2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 东台船用配件有限公司,江苏 东台 224200
2. China Ship Development and Design Center, Wuhan 430064, China;
3. Dongtai Marine Parts Co., Ltd., Dongtai 224200, China
艉轴密封装置是船舶推进轴系的重要设备之一,其主要功能是防止舱外海水进入船体内部,起到舱内密封的作用。因此,艉轴密封装置的密封性能及工作可靠性将直接关系到船舶航行的安全性。Ω弹簧是艉轴密封装置的重要部件,其压缩变形产生的弹力在艉轴密封装置动静环接触面产生一定的压力,起到动密封的作用。如果压力值过大,会导致动静环接触面磨损严重,降低静环的使用寿命。如果压力值过小,会导致动静环接触面泄露量过大,密封失效。因此,如何调整Ω弹簧的变形量,在动静环接触面产生大小合适的接触压力是保证艉轴密封装置工作性能的关键。随着船舶工业的快速发展,对艉轴密封装置的性能要求也日益提高。在满足舱内密封性能的条件下,要求进一步降低摩擦,减少磨损,提高工作可靠性与使用寿命。因此,开展艉轴密封装置的性能分析与优化对提高船舶整体性能具有重要意义。
为满足上述需求,国内外研究机构针对艉轴密封装置开展了大量研究和实践。张振国等[1]考虑了不平衡力和不平衡力矩的作用,对艉轴密封装置进行了强度校核与优化。周斌兴等[2-3]设计了Ω型夹紧弹簧,有效弥补了传统密封装置的横向不稳定性、径向自动补偿能力差等缺点;同时对艉轴密封装置进行了改进,并进行了理论校核与试验研究。王晓军等[4]对Ω型艉轴密封结构进行了分析,利用非线性壳单元、层合壳单元以及实体单元建立了艉轴密封结构的有限元模型,确定了弹簧金属片的应力分布。冯麟涵等[5]搭建了艉轴密封装置的冲击试验台架,模拟实船安装条件,对密封装置进行了冲击试验。杨敏等[6]基于零阶算法对Ω型夹紧弹簧的结构补偿能力进行校核与优化分析,验证了Ω型夹紧弹簧径向刚度的优化设计对改变Ω型夹紧弹簧频率补偿能力的有效性,进而改善其结构补偿能力。
Xiao[7]研制了一种船舶艉轴机械密封试验装置,用于模拟船舶艉轴机械密封各种工况,评估密封性能,对提高机械密封的工作寿命和可靠性提供参考;Jun[8 - 9]介绍了Ω形密封装置的产生背景及其发展情况,并进行了相关的机械密封设计与研究,探讨了机械密封泄漏量的计算方法;并建立了静、动密封环之间的力学稳定温度场数学模型,计算出了密封环的热应力和机械应力,为艉轴密封装置的工程应用提供了数值参考。
许杨等[10]、田靖军等[11]、柯明纯等[12]、郑娆等[15]先后对艉轴密封装置进行结构强度分析,并通过试验验证了模型的正确性与可靠性,为艉轴密封装置的设计与理论分析提供参考 。魏文豪等[13 - 14]建立了热-固耦合数值模型,对不同结构参数进行多目标优化,为艉轴机械密封的结构参数设计提供了思路。王广夫等[16]设计了一种新型试验台,可在轴系运行过程中对艉轴密封装置进行轴向加载并进行性能的检测,为后续不同形式艉轴密封装置试验台的研发设计提供参考。
目前,对艉轴密封装置结构强度评估主要是对Ω弹簧开展结构补偿能力分析。考虑到试验校核成本较高,提高数值模拟方法的准确性和可信性就显得尤为重要。本文以某型艉轴密封装置Ω弹簧为主要对象,建立三维有限元模型,开展不同压缩变形量下Ω弹簧结构强度校核。进一步地,为验证所建数值模型的准确性,对弹簧片小样及设备整体进行试验测试。通过将仿真结果与试验数据的对比,验证所建数值模型的可信性,进而为艉轴密封装置的性能优化提供依据。
1 数值建模 1.1 几何模型艉轴密封装置主要由固定座、Ω弹簧、夹紧环、静环座、静环、动环以及驱动环等部件组成,如图1所示。在正常工作状态下,动环由驱动环带动随轴同步旋转,而静环则保持静止,两者之间的接触面形成动密封摩擦副。

|
图 1 艉轴密封装置结构示意图 Fig. 1 Structure diagram of prototype stern shaft sealing device |
Ω弹簧是艉轴密封装置的弹性元件,主要为摩擦副提供一定的接触压力。通过改变Ω弹簧压缩变形量来调节Ω弹簧产生的弹力,从而起到调整端面密封的效果。一般而言,Ω弹簧的预压缩变形量越大,其位移补偿能力越好。但预压缩变形量也不宜过大,否则会引起塑性变形或断裂,导致艉轴端面密封失效。
Ω弹簧组成从外到内分别是外壳弹簧、桥接弹簧以及支撑弹簧,共3层,各层弹簧均是由单个高强度合金钢弹簧片串联而成。
1)外壳弹簧是由3组弹簧组件沿圆周方向以120°分布。每组弹簧组件由4层金属弹簧片点焊而成。这4层弹簧片相互交错,根部碰焊在一起。
2)桥接弹簧用于上述3组外壳弹簧的连接,共计3组。每组桥接弹簧组件由2层金属弹簧片相互交错焊接而成。
3)支撑弹簧处于弹簧组件的最内圈,组装时在支脚处用弹簧将这些金属片串固起来。
根据Ω弹簧结构特点,把Ω弹簧分为外圈弹簧和内圈弹簧。其中,外圈弹簧包括外壳弹簧和桥接弹簧,内圈弹簧包括支撑弹簧,结构如图2所示。

|
图 2 Ω弹簧及各组件三维模型 Fig. 2 Three-dimensional geometric solid model of spring element |
由于弹簧金属薄片结构厚度为0.7 mm,选用4节点薄壳单元S4R进行网格的划分。各层弹簧组件的网格模型如图3所示,整个网格模型共计

|
图 3 Ω弹簧及各组件三维网格模型 Fig. 3 Ω spring and component three-dimensional mesh model |
组成Ω弹簧的弹簧片采用合金材料制造,具有良好的耐热以及耐蚀性能,较高的机械强度和硬度。表1为该合金材料的属性参数。
|
|
表 1 材料参数表 Tab.1 Material properties |
由于外圈弹簧和内圈弹簧并无直接接触,可分开单独计算。图4为外圈弹簧边界条件示意图。

|
图 4 外圈弹簧边界示意图 Fig. 4 Schematic diagram of outer ring spring boundary |
1)由于外壳弹簧共有3组,沿圆周120°均匀分布,之间用3组桥接弹簧进行连接。根据对称性,对外圈弹簧结构进行有限元分析时,直接选取1/3模型进行分析即可。
2)初始状态下,外圈弹簧各层弹簧片AC段之间存在一定的间隙,是不接触的。随着弹簧组件压缩量的增加,上下层弹簧会因发生变形存在由分离状态进入到接触状态的可能。上下层弹簧片之间属于分开还是接触状态受压缩量、材料属性及边界条件等多个因素的共同影响,是一个比较复杂的几何非线性问题。因此,在弹簧片AC段内外表面定义接触关系来模拟每层弹簧片之间的接触状态。
3)不同层弹簧片在支脚处是通过点焊焊接在一起的。因此,将弹簧片两端的圆弧作为约束面,将其自由度耦合在一起进行约束。
4)外圈弹簧左端与固定座连接,约束底部AB圆弧段6个方向的自由度。外圈弹簧右端连接静环座,这一端可以沿轴向运动,不沿周向扩张,将这一处的单元坐标系改为圆柱坐标系,固定其径向自由度,在CD段施加轴向位移约束来模拟不同的压缩量。
图5为内圈弹簧边界条件示意图。内圈弹簧具体边界设置如下:

|
图 5 内圈弹簧边界示意图 Fig. 5 Diagram of inner ring spring boundary |
1)内圈弹簧是由多个金属弹簧片拼接而成整圆,并用拉簧固定。因此,各金属弹簧片之间定义为绑定关系。
2)内圈弹簧左端连接固定座,约束底部A端3个方向的自由度,设为铰支。
3)内圈弹簧右端连接静环座,由于这一段弹簧可以沿轴向运动,不沿周向扩张,将这一处的单元坐标系改为圆柱坐标系,在B段施加轴向位移约束来模拟不同工作情况下弹簧的压缩量。
2 计算与分析 2.1 弹簧片力学特性以外圈弹簧的弹簧片为例,不同压缩量下,外壳弹簧片的轴向反力和压应力如表2所示。对于外壳弹簧片,当最大压缩量为50 mm时,弹簧所受的最大应力为286.70 MPa,小于材料的屈服极限,满足结构的强度要求。
|
|
表 2 外壳弹簧片在下的最大应力值与轴向力值 Tab.2 The maximum stress value and axial force value of shell spring under different compression |
由图6可知,弹簧两侧的应力最大,其次是弹簧的顶部,比两侧的应力略小,而在支脚处应力最小。
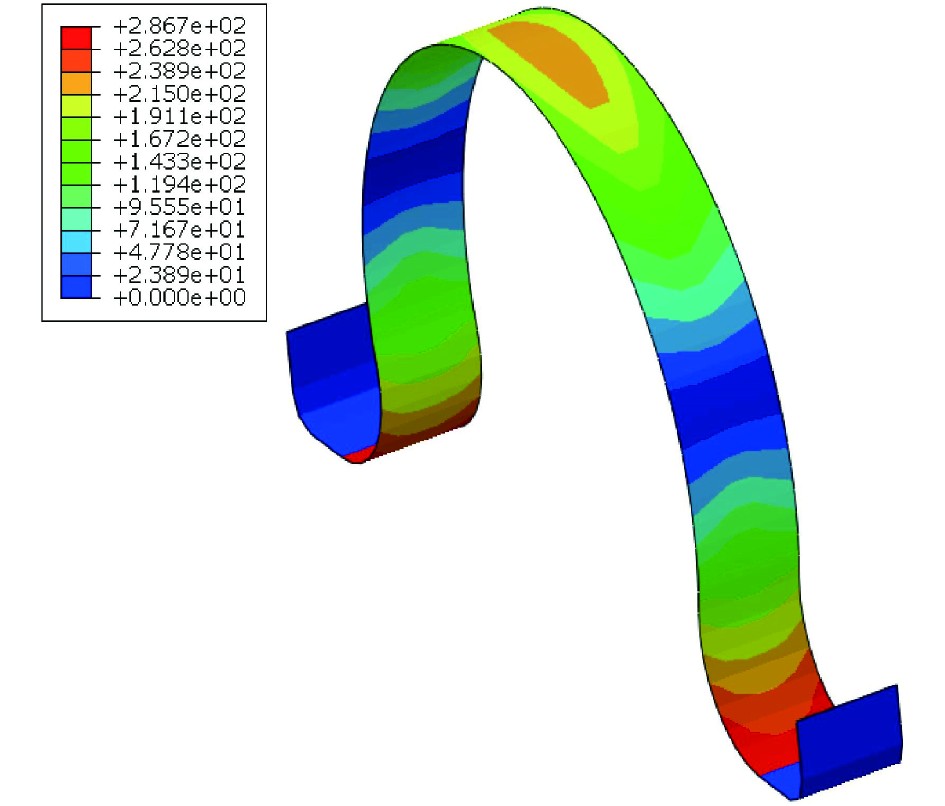
|
图 6 最大压缩量下外壳弹簧片应力分布云图 Fig. 6 Nephogram of shell spring stress distribution under different compression |
由图7中可知,两者之间呈线性变化,通过线性拟合可得到外壳弹簧片的刚度K片 = 0.23 N/mm。
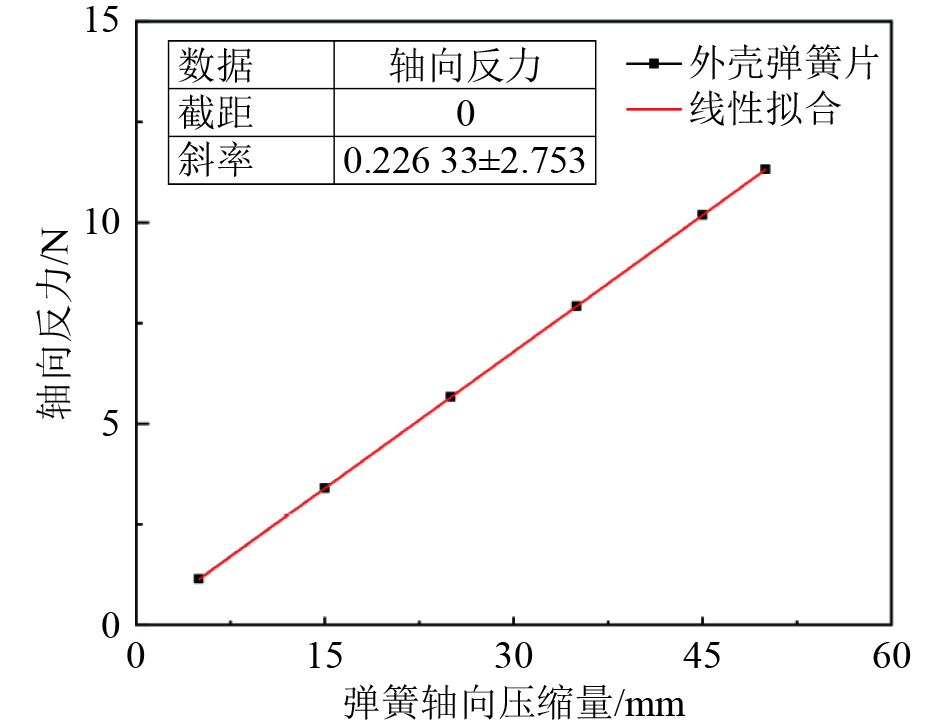
|
图 7 外壳弹簧片压缩量与轴向力关系曲线 Fig. 7 Shell spring compression and axial force relationship curve |
不同压缩量下外圈弹簧的轴向力和最大应力值如表3所示。由图8可知,弹簧两侧的应力最大,其次是弹簧的顶部,比两侧的应力略小,而在支脚处应力最小。当最大压缩量为50 mm时,弹簧所受的最大应力为550.30 MPa,小于材料的屈服极限,满足结构的强度要求。
|
|
表 3 外圈弹簧在不同压缩量下的最大应力值与轴向力值 Tab.3 The maximum stress value and axial force value of outer spring under different compression |

|
图 8 最大压缩量下外圈弹簧应力分布云图 Fig. 8 Nephogram of outer spring stress distribution under different compression |
由图9可知,两者之间呈线性变化,通过线性拟合可得到外圈弹簧的刚度。其中,1组外圈弹簧(即1/3模型)刚度K = 42.39 N/mm,则3组外圈弹簧(即整体模型)刚度K1 = 127.18 N/mm。
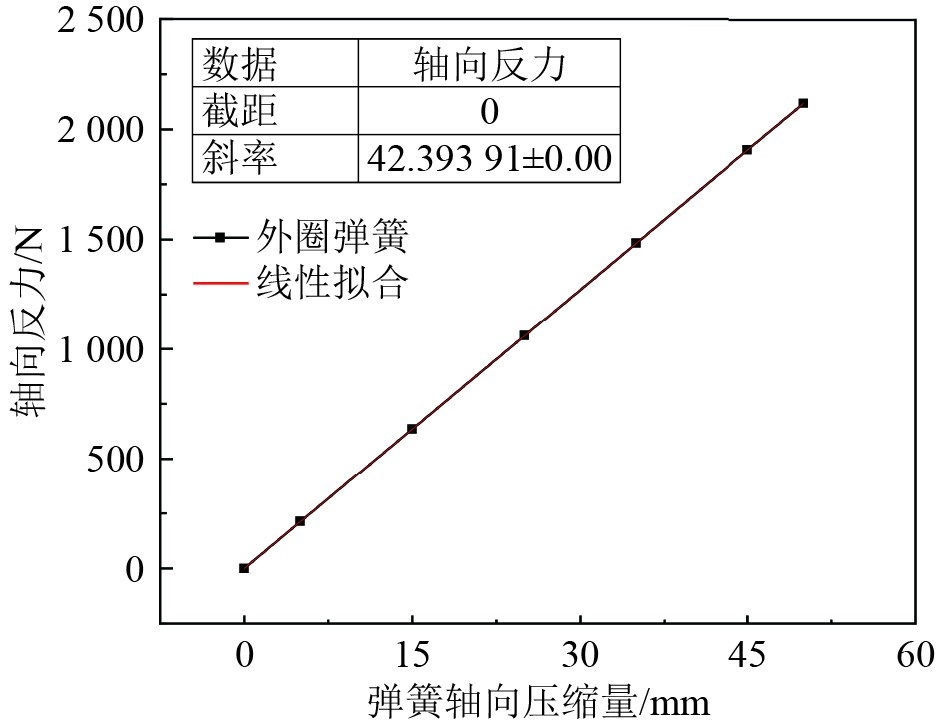
|
图 9 外圈弹簧压缩量与轴向力关系曲线 Fig. 9 Outer spring compression and axial force relationship curve |
不同弹簧压缩量工况下内圈弹簧的弹力和最大应力值如表4所示。由图10可知,内圈弹簧应力分部与外圈弹簧相似。对于内圈弹簧,当压缩量为50 mm时,弹簧所受的最大应力为333.60 MPa,小于材料的屈服极限,满足结构的强度要求。
|
|
表 4 内圈弹簧在不同压缩量下的最大应力值与轴向力值 Tab.4 Maximum stress value and axial force value of inner ring spring under different compression |
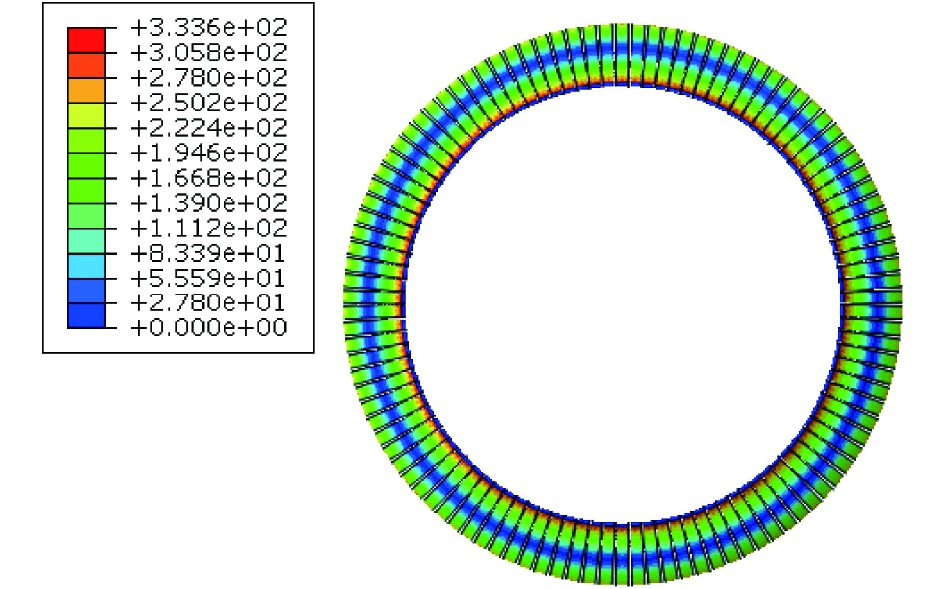
|
图 10 最大压缩量下内圈弹簧的应力云图 Fig. 10 Stress nephogram of inner ring spring under different compression |
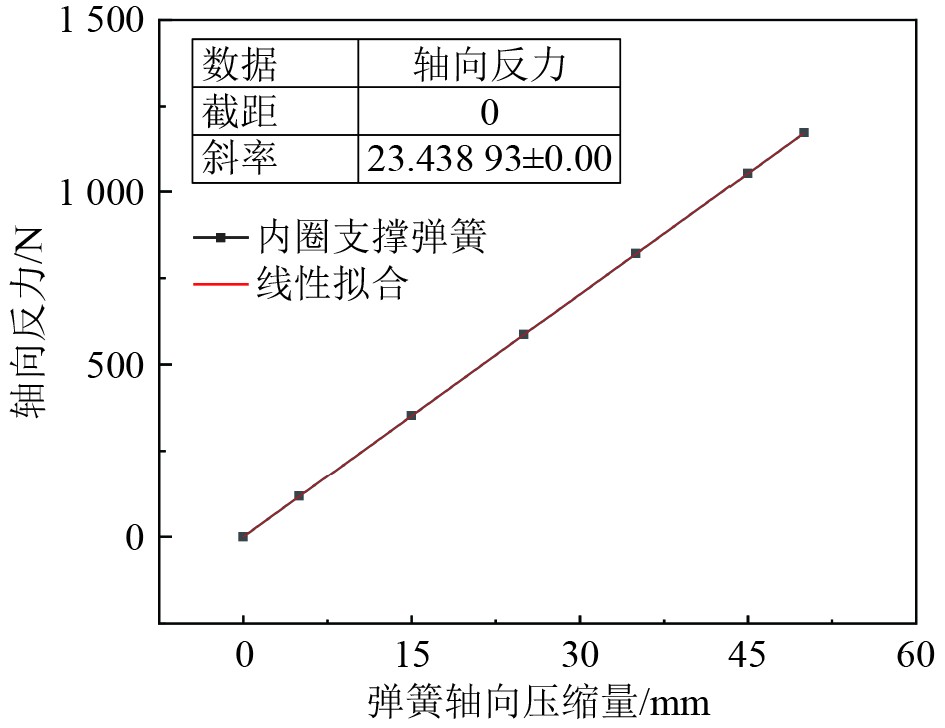
由图11可知,两者之间基本上线性变化。通过拟合可知,内圈支撑弹簧刚度为K2 = 23.44 N/mm。
|
图 11 内圈弹簧压缩量与轴向力关系曲线 Fig. 11 Inner ring spring compression and axial force relationship curve |
考虑到外圈弹簧和内圈弹簧结构上无直接接触,即外圈弹簧和内圈弹簧是并联弹簧关系,且内圈、外圈弹簧的弹簧压缩量与轴向力基本呈线性关系,则整个Ω弹簧的总刚度为内外圈弹簧刚度的叠加值,即Ω弹簧总刚度可表示为:
| $ {\mathit{K}\mathrm{=}\mathit{K}_{\mathrm{1}}\mathrm{+}\mathit{K}_{\mathrm{2}}\mathrm{=127.18+23.44\ N/mm=150.62\ N/mm}。} $ | (1) |
当压缩量为50 mm时,Ω弹簧最大轴向力为
本文基于数显弹簧拉压试验机,完成弹簧片小样的弹力和压缩回弹性能的试验测试。表5为不同轴向压缩量下,Ω弹簧的外壳弹簧片组合的载荷测试结果。
|
|
表 5 Ω型夹紧弹簧片测试结果 Tab.5 Ω spring test results |
由图12可知,外壳弹簧片组合的弹力与压缩量呈线性变化,弹力拟合曲线斜率为0.48,即单个外壳弹簧片刚度约为0.24 N/mm。根据拟合结果,当压缩行程50 mm时,外壳的弹力为11.93 N。

|
图 12 Ω弹簧试样压缩量与轴向力关系曲线 Fig. 12 Relation curve of spring compression and axial force |
将组装后的艉轴密封装置安装于试验台架,在密封动环与驱动夹环之间均布安装4个应变式力传感器,轴向拖动试验主轴,使密封动环按要求向尾方向移动,压缩Ω弹簧产生弹性变形,测量出Ω弹簧在不同压缩量情况下的弹力。表6为不同轴向压缩量下,Ω弹簧的载荷测试结果。
|
|
表 6 试验测试结果 Tab.6 Test result |
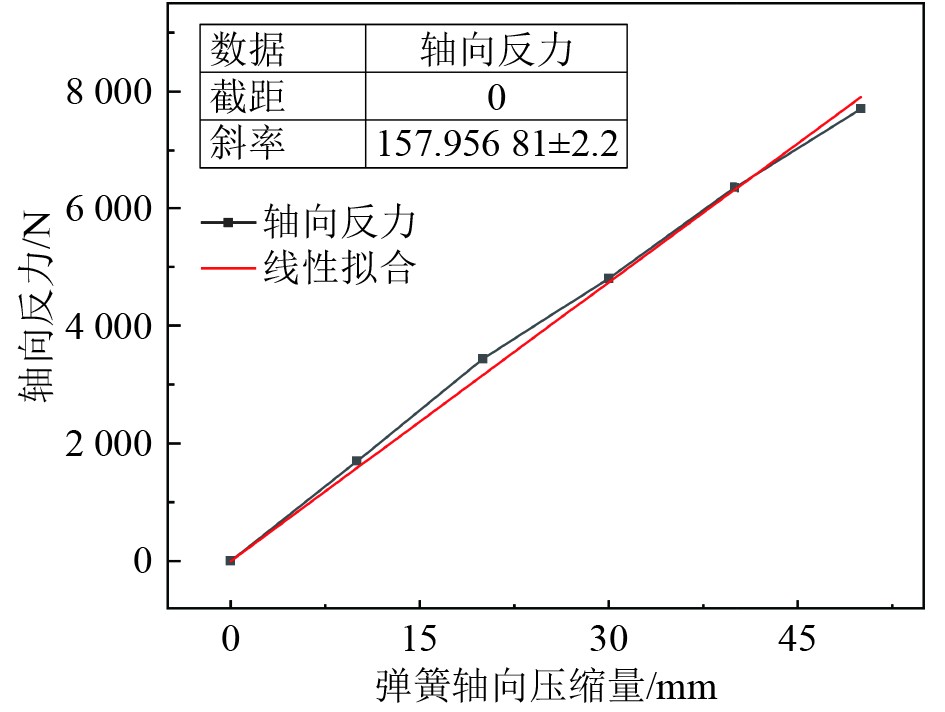
由图13可知,两者之间呈线性变化,通过线性拟合可得到Ω弹簧的刚度K实 = 157.96 N/mm。
|
图 13 Ω型夹紧弹簧压缩量与轴向力关系曲线 Fig. 13 Relation curve of spring compression and axial force |
由表7可知,仿真计算得外壳弹簧片总刚度K片 = 0.23 N/mm,与弹簧片小样测试求得的刚度K样 = 0.24 N/mm相差仅为4.17%。
|
|
表 7 弹簧片小样仿真与测试结果 Tab.7 Simulation and test results of spring piece sample |
由表8可知,计算结果Ω弹簧总刚度K = 150.62 N/mm,与设备测试检验求得的刚度K实 = 157.96 N/mm相差仅为4.65%。
|
|
表 8 艉轴密封装置台架仿真与测试结果 Tab.8 Simulation and test results of stern shaft sealing device test bench |
通过对比表明,本文所建立的有限元数值模型是准确、可信的。
4 结 语1)根据仿真计算可知,在受压状态下,Ω弹簧两侧的应力最大,其次是弹簧的顶部,在支脚处应力最小。
2)艉轴密封装置台架试验测试测得极限工况轴向力为7696.45 N,相对误差2.15%,拟合得到Ω型夹紧弹簧的刚度为157.96 N/mm,相对误差4.65%;对比弹簧片小样测试结果,轴向力仿真结果误差为0.70%,刚度相对误差为4.17%。所有误差均不超过5%,保证了实验的准确性,有效证明了本文所建数值模型的准确性与可信性。
| [1] |
张振国, 姚世卫, 王隽, 等. 潜艇大深度艉轴密封装置摩擦副机械变形研究[J]. 船海工程, 2004(6): 12-14. DOI:10.3963/j.issn.1671-7953.2004.06.006 |
| [2] |
周斌兴, 张能武. 船舶尾轴密封Ω型弹性元件的设计与应用[J]. 船海工程, 2006(6): 60-62. DOI:10.3963/j.issn.1671-7953.2006.06.018 |
| [3] |
周斌兴, 刘步丰, 胡年丰. 新型船舶艉轴端面密封装置的结构与设计[J]. 船舶工程, 2009, 31(2): 24-26. DOI:10.3969/j.issn.1000-6982.2009.02.007 |
| [4] |
王晓军, 胡举喜, 杨海峰, 等. 新型艉轴密封装置的有限元分析与设计[J]. 舰船电子工程, 2010, 30(6): 166-169. DOI:10.3969/j.issn.1627-9730.2010.06.051 |
| [5] |
冯麟涵, 汪玉, 张磊, 等. 大型艉轴密封装置冲击试验台架设计[J]. 润滑与密封, 2012, 37(12): 96-100. DOI:10.3969/j.issn.0254-0150.2012.12.024 |
| [6] |
杨敏, 柳建华, 吴堂荣. 艉轴密封装置Ω弹簧组的多参数优化设计[J]. 上海理工大学学报, 2014, 36(5): 469-472+501. DOI:10.13255/j.cnki.jusst.2014.05.011 |
| [7] |
XIAO G H . The design of mechanical seal testing device of marine stern shaft and the sealing tests[J]. Lubrication Engineering, 2010.
|
| [8] |
JUN R W . Study on the leakage of Ω mechanical seal device[C]//Industrial Electronics & Applications. IEEE, 2016.
|
| [9] |
JUN R W. Based on finite element study on the thermal performance of Ω mechanical seal device[J]. Journal of Hef University, 2016, 33(4): 101−104, 119.
|
| [10] |
许杨, 王玉玲, 胡小红. 基于Ansys的大型船舶艉轴密封变形研究[J]. 机械研究与应用, 2014, 27(5): 41-44+48. DOI:10.16576/j.cnki.1007-4414.2014.05.053 |
| [11] |
田靖军, 王晓军. 艉轴管密封装置的有限元分析[C]// 北京力学会, 北京力学会第二十二届学术年会会议论文集, 北京航空航天大学固体力学研究所, 2016: 2.
|
| [12] |
柯明纯, 黄敏, 常悦, 等. 船舶尾轴密封装置Ω弹簧[J]. 船舶工程, 2019, 41(12): 92-94. DOI:10.13788/j.cnki.cbgc.2019.12.16 |
| [13] |
魏文豪, 李双喜, 张敬博, 等. 船舶艉轴机械密封的结构参数优化研究[C]// 中国力学学会流体力学专业委员会, 第十二届全国流体力学学术会议摘要集, 北京化工大学机电工程学院, 2022.
|
| [14] |
魏文豪, 李双喜, 张敬博, 等. 基于热-固耦合的船舶艉轴密封环材料对密封性能的影响研究[J]. 风机技术, 2022, 64(6): 54-61. DOI:10.16492/j.fjjs.2022.06.0009 |
| [15] |
郑娆, 张敬博, 李双喜, 等. 基于响应面法的船舶艉轴密封结构的优化设计[J]. 机电工程, 2022, 39(11): 1544-1550+1626. DOI:10.3969/j.issn.1001-4551.2022.11.007 |
| [16] |
王广夫, 刘洋, 柯明纯. 基于Ω弹簧的水润滑艉轴密封装置加载试验台设计[J]. 机电设备, 2023, 40(2): 26-28. DOI:10.16443/j.cnki.31-1420.2023.02.007 |
 2025, Vol. 47
2025, Vol. 47
