2. 江苏科技大学 自动化学院,江苏 镇江 212000;
3. 中国船舶集团有限公司第七一一研究所 自动化工程事业部,上海 201108
2. School of Automation, Jiangsu University of Science and Technology, Zhenjiang 212003, China;
3. The 711 Research Institute of CSSC Automation Engineering Division, Shanghai 201108, China
船用涡轮增压器转子由于制造误差、材质不均及安装不对中等问题以及高温高压的环境,使得增压器转子在长时间高速工作后会产生诸多类型转子故障,常见的故障有转子不平衡[1]、转子裂纹[2]、转子碰摩[3]等。这些故障会导致增压器转子毁坏,发生航行事故,造成巨大的经济损失,严重时甚至造成人员伤亡和环境污染。因此,为了船舶安全可靠的航行,及时且高效地判断出转子故障类型在故障监测与诊断中显得尤为关键。
目前,国内大多数涡轮增压器故障诊断都是基于故障现象进行判断,判断依据来源于工程实践经验,具有一定的主观性,从而使故障诊断的效率和准确性下降。针对故障转子轴心轨迹在不同故障类型及转速下呈现出形状细微差异性的特点,应用图像识别算法对故障转子轴心轨迹进行故障诊断,可解决人工识别的弊病。为了通过有限的矩很好地描述图像特征,Hu提出了7个不变矩的组合。但传统Hu不变矩在离散情况下仅仅具有平移和旋转不变性的特点,因此众多学者在此基础上进行了改进。李鑫等[4]利用改进Hu不变矩与概率神经网络(Probabilistic Neural Networks,PNN)对多种产品进行了较好的分类识别。符书楠等[5]通过将改进Hu不变矩与卷积神经网络相结合,有效提升了声呐对水下小目标的发现概率和正确报警率。遆佳等[6]应用LOG算子获取船体局部姿态图像特征点,结合改进Hu矩提出图像配准算法,有效提升了图像平均灰度,提供了船体高精度姿态参数。
针对故障样本数据较多且存在冗余重复的特点,采用特征选择法能够筛选出冗余的特征参数,有效地节省存储空间,减少运行时间以及提高分类效率[7-8]。常见的特征选择方法有递归特征消除法[9](Recursive Feature Elimination,RFE)、过滤式选择(Relief)算法[10]和主成分分析法[11]。而支持向量机递归消除法SVM-RFE(Support Vector Machine,SVM)自从2002年被提出以来在特征选择上得到广泛应用。针对传统SVM-RFE算法只能处理二分类问题的局限性,汪飞翔等[12]通过网格搜索算法对SVM-RFE算法进行优化,研究了水上交通事故影响因素的严重程度,实现了多分类问题处理。为了挖掘出船舶航行事故的致因并分析各个因素对事故的影响程度,石荣丽等[13]提出一种结合SVM-RFE与群体智能优化算法的特征选择方法,并证明了该方法相较于传统的SVM模型拥有更高的识别精度。杨永平[14]提出一种基于遗传算法和SVM算法的舰船目标特征选择方法,有效降低了计算复杂度,提高了识别效率。
目前,基于SVM-RFE的特征选择方法在船舶航行事故致因筛选领域得到广泛应用,但鲜有结合转子机械轨迹图像故障特征参数进行研究。因此,本文在提取增压器转子故障轴心轨迹的改进Hu不变矩特征的基础上,采用SVM-RFE对不同故障类型转子轴心轨迹的改进Hu不变矩特征进行选择与排序,并采用Relief算法进行特征权重排序,对比验证了SVM-RFE排序结果的准确性。最后分别采用逆向传播(Back Propagation,BP)神经网络、PNN和SVM算法分析了Hu-SVM-RFE算法得到的最优特征子集的分类识别率与计算时长,为增压器转子在线故障诊断提供了一种可靠实用的方法。
1 算法原理 1.1 SVM-RFE的原理SVM-RFE从原始数据的全集出发,利用SVM作为分类器,在分类的过程中对各个特征的重要性进行排序。在线性分类面中权向量w2的大小决定了特征的排序,在每一次判断大小后会删除其中的最小特征,通过反复迭代后得到各个特征重要度由大到小的排序。
已知训练样本集合为
SVM的目标函数如下:
| $ S = \frac{1}{2}{\left\| w \right\|^2} 。$ | (1) |
采用最优裁剪(Optimal Brain Damage,OBD)算法对特征参数进行删除,当删除了第i个特征之后,SVM目标函数的变化如下:
| $ \Delta S\left( i \right) = \frac{{\partial S}}{{\partial {w_i}}}\Delta {w_i} + \frac{{{\partial ^2}S}}{{\partial w_i^2}}{\left( {\Delta {w_i}} \right)^2} \approx {\left( {\Delta {w_i}} \right)^2}。$ | (2) |
而当满足
在使用线性核函数时,排序系数可以表示为:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathrm{rank}\left( i \right) = {{\left( {{w_i}} \right)}^2}},\\ {w = \sum\limits_{i = 1}^N {{\alpha _i}{y_i}{x_i}} } 。\end{array}} \right. $ | (3) |
其中,
利用拉格朗日算子来求解最优超平面,得到最优的决策函数为:
| $ f\left( x \right) = \mathrm{sgn} \left( {\sum\limits_{i = 1}^i {{\alpha _i}{y_i}{x_i}} + b} \right)。$ | (4) |
此外,SVM-RFE多分类识别核心在于不同特征参数两两组合,将权重
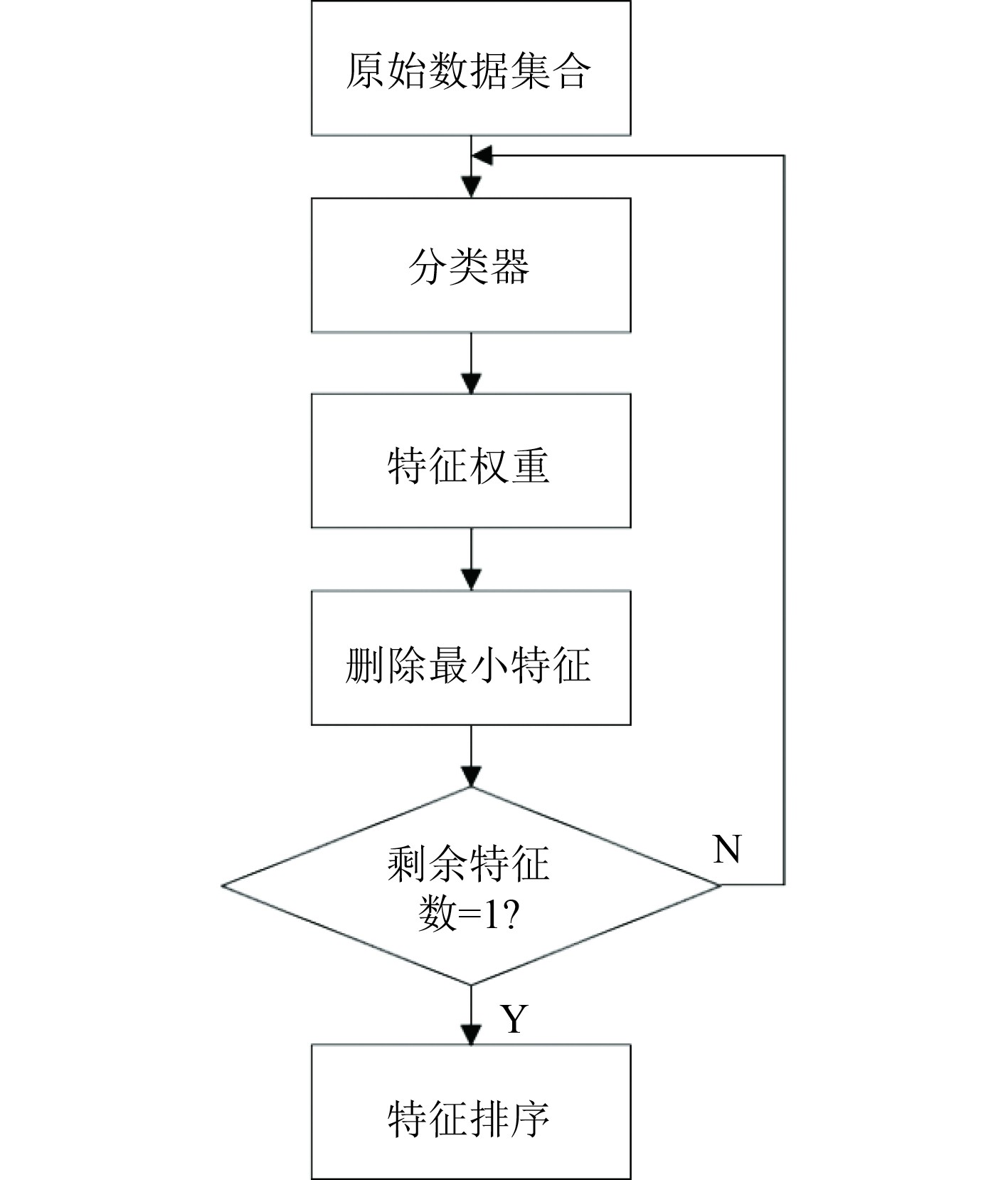
|
图 1 递归特征消除法流程图 Fig. 1 Flow chart of recursive feature elimination method |
二维形状不变矩可以描述图像的几何学特征,主要包含平移、旋转、尺缩等不变性特征。不变矩可以通过物理意义来解释,图像可以表示成质密不均的薄板,其中各阶不变矩表征意义如下:零阶矩为总质量;一阶矩为质心;二阶矩表示为大小与方向。在
| $ {m_{uv}} = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{x^u}{y^v}f(x,y){\text{d}}x{\text{d}}y} }。$ | (5) |
考虑到故障轴心轨迹图像为离散图像,并且为了简化计算,令轴心轨迹的灰度为1,即
| $ {m_{uv}} = \sum\limits_x^N {\sum\limits_y^M {{x^u}{y^v}} }。$ | (6) |
其中,M、N分别为故障轴心轨迹图像的宽度与高度。
为了使矩特征具有平移不变性,需要计算图像的中心矩。图像在
| $ {\mu _{uv}} = \sum\limits_x {\sum\limits_y {{{\left( {x - \frac{{{m_{10}}}}{{{m_{00}}}}} \right)}^u}{{\left( {y - \frac{{{m_{01}}}}{{{m_{00}}}}} \right)}^v}} }。$ | (7) |
式中:
为了使矩特征获得尺度伸缩不变性,对
| $ {\eta _{uv}} = \frac{{{\mu _{uv}}}}{{\mu _{00}^r}},u + v = 2,3, \cdot \cdot \cdot 。$ | (8) |
其中,系数
最后,对上述中心矩进行归一化处理使其具备旋转不变性,得到的Hu不变矩
| $ {\left\{ {\begin{array}{*{20}{l}} {{\varphi _1} = {\eta _{20}} + {\eta _{02}}} ,\\ {{\varphi _2} = {{({\eta _{20}} - {\eta _{02}})}^2} + 4\eta _{11}^2} ,\\ {{\varphi _3} = {{({\eta _{30}} - 3{\eta _{12}})}^2} + {{(3{\eta _{21}} - {\eta _{03}})}^2}} ,\\ {{\varphi _4} = {{({\eta _{30}} + {\eta _{12}})}^2} + {{({\eta _{21}} + {\eta _{03}})}^2}} ,\\ \begin{gathered} {\varphi _5} = {\text{(}}{\eta _{30}} - 3{\eta _{12}}{\text{)(}}{\eta _{30}} + {\eta _{12}}{\text{)}}\left[ {{{{\text{(}}{\eta _{30}} + {\eta _{12}}{\text{)}}}^2} - 3{{{\text{(}}{\eta _{21}} + {\eta _{03}}{\text{)}}}^2}} \right] + \\ \begin{array}{*{20}{c}} {}&{ {\text{(}}3{\eta _{21}} - {\eta _{03}}{\text{)(}}{\eta _{21}} + {\eta _{03}}{\text{)}}\left[ {3{{{\text{(}}{\eta _{30}} + {\eta _{12}}{\text{)}}}^2} - {{{\text{(}}{\eta _{21}} + {\eta _{03}}{\text{)}}}^2}} \right]} ,\end{array} \\ \end{gathered} \\ \begin{gathered} {\varphi _6} = ({\eta _{20}} - {\eta _{02}})\left[ {{{({\eta _{30}} + {\eta _{12}})}^2} - {{({\eta _{21}} + {\eta _{03}})}^2}} \right] + \\ \begin{array}{*{20}{c}} {}&{ 4{\eta _{11}}({\eta _{30}} + {\eta _{12}})({\eta _{21}} + {\eta _{03}})} ,\end{array} \\ \end{gathered} \\ \begin{gathered} {\varphi _7} = (3{\eta _{21}} - {\eta _{03}})({\eta _{30}} + {\eta _{12}})\left[ {{{({\eta _{30}} + {\eta _{12}})}^2} - 3{{({\eta _{21}} + {\eta _{03}})}^2}} \right] + \\ \begin{array}{*{20}{c}} {}&{ (3{\eta _{21}} - {\eta _{30}})({\eta _{21}} + {\eta _{03}})\left[ {3{{({\eta _{30}} + {\eta _{12}})}^2} - {{({\eta _{21}} + {\eta _{03}})}^2}} \right]} 。\end{array} \\ \end{gathered} \end{array}} \right. }$ | (9) |
由于针对图像的识别依据是形状,传统的Hu不变矩算法在连续区域图像中具有良好的不变性,但是该算法计算周期较长且不能准确的在非线性空间对图形平移、旋转和缩放保持不变。
1.2.2 改进Hu不变矩特征提取传统的Hu不变矩无法满足非线性不连续区域的目标图像尺度变化时的不变性,尤其是基于高阶矩的二维物体结构的描述。
针对坐标
| $ \left\{ \begin{gathered} x' = \rho x ,\\ y' = \rho y ,\\ x' - \bar x' = \rho (x - \bar x) ,\\ y' - \bar y' = \rho (y - \bar y) 。\\ \end{gathered} \right. $ | (10) |
图像尺度对目标长度失真变化的失真比例系数为
| $ {\eta '_{uv}} = \frac{{{\rho ^{u + v + 1}}{\mu _{uv}}}}{{\rho \mu _{00}^r}} = {\rho ^{u + v}}{\eta _{uv}}。$ | (11) |
联立式(9)和式(11),得到改进矩阵的7个不变矩
| $ \left\{ \begin{gathered} {{\varphi '}_1} = {\rho ^2}{\varphi _1} ,\\ {{\varphi '}_2} = {\rho ^4}{\varphi _2} ,\\ {{\varphi '}_3} = {\rho ^6}{\varphi _3} ,\\ {{\varphi '}_4} = {\rho ^6}{\varphi _4} ,\\ {{\varphi '}_5} = {\rho ^{12}}{\varphi _5},\\ {{\varphi '}_6} = {\rho ^8}{\varphi _6} ,\\ {{\varphi '}_7} = {\rho ^{12}}{\varphi _7} 。\\ \end{gathered} \right. $ | (12) |
为了解决图像体积较小、几何形状差别不突出、噪声干扰造成的不连续区域识别效果差等情况,则改进不变矩特征向量
| $ \left\{ \begin{gathered} {\phi _1} = {{\varphi '}_2}/{({{\varphi '}_1})^2} ,\\ {\phi _2} = {{\varphi '}_3}/{({{\varphi '}_1})^3} ,\\ {\phi _3} = {{\varphi '}_4}/{({{\varphi '}_1})^3} ,\\ {\phi _4} = {{\varphi '}_5}/{({{\varphi '}_1})^6} ,\\ {\phi _5} = {{\varphi '}_6}/{({{\varphi '}_1})^4} ,\\ {\phi _6} = {{\varphi '}_7}/{({{\varphi '}_1})^6} 。\\ \end{gathered} \right. $ | (13) |
考虑到对数能够反映不变矩特征较大时的差异性,同时可以更加清晰地描述物体图像形态变换。则对数形式改进Hu不变矩可表达为:
| $ {\varphi }_{n}=\left|\mathrm{ln}\left|{\varphi }_{n}\right|\right|\text{,}n=1,2,\cdots ,6。$ | (14) |
首先,基于Matlab自带的郁金香数据分类集iris(共3类,分别为1:setosa,2:versicolor,3:virginica)进行SVM-RFE分类识别,每种植物采集50组数据,其中每组有4个特征参数,分别为花萼和花瓣的长和宽,分别将前30组作为训练组,后20组作为测试组。郁金香特征参数排序计算结果如表1所示。
|
|
表 1 特征排序 Tab.1 Feature sorting |
为验证SVM-RFE特征排序结果的准确性,通过Relief算法对上述iris特征集进行特征权重求解,确定不同参数的特征权重,计算结果如图2所示。

|
图 2 不同属性特征权重分布 Fig. 2 Weight distribution of different attribute features |
从表1和图2可知,基于SVM-RFE的特征排序结果同基于Relief算法得到的特征权重大小排序一致,由大到小依次为花瓣宽>花瓣长>花萼长>花萼宽。因此验证了本文构建的SVM-RFE特征排序算法模型的准确性。
3 计算与分析 3.1 增压器转子故障轴心轨迹特征提取选择增压器转子在运行时3种典型故障的轴心轨迹:类型1:转子质量不平衡(椭圆或圆形)、类型2:油膜涡动(内“8”形)和类型3:转子裂纹(“漩涡”形)。典型故障轴心轨迹如图3所示。
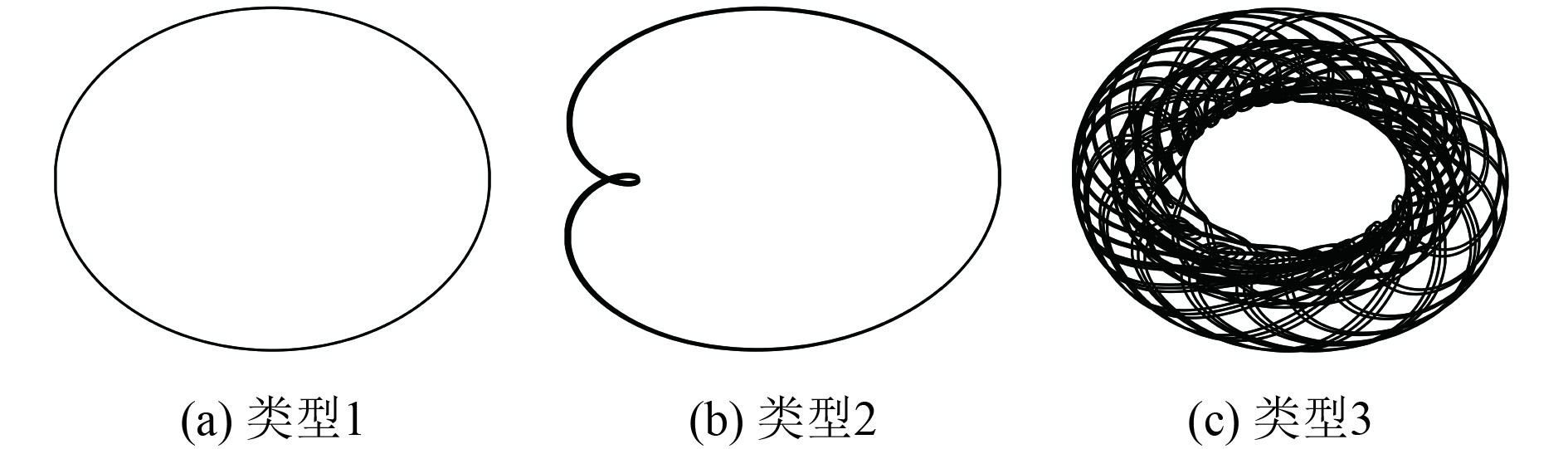
|
图 3 轴心轨迹 Fig. 3 Axial trajectory |
利用改进Hu不变矩对故障转子轴心轨迹进行特征提取,部分轴心轨迹的改进Hu不变矩特征如表2所示。可以看出,各故障类型的
|
|
表 2 不同故障类型改进Hu矩 Tab.2 Improved Hu moment values of different fault types |
综上,增压器转子不同故障轴心轨迹的6个改进Hu不变矩参数的数值分布区间不同具备一定的区分度,这也为故障分类识别提供了可行性。
3.2 基于Hu-SVM-RFE的特征排序对增压器转子质量不平衡、油膜涡动和转子裂纹进行故障轴心轨迹改进Hu不变矩特征提取。每种轴心轨迹为460组,取前300组为训练组后160组为测试组。结合SVM-RFE增压器转子轴心轨迹的改进Hu矩特征排序,排序结果如表3所示。特征权重从小到大依次删减后的特征组合识别率及识别时间如表4所示。
|
|
表 3 特征排序 Tab.3 Feature sorting |
|
|
表 4 不同特征组合的识别率 Tab.4 Recognition rate of different feature combinations |
从表4可知,在依次删除小权重特征后,特征组合的分类识别准确率逐步下降。当保留的特征参数数目大于2时,故障分类识别准确率在90%以上。当特征参数等于2时,分类准确率开始低于90%。进一步减少特征参数,当特征参数只有1个时,分类准确率较低,只有64.03%。这是因为特征参数数目较少时每删除一个特征就会导致特征组合整体的数据差异化信息量减少,从而使得数据不足以支持较好的分类。
此外,在分类识别率大于90%时,随着权重较低的特征参数被删除,各组合的运行时间不断降低。而当特征参数数目小于3时,随着特征参数数目减少,此时的分类识别准确率会随之降低,运行时间却在增加。这个过程中由于特征参数较少,各故障之间的重合度较高,在优化选择时需要更多的运行时间。因此,当数据冗余较多时,删减低权重特征参数可以提高分类运行时间,而当数据冗余较少或无冗余时,删减特征参数反而会增加运行时间。
3.3 Hu-SVM-RFE结合不同诊断算法的分类识别分别采用交叉验证(Cross Validation,CV)优化的SVM算法、BP神经网络算法和PNN算法结合Hu-SVM-RFE优选参数组合(

|
图 4 SVM分类的可视化图 Fig. 4 Visualization diagram for SVM classification |
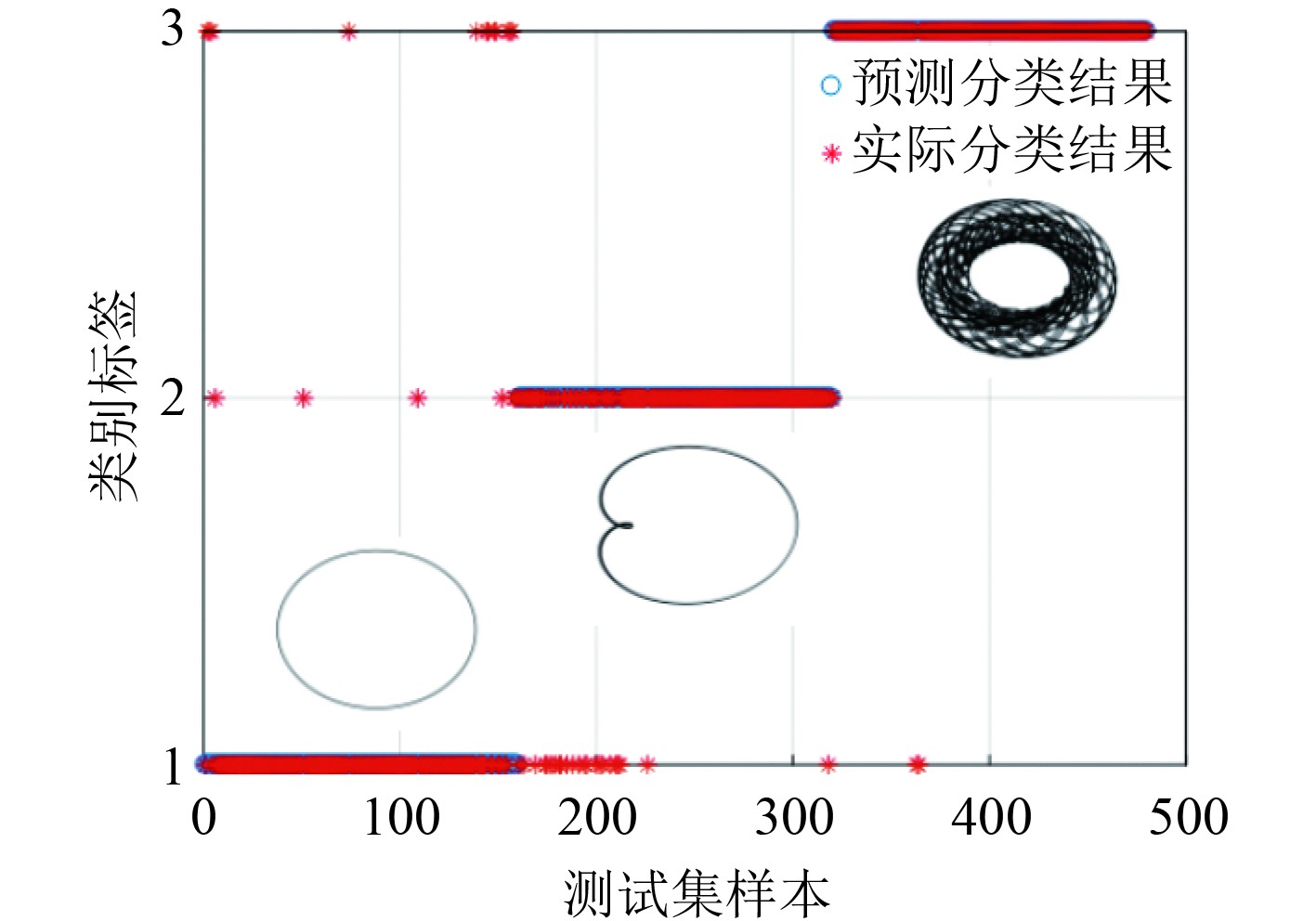
|
图 5 BP算法的可视化图 Fig. 5 Visualization diagram for BP classification |
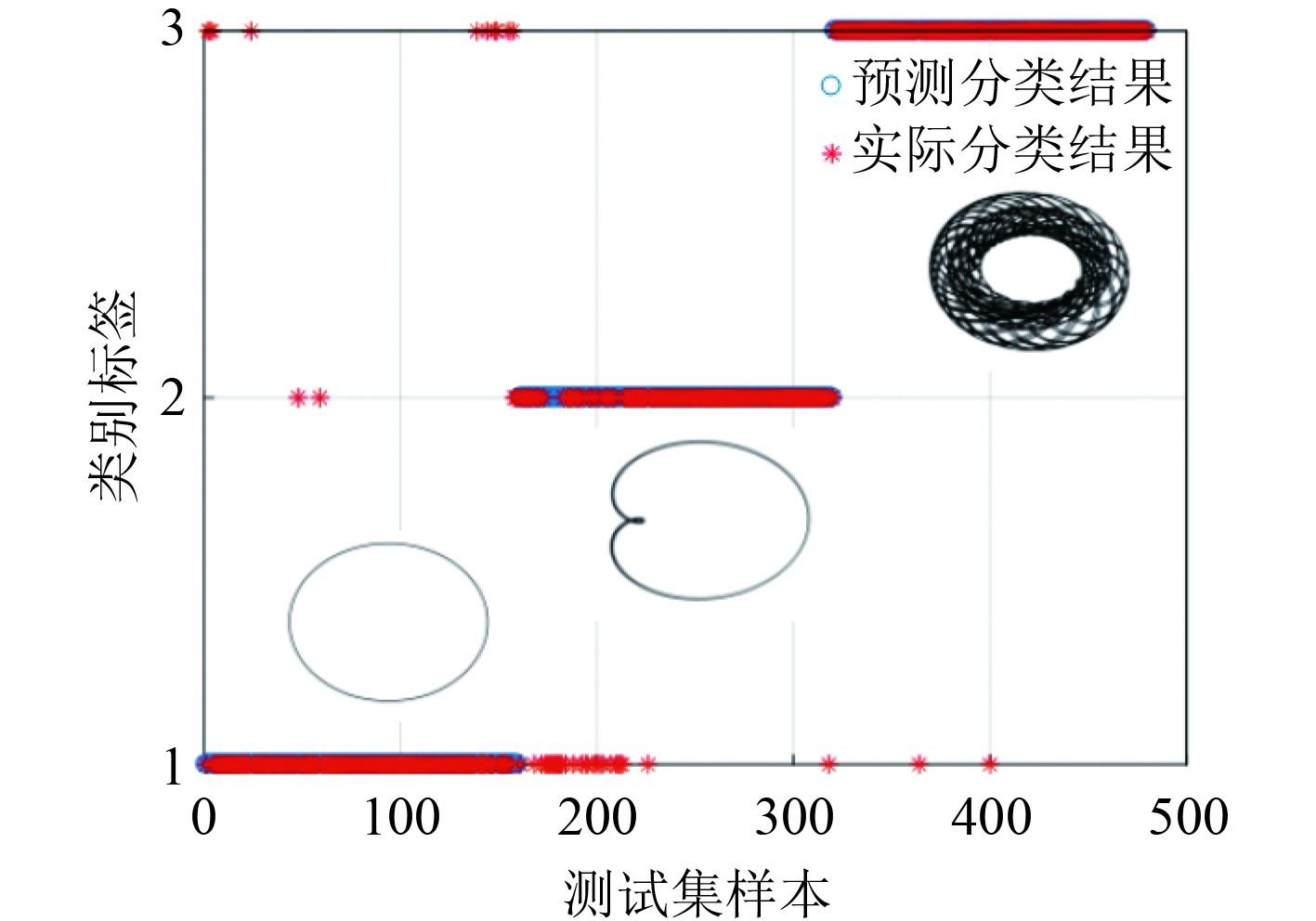
|
图 6 PNN算法的可视化图 Fig. 6 Visualization diagram for PNN classification |
下面分别采用概率神经网络PNN、BP神经网络和SVM算法得到的分类识别率和计算时长对比,见表5。
|
|
表 5 结果对比 Tab.5 Comparison of results methods |
可知,基于Hu-SVM-RFE优选参数组合(
此外,从计算时长上看,PNN算法耗时最短,较SVM算法能够缩减20倍,较BP算法缩减11倍。这是由于想得到较高的分类识别率,BP神经网络和SVM算法需要对相似度较高的样本进行更加细致地识别,而PNN不需要多次计算便可获得收敛的贝叶斯优化解。
综上,可以看出不同诊断算法得到的增压器转子故障分类识别率与计算时长成反比。在实际工程应用中为保证诊断的实时性,在优先保证一定的故障诊断率的同时选择耗时较少的算法。因此,选择PNN算法对增压器转子故障进行分类识别,可以在保证高故障识别率的基础上达到实时性。
4 结 语1)利用改进Hu不变矩算法可以较好地表征增压器故障转子轴心轨迹特征,其不变性的特点能很好地反映增压器转子某一类故障轴心轨迹的相似性特征。
2)基于Hu-SVM-RFE算法可以高效地对故障特征进行排序,进而实现特征参数降维。当数据冗余较多时,特征参数降维可以有效降低分类运行时间,而当数据冗余较少或无冗余时,特征参数降维反而会增加运行时间。
3)不同算法得到的故障分类识别率与计算时长成反比。基于Hu-SVM-RFE和PNN算法的增压器转子典型故障进行识别技术可以在保证高故障识别率的基础上达到实时性。
| [1] |
SINGH A, GUPTA T C. Effect of rotating unbalance and engine excitations on the nonlinear dynamic response of turbocharger flexible rotor system supported on floating ring bearings[J]. Archive of Applied Mechanics, 2020, 90: 1117-1134. |
| [2] |
KHORRAMI H, RAKHEJA S, SEDAGHATI R. Vibration behavior of a two-crack shaft in a rotor disc-bearing system[J]. Mechanism and Machine Theory, 2017, 113: 67-84. DOI:10.1016/j.mechmachtheory.2017.03.006 |
| [3] |
XU H, WANG N, JIANG D, et al. Dynamic characteristics and experimental research of dual-rotor system with rub-impact fault[J]. Shock and Vibration, 2016, 2016: 1-11. |
| [4] |
李鑫, 赵坤鹏, 朱凌寒. 改进的不变矩和PNN相结合的多品种产品识别算法[J]. 传感器与微系统, 2019, 38(8): 132-135. |
| [5] |
符书楠, 许枫, 刘佳, 等. 结合区域提取和改进卷积神经网络的水下小目标检测[J]. 应用声学, 2023, 42(6): 1280-1288. |
| [6] |
遆佳, 李霁. 船体局部姿态图像的配准算法[J]. 舰船科学技术, 2021, 43(12A): 13-15. TI J, LI J. Design of registration algorithm for hull local attitude image[J]. Ship Science and Technology, 2021, 43(12A): 13-15. DOI:10.3404/j.issn.16727649.2021.12A.005 |
| [7] |
KOZODOI N, LESSMANN S, PAPAKONSTANTINOU K, et al. A multi-objective approach for profit-driven feature selection in credit scoring[J]. Decision Support Systems, 2019, 120: 106-117. DOI:10.1016/j.dss.2019.03.011 |
| [8] |
GOTTWALT F, CHANG E, DILLON T. CorrCorr: a feature selection method for multivariate correlation network anomaly detection techniques[J]. Computers & Security, 2019, 83: 234-245. |
| [9] |
KORNYO O, ASANTE M, OPOKU R, et al. Botnet attacks classification in AMI networks with recursive feature elimination(RFE) and machine learning algorithms[J]. Computers & Security, 2023, 135: 103456. |
| [10] |
KUSHWAHA N L, RAJPUT J, SUNA T, et al. Metaheuristic approaches for prediction of water quality indices with relief algorithm-based feature selection[J]. Ecological Informatics, 2023, 75: 102122. DOI:10.1016/j.ecoinf.2023.102122 |
| [11] |
ZHANG T, MARINO A, XIONG H, et al. A ship detector applying principal component analysis to the polarimetric notch filter[J]. Remote Sensing, 2018, 10(6): 948. DOI:10.3390/rs10060948 |
| [12] |
汪飞翔, 杨亚东, 田书冰, 等. 基于SVM的水上交通事故严重程度的影响因素研究[J]. 交通信息与安全, 2018, 36(2): 18-23+32. DOI:10.3963/j.issn.1674-4861.2018.02.003 |
| [13] |
石荣丽, 林亦舒. 基于特征优选和SVM的船舶航行事故致因分析[J]. 运筹与管理, 2023, 32(12): 99-105. |
| [14] |
杨永平. 基于遗传算法优化支持向量机的船舰目标识别分类[J]. 舰船科学技术, 2024, 46(4): 174-178. YANG Y P. Ship target recognition and classification based on genetic algorithm optimization of support vector machine[J]. Ship Science and Technology, 2024, 46(4): 174-178. |
 2025, Vol. 47
2025, Vol. 47
