2. 上海交通大学机械与动力工程学院,上海 200240;
3. 船舶与海洋工程特种装备和动力系统国家工程研究中心,上海 201108
2. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
3. National Engineering Research Centre for Special Equipment and Power System of Ship and Marine Engineering, Shanghai 201108, China
在船用柴油机中,离心式压气机作为压缩系统核心部件,其性能直接影响着柴油发动机的工作效率和推进力输出,因此有关离心式压气机气动性能的预测是设计过程中的关键一环。随着部件性能指标的提高和运行工况范围的拓宽,包括二维、准三维和全三维在内的预测方法都得到了持续研究和开发。近年来,耦合神经网络代理模型的流线曲率法在离心式压气机性能预测中展现出了巨大潜力,本文将深入研究这种方法的原理,介绍其应用,并分析其在提高性能预测准确性方面的潜力。
离心式压气机设计过程中传统的性能预测方法通常会受到精度和复杂度之间的限制,而全三维设计体系中的CFD方法给出的预测结果的准确性既受制于湍流模型,又受制于算力资源[1]。相比之下,二维通流计算方法凭借有效的气动参数关联模型,能够为离心式压气机设计和特性预测提供快速且可靠的结果。有效的通流计算能够缩短研制周期,同时也能够降低研制费用,在离心式压气机设计中得到了普遍应用。
通流计算方法中最具代表性的是流线曲率法,它由吴仲华[2]于1952年提出的两类相对流面理论发展而来,并在接下来的几十年中被国内外许多学者持续完善,近期的流线曲率法计算程序由Quintanilla 等[3]、Hosein 等[4]以及Rasool等[5]开发。戎毅等[6]指出,流线曲率法计算精度主要取决于经验模型的准确程度。但经验模型面临调用过程复杂,适用工况范围窄,可更新性差等问题。
所以,为了解决以往经验模型的局限性,本文从数值模拟中提取关键的流场特征参数。基于BP神经网络将基本的流场参数和叶型几何参数分别跟落后角和总压损失系数关联起来,形成了对应的代理模型,并结合以往成熟的正问题分析程序形成了新的正问题计算程序。同时,本文对2台应用广泛的离心压气机进行了通流计算校验,验证了神经网络模型替代传统经验模型的可行性和有效性,能够为离心压气机的进一步设计和优化提供参考。
1 耦合神经网络模型的流线曲率法 1.1 流线曲率法在离心式压气机中,内部气体的流动通常比较复杂,既不是定常流动,也受到流动工质粘性的影响,并且伴随着强烈的三维效应。而流线曲率法为了方便求解,在分析计算过程中对内部气流流动做了系列假设。该方法的计算区域在S2流面上呈现为二维的计算网格如图1所示。离散的计算网格由轴向的流线和径向的计算站互相交错组成,流线和计算站交错的节点即为每一个网格点,在每一个网格点上求解经过假设简化后的流场控制方程获得流场参数,得到整个流场。简化后的控制方程如式(1)、式(2)所示[7]。

|
图 1 子午面网格示意图 Fig. 1 Schematic diagram of the meridian grid |
压力梯度方程:
| $ \begin{split} & \frac{\partial\mathit{V}_{\mathit{m}}}{\partial n}=\frac{1}{\mathit{V}_{\mathit{m}}}\left[\frac{\partial I}{\partial n}-T\frac{\partial S}{\partial n}-\left(\frac{C_{\theta}}{r}-\omega\right)\frac{\partial\left(rC_{\theta}\right)}{\partial n}\right]+ \\ &\mathit{V}_{\mathit{m}}\left[\mathrm{cos}\left(\phi-\varphi\right)\frac{\partial\phi}{\partial m}+\frac{\mathrm{sin}\left(\phi-\varphi\right)}{\mathit{V}_{\mathit{m}}}\frac{\partial\mathit{V}_{\mathit{m}}}{\partial m}\right]。\end{split} $ | (1) |
流量连续方程:
| $ G = \int_H^T 2 {\text{π}} r\rho {V_m}{\rm{cos}}\left( {\phi - \varphi } \right){\rm{d}}n 。$ | (2) |
式中:
首先把2组控制方程进行离散,转换成关于子午速度的方程来迭代求解。也就是根据上下站之间的几何和气动参数计算出子午速度,同时,根据求得的子午速度求出该网格点所需的所有气动参数[8]。
在计算过程中,子午速度
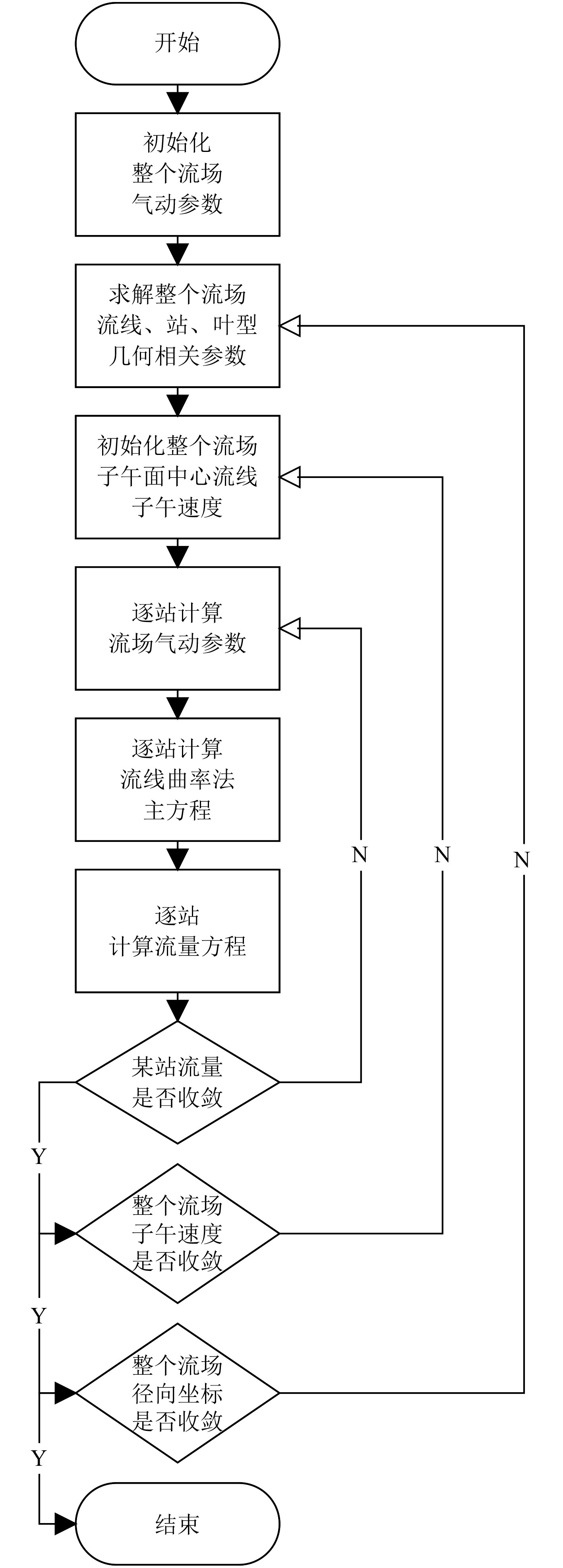
采用流线曲率法进行离心压气机S2流面分析计算的基本流程如图2所示[9]。核心计算流程包括内部和外部2层循环。内部循环涉及计算站点的流量迭代,即求解站内控制方程组。外部循环则涉及整个子午面流场的流线坐标迭代。
|
图 2 流线曲率法计算流程图 Fig. 2 Flowchart of the calculation of the streamline curvature method |
首先,按照等环量面积原则确定初始流线的位置,确保每个流管环形面积相等。各个初始流线与沿径向分布的计算站点相互交错,构成初始计算网格。在给定边界条件和初始条件后,开始内部循环。完成一次内部循环后,根据各站点求解的流管流量按比例插值,求解新的流线与计算站点的交点,从而调整流线位置生成新的计算网格,完成一次外部循环。若当前和上一次外部循环生成的流线坐标相对误差满足精度要求,则迭代结束。最后,根据子午速度的控制方程组求解各个节点的气动参数和压气机特性,完成正问题分析过程。
离心压气机的正问题分析程序中,准确性依赖于叶轮滑移模型和损失模型[10]。合适的经验模型引入能够预测出较为可靠的总压损失系数和落后角,从而得到更可信的压气机性能参数。因此,考虑利用更容易实现非线性映射关系的代理模型代替经验模型耦合到正问题中。
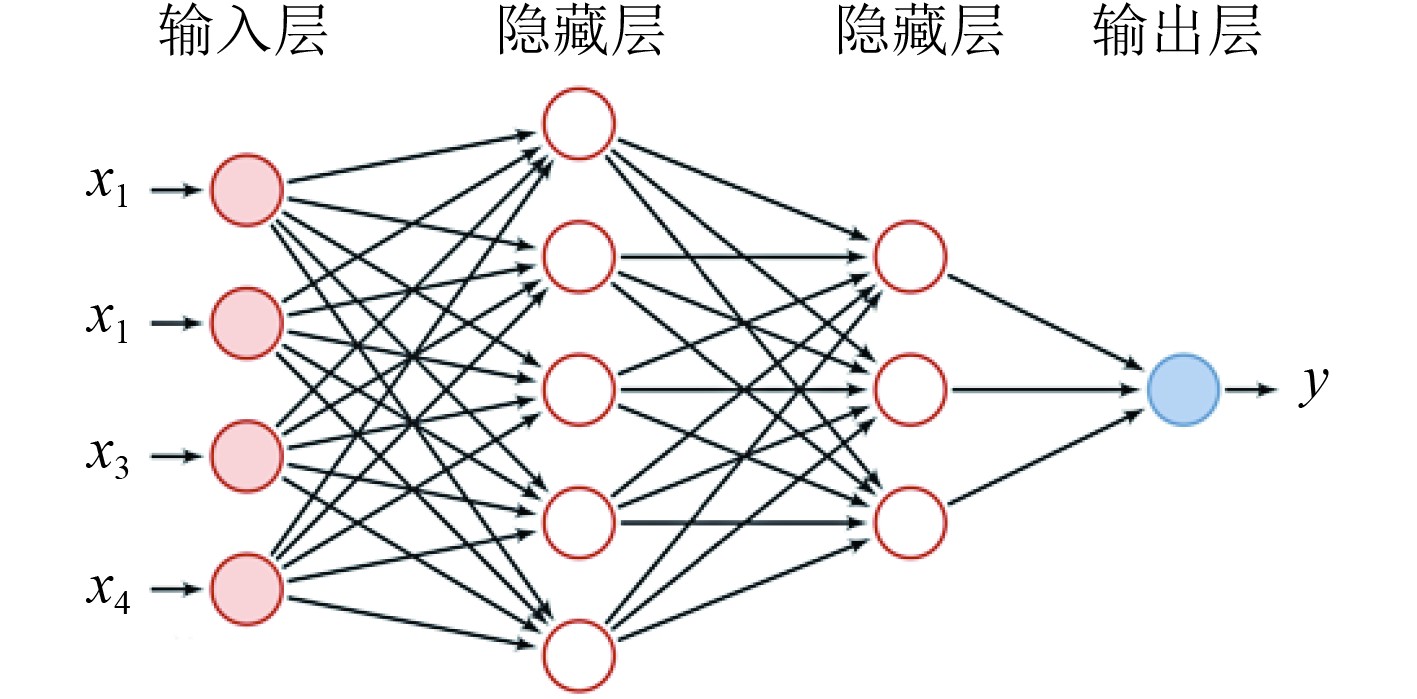
1.2 基于神经网络的气动参数代理模型BP神经网络是一种多层前馈神经网络,能够对不同应用场景下的关系模式进行很好的分类,并且能对多维函数进行很好的映射拟合,而通流计算中的落后角和损失系数与其他参数之间的关系正是这样的非线性映射关系,BP网络能够进行描述。从结构上讲,BP网络具有输入层、隐藏层和输出层,概念清晰,模型简单,便于快速建立可靠映射模型[11]。其结构如图3所示。
|
图 3 BP神经网络结构示意图 Fig. 3 Schematic diagram of the BP neural network structure |
外界信息经过各个神经元的传递完成一次正向传播后,得到输出并对比其与真值之间的误差,再将误差反向传播,从而调整各神经元节点的权重。直到误差函数(损失函数)的值达到最小,网络完成学习,而BP神经网络中常用的误差函数形式为均方误差函数,本文沿用该函数。
| $ RMSE=\sqrt{\frac{1}{N}\sum_{i=1}^N\left(Y_i-f\left(x_i\right)\right)^2}。$ | (3) |
式中:RMSE为均方误差;
在明确神经网络的基本原理和建立过程后,就需在合适的数据库的基础上对网络进行训练,建立起从流道几何参数和边界条件到通流气动参数的映射。
对离心压气机整机进行CFD模拟,将不同来流工况下提取的气动参数作为数据集,采用Matlab神经网络工具箱进行训练,在数据库输入之后,首先会进行归一化处理(包括输入变量和输出变量),并且划分各个训练阶段数据集[12 - 13]。具体选取参数分布如表1所示。
|
|
表 1 神经网络训练数据分布表 Tab.1 Neural network training data distribution table |
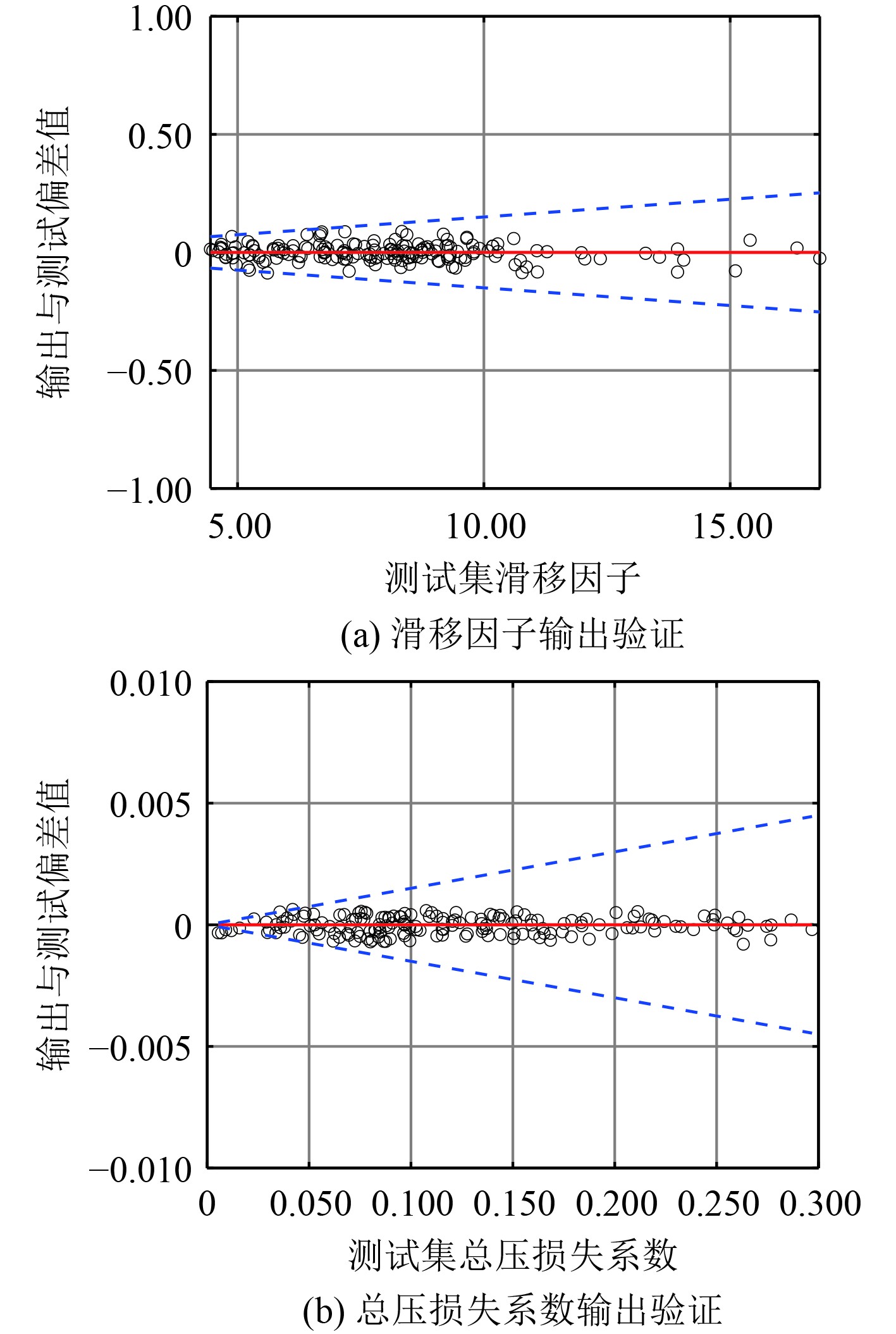
将叶型参数集和气动参数集共同组成训练数据集,落后角与总压损失系数设置为输出参数,其余均设置为输入参数,按照图4中的流程对数据集进行训练。
|
图 4 神经网络输出误差检验 Fig. 4 Neural network output error check |
为了对训练得到神经网络正确性进行检验,随机选取测试数据集中部分数据对网络进行验证,得到检验误差分布如图4所示。可以看出,样本点预测误差集中在以对角线构成的窄误差带内,最大相对误差分别为1.5%和3%,说明训练得到的该神经网络模型能够满足后续通流计算对2个参数的预测精度要求。
2 模型验证与应用对离心压气机整体气动性能进行计算校验,将试验结果与改进的流线曲率法预测结果进行对比,可以完整验证改进方法的可靠性与适用性。
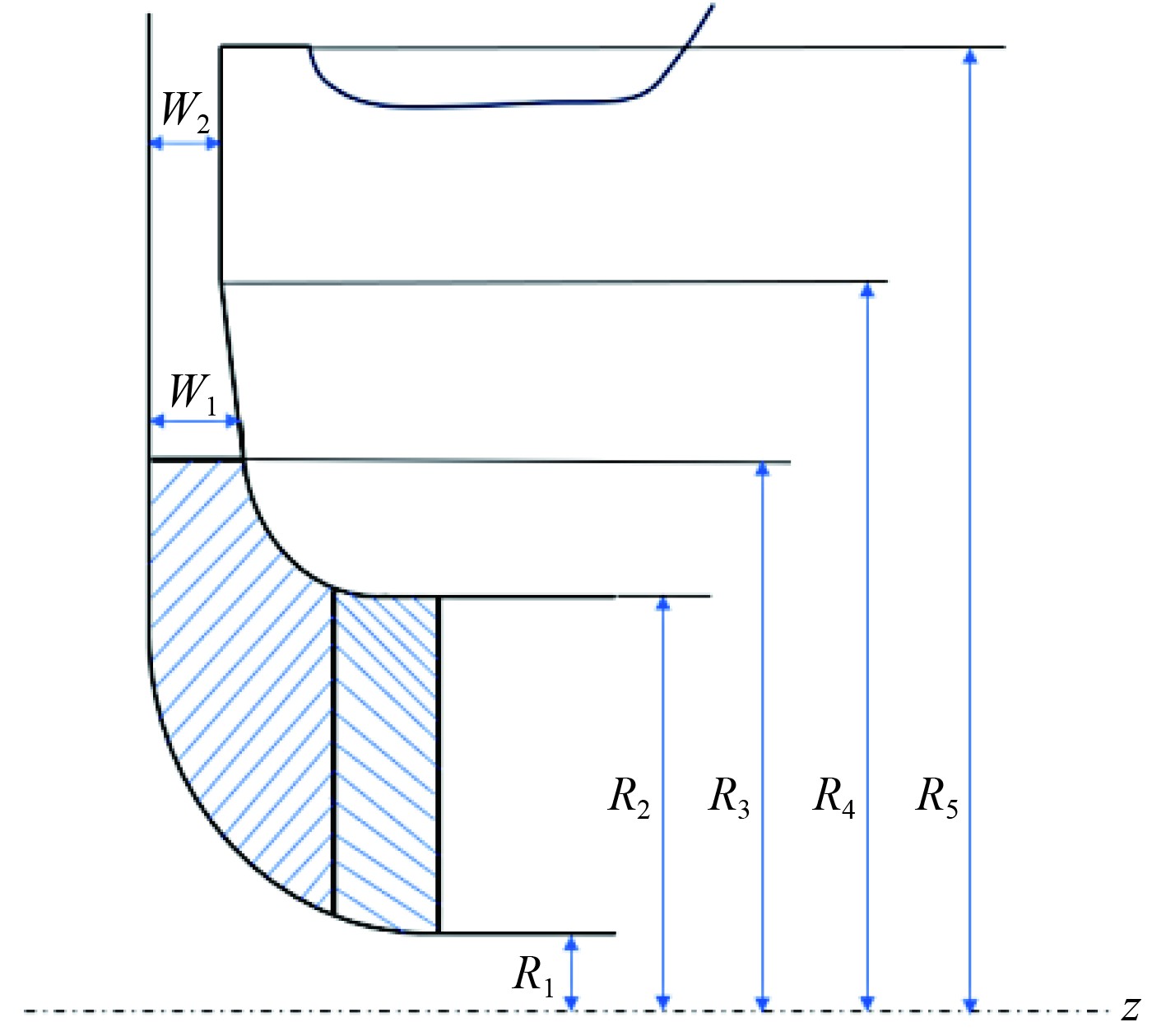
2.1 验证对象1JP60作为高速小尺寸离心式压气机[14],喘振裕度大,设计强度高,在叶型上采用前倾后弯叶片。图5为其完整几何模型,是一款应用广泛的增压器件。其子午界面流道几何如图6所示。其他主要设计参数如表2所示。

|
图 5 JP60离心压气机模型示意图 Fig. 5 Schematic diagram of the JP60 centrifugal compressor model |
|
图 6 JP60离心压气机子午面示意图 Fig. 6 Schematic diagram of the meridian surface of JP60 centrifugal compressor |
|
|
表 2 高速离心压气机主要设计参数表 Tab.2 The main design parameters of high-speed centrifugal compressor are table |
通过公开试验结果可得在不同转速下离心压气机特性曲线如图7和图8所示。

|
图 7 JP60离心压气机压比特性曲线 Fig. 7 JP60 centrifugal compressor pressure ratio characteristic curve |

|
图 8 JP60离心压气机效率特性曲线 Fig. 8 Efficiency characteristic curve of JP60 centrifugal compressor |
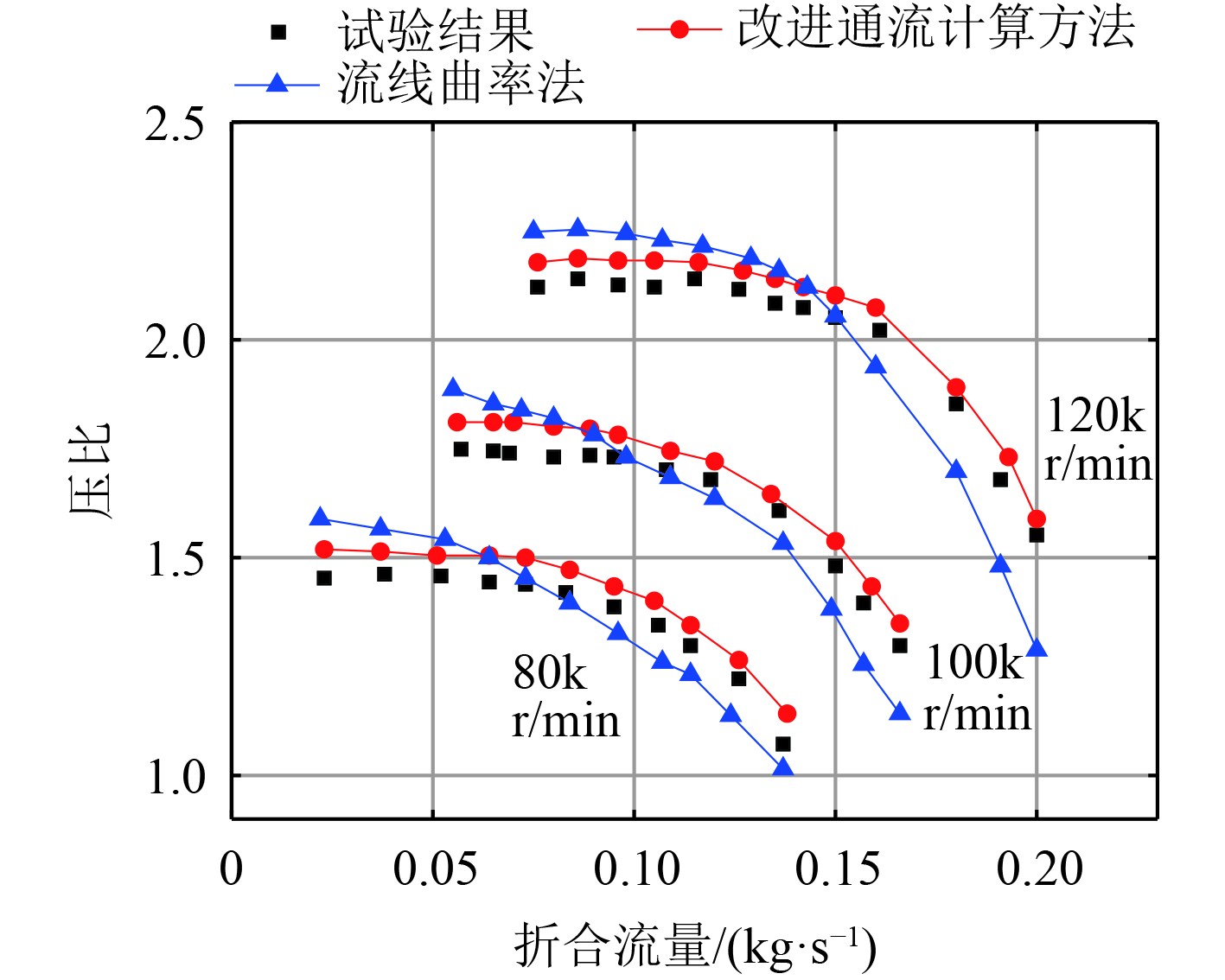
在试验结果的基础上,继续在不同工况下利用改进过的通流计算程序进行计算校验。在各个转速下,图9和图10中圆形点线是三维CFD计算结果,方形和三角形点线分别是原始通流计算程序结果和基于神经网络的通流计算程序结果。
|
图 9 JP60离心压气机压比性能试验与预测结果对比 Fig. 9 Comparison of the pressure ratio performance test of JP60 centrifugal compressor with the predicted results |

|
图 10 JP60离心压气机压比性能试验与预测结果对比 Fig. 10 Comparison of the pressure ratio performance test of JP60 centrifugal compressor with the predicted results |
可以看出,基于BP神经网络模型的正问题分析程序对该离心压气机的预测结果与初始的正问题分析程序的计算结果基本吻合。在设计转速工况下,改进的正问题分析程序能很好预测近失速工况和近堵塞工况质量流量,而另外2个非设计转速下,改良模型对近失速工况和近堵塞工况质量流量的预测精度也几乎与设计工况下一致,说明该分析程序在较宽的工况范围内都有较好的预测效果。
2.2 验证对象2HPCC作为高速高压比离心压气机[15],在设计之初借鉴了轴流压气机设计方法,其中的离心叶轮包含大小叶片各15个,小叶片用于分流。在后续的计算中,沿流线方向将小叶片厚度叠加进大叶片中即可。其主要设计参数如表3所示。
|
|
表 3 高压比离心压气机主要设计参数表 Tab.3 The main design parameters of the high-pressure ratio centrifugal compressor are table |
同样可以得到改进流线曲率法对该离心压气机气动性能预测结果与试验结果对比,如图11和图12所示。总压比和效率预测在标准流量工况下预测效果最好,在流量逐渐减小的近喘振工况下误差逐渐变大,但整体而言通流预测结果满足计算精度,最大相对误差不超过17%,且出现在偏离设计点的工况,靠近设计点附近的相对误差均在5%以内,完整验证了改进的流线曲率法计算程序在离心式压气机气动性能预测中的准确性。

|
图 11 HPCC离心压气机压比性能试验与预测结果对比 Fig. 11 Comparison of HPCC centrifugal compressor pressure ratio performance test and prediction results |

|
图 12 HPCC离心压气机效率性能试验与预测结果对比 Fig. 12 Comparison of HPCC centrifugal compressor efficiency performance test and prediction results |
本文针对离心压气机的性能预测过程中快速准确获得流场气动参数的需求,利用神经网络建立气动参数代理模型,以此改进流线曲率法通流计算程序。就2个离心压气机进行性能预测并与试验结果对比分析,结论如下:
1)利用BP神经网络建立的落后角和总压损失系数代理模型训练速度快,预测精度高,能够实现离心压气机气动参数预测。
2)通过改进的流线曲率法计算程序对2台不同离心压气机气动性能预测结果与公开试验测试数据对比,发现近设计点范围内预测相对误差在5%以内,验证了改进的通流算法可行性和适用性。
3)本文针对离心压气机的滑移因子和总压损失系数建立代理模型并耦合到正问题计算中,在近设计点获得了较为准确的预测结果。而面对更复杂多变的近喘和大流量工况,采用此种方法能否取得同样效果仍待检验,未来神经网络模型在柴油机离心压气机设计问题中的应用值得继续研究。
| [1] |
高丽敏, 杨光, 王浩浩, 等. 波纹对高亚音叶型气动敏感位置和宽度研究[J]. 工程热物理学报, 2023, 44(1): 78-85. |
| [2] |
WU C H. A general theory of three-dimensional flow in subsonic and supersonic turbomachines of axial-, radial-, and mixed-flow types[R]. NACA-TN-2604, 1952.
|
| [3] |
QUINTANILLA V , BRIGGS K , MORRIS M , et al. Performance of a supercritical carbon dioxide compressor using a streamline curvature based throughflow method[J]. Applied Thermal Engineering, 2024, 24(12): 22−29.
|
| [4] |
HOSEIN B , VAHID E , ALIREZA T , et al. Improved streamline curvature method for prediction of gas turbines performance[J]. Arabian Journal for Science and Engineering, 2023, 49(2): 2749−2766.
|
| [5] |
RASOOL H , ALI N , ULLAH K. Bifurcations of streamlines in peristaltic flow without lubrication approximation: A case study[J]. ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, 2023, 10(4): 1−2.
|
| [6] |
戎毅, 廖凯龙, 孙恩慧, 等. 基于流线曲率法的超临界二氧化碳离心压缩机通流计算方法[J]. 热力发电, 2024, 53(2): 124-132. DOI:10.19666/j.rlfd.202307140 |
| [7] |
巫骁雄, 刘波, 唐天全. 流线曲率法在多级跨声速轴流压气机特性预测中的应用[J]. 推进技术, 2017(10): 2235-2245. |
| [8] |
王剑. 基于流线曲率法的周向弯曲叶片的性能计算[D]. 上海: 上海交通大学, 2012.
|
| [9] |
郑覃, 杨小贺, 叶俊, 等. 变外涵工况下风扇增压级双涵匹配机理[J]. 航空动力学报, 2022, 37(9): 1946-1956. DOI:10.13224/j.cnki.jasp.20210112 |
| [10] |
张超炜. 离心压气机性能预测模型及气动设计方法研究[D]. 北京: 中国科学院大学(中国科学院工程热物理研究所), 2020.
|
| [11] |
黄孟璇. 基于神经网络与遗传算法的压气机正问题优化设计研究[D]. 南京, 南京航空航天大学, 2018.
|
| [12] |
费腾, 季路成, 周玲. 神经网络模型在压气机通流特性分析中的应用[J]. 航空动力学报, 2022, 37(6): 1260-1272. |
| [13] |
韩昌富, 刘波, 张博涛. 损失及落后角代理模型在多级轴流压气机特性预测中的应用[J]. 推进技术, 2020, 41(7): 1493-501. |
| [14] |
朱智富, 马朝臣, 张志强, 等. 车用涡轮增压器喘振判断方法的研究[J]. 内燃机工程, 2010, 31(4): 59-62+68. DOI:10.3969/j.issn.1000-0925.2010.04.013 |
| [15] |
谢卫红, 周进, 王毅. 高压比离心压气机气动特性研究[J]. 机械工程与自动化, 2018(2): 32-34+37. DOI:10.3969/j.issn.1672-6413.2018.02.012 |
 2025, Vol. 47
2025, Vol. 47

