0 引　言

随着时代的不断进步和科学的不断发展，水下机器人已经被广泛应用于智慧医疗、智慧农业、工业信息化制造等领域。而路径规划作为水下机器人研究领域的重要分支，已经成为当今学者们研究的重点和难点之一。而水下机器人的路径规划就是根据水下机器人对外部环境的感知，规划出一条安全且成本最低的最优路径^[1]。良好的路径不仅能降低对能源的损耗，还可以节省大量的时间。当前，在移动自动机的路径设计领域内，普遍采纳的导航计算方法主要涉及到迪杰斯特拉算法、退火模拟法以及粒子群算法等，均为这类机器人常规选用的路线优化技术^{[2 − 4]}，可以从地图上的指定起点到目标位置的运动路径。然而，在搜索路径过程中往往会遇到陷入局部最优、搜索能力差、易与障碍物碰撞等问题。

蚁群算法因具有正反馈能力强和种群分化等优势而得到了广泛的应用，但是蚁群算法也存在着搜索效率低和收敛速度慢等缺点。周怀芳等^[5]对核事故下应急车辆路径规划问题，以累积辐射剂量为评价指标，提出了一种基于混合蚁群算法的车辆路径规划方法。改进混合算法精确性和稳定性明显优于传统算法的搜索结果。李三平等^[6]采用扩展后的 Dijkstra算法对转移概率进行改进，扩展了搜索范围，并引入终点信息对初始信息素改进，增强了初期路径搜索的导向性。毛寿祺等^[7]针对水面无人船全局路径规划问题，提出一种融入细菌觅食算法繁殖操作和趋化操作的改进蚁群算法。该算法改变传统蚁群算法单一距离启发的机制，结合水面无人船的实际物理约束，引入转向角启发因子。相较于传统的蚁群算法，其路径寻优和避障能力较高。符运来等^[8]提出的双向A^*-APF算法，在保证搜索时长的同时，剔除路径上冗余拐点，缩短了规划路径的长度，与传统A^*算法和双向A^*算法相比，各项数据均有进步，得到了较为理想的试验结果，解决了传统A^*算法规划路径并非最短，路径上拐点较多，搜索时间较长等问题。

针对传统蚁群算法在规划路线时面临的问题，如初始信息素量缺乏、需要重复迭代的次数较多、搜寻路径的速率缓慢以及容易受困于局部的最优解，本研究提出了对蚁群算法的优化方案。改进措施包括将蚁群算法与A^*算法进行结合使用，并对蚁群算法中的起始信息素浓度进行调整。然后完善信息要素的更新方式以及节点转移的概率。优化版的蚁群算法在少数几次迭代中即可精确制定出最佳行进路线，这显著增强了路径设计的效能与精确度。

1 环境建模和相关算法介绍 1.1 环境建模

在水下机器人环境建模方法中主要有机器视觉法、拓扑图法和栅格法等。由于栅格法容易操作、适应性强，对环境建模的复杂程度可以明显降低。因此，本文选择栅格法来建立移动的水下机器人的工作环境模型^[9]。栅格法以栅格为单位记录环境信息，环境被量化成具有一定分辨率的栅格，栅格的大小直接影响着环境信息存储量的大小和规划时间的长短。在采用栅格模型进行环境表征时，仿真地图上的开阔空间通过数字0来体现，并使相应的格子显示为白色；而数字1则代表仿真地图的阻碍物区域，与之对应的单元格应涂为黑色。本文结合直角座标系与索引法的方式制图，如图1所示，用以机器人行动的仿真环境地图包含20×20的单元格阵列^[10]。

在图1中，白色网格代表自由区域，黑色网格代表障碍物区域，每个网格都有唯一的编号序列号，并对应有位置坐标。网格序列号和对应坐标之间的变换关系为：

$ \left\{\begin{aligned} & x_i=a\left(\mathrm{mod}\left(i,N_x\right)-0.5\right)，\\ & y_i=a\left(N_y+0.5-\mathrm{ceil}\left(\displaystyle\frac{i}{N_y}\right)\right)。\end{aligned}\right. $

(1)

式中：($ {\mathit x}_{{i}},{\mathit y}_{{i}} $)为第i个网格的位置坐标；i为第i个网格的序列号；mod（）为冗余运算符；ceil（）为向上取整运算符。

1.2 蚁群算法原理

意大利学者Marco Dorigo在1991年首次提出一套基于群体智慧的启示式计算方法，称为蚁群算法。

在自然界中，蚂蚁群体在寻找食物的过程中，无论是蚂蚁之间的协作，还是蚂蚁与环境之间的互动，都要依靠一种叫做信息素（Pheromone）的物质来实现蚂蚁群体之间的间接沟通，从而通过协作找到从蚁穴到食物来源的最短路径^[11]。

在搜寻食物时，蚂蚁常常无计划地选道而行，然而它们能侦测到所处地表的信息素浓度，并趋向于沿着信息素密度更高的地带前进。这种信息素由蚂蚁自身分泌，作为蚁群间进行非直接交流的信号。较短途径因为来回耗时较少，每个时间单位内经过的蚂蚁数量众多，导致信息素堆积速度快于那些较远途径。所以，紧随其后的蚂蚁到达岔路口时，更容易察觉到先行者的信息素痕迹，而偏好挑选一条更短的途径继续前进。正是这样的正向反馈效应，让越来越多蚂蚁在寻找巢穴与食物源的最便捷路线时走在同一条线路上。随着时间流逝，非最佳路径上的信息素自然挥发，最终导致所有蚂蚁集体沿着最理想的路线进行移动^[12]。

在蚂蚁搜寻食源的路途中，其决定路径转向的几率主要取决于信息素浓度及各路线上的引导信息。设想在一个固定且已探明的格状空间里，在时间点t，位于格子i的第k只蚂蚁（k为1，2，…，M）向第j个网格移动的过程如下。首先，通过式(2)计算第i个网格周围的每个可选路径的转移概率$ \mathrm{\mathit{P}}_{ij}^{\mathrm{\mathit{k}}}\left(t\right) $，然后通过轮盘赌规则确定下一个第j个网格。转移概率的计算在等式t中示出，第i个网格周围的每个可选路径的$ {\mathit{P}}_{{i}{j}}^{\mathit{k}}\left({t}\right) $计算式为：

$ P_{ij}^k\left(t\right)=\left\{\begin{aligned} & \displaystyle\frac{\left[\tau_{ij}\left(t\right)\right]^{\alpha}\left[\eta_{ij}\left(t\right)\right]^{\beta}}{\sum_{s\in allowed_k}^{ }\left[\tau_{ij}\left(t\right)\right]^{\alpha}\left[\eta_{ij}\left(t\right)\right]^{\beta}},j\in allowed_k。\\ & 0,\rm{otherwise}\end{aligned}\right. $

(2)

在该情境下，自变量时间t点所标示的，源于网格i至网格j间的信息素密度记作τ_ij(t)；α为影响信息素密度的系数；β为路径选择的启发式权重；集合s包含蚂蚁k在网格i周边可遍历的潜在网格，记为allowed_k；而$ {\mathrm{\eta }}_{\mathit{i}\mathit{j}}\left(\mathit{t}\right) $即代表同一时间t，连接网格i与网格j之间的路径启发式信息，其运算法则如下：

$ \eta_{ij}\left(t\right)=\frac{1}{d_{ij}}。$

(3)

式中：$ {d}_{ij} $为从第i个网格到第j个网格的欧几里得距离。

当一只蚂蚁移动从网格i至网格j期间，使用式(4)进行的是局部范围内的信息素的刷新。而在每一轮搜索完成后，所有蚂蚁共同涉及的是信息素的整体优化，其对应的更新过程则按照特定的后续算式来执行。

$ \tau_{ij}\left(t\right)=(1-\vartheta)\tau_{ij}\left(t\right)+\vartheta\tau_0,\vartheta\in\left(\mathrm{0,1}\right)，$

(4)

$ \tau_{ij}(t+1)=(1-\rho)\tau_{ij}\left(t\right)+\rho\Delta\tau_{ij}\left(t\right)，$

(5)

$ \Delta\tau_{ij}\left(t\right)=\sum_{ k=1}^{M }\Delta\tau_{ij}^k\left(t\right)。$

(6)

式中：$ \vartheta $为一个常数，$ {\tau }_{0} $为正值。符号ρ用来表示信息素蒸发掉的相对速率，在此基础上，(1−ρ)则表示信息素得以保留下来的比例。$ \Delta {\tau }_{ij}\left(t\right) $反应出在特定的迭代循环里，从节点i到节点j之间的信息素浓度水平，$ \Delta {\tau }_{ij}\left(t\right) $则用以量化这条路径上信息素增加的量值。而M是指构成蚁群的全部蚂蚁数目，$ \Delta {\tau }_{ij}^{k}\left(t\right) $指的是，在某一迭代周期内，编号为k的蚂蚁在i到j的路径上所遗留下的信息素总量。本文所采纳的信息素浓聚程度是参照蚁群优化算法所提出的模型^[13]得出的，并依照式(7)的规定计算得出$ \Delta {\tau }_{ij}\left(t\right) $的确切数额。

$ \Delta {\tau }_{ij}^{k}=\left\{\begin{aligned}&\displaystyle\frac{Q}{{L}_{k}},\mathrm{如}\mathrm{果}\mathrm{蚂}\mathrm{蚁}k\mathrm{经}\mathrm{过}\mathrm{路}\mathrm{径}\mathrm{城}\mathrm{市}i\mathrm{到}j，\\ &0,\mathrm{否}\mathrm{则}。\end{aligned}\right. $

(7)

式中：Q为指初始状态时信息素的固定浓度；$ {L}_{k} $为第k只蚂蚁在这一轮循环过程中行进的总路径长度。

2 蚁群A*算法 2.1 改进蚁群A*算法启发函数

蚁集算法当中，鉴于导向信息仅仅基于现行方格及其备选方格间隔的远近，这一因素势必造成算法在起始阶段的全局效能表现不佳。为了提高搜索的启发性，还考虑了所选网格与目标网格之间的距离。此外，在算法后期，为了弱化启发信息的作用，平衡算法的全局搜索能力和收敛速度显得尤为重要。为解决蚁群初始信息素匮乏问题，利用带约束的A*算法寻路精度高的优点，来优化设置启发函数。

A^*算法是一种基于启发式搜索的最短路径优先算法，同时又加上了一些约束条件。在复杂参数空间中，对每个潜在的检测点进行效用评估，筛选性价比最高的点，并以此为基础继续寻找，直到达到预定的目标点为止。这种方法能有效缩减搜寻的范围，降低问题解决难度，并从而加快解决问题的速率。评估函数结合了从初始点到当前点的实际代价和从当前点到目标点的估算代价。A*算法估价函数 f(n) 如下：

$ \mathit{f(n)=g(n)+h(n)}。$

(8)

在此算法框架里，g(n)函数象征着前往下一站所需路径的代价，另一方面，h(n)函数扮演着引导角色，确保搜寻过程朝向目标点的最短途径前进。尽管如此，在蚂蚁算法的体系中，其启发函数被设置为1/d_ij，此函数只衡量了起点i到候选点j之间的直接距离成本，更侧重于搜寻邻近的短途径，这种做法不仅难以全面挖掘到最优途径，还容易陷入仅局部最优的搜索陷阱。而在经典蚁群算法应用中，结合了A*算法的思想，便纳入了预测价值d_je。通过融合d_ij的实际代价与d_je的预测评估，得到了一个改善的启发式算法表达式，详述如下：

$ \eta=\frac{\delta d_{je}}{\delta\times d_{ij}+(1-\delta)d_{je}}。$

(9)

该算法中，δ 为途径障碍调整系数，其有效数值介于0～2，这一参数的应用增强了搜索效能，同时借助目的地节点，有效促进了路径整体的最优化，从而规避了落入部分最优解的困境。

2.2 改进蚁群A*算法信息素更新规则

面对机动机器人路线设计的挑战，为确保一条既安全又高效能够畅通无阻的路线，增强寻径的效率与选择的多样性，提升规避障碍与搜寻效能，在蚂蚁算法更新信息素的规则里融入了避障因素与线路指引要素。提高路径回避能力和搜索效率。改进的信息素更新规则如下：

$ \mu_{ij}\left(t\right)=\frac{1}{\mathrm{cos}\varphi}=\frac{\left|y_i-y_j\right|}{d_{ij}}，$

(10)

$ \Delta\tau=\frac{Q}{P_m+\xi\mu_{ij}\left(t\right)+\lambda}。$

(11)

式中：P_m 为第m只蚂蚁走完之后所得到的路径距离；$ {\mu }_{ij}\left(t\right) $为路径引导因子；ξ为拐角平衡系数；$ \lambda $为障碍排除因子，取值范围为(0,1)。

2.3 改进蚁群A*算法状态转移概率

状态转移概率主要是由信息素因子α、启发函数因子β和信息素挥发系数ρ决定。对其参数的设定没有健全的理论来确定和支撑，多依赖学者的经验和多次实验来配置最佳的参数组合。

蚁群算法参数取不同的值会由于正反馈机制和挥发机制而影响路径寻优结果和迭代收敛速度。设置过高容易导致局部最优，设置过低难以获取最短路径，从而导致搜寻路径过长，效率降低。

依据迭代次数的增减动态调整α与β的值，由此在迭代过程中拓展蚂蚁寻路的可能性区域，以此使得获得的解决方案的质量能够随着迭代的进行而提升，从而避免过早地被困于局部最优解。信息素浓度参数α与启发式因子β根据迭代的不同阶段进行自我调整，更新方式如下：

$ \mathrm{\alpha }={\mathrm{\alpha }}_{1}\cdot \mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{{\text{π}} }\cdot \frac{{k}-{K}/2}{5}\right)+{\mathrm{\alpha }}_{2}，$

(12)

$ \beta=\beta_1\cdot\mathrm{sin}\left({\text{π}}\cdot\frac{k-K/2}{5}\right)+\beta_2。$

(13)

式中：α₁、α₂、β₁、β₂均为待定参数；k为当前迭代次数，K为最大迭代次数。

在迭代初期，α值较小，除由改进A*算法得到的路径信息素浓度较高，其他路径信息素浓度相差不大，对蚂蚁的影响较小；而β值较大，蚂蚁依赖于距离参数为选择依据，有利于提高算法搜索速度。

随着迭代进程接近尾声，各路线上的信息素含量逐步不敌那些更佳路线的信息素含量。因此，信息素含量的多寡转变为主导蚂蚁辨识最佳路线的关键因素。为此，应当增加α系数的数值，并相对减少β系数，以此促进算法的快速收敛。

针对传统蚂蚁算法信息素挥发率ρ的常数设定，本研究提出了一种优化，调整ρ使之能依迭代过程自动调节，藉由蚂蚁算法信息素正反馈效应保障路径优化问题获得最佳全局解。在迭代初期，ρ值较小，算法的随机性能和全局寻优能力较高；随着迭代的进行，ρ值逐渐增大，由于信息素正反馈作用使算法收敛速度加快。动态更新信息素挥发系数ρ如下：

$ \rho=\rho_1\cdot\mathrm{tan}\left(\text{π}\cdot\frac{k-3\text{π}}{5}\right)+\rho_2。$

(14)

式中：$ {\rho }_{1} $和$ {\rho }_{2} $均为常数。

3 改进蚁群A*算法的机器人路径规划实现

结合A*算法与蚁群优化技术的机器人导航路径设定程序如下：

步骤1　建立二维空间栅格静态地图，设置障碍物,选择起始点和终点。

步骤2　为本文中提到的演算法各项指标设定初值，涵盖蚁群的规模和最高重复运算次数等因素。

步骤3　对开局点执行禁忌操作，同时安排每只蚂蚁m（m取值范围为1～M）于起始点。采用本研究提出的优化算法，对初始的信息素浓度进行调整，并对启发式函数作出创新。

步骤4　运用式(2)推导出各个潜在节点的几率，并通过轮盘选择法确定下一步将前往的节点，将该节点添加至禁忌表中，随后对旅途的距离作出相应调整。

步骤5　检查蚂蚁是否抵达E点，若抵达，则记录下其所经过的格子编号及所走路径的长度。如果尚未到达，需持续执行步骤4，直至找到E点为止。倘若有蚂蚁k在搜索过程中进入僵局，便采取相应的蚂蚁退回机制加以解决。一切蚂蚁搜索完毕，转移到步骤6。

步骤6　评估当前迭代轮数是否触及设定的迭代上限N_max。倘若迭代已经到达预定的最大次数，此时将中止迭代过程，同时记录下此刻蚂蚁群体所找到的最短路径长度及迭代轮数。反之，若未达上限，则重置禁忌记录，将N的值加1，随后回到步骤3，持续进行路径探索，直至迭代次数等同于N_max时，完成算法执行，并最终提供所探索到的最短路径长度及其对应的迭代轮数。

4 仿真与分析

为充分考察本文所提出算法的有效与准确性，采用了2个规模不一的地图进行蚂蚁群算法导航机器人的路径规划模拟实验，这2个地图分别具有20×20和30×30的栅格尺寸。

由于考虑到其他文献所研究的算法与本文所研究的算法在参数选取上有所不同，故直接利用本文改进算法所设置的环境和参数来进行仿真实验的对比和分析。搭建一套模拟执行的平台，其配置为：使用PYTHON 3.11版本，运行于搭载64位Windows 11系统的计算机上，该计算机装备了英特尔酷睿i7-8700处理器以及16 GB的RAM。参数设置：最大迭代次数N_max = 100；蚂蚁数目m = 50；信息素ƍ = 1；障碍排除因子$ \lambda $ = 0.6；路径障碍修正因子$ \delta $ = 0.7。

4.1 20×20仿真环境

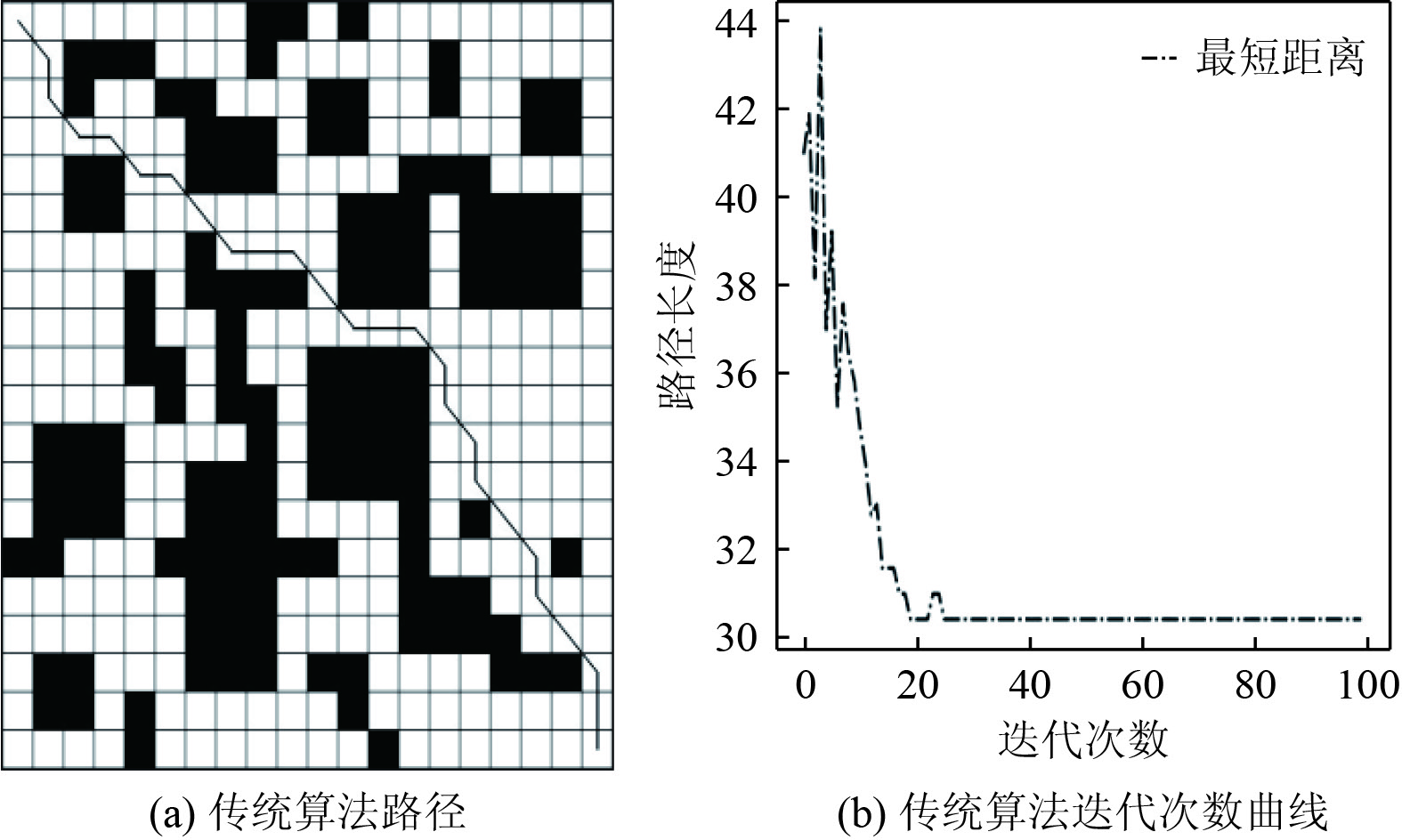
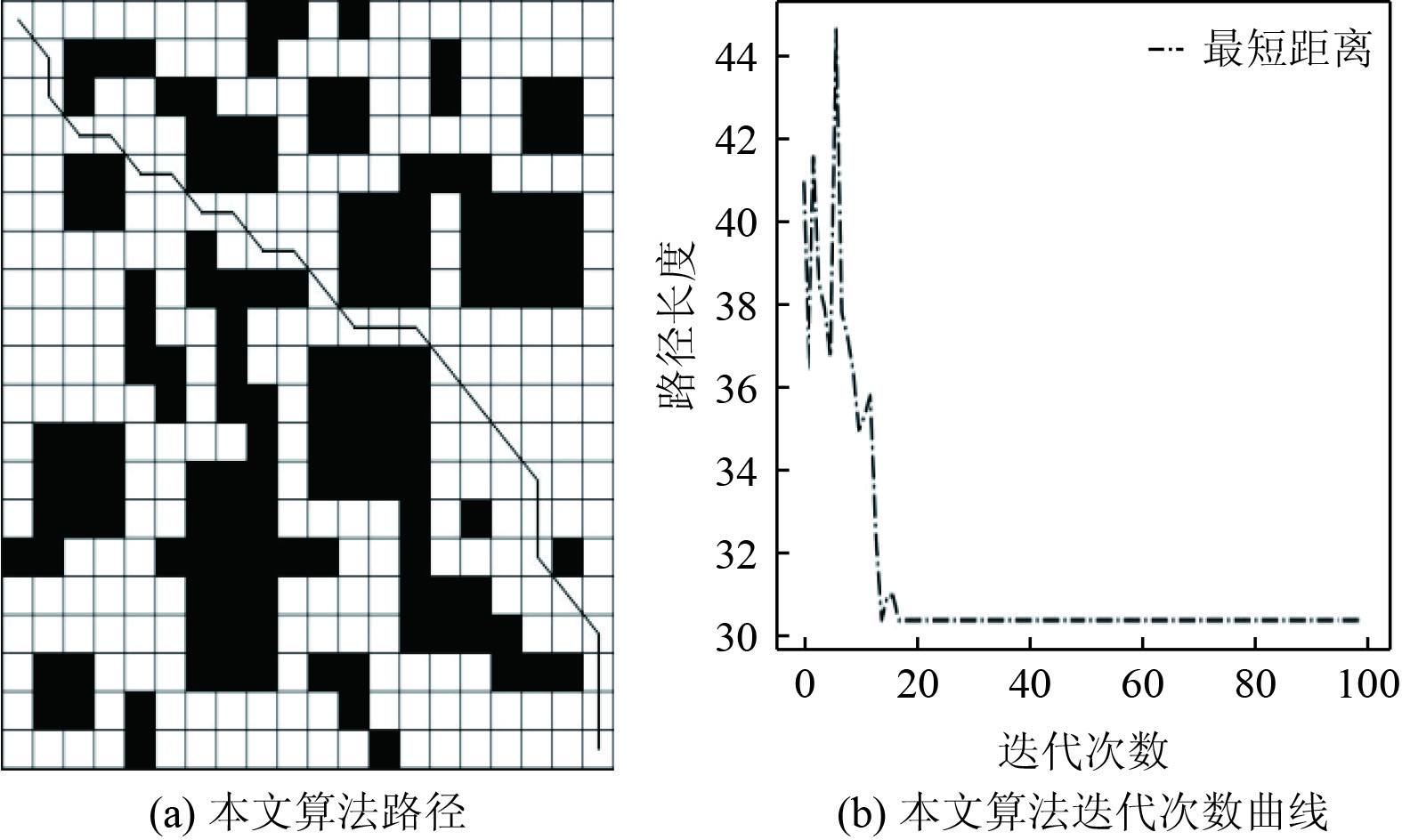
在20×20的场景大小中，本研究所提升的算法与经典蚂蚁算法及文献[12]中的算法展开模拟对比试验。左上角栅格坐标为[0,0]，向下增大，向右增大。所以右下角为[19,19]。本文结果是多次实验对比分析所得到的，3种路径规划的实验结果和收敛曲线如图2～图4所示。对仿真实验中的最优迭代次数、平均用时和路径长度如表1所示。

可以看出，本文所提出的优化算法在路径规划方面产出的结果显著超越了传统蚂蚁算法及文献[12]中介绍的方法。这种改进算法在最优迭代次数、平均处理时长和总路径长度3个评价指标上均表现出色。此成效归功于改善了初始启发式函数，并融合了A*算法，大幅提升了初始路径设置的适应性，以此缩减了最终路径长度，并确保规划出的路线更符合机器人实际行驶的需求。对照来看，传统蚂蚁算法在寻找路径的效率上存在不足，有时可能停留在局部最优解，未能有效实现路径规划的优化。

4.2 30×30仿真环境

为了进一步验证本文算法在复杂环境下的路径规划表现，在30×30的栅格地图环境下进行仿真实验。由于栅格地图面积变大和障碍物变多，每个算法的迭代次数和路径长度都有所变大。在30×30地图规模的基础上改变障碍物设置以及在环境中的覆盖率。实验结果如图5～图7所示。对仿真实验中的最优迭代次数、平均用时和路径长度如表2所示。

可以看出，在不同障碍物覆盖率的地图上，在最优迭代次数上，本文所提出来的A*蚁群融合相比其余2种算法有明显的降低，所以在更短的时间上可以找到最优路径。另外在平均用时和路径长度上，本文改进的蚁群算法比文献[12]所改进的算法分别提升了8.9%和2.2%。此次实验说明即使在地形复杂障碍物多的情况下。依然可以保持良好的搜索能力和更短的平均用时。

5 结　语

针对经典蚁群算法在定位最佳路线时存在的弱点，如寻找路径时耗时较长、需要重复迭代众多次且易于落入部分最优解的困境，本研究提出了一种优化版蚁群算法。该算法在早期迭代过程中结合了A*算法，目的是为了对启发式函数进行改良和增强。提高算法在初期的寻优能力。为此，以增强算法在路径探索时的绕障技巧，将碰撞避免元素和方向指引元素并入信息素的更新机制中；并对信息素元素、引导函数元素以及蒸发系数作出优化，实现在路径规划的不同环节中对参数的自动调节。最后通过实验验证蚁群A*融合算法的有效性，并且在不同地图范围下，将本文算法与其余蚁群算法进行比较分析。结果表明：文中算法在迭代次数、平均用时和路径长度均优于其他算法，也更符合机器人实际运动情况。