0 引　言

船舶在海上航行时，会受到海浪、风、水流等影响，导致船舶产生复杂的摇荡运动^[1]。摇荡运动包含多个自由度运动。各自由度运动并非孤立存在，而是相互交织、相互作用，共同形成一个极为复杂的线性动态系统^[2]。当船舶受到海浪的扰动时，其纵荡、垂荡和纵摇运动会同时产生，相互影响。这种耦合作用不仅增加船舶运动控制的难度，还降低控制系统的稳定性和准确性。

为解决这个问题，研究者们开始对船舶运动系统进行解耦合研究。例如，孙小帅等^[3]采用三维面元法确定船舶运动模型中的水动力系数，四阶龙格库塔方法确定水面船舶及拖体的六自由度运动，有限差分方法确定拖缆的张力及摇荡运动，分析船舶摇荡运动对拖缆的影响，提升水面船舶航行性能和拖曳系统作业安全。水动力系数的准确性高度依赖于模型的精确度和输入参数的选择，微小的参数变化便会导致显著的结果差异。郭嘉宁等^[4]利用垂向耦合技术，通过数值模拟和实验验证，展现出在波浪中的稳定性与操控性显著提升，为提升船舶航行安全和作业效率提供新的解决方案。垂向耦合技术不适用于所有类型的船舶和海洋环境，特别是在极端条件下。Jiang等^[5]结合自适应网格技术和加权双支持向量回归算法，捕捉船舶在操纵过程中的动态特性。通过数据驱动的方式，结合动态特性，分析和预测船舶在不同操纵条件下的运动响应。该方法高度依赖于可用的数据质量和数量，数据不足或不准确便会导致预测结果不准确。

智能优化算法中改进野马算法在搜索过程中不易陷入局部最优，能够在全局范围内寻找最优解。该算法具有较强的鲁棒性，能够应对各种复杂环境和噪声干扰，实现系统的精准解耦合。为此，研究船舶运动系统解耦合过程的智能优化算法应用，提升船舶航行时的安全性和稳定性。

1 船舶运动系统解耦合过程 1.1 船舶运动系统的耦合方程

船舶运动系统是一个复杂的非线性系统，对其进行全面深入的研究需要耗费大量的时间和资源。在实际研究中，纵摇和横摇是对船舶航行稳定性影响最大的2种运动模式，其它耦合关系对船舶航行稳定性的影响相对较小。这2种运动模式不仅直接关系到船舶的航行安全^[6]，还影响着乘员的舒适度和货物的安全运输。纵摇和横摇之间存在显著的耦合关系。因此，在解耦合过程中，必须优先考虑这2种运动模式之间的耦合关系。船舶运动系统中纵、横摇运动的非线性方程为：

$ F_C=\left\{\begin{aligned} & \boldsymbol{M}_x\times I_x\left(\ddot{\alpha}+\dot{\alpha}\right)B_{\alpha_1}=G_x\cos\left(ct+\tau\right)，\\ & \boldsymbol{M}_y\times I_y\left(\ddot{\theta}+\dot{\theta}\right)B_{\theta_1}=G_y\cos\left(ct+\tau\right)。\end{aligned}\right. $

(1)

式中，$ \boldsymbol{M}_x=I_x+\Delta I_x $、$ \boldsymbol{M}_y=I_y+\Delta I_y $为横、纵摇惯性力矩阵；$ {I_x} $、$ {I_y} $为横、纵摇惯性矩；$ \dot \alpha $、$ \ddot \alpha $为$ \alpha $对于时间$ t $的一阶、二阶导数；$ \dot \theta $、$ \ddot \theta $为$ \theta $对于时间$ t $的一阶、二阶导数；$ {B_{{\alpha _1}}} $、$ {B_{{\theta _1}}} $为阻尼系数矩阵；$ {G_x} $、$ {G_y} $为波浪激励力矩；$ c $为船舶航行过程中，实际感受到的波浪作用频率；$ t $为船舶航行时间；$ \tau $为波浪作用于船舶等浮体时，产生的激励力矩相位差。

仅保留船舶运动系统中纵摇与横摇之间相互作用力的耦合项，而忽略其他非线性因素和入射波对初稳性高的动态调整。建立船舶运动系统的耦合方程，公式如下：

$ O_H=\left\{\begin{array}{*{20}{c}}\boldsymbol{M}_x\times F_C\cos\left(ct+\tau\right)，\\ \boldsymbol{M}_y\times F_C\cos\left(ct+\tau\right)。\end{array}\right. $

(2)

1.2 改进野马优化算法的船舶运动系统解耦合方程

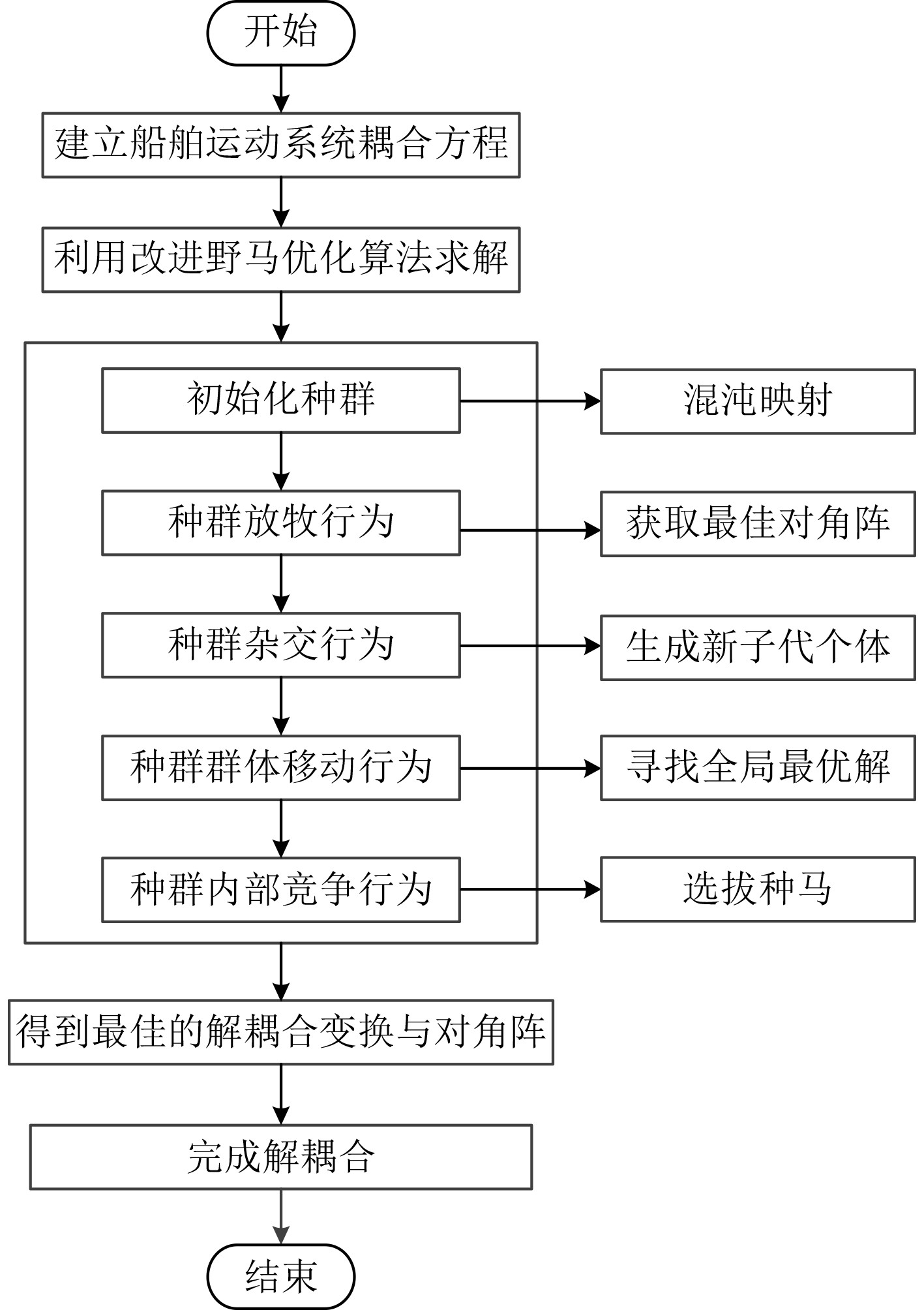
改进野马优化算法在处理多维度、多自由度的复杂问题时具有更高的精度和稳定性，能够在复杂多变的环境中，快速找到最优解。为此，利用改进野马优化算法对建立的船舶运动系统耦合方程进行求解，完成解耦合，更准确地分析船舶的运动特性，提升船舶的航行安全性和舒适性。改进野马优化算法的计算流程图如图1所示。

为便于分析，将式(2)的船舶运动系统耦合方程，简化成：

$ {M_i} \times {B_i} \times {K_i} = {G_i}\cos \left( {ct + \tau } \right) 。$

(3)

式中：$ i $为横摇或纵摇运动。

通过搜索到对应的解耦合变换$ {A_L} $与$ {A_R} $，获取$ {M_i} $、$ {B_i} $、$ {K_i} $的对角阵$ \hat{\boldsymbol{M}}_i $、$ \hat{\boldsymbol{B}}_i $、$ \hat{\boldsymbol{K}}_i $，使得式(3)的船舶运动系统耦合方程能够转化为对角形式的方程，从而实现解耦。

令低阻尼二阶船舶运动系统的特征值对角阵为$ \boldsymbol{A} $；$ \boldsymbol{A} $的左右特征向量，即解耦合变换为$ {A_L} $、$ {A_R} $；表达式如下：

$ \left\{\begin{gathered}{\boldsymbol A}^{-1}A_L^{\mathrm{T}}K=A_L^{\mathrm{T}}M，\\ KA_R{\boldsymbol A}^{-1}=MA_R。\\ \end{gathered}\right. $

(4)

通过$ {A_L} $与$ {A_R} $得到$ {M_i} $、$ {B_i} $、$ {K_i} $的对角阵$ \hat{\boldsymbol{M}}_i $、$ \hat{\boldsymbol{B}}_i $、$ \hat{\boldsymbol{K}}_i $。

在野马优化算法内引入Sinusoidal混沌映射，改进野马优化算法，利用改进野马优化算法求解船舶运动系统解耦合过程的目标函数，完成解耦合的具体步骤如下：

1）通过Sinusoidal混沌映射，初始化种群，即解耦合变换的候选解集合，每个个体都代表一个可能的解耦合变换。

2）在种群放牧行为中，每个个体位置代表一个可能的解耦合变换，用于获取惯性力矩阵、阻尼系数矩阵、回复力系数矩阵的最佳对角阵，使得原船舶运动系统耦合方程变为对角形式，完成解耦合。

3）在种群杂交行为中，选取2个父代个体，它们分别代表2个可能的船舶运动系统解耦合变换。通过交叉操作，结合2个父代个体的优秀基因生成1个新的子代个体。

4）在种群群体移动行为中，种马负责带领种群寻找更加优秀的“水坑”，即全局最优解，代表最佳的解耦合变换。

5）在种群内部竞争行为中，种马个体通过其适应度信息进行选拔，由适应度信息最小的个体（即船舶运动系统解耦合效果最好的解耦变换）担任种马。

2 结果与分析

为了验证所提智能优化算法在船舶运动系统解耦合过程中的有效性，实验选择了一艘作为研究对象的船舶基本信息如下：排水量为1574 t；船长为98 m；船宽为10.2 m；船中高为6.3 m；吃水为3.09 m；横稳心高为1.095 m；自由液面到船重心距离为1.32 m。这些船舶参数为后续的解耦合计算提供了必要的船舶特性数据，确保实验的准确性和可靠性。

实验的核心内容是应用改进后的野马优化算法对船舶运动系统的耦合方程进行求解，以实现解耦合。具体来说，实验步骤如下：

1）基于船舶运动系统的非线性特性，特别是纵摇和横摇之间的显著耦合关系，建立船舶运动系统的耦合方程。

2）利用引入Sinusoidal混沌映射的改进野马优化算法对耦合方程进行求解。

3）对算法求解得到的结果进行验证和分析。

利用本文算法对实验对象进行解耦合处理，准确分析船的运动特性，提升船舶航行的稳定性。该船舶的基本信息如表1所示。

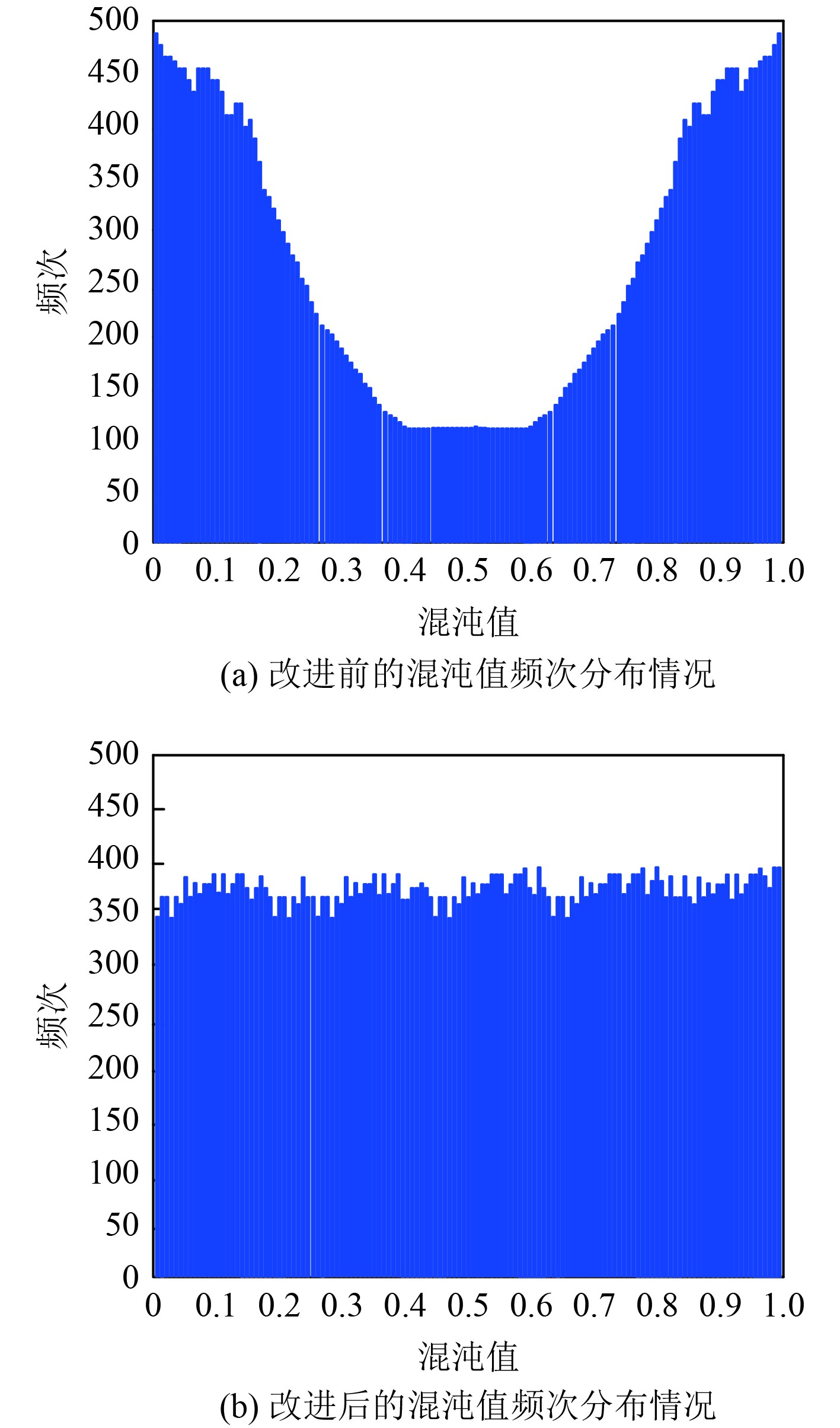
分析本文算法中野马优化算法改进前后，其混沌值的频次分布情况，混沌值的频次分布越均匀，说明船舶运动系统耦合方程的求解效果越佳，分析结果如图2所示。由图2可知，本文算法改进前，求解船舶运动系统耦合方程时，混沌值的频次分布波动起伏较大。本文算法改进后，混沌值能够均匀分布在350～400频次之间。实验证明：本文算法改进后，可提升船舶运动系统耦合方程的求解效果。

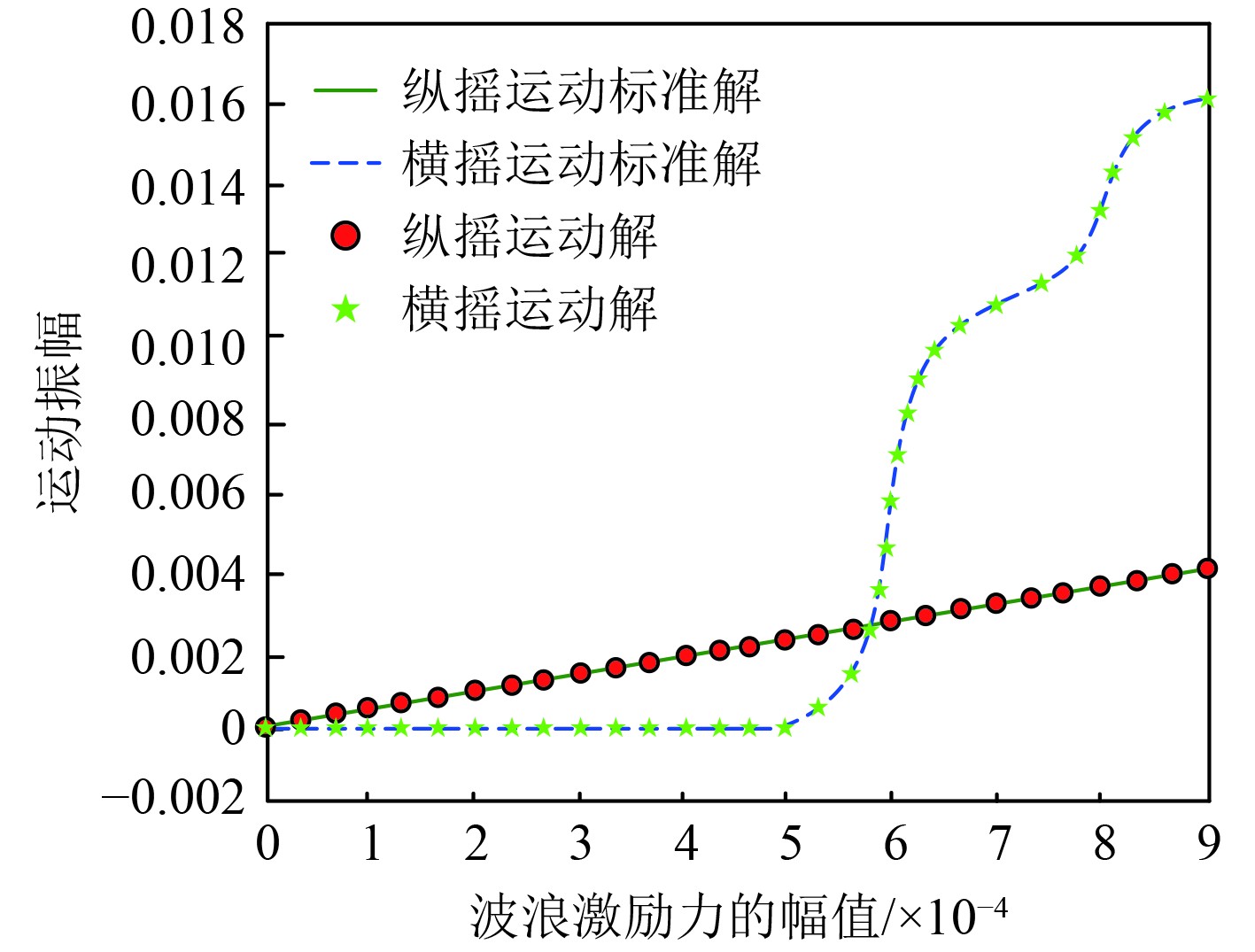
利用本文算法在不同波浪激励力幅值的复杂多变环境下，对该船舶运动系统耦合方程进行求解，实现解耦合，船舶运动系统解耦合过程如图3所示。由图可知，在不同波浪激励力幅值情况下，本文算法求解船舶运动系统耦合方程，得到的横、纵摇运动解，与横、纵摇标准解完全吻合，说明本文算法的船舶运动系统耦合方程求解效果较优，即船舶运动系统解耦合精度较高。随着波浪激励力幅值的提升，纵摇运动幅值存在较小的变化趋势，说明波浪激励力幅值对纵摇运动幅值的影响较小。当波浪激励力幅值超过5×10⁻⁴时，横摇运动幅值的增长幅度较大，说明波浪激励力幅值对纵摇运动幅值的影响较大。

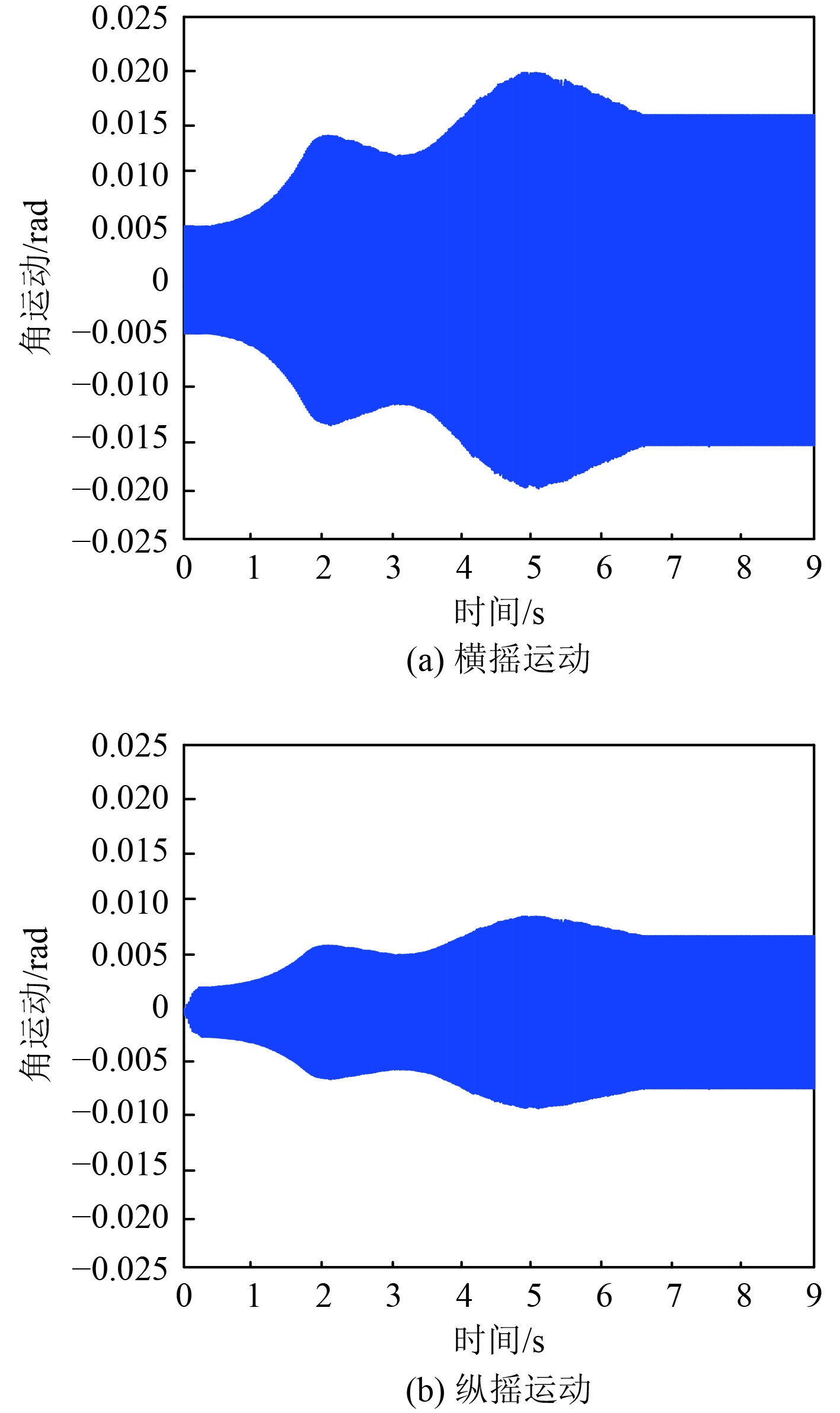
利用本文算法进行船舶运动系统解耦合，得到该船舶的横、纵摇运动时历，如图4所示。如图可知，利用本文算法进行船舶运动系统解耦合后，可获取该船舶的横、纵摇运动时历，通过分析船舶的横、纵摇运动时历可知，该船舶的横摇角主要在±0.02 rad之间波动，纵摇角主要在±0.01 rad之间波动，说明该船舶在航行过程中，其横摇和纵摇运动均保持相对较小的幅度，显示出船舶运动状态的稳定性较优。

3 结　语

本文将智能优化算法应用于船舶运动系统解耦合过程，通过构建船舶运动系统解耦合的目标函数及约束条件，利用智能优化算法对船舶运动系统进行迭代优化，完成解耦合。实验结果表明，利用本文算法进行船舶运动系统解耦合后，所获取的船舶横摇和纵摇运动时历曲线显示出良好的稳定性，横摇角主要在±0.02 rad之间波动，纵摇角主要在±0.01 rad之间波动。