0 引　言

在船舶运行过程中，推进轴系不仅要承受来自主机的静态和动态扭矩，还要面对复杂多变的海洋环境载荷^[1]。这些载荷的综合作用，往往导致推进轴系产生复杂的瞬态扭转振动响应。瞬态扭转振动是推进轴系在短时间内受到突变载荷或激励时产生的振动现象，其特点是振动频率高、持续时间短，但可能对轴系的强度和耐久性造成严重影响^[2]。若未能有效控制和预测这类振动，可能导致轴系部件的疲劳损伤、联接处的松动甚至断裂，进而引发船舶动力系统的失效，严重威胁船舶的安全航行。

周慧慧等^[3]利用有限激励数据，构建涵盖所有不确定性的非概率凸模型，进行轴系振动位移边界估计。但在处理高度非线性或复杂系统时，非概率凸模型无法准确捕捉系统的所有振动特性。古铮等^[4]通过构建动力学分析模型，探究轴段空心度对轴系扭转振动的影响。但是该方法主要关注轴段空心度对扭转振动的影响，对于其他类型的振动（如横向振动、纵向振动等）无法提供全面的分析。巫頔等^[5]将轴系梁段的物理量与时间关联起来，建立描述其振动行为的数学模型，捕捉轴系振动特性。但是该方法无法直接应用于具有复杂几何形状或材料特性的轴系。安宇晨等^[6]通过构建轴系的动力学模型，考虑不同支撑刚度条件下轴系的振动情况。该研究侧重于探讨支撑刚度如何影响轴系的振动特性，但对于其他类型的激励因素或参数变动，其分析范围则不够全面。

有限元法擅长应对各类复杂的几何形态、材料属性以及多物理场相互作用问题，能够提供更为详尽全面的分析结果。因此，采用有限元分析方法来研究船舶推进轴系的瞬态扭转振动响应，对于确保船舶的安全航行至关重要。

1 船舶推进轴系瞬态扭转振动响应分析 1.1 船舶推进轴系介绍

以某船舶推进轴系为研究对象，该推进轴系的长度为35.4 m，其基本信息如表1所示。

利用ADINA有限元软件，构建船舶推进轴系的有限元模型，旨在分析该轴系在船舶推进过程中的瞬态扭转振动响应。

1.2 船舶推进轴系有限元模型构建

在船舶推进轴系有限元模型构建过程中，网格划分需依据轴系组件的形状及计算精度要求，精心选择合适的单元类型，并对轴系模型实施细致的网格划分，通过优化网格的大小与密度，旨在精准捕捉关键振动特性的同时，维持高效的计算能力。此外，确保准确输入各组件的材料属性，涵盖密度、弹性模量、泊松比等关键参数，这些对振动响应具有显著影响。在施加约束与载荷时，需严格依据实际情况与设计规范，特别注意载荷的分布与大小，以全面模拟实际运行中的各种工况。最后，在利用Newmark-β法求解船舶推进轴系的时域瞬态扭转振动响应时，应合理设定求解参数，包括时间步长、精度及稳定性调整参数，以保障求解过程的稳定与结果的精确。

令船舶推进轴系上某个复杂部件的局部坐标是$ \left( {x,y,z} \right) $，对应的全局空间坐标为：

$ {\left[ \begin{array}{*{20}{c}} X \\ Y \\ Z \\ \end{array} \right] = \left[ \begin{array}{*{20}{c}} \cos \alpha & - \sin \alpha & 0 \\ \sin \alpha &\cos \alpha &0 \\ 0& 0& 1 \\ \end{array} \right]\left[ \begin{array}{*{20}{c}} x\cos \theta - y\sin \theta \\ x\sin \theta + y\cos \theta \\ z + {t_z} \\ \end{array} \right] + \left[ \begin{array}{*{20}{c}} {X_0} \\ {Y_0} \\ {Z_0} \\ \end{array} \right]。}$

(1)

式中：$ \alpha $为绕全局X轴的旋转角；$ \theta $为绕局部Y轴的旋转角；$ {t_z} $为沿全局Z轴的偏移量；$ \left( {{X_0},{Y_0},{Z_0}} \right) $为原始坐标。

船舶推进轴系的有限元模型建模步骤如下：

步骤1　定义船舶推进轴系模型参变量。确定轴系的主要尺寸，如轴径、长度、轴承间距等^[7]。

步骤2　收集并导入轴系组件几何数据。获取轴、轴承、联轴器、螺旋桨等轴系组件的几何数据文件，将这些几何数据导入到有限元分析软件中。

步骤3　生成船舶推进轴系组件的几何模型。在有限元分析软件中，根据导入的几何数据，生成轴系各组件的几何模型^[8]。

步骤4　计算轴系组件的空间坐标。对于轴系中的每个组件，计算其关键点的空间坐标，这些坐标数据将作为后续进行网格划分以及有限元分析的基础。

步骤5　组装轴系模型。在有限元软件中，各组件按照空间坐标计算结果进行组装，形成完整的船舶推进轴系模型。

步骤6　网格划分与单元类型选择。根据轴系组件的形状和计算精度要求，选择合适的单元类型（如壳单元、体单元等）。对轴系模型进行网格划分，确保网格质量满足分析要求。

步骤7　施加约束与载荷。根据实际情况和设计要求，在轴系模型上施加正确的约束条件。

步骤8　设置求解参数与运行求解。在有限元软件中设利用Newmark-β法，求解船舶推进轴系的时域瞬态扭转振动响应。

步骤9　提取与分析结果。从有限元软件中提取瞬态扭转振动响应分析结果。

步骤10　构建船舶推进轴系的有限元模型，并进行瞬态扭转振动响应的详细分析。

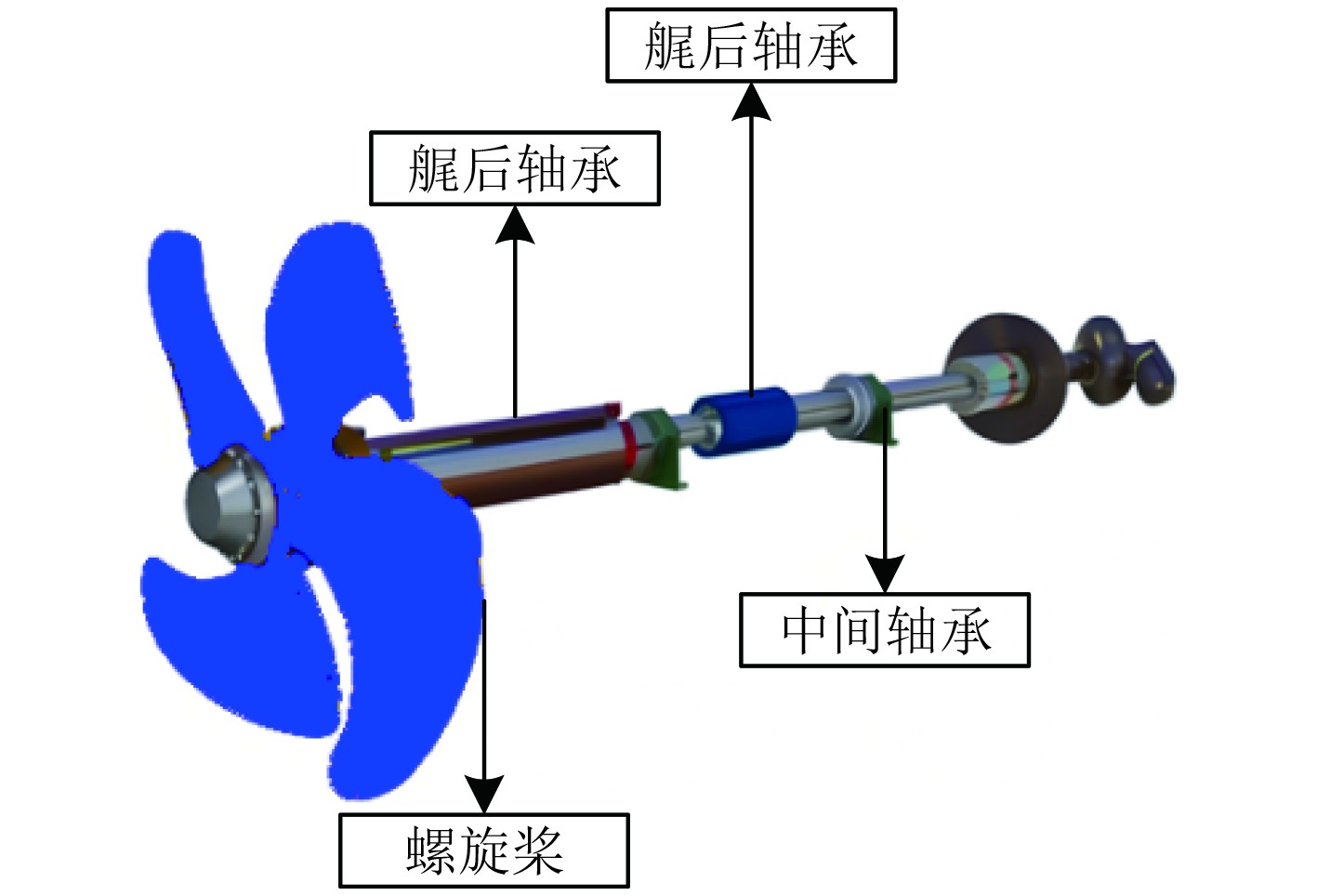
船舶推进轴系的有限元模型如图1所示。

1.3 推进轴系瞬态扭转振动响应有限元分析

在有限元软件中设利用Newmark-β法，求解船舶推进轴系的时域瞬态扭转振动响应。令船舶推进轴系部件的质点角位移、角速度、角速度矢量分别为$ \varphi $、$ \dot \varphi $、$ \ddot \varphi $；在$ \left[ {t,t + \Delta t} \right] $时间内，$ {\varphi _{t + \Delta t}} $与$ {\dot \varphi _{t + \Delta t}} $的计算公式如下：

$ \left\{\begin{aligned} &{\varphi _{t + \Delta t}} = {\varphi _t} + {{\dot \varphi }_t}\Delta t + \left[ {\left( {\frac{1}{2} - \beta } \right){{\ddot \varphi }_t} + \beta {{\ddot \varphi }_{t + \Delta t}}} \right]\Delta {t^2} ，\\ &{{\dot \varphi }_{t + \Delta t}} = {{\dot \varphi }_t} + \left[ {\left( {1 - \lambda } \right){{\ddot \varphi }_t} + \lambda {{\ddot \varphi }_{t + \Delta t}}} \right]\Delta t 。\\ \end{aligned}\right.$

(2)

式中：$ \lambda $为精度调整参数；$ \beta $为稳定性调整参数；$ \Delta t $为变化时间。

Newmark-β法需符合$ t + \Delta t $时刻的动力方程需求，公式如下：

$ \boldsymbol{M}\ddot{\varphi}_{t+\Delta t}+\boldsymbol{A}\dot{\varphi}_{t+\Delta t}+\boldsymbol{G}\varphi_{t+\Delta t}={\boldsymbol{H}_{\boldsymbol t+\Delta {\boldsymbol t}}}。$

(3)

式中：$ \boldsymbol{M} $为船舶推进轴系各质量部分在旋转或平移运动中惯性特性的矩阵；$ \boldsymbol{A} $为阻碍运动能量耗散矩阵；$ \boldsymbol{G} $为受到扭转力作用时抵抗变形能力的矩阵；$ \boldsymbol{H}_{\boldsymbol{t}+\Delta\boldsymbol{t}} $为质点激励力矩矢量。

依据式(2)可得：

$ \left\{\begin{aligned} &{{\ddot \varphi }_{t + \Delta t}} = \frac{{{\varphi _{t + \Delta t}} - {\varphi _t}}}{{\beta \Delta {t^2}}} - \frac{{{{\dot \varphi }_t}}}{{\beta \Delta t}} - \left( {\frac{1}{{2\beta }} - 1} \right)\Delta t{{\ddot \varphi }_t} ，\\ &{{\dot \varphi }_{t + \Delta t}} = \frac{{\lambda \left( {{\varphi _{t + \Delta t}} - {\varphi _t}} \right)}}{{\beta \Delta t}} + \left( {1 + \frac{\lambda }{\beta }} \right){{\dot \varphi }_t} + \left( {1 - \frac{\lambda }{{2\beta }}} \right)\Delta t{{\ddot \varphi }_t} 。\\ \end{aligned} \right.$

(4)

将式(3)代入到式(4)，获取$ {\varphi _{t + \Delta t}} $的计算公式：

$ {\varphi _{t + \Delta t}} = \frac{{{{\hat H}_{t + \Delta t}}}}{{\hat G}}。$

(5)

其中：$ \hat G = G + \displaystyle\dfrac{\lambda }{{\beta \Delta t}}A + \dfrac{M}{{\beta \Delta {t^2}}} $；$ \hat{H}_{t+\Delta t}= H_{t+\Delta t}+ M\left[\dfrac{\varphi_t}{\beta\Delta t^2}+ \dfrac{\dot{\varphi}_t}{\beta\Delta t}+\left(\dfrac{1}{2\beta}-1\right)\ddot{\varphi}_t\right]+A\left[\dfrac{\lambda\varphi_t}{\beta\Delta t}+\left(\dfrac{\lambda}{\beta}-1\right)\dot{\varphi}_t+\left(\dfrac{\lambda}{2\beta}-1\right)\Delta t\ddot{\varphi}_t\right] $。

求解式(5)可得船舶推进轴系的角位移，求解式(4)可得船舶推进轴系的角速度与角加速度，这些数据将用于分析瞬态扭转振动响应。

1.4 推进轴系瞬态扭转振动响应分析的计算工况

明确了轴系在不同工况下的转速，具体设定低速、中速和高速3种转速条件，旨在模拟船舶在实际运行中的各种航行状态和负载情况。界定轴系的固定端和自由端位置，并考虑可能存在的支撑结构。在载荷施加方面，考虑均匀分布的力载荷，并引入了非均匀分布的载荷，如集中力和变化力，使得模拟更加贴近实际复杂的受力情况。计算工况如表2所示。

可知，工况1与工况2的主要区别在与受力区域的大小和转速条件，工况1针对较小的受力区域且处于低速状态，而工况2则覆盖较大的受力区域并设定为中速，更贴近实际航行中的受力情况。工况3在均匀分布力载荷的基础上增加了集中力载荷，模拟螺旋桨运行中可能遭遇的不均匀受力，并结合高速条件显著增强了轴系的扭转振动响应，有助于深入评估轴系的动态性能。工况4则综合考虑了动态变化载荷和非均匀分布载荷，同时转速从低速渐变至高速，旨在模拟船舶加速或变航向时的复杂受力情况。

2 试验分析

利用本文方法分析船舶推进轴系瞬态扭转应力，以船舶推进轴系螺旋桨的其中一个桨叶为例。分析结果如图2所示。

可知，对比工况1与工况3时，发现螺旋桨桨叶的扭转应力分布特点非常相似，最大应力点均聚焦于桨叶与浆毂的交界区域。工况1条件下，该区域的扭转应力峰值约为100 MPa，工况3条件下，扭转应力峰值约为200 MPa，凸显工况变化对桨叶扭转应力水平的直接影响。在工况2和工况4的条件下，桨叶扭转应力分布呈现出相似的模式，具体表现为最大应力转而集中于叶切面的随边周围区域。在工况2条件下，该区域的应力峰值约为150 MPa，工况4的应力峰值约为200 MPa，再次证明工况条件在决定桨叶应力分布及其大小中的关键作用。试验证明：船舶在不同工况下运行时，其推进轴系螺旋桨桨叶的扭转应力分布特征不仅存在差异，而且呈现出一定的规律性。这一发现对于船舶设计的精细化、推进性能的优化以及航行安全的保障具有深远的指导意义。通过深入理解这些应力分布规律，设计师和工程师可以更加科学地预测和调整桨叶的应力状态，确保船舶在各种工况下都能保持最佳性能和最高安全性。

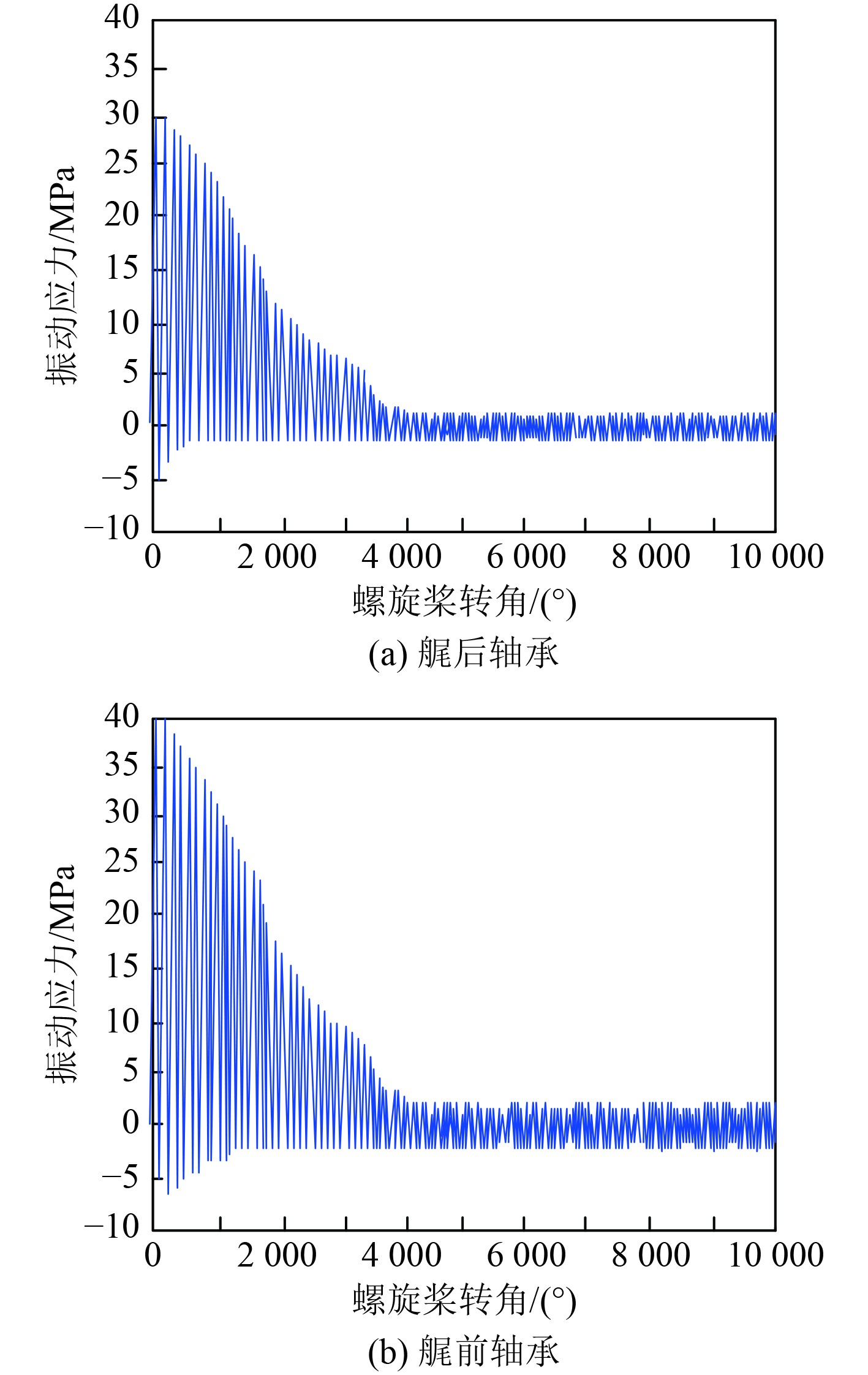
在工况2条件下，利用本文方法分析该船舶推进轴系的时域瞬态扭转振动应力，以船舶推进轴系的艉后轴承与艉前轴承为例，分析结果如图3所示。

可知，随着螺旋桨转角的逐渐增大，艉后轴承与艉前轴承所承受的瞬态扭转振动应力均呈现出一个明显的下降趋势，并最终趋于平稳状态。当螺旋桨转角处于较低的2000°以下时，2个轴承所承受的瞬态扭转振动应力均相对较高。在此阶段，尾前轴承所承受的最大瞬态扭转振动应力略高于艉后轴承，前者约为40 MPa左右，后者则约为30 MPa左右。当螺旋桨转角增加至4000°时，尾后轴承与艉前轴承的瞬态扭转振动应力均显著下降并趋于稳定。此时，尾前轴承的瞬态扭转振动应力稳定在±2 MPa的范围内，而尾后轴承的瞬态扭转振动应力则稳定保持在±1 MPa的范围内。试验结果表明：螺旋桨转角对船舶推进轴系中关键轴承的瞬态扭转振动应力具有显著影响，增大螺旋桨转角，可有效降低船舶推进轴系尾后轴承与尾前轴承的瞬态扭转振动应力，从而提升船舶推进轴系的稳定性和可靠性。这一发现为船舶设计师和工程师提供了宝贵的指导，能够更加精确地预测和优化轴承的受力状况。

在工况2的条件下，利用本文方法分析船舶推进轴系在共振转速与最大持续转速下的瞬态扭转振动响应。通过分析角位移与角速度的变化，呈现瞬态扭转振动响应的演变情况，以船舶推进轴系的中间轴承为例，分析结果如图4所示。

分析图4(a)可知，在共振转速条件下，船舶推进轴系中间轴承的角位移振幅波形呈现出较大的波动幅度，最大振幅接近8×10⁻² rad左右。这些显著的波动与中间轴承的共振现象相对应，表明中间轴承经历了较为严重的扭转变形，其工作状态并不稳定。

分析图4(b)可知，在最大持续转速下，角位移波形相对平稳，最大振幅减少至约3×10⁻² rad。与共振转速下的情况相比，波动幅度有了显著下降，表明在最大持续转速下，船舶推进轴系的中间轴承运转更为平稳，未出现明显共振现象，其工作状态得到显著的改善。

分析图4(c)可知，在共振转速振动的影响下，船舶推进轴系中间轴承的角速度曲线随角位移的波动而发生变化，最终稳定在±1 rad/s左右，这一相对较大的数值反映了中间轴承在振动过程中旋转速度的不稳定性，可能会对轴系的整体性能和寿命产生不利影响。

分析图4(d)可知，在最大持续转速下，角速度曲线的波动幅度较小，最终稳定在±0.2 rad/s左右。这表明在最大持续转速下，船舶推进轴系的中间轴承角速度更加稳定，没有出现明显的突变或大幅波动，这一特性体现了船舶推进轴系在稳定工况下中间轴承旋转速度的稳定性，为轴系的长期稳定运行提供有力保障。

3 结　语

1）桨叶扭转应力分布特性

工况变化对桨叶扭转应力水平有直接影响，工况条件的改变会导致应力峰值出现变化。

2）轴承瞬态扭转振动应力响应

在螺旋桨转角较低时，轴承所承受的瞬态扭转振动应力相对较高，且艉前轴承的应力略高于艉后轴承。提升螺旋桨转角可以降低轴承的瞬态扭转振动应力，提高船舶推进轴系的稳定性和可靠性。

3）共振转速与最大持续转速下的振动响应

共振转速下，中间轴承的角速度曲线波动较大，反映出旋转速度的不稳定性；在最大持续转速下，角速度曲线波动幅度较小，更加稳定。