0 引　言

流水孔结构在水下航行体表面广泛存在，水流在开孔附近的复杂流动将增大壳体表面的脉动载荷，进而增大结构主体的振动噪声水平。流水孔开孔尺寸远小于结构表面曲率，可将水下航行体表面开孔简化为平板开孔模型。平板开孔模型具有结构简单、适用性强等特点，通过分析开孔平板的流激振声特性，确定水动力噪声主导分量，进而为船舶及水下航行体表面开孔后的流激振声研究提供重要支撑，因此开展开孔平板水动力噪声特性研究具有重要意义。

国内外许多学者对开孔平板表面流动及振动噪声特性开展系列研究。Rockwell^{[1 − 3]}系统性地梳理了剪切层和孔腔发声的问题及特点，并将流激孔腔振动噪声成因归纳为3大类。李荣华等^[4]针对局部开孔的深腔体流噪声现象进行机理研究，明确开孔后侧的压力脉动现象是孔腔发声的主要原因。张楠等^{[5 − 7]}结合大涡模拟和FW-H声类比等理论，对方形及格栅型孔穴开展流激振声特性试验及仿真分析工作，初步形成了流激孔穴数值预报方法。袁国清^[8]分析了不同开孔特征、不同分布方式的开孔平板流激振声特性，发现结构湿模态和流体激励力特性对流激噪声有直接影响。陈钊^[9]探究了正方形开孔的腔壁结构特性对流激噪声的影响，为水下开口低噪声优化设计提供支撑。徐俊等^[10]基于多步骤混合方法分析了开孔平板周围的涡流场及声场分布，确定了不同区域对总噪声的贡献量和影响声辐射水平的主要声源。耿冬寒等^[11]分析某特定长深比的孔穴水动力噪声辐射特性，结果表明沿来流上游方向的声辐射能量较高。胡昊明等^[12]分析了带格栅开孔平板的流噪声及结构响应情况，同时探究格栅间距和来流角度等变量对孔腔结构噪声及振动响应的影响。

通过对开孔平板流激振动噪声特性研究现状的初步总结，可以看出基于试验和数值模拟手段形成了丰富的成果，但仍存在不足。现有研究多集中在小数目的矩形和圆形开孔，针对纵缝式开孔平板水动力噪声特性的研究较少。另外，纵缝式开孔平板水动力噪声成分占比仍不明确，无法为纵缝式开孔结构的水动力噪声控制指明可靠方向。因此，针对纵缝式开孔平板水动力噪声特性及主导分量研究不足的现状，本文基于数值模拟方法，探究了纵缝式开孔平板流激振声特性规律并明确水动力噪声主导分量，为水下航行体等复杂结构开孔后的水动力噪声研究提供参考及支撑。

1 数值模拟方法及理论 1.1 大涡模拟理论

大涡模拟方法是流场特性模拟过程采用的常用手段之一，其基本思想是用瞬时N-S方程模拟湍流中的大尺度旋涡，同时引入近似模型来反映小涡对大涡的影响。定义流场中所有尺度涡的集合为$\phi \left( {x,t} \right)$，流场中的小尺度涡量为$\phi '\left( {x,t} \right)$，大尺度涡量为$\bar \phi \left( {x,t} \right)$，3个量可通过滤波函数相互转化，关系式如下：

$ \phi \left( {x,t} \right) = \bar \phi \left( {x,t} \right) + \phi '\left( {x,t} \right)，$

(1)

$ \bar \phi \left( {x,t} \right) = \int_D {\bar G\left( {x,x',\Delta } \right)} \phi \left( {x',t} \right){\text{d}}x'。$

(2)

式中：$\bar G\left( {x,x',\Delta } \right)$为滤波函数；$x'$为滤波之前的向量；$x$为滤波后的向量；$\Delta $为滤波带宽；D为流场计算域。

滤波后的N-S方程可写为：

$ \frac{{\partial \left( {\rho \overline {{u_i}} } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {\tau _{ij}} + \rho \overline {\overline {{u_i}} \overline {{u_j}} } } \right)}}{{\partial {x_j}}} = - \frac{{\partial \overline p }}{{\partial {x_i}}} + \mu \frac{{{\partial ^2}\overline {{u_i}} }}{{{\partial ^2}{x_j}}}。$

(3)

式中：${u_i}$、${u_j}$分别为速度矢量在不同方向上的分量；$p$为流场压力；$\rho $为流体密度；${\tau _{ij}}$为亚格子雷诺应力；$\mu $为流体动力黏性系数。

1.2 广义FW-H方程

针对流体介质中运动表面的声辐射求解，Frances Antonio在传统FW-H方程基础上，结合基尔霍夫方程，推导出了适用范围更广的K-FWH方程，也称广义FW-H方程，具体形式如下^[13]：

$ \begin{split}{l} \displaystyle\frac{1}{{c_0^2}}\displaystyle\frac{{{\partial ^2}p'}}{{\partial {t^2}}} - {\nabla ^2}p' =& \displaystyle\frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}\left[ {{T_{ij}}H\left( f \right)} \right] - \\ &\displaystyle\frac{\partial }{{\partial {x_i}}}\left\{ {\left[ {{P_{ij}}{n_j} + \rho {u_i}\left( {{u_n} - {v_n}} \right)} \right]\delta \left( f \right)} \right\} + \\ &\displaystyle\frac{\partial }{{\partial t}}\left\{ {\left[ {{\rho _0}{v_n} + \rho \left( {{u_n} - {v_n}} \right)} \right]\delta \left( f \right)} \right\}。\end{split}$

(4)

式中：${u_i}$和${u_n}$分别为$i$方向和$n$方向的流体速度分量；${v_i}$和${v_n}$分别为物体在$i$方向和$n$方向的速度分量；$H\left( f \right)$为Heaviside阶跃函数；$\delta \left( f \right)$为Dirac delta函数；$p'$为远场声压；${c_0}$为远场声速；${\rho _0}$为远场密度；${T_{ij}}$为Lighthill应力张量。

广义FW-H方程兼具基尔霍夫积分和FW-H方程的优点，随着计算机技术的高速发展，现阶段绝大部分CFD计算分析软件均能基于该方程开展流体流动噪声的计算。

1.3 流激振动噪声求解理论

由于开孔平板是弹性结构，当流体流经开孔平板表面时，平板的振动方程可写为如下形式^[14]：

$ \boldsymbol{M}^{s\ }\vec{\ddot{\delta}}+K^{s\ }\vec{\delta}=F^m+F^p。$

(5)

式中：$ \boldsymbol{M}^S $和$ \boldsymbol{K}^S $为结构的质量矩阵和刚度矩阵；$ \vec{\delta} $为结构的位移向量；$ F^m $和$ F^p $分别为机械激励和流体激励对结构作用的等效节点载荷。

考虑流体对结构的影响，引入附连水质量${M^w}$，平板振动方程可写成：

$ \left(\boldsymbol{M}^s+\boldsymbol{M}^w\right)\ \vec{\ddot{\delta}}+K^s\ \vec{\delta}=F^m+F^p 。$

(6)

根据该方程可求解出结构在水中的湿模态，开孔平板的流激振动较为复杂，因此可基于模态叠加法求解结构振动。考虑流体的影响，结构振动可看作不同阶次的湿模态相互叠加，公式表示如下：

$ \delta(t)=\boldsymbol{\phi}\ y=\sum\limits_{i=1}^n\phi_iy_i。$

(7)

式中：$\delta \left( t \right)$为位移向量；$ \boldsymbol{\phi} $为主模态形状矩阵；$ y $为模态向量坐标；$ {\phi _i} $和$ {y_i} $为第i阶模态振型及其模态坐标。

通过求解结构振动与声场间的声振耦合问题，可获得平板在湍流脉动力激励下的流激噪声。结构表面的振动速度是声场边界上的速度输入，声学方程表示为^[15]：

$ \left(\boldsymbol{K}_a+j\omega\boldsymbol{C}_a-\omega^2\boldsymbol{M}_a\right)\cdot\boldsymbol{p}_i-\omega^2\boldsymbol{M}_c\boldsymbol{u}_i=\boldsymbol{F}_{ai} 。$

(8)

式中：$ {{\boldsymbol{K}}_a} $、$ {{\boldsymbol{C}}_a} $和$ {{\boldsymbol{M}}_a} $分别为流体介质的等效刚度阵、等效阻尼阵和等效质量阵；$ {{\boldsymbol{p}}_i} $为待求解的声压；$\omega $为圆频率；$ {{\boldsymbol{M}}_c} $为耦合质量阵；$ {{\boldsymbol{u}}_i} $为结构节点位移；$ {{\boldsymbol{F}}_{ai}} $为声场激励。

求解上述声学方程，即可求得结构在流体载荷作用下的流激噪声。

2 方法有效性验证 2.1 流动噪声模拟有效性验证

法国学者Lafon在风洞中对倒T形孔穴进行流动噪声测试，所取得的测试结果受到同行的广泛认可，具有较高的参考价值。为验证本文流动噪声数值模拟方法的有效性，开展倒T形孔穴中心位置处的流动噪声仿真工作。测试场景示意图如图1所示，试验详细参数见文献[16]。

数值模拟参数设置同试验测试场景保持一致，空气中声速设置为343 m/s。流场整体长0.473 m，目标网格尺寸为1 cm，面网格增长率为1.2，流场网格近壁厚度为0.005 mm。对重点关注区域进行网格加密，形成体网格约为277万个，如图2所示。

数值模拟过程采用大涡模拟（LES）和FW-H方程，大涡模拟时间步长为$1.5 \times {10^{ - 4}}$ s，使得计算结果分析频率上限达到3300 Hz，同时选取FW-H声学计算模型对考核点声压进行计算。试验测试声压曲线及本文仿真结果曲线如图3所示。

可知，本文数值仿真结果曲线同测试曲线的整体趋势及峰值频率基本保持一致。试验测试与数值仿真峰值频率及特征峰值的对比如表1所示。数值模拟所得峰值频率结果的相对误差最大为6.1%，峰值大小的差值不超过2.5 dB。考虑到数值方法与仿真结果之间不可避免的差异，本文采用的流动噪声模拟手段可靠性高，能够应用至开孔平板流噪声研究中。

3 典型纵缝式开孔平板流激振声特性研究 3.1 计算模型及研究思路

本节以纵缝式开孔矩形钢板为研究对象，探究四周刚性固定的开孔平板在3 m/s流速下的水动力噪声特性。钢板长为1 m，宽为0.25 m，板厚为4 mm，钢板中心位置处有0.35 m×0.035 m的纵缝式开孔。开孔内侧设置若干个支骨以保证开孔部位的强度，支骨宽度为0.01 m，厚度与板厚相同，支骨布置间隔为0.05 m，开孔矩形钢板尺寸信息如图4所示。

纵缝式开孔平板水动力噪声特性的分析流程如图5所示，涉及流体、固体和声学的联合仿真分析。首先通过大涡模拟方法模拟平板表面的流体运动，获取测点的脉动压力，并通过FW-H方程求解得出流体的流动噪声。接着进行开孔平板的结构-声学联合仿真分析，基于有限元方法获取结构模态，并利用声固耦合方法得到平板表面的振动响应，通过对声学方程的求解获得平板在脉动载荷作用下的流激噪声。

3.2 表面载荷及流噪声分析

本节探究纵缝式开孔平板表面脉动载荷和流噪声水平，对开孔平板所在流场进行网格划分。以开孔平板为边界，流场主要分为上侧流场和下侧流场两部分，上侧流场主体尺寸为2.5 m×0.25 m×0.25 m，下侧流场尺寸为0.65 m×0.115 m×0.04 m。流场的网格划分策略如下：流场最大网格尺寸为0.04 m，目标网格尺寸为0.02 m；近壁面棱柱层厚度设置为1×10⁻⁵ m，棱柱层数设置为15层。对流场实施局部加密，加密网格尺寸最小为2 mm，流场网格总数约为215万个。为避免流场边界对流域内速度的影响，上侧流场侧面边界条件设置为对称平面，流体的入口和出口分别设置为速度进口和压力出口边界条件，平板及开孔结构表面设置为壁面，流场网格划分及边界条件设定如图6所示。

开孔平板表面脉动压力的求解采用变时间步长分析方法，在3 m/s的来流速度下，进行时间步长为0.001 s的非定常模拟，当计算至2.5 s时，进行时间步长为5×10⁻⁴ s的非定常模拟，计算时间持续至3.5 s。利用FW-H方程获得测点处的流动噪声。上述时间步长能够保证最大分析频率${f_{\max }}$=1000 Hz。在平板开孔的前后及侧面布置7个脉动压力监测点，在平板开孔的正上方0.5 m处布置噪声测点，压力测点和流噪声接收点分布图如图7所示。

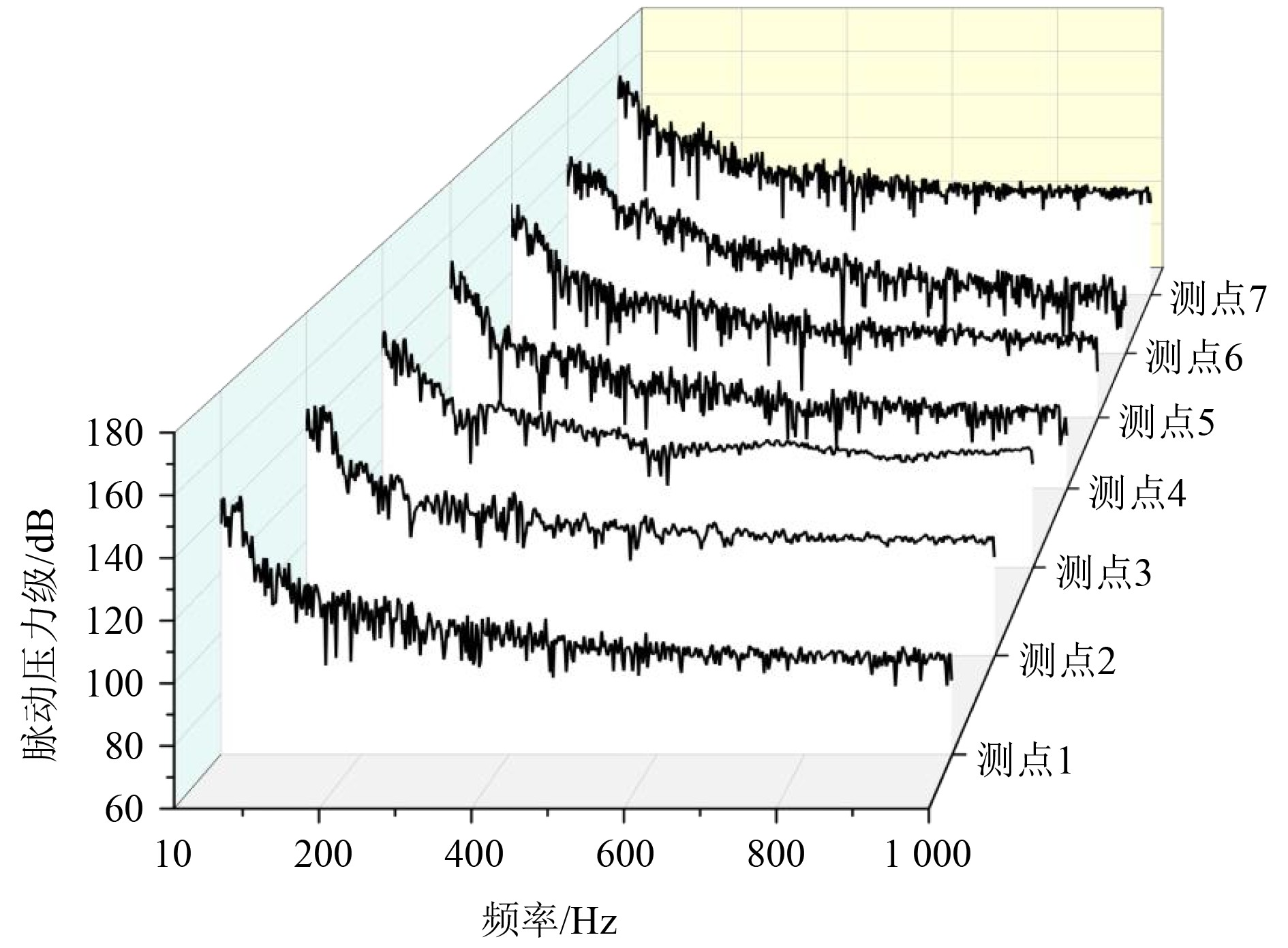
平板表面测点处的脉动压力级对比图如图8所示，可以看出各测点脉动压力水平总体上随着频率的增大而逐渐减小。测点1与测点6的脉动压力水平较为接近，最大脉动压力值约为150 dB；而测点7的脉动压力水平在10～1000 Hz频段内普遍高于其余测点压力5～10 dB，其最大脉动压力值为159.1 dB。这是由于测点7位于孔穴后侧，流体在经过孔穴和梁结构的阻隔后，流体扰动现象明显，导致流体在该位置处有巨大的波动。

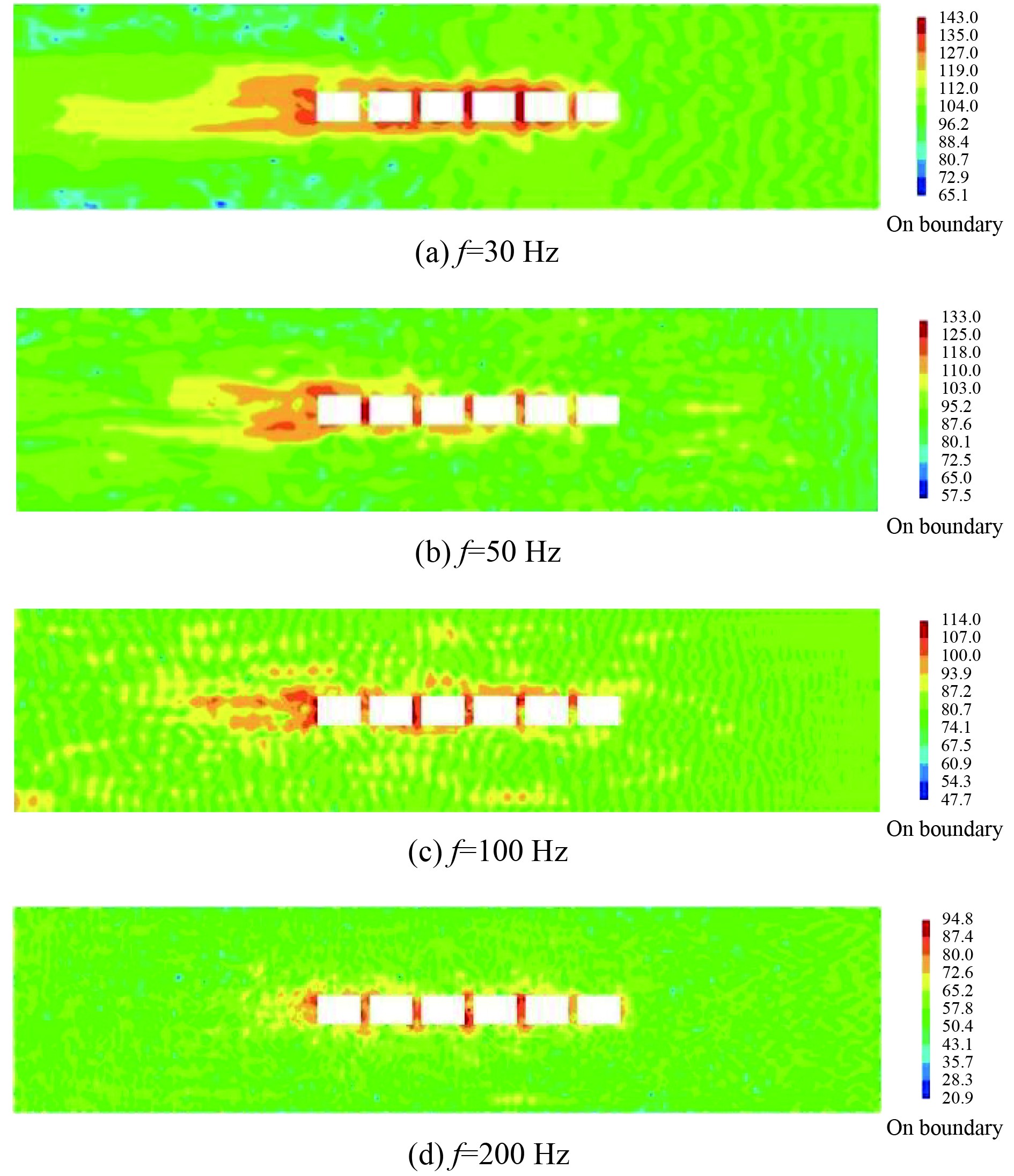
将平板表面脉动压力的时域数据转化为频域数据后，不同特征频率下平板表面脉动载荷分布如图9所示。可以看出，尽管不同频率下平板脉动载荷分布特征存在差异，但仍然能够找到相同点，即开孔后侧和支骨表面载荷水平明显高于其他位置处，这是由于上述位置处的流体在运动过程中因触碰障碍而导致剧烈扰动，进而形成较大的脉动载荷。

基于快速傅里叶变换（FFT）将0.5 m高处测点的流噪声时域数据转换为频域，获得声学测点的流噪声频域曲线图，如图10所示。可以看出，开孔平板在3 m/s流速下的流动噪声曲线整体上随着频率增大而逐渐减小，在18 Hz时流动噪声达到最大值107.3 dB。

3.3 流激振动及噪声特性分析

在求得流体载荷的基础上，从结构仿真和声场模拟入手，探究开孔平板的流激振动及噪声特性规律。首先进行四周刚性固定条件下开孔平板的模态分析，结构网格尺寸为5 mm，满足单元尺寸小于弯曲波长的1/6这一基本原则，网格总数约为1万个。开孔平板的典型振型图如图11所示。可以看出，一阶模态和三阶模态对孔穴周围的振动响应水平贡献较大，应尽量避免。

将平板上各单元节点的流体脉动载荷信息和声场网格依次导入至声学有限元计算软件中，基于模态叠加法分析开孔平板在流激载荷作用下的振动噪声特性。与流噪声和脉动压力分析类似，在开孔平板中心位置正上方0.5 m处设置噪声接收点，在开孔附近布置若干振动测点，测点位置示意图如图12所示。

在3 m/s的来流速度下，基于各测点振动速度求得开孔平板的均方振速级曲线，如图13所示。可知，测点均方振速曲线在10～200 Hz频段内总体上随频率的增大而减小，该现象符合各测点位置处脉动载荷的基本规律。曲线在28 Hz处出现最大值（48 dB），这是由于流体测点在28 Hz处的脉动载荷最大，导致结构在28 Hz振动响应较大；在200 Hz以上频段曲线有明显波动现象，并出现若干个峰值，峰值频率同开孔平板模态特征频率接近，尽管该频段内流体脉动载荷较小，但在开孔平板结构模态影响下，特征频率处（440 Hz）仍产生较大峰值（40.8 dB）。

距离平板中心0.5 m处的声学测点流激噪声曲线如图14所示，参考声压值为10⁻⁶ Pa。可以看出，开孔平板的流激噪声曲线在430 Hz处有明显峰值，流激噪声最大值为63.4 dB。由于开孔平板模态特征频率与流激噪声峰值频率接近，流激噪声曲线峰值的出现很可能与结构的一阶模态有关。

建立声学考核平面，可获得开孔平板的声场分布云图，如图15所示。结合平板开孔模型的流激噪声曲线，选取若干特征频率进行分析，可以看出，不同特征频率下声场分布细节存在差异，但总体上开孔平板的流激噪声声场分布云图呈现对称性特征。在大部分频点处，开孔平板的流激噪声主要集中在平板中孔穴的后侧位置，这是由于孔穴后侧位置漩涡运动剧烈、表面脉动载荷显著引起的，声学计算结果与流体-结构仿真结果保持一致。

3.4 开孔平板水动力噪声主导分量分析

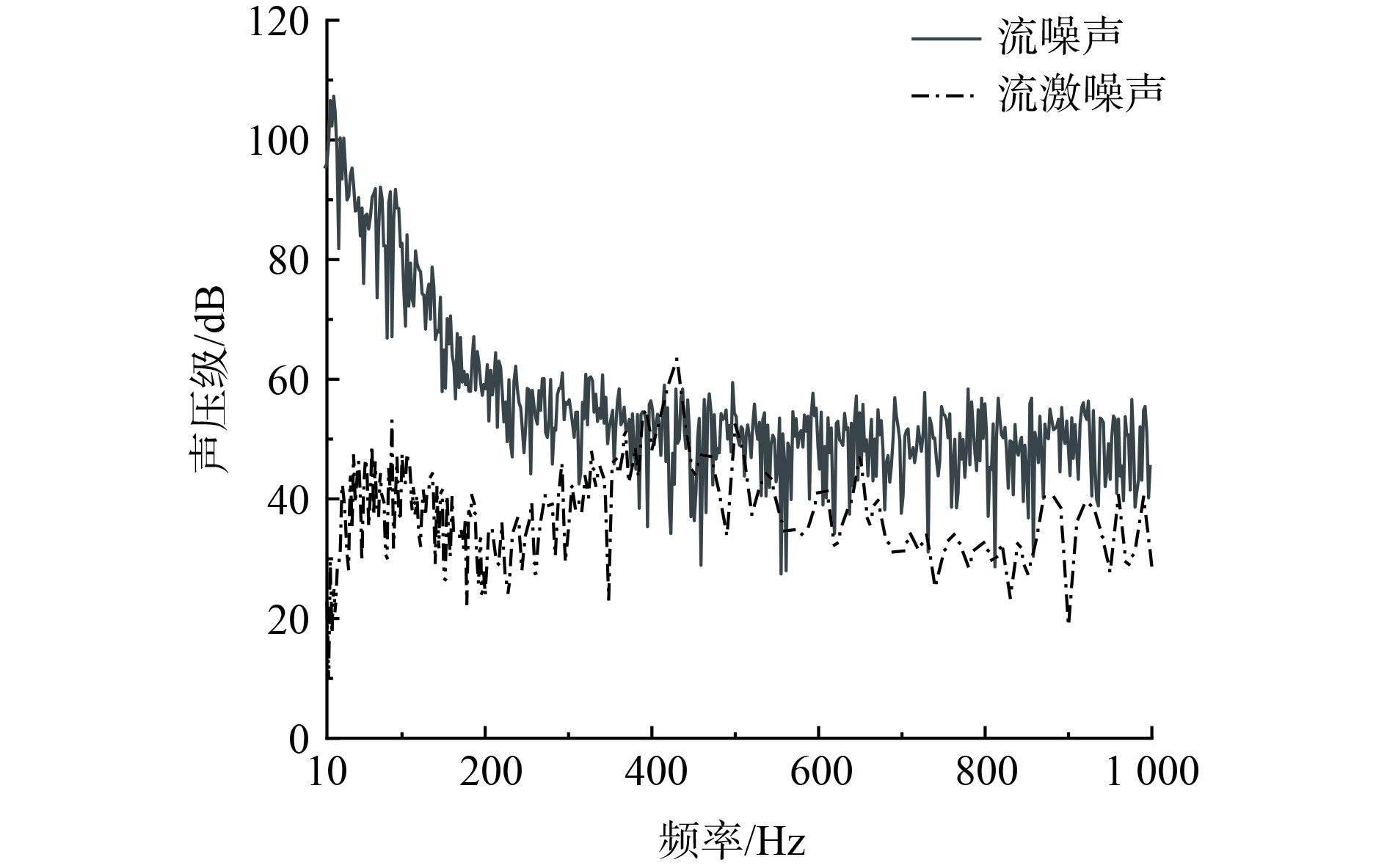
水动力噪声是流体流动噪声和结构流激噪声叠加的总和，通过比较流动噪声和流激噪声的强弱，可以确定水动力噪声的主导分量，为噪声控制指明方向。选取开孔平板正上方0.5 m位置作为噪声考核点，3 m/s流速下开孔平板的流噪声和流激噪声对比图如图16所示。可以看出，在10～300 Hz频段内，开孔平板的流噪声水平远远大于流激噪声，噪声差值普遍在20 dB以上；350～450 Hz频段内开孔平板的流激噪声水平基本与流噪声大小持平；当频率大于450 Hz时，开孔平板的流激噪声普遍小于流噪声，且二者存在较大差距。因此，总体上看，开孔平板的流噪声水平远远大于结构的流激噪声水平，流体的流动噪声占据开孔平板水动力噪声的主要成分。

4 结　语

针对纵缝式开孔平板水动力噪声特性不明确的问题，以典型纵缝式开孔平板为研究对象，利用数值模拟手段获得纵缝式开孔平板在特定流速下的脉动载荷特性及水动力噪声规律，确定其水动力噪声主导分量。具体结论如下：

1）在3 m/s航速下，纵缝式开孔平板表面脉动载荷整体上随着频率的增大而逐渐减小，开孔位置后侧的脉动压力水平要高于其余位置5～10 dB，最大脉动压力值为159.1 dB；纵缝式开孔附近的振动测点均方振速在28 Hz时最大，最大值为40.8 dB。

2）距开孔位置0.5 m处的流动噪声曲线整体上随着频率增大而逐渐减小，在18 Hz时流动噪声达到最大值107.3 dB。开孔平板的流激噪声曲线在430 Hz最大，流激噪声最大值为63.4 dB，这是由于该频率与平板模态频率接近造成的。流体的流动噪声是开孔小尺度平板水动力噪声的主要成分。