2. 船舶结构安全全国重点实验室,江苏 无锡 214082
2. National Key Laboratory of Ship Structural Safety, Wuxi 214082, China
水下通信方式主要可分为声、光、电三类,即水声、激光与电磁波通信,目前水声通信是应用范围最广的水下无线通信技术,但随着海洋资源开发与深海探测技术的不断发展,水声通信的短板如传播延迟长、信号衰减大、多径效应严重、通信带宽有限等特性带来的设计问题越来越突出。水下激光通信具有传输速率高、信息容量大、抗干扰性强、安全保密度高、隐蔽性好等特点,是未来水下通信技术的发展和应用趋势[1 − 4]。水下激光通信系统主要由发射端、接收端两大部分组成,发射端通过编码、调制将电信号转换为光信号,从光窗发出;接收端从光窗接收光信号,并通过解调、解码将光信号转换成电信号。
耐压舱是水下激光通信发射端、接收端的重要部件,可以为舱内编/解码、调/解制相关仪器设备提供常压密封环境。该耐压舱相比于传统的深海耐压结构,除了要具备足够的耐压强度与密封性能外,还涉及光窗结构及其密封设计问题。光窗结构既是耐压结构的一部分,也是发射端、接收端光信号进出的窗口,是耐压舱结构设计的关键。本文以某水下激光通信系统耐压舱为对象,采用理论分析与有限元仿真手段对耐压舱的耐压与密封性能开展研究,重点讨论耐压舱的结构形式及其安全性设计方法,以期为耐压舱的工程设计提供技术依据。
1 耐压舱结构方案根据水下激光通信耐压舱设计目标,光窗数量4只、光窗通光孔径≮Φ30 mm,舱内空间需求≮Φ360 mm×L650 mm。显然,耐压舱是金属-非金属组合式耐压结构,舱体部分为金属结构,光窗部分为非金属结构。
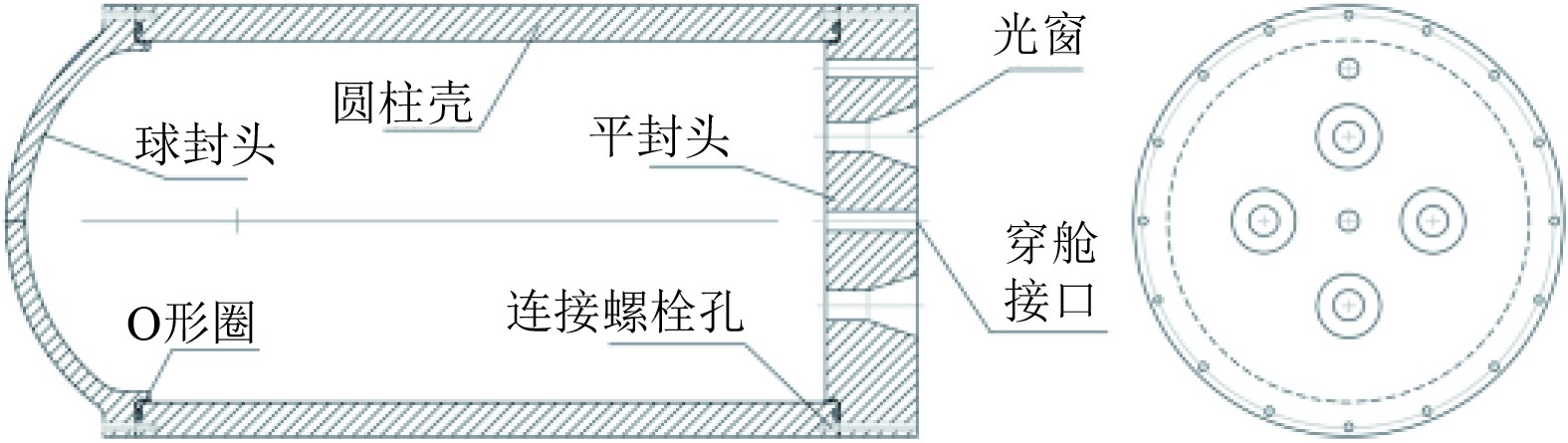
综合考虑耐压结构受力特性和舱内空间布置效率,耐压舱采用圆柱壳体结构,两端分别采用球封头、平封头结构,并通过螺栓和O形圈进行连接密封。耐压舱一端采用平封头,可有效集中布置光窗和穿舱接口,如图1所示。
|
图 1 耐压舱结构形式 Fig. 1 Structural form of pressure chamber |
关于耐压舱结构材料,钛合金密度小、强度高、无磁性,是深海耐压结构的理想材料。通过论证分析,该水下激光通信系统耐压舱金属结构部分材料选用合金TC4ELI,其材料力学性能指标如表1所示。光窗材料选用蓝宝石,其力学性能如表2所示。
|
|
表 1 钛合金TC4ELI的材料力学性能 Tab.1 Mechanical properties of titanium alloy TC4ELI |
|
|
表 2 蓝宝石的材料力学性能 Tab.2 Material mechanical properties of sapphire |
根据该水下激光通信系统耐压舱的设计目标,确定结构设计参数为:计算压力
耐压舱圆柱壳厚度
| $ t\geqslant\frac{K_{\text{2}}^{\text{0}}P_jR_i}{\left[\sigma\right]}。$ | (1) |
式中:
球封头厚度
| $ {t_s} \geqslant \frac{{{{{P}}_{{j}}}{{{R}}_{{s}}}}}{{2\left[ \sigma \right]}}。$ | (2) |
经估算球封头厚度
平封头厚度
| $ t_k\geqslant D_c\sqrt{\frac{kP_j}{\phi R_{eH}}}。$ | (3) |
式中:
| $ \varphi=\frac{D_c-n\mathrm{_1}d\mathrm{_{\text{1}}}-n_{\mathrm{2}}d\mathrm{_{\text{2}}}}{D_c}。$ | (4) |
式中:
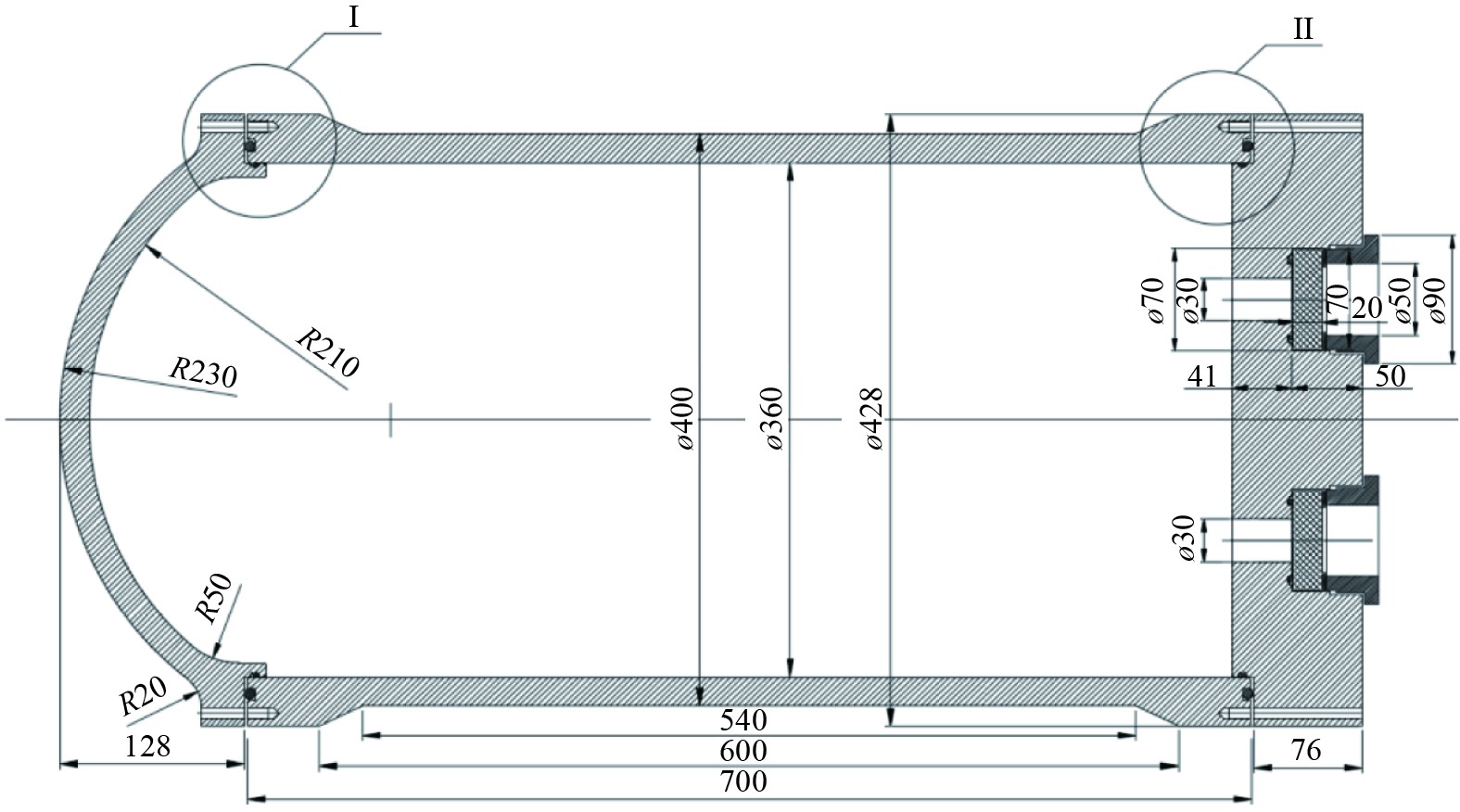
光窗玻璃采用圆平板的结构形式,玻璃与光窗底座之间通过O形圈密封,采用螺母预压紧固定。根据光窗设计目标,经综合考虑光窗结构的强度、刚度和透光性能,光窗孔座的开孔直径为Φ70 mm,蓝宝石玻璃厚度为20 mm。根据耐压舱厚度估算结果,耐压舱具体的结构尺寸方案如图2所示。
|
图 2 耐压舱结构尺寸方案 Fig. 2 Design scheme for pressure chamber |
耐压舱主要由圆柱壳和球壳结构组成,综合借鉴载人潜水器等标准关于圆柱壳和球壳结构的强度与稳定性计算方法,对耐压舱结构进行安全性校核分析。
圆柱壳的中面周向应力
| $ \sigma _2^0{{ = K}}_{\text{2}}^{\text{0}}{{{P}}_{{j}}}\frac{{{{{R}}_{{i}}}{\text{ + 0}}{\text{.5}}t}}{t} \leqslant {\text{0}}{\text{.9}}{{{R}}_{{{eH}}}}。$ | (5) |
圆柱壳的屈曲压力
| $ P_{cr\mathrm{1}}\text{ = }C_{g\mathrm{1}}C_{s\mathrm{1}}P_{e\mathrm{1}}\geqslant P_j。$ | (6) |
式中:
圆柱壳的极限承载能力
| $ P_y^0=\frac{{\text{4}}}{{\sqrt {\text{3}} }}\frac{{\text{1}}}{{{{\overline {{B}} }_{\text{1}}}+{{\overline {{B}} }_{\text{2}}}}}\frac{t}{{{{{R}}_{{i}}} + {\text{0}}{\text{.5}}t}}{{{R}}_{{{eH}}}} \geqslant {{{P}}_{{j}}} 。$ | (7) |
式中:
球壳的中面膜应力
| $ {\sigma _m}{\text{ = }}{{{P}}_{{j}}}\frac{{{{{R}}_{{s}}} + {\text{0}}{\text{.5}}{t_s}}}{{{\text{2}}{t_s}}} \leqslant {\text{0}}{\text{.9}}{{{R}}_{{{eH}}}}。$ | (8) |
球壳的屈曲压力
| $ P_{cr2}\text{ = }C_{g\mathrm{2}}C_{s\mathrm{2}}P_{e\mathrm{2}}\geqslant P_j。$ | (9) |
式中:
球壳的极限承载能力
| $ P_y = \left( 2.391\frac{{R}_{{eH}}t_s}{{R}_{{s}}} - 12.121 \right) \times \left( 1 - 25.472\frac{\Delta}{{R}_{{s}}} \right) \geqslant {P}_{{j}} 。$ | (10) |
式中:
计算结果如表3所示。结果表明,耐压舱的结构强度和承载能力满足参考借鉴的相关控制标准要求。
|
|
表 3 耐压舱结构安全性计算结果 Tab.3 Safety verification calculation results of pressure chamber |
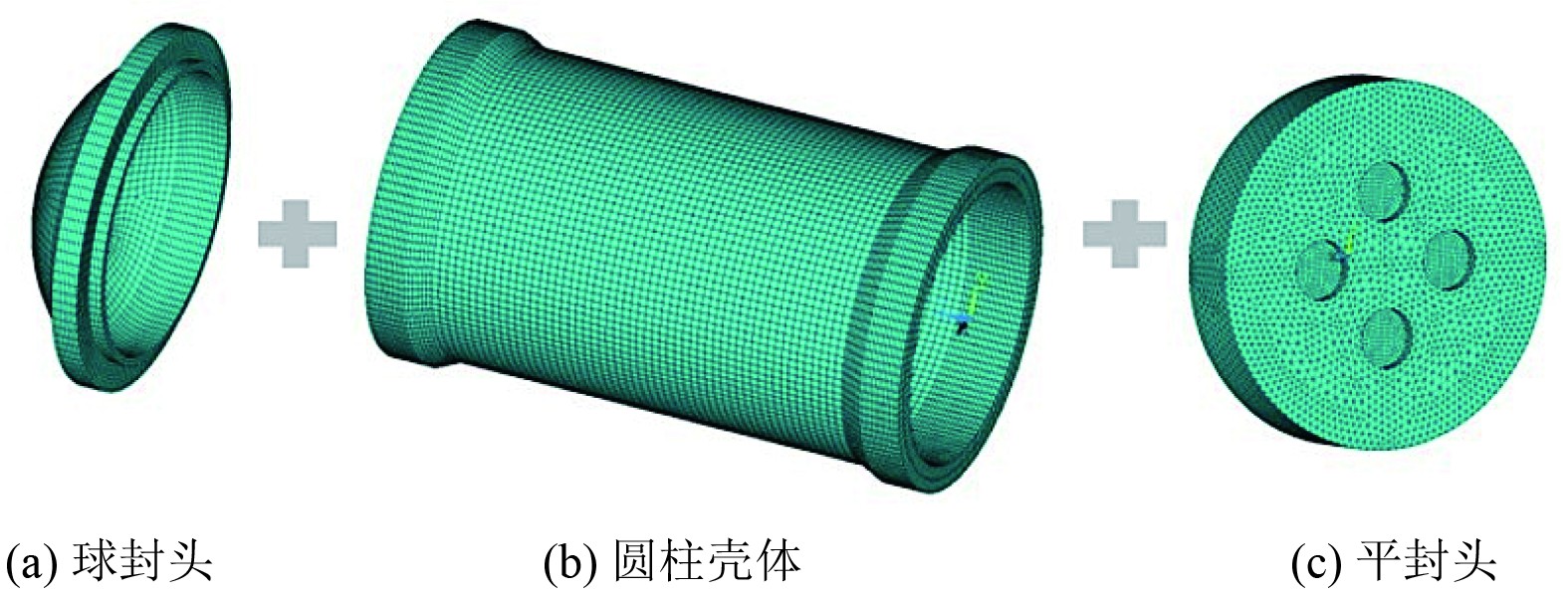
采用通用有限元软件对耐压舱进行仿真计算分析,选用3维20节点固体结构单元SOLID186建立有限元模型,如图3所示。耐压舱有限元模型包括球封头、圆柱壳体、带开孔平封头三部分,计算时球封头与圆柱壳体之间、平封头与圆柱壳体之间的法兰端面设置接触约束,在球封头顶部施加变形约束UZ = 0(约束刚体位移)。
|
图 3 耐压舱有限元模型 Fig. 3 Finite element model of pressure chamber |
在有限元模型外表面施加面载荷60 MPa(模拟外部静水压力)进行仿真计算,根据应力计算结果,提取相关部位的结构应力进行评价分析,如图4所示。

|
图 4 耐压舱结构应力云图 Fig. 4 Stress of pressure chamber |
耐压舱结构应力仿真计算结果如表4所示,耐压舱圆柱壳和球壳典型部位的应力满足相关标准要求。
|
|
表 4 耐压舱结构应力仿真计算结果 Tab.4 Stress simulation calculation results of pressure chamber |
为计及耐压舱结构几何非线性,首先通过屈曲计算,获得耐压舱结构的弹性屈曲压力和屈曲模态,其第一阶屈曲形态如图5所示,对应的弹性失稳压力为137.9 MPa。

|
图 5 耐压舱屈曲模态 Fig. 5 Buckling mode of pressure chamber |
取一阶模态导入初始缺陷,设置初始缺陷幅值为0.1×t = 2 mm,耐压舱材料非线性按Bilinear弹塑性模型,屈服强度设置为740 MPa,利用弧长法进行非线性屈曲分析,计算结果如图6所示。根据计算结果,耐压舱的极限承载能力为62.8 MPa,满足结构承载能力相关标准要求。

|
图 6 耐压舱极限承载能力仿真计算结果 Fig. 6 Simulation calculation results of ultimate bearing capacity of pressure chamber |
耐压舱端部封头与圆柱壳体之间密封结构采用两道O形圈分别进行轴向密封和径向密封,并利用螺栓进行紧固连接,轴向密封圈线径为7 mm,内直径为376 mm,密封凹槽尺寸深为5.4 mm、宽为8.2 mm,径向密封圈线径为为3 mm,内直径为352 mm,密封凹槽尺寸深为3.1 mm、宽为5.2 mm;光窗底座采用一道O形圈、通过螺母压紧光窗玻璃进行密封,密封圈线径为3.55 mm,内直径为50 mm,密封凹槽尺寸深为3.1 mm 、宽为5.2 mm,如图7所示。

|
图 7 耐压舱端部封头密封结构形式 Fig. 7 Sealing structure of pressure chamber |
O形圈的密封性能评价如下:1)O形圈最大等效应力
O形圈材质为丁晴橡胶,有限元仿真计算时采用Mooney-Rivlin超弹模型描述材料本构关系,耐压舱密封性能仿真计算结果云图如图8~图9所示。

|
图 8 耐压舱封头端部密封性能仿真计算应力云图 Fig. 8 Stress of sealing performance at the end of pressure chamber head |
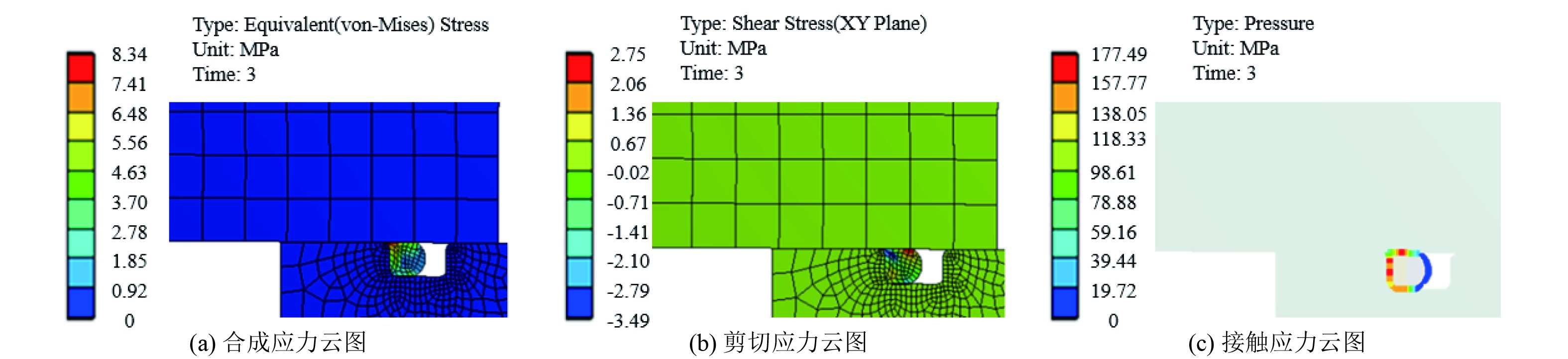
|
图 9 耐压舱光窗密封性能仿真计算应力云图 Fig. 9 Stress of sealing performance of pressure chamber light window |
计算结果表明:
1)耐压舱封头端的O形圈等效应力最大为8.1 MPa,位于密封圈内侧上部与密封槽接触部位,其值小于橡胶的屈服强度(23 MPa);其最大剪应力为−3.6 MPa,位于密封圈内侧上部与密封槽接触部位,其值小于橡胶的抗剪强度(4.6 MPa);密封圈接触压力为172.4 MPa,大于外部静水压力,密封圈不会发生渗漏。
2)光窗底座处的O形密封圈等效应力最大为8.3 MPa,位于密封圈内侧上部与密封槽接触部位,其值小于橡胶的破坏强度;其最大剪应力为−3.5 MPa,位于密封圈内侧上部与密封槽接触部位,其值小于橡胶的抗剪强度;密封圈接触压力为177.5 MPa,大于外部静水压力,密封圈不会发生渗漏。
4 理论与仿真计算结果的比较分析根据前文所述计算结果,耐压舱的结构强度与承载能力计算结果汇总如表5所示。
|
|
表 5 耐压舱结构强度与承载能力计算结果比较 Tab.5 Comparison of calculation results for strength and bearing capacity of pressure chamber |
结果表明:1)关于圆柱壳和球壳结构的理论分析和有限元仿真计算结果基本一致,进一步印证了本文关于耐压舱结构强度与承载能力计算结果的正确性。2)耐压舱结构的承载能力破坏部位发生在圆柱壳部分,且为屈曲失稳破坏,解析计算值为63.9 MPa,有限元仿真计算值为62.8 MPa。3)相对来看,解析计算方法关于耐压舱结构应力的计算结果略偏小、但关于圆柱壳屈曲压力的计算结果略偏大,表明采取的解析计算方法总体而言可能偏危险,工程设计时需要注意这一潜在问题。
5 结 语1)针对水下激光通信耐压舱的结构特点和设计目标,提出了一种钛合金舱体和蓝宝石光窗的耐压结构方案。
2)采用理论分析与有限元仿真方法研究评估耐压舱的结构强度和承载能力,两者计算结果比较一致,且满足结构安全标准要求。
3)基于Mooney-Rivlin超弹模型的密封性能仿真表明耐压舱的密封结构合理可行,满足深海耐压密封性要求。
论文研究结果可以直接为该水下激光通信系统耐压舱的工程设计提供依据,也可为类似耐压结构设计提供技术参考。
| [1] |
曾凤娇, 杨康建, 宴旭, 等. 水下激光通信系统研究进展[J]. 激光与光电子学进展, 2021, 58(3): 1-12. ZENG F J, YANG K J, YAN X, et al. Research progress on underwater laser communication systems[J]. Progress in Laser and Optoelectronics, 2021, 58(3): 1-12. |
| [2] |
刘润芃, 佟首峰, 张鹏. 水下光通信技术研究[J]. 光通信研究, 2023(4): 11-14. LIU R P, TONG S F, ZHANG P. Research on underwater optical communication technology[J]. Study on Optical Communications, 2023(4): 11-14. |
| [3] |
李碧丽, 贺锋涛, 朱云周, 等. 大功率水下激光通信发射系统研究[J]. 自动化与仪器仪表, 2022(2): 30-33. LI B L, HE F T, ZHU Y Z, et al. Research on high power underwater laser communication transmission system[J]. Automation and Instrumentation, 2022(2): 30-33. |
| [4] |
姜艳, 邹雨泽, 朱平杰, 等. 水下无人潜航器无线通信技术研究[J]. 舰船电子工程, 2022, 42(11): 69-73. JIANG Y, ZOU Y Z, ZHU P J, et al. Research on wireless communication technologies for unmanned underwater vehicles[J]. Ship Electronic Engineering, 2022, 42(11): 69-73. DOI:10.3969/j.issn.1672-9730.2022.11.016 |
| [5] |
欧阳吕伟, 叶聪, 李艳青, 等. 全海深潜水器耐压壳体设计计算规则: Q/702 J0203.001-2017[R]. 无锡: 中国船舶科学研究中心, 2017. OUYANG L W, YE C, LI Y Q, et al. Design and calculation rules for pressure hull of all-sea deep submersible: Q/702 J0203.001-2017[R]. Wuxi: CSSRC, 2017. |
| [6] |
吴梵, 朱锡, 梅志远. 船舶结构力学[M]. 北京: 国防工业出版社, 2010.
|
| [7] |
徐秉汉, 朱邦俊, 欧阳吕伟, 等. 现代潜艇结构强度的理论与试验[M]. 北京: 国防工业出版社, 2007.
|
| [8] |
朱邦俊, 万正权. 环肋圆柱壳应力分析的一种新方法[J]. 船舶力学, 2004, 8(4): 61-67. ZHU B J, WAN Z Q. A Method of stress analysis of ring-stiffened cylindrical shell[J]. Journal of Ship Mechanics, 2004, 8(4): 61-67. |
 2025, Vol. 47
2025, Vol. 47
