随着科学技术的进步与发展,没有硝烟的电子战已成为现代战争中重要的一部分[1]。精确打击能力、主动防御水平决定着战争的走向,而其中对辐射源目标位置信息的测量尤为重要[2]。被动测向又称为无源测向,侦收系统通过接收辐射源发射的电磁波信号,计算出辐射源的来波方向用于电子支援侦察。由于无源测向技术不需要在目标周围发射探测信号,因而无源测向技术具有隐蔽性好、安全性高、设备成本低、无电磁污染等优势[3]。因此,电子战中对于无源测向的研究吸引了广大学者的关注。
无源测向系统利用目标自身辐射的电磁波信号,完成信号的接收处理,实现空间信号到达方向(Direction of Arrival,DOA)的测量计算。目前,常用的DOA测量方法有时差测量法[4]、比幅测向法[5]、相位干涉仪测向法[6]等。时差测量法通过比较不同接收机之间的信号到达时差,来计算辐射源的DOA,该技术测向精度高,但需要采用高精度系统时钟,且不同接收机之间对时钟同步要求较高。比幅测向法根据测向天线的方向性,利用不同来波方向信号测量的幅度值差异,计算出DOA,常用算法有两波束比幅测向法、三波束比幅测向法等。该方法原理简单,但天线方向性对测向精度影响较大,同时一般比幅测向系统的天线采用水平安装方式,只能测量方位角,无法有效测量俯仰角,当目标位于高俯仰位置时,方位角测量误差较大。相位干涉仪测向法利用阵列天线接收到信号的相位信息完成DOA的计算,该技术测向精度高,测向速度快,场地适应能力强,但在一维水平干涉仪阵列系统中,当辐射源位于高俯仰位置时,测算到的方位角误差同样较大。为解决这一不足,现有侦察系统多采用二维干涉仪天线阵列[7](水平阵列、俯仰阵列),可以联立计算出方位角和俯仰角,提高测向精度,该架构已被广泛运用于航空航海等军用领域的测向系统中。然而,采用相位干涉仪体制的侦察系统造价相对较高,尤其是二维干涉仪天线阵列,需同时安装水平和俯仰干涉仪阵列。同时,为实现空域全覆盖,增加信号截获概率,相位干涉仪侦察系统一般采用多个阵面的安装形式[8],相邻阵面采用同样的二维阵列天线安装方式,实现辐射源方位、俯仰的计算测量,这无疑增加了系统成本和阵面体积,有悖于现代电子信息装便携化、低成本的发展趋势[9]。为了改善上述相位干涉仪测向系统的不足,本文创新提出了一种基于相邻阵面水平干涉仪的联合二维测向算法,各天线阵面仅需配备一维水平干涉仪阵列天线,且相邻阵面间安装夹角设计更为灵活。首先,相邻2个阵面利用各自的水平干涉仪天线完成本阵面的信号方位角计算;然后,通过等式联立计算得到辐射信号的真实俯仰角;最后,利用真实俯仰角修正此前计算得到的方位角,修正测向偏差,从而实现相邻阵面水平干涉仪的联合二维测向过程。
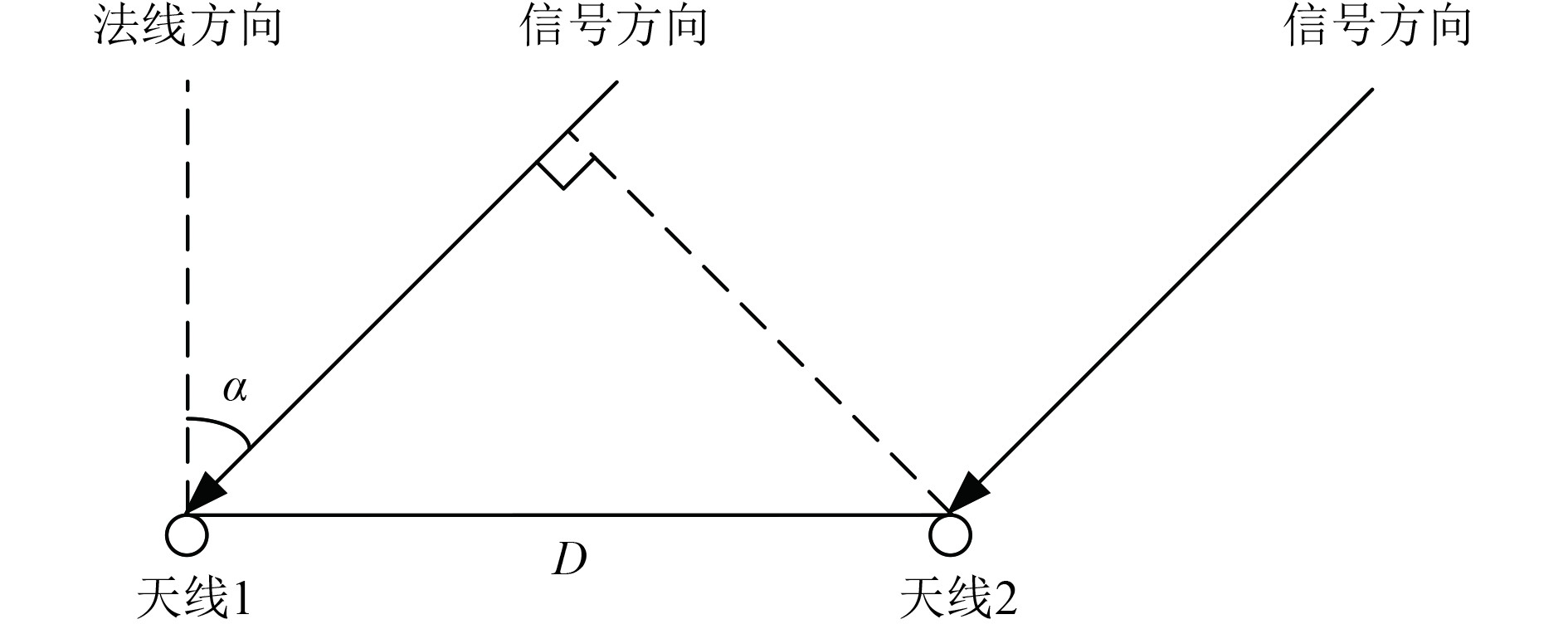
1 干涉仪测向原理干涉仪测向原理如图1所示[10],信号以某个角度入射到干涉仪天线阵列,不同接收天线接收同一信号时,由于信号的传输时延,2个天线接收到的信号会产生相位差,系统利用该相位差计算出信号的入射角度。干涉仪测向原理简单,且测向精度高,在侦察系统中应用广泛。
|
图 1 干涉仪测向原理 Fig. 1 Principle of direction finding with interferometer |
如图1所示,信号的入射角度为
| $ \Delta t = \frac{{D\sin (\alpha )}}{c}。$ | (1) |
式中:c为电磁波传播速度。设信号的频率为f,则对应的角速度为
| $ \Delta \varphi = \omega \Delta t = \frac{{2{\text π} D\sin \alpha }}{\lambda }。$ | (2) |
从而信号的方位角为:
| $ \alpha = \arcsin (\frac{{\Delta \varphi \lambda }}{{2{\text π} D}})。$ | (3) |
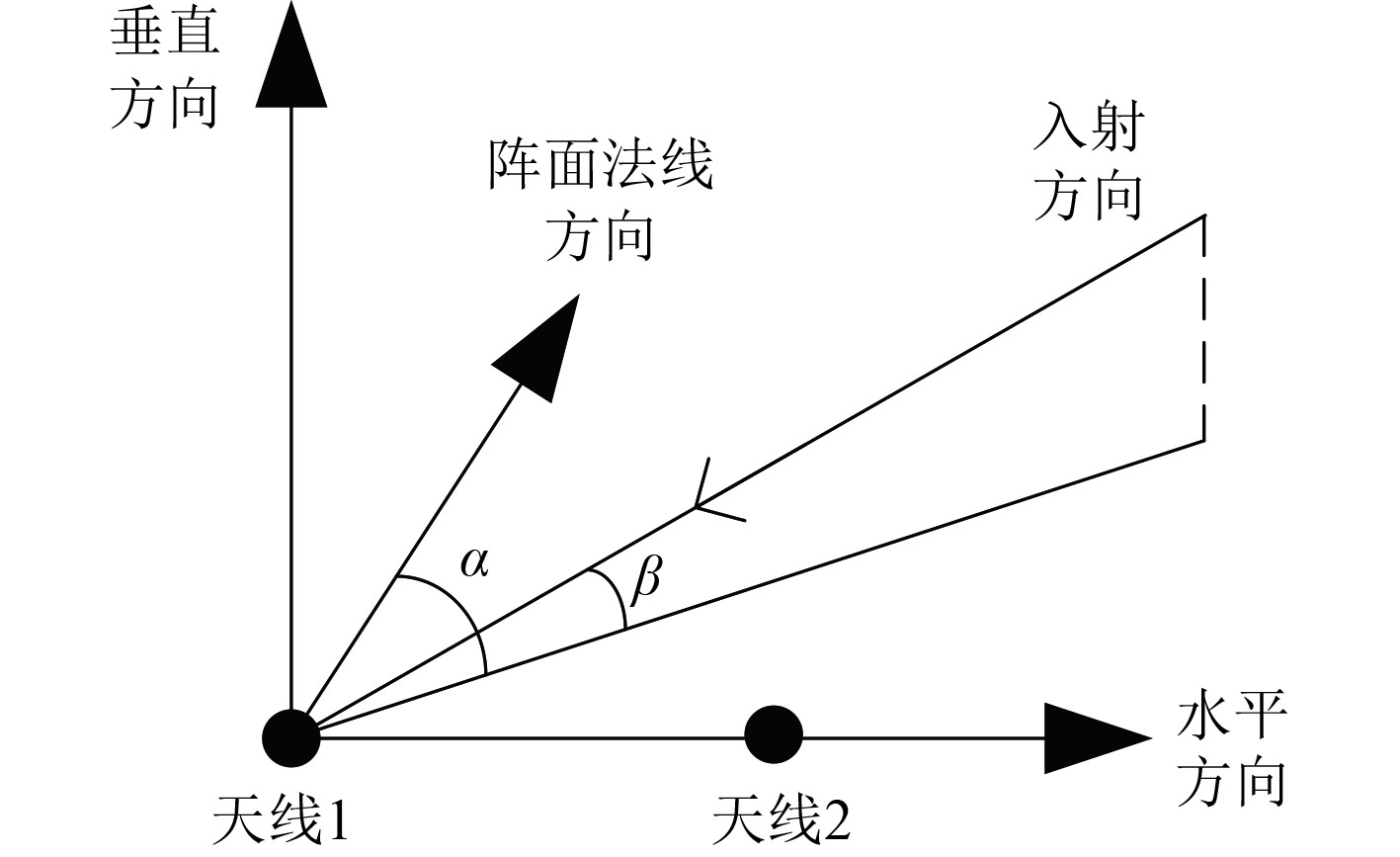
上述公式是在信号入射俯仰角为0°时的情况,当信号以俯仰角β入射时,如图2所示,式(2)变化为:
|
图 2 带俯仰角时干涉仪测向示意图 Fig. 2 Interferometer direction finding diagram with pitch angle |
| $ \Delta \varphi = \frac{{2{\text π} D\sin \alpha \cos\beta }}{\lambda } 。$ | (4) |
因此入射信号的方位角为:
| $ \alpha = \arcsin (\frac{{\Delta \varphi \lambda }}{{2{\text π} D\cos \beta }})。$ | (5) |
在侦收系统仅配置水平干涉仪时,由于信号相对于阵面的入射方向存在俯仰角,水平干涉仪测量得到的方位
| $ {\alpha ^{'}} = \arcsin (\frac{{\Delta \varphi \lambda }}{{2{\text π} D}}) 。$ | (6) |
同时满足:
| $ \displaystyle\sin{\alpha ^{'}}=\displaystyle\sin\alpha\displaystyle\cos\beta。$ | (7) |
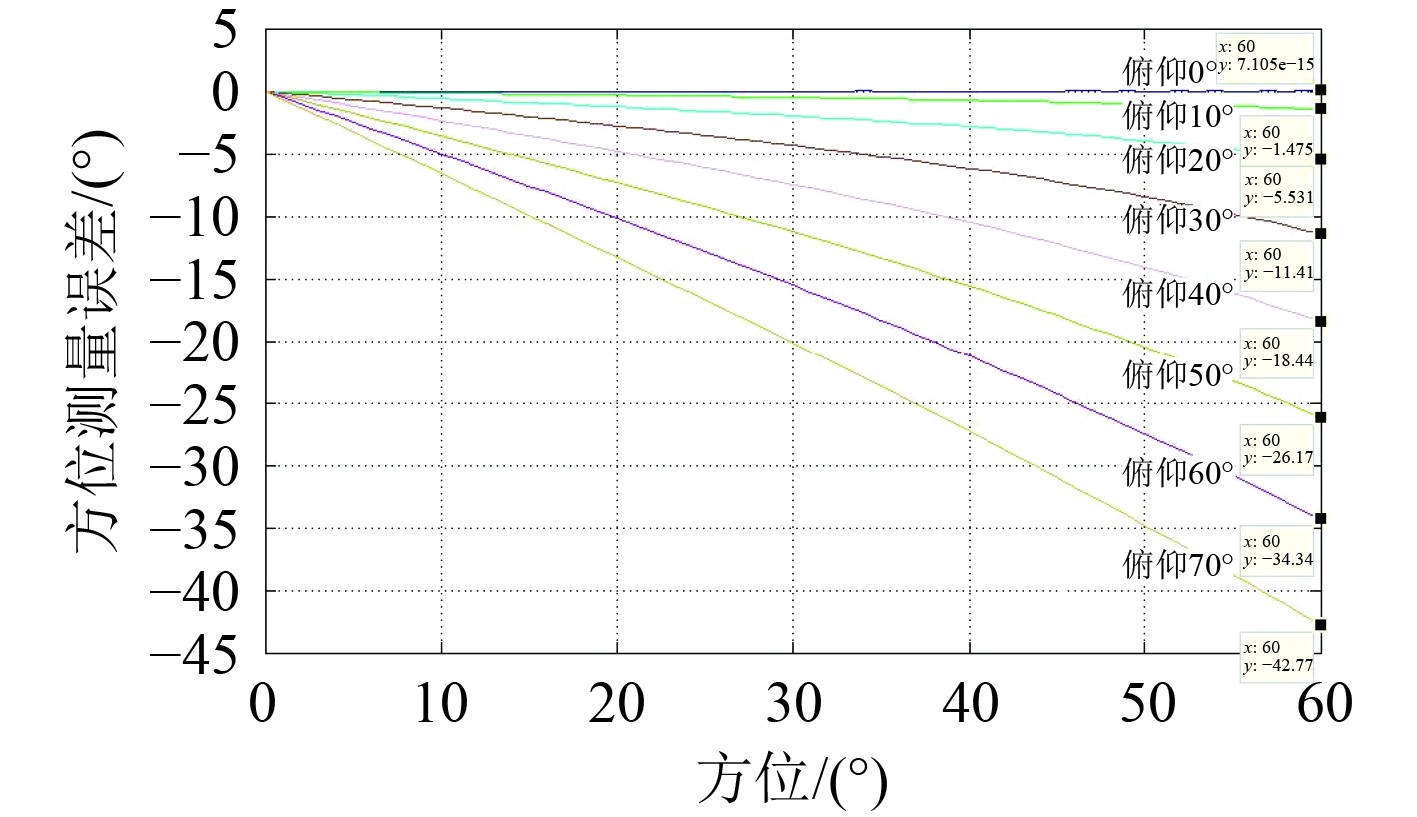
可以看出,对单个阵面而言,在仅配置水平干涉仪时,由于入射信号存在俯仰角,实测的方位结果与真实方位值存在偏差,降低了测向精度,实测方位值和理论方位值的误差曲线如图3所示。
|
图 3 不同俯仰角时方位角测量误差 Fig. 3 Azimuth measurement error at different pitch angles |
可以看出,当信号入射俯仰角不为0°时,随着信号入射方位角的增大,水平干涉仪测量出的方位测量值误差也随之增大,且俯仰角越大,方位的测量误差越大,考虑工程应用实际情形,在方位60°、俯仰70°的极限情况下,方位测量误差达到42.77°。同时,结合式(7),可以发现,当入射俯仰角不为0°时,实际测得的方位角要小于真实的方位角,即偏向阵面的法线方向。
解决这个问题最直接的方法是增加垂直干涉仪天线阵列,构成二维干涉仪测向阵列天线,实现对方位角和俯仰角的精确测量,可以极大减小测向误差。然而,随着天线数量的增加,天线后端的微波以及接收机处理通道数量都将随之增加,增加了系统的构建成本。同时,垂直干涉仪天线阵列的安装也增大了天线阵面的体积,不利于电子信息装备朝便携化、低成本方向发展。因此,面对当前电子信息装备小型化、低成本的发展趋势,需要构建一种有效的测向方法,实现对信号方位角、俯仰角的精确测量。
2 基于相邻阵面水平干涉仪的联合二维测向算法本节推导基于相邻阵面水平干涉仪的联合二维测向算法,该算法架构中,每个阵面仅需配置水平干涉仪天线阵,且相邻阵面设计安装时,夹角设计更为灵活,更利于系统的扩展。2个相邻阵面利用水平干涉仪天线先各自测量出对应阵面的方位角,当存在俯仰角时,2个阵面测得的方位角不一致,通过公式联立可以求得真实的方位角和俯仰角。
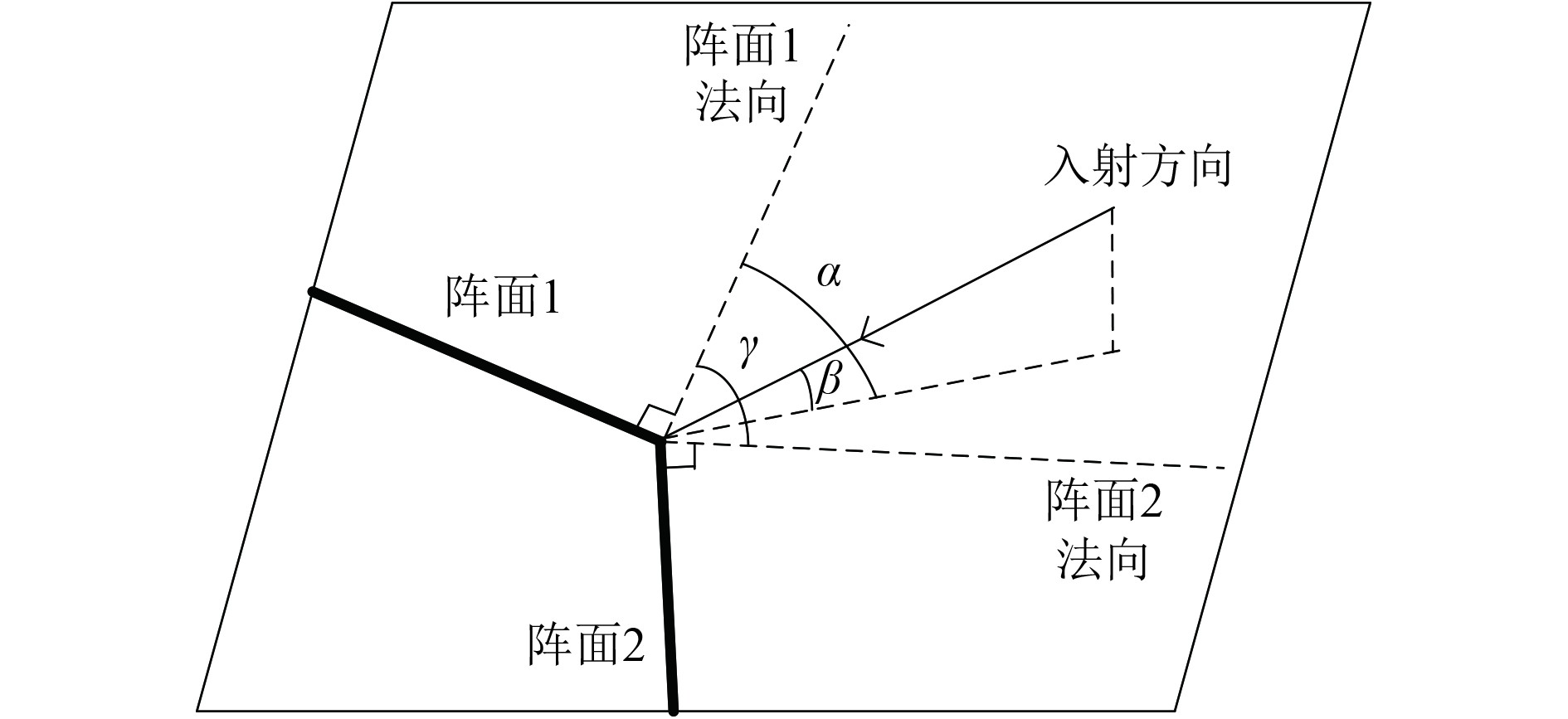
如图4所示,信号以方位角
|
图 4 信号入射阵面示意图 Fig. 4 Diagram of signal incident on multiple fronts |
因此,对于阵面1和阵面2有如下关系:
| $ \sin{\alpha_1 ^{'}}=\displaystyle\sin\alpha\displaystyle\cos\beta,$ | (8) |
| $ \sin(\gamma-{\alpha_2 ^{'}})=\displaystyle\sin(\gamma-\alpha)\displaystyle{\cos\beta}。$ | (9) |
根据式(8),求得:
| $ \cos^2\alpha=\frac{\cos^2\beta-\sin^2\alpha_1^{'}}{\cos^2\beta}。$ | (10) |
对式(9)等号右边
| $ \sin (\gamma - \alpha _2^{'}) = \sin\gamma \cos\alpha \cos\beta - \cos\gamma \sin\alpha _1^{'} 。$ | (11) |
联立式(10)和式(11),得到俯仰角:
| $ {\beta = \arccos \left[ {\sqrt {\dfrac{{{{[\sin(\gamma - \alpha _2^{'}) + \cos\gamma \sin\alpha _1^{'}]}^2}}}{{{{\sin }^2}\gamma }} + {{\sin }^2}\alpha _1^{'}} } \right]。} $ | (12) |
联立式(8)和式(12),计算得到方位角:
| $ {\begin{split} \alpha = \arcsin \left[ {{{\sin\alpha _1^{'}} \mathord{\left/ {\vphantom {{sin(\alpha _1^{'})} {\sqrt {\frac{{{{[sin(\gamma - \alpha _2^{'}) + cos\gamma sin\alpha _1^{'}]}^2}}}{{{{\sin }^2}\gamma }} + {{\sin }^2}\alpha _1^{'}} }}} \right. } {\sqrt {\frac{{{{[\sin(\gamma - \alpha _2^{'}) + \cos\gamma \sin\alpha _1^{'}]}^2}}}{{{{\sin }^2}\gamma }} + {{\sin }^2}\alpha _1^{'}} }}} \right]。\end{split}}$ | (13) |
由式(12)和式(13)可以看出,当信号以某一方位角和俯仰角入射时,利用相邻2个水平干涉仪天线阵分别测量出该信号在各自阵面下的方位角,通过联合解算,即可同时解算出信号入射的真实方位角和俯仰角。
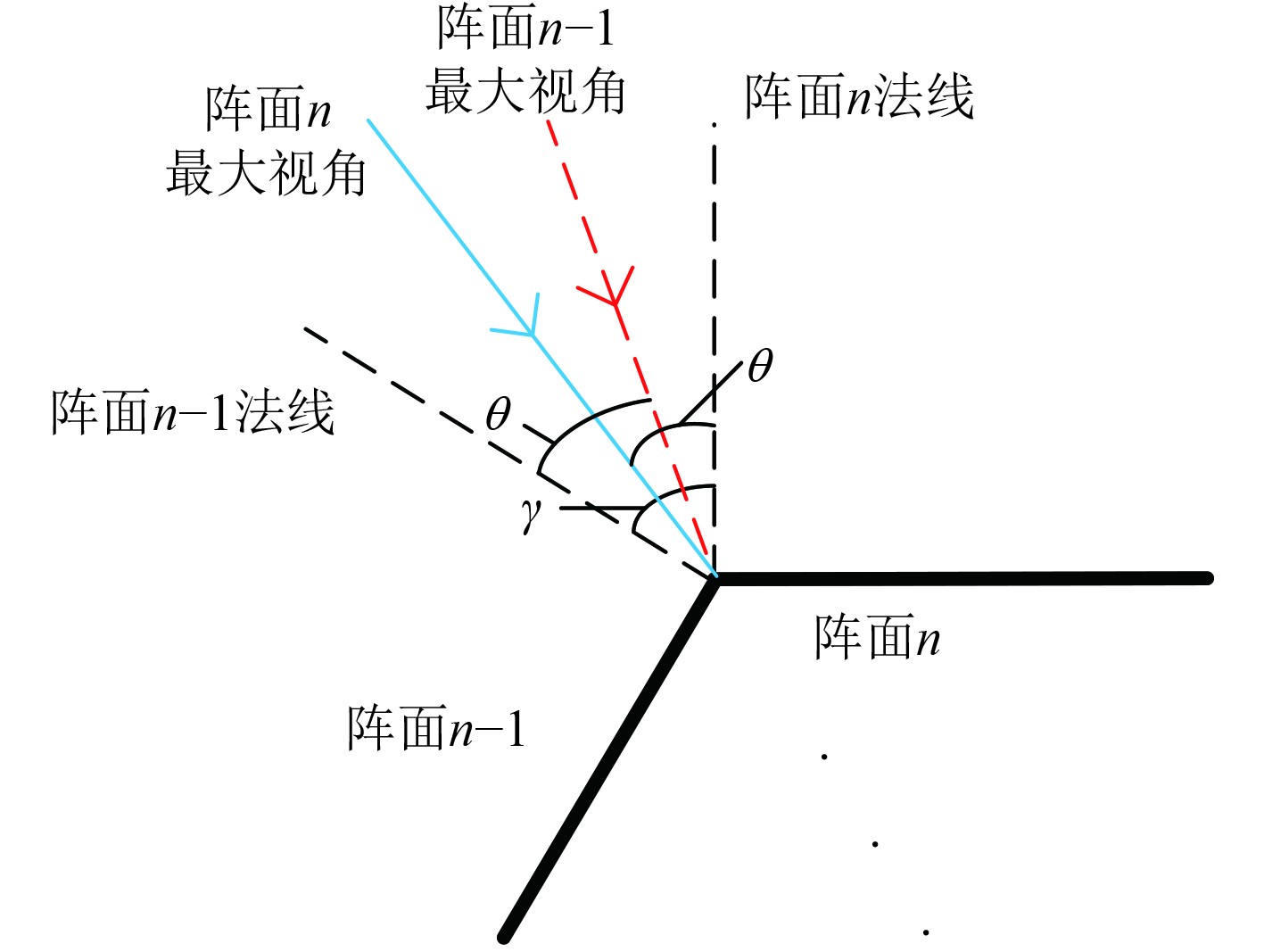
考虑到本文的测量算法需要有2个阵面能同时侦收到同一信号并分别完成测向,才能计算得到真实方位角和俯仰角,而干涉仪天线方向图中,随着入射角度的增大,天线增益逐渐减小[11],因此不同天线存在最大视角,即能够正确测量出方位的最大入射角度
|
图 5 阵面夹角和干涉仪天线最大视角关系示意图 Fig. 5 Diagram of the relationship between the array angle and the maximum effective measurement angle of interferometer antenna |
可以看出,当干涉仪天线最大视角
| $ \theta \geqslant \gamma 。$ | (14) |
基于上述的分析推导,对基于相邻阵面水平干涉仪的联合二维测向算法进行了仿真,并与一维水平干涉仪的方位角测量结果进行比较分析。仿真参数如表1所示。其中,不考虑测向系统本身的误差,认为阵面1和阵面2为理想的测向系统,令2个阵面夹角为59°并垂直于大地平面放置,阵面1的法线方向为方位0°,阵面2由阵面1参照图4所示顺时针旋转59°放置,仿真中方位设置值为相对于阵面1法线方向的夹角,法线顺时针方向为方位设置值增大的方向。
|
|
表 1 仿真参数 Tab.1 Simulation parameter |
仿真中,首先根据方位角和俯仰角的设置值,根据式(8)和式(9)反推出阵面1和阵面2理论测量出来的方位结果,然后将2个阵面的方位测量结果以及阵面之间的夹角一并代入式(12)和式(13)计算出真实的方位角和俯仰角,其中方位设置范围为0°~60°,俯仰设置范围为−20°~80°,取值间隔为20°。
仿真结果如图6~图11所示。由图7可以看出,在俯仰角为0°时,阵面1、阵面2测量的方位结果一致,均为设置值,基于该结果,表明水平干涉仪天线阵列在不存在俯仰角时,方位测量结果准确。由图6~图11可以看出,在任意俯仰角下,联合算法测量的方位角和俯仰角和真实设置值一致,在不考虑系统误差下,表明该联合二维测向算法能够准确地计算出信号真实的方位角和俯仰角。同时,在仅有水平干涉仪天线阵列时,干涉仪测向结果随着俯仰角度的增大,阵面1和阵面2各自的方位角测量误差也同步增大,对于侦察系统,同一个信号测量出2种方位值,会导致后端信号处理出现增批现象。此外,在满足式(14)的条件下,联合测向算法中的2个阵面夹角可以为任意设置值。

|
图 6 俯仰−20°仿真结果 Fig. 6 Simulation results with pitch −20° |
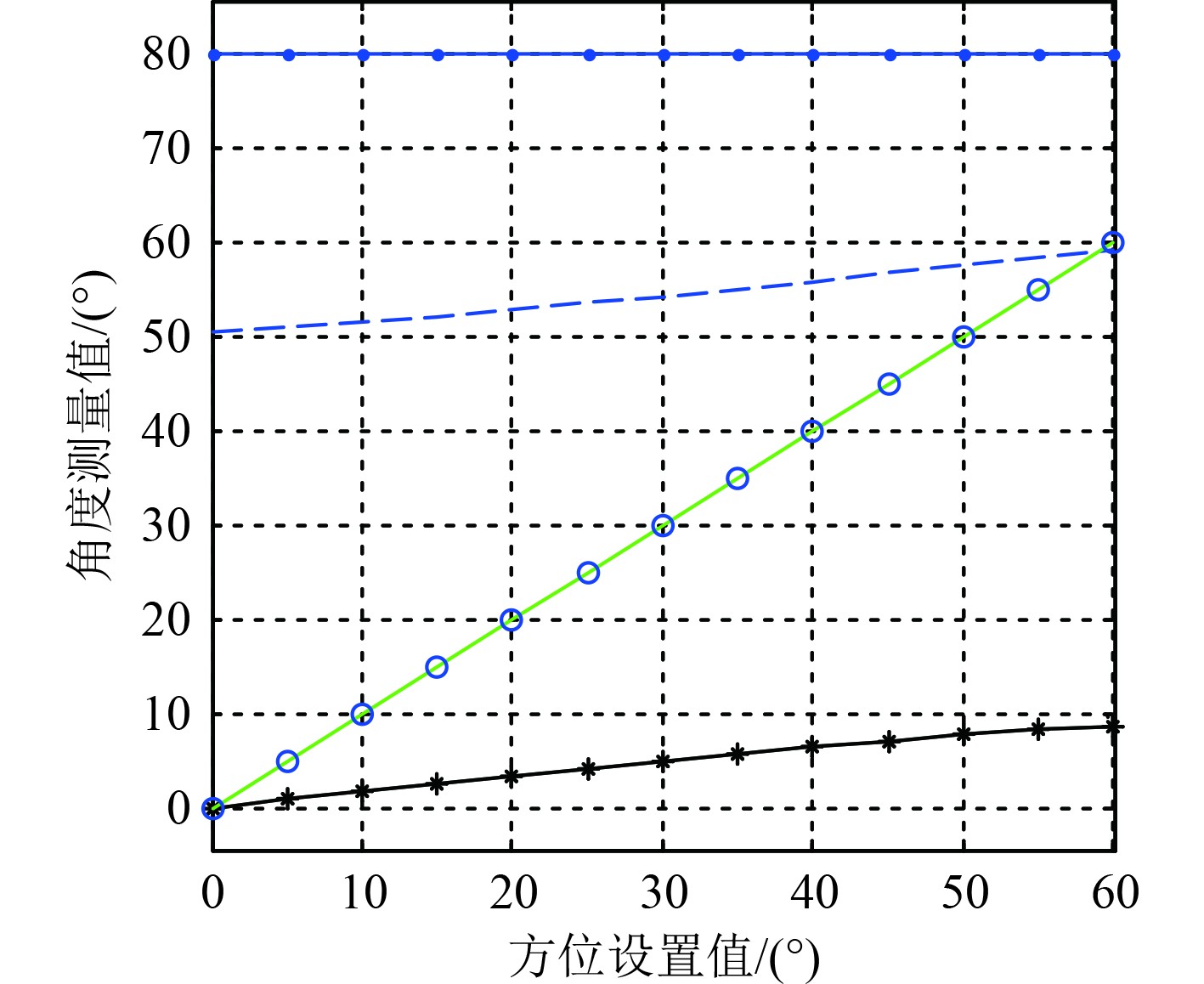
|
图 11 俯仰 80o仿真结果 Fig. 11 Simulation results with pitch 80o |
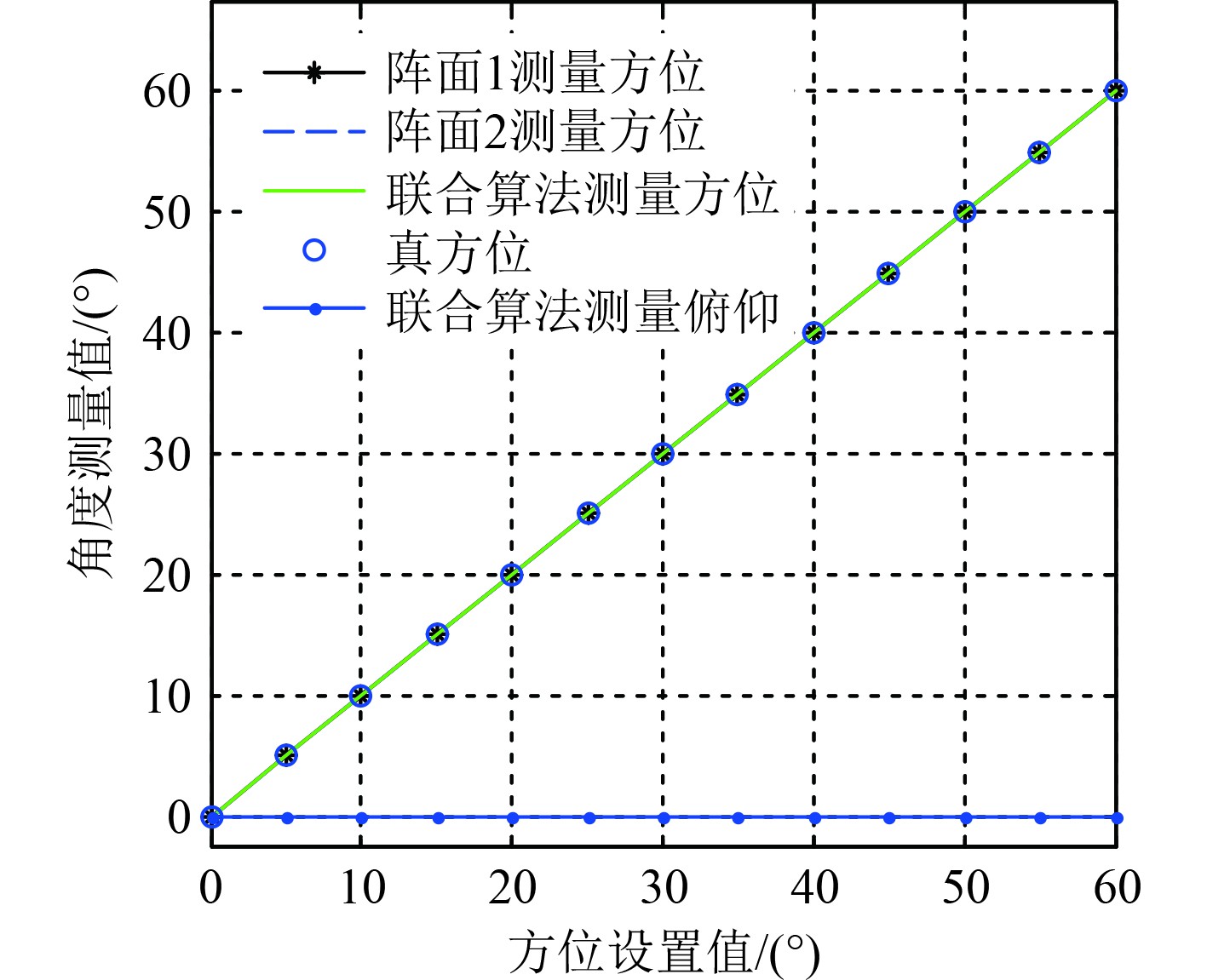
|
图 7 俯仰0o仿真结果 Fig. 7 Simulation results with pitch 0o |
因此,可以看出本文的基于相邻阵面水平干涉仪的联合二维测向算法是一种有效的二维测向算法,利用2个相邻阵面各自测量出的方位角,联合计算出真实方位角和俯仰角,算法简单易实现。同时,相邻阵面的安装形式更加灵活,节约了系统成本,且相对于二维干涉仪天线阵列,天线阵面体积得到有效的缩小。

|
图 8 俯仰20o仿真结果 Fig. 8 Simulation results with pitch 20° |

|
图 9 俯仰 40o仿真结果 Fig. 9 Simulation results with pitch 40o |
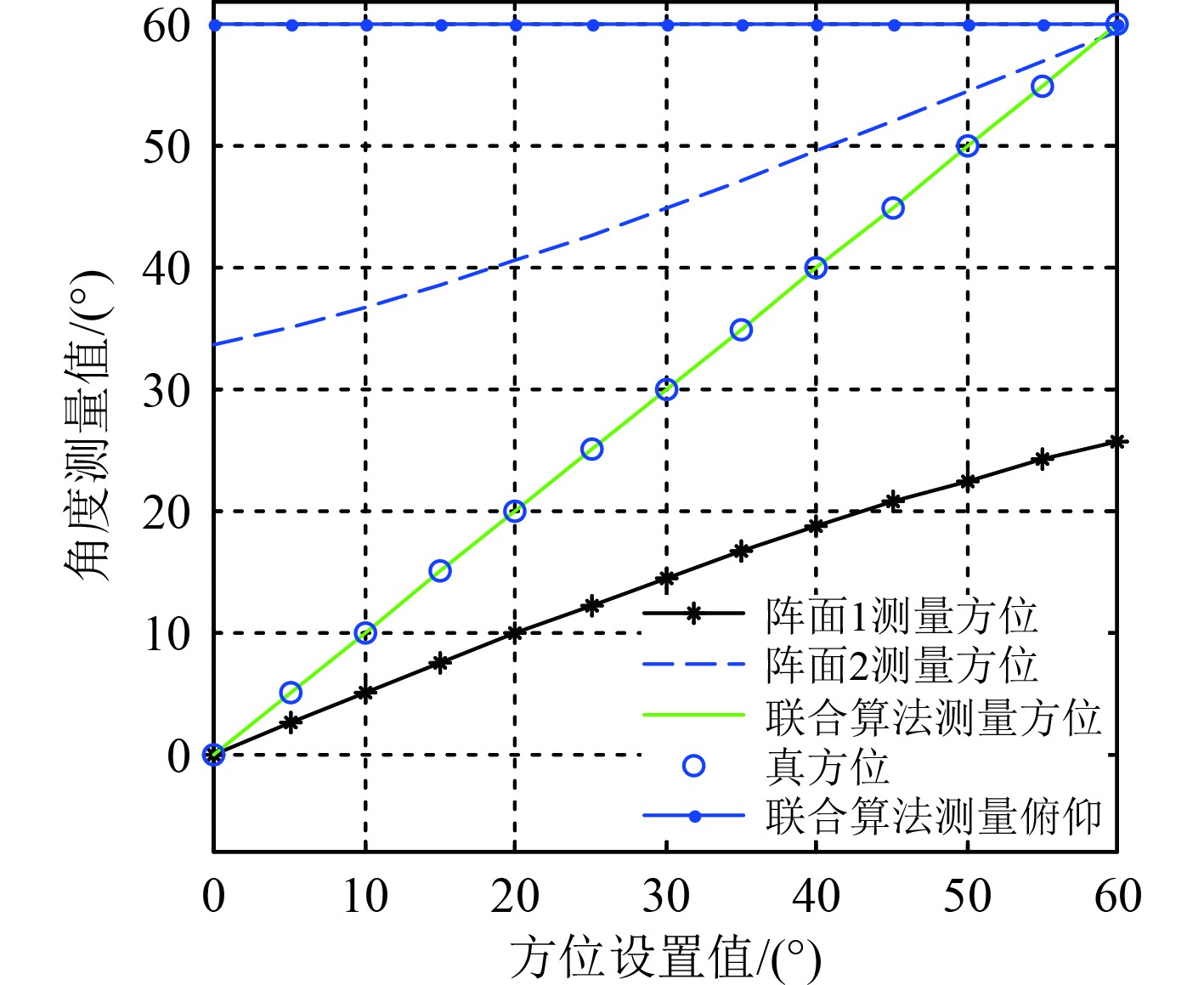
|
图 10 俯仰60o仿真结果 Fig. 10 Simulation results with pitch 60° |
1)本文提出的基于相邻阵面水平干涉仪的联合二维测向算法,有效解决了水平干涉仪无法测量俯仰角的弊端,在高俯仰角条件下,极大缩小了系统的测向误差,对于侦察系统能够有效减少增批现象。
2)相对于传统二维干涉仪天线阵列,本文提出的联合二维测向算法仅需给每个阵面安装水平干涉仪天线阵列,减少了天线阵列使用数量,极大减少了系统的制造成本,2个阵面之间安装夹角更为灵活。且相对于二维干涉仪天线阵列,由于去除了俯仰干涉仪天线,天线阵面的体积能够有效减小,符合现在电子信息装备朝着便携化、低成本的发展方向。
3)本文提出的基于相邻阵面水平干涉仪的联合二维测向算法,能够准确测量出入射信号的方位角和俯仰角,对干涉仪测向侦察系统具有实际指导意义。
| [1] |
蒋旭峰. 线性调频引信干扰与抗干扰技术研究[D]. 南京: 南京理工大学, 2020.
|
| [2] |
吴癸周, 郭福成, 张敏. 信号直接定位技术综述[J]. 雷达学报, 2020, 9(6): 998−1013.
|
| [3] |
张敏, 张文俊, 李曦, 等. 基于长基线干涉仪相位差的多站无源定位方法[J]. 电子与信息学报, 2023, 45(11): 3868-3876. DOI:10.11999/JEIT221362 |
| [4] |
夏伟, 罗明, 赵美霞. 无源时差定位系统最优布站方法研究[J]. 雷达科学与技术, 2020, 18(1): 34-38. |
| [5] |
王博, 谢军伟, 葛佳昂, 等. FDA对比幅法单脉冲测向的角度欺骗[J]. 北京航空航天大学学报, 2020, 46(3): 643-650. |
| [6] |
刘伟, 付永庆, 许达. 二维相位干涉仪在相干干扰下的测向误差模型[J]. 中南大学学报(自然科学版), 2015, 46(4): 1274-1280. |
| [7] |
李琳, 居易. 近场试验条件对二维干涉仪测向系统的影响[J]. 舰船电子对抗, 2017, 40(5): 44-47+69. |
| [8] |
曹鑫. 干涉仪测向系统设计[D]. 南京: 东南大学, 2021.
|
| [9] |
程翔. 美国海军舰载电子战系统的现状及发展[J]. 舰船电子对抗, 2021, 44(3): 1-4+10. |
| [10] |
肖秀丽. 干涉仪测向原理[J]. 中国无线电, 2006(5): 43-49. DOI:10.3969/j.issn.1672-7797.2006.05.014 |
| [11] |
刘治甬, 叶波涛, 陈舒. 一种用于星载干涉仪的测向宽带天线的研究[J]. 现代信息科技, 2021, 5(3): 54-56+60. |
 2025, Vol. 47
2025, Vol. 47
