锚是船舶最重要的设备之一,除了保证船舶安全停靠之外,锚设备还可以辅助操纵船舶,因此,分析拖锚运动的动态变化对于预测和控制船舶的行为具有重要意义。目前,国内外对船舶运动模型在锚泊操纵方面的研究较少,对于船舶拖锚运动建模,更是少有人进行全面系统的研究。
锚链作为船舶拖锚运动中密不可分的一部分,其形式多样,受力情况复杂。近年来,已有多种数值计算模型用来求解锚链的张力与构型,其中包括动态计算方法(集中质量法[1 - 2]、有限差分法[3])、稳态计算方法(悬链线法[4 - 5]、有限元法[6]、直接积分法[7 - 8]等)。考虑到船舶获取锚链张力计算所需条件的局限性,本文采用直接积分法对锚链力进行求解。Chiou等[7]、Sun等[8]采用了直接积分法构建动力学方程,前者率先应用此方法深入探究了缆绳不规则运动的特性,后者在此基础上进行了进一步的改良和提升,其引入缆绳速度和姿态角作为关键变量,研究缆绳在收放过程中的水动力响应以及低应力条件下的动态特性。
本文利用直接积分法建立锚链力计算模型,将上述作用力与分离型模型(Manoeuvring Model Group,MMG)相耦合,建立船舶三自由度拖锚运动数学模型,使其能够获取拖锚运动过程中船舶的运动参数以及锚链的受力情况。
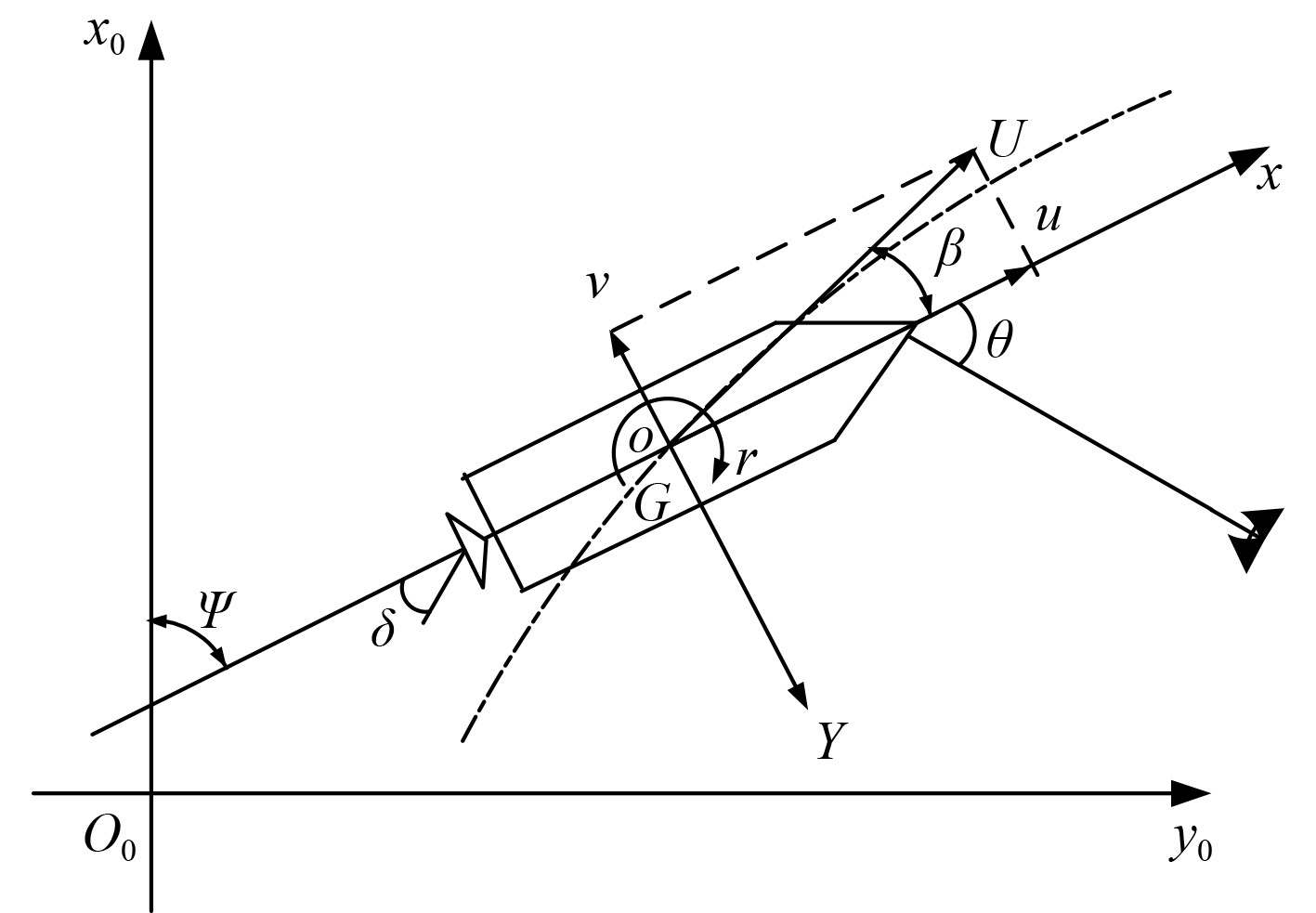
1 建立船舶三自由度数学模型本文在描述船舶平面运动时采用如图1所示的坐标系统。该系统包含2个坐标系[9],一个是空间坐标系
|
图 1 惯性坐标系与附体坐标系 Fig. 1 Earth and ship body coordinates |
基于MMG理论,在船舶纵荡、横荡以及艏摇运动之间的互相作用下,耦合锚链的作用力和力矩,以船体中心位置作为附体坐标系的原点,建立船舶三自由度拖锚运动方程:
| $ \left\{ {\begin{aligned} &{(m + {m_x})\dot u - (m + {m_y})vr - m{x_G}{r^2} = } \\ &{{X_H} + {X_P} + {X_R} + {X_W} + {X_A} + {X_C} + {X_T}},\\ &{(m + {m_y})\dot v + (m + {m_x})ur + m{x_G}\dot r = } \\ &{{Y_H} + {Y_R} + {Y_W} + {Y_A} + {Y_C} + {Y_T}} ,\\ &{({I_{zz}}{\text{ + }}{J_{zz}} + mx_G^2)\dot r + m{x_G}(\dot v + ur) = } \\ &{{N_H} + {N_R} + {N_W} + {N_A} + {N_C} + {N_T}} 。\end{aligned}} \right. $ | (1) |
式中:
| $ {\left\{\begin{gathered}X_H=\left(\dfrac{\rho}{2}\right)Ld_m\left\{X'_0uU+\left(m_y+X'_{vr}+\Delta X'_{vr}\right)Lvr\right\},\\ Y_H=\left(\dfrac{\rho}{2}\right)Ld_m\left[ \begin{array}{*{20}{c}}\left\{Y'_vv\left|u\right|+\left(Y'_r-m_x\right)Lru\right\}-\dfrac{C_D}{\boldsymbol{L}}\cdot \\ \int_{-\boldsymbol{L}/2}^{\boldsymbol{L}/2}\left(1-\tau'\dfrac{x}{\boldsymbol{L}}\right)\left|v+C_{rY}rx\right| \\ \left(v+C_{rY}rx\right){\rm{d}}x\end{array} \right],\\ N_H=\left(\dfrac{\rho}{2}\right)L^2d_m\left[\begin{array}{*{20}{c}}\left\{N'_vvu+N'_rLr\left|u\right|\right\}-\dfrac{C_D}{L^2}\int_{-\boldsymbol{L}/2}^{\boldsymbol{L}/2}\cdot \\ \left(1-\tau'\dfrac{x}{\boldsymbol{L}}\right)\left|v+C_{rN}rx\right| \\ \left(v+C_{rN}rx\right)x{\rm{d}}x\end{array}\right]。\\\end{gathered} \right. }$ | (2) |
式中:
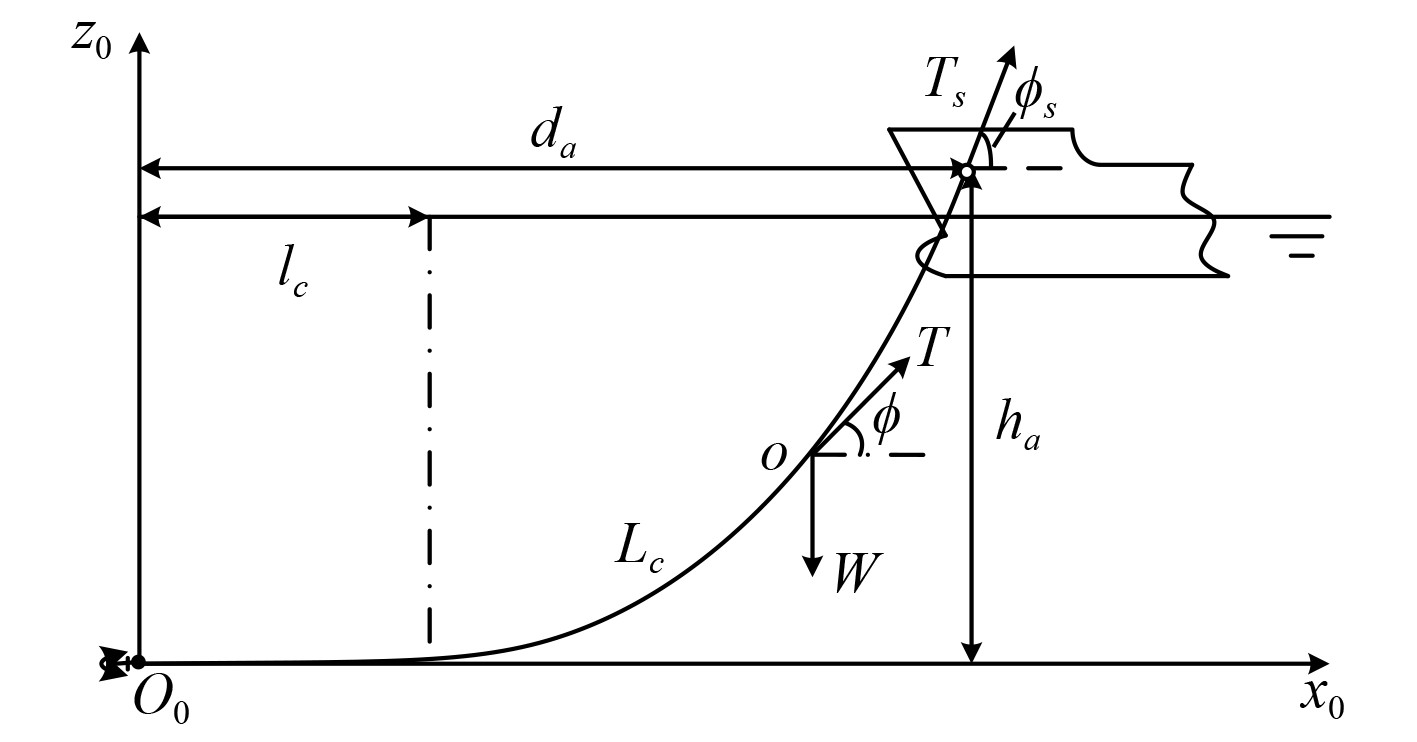
为了更为方便地求解锚链张力及构型,本文建立了如图2所示的船舶单锚泊状态下的坐标系。图中:
|
图 2 锚链坐标系 Fig. 2 Anchor chain coordinate system |
设锚链是细长、柔性的,不考虑扭矩的影响。锚链微元
| $ \frac{{\partial \mathop T\limits^ \to }}{{\partial s}} = S'\mathop W\limits^ \to。$ | (3) |
将式(3)在锚链附体坐标系下沿各个坐标轴方向展开,同时根据惯性坐标系与附体坐标系的转换关系可得平衡方程的标量形式:
| $ \left\{ \begin{gathered} {{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}s}}} \right. } {{\text{d}}s}} = {w_c}g\sin \phi ,\\ {{{{{\text{d}}\phi } \mathord{\left/ {\vphantom {{{\text{d}}\phi } {{\text{d}}s}}} \right. } {{\text{d}}s}} = {w_c}g\cos \phi } \mathord{\left/ {\vphantom {{{{{\text{d}}\phi } \mathord{\left/ {\vphantom {{{\text{d}}\phi } {{\text{d}}s}}} \right. } {{\text{d}}s}} = {w_c}g\cos \phi } T}} \right. } T} ,\\ {{{\text{d}}x} \mathord{\left/ {\vphantom {{{\text{d}}x} {{\text{d}}s}}} \right. } {{\text{d}}s}} = \left( {1 + Te} \right)\cos \phi ,\\ {{{\text{d}}z} \mathord{\left/ {\vphantom {{{\text{d}}z} {{\text{d}}s}}} \right. } {{\text{d}}s}} = \left( {1 + Te} \right)\sin \phi 。\\ \end{gathered} \right. $ | (4) |
式中,
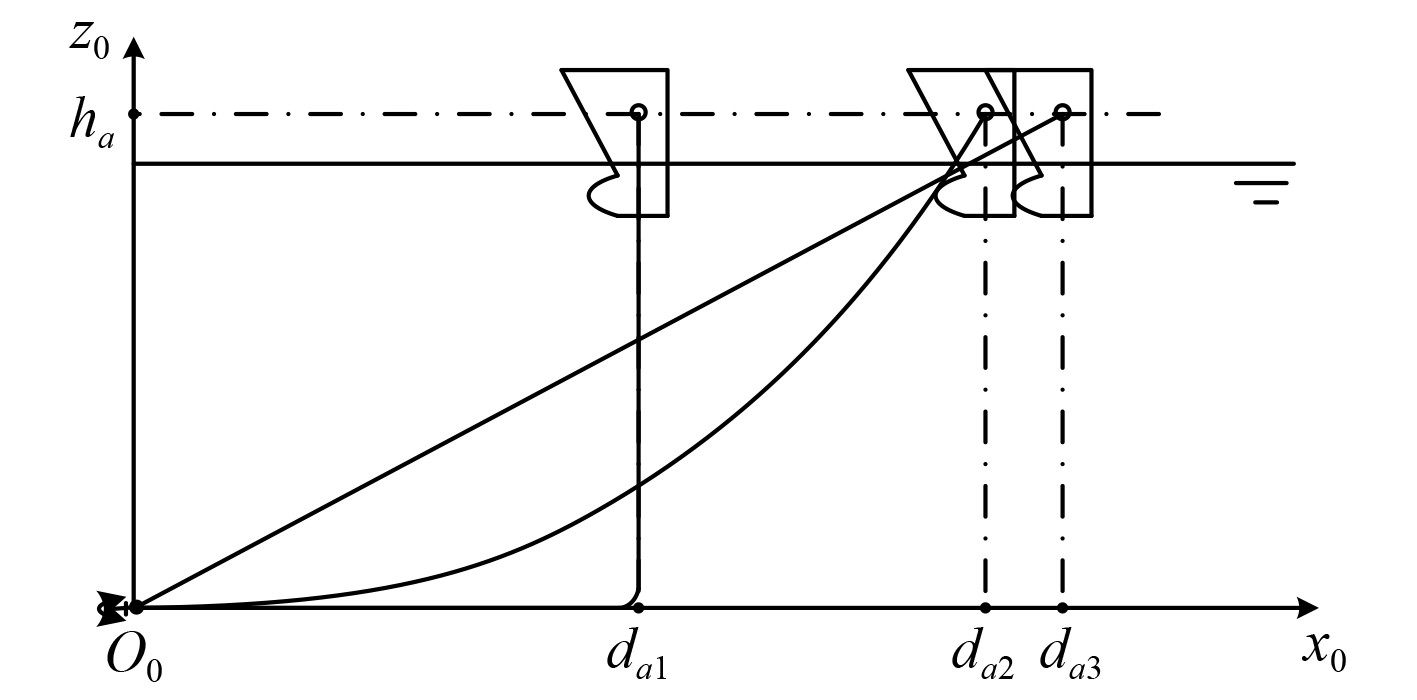
锚链的构型随锚链孔与锚位间距离
|
图 3 锚链形状及受力示意图 Fig. 3 Cable shape and force diagram |
当
因此,根据上述3种情况分别确定锚链两端的边界条件,然后利用二分法和龙哥库塔方法对锚链微分方程积分求解。
1)
如释放锚链总长为
| $ \left\{ \begin{gathered} {T_0} = 0 ,\\ {\phi _0} = 0 ,\\ {x_0} = {L_c} - {h_a} ,\\ {z_0} = 0。\\ \end{gathered} \right. $ | (5) |
将式(5)作为初始值代入式(4)中,采用二分法迭代求解
| $ \left| {\int_0^{{L_c} - x} {(1 + eT)\sin \phi {\text{ds}} - {h_a}} } \right| < \varepsilon。$ | (6) |
式中,
可以认为,在
2)
根据锚链海底端的边界条件可确定式(4)的积分初值如下:
| $ \left\{ \begin{gathered} {T_0} = 0,\\ {\phi _0} = 0,\\ {x_0} = 0 ,\\ {z_0} = 0 。\\ \end{gathered} \right. $ | (7) |
当
| $ \left|\displaystyle\int_0^{L_c}(1+eT)\mathrm{sin}\varphi\text{ds}-h_a\right| < \varepsilon\text{ }\text{,}\text{ }T_0\in\left(0,T_{\mathrm{\max}}\right]。$ | (8) |
当
| $ \left\{\begin{gathered}\left|\int_0^{L_c-x}(1+eT)\cos\phi\text{d}s-d_a\right| < \varepsilon,\\ \left|\int_0^{L_c-x}(1+eT)\sin\phi\text{d}s-h_a\right| < \varepsilon。\\ \end{gathered}\right. $ | (9) |
式中:
3)
此时,不存在卧底锚链,式(4)的积分初始值为式(7)。可根据锚位处
| $ \left\{ \begin{gathered} \left| {\int_0^{{L_c}} {(1 + eT)\cos \phi {\text{d}}s - {d_a}} } \right| < \varepsilon,\\ \left| {\int_0^{{L_c}} {(1 + eT)\sin \phi {\text{d}}s - {h_a}} } \right| < \varepsilon。\\ \end{gathered} \right. $ | (10) |
式中:
利用上述公式求解出锚链孔处的锚链张力
| $ \left\{ \begin{gathered} {X_C} = {T_s}\cos {\phi _s}\cos \theta,\\ {Y_C} = {T_s}\cos {\phi _s}\sin \theta,\\ {N_C} = - {X_C} \cdot {y_C} + {Y_C} \cdot {x_C}。\\ \end{gathered} \right. $ | (11) |
式中:
锚的抓力主要由2个因素构成,即锚的自身抓力和锚链与海底的摩擦力。
锚的总抓力计算式为:
| $ P = {P_a} + {P_c} = {\lambda _a} \cdot {w_a} + {\lambda _c} \cdot {w_c} \cdot {l_c} .$ | (12) |
式中:
|
|
表 1 锚静抓力系数表 Tab.1 Table of anchor static grip coefficients |
|
|
表 2 锚动抓力系数表 Tab.2 Table of anchor dynamic grip coefficients |
在船失去锚固的情况下,抓力系数与拖锚时的动态锚抓力系数具有相同数值。当海底底质为泥沙时,锚的动抓力与锚链的出链长度及水深之间存在一定关系(见表2)。
锚链在锚链孔处的张力
为了验证模型的正确性和适用性,本文以“北斗”轮风中拖锚漂航实船试验为例进行风中拖锚漂航运动仿真。船舶主尺度及其锚链参数如表3和表4所示[11]。
|
|
表 3 “北斗”轮船舶尺度 Tab.3 Ship size of the vessel "Beidou" |
|
|
表 4 “北斗”轮锚链参数 Tab.4 Anchor chain parameters of the vessel "Beidou" |
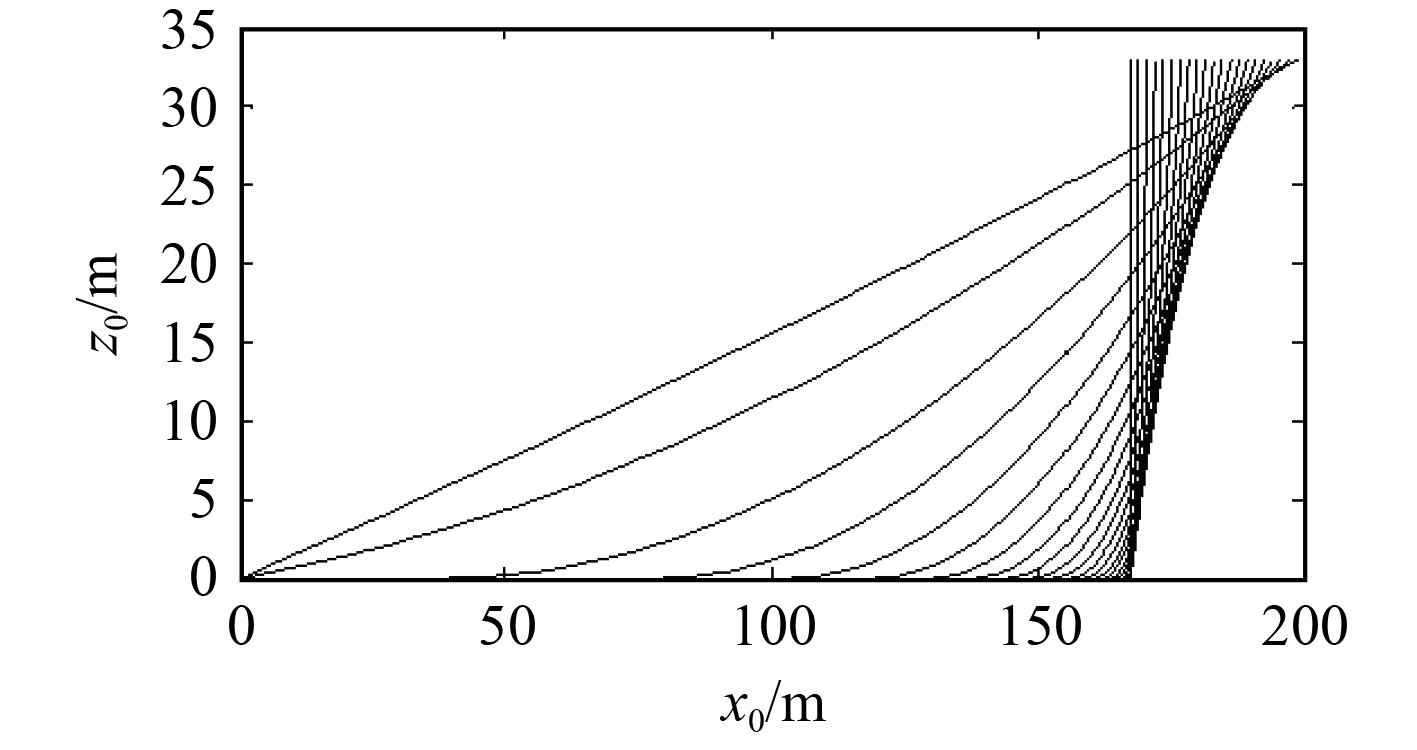
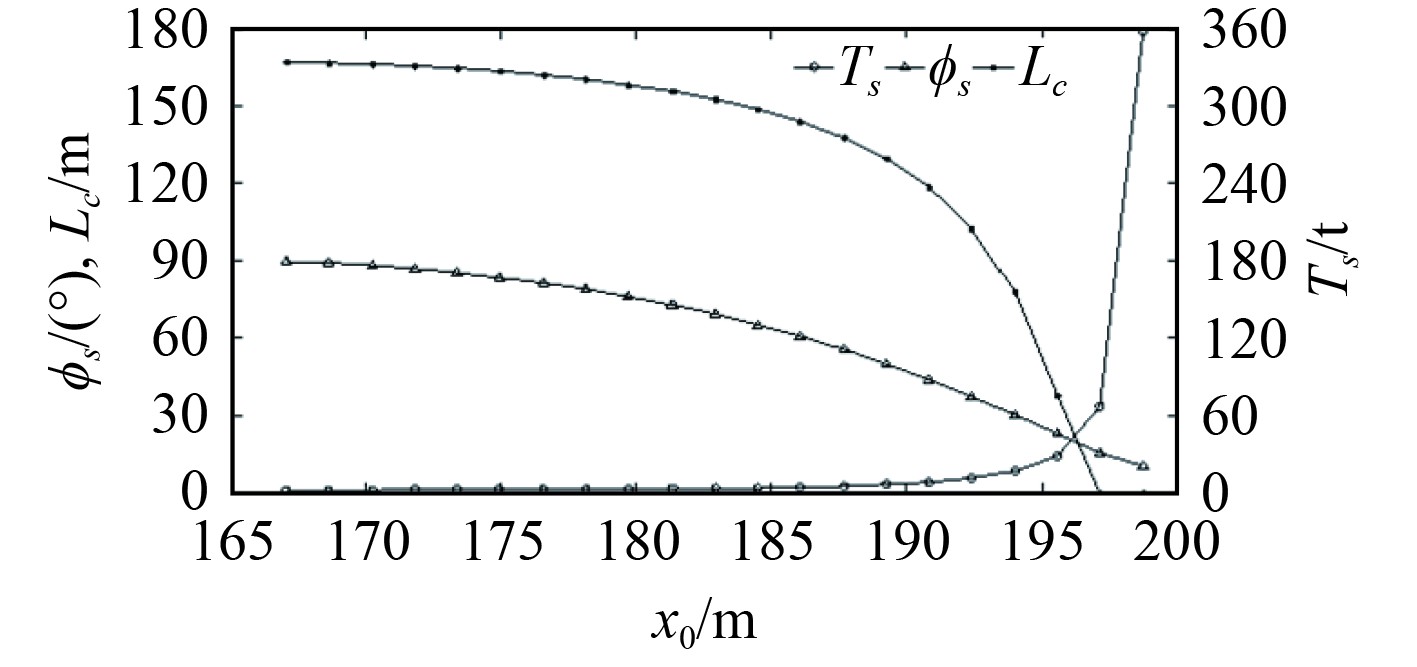
图4为200 m锚链随船锚间距的增加而变化的构型,图5为锚链孔端的锚链张力和水平交角以及卧底锚链长度随船锚间距的增加而变化的过程。可知,锚链作用于船体的张力随船锚距离的增加而增加,而水平交角和卧底锚链的长度则随之减小。在已知锚位、船位和出链长度的情况下,利用该算法,不仅可以预报锚链的张力和构型,而且还可计算出卧底锚链的长度,即可较准确地计算出锚和锚链的抓力,用于预报船舶是否走锚。在实际工作中,锚位、船位和出链长度较易获取,因此,该算法具有较强的实用性。
|
图 4
不同 |
|
图 5
张力、欧拉角和卧底锚链变化
Fig. 5
Static chain TS, ϕS & lc of different |
为了验证所建船舶运动模型的准确性,本文以“北斗”轮为例进行旋回与停船仿真试验,并与实船试验结果[12]进行对比验证。
1)旋回仿真试验验证
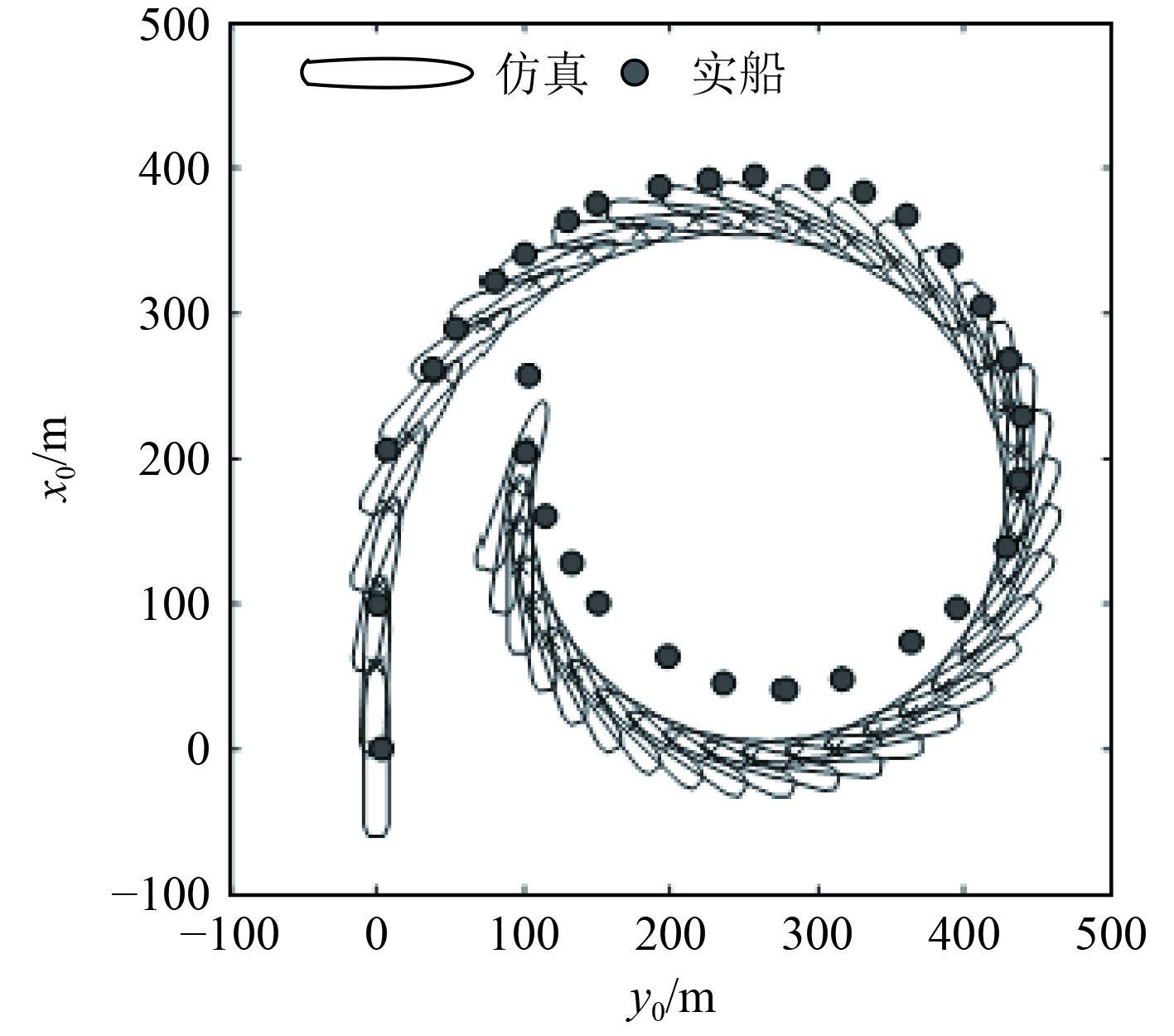
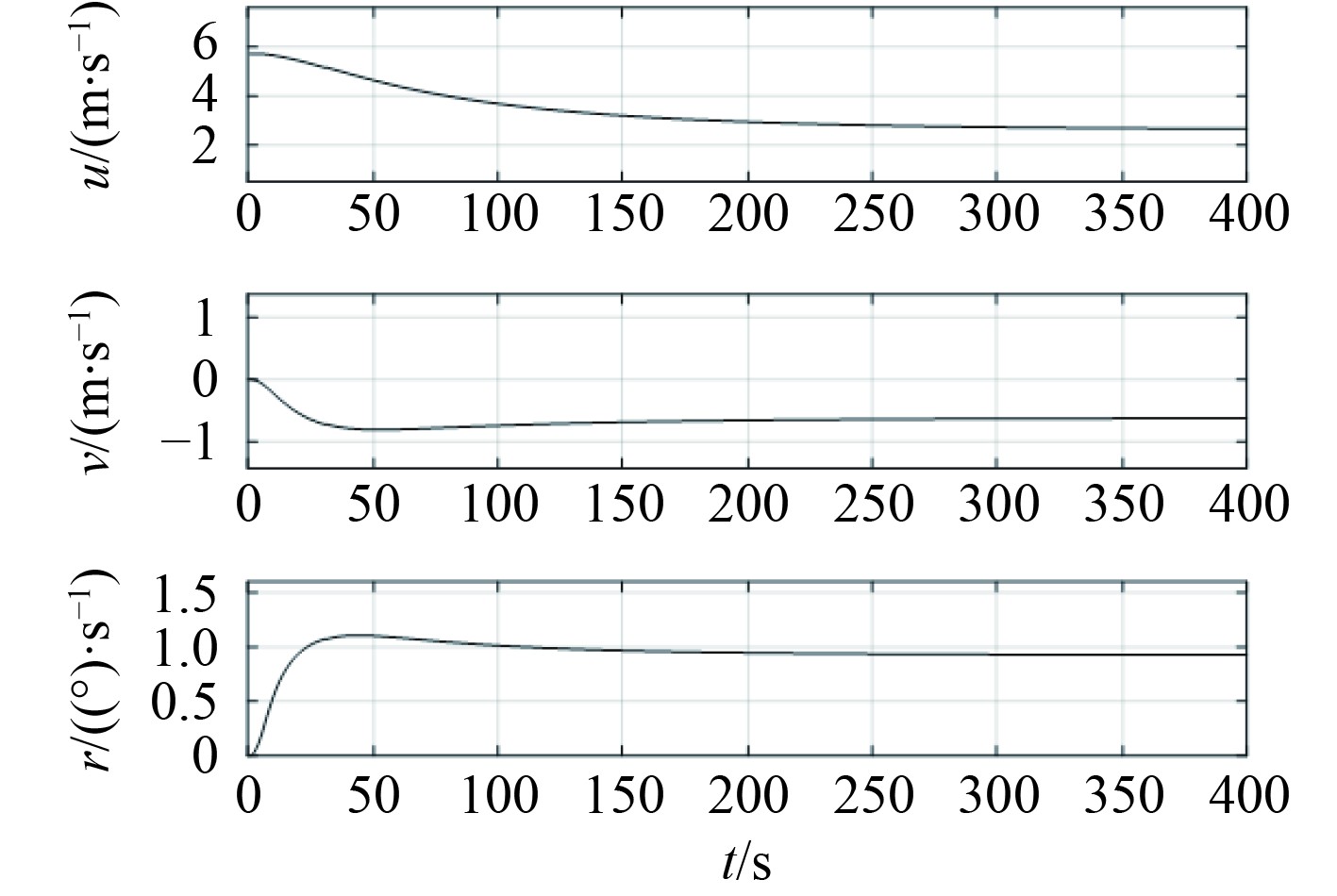
船舶旋回仿真试验的初始条件为:航速11.2 kn、航向0° 、舵角35° 、南风5.6 m/s。当仿真时长为400 s时,仿真结果如图6和图7所示。比对结果如表5所示。
|
图 6 旋回运动轨迹对比 Fig. 6 Turning motion trajectories |
|
图 7 旋回动态性能 Fig. 7 Dynamic turning performance |
|
|
表 5 旋回试验结果对比 Tab.5 Comparison of turning test results |
2)停船仿真试验
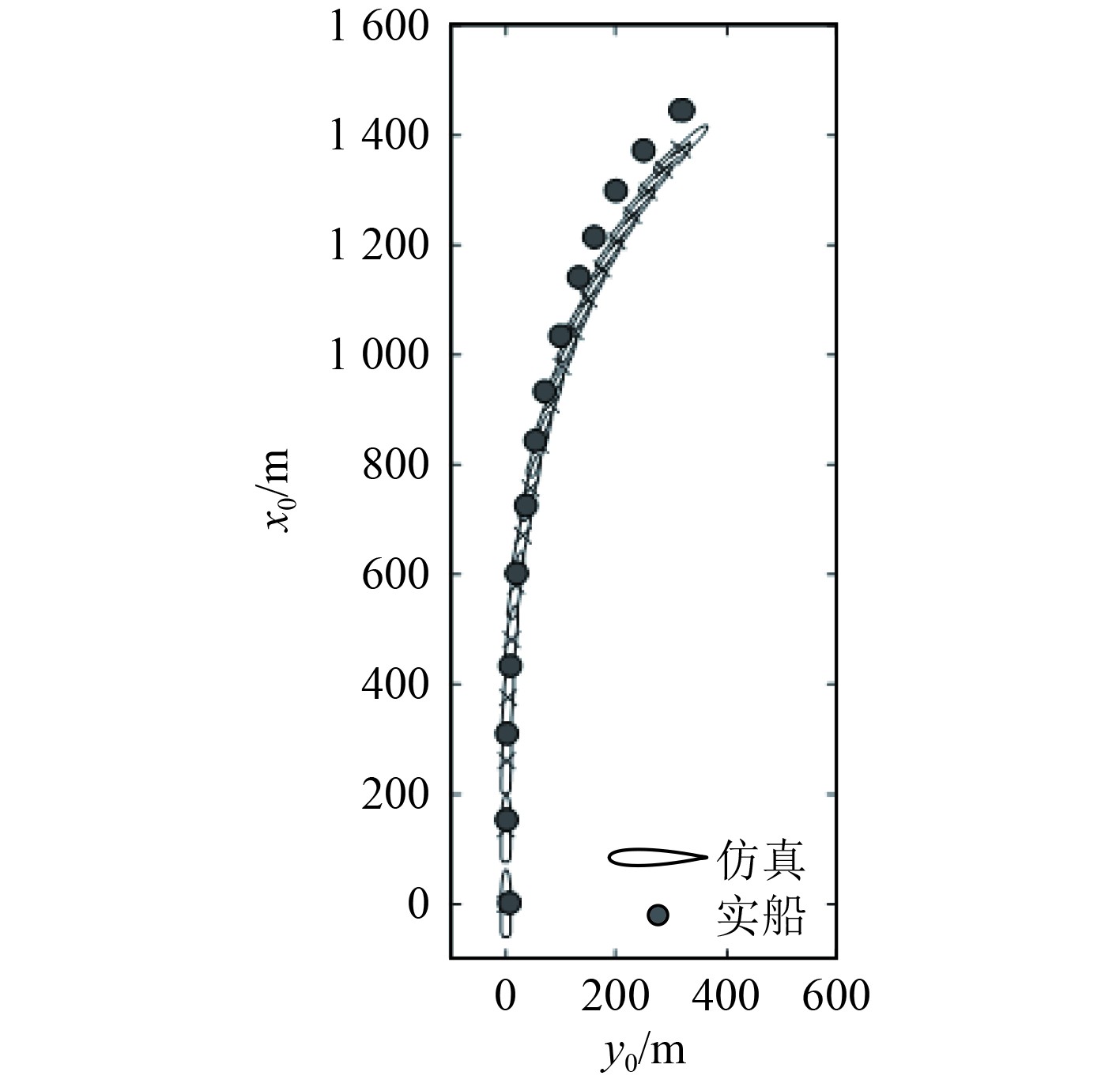
船舶停船仿真试验的初始条件为:航速12 kn、航向0° 、主机转速0 、风速4.0 m/s,风向70°。仿真时长400 s,仿真结果如图8和图9所示。比对结果如表6所示。
|
图 8 旋回运动轨迹对比 Fig. 8 Stopping motion trajectories |
|
|
表 6 停船试验结果对比 Tab.6 Comparison of stopping test results |
|
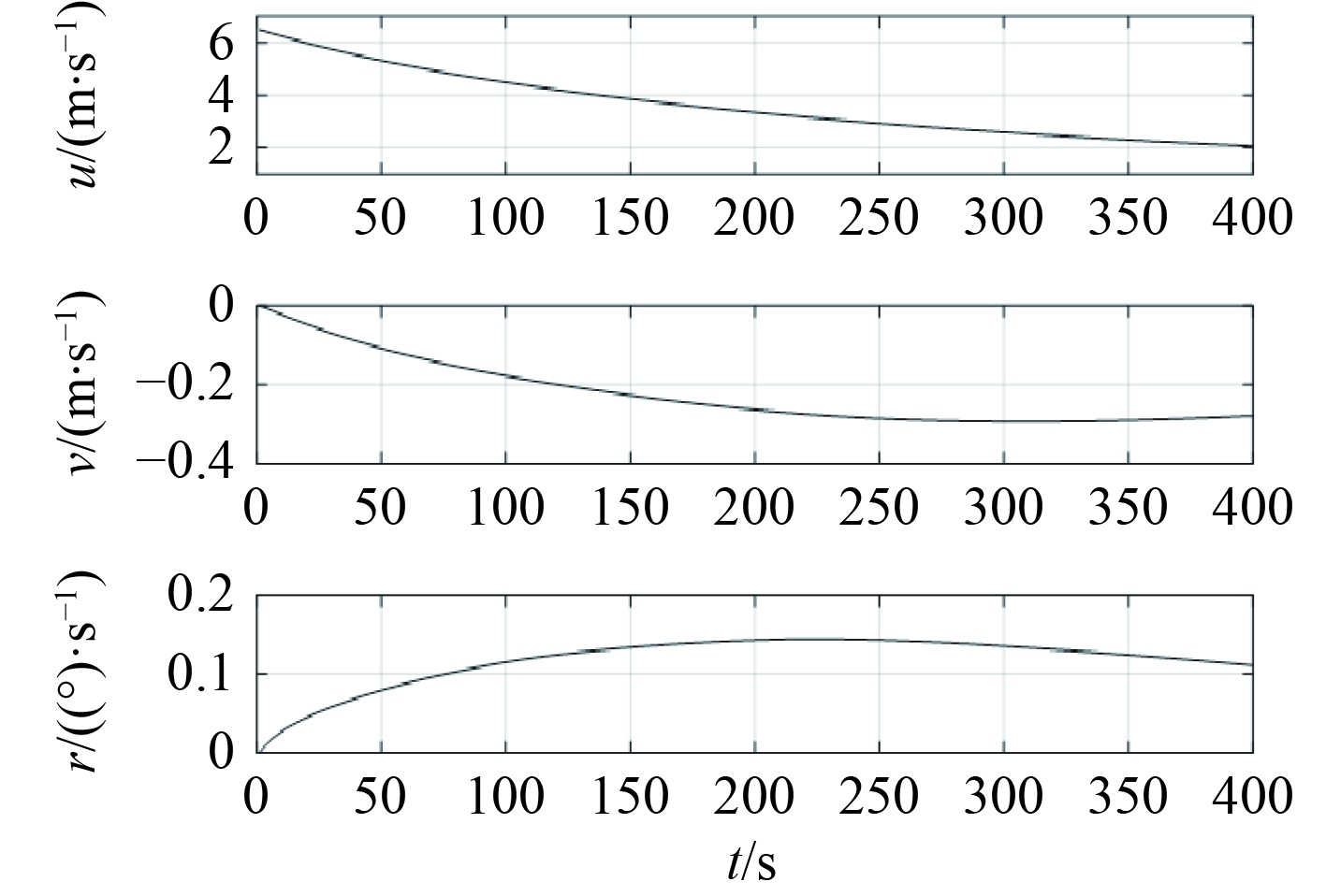
图 9 旋回动态性能 Fig. 9 Dynamic stopping performance |
由船舶旋回和停船仿真试验可知,所建模型操纵性符合度良好,误差值均小于10%,仿真结果符合实际,仿真精度满足工程需要。
3.3 风中拖锚漂航仿真试验本文以“北斗”轮风中拖锚漂航实船试验为例[13]进行风中拖锚漂航运动仿真,初始条件为:航速0 kn、横风风速15 m/s、水深22 m,泥底,锚链长2节。仿真试验时长8 min,仿真结果如图10和图11所示。比对结果如表7所示。
|
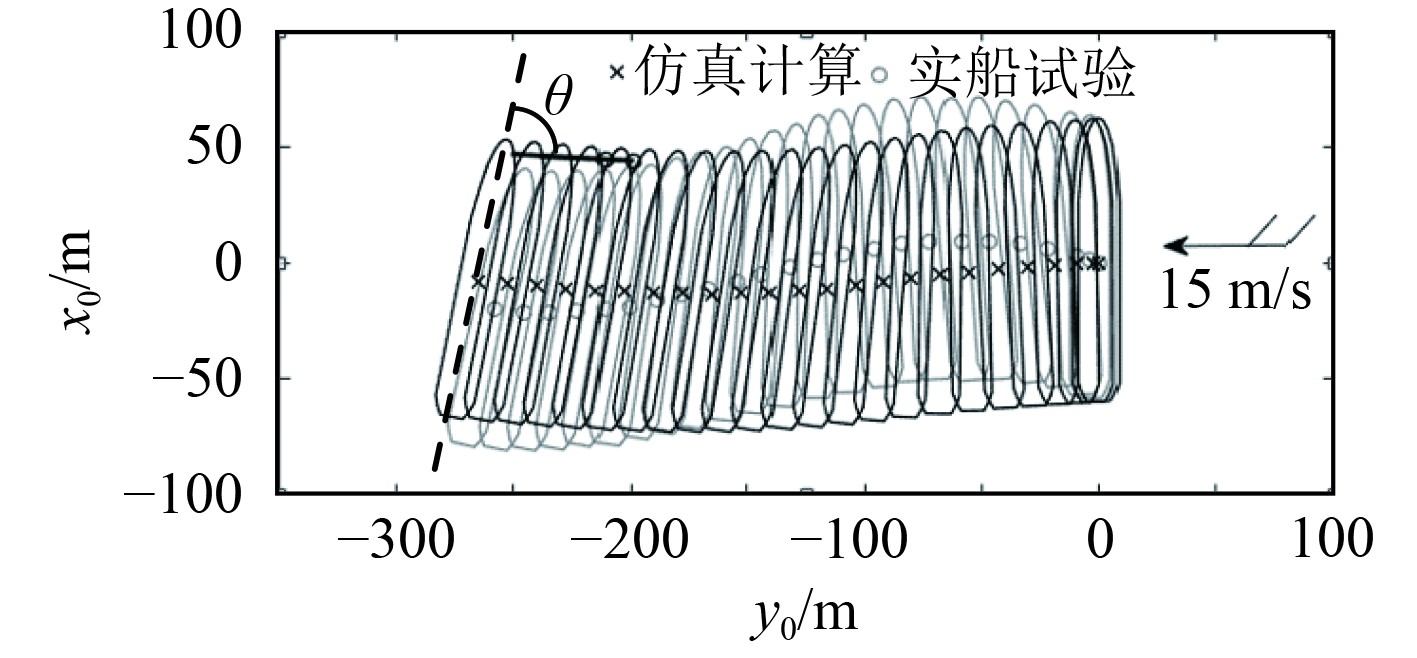
图 10 “北斗”轮拖锚漂航运动轨迹 Fig. 10 Trajectory of the "Beidou" ship's anchor-dragging |
|
|
表 7 拖锚漂航试验结果对比 Tab.7 Comparison of anchor dragging and drifting test results |
可知,由于船舶正横受风,导致船体横向漂移速度逐渐增加,最终由于锚链力及力矩和横流水动力及力矩的作用,横向漂移速度、锚链方位角和锚链张力逐渐趋于稳定;同时由于锚链力及力矩的作用使船舶最终的稳定状态既没有表现出固定锚泊船的偏荡运动,也没有表现出自由船舶风中的偏转规律,而是保持小于90°的风弦角向下风漂移,符合风中拖锚漂航的实际运动规律。
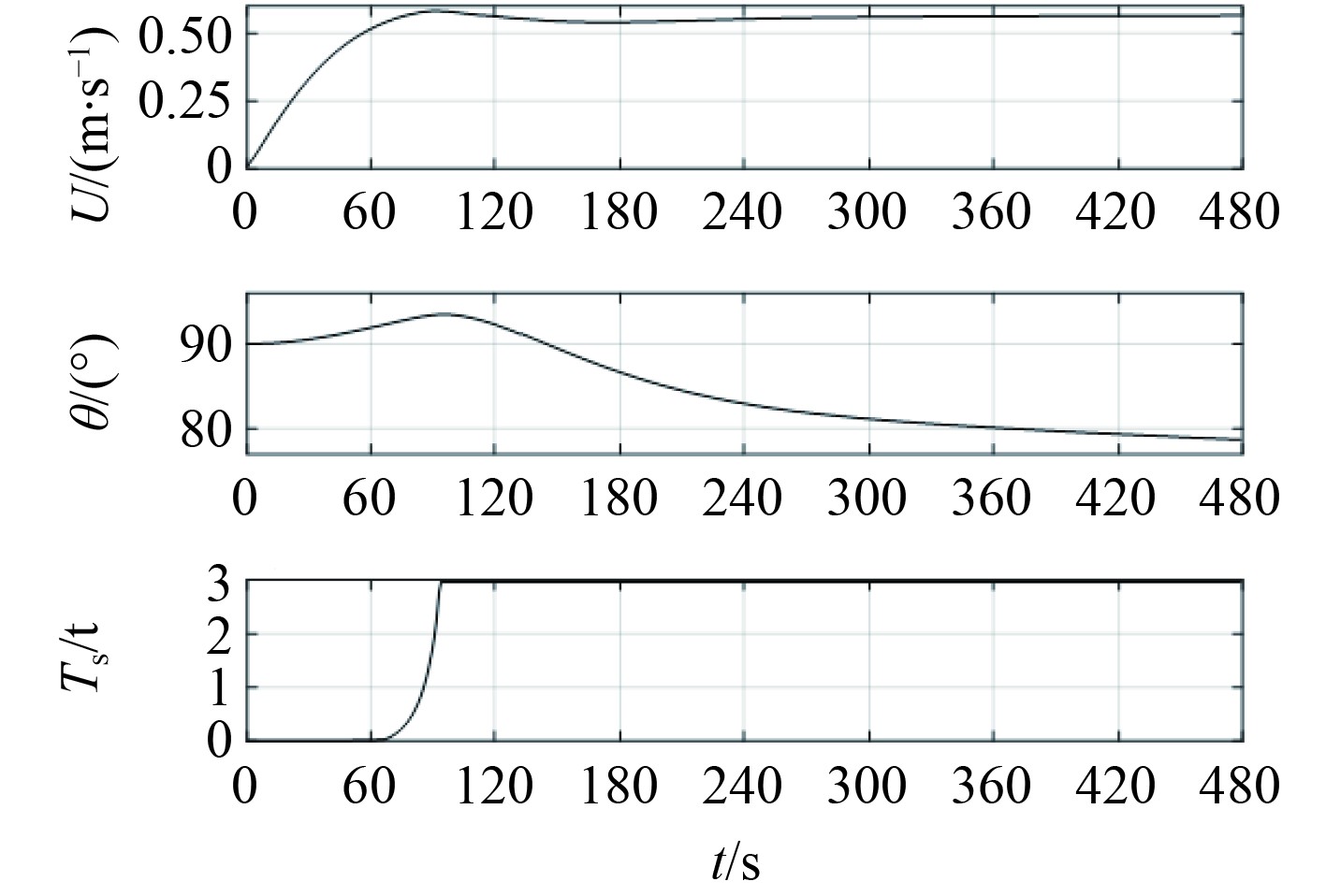
|
图 11 漂移速度、锚链角、锚链张力变化曲线 Fig. 11 U、θ 、Ts variation curve |
通过表7的相对误差可以看出,船舶拖锚漂航仿真试验结果与实船试验结果的符合度较好,与实船试验的最大误差为5.7%,能够满足工程及仿真的精度需求。通过对仿真结果的分析,更好理解了拖锚漂航的机制和影响因素,也进一步证明了本文拖锚运动数学模型的准确性。
4 结 语本文基于直接积分法,提出了一种在已知锚位、船位及出链长度即可计算锚链张力和构型方法建立锚链与锚力的计算模型,并将此锚链力计算模型与船舶运动数学模型耦合,建立全面的三自由度船舶拖锚运动数学模型。同时,以“北斗”轮为实船研究对象,根据实船实验条件及数据,对本文提出的拖锚运动数学模型进行仿真验证,开展了拖锚漂航仿真试验以及不同风速下的漂航运动分析,仿真结果与实船数据的相对误差均在6%以下,表明了本文拖锚运动数学模型的正确性和适用性。
| [1] |
WALTON T S, POLACHECH H. Calculation of transient motion of submerged cables[J]. Mathematics of Computation, 1960, 14: 27-46. DOI:10.1090/S0025-5718-1960-0116470-5 |
| [2] |
张峰, 朱克强, 蒋凯东. 海洋缆索系统运动仿真研究[J]. 港工技术, 2009, 46(2): 7-9. ZHANG F, ZHU K Q, JIANG K D. Motions simulation study of ocean cable system[J]. Port Engineering Technology, 2009, 46(2): 7-9. DOI:10.3969/j.issn.1004-9592.2009.02.003 |
| [3] |
ABLOW C M, SCHECHTER S. Numerical simulation of undersea cable dynamics[J]. Ocean Engineering, 1983, 10(6): 443-457. DOI:10.1016/0029-8018(83)90046-X |
| [4] |
WENNERSBERG, LARS A L. Modeling and simulation of anchor handling vessels[D]. Trondheim Norway: Norwegian University of Science and Technology, 2009.
|
| [5] |
蒋效彬. 船舶系泊系统的建模仿真与应用研究[D]. 大连: 大连海事大学, 2021.
|
| [6] |
刘文玺, 周其斗, 张纬康, 等. 浮体与系泊系统的耦合动力分析[J]. 船舶力学, 2014, 18(8): 940-957. LIU W X, ZHOU Q D, ZHANG W K, et al. Dynamic analysis of the coupled floating body/mooring system[J]. Journal of Ship Mechanics, 2014, 18(8): 940-957. DOI:10.3969/j.issn.1007-7294.2014.08.009 |
| [7] |
CHIOU R B, LEONARD J W. Nonlinear hydrodynamics response of curved singly connected cables[J]. Computer Modeling in Ocean Engineering, Balkema, Rotterdam, 1991, (1): 39−42.
|
| [8] |
SUN Y, LEONARD J W, CHIOU R B. Simulation of unsteady oceanic cable deployment by direct integration with suppression[J]. Ocean Engineering, 1994, 2(1): 243-256. |
| [9] |
贾兴乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999.
|
| [10] |
芳村康男ほか. 風力下で漂流する船舶の簡易数学モデルによる運動シミュレーション[J]. 日本船舶海洋工学会論文集, 2020, 3(1): 47-57. YOSHIMURA Y. Simulation of ship drift motion with a simplified mathematical model under the wind[J]. Journal of the Japan Society of Naval Architects and Ocean Engineers, 2020, 3(1): 47-57. |
| [11] |
洪碧光. 船舶操纵原理与技术[M]. 大连: 大连海事大学出版社, 2007.
|
| [12] |
新井康夫, 米澤弓雄, 河口信義, 等. 実船における船体運動の測定について[J]. 日本航海学会論文集, 1983, 68: 25−35. ARAI Y , YONEZAWA Y , KOGUCHI N , et al. The measurement of ship's path using the computer plotting system with the doppler sonar[J]. The Journal of Japan Institute of Navigation, 1983, 68: 25−35. |
| [13] |
矢吹英雄, 山下勝博, 斎藤重信. 実船実験における守錨基準の検討と錨泊状態モニタ装置の提案[J]. 日本航海学会論文集, 2003, 10(8): 67-74. YABUKI H, YAMASHITA K, SAITOH S. A study on standards of anchor watch in stormy weather and proposal of monitoring system for anchoring by means of full-scale experiments[J]. The Journal of Japan Institute of Navigation, 2003, 10(8): 67-74. |
 2025, Vol. 47
2025, Vol. 47
