近年来,海上无人电子侦察手段由于行动隐蔽、易于抵近等特点而受到广泛关注,相关技术趋于成熟,并逐渐开始投入使用。与此同时,海上电子侦察无源定位技术也在快速发展,其中在复杂电磁环境下纯方位无源定位的技术需求已经凸显迫切性[1],研究平台定位信号受到干扰条件下的目标无源定位方法,以此实现海上前出抵近侦察时的目标精确定位,确保极端情况下的海上电子侦察任务实施,相关技术成果将在未来无人平台侦察任务中具有广阔的应用前景。从近几年该领域的研究情况看,纯方位无源定位模型研究主要包括关注单个平台机动场景下基于纯方位信息进行目标定位[2 − 6],以及多平台协同侦察场景下通过方位交叉进行无源定位[7 − 10],缺少平台北斗定位功能受到干扰背景下进行多平台纯方位无源定位的技术和方法。因此,本文面向无人平台对海上目标前出抵近电子侦察的使用场景,在前出无人平台北斗定位功能受到干扰的情况下,提出对海上机动目标的多平台协同侦察无源定位方法,建立干扰条件下的伪量测线性方程,基于平方根衰减记忆滤波算法迭代求得目标实时位置,并对目标位置进行补偿校正,从而获得海上机动目标的精确位置解,仿真分析结果表明本文提出的方法明显优于传统方法。
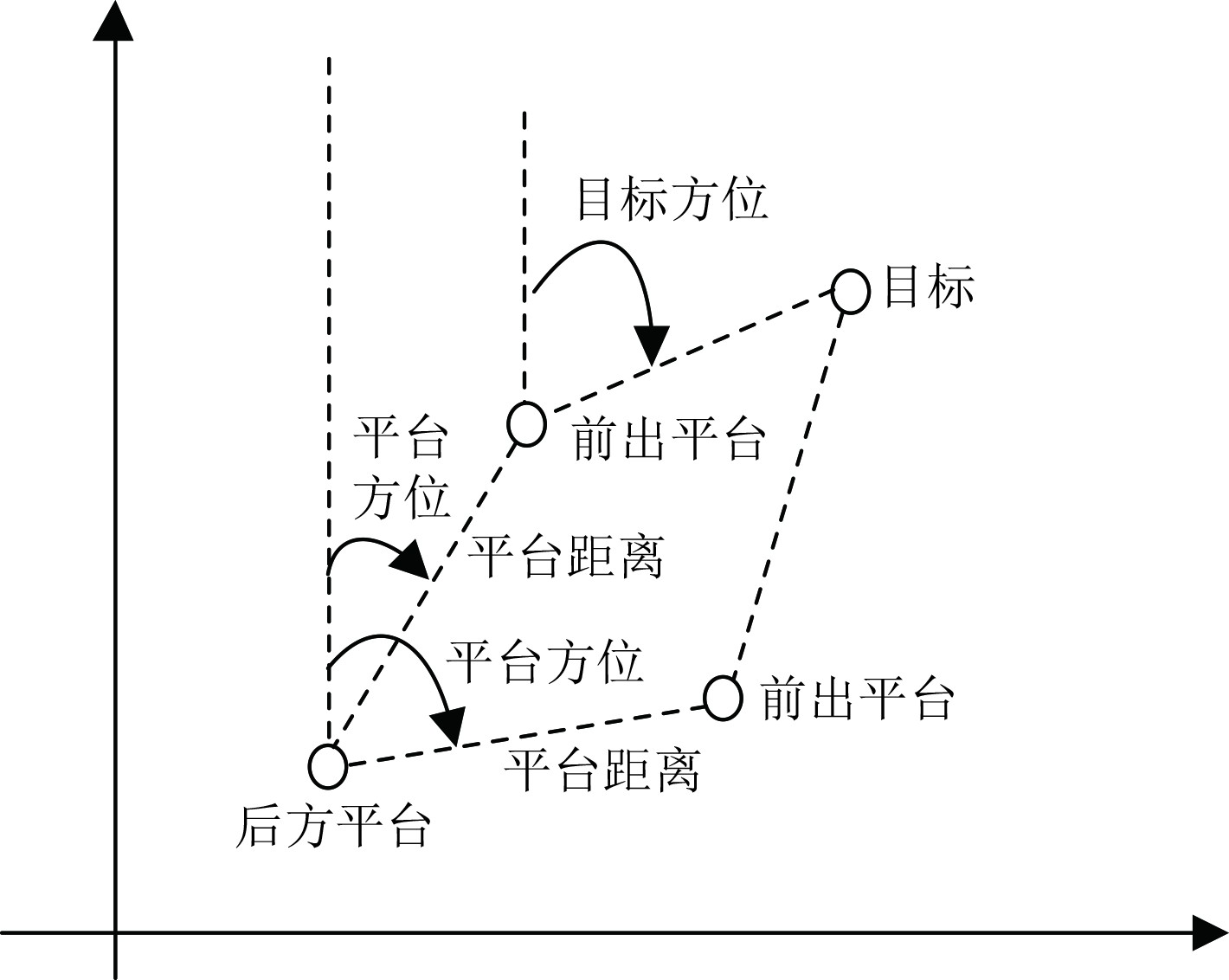
1 干扰条件下海上多平台无源定位模型本文干扰条件下的海上多平台无源定位模型是指在后方平台指挥下多个无人平台前出抵近侦察,当前出平台北斗定位信号受到干扰失去本平台定位信息时,联立后方平台探测己方前出平台的距离、方位以及前出平台探测的目标方位建立伪量测线性方程,从而获得干扰条件下针对机动目标的多平台无源定位模型,使其在极端条件下仍能够对目标进行精确定位(见图1)。
|
图 1 干扰条件下海上多平台纯方位无源定位示意图 Fig. 1 Bearing-only location of multiple platforms at sea under interference conditions |
设后方平台坐标为
| $ \mathrm{cos}{\beta }_{{i}}x-\mathrm{sin}{\beta }_{i}y-{T}_{i}\mathrm{cos}{\beta }_{{i}}{v}_{x}+{T}_{i}\mathrm{sin}{\beta }_{{i}}{v}_{y}={d}_{i}\mathrm{s}\mathrm{i}\mathrm{n}\left({\alpha }_{i}-{\beta }_{i}\right)+{v}_{i} 。$ | (1) |
式中:
| $ {E}\left({v}_{i}^{2}\right)={\|{d}_{i}\|}^{2}{u}_{i}^{2},$ | (2) |
| $ {{u}}_{{i}}^{2}=0.5\left(1-{{e}}^{-2{\mathrm{\sigma }}_{{i}}^{2}}\right)。$ | (3) |
设定待求目标初始状态
| $ \frac{1}{2}\sum_{\mathrm{i}=1}^n\left(Z-\mathrm{A}X_0\right)^2。$ | (4) |
其中:
| $ {X}_{0}=\left[\begin{array}{c}\begin{array}{c}x\\ y\end{array}\\ \begin{array}{c}{v}_{x}\\ {v}_{y}\end{array}\end{array}\right],$ |
| $ \boldsymbol{A}=\left[\begin{array}{cc}\begin{array}{cc}\mathrm{cos}{\beta }_{1}& -\mathrm{sin}{\beta }_{1}\\ \mathrm{cos}{\beta }_{2}& -\mathrm{sin}{\beta }_{2}\end{array}& \begin{array}{cc}-{T}_{1}\mathrm{cos}{\beta }_{1}& {T}_{1}\mathrm{sin}{\beta }_{1}\\ -{T}_{2}\mathrm{cos}{\beta }_{2}& {T}_{2}\mathrm{sin}{\beta }_{2}\end{array}\\ \begin{array}{cc} \vdots & \vdots\\ \mathrm{cos}{\beta }_{n}& -\mathrm{sin}{\beta }_{n}\end{array}& \begin{array}{cc}\vdots&\\ -{T}_{n}\mathrm{cos}{\beta }_{n}& {T}_{n}\mathrm{sin}{\beta }_{n}\end{array}\end{array}\right] ,$ |
| $ Z=\left[\begin{array}{c}\begin{array}{c}d_1\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha_1-\beta_1\right) \\ d_2\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha_2-\beta_2\right)\end{array} \\ \begin{array}{c}\vdots \\ d_n\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha_n-\beta_n\right)\end{array}\end{array}\right]。$ |
这里
通过求解无源定位模型,可得目标状态初始值
| $ {X}_{0}={\left({A}^{\rm T}\mathrm{A}\right)}^{-1}{A}^{\rm T}Z ,$ | (5) |
| $ {P}_{0}={\left({A}^{\rm T}{R}^{-1}\mathrm{A}\right)}^{-1}。$ | (6) |
式中:
| $ A_k^{\rm{T}}\mathrm{A}=\left[\begin{array}{cc}\begin{array}{cc}\displaystyle\sum_{i=1}^n\mathrm{cos}^2\beta_i & -\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i \\ -\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i & \displaystyle\sum_{i=1}^n\mathrm{sin}^2\beta_i\end{array} & \begin{array}{cc}-T_i\displaystyle\sum_{i=1}^n\mathrm{cos}^2\beta_i & T_i\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i \\ T_i\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i & -T_i\displaystyle\sum_{i=1}^n\mathrm{sin}^2\beta_i\end{array} \\ \begin{array}{cc}-T_i\displaystyle\sum_{i=1}^n\mathrm{cos}^2\beta_i & T_i\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i \\ T_i\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i & -T_i\displaystyle\sum_{i=1}^n\mathrm{sin}^2\beta_i\end{array} & \begin{array}{cc}T_i^2\displaystyle\sum_{i=1}^n\mathrm{cos}^2\beta_i & -T_i^2\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i \\ -T_i^2\displaystyle\sum_{i=1}^n\mathrm{cos}\beta_i\mathrm{sin}\beta_i & T_i^2\displaystyle\sum_{i=1}^n\mathrm{sin}^2\beta_i\end{array}\end{array}\right],$ |
| $ {A}_{k}^{\rm T}Z=\left[\begin{array}{c}\displaystyle\sum _{i=1}^{n}{d}_{i}\mathrm{cos}{\beta }_{i}\mathrm{sin}\left({\alpha }_{i}-{\beta }_{i}\right)\\ \begin{array}{c}-\displaystyle\sum _{i=1}^{n}{d}_{i}\mathrm{sin}{\beta }_{i}\mathrm{sin}\left({\alpha }_{i}-{\beta }_{i}\right)\\ -{t}_{i}\displaystyle\sum _{i=1}^{n}{d}_{i}\mathrm{cos}{\beta }_{i}\mathrm{sin}\left({\alpha }_{i}-{\beta }_{i}\right)\\ {t}_{i}\displaystyle\sum _{i=1}^{n}{d}_{i}\mathrm{sin}{\beta }_{i}\mathrm{sin}\left({\alpha }_{i}-{\beta }_{i}\right)\end{array}\end{array}\right] 。$ |
通过以上最小二乘模型可以求解目标跟踪时刻的初始状态值,当前出平台获取新目标量测时,可通过初始状态值继续迭代求解目标实时位置。假设目标为匀速直线运动,则系统状态方程可以表示为:
| $ X_{k+1}=\Phi\left(k+1,k\right)X_k+U_{k+1}。$ | (7) |
其中,
| $ \mathit{\Phi}\left(k+1,k\right)=\left[\begin{array}{cc}\begin{array}{cc}1 & 0 \\ 0 & 1\end{array} & \begin{array}{cc}T & 0 \\ 0 & T\end{array} \\ \begin{array}{cc}0 & 0 \\ 0 & 0\end{array} & \begin{array}{cc}1 & 0 \\ 0 & 1\end{array}\end{array}\right]。$ |
式中:
通过式(1),伪量测线性方程可以表示为
| $ z_{k+1}=H_{k+1}X_{k+1}+\mathrm{v}_{k+1},$ | (8) |
且
| $ {E}\left({v}_{k+1}^{2}\right)={R}_{k+1}={\|{d}_{k+1}\|}^{2}{u}_{k+1}^{2},$ | (9) |
| $ u_{k+1}^2=0.5\left(1-e^{-2\sigma_{k+1}^2}\right)。$ | (10) |
其中,
| $ z_{k+1}=d_{k+1}\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha_{k+1}-\beta_{k+1}\right),$ | (11) |
| $ H_{k+1}=\left[\begin{array}{cc}\begin{array}{cc}\mathrm{cos}\beta_{\mathrm{k}+1} & -\mathrm{sin}\beta_{k+1}\end{array} & \begin{array}{cc}0 & 0\end{array}\end{array}\right]。$ | (12) |
对于本文研究的定位模型系统式(7)和式(8),可采用传统的辅助变量伪线性卡尔曼滤波方法(PLKF)进行求解,并获得目标位置要素,计算方法为:
| $ X_{k+1|\mathrm{k}}=\mathit{\Phi}\left(k+1,k\right)X_{k|\mathrm{k}},$ | (13) |
| $ P_{k+1|k}=\Phi\left(k+1,k\right)P_{\mathrm{k}}\mathit{\Phi}\left(k+1,k\right)^{\mathrm{T}}+Q,$ | (14) |
| $ K_{\mathrm{k}+1}=P_{k+1|k}H_{k+1}^{\mathrm{T}}\left[H_{\mathrm{k}+1}P_{k+1|k}H_{k+1}^{\mathrm{T}}+R_{k+1}\right]^{-1},$ | (15) |
| $ X_{k+1|k+1}=X_{k+1|k}+K_{\mathrm{k}+1}\left(z_{k+1}-H_{\mathrm{k}+1}X_{k+1|k}\right),$ | (16) |
| $ \boldsymbol{P}_{\mathrm{k}+1}=\left(I-K_{\mathrm{k}+1}H_{k+1}^{\mathrm{T}}\right)\boldsymbol{P}_{k+1|k},$ | (17) |
| $ \begin{split} & X_{k+1}^{BC}=X_{k+1}+\left(H_{k+1}^{\mathrm{T}}R_{k+1}^{-1}H_{k+1}+\boldsymbol{P}_{k+1|k}^{-1}\right)^{-1} \\ &R_{k+1}^{-1}u_{k+1}^{-1}\boldsymbol{M}\mathrm{^T}\left(\boldsymbol{M}X_{k+1|k}-\gamma_{\mathrm{k}+1}\right)。\end{split} $ | (18) |
式中:
| $ \boldsymbol M=\left[\begin{array}{cc}\begin{array}{cc}\begin{array}{c}1\\ 0\end{array}& \begin{array}{c}0\\ 1\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\right] ,$ | (19) |
| $ \gamma_{\mathrm{\mathit{k}}+1}=\left[\begin{array}{c}\mathrm{\mathit{d}}_{\mathrm{\mathit{k}}+1}\mathrm{cos}\left(\mathrm{\beta}_{\mathrm{k}+1}\right) \\ \mathrm{\mathit{d}}_{\mathrm{\mathit{k}}+1}\mathrm{sin}\left(\mathrm{\beta}_{\mathrm{k}+1}\right)\end{array}\right]。$ | (20) |
由于海上目标在实际环境中一般存在运动状态突变的问题,所以需要针对相关问题对辅助变量伪线性卡尔曼滤波算法进行改进,以获得更为精确的目标位置估计结果。
2 基于平方根衰减自适应滤波的无源定位算法对于本文研究的定位模型系统,如果在目标运动状态存在突变的情况下使用标准卡尔曼滤波,将导致目标定位精度的下降,甚至可能引起滤波算法的发散。避免这种缺陷的一种途径是使用衰减记忆卡尔曼滤波,就是强调新近数据的作用,而逐渐遗忘陈旧数据,传统衰减记忆卡尔曼滤波计算步骤为:
| $ X_{k+1|\mathrm{k}}=\mathit{\Phi}\left(k+1,k\right)X_{k|\mathrm{k}},$ | (21) |
| $ \boldsymbol{P}_{k+1|k}=\mathit{\Phi}\left(k+1,k\right)\left(\lambda\boldsymbol{P}_{\mathrm{k}}\right)\Phi\left(k+1,k\right)^{\mathrm{T}}+Q,$ | (22) |
| $ K_{{k}+1}=\boldsymbol{P}_{k+1|k}H_{k+1}^{\mathrm{T}}\left[H_{{k}+1}\boldsymbol{P}_{k+1|k}H_{k+1}^{\mathrm{T}}+R_{k+1}\right]^{-1},$ | (23) |
| $ X_{k+1|k+1}=X_{k+1|k}+K_{{k}+1}\left(z_{k+1}-H_{{k}+1}X_{k+1|k}\right),$ | (24) |
| $ \boldsymbol{P}_{{k}+1}=\left(I-K_{{k}+1}H_{k+1}^{\mathrm{T}}\right)\boldsymbol{P}_{k+1|k}。$ | (25) |
从式(22)可知,相比标准卡尔曼滤波,由于引入衰减因子
针对定位模型系统,为了在目标运动状态突变情况下获得更好的定位效果,需要在伪线性滤波算法基础上引入衰减记忆滤波,同时为了使算法更加稳定,还需要在计算过程中进一步引入平方根算法,最终得到伪线性平方根衰减记忆滤波,算法步骤如下:
步骤1 获得同一个时刻k的多个平台方位量测,通过式(5)和式(6)求解目标初始状态
步骤2 若k+1时刻有新量测,计算目标预测状态
| $ {X}_{k+1|{k}}=\Phi\left(k+1,k\right){X}_{k|{k}},$ | (26) |
| $ \boldsymbol{S}_{k+1|k}=\Phi\left(k+1,k\right)S_k。$ | (27) |
步骤3 利用k时刻误差协方差矩阵
| $ K_{k+1}=\sqrt{\lambda_{k+1}}\mathrm{a}_{k+1}S_{k+1|k}F_{k+1}。$ | (28) |
其中,
| $ \lambda_{k+1}=\lambda_k+b,$ | (29) |
| $ F_{k+1}=\sqrt{\lambda_{k+1}}S_{k+1|k}^{\mathrm{T}}H_{k+1}^{\mathrm{T}},$ | (30) |
| $ H_{k+1}=\left[\begin{array}{cc}\begin{array}{cc}\mathrm{cos}\beta_{\mathrm{k}+1} & -\mathrm{sin}\beta_{k+1}\end{array} & \begin{array}{cc}0 & 0\end{array}\end{array}\right],$ | (31) |
| $ \mathrm{a}_{k+1}=\left(F_{k+1}^{\mathrm{T}}F_{k+1}+R_{k+1}\right)^{-1},$ | (32) |
| $ \mathrm{\mathit{f}}_{k+1}=\frac{1+\sqrt{\mathrm{\mathit{a}}_{k+1}\mathrm{\mathit{R}}_{k+1}}}{1-\mathrm{\mathit{a}}_{k+1}\mathrm{\mathit{R}}_{k+1}}。$ | (33) |
式中:
步骤4 利用k+1时刻的量测
| $ {X}_{k+1|k+1}={X}_{k+1|k}+{K}_{{k}+1}\left({z}_{k+1}-{H}_{\mathrm{k}+1}{X}_{k+1|k}\right)。$ | (34) |
步骤5 协方差矩阵
| $ {S}_{k+1}={S}_{k+1|k}\left(\mathrm{I}-{{a}}_{k+1}{{f}}_{k+1}{{F}_{k+1}F}_{k+1}^{\rm T}\right) ,$ | (35) |
| $ {P}_{k+1}={S}_{k+1}{S}_{k+1}^{\rm T} 。$ | (36) |
步骤6 对
| $ \begin{split}X_{k+1}^{BC}=&X_{k+1|k+1}+\left(H_{k+1}^{\mathrm{T}}R_{k+1}^{-1}H_{k+1}+P_{k+1|k}^{-1}\right)^{-1}R_{k+1}^{-1}u_{k+1}^{-1} \\ &M^\mathrm{T}\left(MX_{k+1|k}-\gamma_{k+1}\right)。\\[-4pt] \end{split}$ | (37) |
若获得新量测,则重复步骤2。
算法中在计算渐消因子
| $ \Delta\mathrm{z}_{k+1}^{\mathrm{T}}\Delta z_{k+1}\leqslant\tau\cdot trE\left(\Delta z_{k+1}\Delta\mathrm{z}_{k+1}^{\mathrm{T}}\right)。$ | (38) |
式(38)中
| $ \Delta z_{k+1}=z_{k+1}-H_{\mathrm{k}+1}X_{k+1|k}。$ | (39) |
当式(38)成立时,算法处于正常工作状态,否则根据式(29)计算
以上算法通过衰减记忆滤波来更好地对存在运动状态突变情况下的海上目标进行精确定位,并在滤波步骤中引入平方根分解算法以提高算法的稳定性,同时由于量测噪声不满足高斯白噪声分布,为了进一步修正定位偏差,通过对衰减记忆滤波算法得到的结果进行补偿修正,减少定位偏差,进一步提高定位结果的精度。
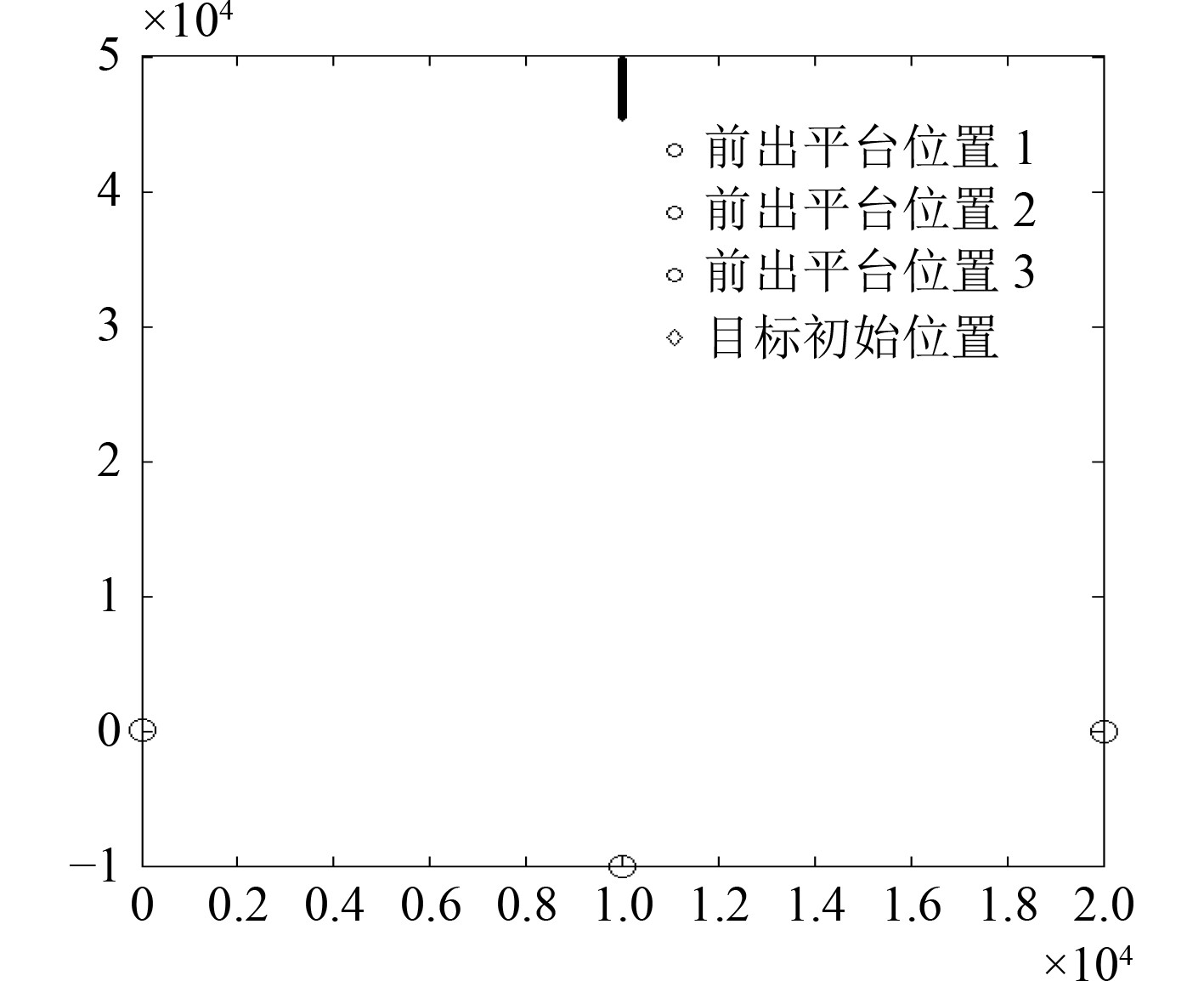
3 仿真分析为了验证算法的有效性,设置如下仿真场景,假设后方平台坐标
|
图 2 仿真场景示意图 Fig. 2 Simulation Scenario |
分别按目标匀速运动、目标速度状态突变、目标加速度状态突变共3组剧情仿真,分别进行100次蒙特卡洛试验,并采用均方根误差作为目标定位结果的评价指标,均方根误差定义如下:
| $ R\mathrm{M}\mathrm{S}\mathrm{E}={\left[\frac{1}{N}\sum _{\mathrm{k}=1}^{\mathrm{N}}\left[{\left({x}_{k}-x\right)}^{2}+{\left({y}_{k}-y\right)}^{2}\right]\right]}^{\frac{1}{2}} 。$ |
式中:
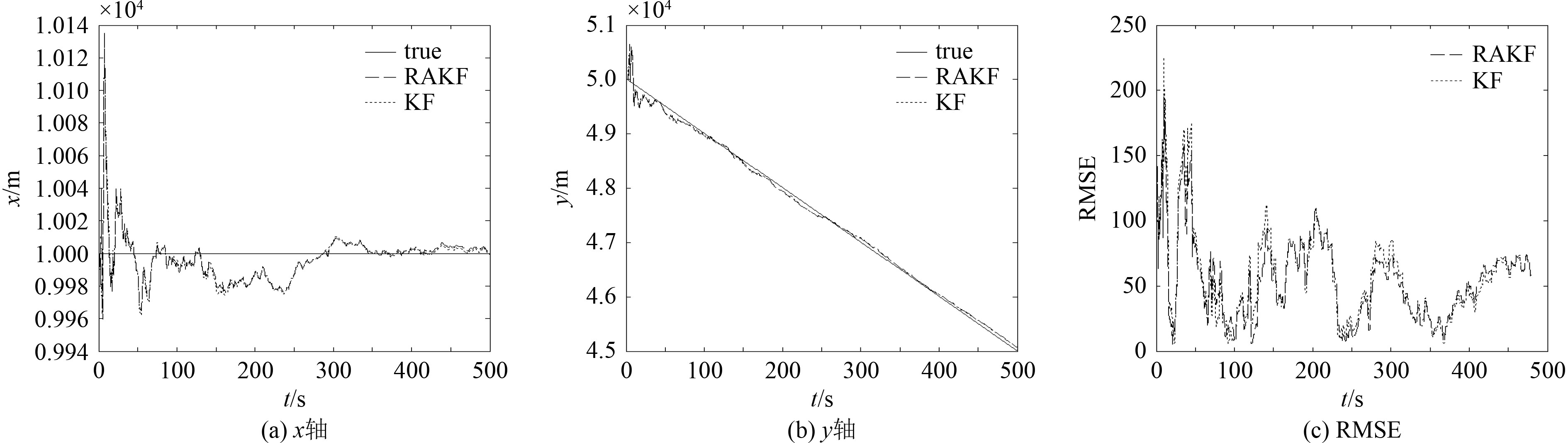
1)仿真场景1:目标运动状态为匀速运动,速度分量为
|
图 3 仿真场景1目标对比图 Fig. 3 Comparison of target location result in simulation Scenario 1 |
仿真场景1中方位观测噪声按照0.5°、1°、1.5°、2°、3°分别进行100次蒙特卡罗实验,统计2种方法的平均RMSE,结果如表1所示。
|
|
表 1 仿真场景1不同方位观测噪声协方差下的方法比较 Tab.1 Comparison of methods with different observation noise in the Scenario 1 |
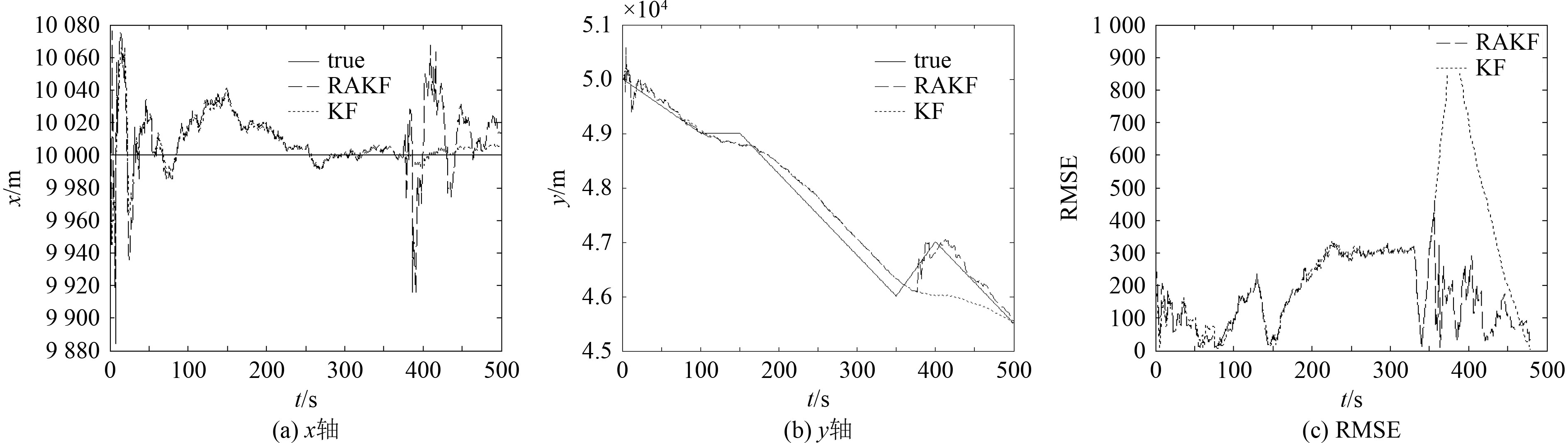
2)仿真场景2:目标运动状态存在速度突变,初始速度分量为
|
图 4 仿真场景2目标定位对比图 Fig. 4 Comparison of target location result in simulation Scenario 2 |
仿真场景2中方位观测噪声按照0.5°、1°、1.5°、2°、3°分别进行100次蒙特卡罗实验,统计2种方法的平均RMSE,结果如表2所示。
|
|
表 2 仿真场景2不同方位观测噪声协方差下的方法比较 Tab.2 Comparison of methods with different observation noise in the Scenario 2 |
3)仿真场景3:目标运动状态存在加速度突变,初始速度分量为
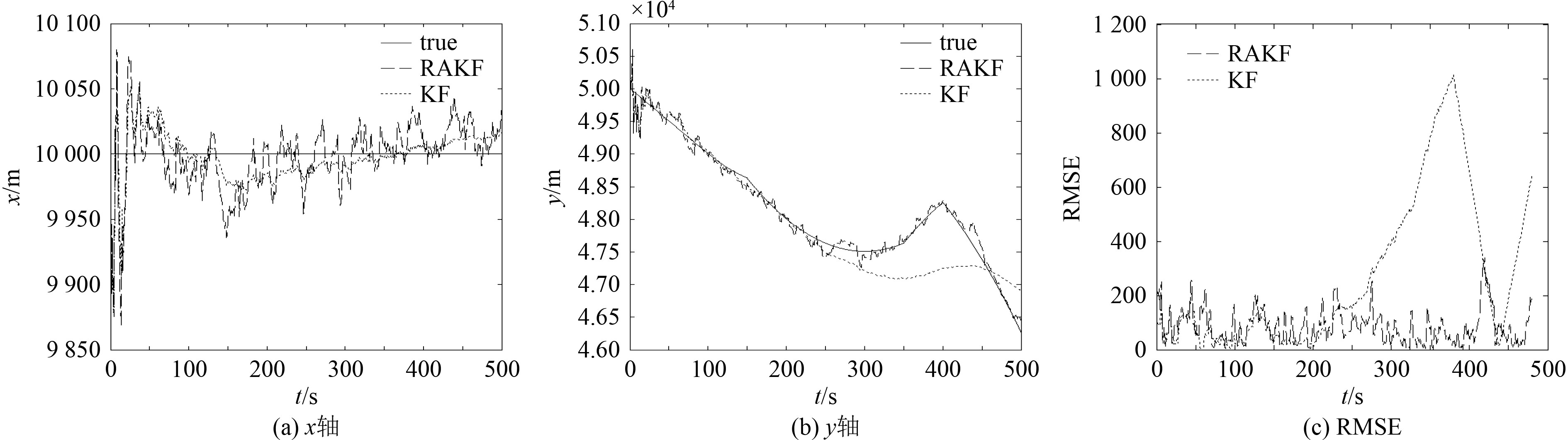
|
图 5 仿真场景3目标定位对比图 Fig. 5 Comparison of target location result in simulation Scenario 3 |
仿真场景3中方位观测噪声按照0.5°、1°、1.5°、2°、3°分别进行100次蒙特卡罗实验,统计2种方法的平均RMSE,结果如表3所示。
|
|
表 3 仿真场景3不同方位观测噪声协方差下的方法比较 Tab.3 Comparison of methods with different observation noise in the Scenario 3 |
由图3~图5可知,仿真剧情1中目标处于匀速状态,本文提出的算法和普通Kalman滤波算法性能基本一致,RMSE计算结果逐渐减小。仿真剧情2中目标有4次速度状态突变,仿真剧情3中目标有4次加速度状态突变,仿真结果均表现为x轴定位精度比普通Kalman滤波算法略差,但y轴定位精度比普通Kalman滤波算法高,尤其在第3次状态突变后,RMSE计算结果表明普通Kalman滤波算法逐渐有发散趋势,而改进方法依然有较好的结果。
表1~表3表明随着方位噪声的增加,平均RMSE指标将逐渐增加,但在同一场景的不同方位噪声下,本文提出的算法平均RMSE指标均明显要优于普通Kalman滤波算法。
综合3个仿真试验,本文算法在具有较高精度的同时,还能适应目标存在状态突变的情况,具有较小的精度结果,因此本文提出的算法明显优于普通Kalman滤波算法。
4 结 语本文提出一种海上多平台无源定位算法,构建了平台北斗信号受到干扰条件下的目标定位模型,通过衰减记忆滤波算法解算模型,在解算过程中引入平方根分解算法来提高算法的稳定性,并在衰减记忆滤波算法结果的基础上进一步校正目标位置,最后得到精度较高的定位结果。仿真结果表明,本文方法能够适用于干扰条件下的机动目标无源定位,并且定位精度高,稳定性好,有较大的应用价值。
| [1] |
李晓花, 苏骏, 李秀秀. 强干扰环境单观测站水下纯方位多目标跟踪[J]. 计算机工程与应用, 2021, 57(17): 253-259. DOI:10.3778/j.issn.1002-8331.2006-0044 |
| [2] |
张鲲, 沈重, 王海丰, 等. 海上侦察船的纯方位无源定位技术研究[J]. 舰船科学技术, 2018, 40(1): 19−21. ZHANG K J, SHEN Z, WANG H F, et al. Research on bearings only passive location technology for reconnaissance ship at sea [J], Ship Science and Technology, 2018, 40(1): 19−21. |
| [3] |
蔚婧, 文珺, 李彩彩, 等. 辅助变量纯方位目标跟踪算法[J]. 西安电子科技大学学报, 2016, 43(1): 167-172. |
| [4] |
舒象兰, 孙荣光, 马鑫. 一种改进的纯方位目标运动分析方法研究[J]. 舰船科学技术, 2015, 37(11): 124-127. SHU X L, SUN R G, MA X. Research on an improved bearing only target motion analyse method[J]. Ship Science and Technology, 2015, 37(11): 124-127. |
| [5] |
程善政, 陈双, 何心怡. 一种目标运动要素纯方位解算方法[J]. 舰船科学技术, 2020, 42(12): 129-132. CHENG S Z, CHEN S, HE X Y. A movement parameters calculating method base on bearings-only[J]. Ship Science and Technology, 2020, 42(12): 129-132. |
| [6] |
田德艳, 张小川, 邹司宸, 等. L2正则化粒子滤波在水下无人平台纯方位角跟踪的应用[J]. 舰船科学技术, 2020, 42(12): 111−116. TIAN D Y, ZHANG X C, ZHOU S C, et al. Application of L2 regularized particle filter in pure azimuth tracking of underwater unmanned platform[J]. Ship Science and Technology, 2020, 42(12): 111−116. |
| [7] |
吴旭, 杜选民, 周胜增. 基于双阵纯方位的水下运动目标运动分析研究[J]. 舰船科学技术, 2017, 39(5): 163−168. DU X, DU X M, ZHOU Z S. Research Framework Analysis of Anti-sea Striking Operation with Reconnaissance Satellite Information Support[J]. Ship Science and Technology, 2017, 39(5): 170−179. |
| [8] |
户文贵, 钟宗林. 船舶纯方位无源定位跟踪与数据关联研究[J]. 舰船科学技术, 2017, 39(11): 115-117. HU W G, ZHONG Z L. Research on ship bearings only passive location tracking and data association[J]. Ship Science and Technology, 2017, 39(11): 115-117. |
| [9] |
盛 琥, 赵温波. 基于BLUE的双站纯方位跟踪算法[J]. 弹箭与制导学报, 2018, 38(6): 117−124.
|
| [10] |
林晓烘, 程志锋, 于莹, 等. 海上多无人机协同交叉定位的优化配置方法[J]. 火力与指挥控制, 2021, 46(12): 9-14. DOI:10.3969/j.issn.1002-0640.2021.12.002 |
 2025, Vol. 47
2025, Vol. 47
