0 引　言

在当前全球海运业务不断扩展的背景下，海上自主航行船舶的研发和应用显得尤为重要。自主航行技术旨在实现船舶的独立操作，无需人工干预即可安全有效地完成航行任务^[1]。这种技术的关键之一是避碰决策，即船舶在识别到潜在碰撞风险后能够自动采取措施避免碰撞，从而保障航行安全。为了实现这一目标，船舶不仅需要能够实时感知周围环境，还必须能够处理复杂的多船相遇情况，并做出精确的避碰决策。

在目前的研究中，关于多船避碰决策的探索普遍采用针对重点船舶的避碰策略或是基于分布式系统的决策方法，致力于为各船舶设计一条最优或接近最优的航线。周怡等^[2]依托于改良的DDPG算法与进阶的船舶领域模型进行了船舶避碰路径的规划研究，有效启用了水域船舶航线的监管功能，并在航线预测与其他船舶相交汇的情况下，启动警告调度机制，实现了碰撞预警功能。孙硕等^[3]通过四元安全领域的应用改善了人工势场法中固定障碍物斥力作用范围的问题，提出了依据船速动态调整避让领域范围的新模式，从而替换了固定阈值的障碍物斥力势场范围，使得避让距离由静态转向动态。尽管如此，现有的避碰策略多从本船的视角出发设计，导致船舶间的避让责任不明确，决策方案缺乏整体协同。鉴于此，刘钊等^[4]针对避碰决策中信息的高维性与动作的连续性特征，研究了基于双延迟深度确定性策略梯度（TD3）的船舶自主避碰策略，考虑了决策的合理性与实时性。张金奋等^[5]面对复杂水域条件下传统快速搜索随机树算法的低效问题，提出一种改进的基于自适应步长的快速搜索随机树算法，用于船舶避碰路径规划。王晋鑫等^[6]针对狭窄水域航行的挑战，引入一种结合人工势场法与模型预测控制的船舶智能变速避碰算法。以上算法能有效提供航速与航向决策，实现水域内的有效多船避让。然而，多船避碰决策的实际应用仍旧面临众多挑战，特别是多航行特征和复杂航线环境下避碰决策的协同性问题依然存在。

鉴于此，考虑多船会遇、避碰规则及船舶偏航等多航行特征，构建海上自主航行船舶避碰决策模型，旨在保证在复杂多变的海上环境中，船舶能够安全、高效地执行避碰策略，为海运业的持续发展提供理论依据。

1 海上自主航行船舶避碰决策多级优化

在常规航行条件下，船舶驾驶员在识别到本船与目标船之间可能发生碰撞的风险时，需要对面临的航行会遇场景进行详细分析，并基于此形成避碰决策指令，交由舵手执行^[7]。在执行指令过程中，驾驶员必须实时监控海域情况，并在情况变化时适时调整避碰策略，确保两船安全驶过。研究表明，船舶驾驶员的避碰决策过程实质上是一连串序贯决策任务的集合^[8]。对于避碰策略而言，不可能在避让行动开始之前预设全部动作直至结束，而必须根据实时环境在不同阶段调整策略^[9]。基于避碰决策空间，将探讨多样的航行特征因素对决策造成的影响，通过实时数据分析，评估海上环境变化对决策空间的实际反馈，并通过优化决策空间来确保获得最合适的避碰策略。

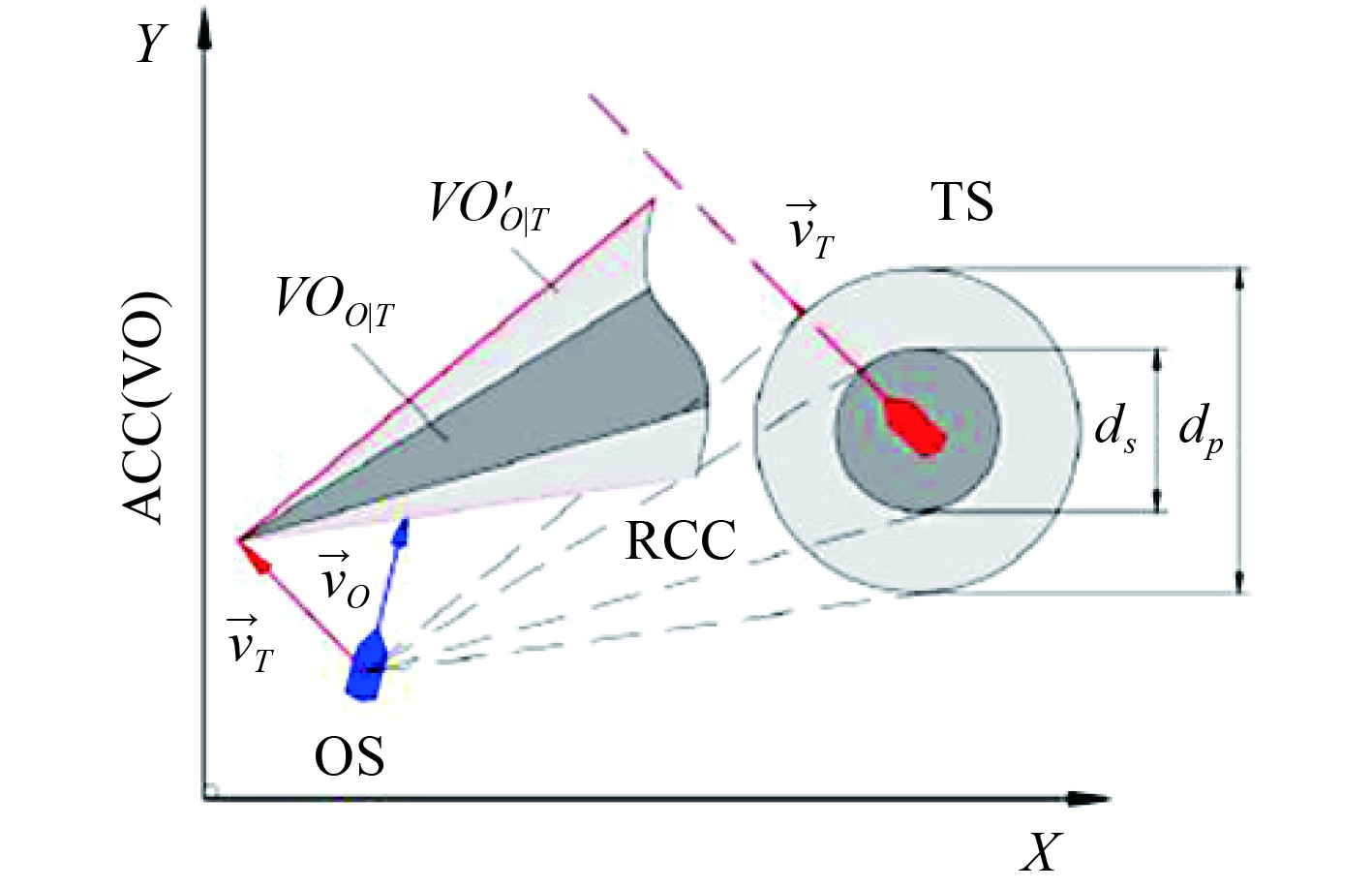
1.1 初始决策空间

避碰决策系统在面对可能产生碰撞的会遇情形时，利用视觉里程计（Visual Odometry，VO）算法制定初步避碰决策^[10]。在此框架下，会将导致本船发生碰撞的所有可能速度${\vec v_o}$集合定义为绝对速度障碍（Absolute Collision Cone，ACC）。相应地，可能导致碰撞的相对速度${\vec v_{{O}}} = {\vec v_O} - {\vec v_{T}}$的集合则被定义为相对速度障碍（Relative Collision Cone，RCC）^[11]。这2种速度障碍均在不同的速度空间中被构建，几何关系见图1，RCC通过沿矢量${\vec v_{\text{T}}}$的平移可以转换得到ACC。

以TS为中心${d_s}$为直径的区域即为${A_s}$，以OS为中心${d_p}$为直径的圆形区域即为${A_p}$。那么OS的狭义速度障碍为：

$ V{O_{O\mid T}} = \bigcup\limits_{{t_f}}^\infty {\left[ {\left( {\frac{{{{\vec d}_{OT}}\left( {{t_0}} \right)}}{{{t_f} - {t_0}}} + {{\vec v}_T}} \right) \oplus \frac{{{conf} P\left( {O,{d_s}} \right)}}{{{t_f} - {t_0}}}} \right]}。$

(1)

广义速度障碍为：

$ VO_{O\mid T}^\prime = \bigcup\limits_{{t_f}}^\infty {\left[ {\left( {\frac{{{{\vec d}_{OT}}\left( {{t_0}} \right)}}{{{t_f} - {t_0}}} + {{\vec v}_T}} \right) \oplus \frac{{{conf} P\left( {O,{d_p} - {d_s}} \right)}}{{{t_f} - {t_0}}}} \right]} 。$

(2)

式中：${t_f}$为碰撞时间；${\vec d_{OT}}\left( {{t_0}} \right)$为两船初始${t_0}$时刻的相对位置；TS对应的速度为${\vec v_T}$。将船舶的危险区域定义为目标船舶周围所有可能导致碰撞的我方船舶位置的集合，即冲突位置集合（Conflict Position，confp（O）），其中O表示参考点。

依据2个速度障碍的定义，OS的速度选择会受到影响。根据狭义速度障碍的规定，OS被禁止在区域$V{O_{O\mid T}}$内选择航速；而在区域$VO_{O\mid T}^\prime $内定义的广义速度障碍则允许航速选择，尽管该区域内的速度选择可能仍然具有潜在的风险，通常不推荐在此区域内选择高风险的航速。鉴于船舶在实际操作中需兼顾灵活性与操纵性，通常会通过改变航速和航向来实现避碰。

改变航向是采取的主要避碰手段，其中${A_{sl}}$、$ {A}_{sr}、{A}_{pl} $和${A_{pr}}$分别标示了$V{O_{O\mid T}}$和$VO_{O\mid T}^\prime $方向的航向边界。据此可以明确识别出狭义的航向障碍区域和广义的航向障碍区域，分别为$CCO = \left\{ {{C_0} \in \left( {{A_{sl}},{A_{sr}}} \right)} \right\}$和$BCO = \left\{ {{C_{\mathrm{o}}} \in \left( {{A_{pl}},{A_{sl}}} \right) \cup \left( {{A_{sr}},{A_{spr}}} \right)} \right\}$。

1.2 多船会遇约束

在多船会遇场景中，若存在与数艘船舶的碰撞风险，常规的避碰策略包括为每一艘潜在碰撞目标船计算绝对速度障碍，并将这些速度障碍汇总为1个并集。船舶需在此速度障碍并集之外选定新的航速以避免碰撞。同时，需确保该决策不会对初步未具碰撞风险的船舶造成新的危险^[12]。

设有m艘目标船舶存在碰撞风险，而n艘在当前状态下无碰撞风险。那么本船可选择航向表示^[13]为：

$ {{C}_0} \notin \left( {\sum\limits_{k = 1}^m V O_{O\mid T}^k \cup \sum\limits_{k = 1}^n V O_{O\mid T}^k} \right) 。$

(3)

虽然严格遵守此避碰原则可以确保航线安全，但在船舶众多的情况下，可能导致可选的航向空间过于狭窄，有时需要船舶做出较大角度的航向调整^[14]。这种决策与船舶的实际航行条件不符。

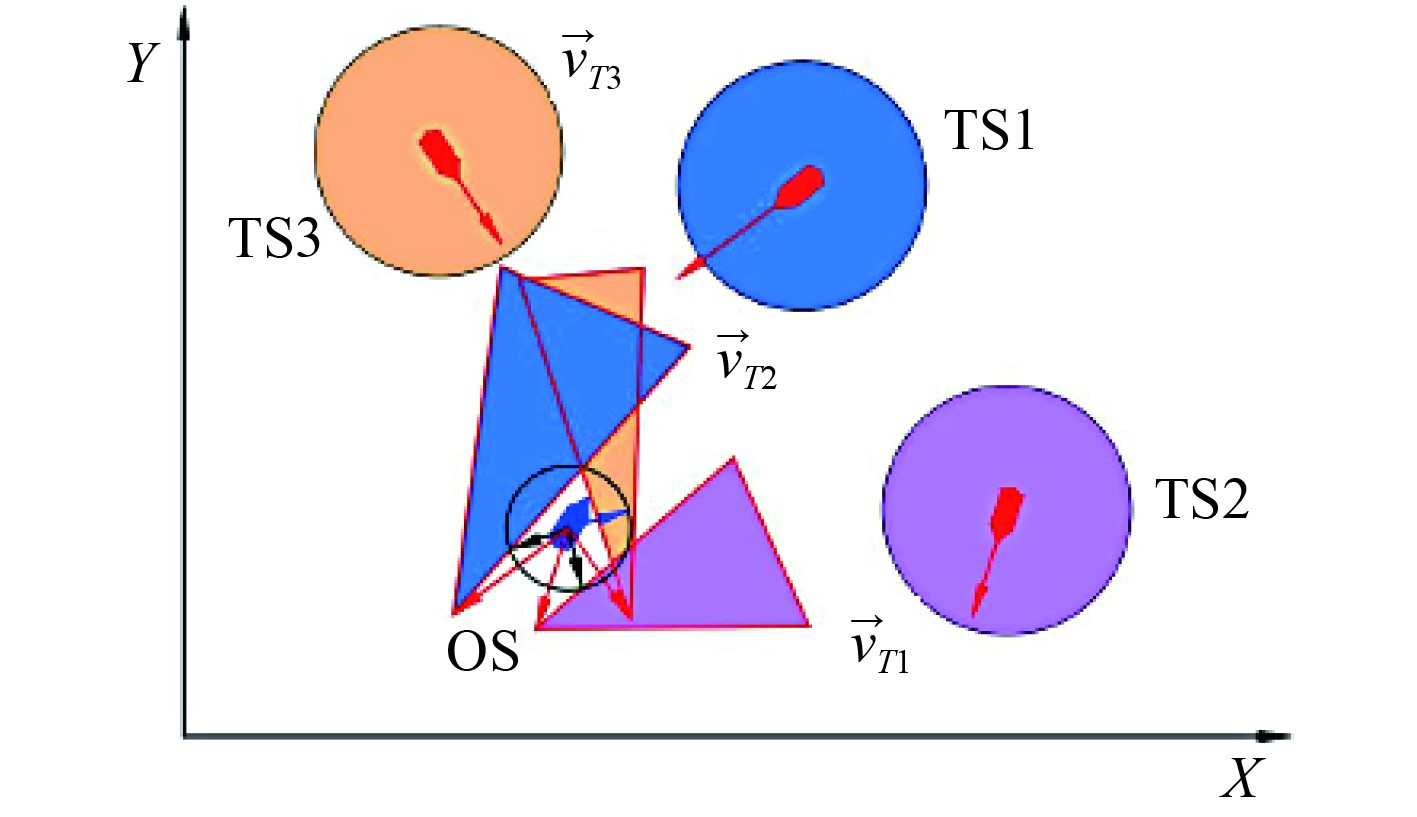
如图2所示，在多船会遇的情境下，OS当前与3艘目标船舶（分别标记为TS1、TS2、TS3）相遇，航速分别为$ {\overrightarrow{v}}_{T1}、{\overrightarrow{v}}_{T2}、{\overrightarrow{v}}_{T3} $。如果严格按照传统的VO算法进行避碰决策，安全的航速必须位于每艘目标船速度障碍的外部，即不能与图中所有阴影部分相交。在此情况下，VO算法选择的方向并不合理，实践中应选择方向与TS3的速度障碍区域略有重叠，但是最为合理。

针对上述多船会遇下的传统速度障碍算法存在的局限性，提议不再将速度障碍定义为船舶速度选择的完全禁区。而是改进为允许船舶在广义航向障碍区BCO内选择新的航向，但仍禁止在狭义航向障碍区CCO内选择航向。如果选定的航向位于BCO区域内，将引入一个代价函数以评估此决策的可行性及其潜在风险^[15]。定义如下：

$ {P_T}\left( {{C_O}} \right) = \left\{ {\begin{array}{*{20}{l}} {{{\left( {\dfrac{{{C_O} - {A_{pl}}}}{{{A_{pl}} - {A_{sl}}}}} \right)}^\alpha }，{\text{ if }}{C_O} \in \left( {{A_{sl}},{A_{pl}}} \right)}，\\ {{{\left( {\dfrac{{{A_{pr}} - {C_O}}}{{{A_{pr}} - {A_{sr}}}}} \right)}^\alpha }，{\text{ if }}{C_O} \in \left( {{A_{sr}},{A_{pr}}} \right)} 。\end{array}} \right. $

(4)

求解总的代价函数如下：

$ {{U}_{{\text{multi }}}}\left( {C_O^{opt}} \right) = \sum\limits_{k = 1}^m {w_T^k} P_T^k\left( {C_O^{opt}} \right) + \sum\limits_{k = 1}^n {P_T^k} \left( {C_O^{opt}} \right)。$

(5)

1.3 避碰规则约束

为了保障船舶的航行安全并有效防止碰撞事件，国际海上避碰规则（COLREGS）被广泛认定为在公海及其连接的所有航道上普遍适用的国际公约。该公约的核心内容涵盖了避让责任的具体规定、避碰操作的指导原则以及避让信号的使用等方面，对船舶执行避碰行为乃至海上碰撞事故的责任判断提供了重要的指导^[16]。随着海上自主航行船舶技术的持续发展以及未来智能船舶在海上运输行业中的新业态形成，预见到未来海上自主航行船舶与传统有人驾驶船舶将在长时间内并存的趋势。基于这些考虑，COLREGS应作为海上自主航行船舶在制定避碰策略时的关键参考标准。

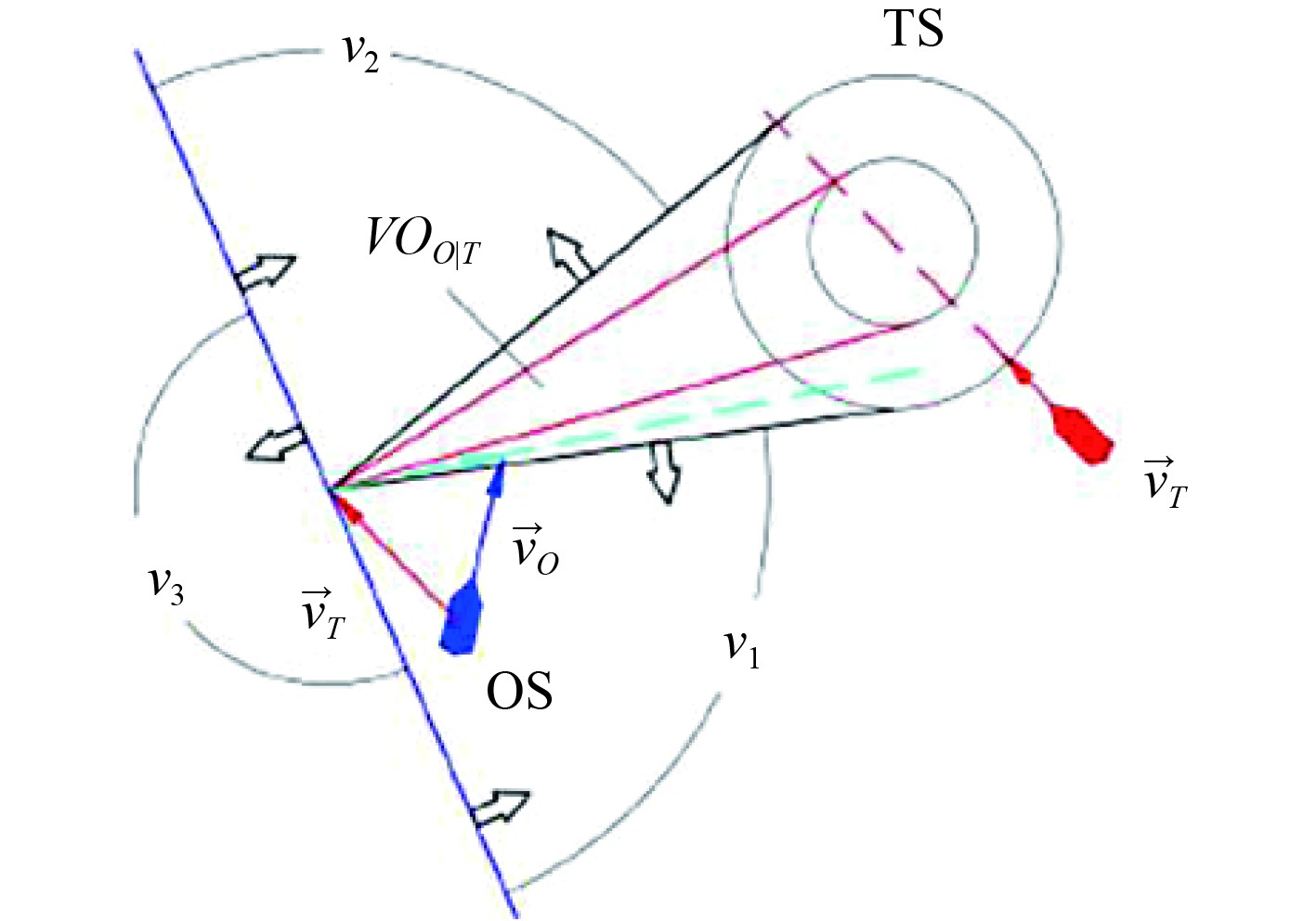
图3展示将速度障碍以外的速度空间细分为3个区域，垂直于VO区域的中心线与船舶当前位置与目标船TS的连线平行，即$\left( {{P_T} - {P_O}} \right)$。

若船舶选定图3中v₃区域的速度进行航行，将会逐渐与障碍船舶TS增加距离，该速度区域满足特定的不等式条件：

$ \left( {{P_T} - {P_O}} \right) \cdot \left( {{v_O} - {v_T}} \right) < 0。$

(6)

另一方面，当船舶在图3的${v_1}$区域选择速度航行时，将会从TS的右舷侧通过。在这种配置中，坐标系统以船首为X轴的正方向向前，Y轴的正方向向右，Z轴的正方向垂直向下。

在面对右舷交叉或正面对遇的航行情境时，按照国际海上避碰规则（COLREGs）的规定，船舶无法在${v_2}$区域内选择航速以进行避碰。此类规则引入的限制${v_0} \notin {v_1}$使得船舶必须采取从右侧（${{v_0} \in {v_1}} $）绕过障碍船TS的策略或选择向（$ {{v_0} \in {v_3}} $）方向驶离障碍船以实现避碰。

为了系统化地分析避碰决策，在避碰决策空间中融入规则性约束。规定在OS作为直航船航行时，其不受避碰规则的约束。而当OS承担让路船的角色，在遭遇对向（H₁，H₂）或交叉相遇（C₁，C₂，C₃）局面时，应根据避碰规则向右调整航向。此外，避碰规则所引入的代价函数定义^[17]如下：

$ P_{TS}^c\left( {{C_{OS}}} \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&{\left( {\overrightarrow {RP} \times \overrightarrow {RV_{TS}^{OS}} } \right) = 0}，\\ {0,}&{{{\left( {\overrightarrow {RP} \times \overrightarrow {RV_{TS}^{OS}} } \right)}_z} \geqslant 0} 。\end{array}} \right. $

(7)

式中：RP为OS相对于TS的位置；$\overrightarrow {RP} $为由OS位置指向某一TS位置的向量，定义z轴正方向朝下；OS相对于TS的运动矢量为$\overrightarrow {RV_{TS}^{OS}} $。

假设在与OS形成对遇或交叉相遇局面中，OS需让路的目标船（TS）数量为k，那么避碰规则对OS的约束可以表达为：

$ U_{rul}\left(C_{\mathrm{OS}}\right)=\sum\limits_{i=1}^kP_{TS-i}^c\left(C_{\mathrm{OS}}\right)。$

(8)

1.4 偏航约束

在船舶避碰决策制定时，必须OS当前的航行任务，通常情况下，OS按照预定的航线进行航行。当存在2个避碰角度能够提供类似的避碰效果时，应优先选择变化幅度较小的角度，以此避免过大的转向引发不必要的绕行，从而提升避碰效率。

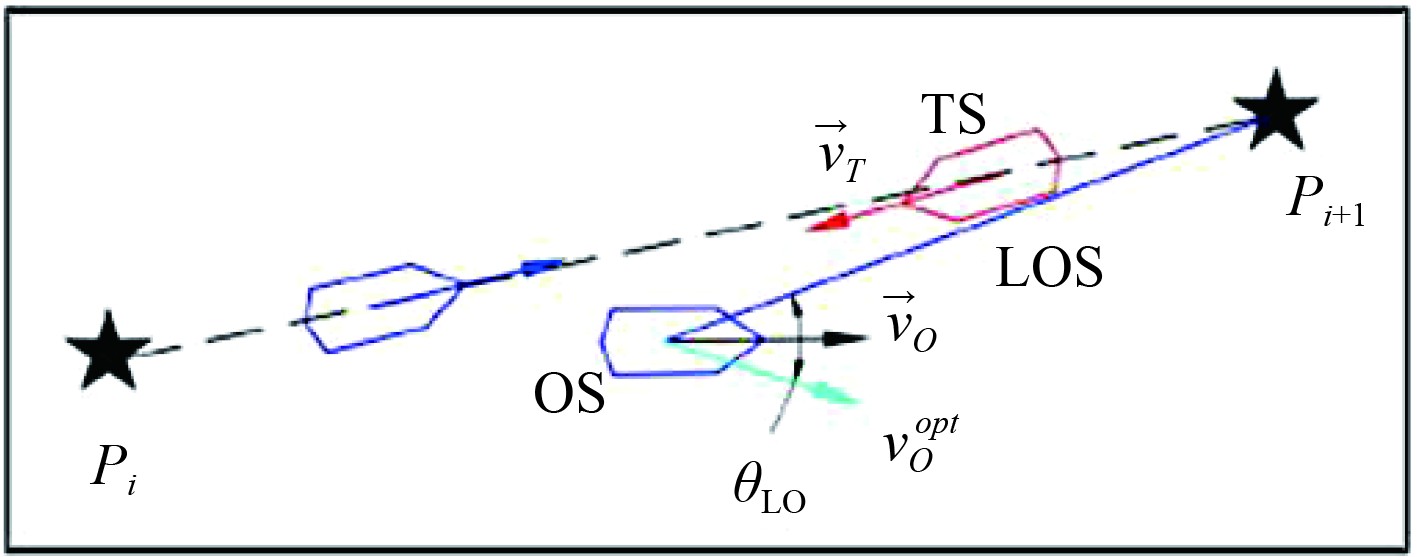
由图4可知，虚线代表船舶在2个航点${P_{{O}1}}\left( {{x_0},{y_{0}}} \right)$与${P_{{O}2}}\left( {{x_{{{O}}2}},{y_{{{O}}2}}} \right)$之间的预定航线，船舶在这2点间的理想航向${C_{LOS}}$可通过视线法确定：

$ {C_{LOS}} = \arctan \left( {\frac{{{x_{O2}} - {x_0}}}{{{y_{O2}} - {y_0}}}} \right) 。$

(9)

假设出现避碰需求，且存在2种潜在的航向选择${C_{LOS}} < 0$，若条件${C_{LOS}} = {C_{LOS}} + 2{\text{π}} $成立，则可以确定一个最优避碰航向以及期望航向${\theta _{{LO}}}$：

${\begin{aligned}[b] & {\theta _{LO}} =\\ & \left\{ {\begin{aligned} &{C_O^{opt} - {C_{LOS}}}，{{\text{ if }}\left( {C_O^{opt} - {C_{LOS}}} \right) \in [0,{\text{π}} ]} ，\\ &{2{\text{π}} - \left( {C_O^{opt} - {C_{LOS}}} \right)}，{{\text{ if }}\left( {C_O^{opt} - {C_{LOS}}} \right) \in ({\text{π}} ,2{\text{π}} ]} ，\\ &{ - \left( {C_O^{opt} - {C_{LOS}}} \right)}，{{\text{ if }}\left( {C_O^{opt} - {C_{LOS}}} \right) \in [ - {\text{π}} ,0)}，\\ &{\left( {C_O^{opt} - {C_{LOS}}} \right) + 2{\text{π}} }，{{\text{ if }}\left( {C_O^{opt} - {C_{LOS}}} \right) \in [ - 2{\text{π}} , - {\text{π}} )} 。\end{aligned}} \right. \end{aligned}}$

(10)

此时，两航向间的夹角${\theta _{LO}} \in [0,{\text{π}} ]$就成为评估航向调整必要性的关键参数。将偏航角的代价函数定义为：

$ {U_{{\text{rout }}}}\left( {C_O^{opt}} \right) = \frac{{\omega {\theta _{LO}}}}{\text{π}}。$

(11)

式中：$\omega $为权重，可以根据需要选取不同的数值，取1。

2 海上自主航行船舶避碰决策设计 2.1 目标船动态响应行为分析

在所有目标船（TS）保持原航向和速度的假设下，选择成本最低的COS作为最终的避碰策略，有效地解决了半动态场景中的船舶避碰难题。然而，海上避碰的实际情形中，TS的航行状态并非总是固定不变，存在行动的不确定性，TS或许会根据避碰规则调整航向和速度，抑或可能不遵循避碰规则，采取自主的动作。若继续依赖于固定的决策模型来处理避碰问题，则难以有效应对TS的这种动态响应行为。因此，深入探讨目标船在避碰过程中的动态响应特征，更全面地适应从半动态到全动态的场景变迁。

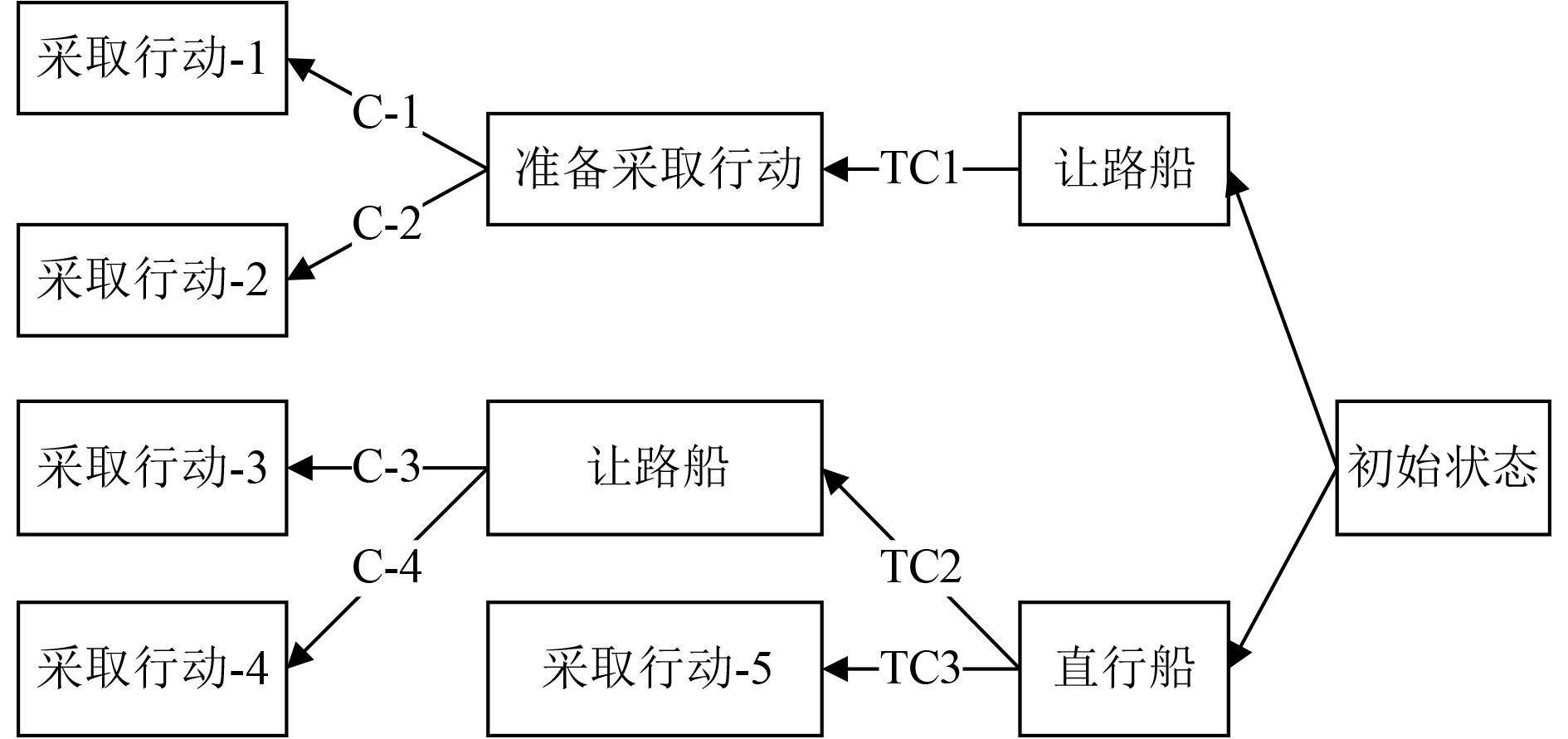
目标船的临时动作可能会违反已有的避碰规则，导致与OS的避让行为发生冲突。为了在避碰决策过程中全面考虑到目标船的这些动态响应行为，引入有限状态机（Finite State Machine，FSM）模型，该模型能有效地处理TS可能出现的各种不确定性行为，从而提高避碰决策方法的智能性和适用性，更贴近海上实际船舶的避碰场景^[18]。为此设计FSM模型，用于分析并应对避碰过程中目标船的动态响应行为，模型结构如图5所示。

2.2 考虑多航行特征要素的船舶避碰决策

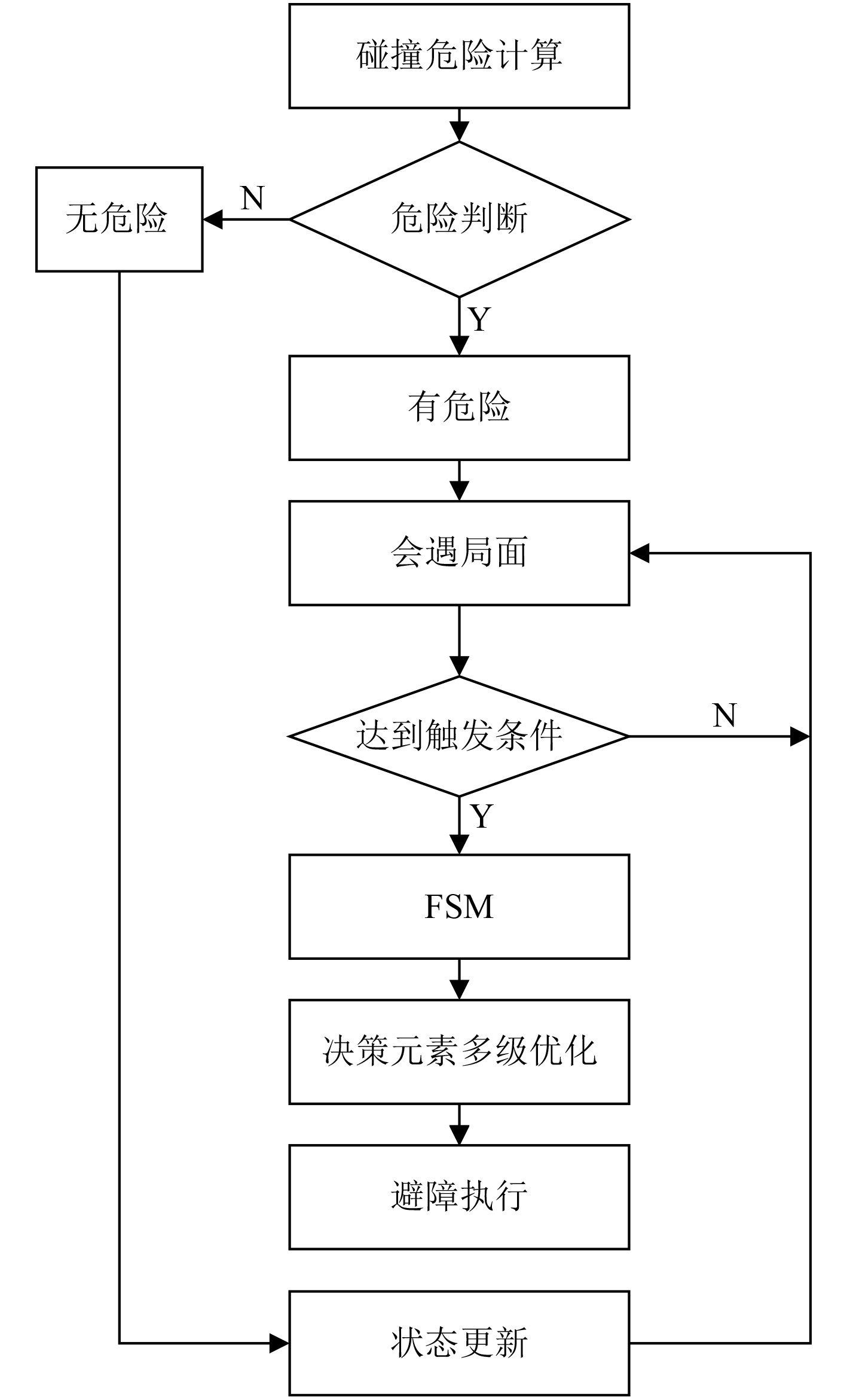
在船舶避碰决策方法中，纳入多种航行特征要素，如多船会遇情况、避碰规则、船舶偏航行为以及目标船在避碰过程中展现的动态响应行为。通过这些复杂航行特征的整合，可以确保制定出的避碰策略更加精准地符合海上实际的避碰场景需求。构建的船舶避碰决策模型涵盖多航行特征，如图6所示。船舶避碰决策模型主要是分析船舶间的碰撞风险并识别出具体的会遇情景，专注于基于这些航行特征要素的决策空间优化，信息流通和策略调整通过FSM来实现，以确保决策过程的连贯性和有效性。

在前端，船舶避碰决策模型采取基于指标的碰撞危险计算方法以评估风险^[19]。该阶段初始确定OS的状态，可为直航船或让路船。继而，有限状态机将评估是否满足触发条件TC-1、TC-2和TC-3。若其中任一条件得到满足，系统将转入相应的状态并执行必要的动作，包括调整后端决策空间的优化配置，以适应多航行要素的约束。若未满足任何触发条件，表明目标船（TS）的动作尚未影响或无需调整OS的避碰策略，因此系统将直接进入后端处理。通过有限状态机连接前后端，确保避碰决策方法能够全面考虑到目标船的动态响应行为这一关键的航行特征要素。

在后端，如果OS处于直航状态，则维持原航向和速度，输出决策为0。若OS为让路船，将依据避碰决策空间的优化方法操作。首先，建立初始的避碰决策空间，然后逐步引入船舶操纵性、多船会遇情况、避碰规则以及偏航的约束。通过结合这些航行特征要素的约束表达式，能够计算出针对OS任意航向的约束总和，确保航行的安全性与合规性。约束总和为：

$ \begin{split} {U_{{\text{sum }}}}\left( {{C_{OS}}} \right) = &{U_{{\text{multi }}}}\left( {C_O^{opt}} \right) +\\ &{U_{rul}}\left( {{C_{OS}}} \right) + {U_{{\text{rout }}}}\left( {C_O^{opt}} \right)。\end{split} $

(12)

计算得到当前时刻t₁本船的避碰决策为$C_{OS}^{opt}\left( {{t_1}} \right)$：

$\begin{aligned}[b] &{{U}_\mathrm{sum}^{{\hslash }_{1}}\left({C}_{OS}\right)= \left\{ \begin{array}{ll} 1\text{，} {U}_\mathrm{sum}\left({C}_{OS}\right)\geqslant 1 ，\\ {U}_\mathrm{sum}\left({C}_{OS}\right)\text{，} {U}_\mathrm{sum}\left({C}_{OS}\right) < 1，\end{array}\right. }\\ & {{U}_{\text{sum }}^{{\hslash }_{1}}\left[{C}_{OS}^{opt}\left({t}_{1}\right)\right]=\mathrm{min}{U}_{\text{sum }}^{{\hslash }_{1}}\left({C}_{OS}\right)} 。\end{aligned}$

(13)

3 海上自主航行船舶避碰决策算法仿真验证 3.1 两船会遇局面

场景1描述两船相遇的情形，初始函数（见表1）。在此场景中，OS的航速落在VO区域内，由此在会遇过程中引发碰撞的可能性，符合对遇情形的相关参数设定^[20]。当OS的速度矢量曲线与扩展后的冲突速度区域发生交集，便形成了对遇局面，此时双方均需调整其航向至右舷，以确保双方均能从对方的左舷安全通过。模拟实验主要旨在验证所提出的避碰策略的效果。在此过程中，所有的避碰措施均由OS独立执行，以展示避碰策略在实际应用中的独立有效性。

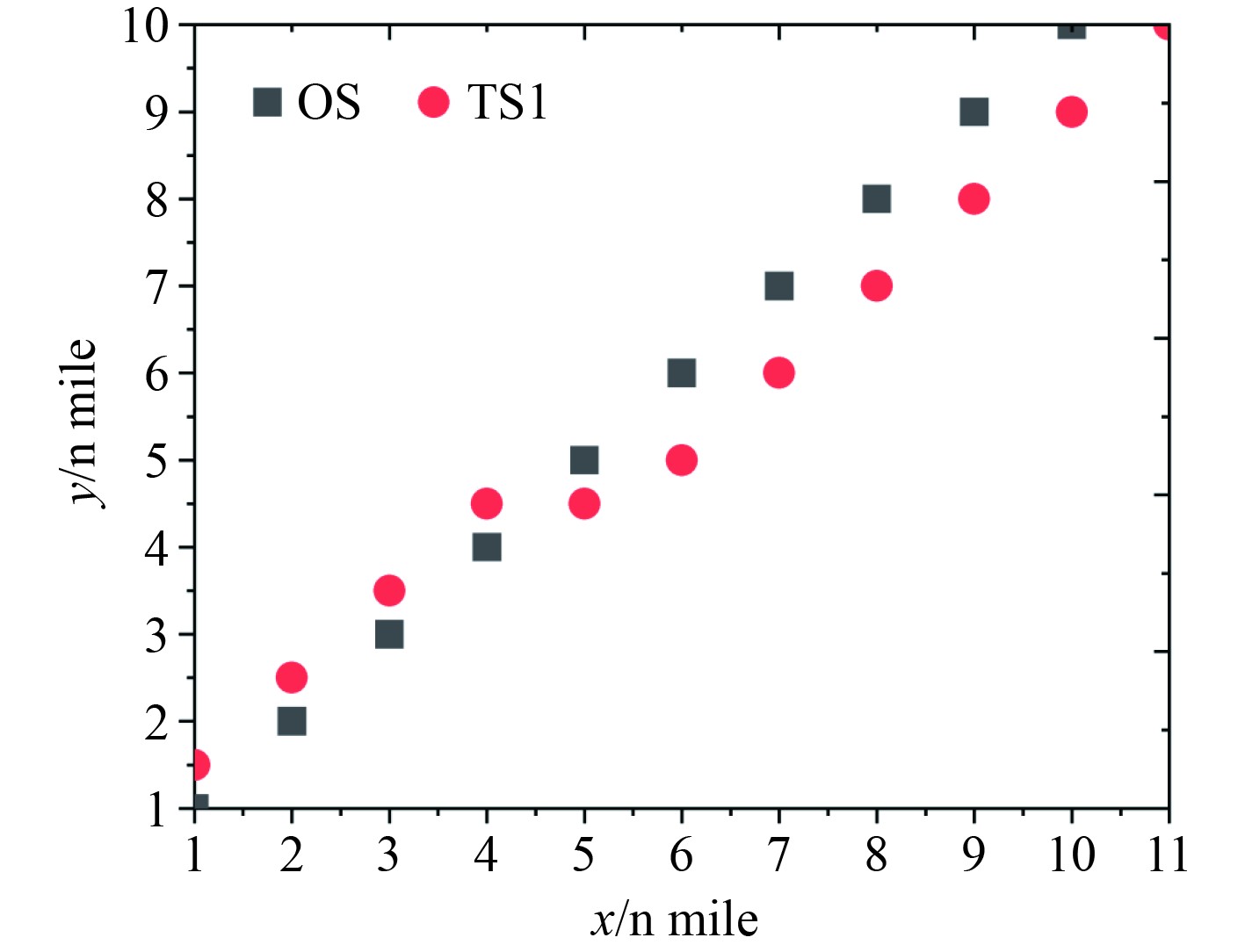
两船对遇局面仿真结果如图7所示。

通过仿真分析可知，在应用前述的自主航行船舶避碰决策算法后，OS将其航线向右舷侧调整了30°，有效避免进入目标船舶TS1的领域，符合整个避碰过程的安全性标准。OS的避碰行动对于TS1而言明确有效，且在整个过程中安全性得到了充分保障。

3.2 多船会遇局面

场景2涵盖5艘目标船（TS），初始信息（见表2）。在此场景中，OS与TS1、TS2及TS3在相似的交叉角度下彼此接近，而TS4正从西向东航行，TS5则从东向西航行，另外TS6作为静态障碍物存在于场景中。这种设置旨在模拟复杂的海上交通环境，检验避碰算法在多变条件下的适应性和反应效率。

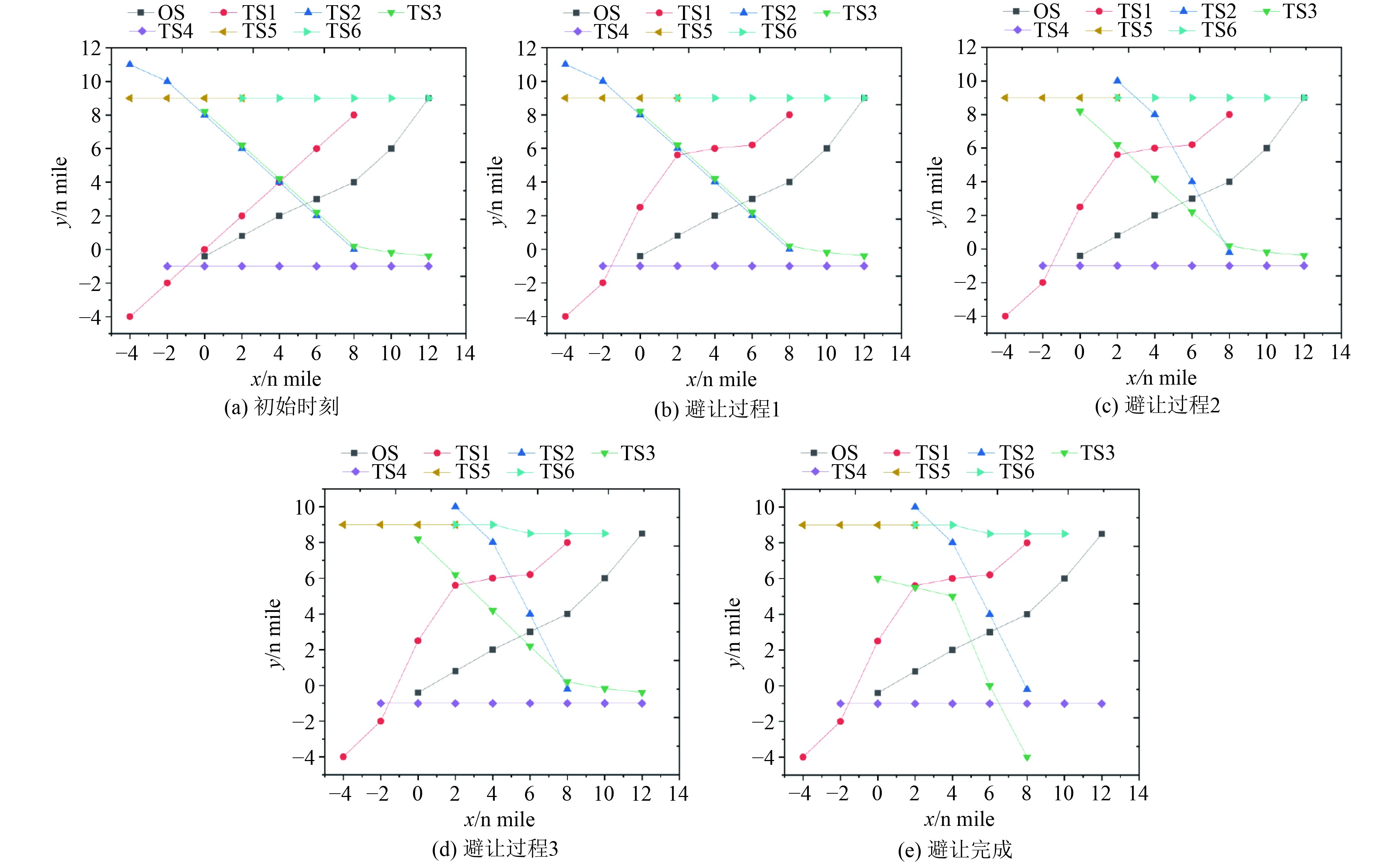
多船会遇仿真结果如图8所示。

在多船会遇的航行场景中，避碰过程通常分为4个阶段。在第一阶段，船舶之间的相对距离较远，碰撞风险相对较低，因此可以较为自由地采取各种航行行动。进入第二阶段，OS及TS1、TS2、TS3归为第一优化级别，而TS4、TS5、TS6则被划分到第二优化级别。在此阶段，第一优化梯队内的船舶需相互考虑避让关系，例如OS需让路给TS1和TS2，TS1应避让OS和TS3，TS2则需要避让TS1及TS3，而TS3则应避让OS和TS2。依据上述分析，OS向右调整航向23°以规避TS1和TS2的碰撞风险。第三阶段主要是解决OS与TS1、TS2、TS3之间的潜在碰撞风险。然而，在此阶段，新的会遇情况出现，分别涉及TS3与TS4、TS5与TS6。第四阶段中，TS3和TS4之间的碰撞风险依旧存在，由于TS3的速度初期位于碰撞风险区域，故存在明显的碰撞危险。在仿真情景中，TS1位于图像最左侧，与OS无碰撞风险；TS2位于图像最右侧且与OS形成交叉相遇的情况；TS3尽管距离OS最近，但由于初期正在通过OS的船首，因此与OS无碰撞风险；TS4和TS5都与OS对遇，分别位于OS的左右两侧。在海上自主航行船舶的避碰决策算法中，OS对TS2、TS4和TS5采取让路行动，而TS1和TS3因无碰撞风险，视为无需特别避让的船舶。OS根据规则要求向右转向，采取行动后能与这5艘TS保持在安全的会遇距离之外，有效地展示了避碰行动的广泛约束性。

4 结　语

综合考虑多船会遇、避碰规则及船舶偏航等关键因素，通过应用有限状态机模型，提出考虑多航行特征的海上自主航行船舶避碰策略。通过仿真发现，考虑多航行特征的海上自主航行船舶避碰策略能够实现两船会遇和多船会遇的有效避障。该方法使船舶避碰过程得以综合考量TS的各种潜在响应行为，从而更贴近海上实际避碰场景的需求。此模型的实施，不仅增强了对避碰策略的适应性和灵活性，也优化了避碰决策过程，确保船舶在多变的海上环境中能够高效安全地进行航行。