应用于船舶动力设备的双层隔振系统主要由动力设备、隔振器、筏体结构和基座结构等组成。设备机组运行时产生的振动通过双层隔振系统传递到基座,然后通过基座传递到船体结构,进而通过船体向水下辐射噪声。因此,在振动源一定的情况下,控制动力设备传递到船体振动的重要措施是传递路径控制,即采用高频隔振性能的隔振装置、优化基座结构等措施具有重要意义。
关于双层隔振系统的研究,国内外许多学者做了大量工作,但基于舰船圆柱壳结构的动力设备隔振系统研究报告有限。陈行[1]对汽车及船舶动力系统中的柴油机双层减振装置进行分析。牛昊轩[2]分析了内燃动力机组内的双层隔振系统,对其低频隔振器优化分析做了相关工作;李开程等[3]对列车用双层隔振系统隔振性能进行实验研究,实验表明该系统隔振性能良好;肖程诗等[4]提出4种浮筏隔振系统方案进行实验对比得到了在大型设备中浮筏隔振系统隔振器的选型依据。
双层隔振系统隔振性能的分析可从多角度入手。从筏体结构上,张伟等[5]对双层隔振系统中间质量进行整体式与分布式这2种形式隔振性能对比,研究表明分布式隔振效果优于整体式;田正东等[6]对隔振系统中插入阻振质量引起的阻抗失配,进行了实验分析,得到阻振质量对隔振系统起到一定的减振作用结论。李俊发[7]针对船舶风机双层隔振系统进行了灵敏度分析及性能测试;赵健学等[8]对双层隔振系统进行阻尼比、质量比、刚度比的调试来测算其对隔振性能的影响;聂振华[9]采用仿真实验对方钢阻振弯曲波传递进行分析,得到了多种布置方式对减振的影响;李飞[10]针对船舶辅机进行阻尼减振和阻振质量的实验,研究了一种复合结构的阻振基座,减少了设备的振动和辐射噪声;尼建军等[11]对海洋平台机座进行减振实验,研究表明阻振质量结合阻尼减振可使减振效果相比单独应用阻尼有较大程度的提高。分析双层隔振系统隔振能力时,力传递率一般作为最有效的隔振评价指标,但是作为工程实际问题难以准确测量,常见用振级落差作为隔振系统的评价指标[12 − 13]。
本文针对潜艇辐射噪声的控制问题,基于圆柱壳舱段结构,研究了其典型动力设备的双层隔振系统。建立了基于圆柱壳舱段结构的典型动力设备双层隔振系统模型,研究了筏体结构、阻振质量等参数对双层隔振系统隔振性能的影响规律。
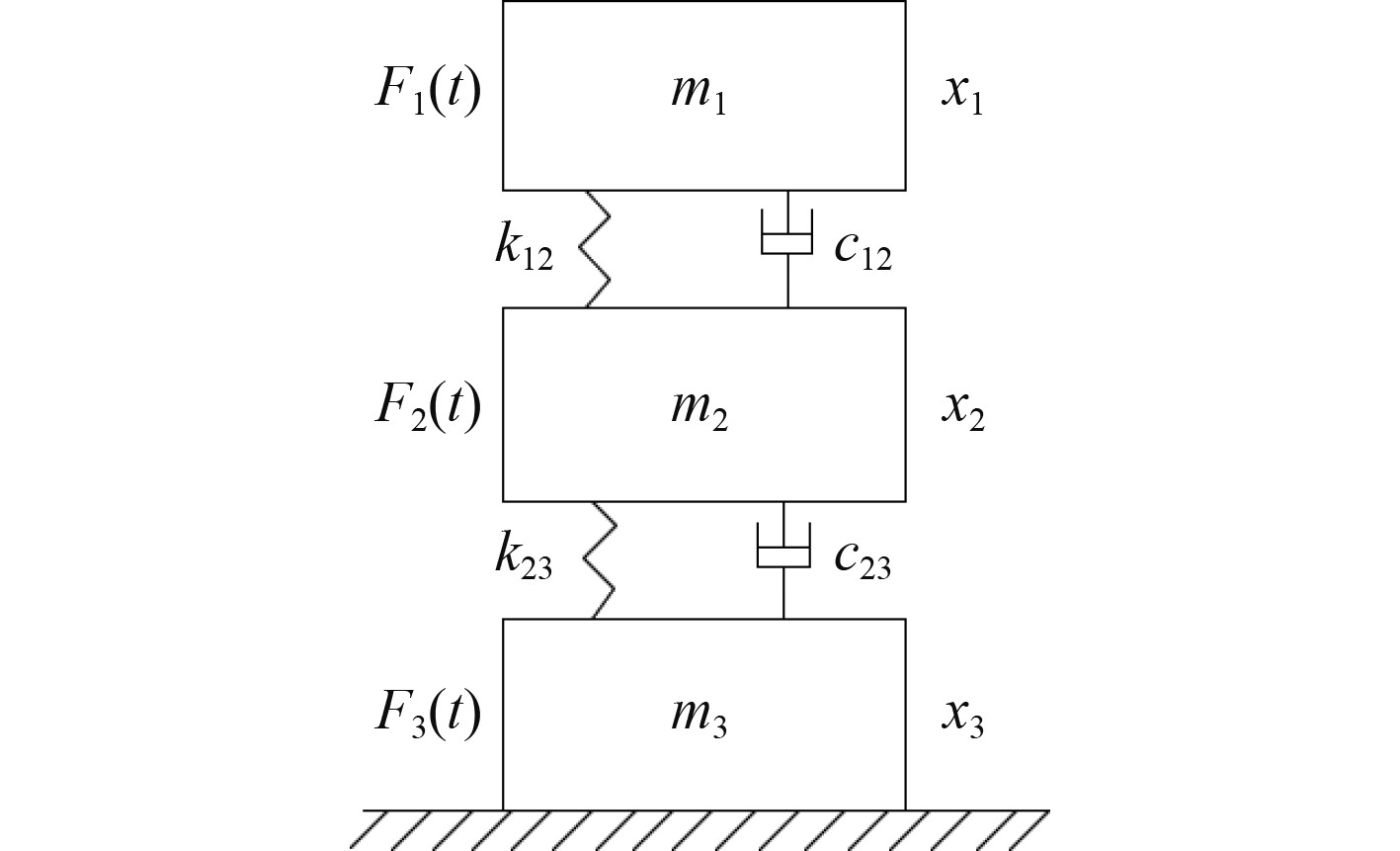
1 双层隔振系统隔振分析 1.1 双层隔振理论基础图1为典型双层隔振系统的示意图。该图包含3个部分质量,最下层是基础基座为m3;中间筏体质量为m2,上层机组设备为m1。双层隔振系统在设备与基座之间安装2层隔振器:k12、k23分别为上层与下层隔振器的刚度;c12、c23分别为上层、下层的隔振器的阻尼。
|
图 1 双层隔振系统 Fig. 1 Double-layer isolation system |
在分析双层隔振系统时,只考虑垂直方向上的振动衰减,图中F1(t)为激励力函数,为了简化问题,该激励力表达形式为:
| $ {F_1}(t) = {F_0}\sin (\omega t)。$ | (1) |
由双层隔振系统力学简化模型并与牛顿第二定律组合可以得到双层隔振系统的振动微分方程如下:
| $ \left\{ \begin{gathered} {m_1}{{\ddot x}_1} + {c_1}({{\dot x}_1} - {{\dot x}_2}) + {k_1}({x_1} - {x_2}) = {F_0}\sin (\omega t),\\ {m_2}{{\ddot x}_2} + ({c_1} + {c_2}){{\dot x}_2} - {c_1}{{\dot x}_1} + ({k_1} + {k_2}){x_2} - {k_1}{x_1} = 0。\\ \end{gathered} \right. $ | (2) |
根据2个自由度隔振系统列出如下方程表达式:
| $ \left\{ \begin{gathered} {F_1}(t) = {m_1}{x_1} + {c_{12}}({x_1} - {x_2}) + {k_{12}}({x_1} - {x_2}) ,\\ {F_2}(t) = {m_2}{x_2} + {c_{12}}({x_2} - {x_1}) + {k_{12}}({x_2} - {x_1}) + \\ {c_2}_3({x_2} - {x_3}) + {k_{23}}({x_2} - {x_3}),\\ {F_3}(t) = {m_3}{x_3} + {c_{23}}({x_3} - {x_2}) + {k_{23}}({x_3} - {x_2})。\\ \end{gathered} \right. $ | (3) |
式中:可以用相对坐标转化形式
将以式(3)联立可求得系统的响应
| $ {F_{23}} = {k_{23}}{\theta _2} + i\omega {c_{23}}{\theta _2} 。$ | (4) |
进而,可以推导出两自由度隔振系统的力传递率:
| $ {\mu _f} = \frac{{\left| {{F_{23}}} \right|}}{{\left| {{F_1}} \right|}} = \frac{1}{{\displaystyle\frac{{{n_1}^2}}{{{n_2}^2}}{{\left(\frac{\omega }{{n_1}}\right)}^4} - \left[1 + \left(1 + \frac{{{k_{23}}}}{{{k_{12}}}}\right) \frac{{{n_1}^2}}{{{n_2}^2}}\right]{{\left(\frac{\omega }{{{n_1}}}\right)}^2} + 1}} 。$ | (5) |
本文研究对象是基于圆柱壳舱段的某典型动力设备双层隔振系统。该典型动力设备的尺寸为580 mm×430 mm。质量为183 kg,如图2(a)所示。

|
图 2 典型动力设备双层隔振系统模型 Fig. 2 Typical double-layer isolation system model for dynamic equipment |
该双层隔振系统的中间筏体结构,如图2(b)所示。材料为结构钢;外型尺寸为580 mm×430 mm×127 mm;重量为80 kg。该双层隔振系统布置于圆柱壳舱段结构中。
圆柱壳舱段为潜艇的缩比模型。圆柱形舱段两端圆周直径为

|
图 3 圆柱形舱段模型 Fig. 3 Cylindrical cabin model |
根据机组质量为183 kg,中间筏架质量为80 kg,上层隔振器选用6个6JX-45,下层隔振器选用6个6JX-70。上下层隔振器都采用反向安装,以保证隔振器处于受压状态。由于机组质心偏移对此调整隔振器安装位置以满足隔振器静变形相同,双层隔振装置安装机组后上下层隔振器的静变形如表1和表2所示,可看出上下层隔振器变形均匀,满足隔振器布置要求。
|
|
表 1 上层隔振器布置 Tab.1 Layout of upper layer vibration isolators |
|
|
表 2 下层隔振器布置 Tab.2 Layout of lower level vibration isolators |
运用Ansys软件对隔振系统进行有限元分析时,主要输入隔振器3个方向上的刚度系数与阻尼系数,隔振器单元采用Bushing单元进行模拟。隔振器的阻尼系数计算公式为:
| $ {C_0} = 2\sqrt {mk},$ | (6) |
| $ \text{ξ} = \frac{C}{{{C_0}}} 。$ | (7) |
由式(6)、式(7)的组合变化得到式(8):
| $ C = 4{\text π} \text{ξ} fm 。$ | (8) |
式中:
|
|
表 3 隔振器参数 Tab.3 Vibration isolator parameters |
为避免系统共振,开展了基于圆柱壳体结构的动力设备双层隔振系统的模态特性分析。动力设备双层隔振系统的前20阶模态如表4所示,此处仅列出前4阶振型,如图4所示。
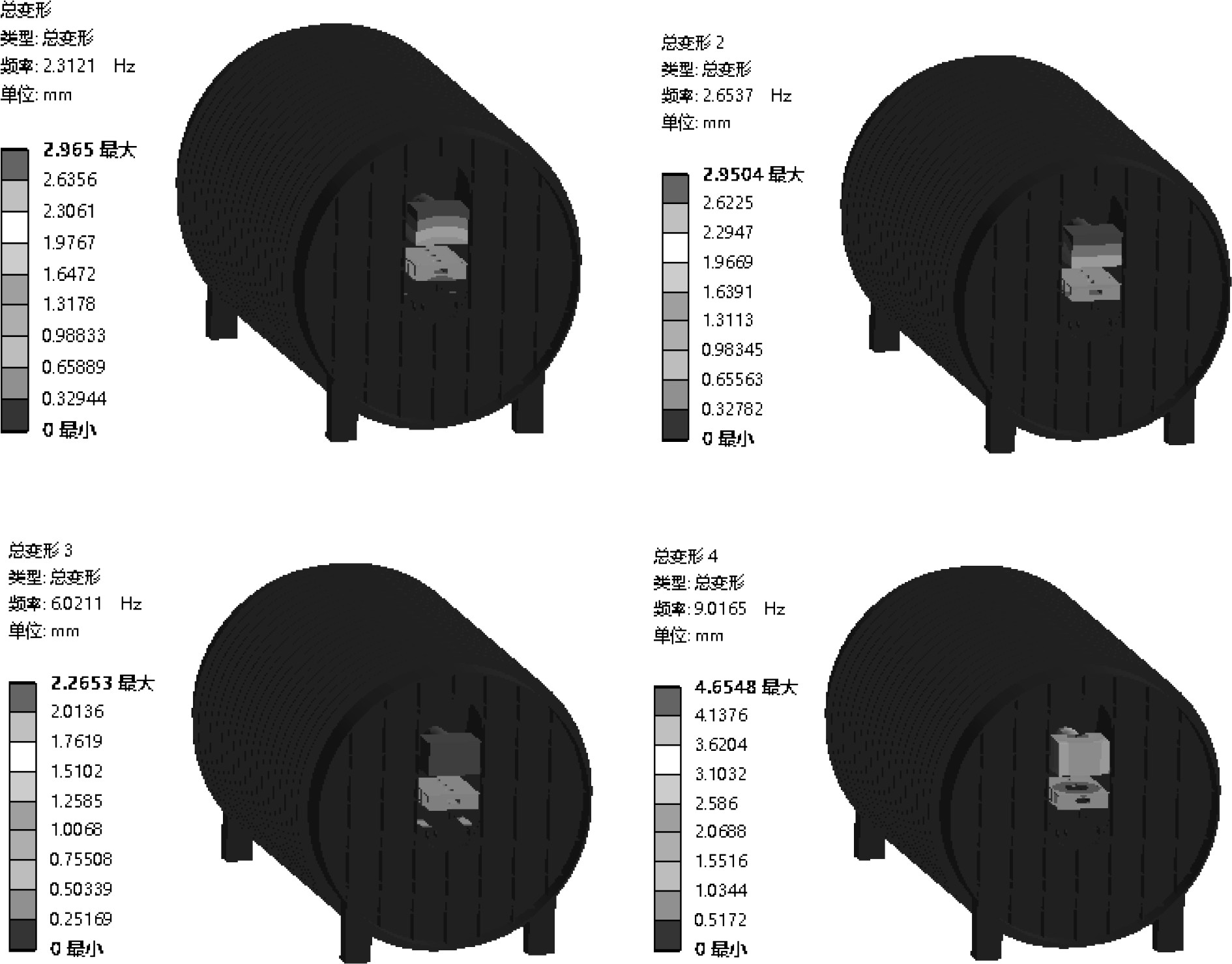
|
图 4 整体前4阶模态阵型 Fig. 4 Overall first 4 modal formations |
|
|
表 4 隔振系统前20阶模态频率 Tab.4 The first 20 modal frequencies of the isolation system |
谐响应分析可以计算系统受外部激励作用时产生的振动响应,谐响应分析求解的方法通常包括完全法、模态叠加法、缩减法。本文选用完全法进行谐响应的计算与求解。
典型动力设备双层隔振系统的有限元模型如图5所示,进行有限元分析,分析频率为0~

|
图 5 典型动力设备隔振系统有限元模型 Fig. 5 Finite element model of typical power equipment vibration isolation system |
通过振级落差对典型动力设备隔振性能进行评估,如下式:
| $ {L_D} = 20\lg \frac{{{a_1}}}{{{a_2}}}。$ | (9) |
式中:LD为加速度振级落差;a1为上层振动加速度响应;a2为下层振动加速度响应。
为了减少仿真分析的误差,在仿真分析中上层隔振器上端和下层隔振器的下端分别取6个测点并取其测量平均值,如图6所示。图7为圆柱壳舱段双层隔振系统示意图。对该舱段动力设备隔振系统进行谐响应分析,隔振装置的振级落差如图8所示。
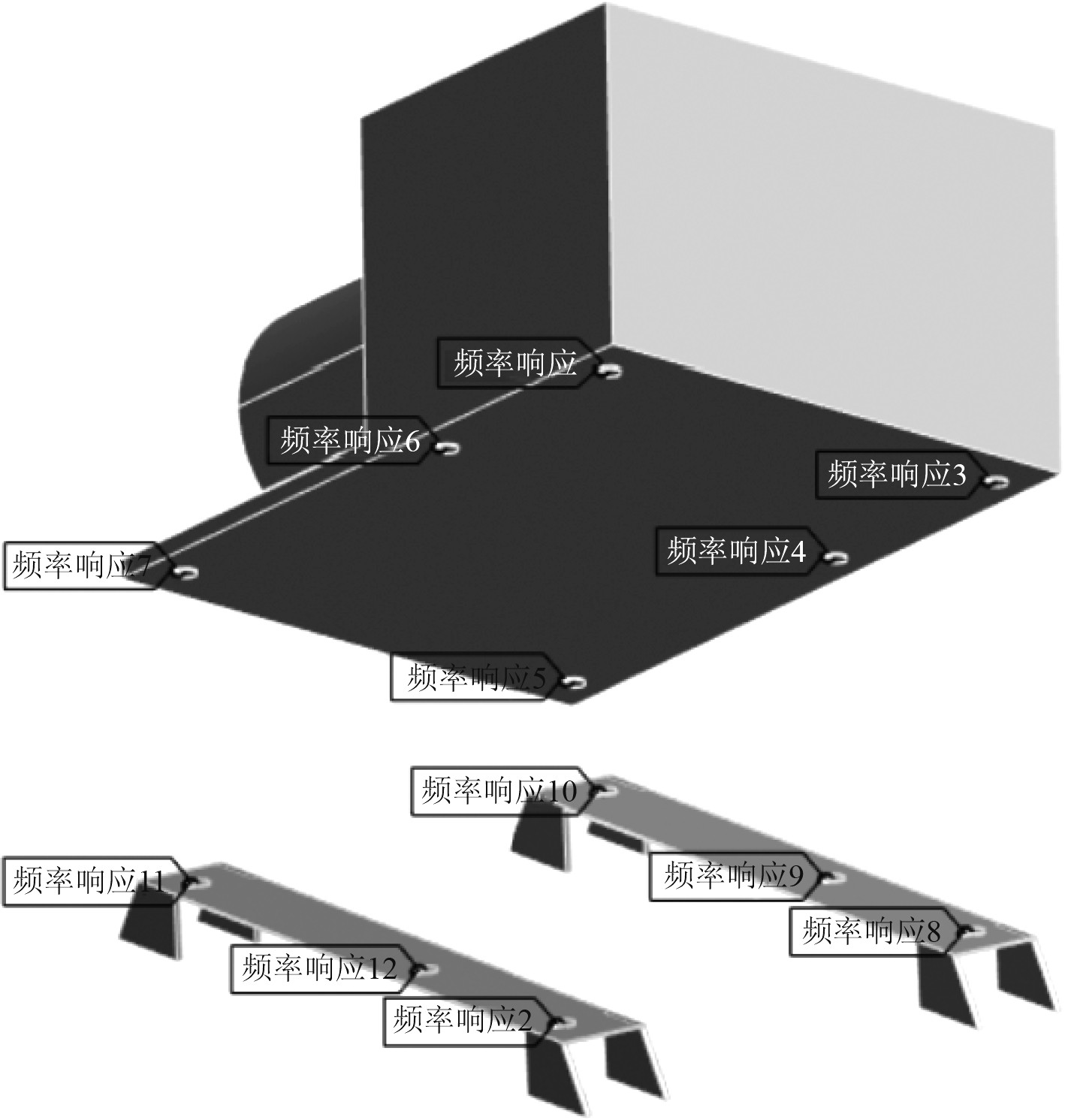
|
图 6 双层隔振系统测点位置 Fig. 6 Location of measurement points for double-layer vibration isolation system |

|
图 7 圆柱壳舱段双层隔振系统 Fig. 7 Double layer vibration isolation system for cylindrical shell cabin section |
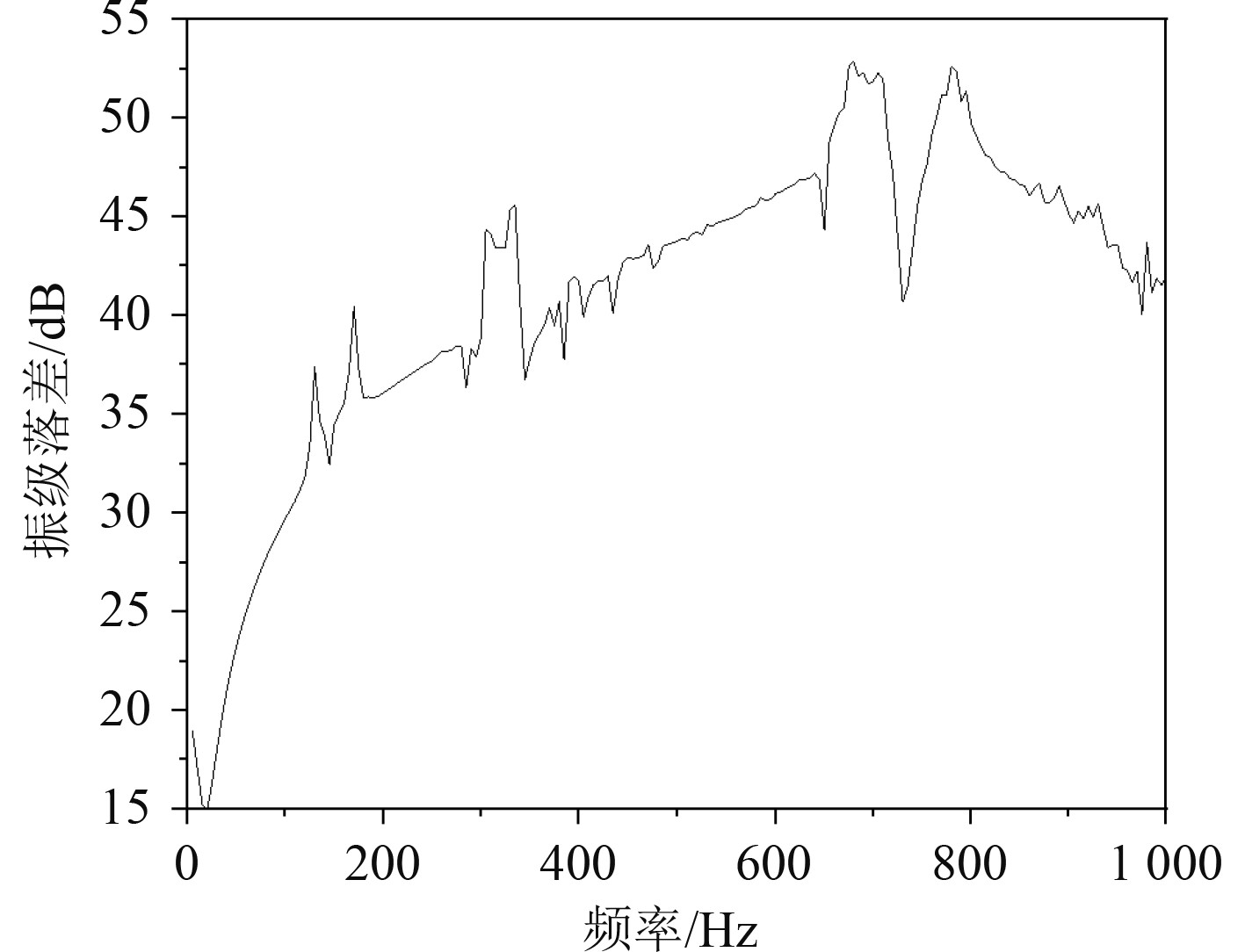
|
图 8 双层隔振平均振级落差 Fig. 8 Double layer isolation average vibration level drop |
可知,该双层隔振系统的振级落差大部分频段内都维持在40~55 dB范围,在全频段范围内振级落差为41.1 dB。
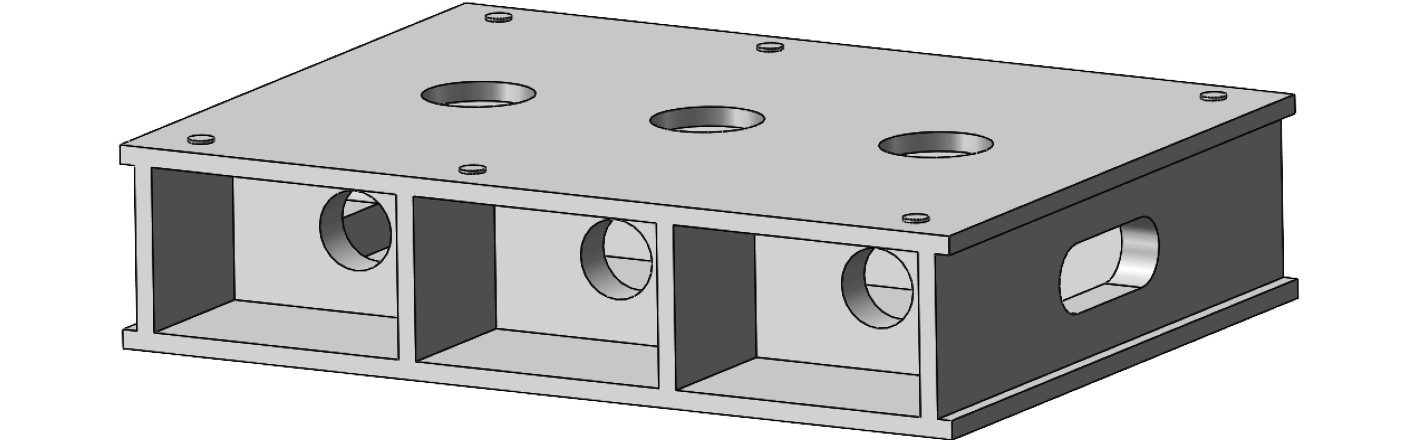
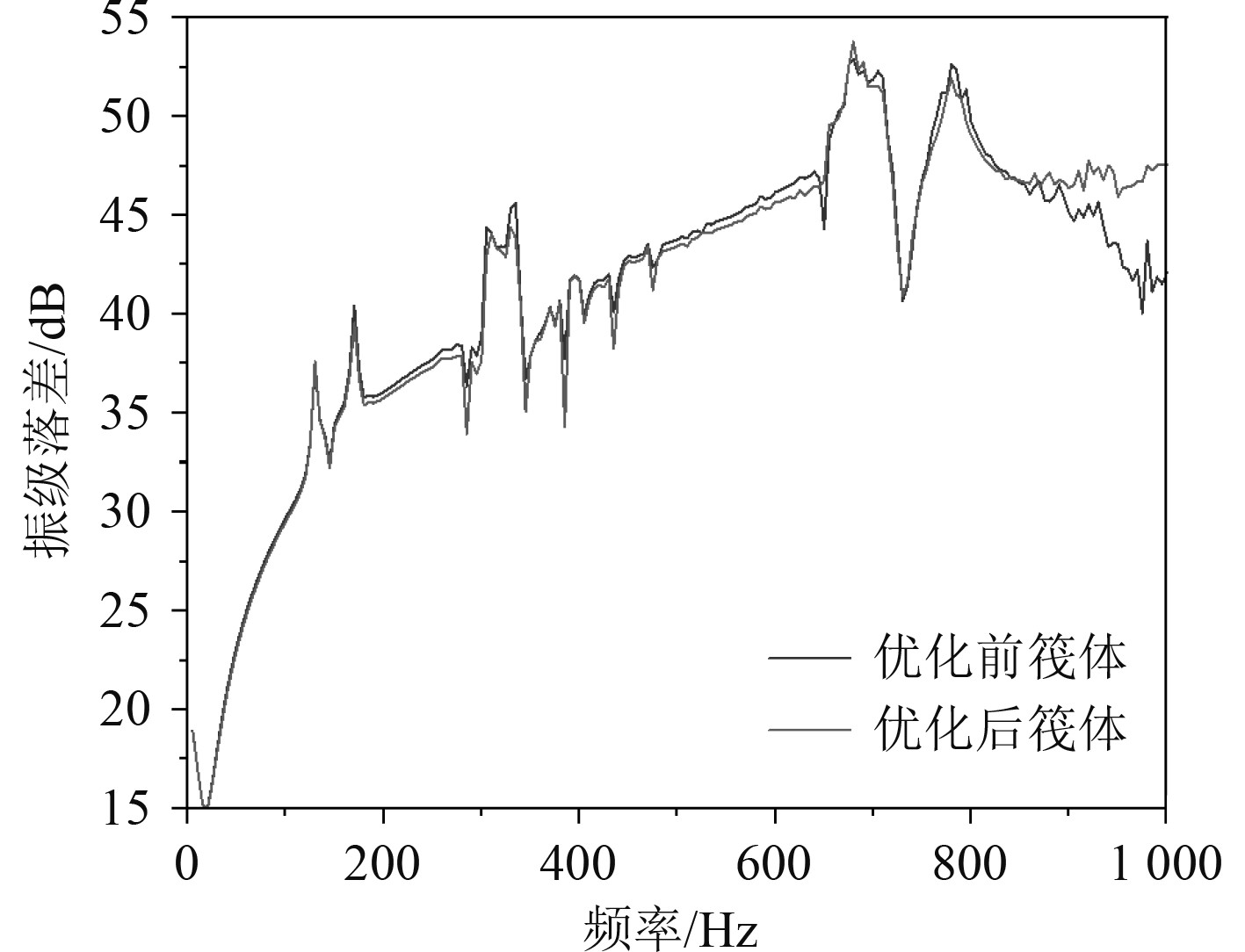
2 筏体结构对系统隔振性的影响双层隔振系统的隔振性能与筏体结构密切相关。本文在原筏体结构模型的基础上,对筏体结构进行优化设计,研究了2种优化筏体结构对系统隔振性能的影响规则,本文仅给出一种结果。优化后的筏体结构如图9所示。改变筏体孔洞形式,优化后的筏体结构质量仍为80 kg,筏体结构对系统隔振性能的影响如图10所示。
|
图 9 优化后的筏架结构 Fig. 9 Optimized raft structure |
|
图 10 2种筏架结构平均振级落差 Fig. 10 Average vibration level drop of two types of raft structures |
可知,在0~800 Hz筏体对系统隔振性能影响不大。在800~
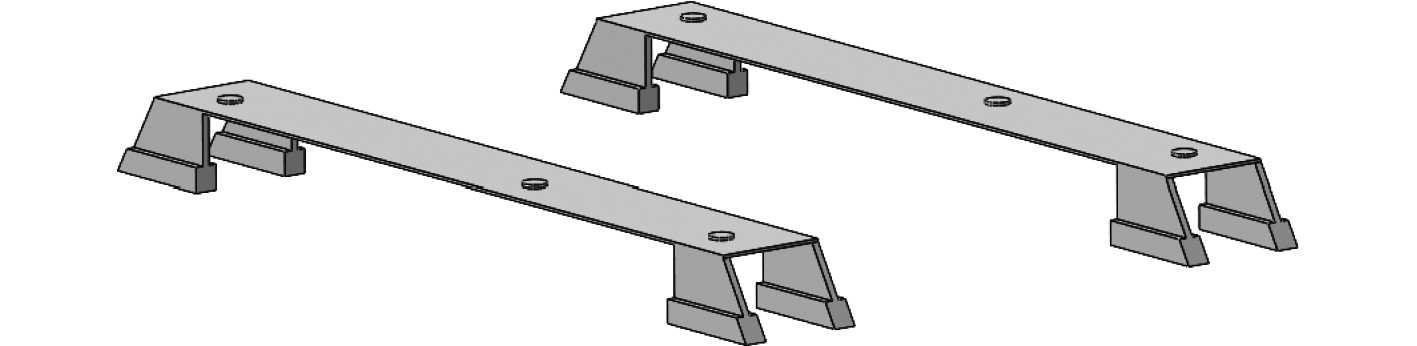
阻振质量通常安装在振动传递主要路径上,引起结构的阻抗失配,使得振动波在传播过程中不连续,部分振动波被反射,从而起到较好的减振效果。在圆柱舱段典型动力设备隔振系统中,基座是振动传递的重要一环。因此,本文对动力设备隔振系统的基座结构采用了阻振质量方式,进一步分析动力设备的振动传递。研究在基座肋板位置安装阻振质量对系统隔振性能的影响。阻振质量安装位置如图11所示,其外形尺寸为16 mm×16 mm,长度于基座肋板的底部,阻振质量的长度相同,材料为结构钢;弹性模量为210 GPa;泊松比为0.3;密度为
|
图 11 阻振质量基座位置 Fig. 11 Position of the damping mass base |
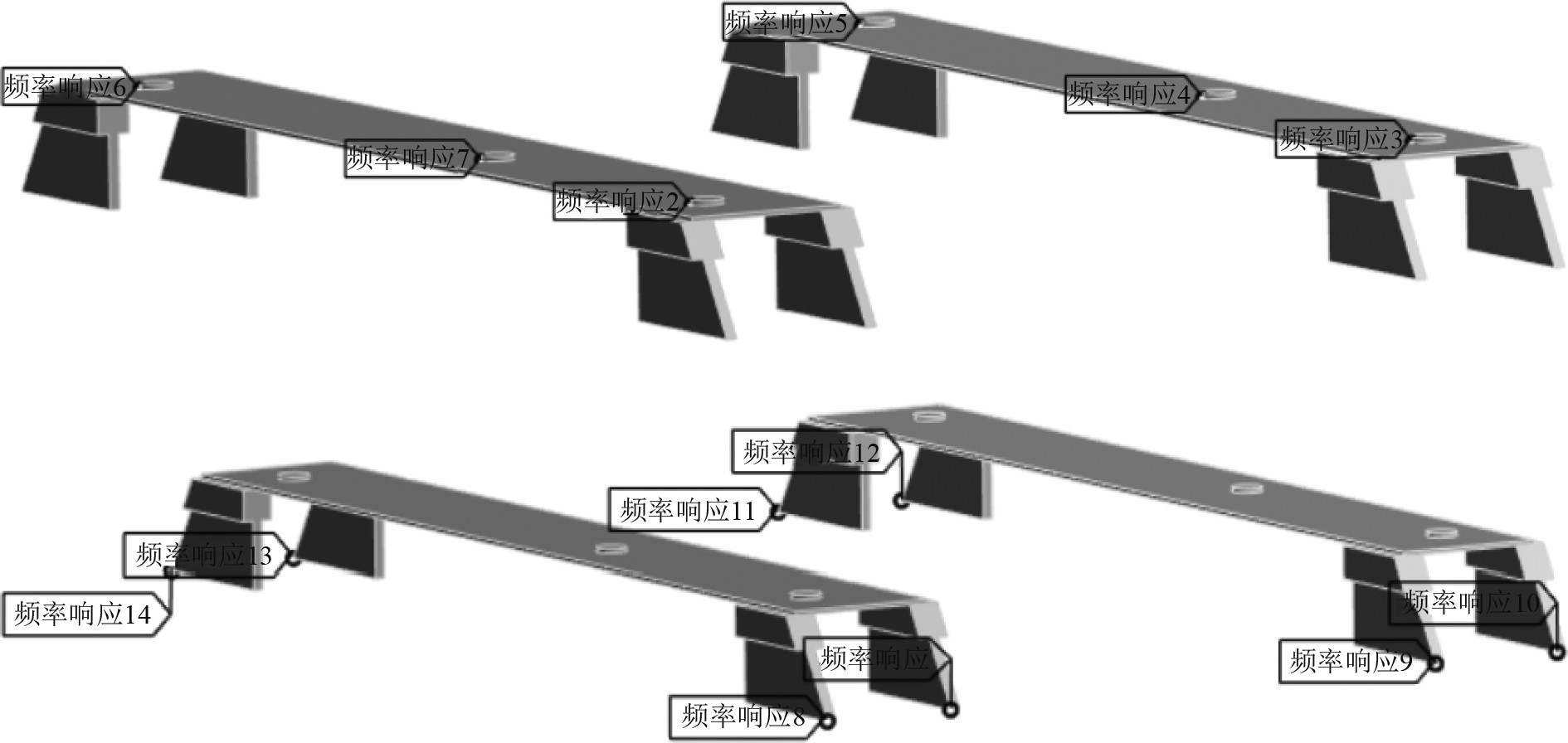
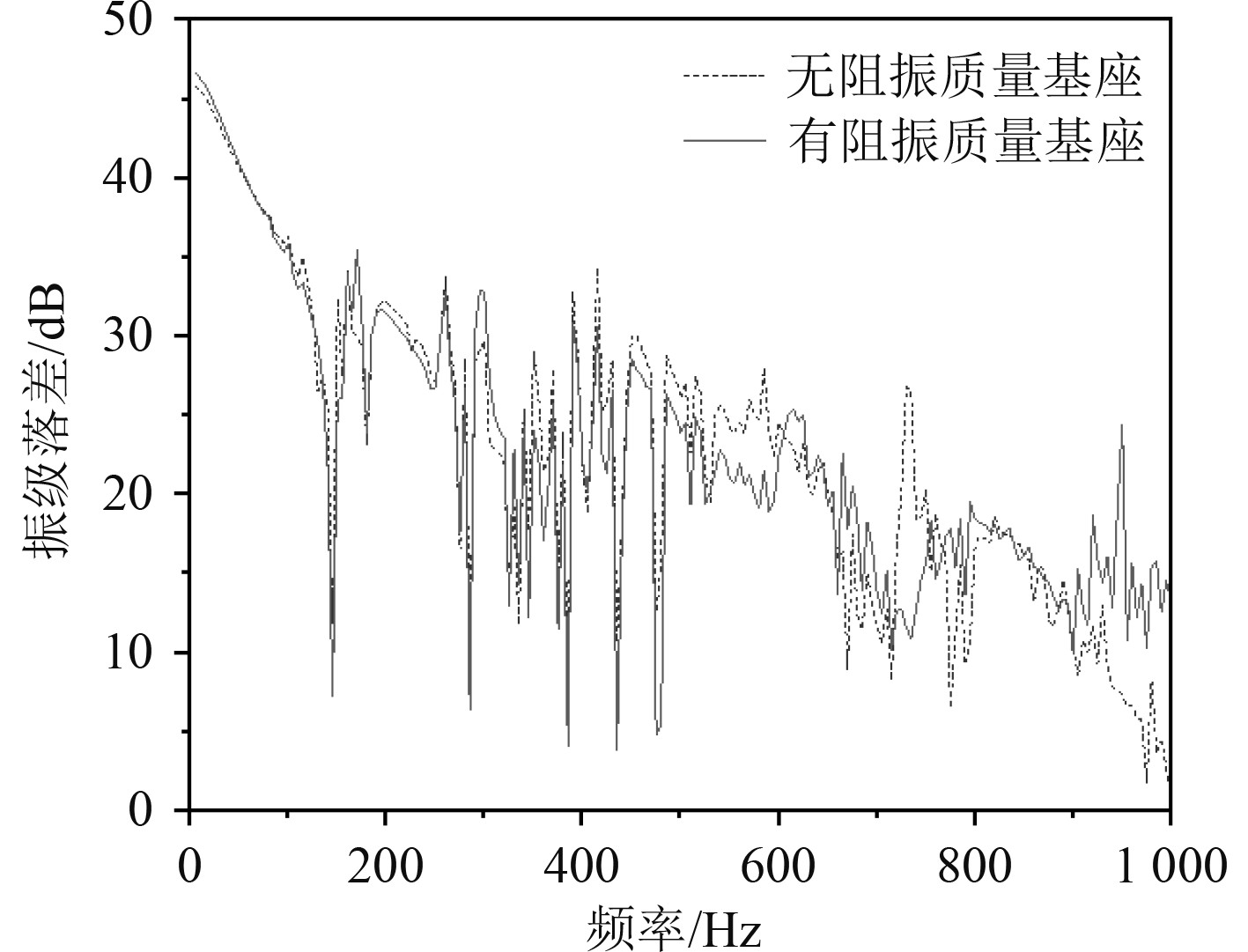
在基座上、下端分别取6个与8个测点,如图12所示。计算安装阻振质量前后系统的振级落差如图13所示,结果表明在0~
|
图 12 基座结构测点布置 Fig. 12 Layout of measuring points for base structure |
|
图 13 阻振质量对系统隔振性能的影响 Fig. 13 The influence of damping mass on system isolation performance |
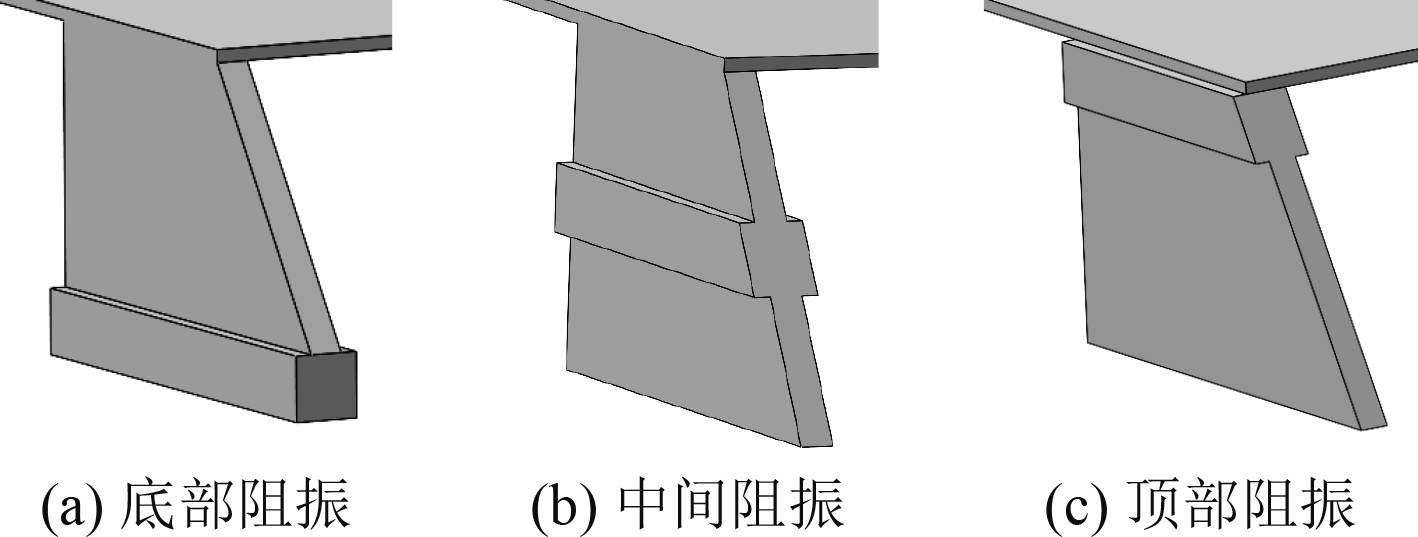
本文研究了阻振质量3种位置对基座振动传递特性的影响,如图14和图15所示。
|
图 14 阻振质量的3种布置形式 Fig. 14 Three types of arrangements for damping mass |
|
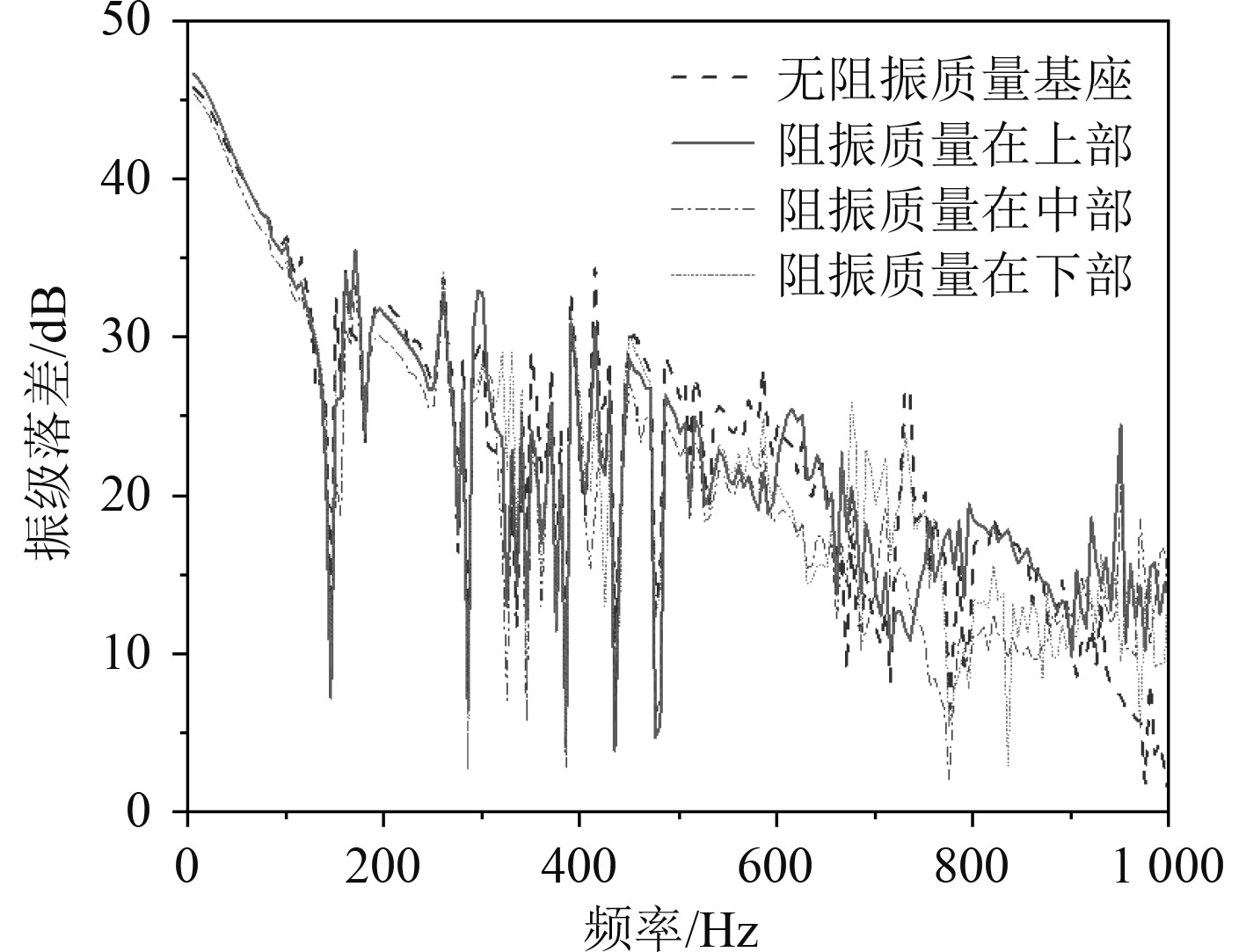
图 15 阻振位置对振动传递的影响 Fig. 15 The influence of damping position on vibration transmission |
从图15可以看出,3种阻振安装位置对应的振级落差曲线趋势一致;在0~900 Hz频段范围内4种形式系统振级落差各有高低,考虑其原因是不同系统的模态都不相同所导致的。综合计算下,在全频段隔振质量安装于上部时隔振效果较好。阻振质量安装于上部系统的振级落差时,比安装于中间和下方时的振级落差分别提高了2.1 dB和0.5 dB。可知,加入阻振质量后在900~
本文通过对圆柱壳舱段典型动力设备双层隔振系统隔振分析,得出如下结论:
1)考虑圆柱舱段动力设备隔振系统的振动较为复杂,其振动特性与圆柱舱段的阻抗等特性有关。
2)优化筏体结构可以提高双层隔振系统的隔振性能,在频率800~
3)在动力设备基座位置布置阻振质量可进一步提高系统的隔振效果,其中阻振质量布置在基座上端的减振效果最好,相对于无阻振质量基座其隔振性能可提高0.2 dB;在900~
| [1] |
陈行. 柴油发电机组双层隔振系统优化设计分析[D]. 成都: 西南交通大学, 2017.
|
| [2] |
牛昊轩. 动力机组双层隔振系统低频隔振器研究[D]. 成都: 西南交通大学, 2018.
|
| [3] |
李开程, 张立民, 邱飞力, 等. 列车用双层隔振系统隔振性能实验[J]. 噪声与振动控制, 2016, 36(1): 92-96. |
| [4] |
肖程诗, 吴绍维, 王俊, 等. 大型船用柴油发电机组浮筏隔振系统设计与优化[J]. 噪声与振动控制, 2022, 42(3): 25-29. DOI:10.3969/j.issn.1006-1355.2022.03.005 |
| [5] |
张伟, 周相荣, 贺华, 等. 整体式与分布式双层隔振系统性能对比研究[J]. 噪声与振动控制, 2017, 37(4): 26-29. DOI:10.3969/j.issn.1006-1355.2017.04.006 |
| [6] |
田正东, 计方. 阻振质量刚性隔振在舰船基座结构中应用研究[J]. 船舶力学, 2011, 15(8): 906-914. TIAN Zhengdong, JI Fang. Research on the application of damping mass rigid isolation in ship foundation structures[J]. Journal of Ship Mechanics, 2011, 15(8): 906-914. DOI:10.3969/j.issn.1007-7294.2011.08.011 |
| [7] |
李俊发. 巢湖某型观光船风机双层隔振系统设计与隔振性能研究[D]. 镇江: 江苏科技大学, 2019.
|
| [8] |
赵建学, 俞翔, 柴凯, 等. 双层隔振系统隔振性能分析[J]. 中国舰船研究, 2017, 12(6): 101-107. ZHAO Jianxue, YU Xiang, CHAI Kai, et al. Analysis of vibration isolation performance of double layer vibration isolation system[J]. Chinese Journal of Ship Research, 2017, 12(6): 101-107. |
| [9] |
聂振华. 舰船齿轮箱支撑基座的隔振性能分析及改进技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
|
| [10] |
李飞. 典型辅机设备隔振系统设计及阻振基座研究[D]. 武汉: 武汉理工大学, 2021.
|
| [11] |
尼建军, 闫森森, 周嘉, 等. 海洋平台机座阻尼结合阻振质量减振分析[J]. 船舶工程, 2021, 43(2): 158-162. NI Jianjun, YAN Sensen, ZHOU Jia, et al. Vibration reduction analysis of offshore platform frame damping combined with damping mass[J]. Ship Engineering, 2021, 43(2): 158-162. |
| [12] |
唐琴. 列车用柴油发电机组隔振系统隔振性能分析[D]. 成都: 西南交通大学, 2013.
|
| [13] |
孙玉华. 内燃动车动力包双层隔振设计方法研究[D]. 成都: 西南交通大学, 2013.
|
 2024, Vol. 46
2024, Vol. 46

