0 引　言

自主水下航行器（AUV）因其携带能源和水下通信的限制，需要不定期进行对接回收任务。对接方式根据对接平台的运动状态可以分为静对接和动对接，目前静对接的研究相对成熟，今年来更多学者针对动对接开始进行研究^[1]。其中，拖曳式动对接是其中主要的对接方式之一，具有广泛的应用前景。为了提升对接成功率，本文设计了一种拖曳式导向罩可开合的接驳装置，对接时通过打开导向罩而扩大对接的有效范围。在该对接系统中接驳装置由一定长度的绳索束缚在另一固定或浮式结构物上（船舶、浮标、海上石油平台等），AUV对接过程中，接驳装置不受任何主动操纵力，自由悬浮于水下。为给AUV提供有利的悬浮对接环境，接驳装置在水中系泊悬浮运动姿态，如纵倾角等，有严格的要求，如接驳装置与AUV需要尽量的同向，为此需要研究接驳装置在水流和波浪等外界扰动作用下的运动状态，验证开合式对接方法的有效性。

国内外针对水下系泊悬浮接驳系统的研究极少，与之相似的是水下锚（系）泊系统和拖曳系统的研究。不同于水下系泊悬浮接驳系统之处，锚（系）泊系统的缆索一般锚定在海底，长期驻留，理想状态下不会走锚，与大陆架固联；拖曳系统的缆索运动输入端束缚在拖船上，随船处于运动状态。对于水下锚（系）泊系统的研究，重点在于建立系统的缆-体耦合动力学模型，Du等^[2]联合集中质量法建立的缆索模型、凯恩法和广义力法建立的水下滑翔机驻留过程动力学模型，建立了水下滑翔机驻留过程的多体系统耦合运动模型，并仿真分析了不同速度和方向的水流、电缆的长度对水下滑翔机系泊运动稳定性的影响。张斌等 ^[3-4]依据欧拉-伯努利梁理论，建立包括弯矩作用的锚链运动模型，分别采用欧拉角和四元数方法来描述锚链姿态，通过适当的边界条件，将驻留航行器、锚链和锚块的运动控制方程耦合为锚泊系统运动模型，仿真分析了周期变动水流作用下的驻留航行器位置及姿态的响应情况以及缆索的运动情况。邵成等^[5]采用经典的Ablow-Schechter拖缆建模方法和Newton-Euler方法分别建立锚链和水下导弹发射平台的运动模型，并结合锚链运动的边界条件建立了水下锚系导弹发射系统的运动模型。基于以上类似的思路，Tian等^[6]基于所建立的装有水动能涡轮发电机的水下驻留系统运动模型，分析了净浮力和洋流流速对水下系泊平台运动的影响。除此之外，李艳生等^[7]根据球形机器人水下系泊状态实际情况，应用线性波理论和Morision方程对流体载荷进行描述，并引入波浪水动力、重摆扰动力和绳索刚度阻尼弹性力项，建立球形水下机器人锚定状态波流联合激励的动力学模型。对于拖曳系统，一般由拖船、拖缆和拖体3个基本要素组成，基本建模方法也是将各子系统分开，分别建立其动力学模型，然后基于拖缆两端的边界条件，将三者耦合建立系统的动力学模型。VU等^[8]采用悬链线方程描述脐带缆模型，通过边界条件与水面无人艇和水下航行器动力学模型耦合，建立并求解分析拖曳系统非线性耦合动力学模型。王飞等^[9]为精确描述水下拖体的运动，借鉴潜艇水下六自由度方程进行建模，同时结合集中质量法建立的拖缆模型及其边界条件，完成水下双阵列拖曳系统建模及其缆破断情况下的运动响应分析。这些学者们的研究思路对水下系泊悬浮接驳系统的建模与分析有一定借鉴作用。

本文重点分析导向罩开合和变拖点对接驳装置姿态的影响，为精确描述开合式接驳装置水下系泊悬浮状态，基于质心运动分析和Newton-Euler动力学理论建立具有变质心特性的接驳装置水下六自由度运动模型，利用空间拘束运动计算流体力学（CFD）方法和假设检验方法，对接驳装置进行水动力模型辨识和简化，并通过系绳运动边界条件将系绳简化模型和水下接驳装置两子系统耦合，建立水下单点系泊悬浮接驳系统动态运动方程，并建立了利用STAR-CCM+的动态仿真模型。通过拖曳实验对2种方法进行有效性验证，最后对该接驳系统在不同条件下的接驳装置运动状态预报和分析，为稳定可靠地实现对接回收AUV提供有意义的参考。

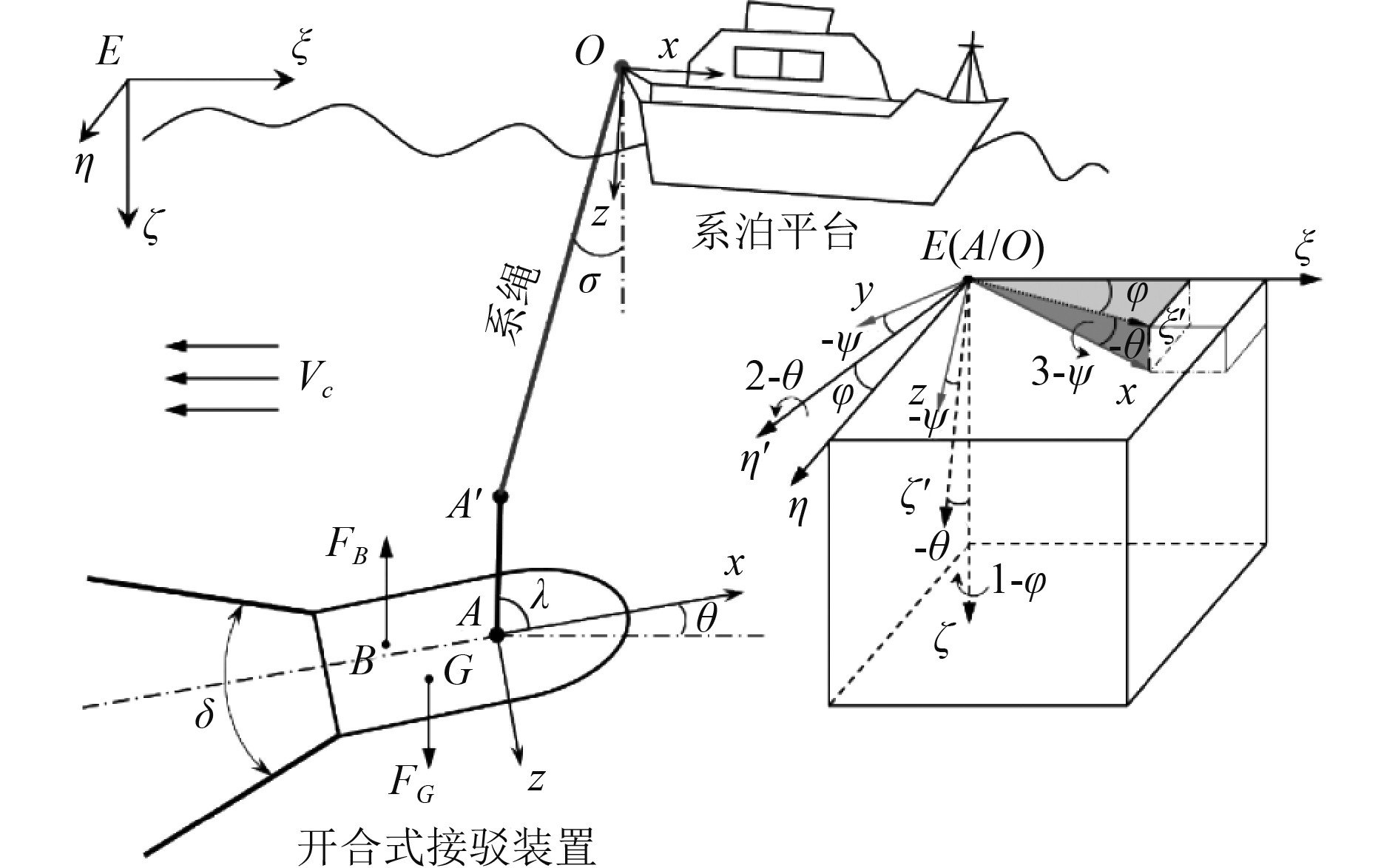
1 接驳系统三维运动数学模型

本文以某无人艇自主部署AUV一体化平台为研究对象。如图1所示，当无人艇停泊于水面上，接驳装置被系泊悬浮于水下，对接前开合式导向罩打开，完成对接后，导向罩合拢同时夹紧AUV。

拖架AA′与装置铰接于拖点A，AA′与装置纵中轴线Ax的夹角λ为拖架角，λ∈[0°, 120°]。当λ为自由状态时，理论拖点变为A；当λ受拖点调节机构约束时，拖架固定，理论拖点同实际拖点A′重合。为提高AUV对接回收可靠性和效率，将传统的固定罩导引方式改为动态开合导引方式，开合导向罩夹角记为δ，δ∈[0°, 34°]。

长度L=10 m的系绳OA′首尾分别系在水面平台和接驳装置上，因系绳长度、横截面积和迎流速度较小，忽略缆绳所受水阻力；系绳在水下呈现处于紧张状态，将系绳简化为一变刚度—阻尼弹簧模型。同时，本文直接给出系泊平台O点的正弦运动规律，作为系泊悬浮接驳系统的输入，以便分析接驳装置的运动状态。

1.1 坐标系统

为便于分析在水流和波浪作用下接驳系统的运动状态，建立3个直角坐标系：惯性坐标系E-ξηζ、接驳装置坐标系A-xyz和系泊平台坐标系O-xyz，如图1所示。惯性坐标系{E}的原点选取在水面，ξ轴水平向右，ζ轴垂直向下；接驳装置坐标系{A}的原点位于拖架与接驳装置铰接点A处，随接驳拖体运动，x轴指向拖体首向；y轴指向右舷；z轴指向拖体下方。接驳装置在空间的位姿取决于随体坐标系{A}原点在惯性坐标系{E}中的位置分量ξ_A、η_A、ζ_A以及动系相对于定系的3个姿态角艏向角φ、纵倾角θ、横滚角ψ，各角度的正向均按右手定则确定。坐标系旋转变换顺序如图1所示，其转换关系为：

$ \left[ {\begin{array}{*{20}{c}} \xi \\ {\boldsymbol \eta} \\ \zeta \end{array}} \right] = {\boldsymbol R}_a^e\left[ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right]，$

(1)

$ {\boldsymbol R}_a^e = \left[ {\begin{array}{*{20}{c}} {\cos \varphi \cos \theta }&{\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi }&{\cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi } \\ {\sin \varphi \cos \theta }&{\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi }&{\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi } \\ { - \sin \theta }&{\cos \theta \sin \psi }&{\cos \theta \cos \psi } \end{array}} \right]。$

(2)

式中：$ {\boldsymbol R}_a^e $为随体坐标系旋转变换矩阵。

1.2 接驳装置水下空间运动模型 1.2.1 运动方程

参考水下航行器运动微分方程 ^[10] ，并考虑开合式接驳装置水动力外形和质量分布关于Axz剖面对称，接驳装置具有变质心特性的水下六自由度运动模型可以通过刚体的Newton-Euler运动方程推导出来。

$ \left\{ \begin{gathered} X = m\left[ {\dot u - vr + wq - {x_G}\left( {{q^2} + {r^2}} \right) + {z_G}\left( {pr + \dot q} \right)} \right], \\ {Y_{}} = m\left[ {\dot v - wp + u{r_{}} + {z_G}\left( {qr - \dot p} \right) + {x_G}\left( {qp + \dot r} \right)} \right], \\ Z = m\left[ {\dot w - uq + vp - {z_G}\left( {{p^2} + {q^2}} \right) + {x_G}\left( {rp - \dot q} \right)} \right], \\ K ={I_{xx}}\dot p + \left( {{I_{zz}} - {I_{yy}}} \right)qr - {I_{xz}}\left( {\dot r + pq} \right) -m{z_G}\left( {\dot v + ru - pw} \right) ,\\ \begin{split} M =& {I_{yy}}\dot q + \left( {{I_{xx}} - {I_{zz}}} \right)rp + {I_{xz}}\left( {{p^2} - {r^2}} \right) + m{z_G}\left( {\dot u + qw - rv} \right) -\\& m{x_G}\left( {\dot w + pv - qu} \right), \end{split} \\ N = {I_{zz}}\dot r + \left( {{I_{yy}} - {I_{xx}}} \right)pq + {I_{zx}}\left( {rq - \dot p} \right) + m{x_G}\left( {\dot v + ru - pw} \right)。\\ \end{gathered} \right. $

(3)

式中：$ \dot u $、$\dot v $、$\dot w $、$\dot p $、$\dot q $、$\dot r $均为刚体运动向量在随体坐标系下关于时间的导数相对于随体坐标系{A}，v₁ = [u, v, w]^T为接驳装置的运动速度；v₂ = [p , q, r]^T为接驳装置运动角速度；m为接驳装置总质量；${I }$为各下标方向上的转动惯量；重心、浮心的坐标分别记作r_AG=[x_G, 0, z_G]^T，r_AB=[x_B, 0, z_B]^T。方程左侧(X, Y, Z, K, M, N)为作用于接驳装置上的合外力（矩）τ，分别记作τ₁ = [X, Y, Z]^T，τ₂ = [K, M, N]^T。因此，接驳装置运动模型为：

$ {{\boldsymbol M}_r}{\dot { v}} + {\boldsymbol C} \cdot { v} = { \tau }。$

(4)

式中：v = [v₁, v₂]^T为接驳装置在随体坐标系下的速度向量；$ {\dot {v}} $对应为加速度向量；M_r为接驳装置质量矩阵，C为科里奥利力矩阵，M_r与C的展开式见文献[11]。

将接驳装置在随体坐标系下的运动描述转换到惯性坐标系下的运动描述，称为辅助运动关系式^[11]。可得接驳装置姿态角随时间变化量${{\dot P}_2}$同角速度向量v₂的关系：

$ {{\dot {\boldsymbol P}}_2}{\text{ = }} \left[ {\begin{array}{*{20}{c}} {\dot \varphi } \\ {\dot \theta } \\ {\dot \psi } \end{array}} \right] {\text{ = }} \left[ {\begin{array}{*{20}{c}} 1&{\tan \theta \sin \varphi }&{\tan \theta \cos \varphi } \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{{{\sin \varphi } \mathord{\left/ {\vphantom {{\sin \varphi } {\cos \theta }}} \right. } {\cos \theta }}}&{{{\cos \varphi } \mathord{\left/ {\vphantom {{\cos \varphi } {\cos \theta }}} \right. } {\cos \theta }}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p \\ q \\ r \end{array}} \right] 。$

(5)

接驳装置在惯性坐标系下的速度${{\dot P}_1}$为：

$ {{\dot { P}}_1}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{{\dot \xi }_A}} \\ {{{\dot \eta }_A}} \\ {{{\dot \zeta }_A}} \end{array}} \right]{\text{ = }}{ R}_a^e\left[ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right] 。$

(6)

1.2.2 外力描述

作用于接驳装置的合外力和力矩向量τ主要包含水动力及力矩τ_h，系绳牵引力τ_A′，重力及其力矩τ_g，浮力及其力矩τ_b，满足式(7)。

$ {{\tau}}{\text{ = }}{{{\tau}}_h} + {{{\tau}}_{A'}} + {{{\tau}}_g} + {{{\tau}}_b}。$

(7)

1）水动力及力矩

接驳装置水下六自由度空间运动方程以格特勒等的潜艇标准运动方程为基础，该方程包含108个水动力系数。根据高婷等^[12]提出的空间拘束运动CFD模拟方法，得到整体拟合优度大于0.9的接驳装置水动力简化模型表示如下：

$ {{\boldsymbol{\tau}}_h}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{X_h}} \\ {{Y_h}} \\ {{Z_h}} \\ {{K_h}} \\ {{M_h}} \\ {{N_h}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\displaystyle\frac{1}{2}\rho {l^3}{{X'}_{\dot u}}\dot u{\text{ + }}\displaystyle\frac{1}{2}\rho {l^2}{{X'}_{uu}}{u^2}} \\ {\displaystyle\frac{1}{2}\rho {l^3}\left( {{{Y'}_{\dot v}}\dot v + {{Y'}_r}ur} \right) + \displaystyle\frac{1}{2}\rho {l^2}\left( {{{Y'}_v}uv + {{Y'}_{v\left| v \right|}}v\left| {\sqrt {{v^2} + {w^2}} } \right|} \right)} \\ {\displaystyle\frac{1}{2}\rho {l^3}\left( {{{Z'}_{\dot w}}\dot w + {{Z'}_q}uq + {{Z'}_{w\left| q \right|}}\displaystyle\frac{w}{{\left| w \right|}}\left| {\sqrt {{v^2} + {w^2}} } \right|\left| q \right|} \right) + \displaystyle\frac{1}{2}\rho {l^2}\left( {{{Z'}_w}uw + {{Z'}_{w\left| w \right|}}w\left| {\sqrt {{v^2} + {w^2}} } \right|} \right)} \\ {\displaystyle\frac{1}{2}\rho {l^5}\left( {{{K'}_{\dot p}}\dot p + {{K'}_{p\left| p \right|}}p\left| p \right|} \right) + \displaystyle\frac{1}{2}\rho {l^4}\left( {{{K'}_p}up + {{K'}_r}ur} \right) + \displaystyle\frac{1}{2}\rho {l^3}\left( {{{K'}_v}uv + {{K'}_{v\left| v \right|}}v\left| {\sqrt {{v^2} + {w^2}} } \right|} \right)} \\ {\displaystyle\frac{1}{2}\rho {l^5}\left( {{{M'}_{\dot q}}\dot q + {{M'}_{q\left| q \right|}}q\left| q \right|} \right) + \displaystyle\frac{1}{2}\rho {l^4}\left( {{{M'}_{\dot w}}\dot w + {{M'}_q}uq} \right) + \displaystyle\frac{1}{2}\rho {l^3}\left( {{{M'}_w}uw + {{M'}_{w\left| w \right|}}w\left| {\sqrt {{v^2} + {w^2}} } \right|} \right)} \\ {\displaystyle\frac{1}{2}\rho {l^5}\left( {{{N'}_{\dot r}}\dot r + {{N'}_{\dot p}}\dot p + {{N'}_{r\left| r \right|}}r\left| r \right|} \right) + \displaystyle\frac{1}{2}\rho {l^4}\left( {{{N'}_{\dot v}}\dot v + {{N'}_r}ur} \right) + \displaystyle\frac{1}{2}\rho {l^3}{{N'}_v}uv} \end{array}} \right] 。$

(8)

式中：ρ为水的密度，取值为1000 kg/m³；l为接驳装置特征长度；其余各项为无量纲化水动力系数，具体含义参考文献[13]。

如若采用类似求取潜艇舵角系数的方法^[14]辨识求解水动力张角系数，需要做50组以上不同工况的仿真。虽然该方法注重单个系数的精度，但是水动力模型整体精度无法保证。然而空间拘束运动模拟方法在保证计算精度的同时，能够极大缩短水动力系数计算的周期^[12]。所以，本文使用空间拘束法求解水动力系数，对应不同导向罩张角计算出不同外形的水动力系数，根据接驳装置装配完成后的调试结果，尽可能从最小值0°到最大值34°均匀取值，最终取值δ为0°、4°、10°、16°、22°、28°、34°。

假设实际海流速度在同一深度是均匀一致的，记水流速度在惯性坐标下的描述为V_c=[V_ci, V_cj, V_ck]^T。根据相对运动理论，可得接驳装置相对海流的速度

$ {{ v}_a}=\left[ {\begin{array}{*{20}{c}} {{u_a}} \\ {{v_a}} \\ {{w_a}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right] - { R}_a^{e - 1}\left[ {\begin{array}{*{20}{c}} {{V_{ci}}} \\ {{V_{cj}}} \\ {{V_{ck}}} \end{array}} \right] 。$

(9)

2）牵引力

基于简化假设，系绳对接驳装置的牵引力方向沿A′O方向。受拉时应力-应变关系弹性化处理；而受压时的弹性刚度系数取为0，系绳张力在惯性坐标系下的表示记为：

$ {\boldsymbol T} = \left[ \begin{array}{l}{T}_{i}\\ {T}_{j}\\ {T}_{k}\end{array} \right] = \left[ \begin{array}{l}\left|T\right|\mathrm{cos}\alpha \\ \left|T\right|\mathrm{cos}\beta \\ \left|T\right|\mathrm{cos}\gamma \end{array} \right] ，\left|T\right|\text = \left\{\begin{split}&{K}_{s}\left(L - {L}_{0}\right) + {C}_{s}\dot{L},L \geqslant {L}_{0}，\\ &0,L \leqslant {L}_{0}。\end{split} \right.$

(10)

式中：(cosα, cosβ, cosγ)为向量$ \overrightarrow {{{OA'}}} $在惯性坐标系下的方向余弦；K_s为系绳受拉时的线弹性刚度系数；C_s为系绳张力阻尼系数；L₀为系绳原长，L为系绳长度。

3）重力与浮力及力矩

设接驳装置的重力大小为F_G=mg；浮力大小为$F_B=\rho \nabla g$；$\nabla $为接驳装置排水体积。则接驳装置重力及其力矩τ_g在随体坐标系{A}下的矢量表示为：

$ {{{\tau} }_g} = \left[ {\begin{array}{*{20}{c}} {{{ f}_G}} \\ {{{ r}_{AG}} \times {{ f}_G}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {F_G}\sin \theta } \\ {{F_G}\cos \theta \sin \psi } \\ {{F_G}\cos \theta \cos \psi } \\ {{y_G}{F_G}\cos \theta \cos \psi - {z_G}{F_G}\cos \theta \sin \psi } \\ { - {z_G}{F_G}\sin \theta - {x_G}{F_G}\cos \theta \cos \psi } \\ {{x_G}{F_G}\cos \theta \sin \psi + {y_G}{F_G}\sin \theta } \end{array}} \right] 。$

(11)

式中：$ {{ f}_G} = {\boldsymbol R}_a^{e - 1}{\left[ {0,0,{F_G}} \right]^{\text T}} $。同理，接驳装置浮力及其力矩τ_b在随体坐标系{A}下的矢量表示为：

$ {{{\tau} }_b} = \left[ {\begin{array}{*{20}{c}} {{{ f}_B}} \\ {{{ r}_{AB}} \times {{ f}_B}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_B}\sin \theta } \\ { - {F_B}\cos \theta \sin \psi } \\ { - {F_B}\cos \theta \cos \psi } \\ { - {y_B}{F_B}\cos \theta \cos \psi + {z_B}{F_B}\cos \theta \sin \psi } \\ {{z_B}{F_B}\sin \theta + {x_B}{F_B}\cos \theta \cos \psi } \\ { - {x_B}{F_B}\cos \theta \sin \psi - {y_B}{F_B}\sin \theta } \end{array}} \right] 。$

(12)

式中：$ {{ f}_B} = {\boldsymbol R}_a^{e - 1}{\left[ {0,0, - {F_B}} \right]^{\text T}} $。

悬浮对接时，接驳装置导向罩会以慢速逐渐合拢，装置质浮心位置及其质量分布发生一定变化。

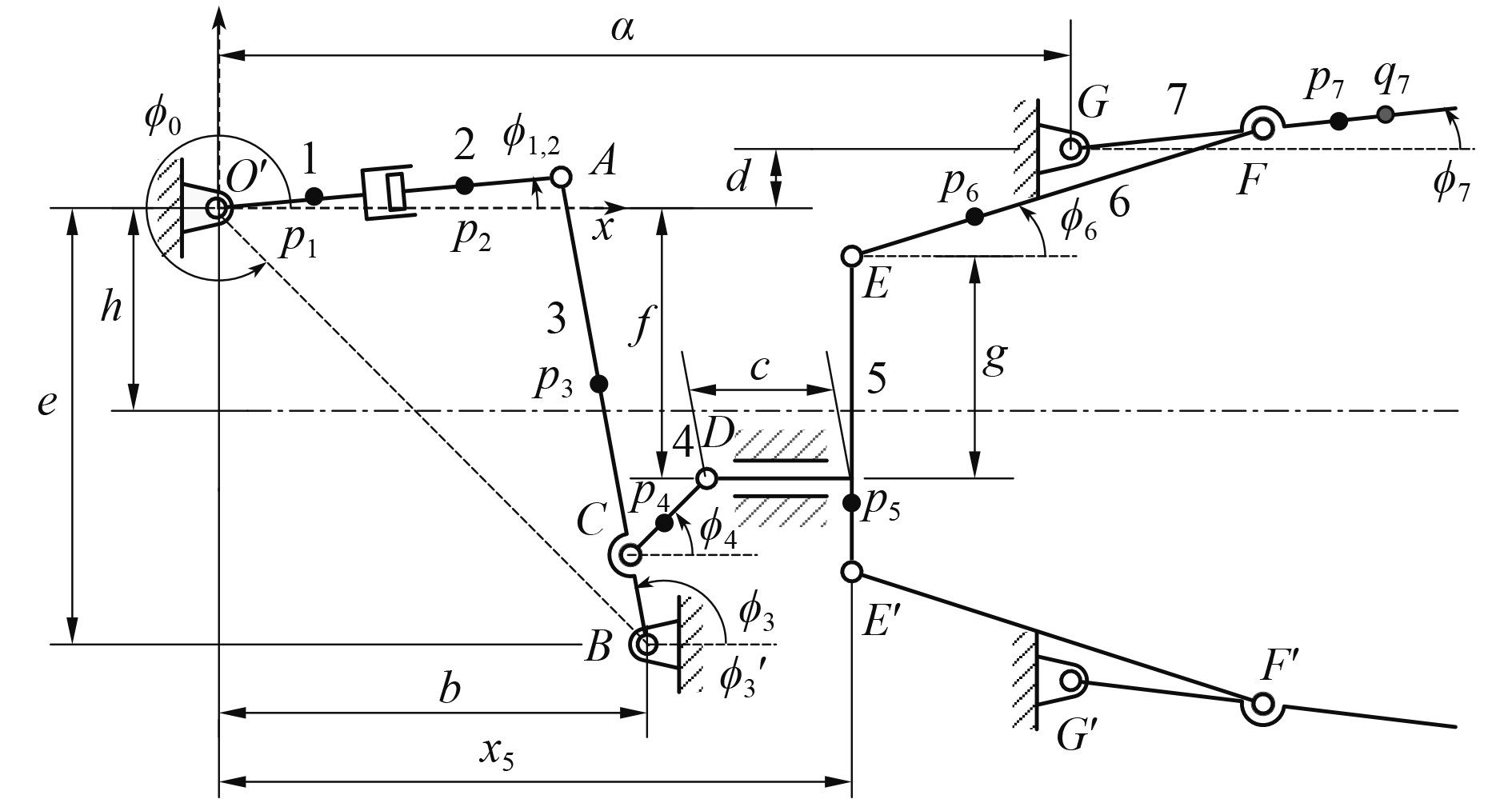
导向罩动作由开合对接机构驱动，机构简图如图2所示。

记$ O'{p_1} = {r_1}，O'{p_2} = {r_2}，B{p_3} = {r_3}，C{p_4} = {r_4}，D{p_5} = {r_5}，F{p_6} = {r_6}，G{p_7} = {r_7}，G{q_7} = {r'_7}$，考虑实际机构的结构分布，推杆6和导向罩7关于图2中心线圆周均布，数量为6，合算后的实际质浮心x坐标为r_p6、r_p7和r_q6的实部，即对应矢量关于O′x轴的投影坐标；z坐标落在机构图2中心线上，即z坐标为：−h。那么，开合对接机构各杆件质浮心位置在基准坐标系O′xz下的坐标分量为：

$ \left\{\begin{gathered} \left({x}_{p1},{z}_{p1}\right)=\left({x}_{q1},{z}_{q1}\right)=\left({r}_{1}\mathrm{cos}{\varphi }_{1},{r}_{1}\mathrm{sin}{\varphi }_{1}\right)，\\ \left({x}_{p2},{z}_{p2}\right)=\left({x}_{q2},{z}_{q2}\right)=\left({r}_{2}\mathrm{cos}{\varphi }_{1},{r}_{2}\mathrm{sin}{\varphi }_{1}\right)，\\ \left({x}_{p3},{z}_{p3}\right) = \left({x}_{q3},{z}_{q3}\right) = \left( b + {r}_{3}\mathrm{cos}{\varphi }_{3},-e+{r}_{3}\mathrm{sin}{\varphi }_{3} \right)，\\ \left({x}_{p4},{z}_{p4}\right) = \left({x}_{q4},{z}_{q4}\right) = \left( \begin{array}{l}b + {{l}^{\prime }}_{3}\mathrm{cos}{{\varphi }^{\prime }}_{3} + {r}_{4}\mathrm{cos}{\varphi }_{4}, \\ -e + {{l}^{\prime }}_{3}\mathrm{sin}{{\varphi }^{\prime }}_{3} + {r}_{4}\mathrm{sin}{\varphi }_{4}\end{array} \right)，\\ \left({x}_{p5},{z}_{p5}\right) = \left({x}_{q5},{z}_{q5}\right)= \\ \left(\begin{array}{l}b+{{l}^{\prime }}_{3}\mathrm{cos}{{\varphi }^{\prime }}_{3}+{l}_{4}\mathrm{cos}{\varphi }_{4}+\mathrm{Re}\left(\overrightarrow{{r}_{5}}\right), \\ -e+{{l}^{\prime }}_{3}\mathrm{sin}{{\varphi }^{\prime }}_{3}+{l}_{4}\mathrm{sin}{\varphi }_{4}+\mathrm{Im}\left(\overrightarrow{{r}_{5}}\right)\end{array}\right)，\\ \left({x}_{p7},{z}_{p7}\right) = \left(a+{r}_{7}\mathrm{cos}{\varphi }_{7},-h\right)；\left({x}_{q7},{z}_{q7}\right) = \\ \left(a+{{r}^{\prime }}_{7}\mathrm{cos}{\varphi }_{7},-h\right)。\\ \end{gathered} \right. $

(13)

式中：l₃=AB、l₃′=BC、l₄=CD、l₆=EF、l₇=GF为机构中各杆件长度符号；为方便计算引入a～h表示机架长度；$ {\phi _i} $表示各杆件的角位移，i≠5，i=1,2,…,7；x₅表示推板滑块的位移。规定各杆件绕其旋转轴逆时针方向为正，与O′x正方向夹角即为各杆件的角位移大小。其中：${\phi _1}{\text{ = }}{\phi _2}$，常数C₀ = 23.062°。

把各构件当作杆矢量，那么，开合机构运动部件的质心位置矢量为：

$ {{ r}_p} = \frac{1}{{{m_J}}}\sum\limits_{i = 1}^7 {{m_i} \cdot } {{ r}_{pi}} 。$

(14)

开合机构运动部件的浮心位置矢量为：

$ {{\boldsymbol r}_q} = \frac{1}{{{m_{BJ}}}}\sum\limits_{i = 1}^7 {{m_{bi}} \cdot } {{\boldsymbol r}_{qi}}。$

(15)

式中：m_i、m_bi (i=1,…,7)分别表示机构杆件1～7的质量和排水质量；m_J、m_BJ分别为对接装置运动部件的质量和排水质量。

将式(15)代入式(13)和式(14)，可以得到对接装置运动部件基于坐标系O′xz下的质浮心位置。非运动部件质浮心位置确定，进而可得到接驳装置整体质浮心位置向量r_AG、r_AB与导向罩张角δ的关系。其中，δ等于2倍的${\phi _7}$。

1.3 边界条件

水下系泊悬浮接驳系统运动模型求解的边界条件为系绳首尾两端O和A′两点的运动和受力。

1）首端O点边界条件：

$ {{ V}_O} = {\left[ {{v_{oi}},{v_{oj}},{v_{ok}}} \right]^{\text T}}。$

(16)

各分量均以周期振荡运动规律作为系统运动输入施加到接驳系统，本文重点研究波浪作用下系泊平台升沉运动对接驳系统的影响，所以取v_oi = v_ok = 0。

2）自由端A′点边界条件

系绳和拖体之间相互影响，它们在运动时首先应满足运动学上的连续性条件，其次在动力学上还应计入拖缆对拖体运动的影响，以精确描述其运动。

①运动学耦合条件：即在拖体和拖缆连接点处A′，速度位置必须时刻一致。A′点在惯性坐标系{E}下的位置r_A′和速度$ {{\dot r}_{A'}} $可分别表示为

$ {{r}}_{{A}^{\prime }} = \left[ \begin{array}{c}{\xi }_{A}\\ {\eta }_{A}\\ {\zeta }_{A}\end{array} \right] + {{R}}_{a}^{e}{{r}}_{A{A}^{\prime }}\begin{array}{cc} ；{{r'}}_{{A}^{\prime }} = {{R}}_{a}^{e}\left(\left[ \begin{array}{c}u\\ v\\ w\end{array} \right] + {\left[ \begin{array}{c}p\\ q\\ r\end{array} \right]}_{\times } {{r}}_{A{A}^{\prime }}\right)。\end{array} $

(17)

式中：$ {{ r}_{AA'}} = \left[ {\begin{array}{*{20}{c}} {{l_{AA'}}\cos \lambda } \\ 0 \\ { - {l_{AA'}}\sin \lambda } \end{array}} \right] $，斜对称阵$ {\left[ {\begin{array}{*{20}{c}} p \\ q \\ r \end{array}} \right]_ \times } = \left[ {\begin{array}{*{20}{c}} 0 & { - r} & q \\ r & 0 & { - p} \\ { - q}&p&0 \end{array}} \right] $。

②动力学耦合边界条件：系绳作用于接驳装置的力，经坐标转换到随体坐标系{A}下可表示为

$ {{{\tau }}_{A'}} = \left[ {\begin{array}{*{20}{c}} {{{ f}_{A'}}} \\ {{{ r}_{AA'}} \times {{ f}_{A'}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{X_{A'}}} \\ {{Y_{A'}}} \\ {{Z_{A'}}} \\ {{y_{A'}}{Z_{A'}} - {z_{A'}}{Y_{A'}}} \\ {{z_{A'}}{X_{A'}} - {x_{A'}}{Z_{A'}}} \\ {{x_{A'}}{Y_{A'}} - {y_{A'}}{X_{A'}}} \end{array}} \right]。$

(18)

式中：$ {{ f}_{A'}} = {\boldsymbol R}_{a}^{{e - 1}}{\left[ {{T_i},{T_j},{T_k}} \right]^{\text T}} $。

最终，水面系泊平台的运动变化为整个系统的输入，而水下接驳拖体的位置与速度由接驳装置的运动控制式(4)计算得到。

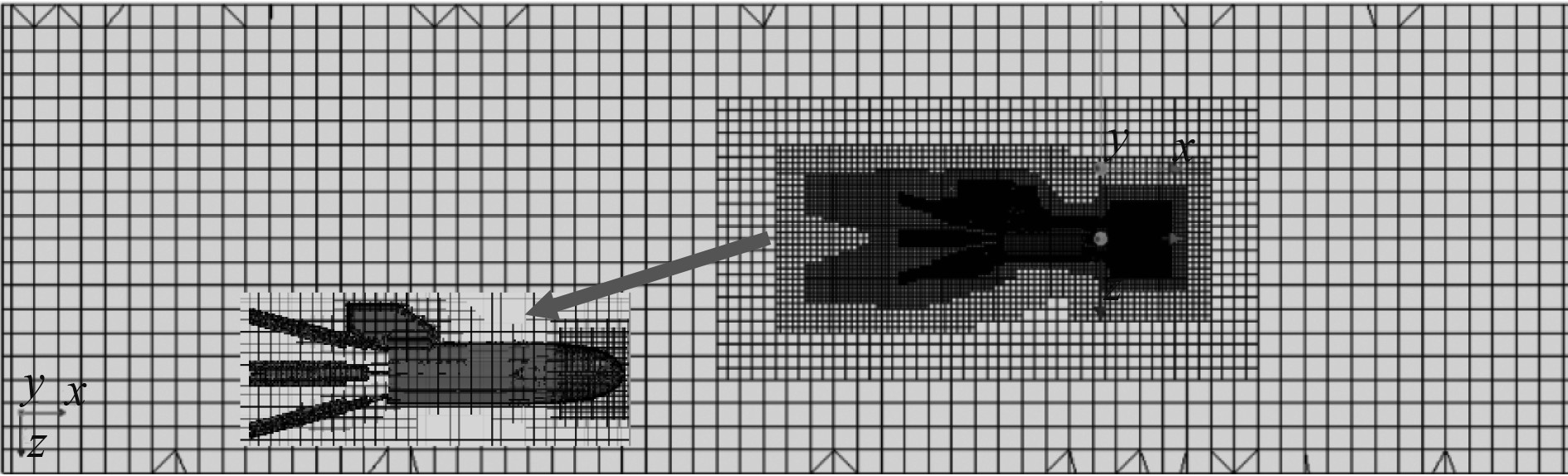
2 仿真分析 2.1 仿真设置

本文采用商用CFD软件STAR-CCM+建立单点系泊悬浮接驳系统的动态仿真模型，如图3所示。CFD仿真试验参数设置如下：单位长度系绳质量为0.5 kg；缆绳长度L₀=5 m；系绳刚度系数K_s=6×10⁵ N/m；水流方向为[−1,−1,0]，水流幅值为1 m/s；系泊点O静止不动。选择动态流体-体相互作用（DFBI）作为动态仿真模式，通过网格有效性检验，网格数量约为206.7万，以及仿真步长为0.025 s，结果收敛。

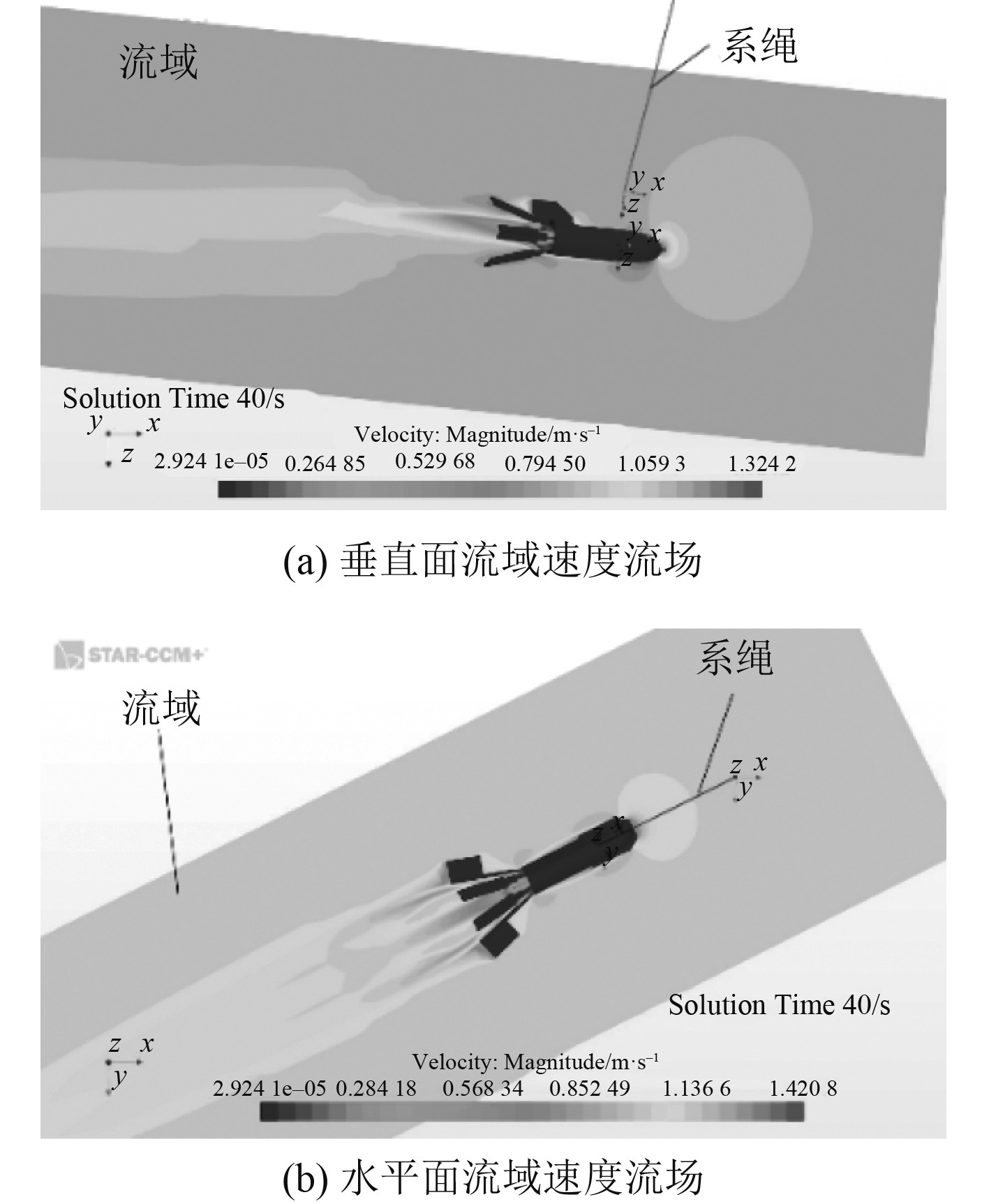
其它参数与数学模型初始基本参数同样保持一致，当时间为40 s时，随体坐标系{A}的垂直面和水平面内流域的速度流场如图4所示，此时接驳装置附近流场已趋于稳定状态。

2.2 仿真结果分析 2.2.1 水流大小

在纵垂面内，研究恒定水流作用下系统的动力响应，在初始条件基础上设置外界水流扰动V_cj=0，V_ci=[−2, −1.5, −1, −0.5, 0] m/s。仿真结果表明，水流幅值越大，系绳摆角越大，接驳装置深度越小，其前向位置偏移越大，相应的系绳张力也越大。图5(d)可以看出，没有水流作用时，纵倾角状态不利于对接；有水流作用下，纵倾角均能在20 s内达到稳定状态，而且水流幅值越大，纵倾角稳定绝对值越小，有利于接驳回收AUV。综合考虑，对于该系统工作于水流幅值为1.5 m/s左右是比较合适的，因为水流幅值继续提升对降低稳定纵倾角效果不再明显，反而会较大地增加系绳张力负担。

为模拟实际水流的复杂缓慢变化，引入正弦波模型来模拟水流速度（T为水流运动周期）^[4]：

$ {V_{ci}} = - 1 + 0.5 \times \sin \left( {\frac{{2{\text{π}} }}{T}t} \right),T = 50\ {\rm s}。$

(19)

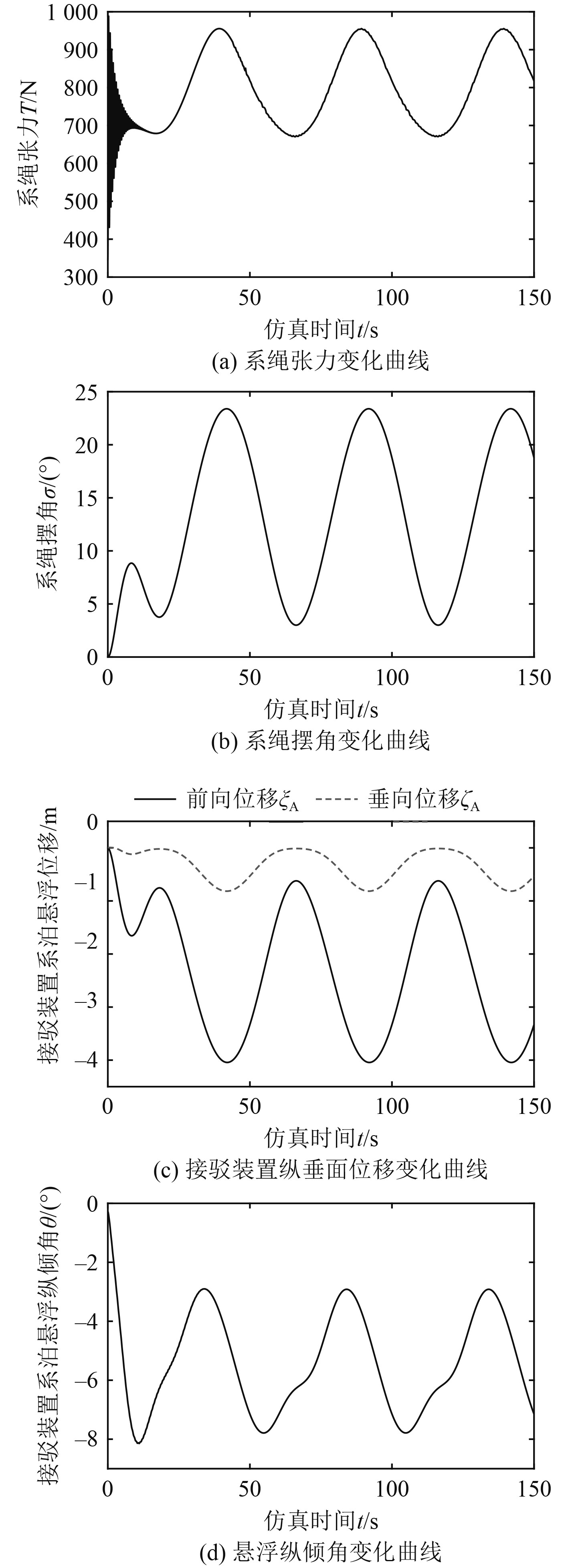
系泊悬浮接驳系统在周期水流作用下的动态响应过程，如图6所示。仿真结果表明，水流作用下，系泊悬浮接驳系统位置、系绳张力、摆角等运动参数均经25 s左右的调整时间，逐渐进入平稳状态。由于水流的周期特性，接驳系统跟随周期水流同步振荡，对应接驳装置纵倾角在[−8,−3]°范围内变化。

2.2.2 水流方向

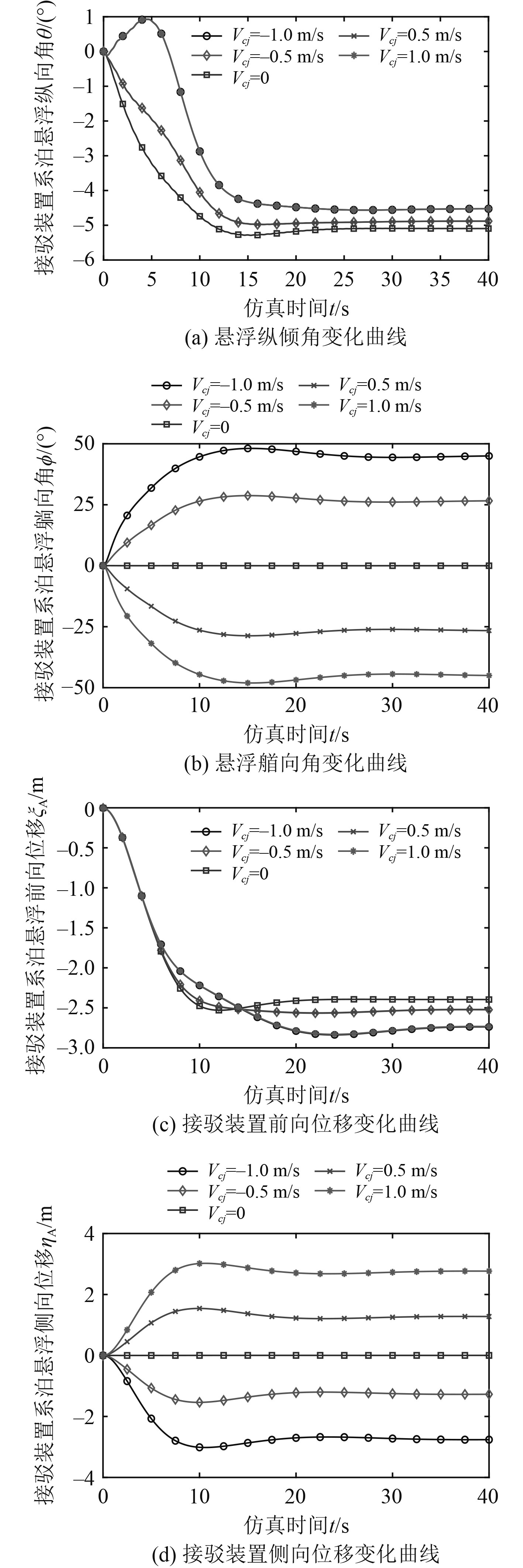
为分析侧向水流对接驳系统系泊悬浮运动的影响，设置外界水流V_ci=−1 m/s，V_cj=[−1, −0.5, 0, 0.5, 1] m/s。由图7可得，侧向水流改变了系统水平面内的运动参数，如接驳装置首向角和侧向位移。同一幅值，不同方向的侧向水流，仅改变水平面内的运动参数方向。最终该系统能在不同侧向水流作用下自动调整并稳定接驳装置首向角位置，且首向角与水流方向角基本相等，具备首向角稳定性。

3 实验验证与分析

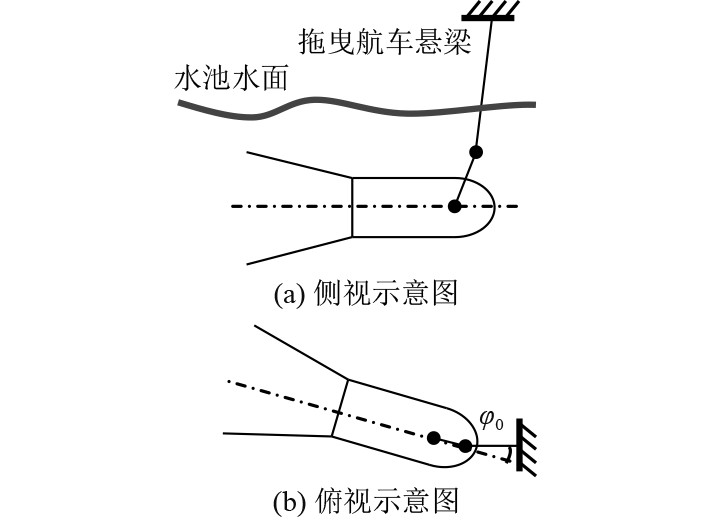
为了验证数学模型和动态仿真模型的有效性，本文在水池进行拖曳实验。水池尺寸为60 m×30 m×15 m；拖曳航车速度最大为1 m/s，精度可以控制在0.001 m/s以内接驳装置上的传感器为惯组IXSEA-OCTANS 3000(2006)，取样频率为15 Hz。通过改变接驳装置的初始姿态模拟不同方向的流，如图8中的航向角初始值φ₀。

假设本文中系泊悬浮接驳系统被预先布放于静水中，仿真初始条件设定系绳处于松弛和张紧的临界状态L₀=10 m，系绳的摆角σ=0°，系泊平台坐标系原点O与惯性坐标系原点E重合，整体系统处于同一铅垂平面内，接驳装置纵倾角θ=0°，拖架角λ=90°。初始导向罩张角δ=34°所对应的接驳装置基本参数如表1所示。

接驳系统水动力模型式(8)中的水动力系数无因次化后，如表2所示。

3.1 实验验证

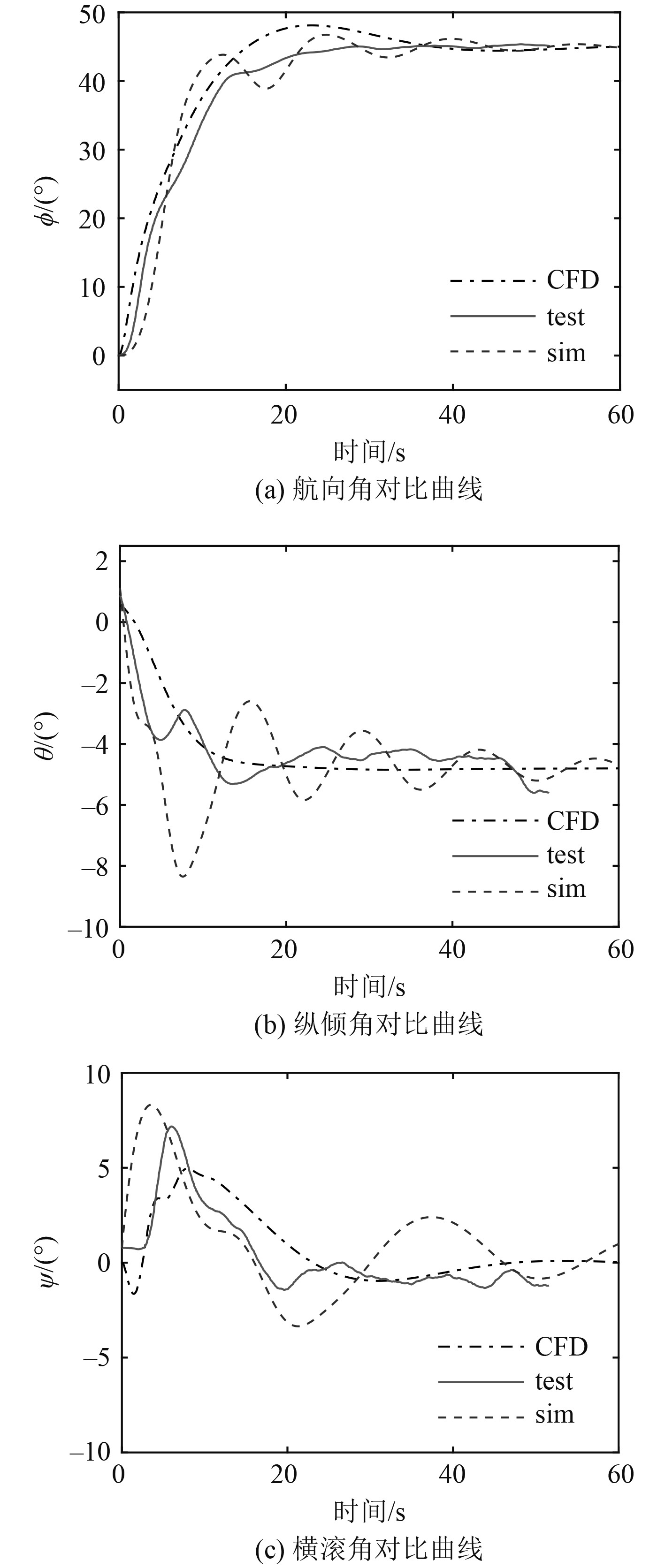
由于惯组只能测量并记录接驳装置的姿态角。图9分别为接驳装置的航向角对比图、俯仰角对比图以及横滚角对比图。拖曳初始角度为45°，拖曳速度为1 m/s。图9(a)中实验数据与CFD模型、数学模型计算值的相关性分别为0.9367、0.9237，分别在26.3、32.9、32.7 s进入稳定状态，即振动幅值差不超过2°（根据设计要求），最终在0°周围波动；图9(b)中分别为0.7033、0.3342，俯仰角最终均在−5°周围波动；图9(c)中的相关性系数较低，分别为0.6072、0.3001，横滚角在0°周围波动。由于接驳装置横滚运动不明显，相关水动力系数较小，容易存在较大的舍入误差，造成仿真值、数值求解值与实验值存在一些偏差。通过实验可以验证数值求解与仿真的有效性，但根据对比结果发现数学模型和仿真模型的阻尼更小，且数学模型有明显的振动周期，因此针对该接驳装置，可以认为仿真模型能更准确地描述其运动状态，后续使用仿真模型预测不同条件下接驳装置的运动状态。

3.2 波浪影响分析

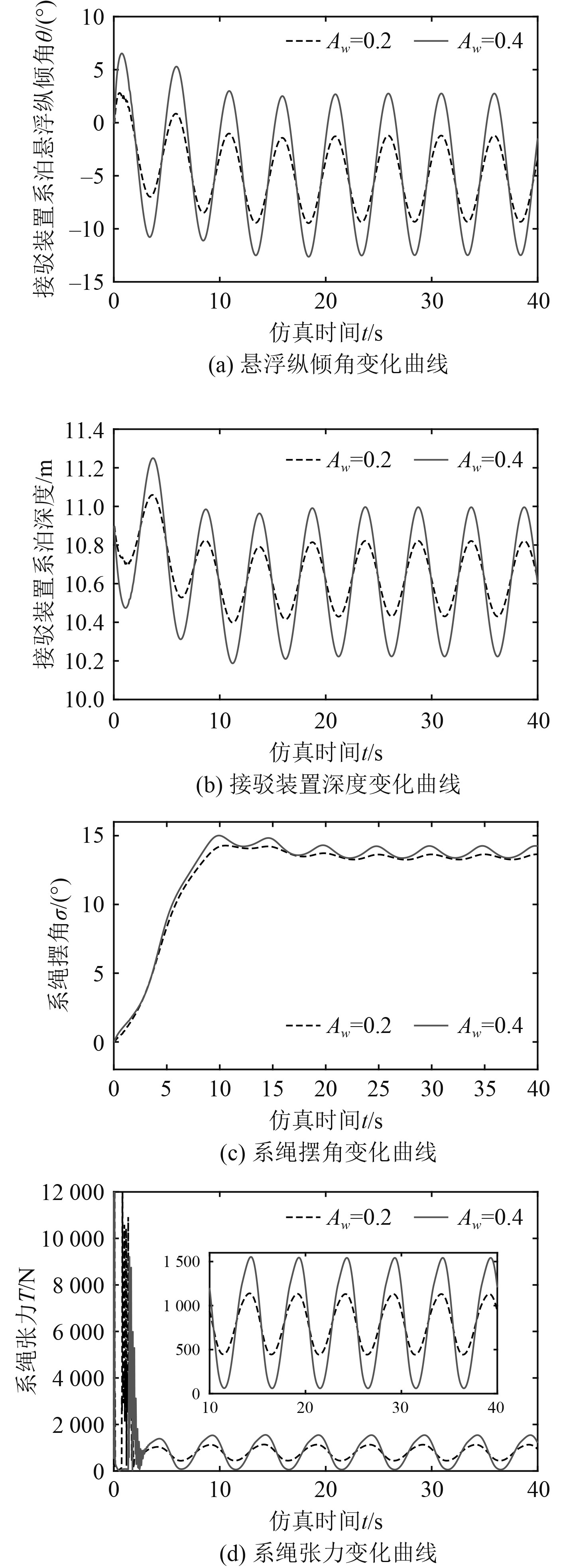
本文主要考虑系泊平台具有正弦特性的垂向升沉输入性强迫振动给系统带来的影响。选取波浪运动周期为5 s，波高A_w分别取0.2 m和0.4 m，系泊悬浮接驳系统在V_ci=−1 m/s工况下，振动传递规律时域仿真计算对比结果如图10所示。水流和升沉运动激励作用下，系绳摆角逐渐增大，经过10 s左右的调整时间，系统平稳过渡到随波升沉阶段，振动周期同波浪运动周期。在这个阶段，波高0.2 m对应纵倾角在−9.336°～−1.214°之间变化，波高0.4 m对应纵倾角在−12.49°～2.751°之间变化，后者变化幅值约为前者2倍。对应深度变化范围幅值分别约为0.39 m和0.8 m，表明系统在初始固定拖架的条件下，对于系泊平台的垂向升沉输入性强迫振动传递没有衰减作用。由图10(d)可以看出，系绳张力经高频振荡，4 s内恢复稳定状态，在接驳装置负浮力作用下，系绳仍时刻保持张紧状态。而波高0.2 m和0.4 m对应最大平稳系绳张力分别为1131 N和1542 N。

3.3 拖点位置影响分析 3.3.1 自由拖架

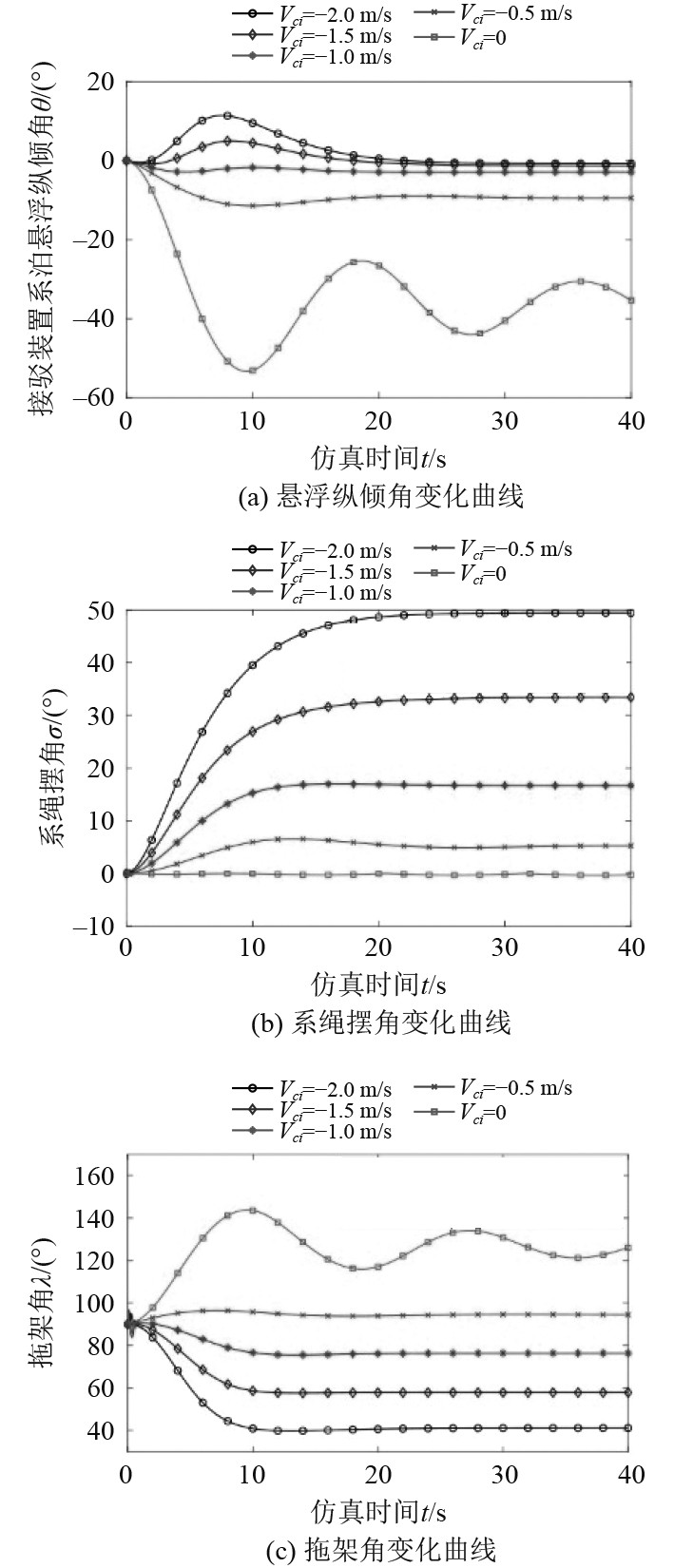
接驳装置除受外界影响外，拖点位置的变化和导向罩的开合状态也影响装置的运动状态。当拖架自由铰接于接驳装置上时，接驳系统在不同幅值水流作用下的运动状态见图11。相比图5所示的固定拖架角λ=90°工况下接驳系统的运动状态，两者悬浮纵倾角和系绳摆角变化规律基本一致，水流均有助于系统快速稳定，而且水流幅值越大，越有利于悬浮纵倾角趋于0。

对应于图11和图5分别将不同水流速度下，2种工况的平衡拖架角、纵倾角和系绳摆角汇总于表3和表4。在水流速度较低时，尽管初始拖点A相对理想拖点（满足平衡纵倾角θ=0°的拖点）靠后约0.1815 m，但由于固定拖架的理论拖点位于A′点，相比自由拖架的理论拖点A，增大了与重心的垂向距离，接驳装置总体稳心高增大，导致单位纵倾角变化产生的静俯仰力矩增大，所以接驳装置系泊悬浮平衡纵倾角相较自由拖架工况小。尤其在静水中时，固定拖架的这种优势更加明显。但是，在水流速度较高时，自由拖架更有利于降低平衡纵倾角。同样，因拖点不同造成静平衡力及力矩的差异，0～2 m/s水流作用下，固定拖架工况下接驳系统系绳摆角幅值范围，相比之下减少约16°，对应接驳装置深度变化范围也更小。

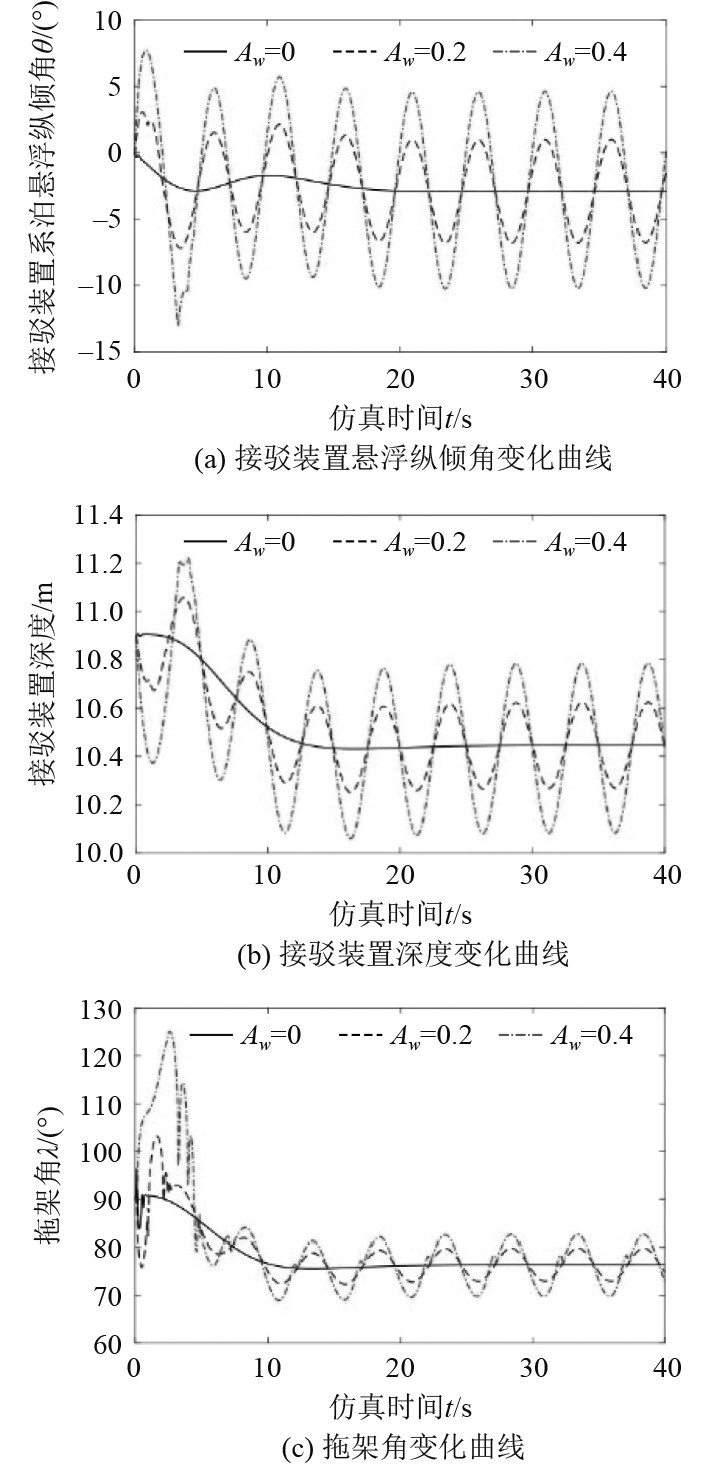
系泊悬浮接驳系统在V_ci=−1 m/s工况下，系泊平台O点输入周期为5 s，幅值A_w分别为0、0.2和0.4 m的具有正弦特性的垂向升沉运动，仿真结果如图12所示。经过15 s左右的调整时间，系统平稳过渡到随波升沉阶段，图示运动参数变化周期同O点输入的强迫升沉振动周期。在这个阶段，升沉幅值0.2 m对应纵倾角在−12.49°～1.009°之间变化，升沉幅值0.4 m对应纵倾角在−10.19°～4.636°之间变化，对应深度变化范围幅值分别为0.35 m和0.7 m。相比于固定拖架，自由拖架相对接驳装置会随波周期摆动，一定程度上缓冲了系绳的振动。

3.3.2 固定拖架

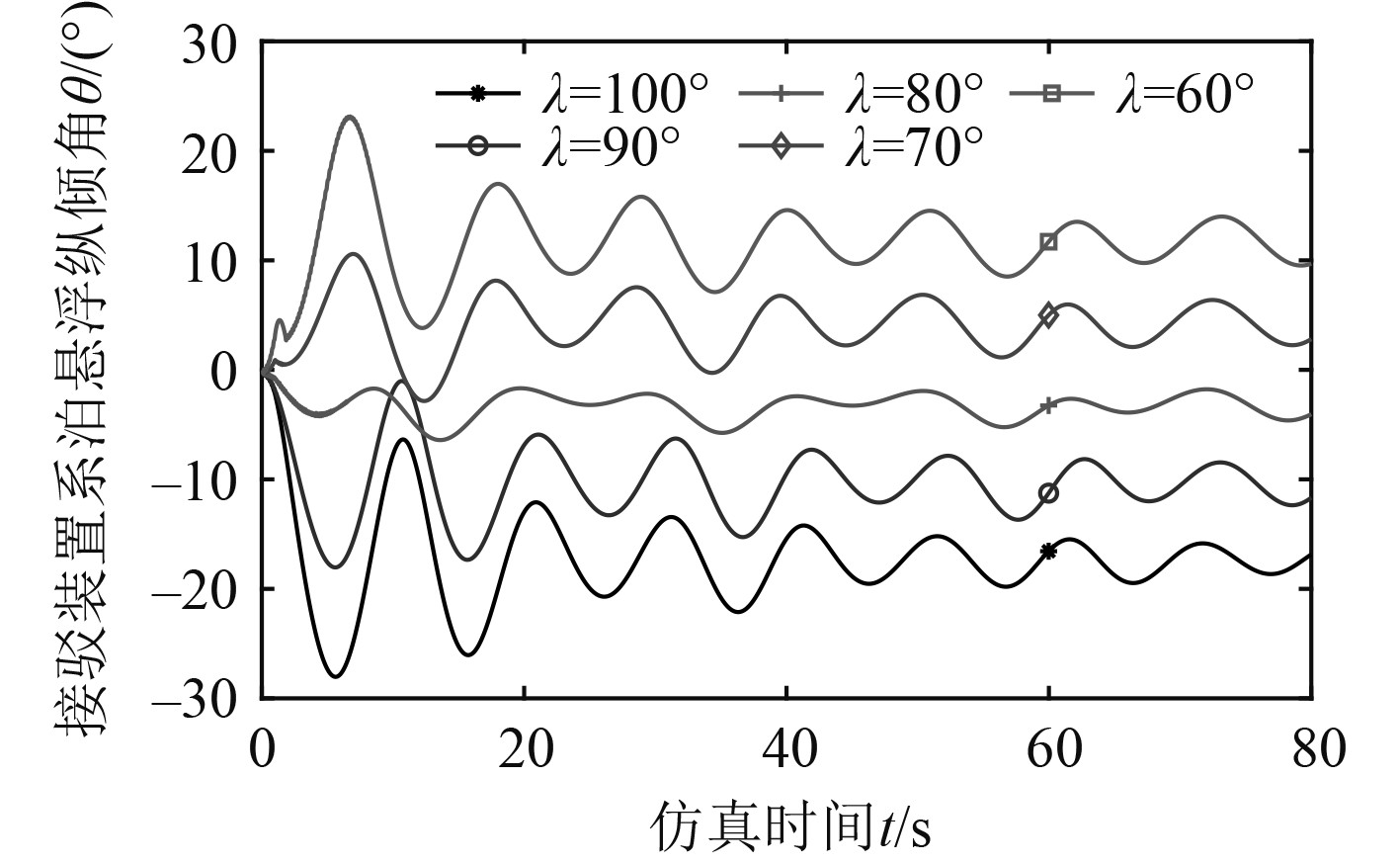
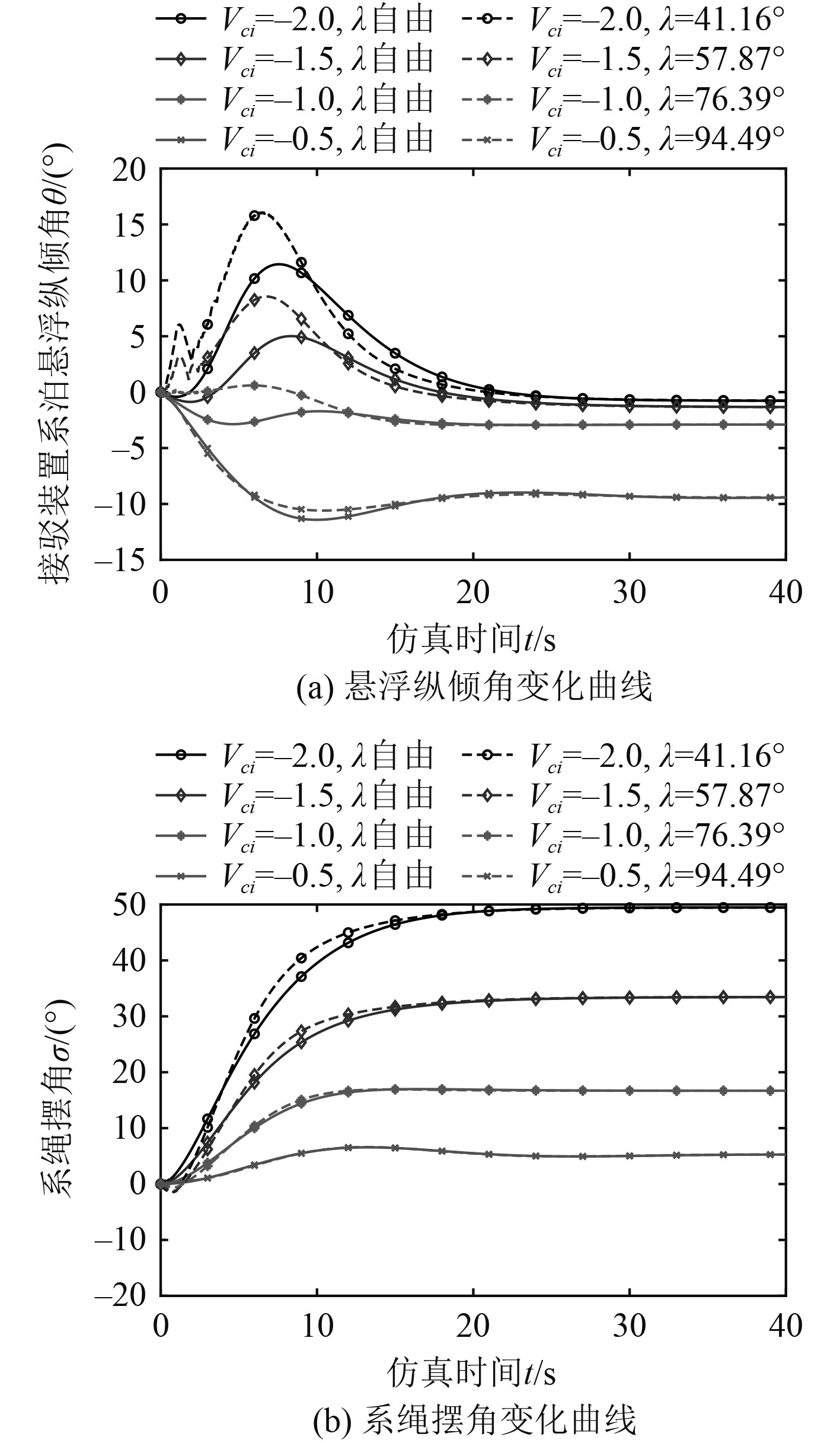
如图13所示，拖架角λ越小，对应接驳系统悬浮纵倾角稳定绝对值先减小后增大。纵倾角稳定值θ趋于0时的拖架角在[70°, 80°]区间内。图14为不同水流条件下，固定拖架角λ设置成表3中对应的平衡拖架角值与自由拖架工况的接驳系统纵倾角与系绳摆角对比曲线图。由此可见，通过设置特定的拖架角，自由和固定拖架方案可以达到同样的系泊悬浮稳定状态。

3.4 导向罩开合影响分析

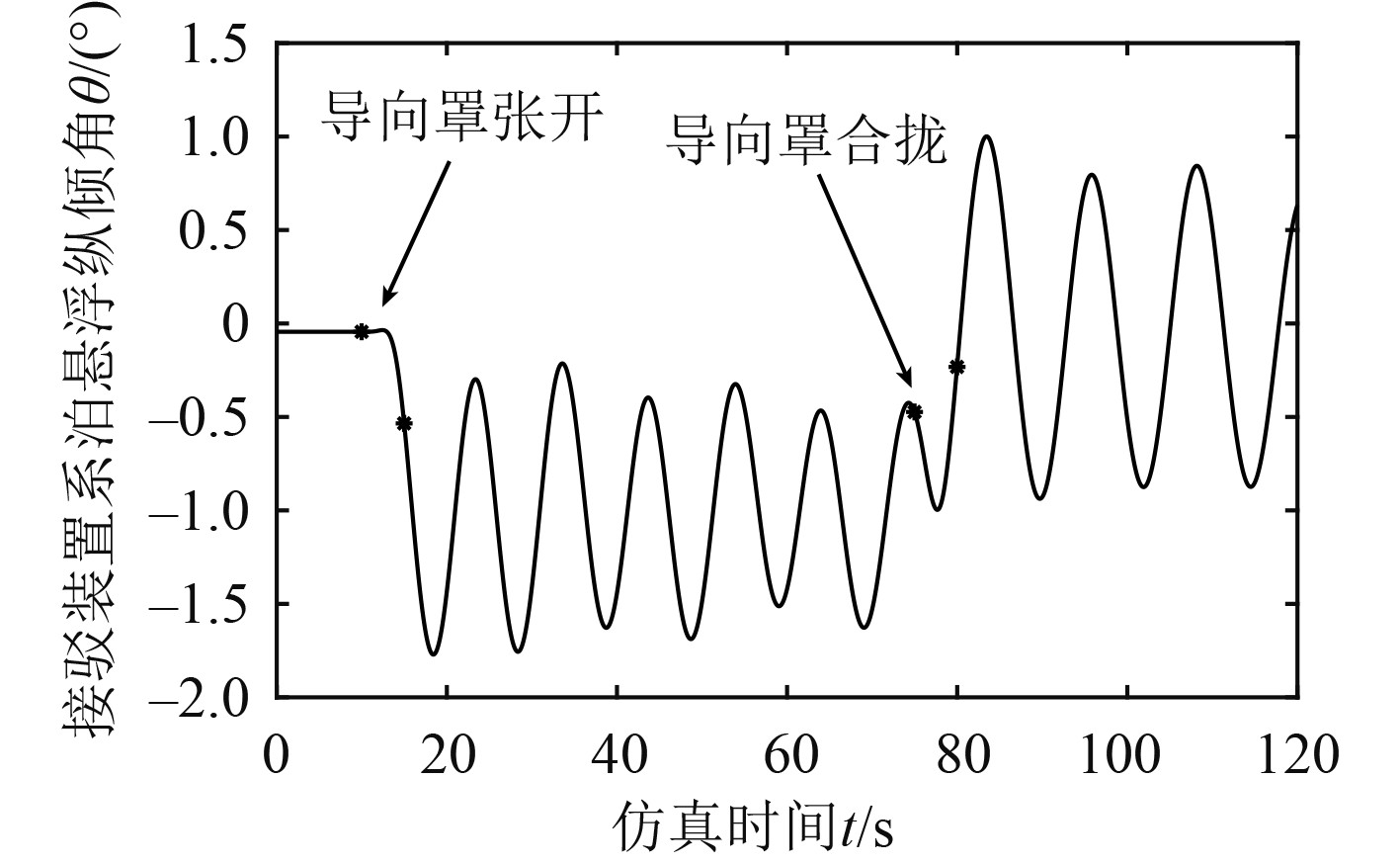
静水中，导向罩合拢，张角δ=0°，当拖架角λ=78.3°时，接驳装置悬浮平衡纵倾角为−0.044°，以此平衡状态为初始条件，10～15 s时导向罩张开至δ=34°，75～80 s时导向罩逐步完全合拢，整个过程的接驳装置悬浮纵倾角的变化曲线如图15所示。导向罩打开时，纵倾角逐渐缓慢振荡至−1°附近，导向罩合拢后，系统还会渐进振荡至初始平衡位置，其振荡幅值小于2°。

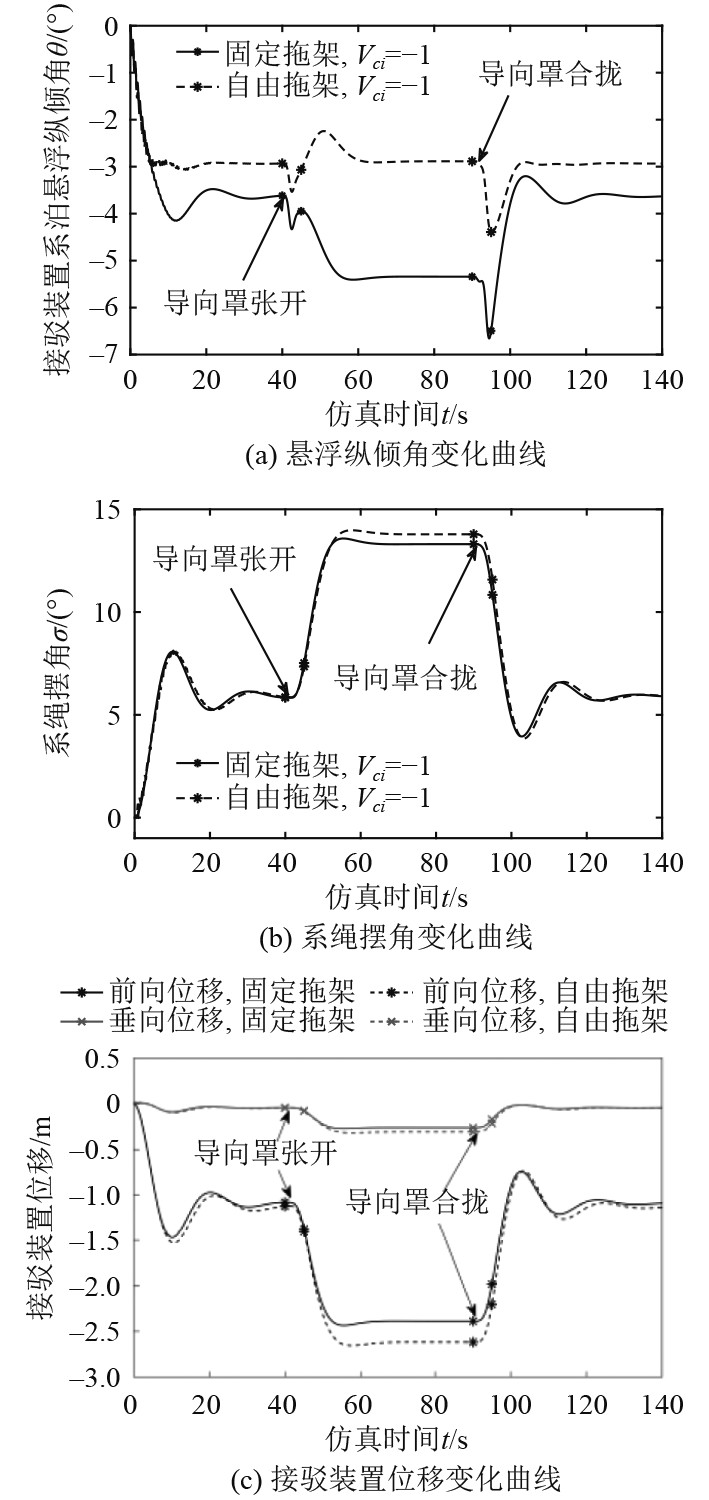
水流速度为1 m/s时，接驳系统初始导向罩张角δ=0°，40～45 s导向罩张开至34°，后在90～95 s逐步完全合拢。整个过程中，固定拖架λ=90°和自由拖架2种工况下，接驳装置的运动状态对比如图16所示。随着导向罩张开，迎流面积增大，所受水阻力增大，系绳摆角增大，对应其相对大地的前向和垂向位置偏移量也增大，并逐渐调整至稳定状态。导向罩合拢后，接驳系统回到导向罩张开前的系泊悬浮稳定状态。结果表明水流作用下，导向罩的开合对接驳装置纵倾角的影响幅值小于4°，而且由于自由拖架接驳系统的理论拖点位于A点，造成纵倾角调整变化的主要原因是导向罩开合导致接驳装置转动惯量的改变。导向罩开合对系绳摆角和接驳装置前向位移偏移量的影响较大，可能造成系统接驳回收AUV时，由于导向罩合拢，接驳装置前向移动较快，导向罩在未夹紧AUV前就与AUV分离。因此，在迎流对接时，需要对接驳系统导向罩合拢运动以及AUV接驳速度提出要求。

4 结　语

本文针对单点系泊悬浮接驳系统，详细研究了接驳装置在外界水流和波浪扰动以及自身拖点位置和导向罩开合扰动下的运动状态。依据实际工况将系绳简化为变刚度—阻尼弹簧模型，接驳装置采用潜艇六自由度运动模型，通过建立缆-体耦合边界条件建立系泊悬浮接驳系统三维运动模型。然后展开仿真模拟计算与拖曳实验，验证了2种方法的有效性，并详细探讨了引入波浪后接驳装置的运动状态，以及导向罩开合、拖曳点的变动对其运动状态的影响。计算结果表明：

1）经过与实验数据的对比，验证了2种方法的有效性，相对于数学模型与仿真模型，实验中的模型在拖曳过程中的阻尼明显更大。而利用STAR-CCM+建立的动态仿真模型相比于数学模型更能准确反映接驳装置的运动状态。

2）接驳系统的悬浮姿态与运动状态分析是整个单点系泊系统设计的关键内容。不同水流工况仿真分析后发现，水流越大，系统更快达到悬浮稳定状态，悬浮纵倾角会降低。

3）水面系泊平台的升沉振动，会以同比例经系绳传递给水下接驳装置，不仅如此，升沉运动加速度也会给系绳带来抗拉负担。由分析可得，系统最好工作在波浪幅值小于0.2 m的海况下，否则需要增加升沉补偿装置来抑制振动传递，降低接驳装置纵倾角和升沉位移。

4）相比自由拖架，静水中固定拖架时，系泊悬浮综合稳定性更好。自由拖架的优势在于，能降低水流作用下接驳装置的悬浮纵倾角稳定值，对升沉振动传递有轻微的抑制作用。因此，在一定程度上有必要综合两者优势，开发变拖点隔振控制系统。通过动态调节实际拖曳点位置，实时配置拖体俯仰静力矩，可以在一定程度上对系泊悬浮接驳装置进行纵倾和深度运动补偿。

5）导向罩开合对接驳系统悬浮纵倾角的影响较小，一般不会影响AUV对接。但在较大的水流作用下，导向罩动作对系绳摆角和接驳装置前向位移偏移量的影响较大。因此，在迎流对接时，需要规划导向罩合拢以及AUV对接方案。