船-机-桨之间的匹配关系对发动机使用寿命、船舶推进系统效率、经济性及污染物排放指标有着重要影响。因此,开展船-机-桨参数匹配的研究是十分必要的。相关机构的研究团队先后开展了甲醇燃料发动机燃油配比、供给控制、船-机-桨动力总成匹配算法的研究,但均未涉及复杂工况下智能船舶驾驶的船-机-桨实时匹配。鉴于此,本文提出一种船-机-桨参数匹配的新方法。首先,基于船-机-桨实时匹配的动态数学模型,构建匹配参数与燃油消耗、推进系统效率及燃烧物排放的多目标优化模型;其次,以桨叶数、螺距比、盘面比、螺旋桨转速、螺旋桨直径、船舶航速及发动机负荷率为优化变量,以最小化发动机燃油消耗、最大化推进系统效率及最小化燃烧物排放为优化目标;然后,采用改进的多目标北方苍鹰优化算法算法(Improved Multi-Objective Northern Goshawk Optimization,IMONGO)对已建立的模型进行迭代寻优。最后,利用排序优选技术(TOPSIS)对优化参数性能进行排序,并且把评分第一的解决方案作为船-机-桨参数匹配结果,进而达到提高船舶经济性且降低环境影响的目标。
1 船-机-桨实时匹配的动态数学模型
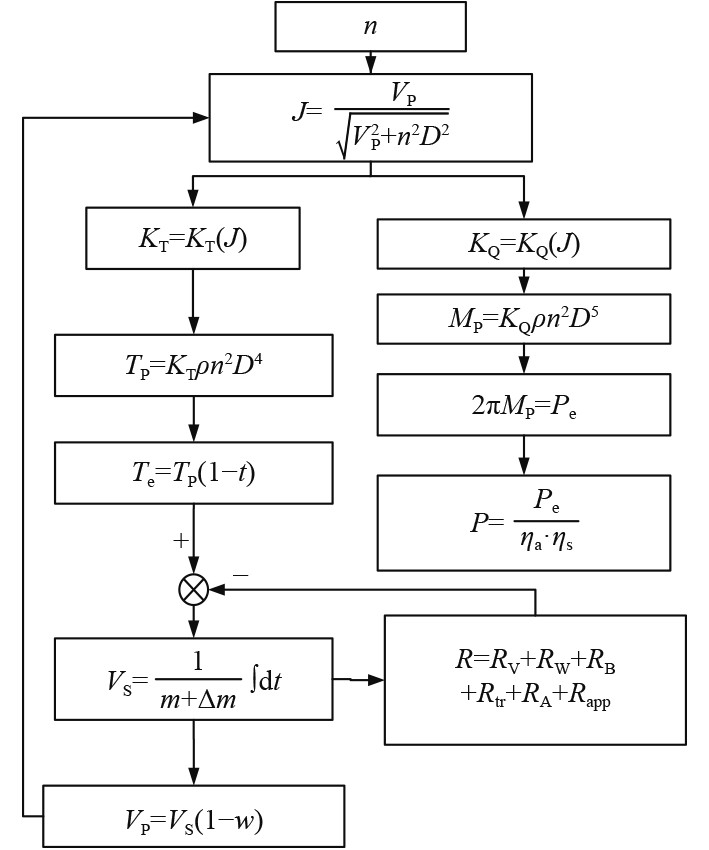
|
图 1 船-机-桨实时匹配数学模型 Fig. 1 Real-time ship-machine-paddle matching mathematical model |
根据船舶主尺度和关键匹配系数研究船舶阻力特性,将船舶阻力分成六部分:裸船体粘性阻力、裸船体兴波阻力、方尾浸没阻力、球鼻艏附加阻力、附体阻力、船模实船修正阻力,根据船舶实际航行工况参数计算相应的分量阻力,最后得到船舶总阻力
| $ {V}_{P}={V}_{S}(1-W),$ | (1) |
| $ J=\frac{{V}_{P}}{\sqrt{{{V}_{P}}^{2}+{n}^{2}{D}^{2}}}。$ | (2) |
通过进速系数、螺距比、盘面比、桨叶数计算对应的推力系数
| $ {K}_{T}=\sum _{n=1}^{39}{{C}_{n}\left(J\right)}^{{S}_{n}}{\left(\frac{P}{D}\right)}^{{t}_{n}}{\left(\frac{{A}_{E}}{{A}_{O}}\right)}^{{u}_{n}}{\left(Z\right)}^{{V}_{n}} ,$ | (3) |
| $ {K}_{Q}=\sum _{n=1}^{47}{{C}_{n}\left(J\right)}^{{S}_{n}}{\left(\frac{P}{D}\right)}^{{t}_{n}}{\left(\frac{{A}_{E}}{{A}_{O}}\right)}^{{u}_{n}}{\left(Z\right)}^{{V}_{n}}。$ | (4) |
式中:
再根据推力系数和扭矩系数分别计算得到螺旋桨的推力
| $ {T}_{P}={K}_{T}\rho {n}^{2}{D}^{4},$ | (5) |
| $ {M}_{P}={K}_{Q}\rho {n}^{2}{D}^{5}。$ | (6) |
其中,
分析船舶实际运行工况,基于牛顿第二定律以及船-机-桨之间的动力平衡关系,提出复杂工况下的船-机-桨动力匹配计算方法,并建立船-机-桨匹配的实时动态数学模型,计算如下:
| $ \begin{split} \left(m+\Delta m\right)\frac{{\rm{d}}{V}_{S}}{{\rm{d}}t}=& {T}_{e}-{R}_{m}={T}_{e}-({R}_{V}+{R}_{W}+{R}_{B}+\\ & {R}_{tr}+{R}_{A}+{R}_{app})。\end{split} $ | (7) |
式中:
北方苍鹰优化算法(Northern Goshawk Optimization,NGO)模拟了苍鹰狩猎,选优过程包含以下2个阶段:
1)识别猎物及攻击猎物(全局搜索)
在狩猎的第一阶段,苍鹰随机选择猎物,然后迅速攻击,属于全局搜索阶段,可用以下数学模型进行描述:
| $ {X}_{ij}^{new,P1}=\left\{\begin{array}{c}{X}_{ij}+r\left({P}_{ij}-I{X}_{i,j}\right),{F}_{{P}_{i}} < {F}_{i},\\ {X}_{ij}+r\left({X}_{i,j}-{P}_{ij}\right),{F}_{{P}_{i}}\geqslant {F}_{i}。\end{array}\right. $ |
| $ {X}_{i}=\left\{\begin{array}{c}{X}_{ij}^{new,P1},{F}_{i}^{new,P1} < {F}_{i},\\ {X}_{i},{F}_{i}^{new,P1}\geqslant {F}_{i}。\end{array}\right. $ | (8) |
式中:
2)追逐及逃生(局部搜索)
当苍鹰靠近猎物后,猎物试图逃跑,此时苍鹰继续追随,防止猎物逃跑,故采取局部搜索,其数学模型如下:
| $ {X}_{ij}^{new,P2}={X}_{i,j}+R(2r-1){X}_{i,j},$ |
| $ R=0.02\left(1-\frac{t}{T}\right), $ |
| $ {X}_{i}=\left\{\begin{array}{c}{X}_{ij}^{new,P2},{F}_{i}^{new,P2} < {F}_{i},\\ {X}_{i},{F}_{i}^{new,P2}\geqslant {F}_{i}。\end{array}\right. $ | (9) |
式中:
NGO采用随机方式生成初始种群,生成的种群分布不均,不能保证初始种群覆盖问题的决策空间,易陷入局部最优[1-4]。因此,引入Sine混沌映射和精英反向学习策略对种群初始化方式进行改进。Sine混沌映射的公式如下:
| $ {s}_{i+1}=\mu \cdot \mathrm{sin}\left(\text{π} {s}_{i}\right),i=\mathrm{1,2},\cdots ,n。$ | (10) |
式中:
精英反向学习策略利用精英个体比一般个体包含更多有效信息的这一特点,通过当前种群中的精英个体构造出反向种群来增加种群的多样性,并从当前种群和反向种群构造的新种群中选取最优个体作为新一代个体[5-6]。
改进的种群初始化步骤如下:
步骤1 按式(11)、式(12)、式(13)生成种群
| $ X=lb+rand\cdot (ub-lb),$ | (11) |
| $ {X}_{s}=lb+S\cdot (ub-lb),$ | (12) |
| $ {X}_{t}=rand\cdot \left(ub-lb\right)-X。$ | (13) |
式中:
步骤2 将种群
自适应权重的特点是当权重较大时,其搜索范围较大;当权重较小时,可对局部进行精细化搜索[7-9]。因此,在苍鹰接近目标时,利用权重较小时的特点改变最优苍鹰的位置,提高局部寻优能力。本文自适应权重公式如下:
| $ \omega ={-e}^{\frac{-t}{T}}+1。$ | (14) |
式中:
| $ \begin{aligned} & {X}_{ij}^{new,P1}=\left\{\begin{array}{c}{\omega \cdot X}_{ij}+r\left({P}_{ij}-I{X}_{i,j}\right),{F}_{{P}_{i}} < {F}_{i},\\ \omega \cdot {X}_{ij}+r\left({X}_{i,j}-{P}_{ij}\right),{F}_{{P}_{i}}\geqslant {F}_{i}。\end{array}\right.\\ & {X}_{i}=\left\{\begin{array}{c}{X}_{ij}^{new,P1},{F}_{i}^{new,P1} < {F}_{i},\\ {X}_{i},{F}_{i}^{new,P1}\geqslant {F}_{i}。\end{array}\right. \end{aligned} $ | (15) |
为了验证改进的IMONGO算法性能,选择标准测试函数ZDT1和ZDT2进行测试。评价指标分别为迭代距离(GD)、反向迭代距离(IGD)、超体积指标(HV)、空间评价方法(SP)。其中,GD值、IGD值及SP值越小,表示收敛性越好且解集越均匀。HV值越大,表示近似解集支配目标空间的体积越大,近似解集越接近真实解集。
|
|
表 1 算法测试函数对照表 Tab.1 Algorithm test function comparison table |
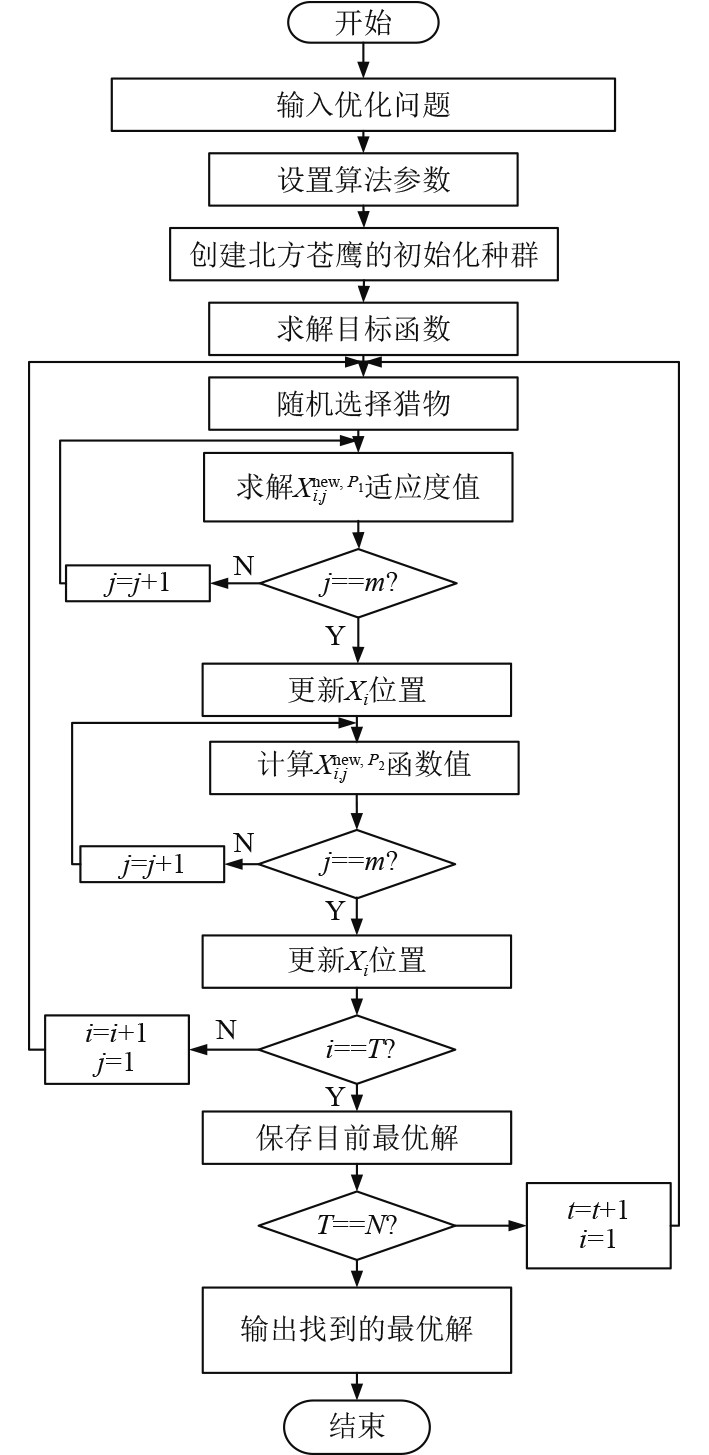
|
图 2 改进的多目标北方苍鹰优化算法流程图 Fig. 2 Flowchart of the improved multi-objective northern eagle optimization algorithm |
以桨叶数、螺距比、盘面比、螺旋桨转速、螺旋桨直径、船舶航速及发动机负荷率为优化变量,设计变量表示如下:
| $ X=\left[Z,\frac{P}{D},\frac{{A}_{E}}{{A}_{O}},n,D,{V}_{S},\frac{{P}_{xq}}{{P}_{S}}\right] 。$ | (16) |
推进系统效率函数表达式如下:
| $ \eta ={\eta }_{a}\cdot {\eta }_{s}\cdot {\eta }_{d}\cdot {\eta }_{f}。$ | (17) |
其中,轴系效率
| $ {\eta }_{f}=\frac{1-t}{1-W} 。$ | (18) |
螺旋桨敞水效率可由下式得到:
| $ {\eta }_{d}=\frac{{K}_{T}\cdot J}{{K}_{Q}\cdot 2\text{π} }。$ | (19) |
对于B系列螺旋桨,
利用Matlab对主机的混合燃料消耗率曲线进行多项式拟合得出目标函数表达式如下:
| $ \begin{split} {\rm{min}}f\left(1\right)=& -16.6{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{4}+36.3\left(\frac{{P}_{xq}}{{P}_{S}}\right)+66.4{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{2}-\\ & 144\frac{{P}_{xq}}{{P}_{S}}+264^{3}。\\[-10pt] \end{split} $ | (20) |
利用Matlab对氮氧化物(
| $ \begin{split} {\rm{min}}f\left(2\right)=& -2.46{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{4}+4.45\left(\frac{{P}_{xq}}{{P}_{S}}\right)+\\ & 0.739{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{2}+0.033\frac{{P}_{xq}}{{P}_{S}}+0.426^{3}。\end{split} $ | (21) |
利用Matlab对主机碳烟(Soot)排放量/
| $ \begin{split} {\rm{min}}{f\left(2\right)}^{*}=& -1.7{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{5}+5{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{4}-5.1{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{3}+\\ & 2.4{\left(\frac{{P}_{xq}}{{P}_{S}}\right)}^{2}+0.37\frac{{P}_{xq}}{{P}_{S}}+0.0.37。\end{split} $ | (22) |
船-机-桨匹配需满足动力平衡关系及能量守恒定律,另外螺旋桨需要满足空泡校核要求,可得3个约束条件:
| $ \begin{split} \left(m+\Delta m\right)\frac{{\rm{d}}{V}_{S}}{{\rm{d}}t}=& {T}_{e}-{R}_{m}={T}_{e}-\left({R}_{V}+{R}_{W}+{R}_{B}+\right.\\ & \left.{R}_{tr}+{R}_{A}+{R}_{app}\right) ,\end{split} $ | (23) |
| $ 2\text{π} n{M}_{P}=P\cdot {\eta }_{a}\cdot {\eta }_{s},$ | (24) |
| $ \frac{{A}_{E}}{{A}_{O}}\geqslant \frac{\left(1.3+0.3Z\right)T}{{P}_{O}-{P}_{V}}+K。$ | (25) |
其中:
| $ {T}_{e}={(1-t)K}_{T}\rho {n}^{2}{D}^{4} ,$ | (26) |
| $ {M}_{P}={K}_{Q}\rho {n}^{2}{D}^{5} 。$ | (27) |
以最小化发动机燃油消耗、最小化燃烧物排放及最大化推进系统效率为优化目标,构建多目标优化模型:
| $ {\rm{min}}f\left(x\right)=\left[f\left(1\right),f\left(2\right),-\eta \right]。$ | (28) |
| $ {\rm{s.t}}.\left\{\begin{array}{c}0.1\leqslant P/D\leqslant 1.2,\\ 0.1\leqslant {A}_{E}/{A}_{O}\leqslant 1,\\ {n}_{\rm min}\leqslant n\leqslant {n}_{\rm max},\\ {D}_{\rm min}\leqslant D\leqslant {D}_{\rm max},\\ {Z}_{\rm min}\leqslant Z\leqslant {Z}_{\rm max},\\ 0\leqslant V\leqslant {V}_{\rm max},\\ 0\leqslant {P}_{xq}/{P}_{S}\leqslant 1.2,\\ 0.10\leqslant t\leqslant 0.22,\\ 0.08\leqslant w\leqslant 0.20。\end{array}\right. $ | (29) |
TOPSIS即“逼近于理想值的排序方法”,是一种高效先进的MCDM(多准则决策)方法[10-13]。在实际优化设计过程中,参数匹配往往只需要某几组匹配参数,因此为获得直观清晰的船-机-桨匹配参数解,以建立的燃油消耗率、燃烧物排放及系统推进效率为目标,以(minf1,minf2,max
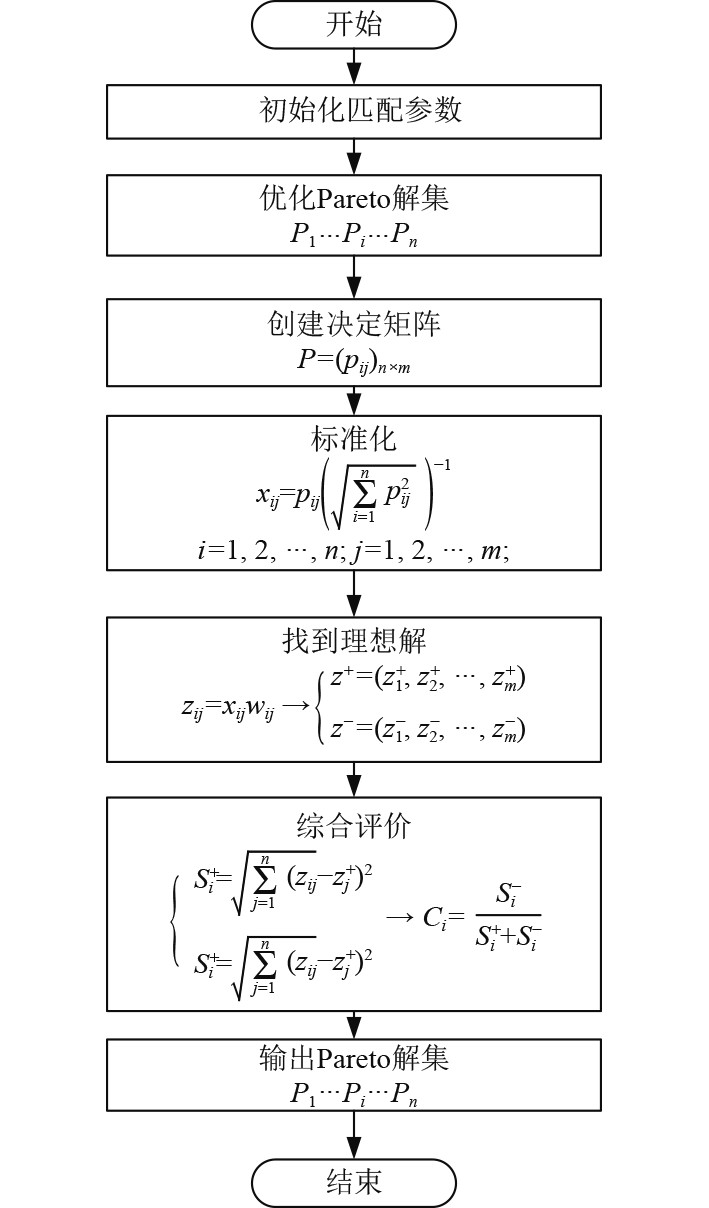
|
图 3 船-机-桨匹配参数性能排名流程图 Fig. 3 Ship-engine-paddle matching parameters performance ranking flow chart |
本文以4.999万吨甲醇双燃料化学品船为例,燃烧物以氮氧化物气体排放为例,进行船-机-桨匹配优化设计。通过Matlab建立的多工况船−机−桨匹配多目标优化模型,设置IMONGO算法参数,进行多目标优化。Pareto前沿解如图4所示。

|
图 4 船-机-桨参数匹配优化结果Pareto图 Fig. 4 Pareto diagram of the optimization result of ship-engine-paddle parameter matching |
利用TOPSIS对IMONGO计算得到的Pareto前沿解进行多属性决策,结果如表2所示。
|
|
表 2 决策后的Pareto前沿解 Tab.2 Pareto frontier solution after decision |
通过船-机-桨参数匹配的Matlab/Simulink模型对多目标优化得到的船-机-桨优化设计参数进行仿真验证,结果如图6~图9所示。
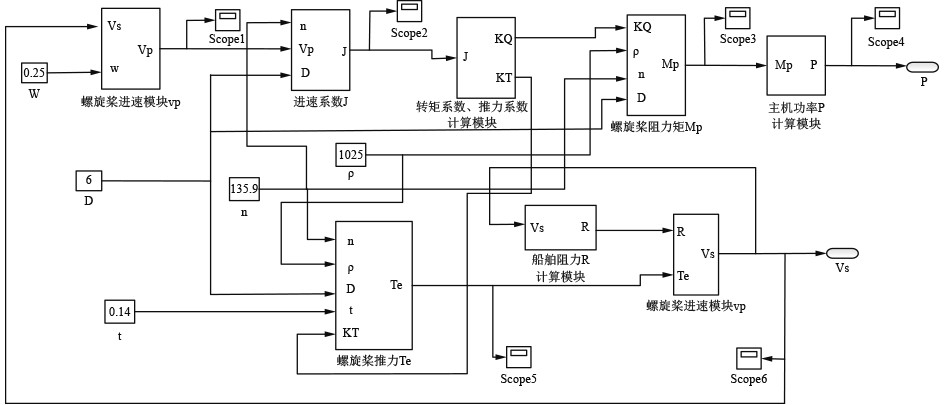
|
图 5 船-机-桨参数匹配matlab/simulink模型 Fig. 5 Boat-machine-paddle parameter matching matlab/simulink model |
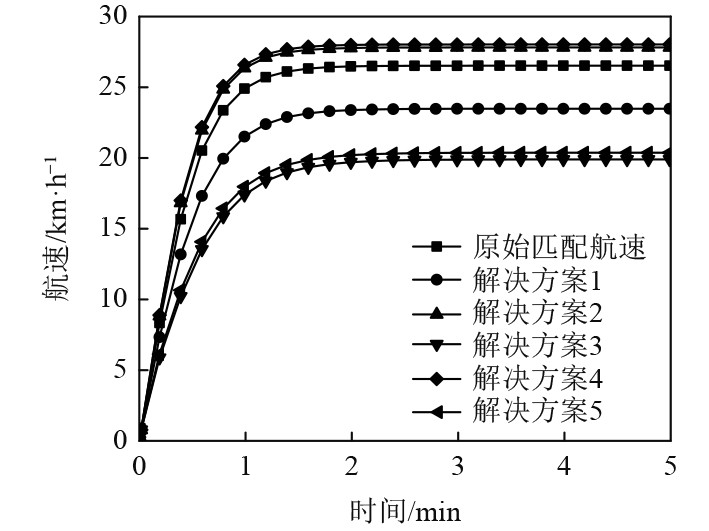
|
图 6 航速仿真结果图 Fig. 6 Speed simulation results |

|
图 7 发动机功率仿真结果图 Fig. 7 T Engine power simulation results graph |
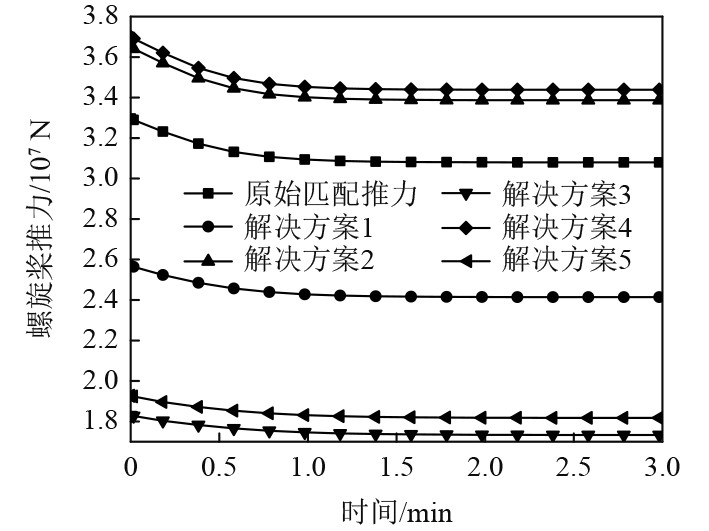
|
图 8 螺旋桨推力仿真结果图 Fig. 8 Propeller thrust simulation results |
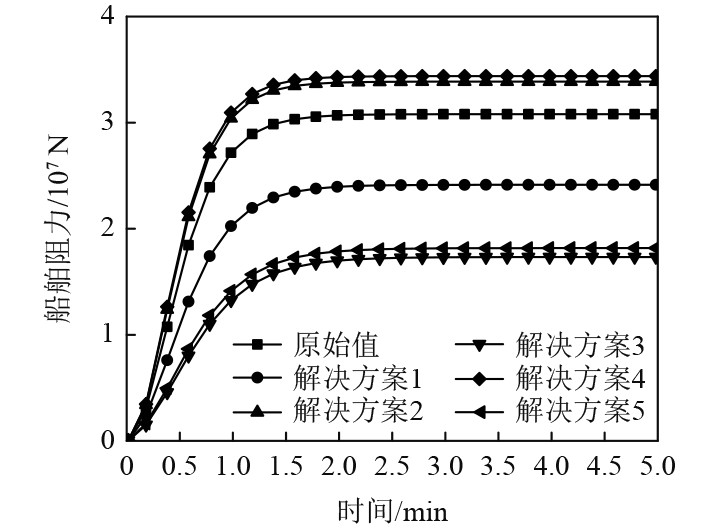
|
图 9 船舶航行阻力仿真结果图 Fig. 9 Ship sailing resistance simulation results |
设置好初始参数和边界条件后,采用FIRE分析软件对Pareto前沿解中5个解决方案的发动机柴油-甲醇混合燃料燃烧物排放进行仿真验证,结果如图10和图11所示。
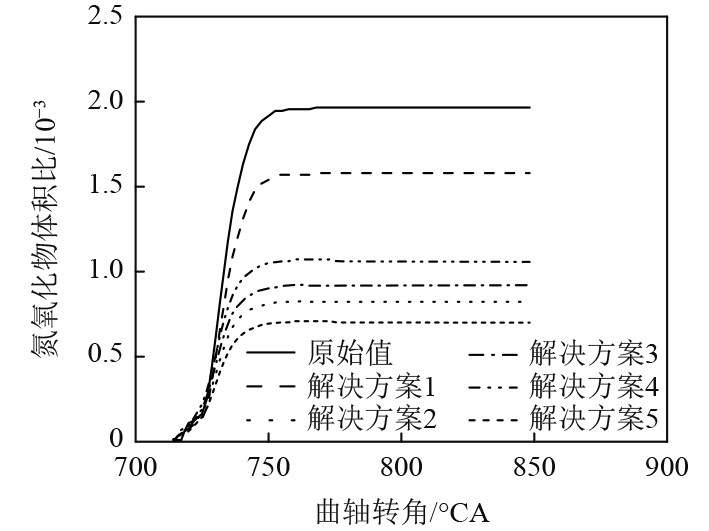
|
图 10 氮氧化物体积比仿真结果图 Fig. 10 Nitrogen oxide volume ratio simulation results graph |
|
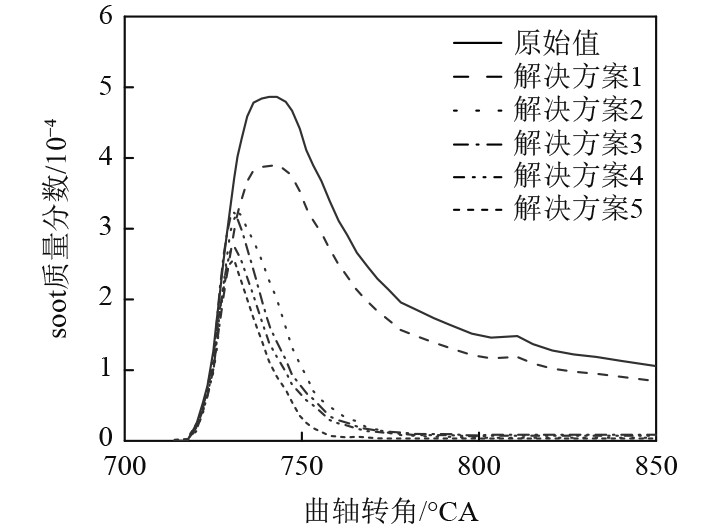
图 11 soot质量分数仿真结果图 Fig. 11 Soot mass fraction simulation results graph |
|
|
表 3 原始匹配值与优化结果(Pareto前沿解)的对比 Tab.3 Comparison of original matching values and optimization results (Pareto front solution) |
以Pareto前沿解的第一组解为例,在经济性目标函数中,燃油消耗率降低了5.97%,发动机燃烧物排放中氮氧化物排放体积比降低了19.49%,碳烟(soot)排放质量分数降低了20.1%,船舶推进系统效率提高到了0.59。
5 结 语本文以甲醇船为对象开展多工况下船−机−桨参数匹配优化,以发动机燃油消耗率、系统推进效率和燃烧物排放指标为目标函数,进行多目标优化设计。结果显示采用本文方法得到的匹配参数能使船舶获得良好的运行状态,可提高船舶运营的经济性和环保性。试验结果表明,多目标优化模型拟合良好,验证了模型的可行性。
改进北方苍鹰优化算法的种群初始化方法和种群搜索策略,4个评价指标表明改进的IMONGO算法具有更好的收敛性和多样性。
通过实例验证,IMONGO算法适用于船-机-桨匹配参数优化问题。基于TOPSIS对优化后的匹配参数进行多属性决策,经过性能评估后得到的匹配参数满足船舶实际航行要求。
| [1] |
李学斌. 多目标遗传算法在水面船舶快速性优化设计中的应用[J]. 江苏科技大学学报(自然科学版), 2008(5): 1-5. LI X B. Application of multi-objective genetic algorithm in the rapidity optimization design of surface ships[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2008(5): 1-5. |
| [2] |
戴忠华, 周穗华, 张晓兵. 多目标优化的舰船磁场建模方法[J]. 物理学报, 2021, 70(16): 147-159. DAI Z H, ZHOU H H, ZHANG X B. A multi-objective optimization approach to modeling the magnetic field of a ship[J]. Journal of Physics, 2021, 70(16): 147-159. |
| [3] |
尹德鑫, 张达敏, 蔡朋宸, 等. 改进的麻雀搜索优化算法及其应用[J/OL]. 计算机工程与科学, 2022(44): 10.
|
| [4] |
王习昌, 鲍东杰. 改进粒子群算法在LQR半主动悬架的应用[J/OL]. 机械科学与技术, 2023, 42(3): 468-474. WANG X C, BAO D J. Improved particle swarm algorithm for LQR semi-active suspension [J/OL]. Mechanical Science and Technology, 2023, 42(3): 468-474. |
| [5] |
周源. 基于CFD方法螺旋桨多目标优化研究[D]. 武汉: 武汉理工大学, 2016.
|
| [6] |
孙林, 陈辉, 管聪. 内河多工况船机桨匹配优化设计[J]. 中国舰船研究, 2022, 17(1): 187-195. SUN L, CHEN H, GUAN C. Optimal design of propeller matching for inland river vessels with multiple operating conditions[J]. China Ship Research, 2022, 17(1): 187-195. |
| [7] |
杨路春, 杨晨俊, 李学斌. 基于多目标进化算法和决策技术的螺旋桨优化设计研究[J]. 中国造船, 2019, 60(3): 55-66. YANG L C, YANG C J, LI X B. Propeller design optimization based on multi-objective evolutionary algorithm and decision technology[J]. China Shipbuilding, 2019, 60(3): 55-66. |
| [8] |
杨秀敏, 耿静, 徐游, 等. 基于TOPSIS模型的海南岛土地综合承载力时空变化及障碍度诊断[J/OL]. 生态学报, 2019, 60(3): 55-66. YANG X M, GENG J, ZHUANG H Y, et al. Diagnosis of spatial and temporal variation of comprehensive land carrying capacity and barrier degree of Hainan Island based on TOPSIS model[J/OL]. Journal of Ecology, 2019, 60(3): 55-66. |
| [9] |
GAO S D, PU C H, LI J. et al. Multi-objective optimal control of industrial organic pollutant treatment process[J]. Control Theory and Applications. 2022, 39(1): 187-199.
|
| [10] |
REN HL, DING Y, SUI C B. Influence of EEDI (Energy Efficiency Design Index) on Ship-Engine-Propeller Matching[J]. Journal Of Marine Science And Engineering, 2019: 7(12).
|
| [11] |
MARQUES CH, BELCHIOR CRP, CAPRACE JD. Marine propeller parametric optimisation and matching to electric motor[J]. Journal Of the Brazilian Society Of Mechanical Sciences And Engineering. 2019: 41(3).
|
| [12] |
MARQUES CH, BELCHIOR CRP, CAPRACE JD. Optimising the engine-propeller matching for a liquefied natural gas carrier under rough weather[J]. Applied Energy, 2018(232)187-96.
|
| [13] |
ZHOU HG, WANG Z, LI L, et al. Line heating process parameter forecasting method based on optimization concept[J]. Advances In Mechanical Engineering, 2022: 14(3).
|
 2023, Vol. 45
2023, Vol. 45
