0 引　言

我国在2019年于山东烟台附近海域第一次成功海上火箭发射后，已进行了多次海上火箭发射任务，形成了完整的海上发射体系^[1]，为提高商业发射的经济性，后期将会对发射后的一级火箭进行回收再利用，SpaceX公司的垂直回收技术使火箭发射成本降低约30%。相比陆地回收，海上火箭回收的经济性更高，该过程不需供给一级火箭反推回陆地的燃料，可按照火箭的自由运动轨迹进行回收^[2]。目前我国海上火箭回收技术处于验证阶段，仍有很多关键技术未解决，如回收船舶作业全过程运动响应分析、载荷数值预报技术研究等。

在冲击载荷作用下的船舶运动响应分析方面，俞俊等^[3]基于AQWA探讨了海上火箭冷发射过程中不同工况下平台的运动问题，将垂向5000 kN和10000 kN的定常力作为火箭冲击载荷输入至Aqwa中，得出冲击载荷越大，相同偏心位置下平台运动极值越大等结论。王建平等^[4-5]利用KANE方法数值求解了在舰载火炮系统横向力作用下的船舶运动状态，与实验数据进行比对，验证了模型的准确性，并讲解了该模型试验。在火箭海上回收过程中，甲板所受冲击载荷的动态变化以及系泊系统的耦合作用不可忽略，而上文未考虑此影响。

本文通过建立海上火箭回收过程中船舶的耦合运动分析方法，寻求影响海上火箭回收精度的关键因素。以某型火箭发动机及多功能海洋工程驳船为研究对象，基于粘流软件STAR-CCM+对考虑火箭回落过程的冲击流场进行模拟，并将所得的冲击载荷时历曲线作为输入导到船舶时域耦合运动方程中。最后，使用势流软件Aqwa在时域上分析不同火箭着陆点对耦合作用下船舶运动响应的影响。

1 理论基础 1.1 垂直燃气射流冲击载荷

对于轴对称冲击射流，在火箭燃气射流动力学^[6]里，带倾角的冲击载荷计算公式为：

$ {{F}}_{{T}}=2\mathrm{{\text{π}} }\mathrm{sin}\mathrm{\theta }{\int }_{0}^{{{r}}_{{e}}}({{p}}_{{e}}-{{p}}_{{a}}+\mathrm{\rho }{\mathrm{v}}^{2}\mathrm{cos}\mathrm{\alpha }){r}\mathrm{d}{r} 。$

(1)

式中： ${{r}}_{{e}}$ 为喷管出口半径； ${{p}}_{{e}}$ 和 ${{p}}_{{a}}$ 分别为喷管出口压力和环境压力； $ \mathrm{\alpha } $ 为气流流动对中心线的当地倾角； $ \mathrm{\theta } $ 为射流轴线与甲板的倾角。喷管出口面积 ${{A}}_{{e}}={{\text{π}} }{{r}}_{{e}}^{2}$ ，比热比 $ \mathrm{\gamma } $ 为燃气流的定压比热与定容比热之比，喷管出口马赫数 ${\mathrm{M}\mathrm{a}}_{{e}}$ 为速度与声速之比，根据3个参数的定义上式可改写为：

$ {{F}}_{{T}}=2{{A}}_{{e}}\mathrm{sin}\mathrm{\theta }{\int }_{0}^{1}\left[{{p}}_{{e}}-{{p}}_{{a}}+{{p}}_{{e}}\mathrm{\gamma }{\mathrm{M}\mathrm{a}}_{{e}}^{2}{\left(\mathrm{cos}\mathrm{\alpha }\right)}^{2}\right]\frac{{r}}{{{r}}_{{e}}}\mathrm{d}\left(\frac{{r}}{{{r}}_{{e}}}\right)。$

(2)

在海上火箭回收最后的垂直降落阶段中，射流与甲板的夹角几乎为90°，将 $\mathrm{\alpha }=0^\circ$ 及 $\mathrm{\theta }=90^\circ$ 代入式（2），最终的垂向冲击载荷计算公式为：

$ {{F}}_{{T}}={{A}}_{{e}}{{p}}_{{e}}(1-\frac{{{p}}_{{a}}}{{{p}}_{{e}}}+\mathrm{\gamma }{\mathrm{M}{a}}_{{e}}^{2})。$

(3)

1.2 时域船舶耦合运动方程

在船舶重心处使用质心动量定理、动量矩定理以及线性水动力理论，得到浮体的六自由度频域运动方程：

$ \left[{{\boldsymbol{M}}}+{{\boldsymbol{u}}}\right]\ddot{{x}}+{\int }_{-\mathrm{\infty }}^{{t}}\left[{k}\left({t}-\mathrm{\tau }\right)\right]\dot{{x}}\mathrm{d}{\tau }+{{\boldsymbol{C}}}{{{x}}}={F} 。$

(4)

式中：x为船舶的六自由度运动响应；M为船舶的质量矩阵； ${u}$ 为附加质量矩阵；C为静水回复力系数矩阵； ${k}\left({t}-{\tau }\right)$ 为延迟函数。方程右端 ${F}$ 为作用在重心的外力。根据Cummins脉冲响应法，将船舶运动及波浪力转化为一系列脉冲运动响应的叠加，并对频域上的系数进行傅里叶变换，即得到时域内的延迟函数 ${k}\left({t}-\mathrm{\tau }\right)$ 等^[7]，进一步将上式改写成时域耦合方程：

$\begin{split} & \left[{M}+{u}\right]\ddot{{x}\left({t}\right)}+{\int }_{-\mathrm{\infty }}^{\mathrm{t}}\left[{k}\left({t}-\mathrm{\tau }\right)\right]\dot{{x}\left({t}\right)}\mathrm{d}\mathrm{\tau }+{C}{x}\left({t}\right)=\\ & {{F}}_{{w}}^{1}\left({t}\right)+{{F}}_{{w}}^{2}\left({t}\right)+{{F}}_{{m}}+{{F}}_{{T}}，\end{split} $

(5)

$ {k}\left({t}\right)=\frac{2}{{\text{π}} }{\int }_{0}^{t}{\lambda }_{ij}\left(\omega t\right){\rm{d}}\omega ,\;\;i,j=1,\cdots ,6 。$

(6)

右端等式中 ${{F}}_{{w}}$ 表示浮体的一阶和二阶波浪力，运用三维势流理论和面元法可以求解流场的速度势，在此基础上使用伯努利方程并在湿面积下积分即得到波浪力。 ${{F}}_{{m}}$ 表示系泊力，由悬链线理论求解， ${{F}}_{{T}}$ 表示回收过程中甲板受到的冲击载荷，计算公式见式（3）。在已知这些参数后，求解耦合作用下的浮体时域运动方程。

2 模型描述 2.1 火箭燃气射流模型 2.1.1 几何模型

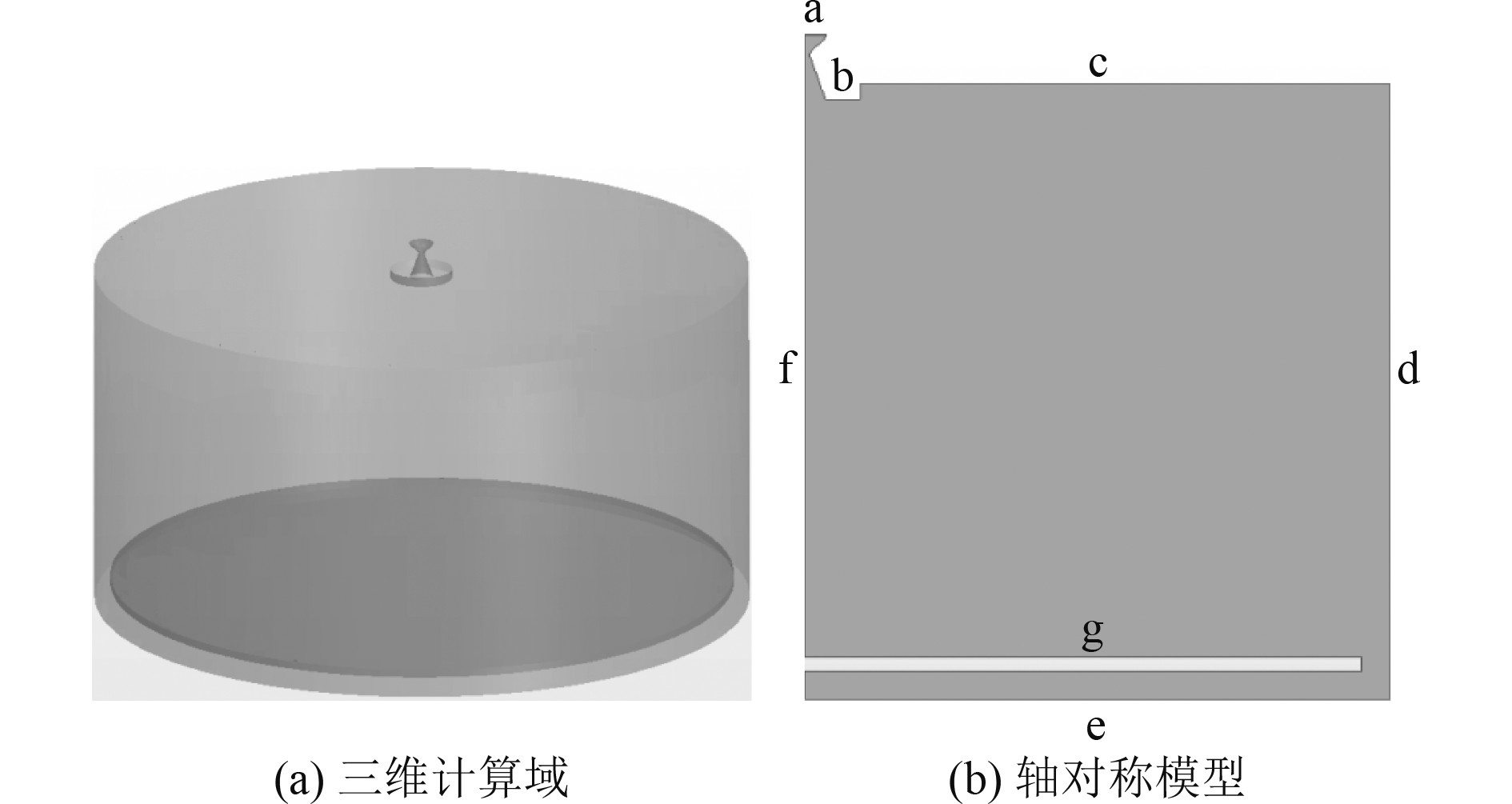
使用的喷管根据我国某型火箭发动机喷管实际尺寸简化而来，喷管的入口和出口直径均为1524 mm，喉部直径为381 mm，喉部到出口长度为1572.2 mm，扩张角为45°。参考Space X进行的多次海上火箭回收，选取海上回收最后一个阶段（垂直降落阶段）为研究过程。该过程大约开始于20 m高空^[8]，回收船舶的型宽为40 m，由此确定火箭初始时刻的三维计算域，如图1(a)所示。燃气射流从顶部喷管向下喷出，撞击底部挡板之后沿径向传递扩散，待射流稳定后用底部圆形挡板逐渐靠近顶部喷管的过程模拟火箭回落。为提高计算效率，对三维模型进行优化，简化后的轴对称模型如图1(b)所示。

2.1.2 边界条件

如图1(b)所示，火箭喷管入口a采用停滞进口边界条件。燃烧室总压为6.08 MPa，入口总温为3050 K。燃气射流的出口（用c，d，e表示）采用压力出口边界条件，压强大小为1 atm，温度为默认值300 K。与燃气流相接触的有甲板面g和喷管壁面b，均设置为壁面条件，使用标准壁面函数，并采用无滑移绝热条件。边界f设置为轴条件，其他参数设置为默认。

2.1.3 网格条件

模拟过程中对挡板周围添上重叠网格，并对射流中心区域进行阶梯式的网格加密，如图2所示。划分后整个流场网格单元数为129984个，节点数为249542个，最小体积变化率为0.02，最大体积变化率为1，表面效度为1。

2.2 海上火箭回收船舶模型

在水动力分析方面，使用的是多功能海洋工程驳船，该船型改良于国内进行过多次海上发射任务的“泰瑞”号，其尺寸满足实际工程应用的要求。该船的锚泊系统采用多点系泊，为悬链线式系泊，系泊系统共有4根缆绳呈对称分布，朝着4个象限的45°方向布置，绳长820 m。船体网格由Aqwa自动生成，基本网格尺寸为1.6 m，网格总数为13367，船体模型及主要船型如表1所示。

3 结果与讨论 3.1 海上火箭回收过程中燃气冲击流场数值模拟 3.1.1 静态冲击载荷数值模型验证

火箭的燃气冲击射流是一种高压、高温、高速的复杂湍流，包含复杂的流动状况，对燃气冲击射流模拟使用较多的湍流模型是雷诺平均纳维-斯托克斯湍流模型(RANS)与大涡模型(LES)，两者均能反映超音速冲击射流的主要流动特征^[9]。LES模型更多应用在三维几何中，RANS模型则无太多要求。STARCCM+中的RANS模型有4种：Spalart-Allmaras湍流模型对于平面射流和圆柱射流扩散率的计算并不精确；K-Omega模型对内部流入口边界条件极端敏感，不适用于高温高压入口的燃气射流模拟。第3种K-Epsilon模型则不存在此问题，其中的两方程Realizablie K-Epsilon模型是基于标准K-Epsilon模型的优化，更适合于射流和边界层流动等。第4种为雷诺应力传输(RST)模型，RST模型因考虑了湍流各向异性和高应变率等影响，对于部分复杂流的模拟可以进行准确预测^[10]。

由于参考文献[11]中并未说明使用的是哪种湍流模型，综上考虑各个湍流模型的优缺点，选择RANS模型中的Realizablie K-Epsilon模型及RST模型与Nobuyuki Tsuboi等^[11]进行的静态燃气冲击射流试验数据及模拟结果进行比对，试验使用的喷管尺寸及燃气参数见文献[11]。

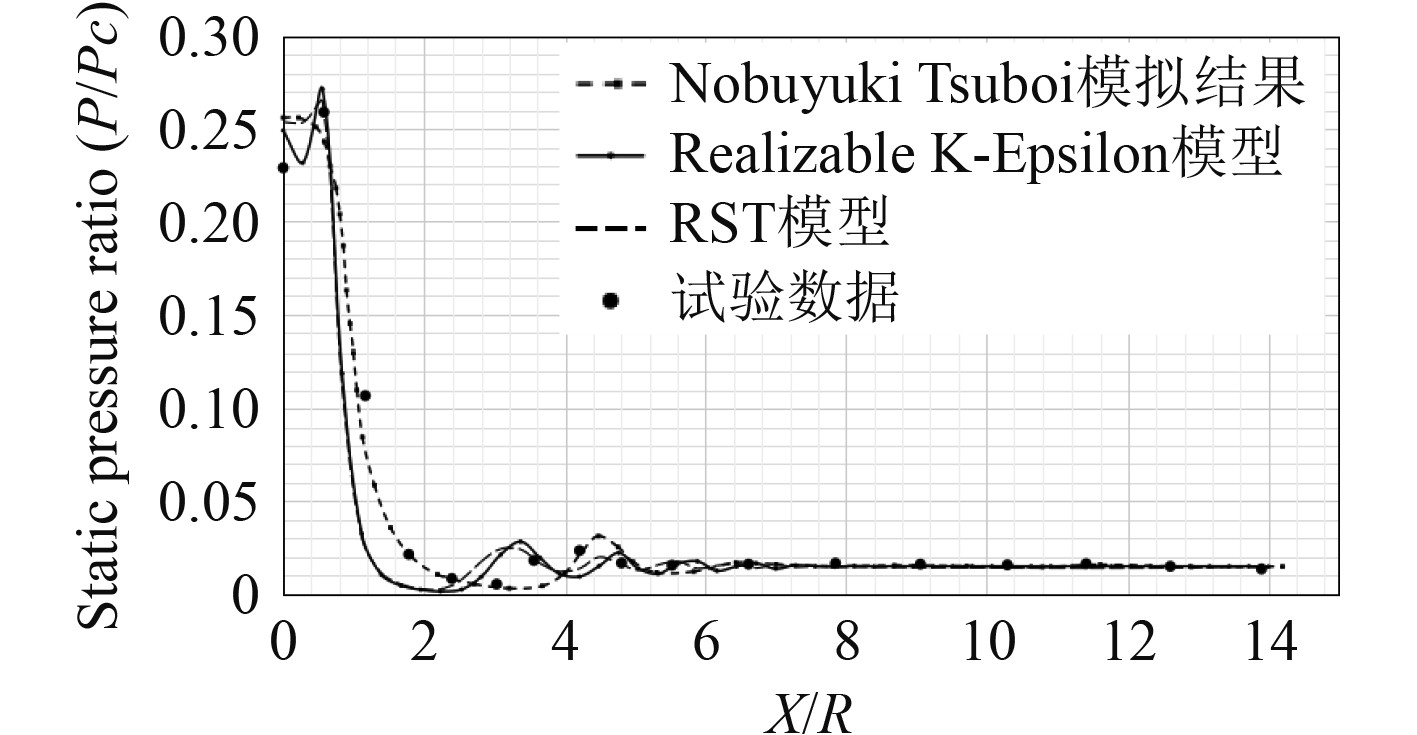
图3为在H=8.74R(H表示喷管出口至地面的距离，R为出口半径)时，待燃气射流稳定作用在底面甲板上后，底面甲板径向上的静压比分布(挡板上该点处的静压值与环境压力的比值)曲线。可知，在冲击射流的中心位置处，Realizable K-Epsilon模型的结果较其他模型的结果更贴近试验数据，其在远离射流中心处的静压比分布与试验结果也贴合得较好。因此在考虑火箭回落过程冲击载荷的数值模拟中使用Realizable K-Epsilon湍流模型，并将库朗数设置为自动控制。

3.1.2 火箭垂直降落阶段冲击流场分析

由于在静态过程中用于试验的是直径为16.52 mm的小喷管，这与实际工程中使用的火箭喷管有较大差距。因此在验证完燃气射流数值模型的准确性后，进一步考虑火箭的动态着陆过程，并使用更加贴合实际的喷管参数，在分析过程中采用如下假设：

1）火箭燃气射流为可压缩的理想气体，不考虑燃烧、化学反应，忽略热损失。不考虑多相流，火箭喷管入口的参数为恒定值。

2）假设垂直降落阶段火箭以5 m/s的恒定速度降落，并将火箭降落的速度等价于挡板靠近火箭尾喷管的速度。忽略由于喷出燃气流所引起的箭体质量减少。

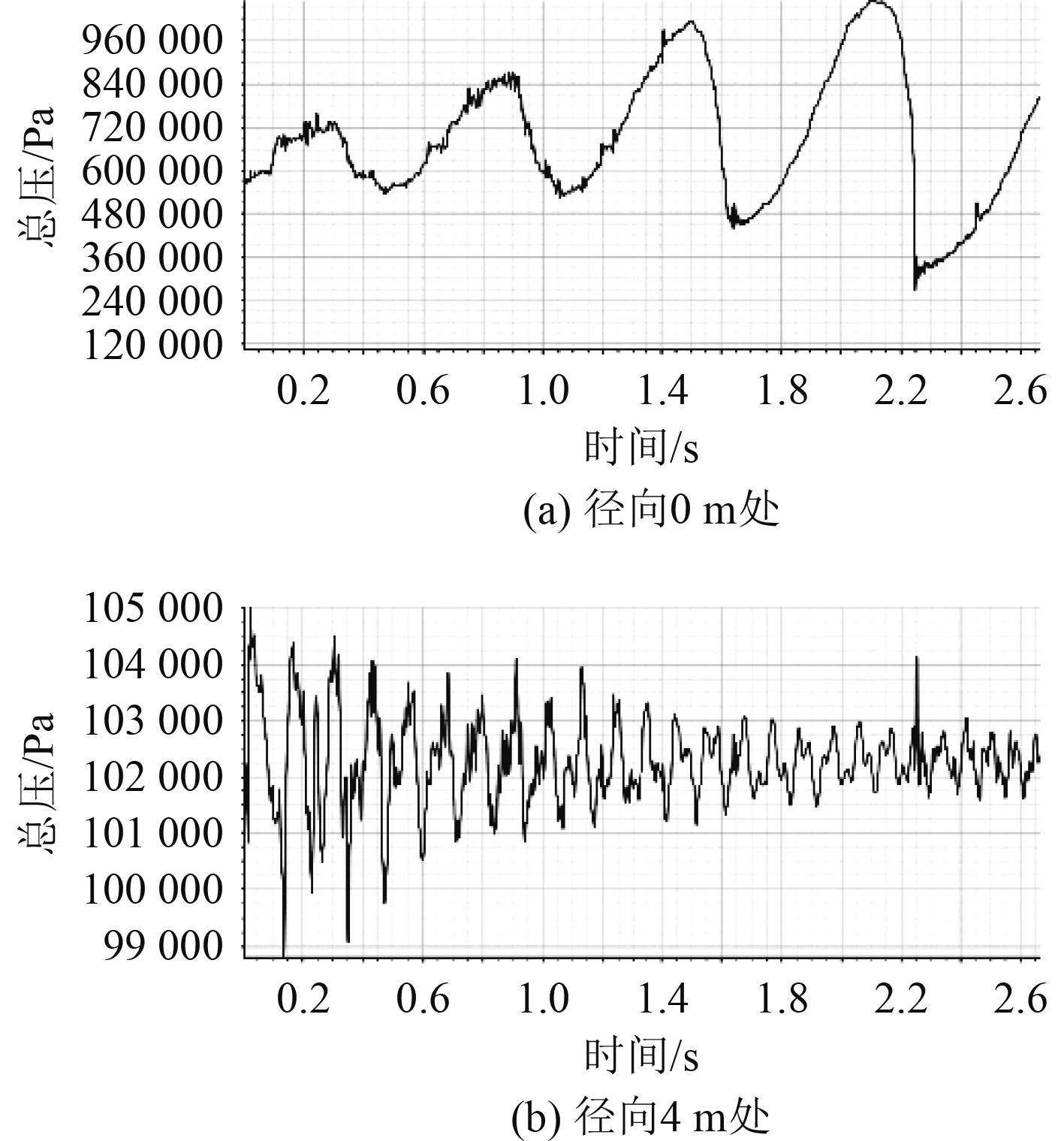
基于STAR-CCM+，该过程的模拟运动过程为2.6649 s，时间步长为60 µs，总迭代步数为44951步，构建火箭垂直降落阶段底部挡板所受冲击流场的数值计算模型，得到挡板所受冲击载荷的时历曲线及挡板上距离射流轴线0 m和4 m处总压的时历曲线，如图5所示。

从图5可以看出，随着时间的增加，即火箭逐渐回落至甲板，径向0 m处的总压值呈现震荡增大的趋势，总压每隔大约0.6 s出现一次极大值，分别在0.3 s时达到极大值730799 Pa，0.9 s时达到870322 Pa，1.5 s时达到1012910 Pa，2.1 s时达到1069260 Pa，总压最大的震荡幅值可达到794220 Pa。由于超音速射流特有的波系结构，如规律的菱形激波等，使得燃气射流内的场变量并非均匀分布，因此在挡板逐渐靠近喷管的过程中，径向0 m处的总压出现周期震荡且逐渐增大的现象。当监测点位于径向距离4 m处时，监测点上的总压呈震荡收缩的趋势，总压最大的波动幅值为6100 Pa。随后总压震荡幅值越来越小，围绕102250 Pa进行小幅度震荡，与标准大气压较接近，该点处不出现大幅波动增长现象的原因，可能是射流在挡板沿径向传播过程中能量耗散较大。

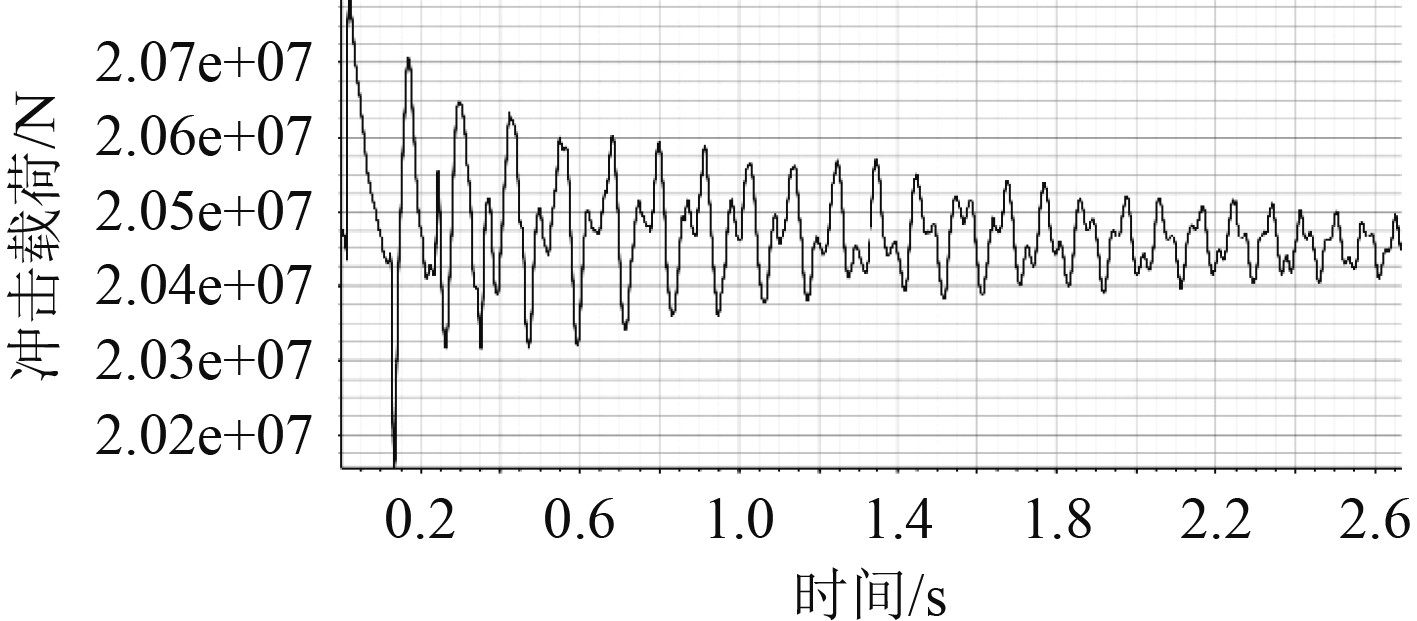
如图6所示，在火箭回落过程中，燃气尾流对回收船舶甲板上的冲击载荷呈小幅波动且逐渐震荡收缩的趋势，并最终维持在20400 kN左右。由于船舶型宽40 m，同喷管出口直径1524 mm相比较大，射流主要是在挡板中心处形成较大的局部压强，在径向距离4 m处总压随时间的变化就已不明显，而对比0 m及4 m处的总压时历曲线可知，总压值的波动随着径向距离的变大而变小，所以在挡板沿径向超过4 m处的部位，受到的总压也应是震荡收缩的，且比4 m处的波动更小。而移动过程中射流的作用面积在稳定之后就无变化，射流对甲板的冲击载荷计算可由总压在作用面积上的积分得到。因此在积分之后，冲击载荷的大小呈现震荡收缩的趋势。

3.1.3 全过程冲击载荷分析

上文模拟的冲击载荷为垂直降落阶段的结果，由SpaceX的海上火箭回收流程表2可知^[8]，仍需补充从着陆点火开始至火箭平稳着陆完整过程的冲击载荷时历曲线，该过程持续约31 s。气动控制阶段火箭发动机关闭，从480 s开始进行着陆点火，甲板开始受到射流的冲击载荷。根据关键时间点及该点的冲击载荷大小，定全过程冲击载荷的表达式，如下式：

$ {{F}}_{{T}}=\left\{\begin{array}{l}788462t-378461538\text{，}{{t}}_{1}\leqslant t < {{t}}_{2}，\\ {{F}}_{{p}}\text{，}{{t}}_{2}\leqslant t < {{t}}_{3}，\\ -20400000t+10424400000\text{，}{{t}}_{3}\leqslant t < {{t}}_{4}。\end{array}\right. $

(7)

其中， ${{t}}_{1}$ ～ ${{t}}_{2}$ 为着陆点火阶段， ${{t}}_{1}$ =480 s， ${{t}}_{2}$ =506 s。由于此时火箭离甲板较远并且射流存在着不与甲板垂直的问题，因此假设该阶段的冲击载荷均匀增加；而 $ {\mathrm{t}}_{2} $ 至 $ {\mathrm{t}}_{3} $ 为垂直降落阶段，其中 ${{t}}_{3}$ 为510 s，基于图6可以得到506～508.6649 s的数值，并可以得到在508.6649～510 s时间内的冲击载荷约为20400 kN。 ${{t}}_{3}$ ～ ${{t}}_{4}$ 为火箭着陆关闭发动机甲板面冲击载荷散去的过程，假设此阶段的总时间为1 s，则 ${{t}}_{4}$ 为511 s。

3.2 不同火箭落点对船舶运动响应的影响

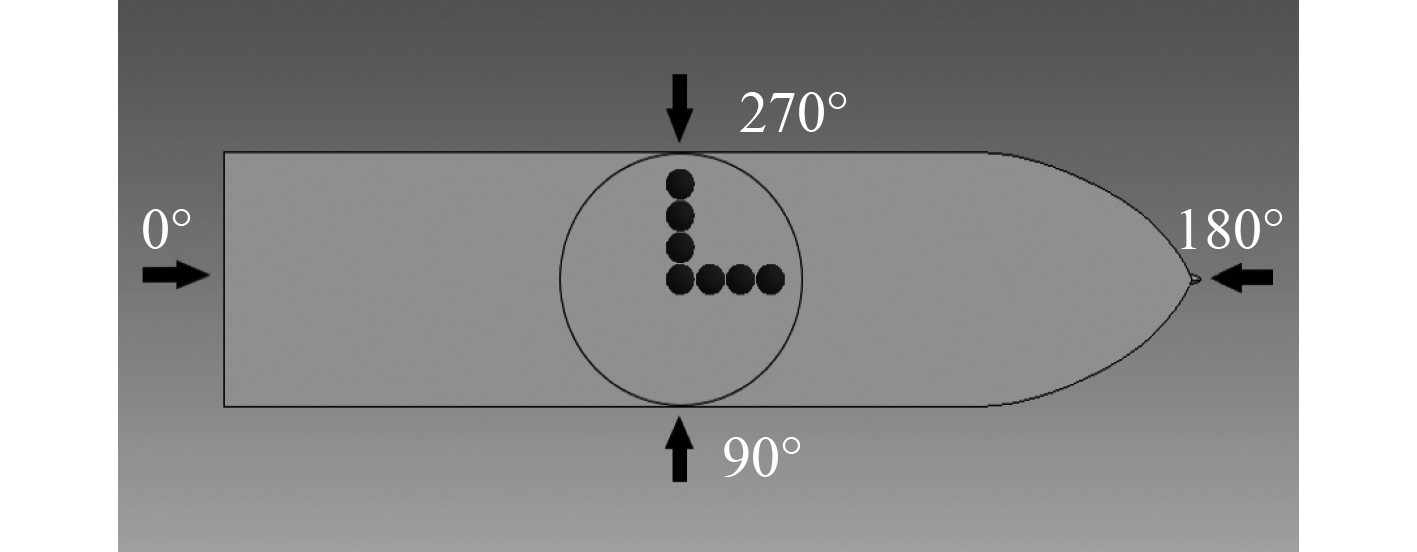
海上火箭回收过程中船舶处于运动状态下，而火箭的落点位置对船舶的运动有很大的影响。Space X公司海上火箭回收的落点范围在船中附近，本文冲击载荷模型的计算域底部是一个直径为40 m的圆，类比Space X公司将该圆的圆心布置在船体重心所对应的甲板位置，如图7所示。通过以下步骤讨论：1）首先考虑静水条件，在所选范围内沿船长及左舷方向分别布置7个回收点(偏心0 m，5 m，10 m，15 m处)，分析其对冲击载荷-系泊力耦合作用下船舶水动力性能的影响；2）考虑有波浪作用时不同落点对船舶水动力性能的影响。

3.2.1 静水中的船舶运动分析

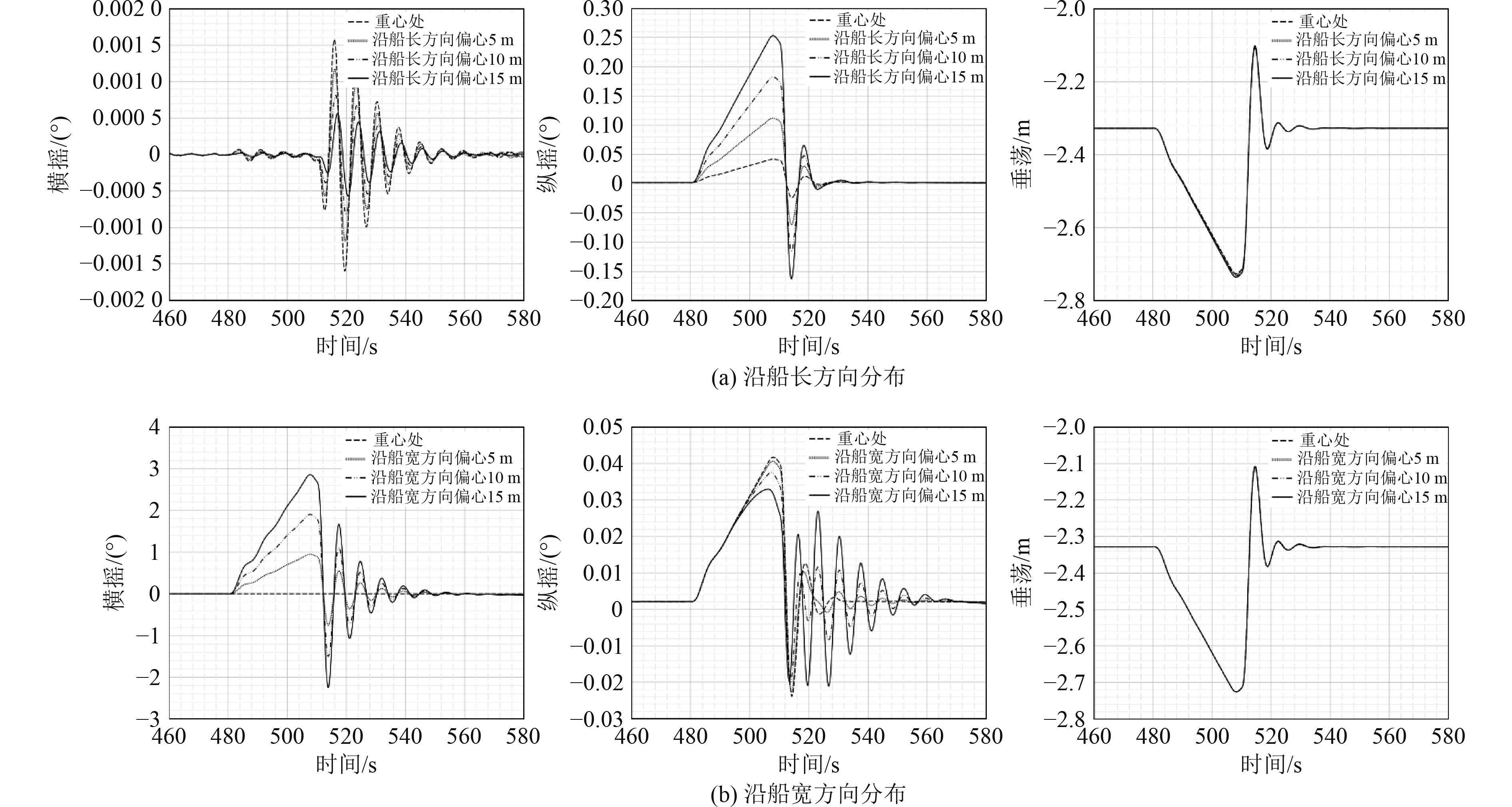
图8为回收船舶在静水中受冲击载荷-系泊力耦合作用下不同回收落点的运动时历曲线。可知，火箭冲击载荷的作用时间为火箭发射升空后的480～511 s。对落点沿船长分布时的船舶运动对比分析如图8(a)所示，结果表明，纵摇运动受动态冲击载荷作用的效果最为明显，且偏心距离越大，纵摇偏移量也越大，极大值约为0.25°，而横摇运动的偏移量随偏心距离的增大而减小，但其幅值较小基本为0，垂荡运动基本不受落点的影响。如图8(b)所示，当回收落点沿船宽分布时，横摇的变化最为明显，且偏心距离越大，横摇偏移量越大，极大值为2.858°。而纵摇运动幅值随偏心距离的增加而减小。

3.2.2 波浪下船舶运动分析

针对回收船舶在燃气射流冲击载荷-波浪力-系泊力耦合作用下不同回收情况的横摇、纵摇和垂荡运动时历结果展开研究，并以无冲击载荷时的运动曲线作为对照。回收船舶的设计作业海况为4级海况，随机入射波浪应用JONSWAP谱，谱峰因子为3，有义波高为1.75 m，谱峰周期为4.5 s，浪向为135°。

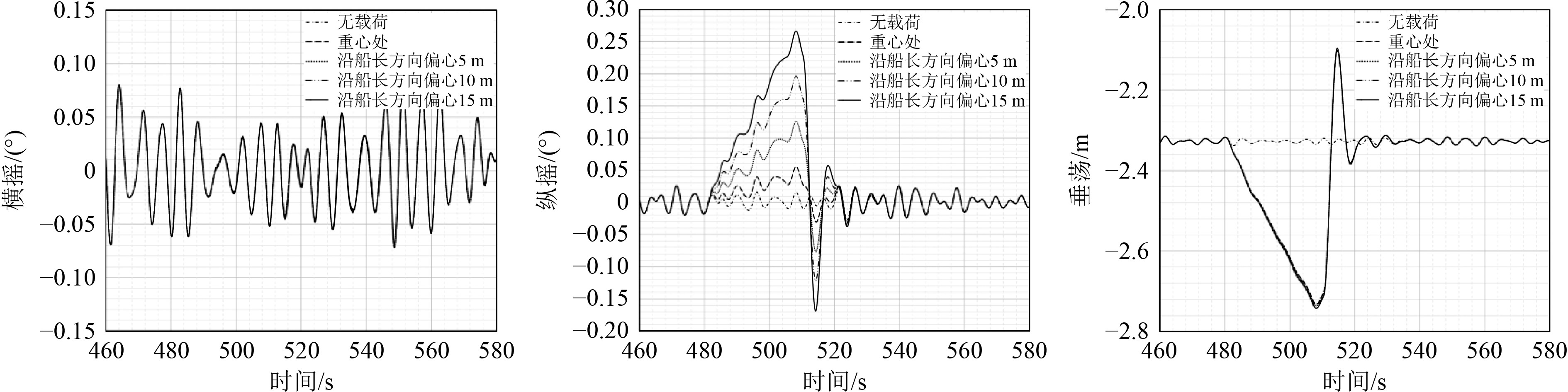
对于作用点沿船长方向分布的垂向载荷来说，从图9可以看出，随着偏心距的增大，纵摇偏移量明显增加，极大值为0.267°。该规律与静水时相似，但波浪力的作用使纵摇幅值增加了0.017°，需注意的是无冲击载荷作用时的纵摇偏移量要小于有冲击载荷作用时的结果。而横摇的运动幅值基本不受冲击载荷的影响，可能是波浪力和系泊力的耦合作用抵消了冲击载荷对横摇的影响。火箭的回收落点位置对垂荡运动影响并不明显，但有无冲击载荷对垂荡运动影响显著，前后状态的差值约有0.41 m。

从图10可以看出，当回收落点沿船宽方向分布时，不同的火箭落点对横摇运动的影响最大。随着偏心距的增大，横摇的运动幅度增大，当回收落点沿左舷偏离重心15 m时，其偏移量最大，此时船舶横摇运动的极大值为2.898°，较静水时的横摇增加了0.04°。另外，无冲击载荷作用与冲击载荷作用在重心时的横摇时历曲线重合，这是因为冲击载荷作用在重心时，没有横倾力矩产生，所以横摇的幅值与无载荷作用时相差不大；在纵摇方面，基本满足随着偏心距离的增大，纵摇偏移量有所增加，但增幅不明显；在垂荡运动方面，偏心距的影响较小。

4 结　语

通过CFD计算软件STAR-CCM+及势流水动力软件Aqwa模拟得到海上火箭回收过程中耦合作用下的船舶运动响应分析模型，分析有无波浪、冲击载荷以及不同火箭落点对船舶横摇、纵摇及垂荡的影响，主要得到以下结论:

1）本文使用的数值模拟方法可用于海上火箭回收全过程中的船舶水动力计算，后续可以应用于不同的火箭、回收船舶或平台上。

2）对于恒推力的火箭喷管，回落过程中燃气尾流对甲板的冲击载荷变化并不明显，呈震荡收缩的趋势，最终维持在20400 kN左右；

3）最佳的火箭回收落点位置为船体重心所对应的甲板位置，此时船舶的横摇纵摇及垂荡运动偏移量最小，随着偏心距离的增大，船舶运动幅值也会增大。当落点位于沿船宽偏心15 m时，横摇偏移量最大，约为2.898°。当回收落点位于沿船长偏心15 m时，纵摇偏移量最大，约为0.267°。

4）根据回收船舶在作业海况及静水状态下的时历曲线可知，中低海况波浪力的添加会增大横摇和纵摇的极值偏移量，但其影响较不同火箭回收落点带来的变化并不明显。