0 引　言

船舶的工作环境导致船体受到的载荷情况非常复杂，其中，周期性载荷以波浪载荷和机械振动载荷为主，非周期性载荷以船舶碰撞等冲击载荷为主，周期性载荷和非周期性载荷对船舶结构产生的破坏作用明显不同，非周期性载荷会导致船体结构的屈服破坏，往往是瞬时的破坏作用，非周期性载荷产生的破坏以疲劳损伤为主要形式，往往导致船舶结构的磨损等失效形式。

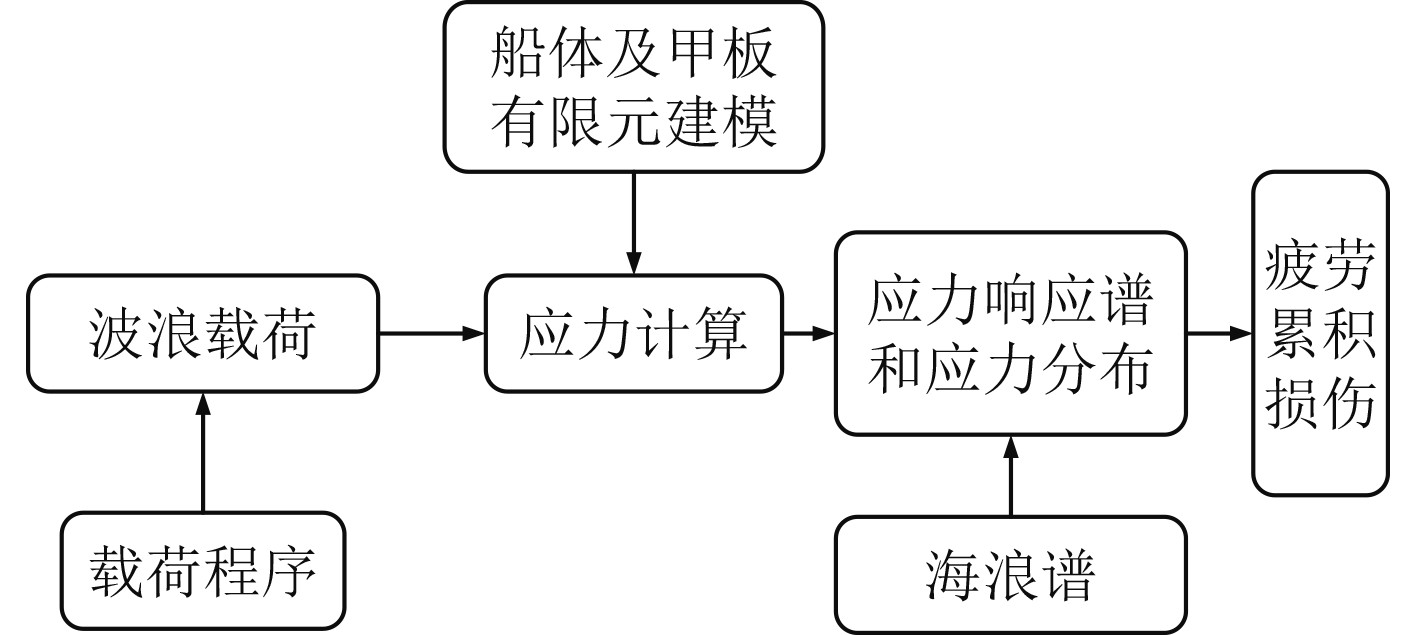
随着船舶制造业的不断发展，大量的新材料，新结构应用于船舶制造中。比如高强度钢和硬质合金钢目前在船舶结构中的使用量非常大，从材料方面提升了船舶的疲劳强度。目前，船舶甲板等支撑结构的失效仍以疲劳磨损为主，因此，基于经验公式和热点应力分析方法，对船舶甲板支撑结构的疲劳强度特性进行分析。基本流程如图1所示。

为确保船舶甲板支撑结构的疲劳强度有一定的安全裕量，本文从疲劳强度分析理论基础入手，介绍S-N曲线的使用方法，分析船舶甲板支撑结构受到的波浪载荷，结合有限元仿真软件Ansys建立船舶及甲板支撑结构的有限元模型，最后利用Miner线性累加损伤理论评估了船舶甲板的疲劳寿命。本文研究对于提升船舶甲板支撑结构的设计质量有重要意义。

1 疲劳强度基础理论研究

受复杂的工作环境影响，船舶甲板支撑结构的主要失效形式包括疲劳磨损、冲击断裂和腐蚀3种，冲击断裂主要出现在船舶碰撞等事故中，碰撞过程中产生的应力达到了船舶甲板结构材料的屈服应力，产生形状变化和断裂。甲板支撑结构的腐蚀主要原因来自海水以及海洋大气中的腐蚀性物质，船舶结构的腐蚀与采用的防腐方式有关^[1]。疲劳磨损是导致船舶甲板支撑结构出现故障的主要原因，也是研究的重点内容。

由于船舶甲板支撑结构在使用过程中，始终受周期性变化的波浪载荷影响，产生的结构交变应力不断作用于支撑结构的应力集中区域，这种交变应力的循环次数可达数十万次，不断累积的疲劳损伤最终会导致甲板结构产生裂纹和屈服，最终导致整体结构的破坏。

船舶甲板支撑结构的疲劳破坏与应力破坏的不同之处在于：

1）力学原理不同

甲板支撑结构的疲劳破坏是多次重复载荷作用下的结果，是载荷在时间作用下产生的累积效应，而应力破坏与时间无关，是由于应力的极大值超过材料的屈服极限导致。

2）表现形式不同

甲板支撑结构的疲劳破坏不会产生明显的宏观变形，往往以裂纹扩展的形式表现，而应力破坏伴随着明显的塑性变形。

3）材料的敏感性不同

疲劳破坏是甲板支撑结构的材料、形状、使用环境等因素的综合产物，对于这些因素都非常敏感，而应力破坏只对发生冲击作用当时的材料屈服有敏感性。

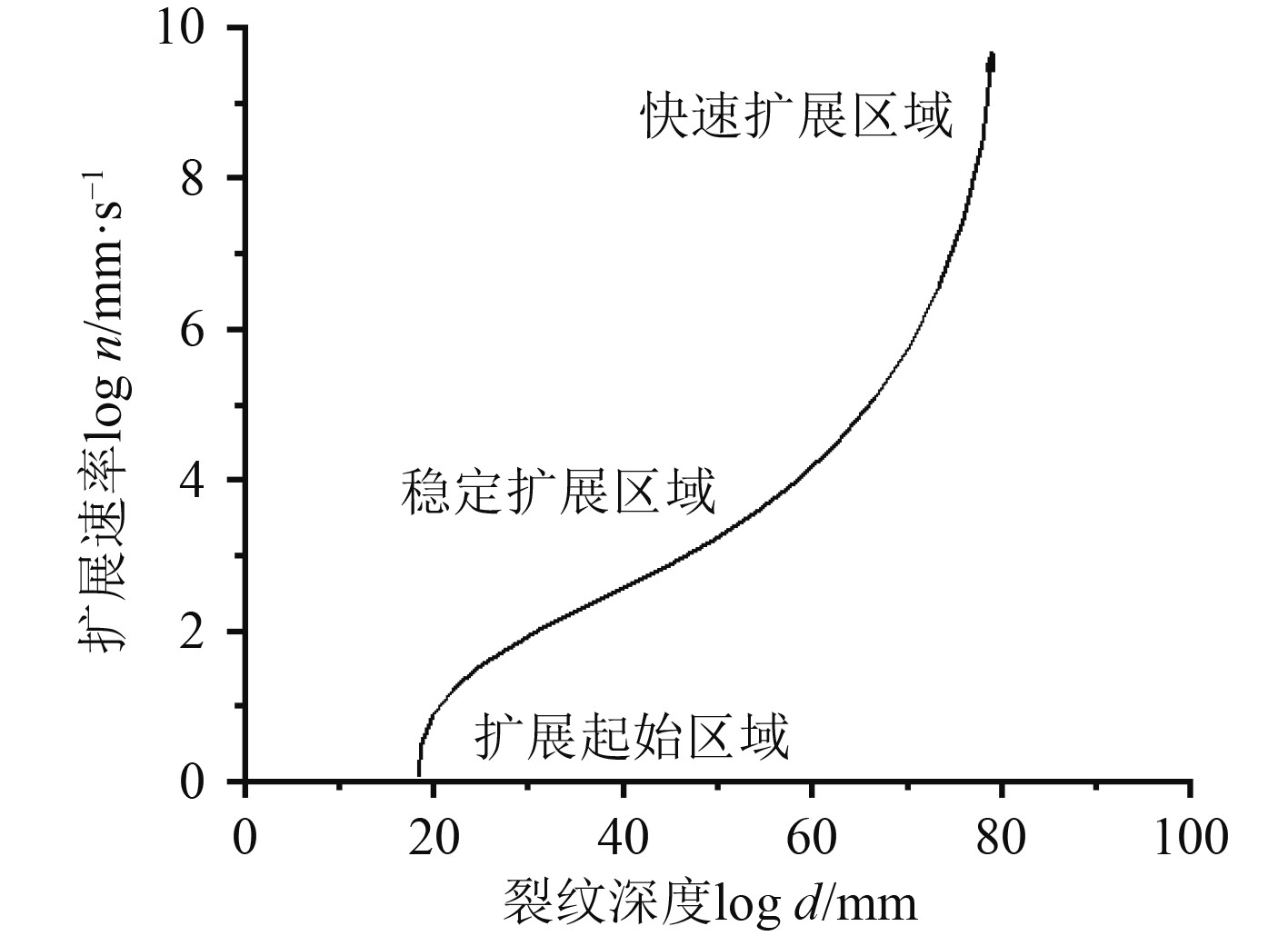
裂纹扩展是结构疲劳失效的重要指标，材料力学研究表明，结构件的裂纹扩展可以分为裂纹起始区域、稳定扩展区域和快速扩展区域，金属材料的裂纹扩展速率曲线如图2所示。

2 S-N曲线法的疲劳强度计算

在材料的疲劳分析方法中，S-N曲线和Miner线性累积损伤是2种最常用的分析方法，S-N曲线用循环应力幅值与材料的循环次数表征材料的疲劳特性，而Miner线性累积损伤是指当前材料在不同应力幅度下的循环次数与总循环次数的比值，这个比值如果小于1，则证明材料的疲劳强度没有问题。

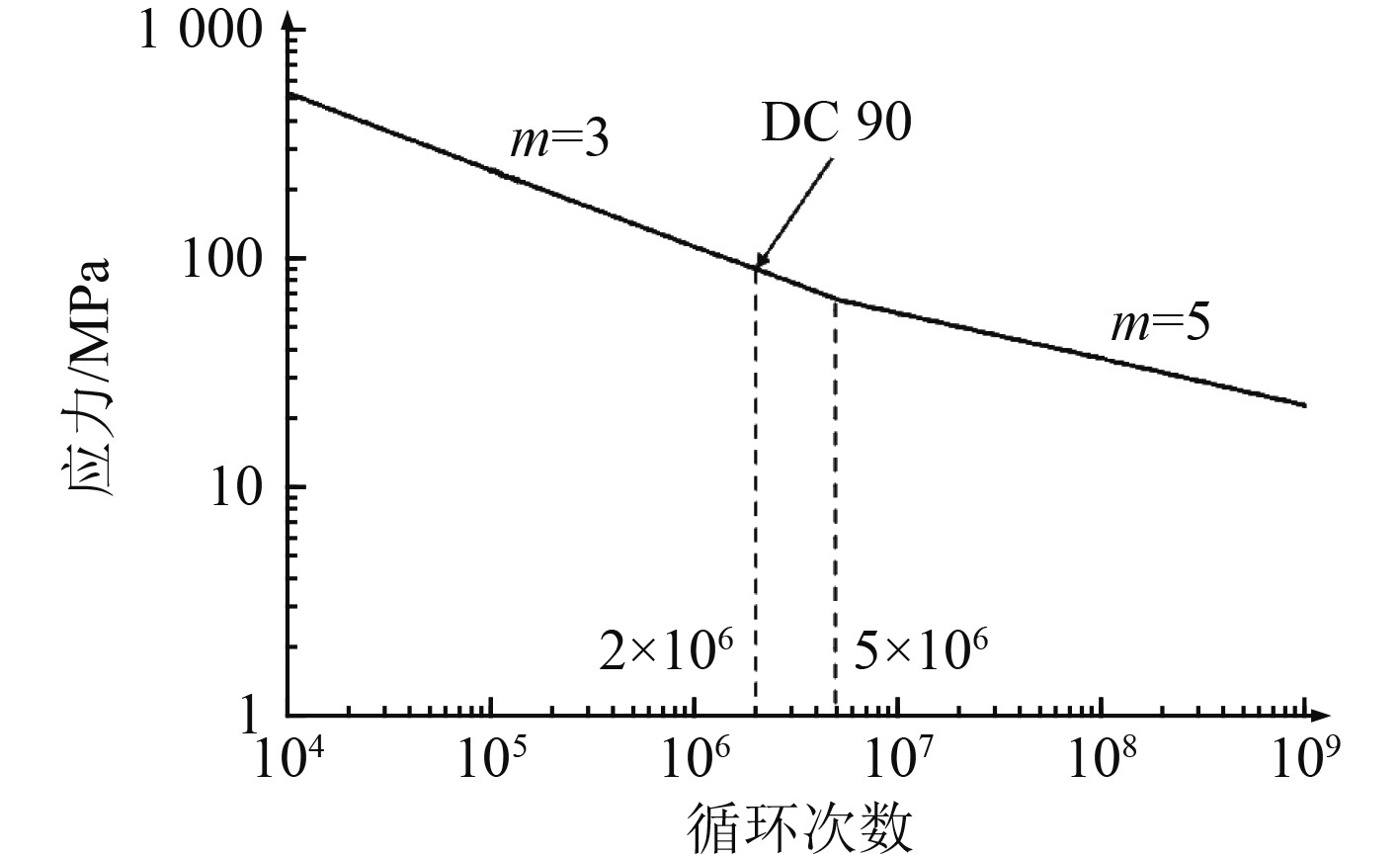
S-N曲线的一般形式为：

$ {S_r}{N_r}^m = A \text{。} $

式中： $ {S_r} $ 为交变应力的范围； $ {N_r} $ 为材料在该交变应力下可用的循环次数^[2]；A为常数值。在进行船舶甲板支撑结构的疲劳强度评估时，采用的是DC90 S-N曲线，该曲线如图3所示。

在甲板支撑结构的疲劳累积评估时，需要确定以下假设：

1）忽略低于疲劳极限的交变应力；

2）应力必须为循环对称应力，应力极限值的比值 $ \dfrac{{{\sigma _{\max }}}}{{{\sigma _{\min }}}} \ne 1 $ ；

3）当前交变应力的疲劳损失与前一个载荷工况不相关，当前应力的循环次数为n，则当前产生的疲劳损失为 $ \dfrac{n}{N} $ ；

4）疲劳载荷的加载顺序不会对结构的损失产生影响。

材料的疲劳累积损伤用下式计算：

$ D = \frac{{{N_L}}}{A}\int_0^{ + \infty } {{S^m}} \frac{h}{q}{\left( {\frac{S}{q}} \right)^{h - 1}}{\rm{d}}S = \frac{{{N_L}}}{A}{q^m}\varGamma \left( {1 + \frac{m}{h}} \right) \text{。} $

式中： $ {N_L} $ 为材料总循环次数；A和m为试验常数；q为尺度参数；h为形状参数； $ {S^m} $ 为应力幅值。通常 $ D \geqslant 1 $ 时认为材料出现疲劳破坏。

3 基于疲劳强度的船舶甲板支撑结构设计 3.1 船舶甲板支撑结构的波浪载荷分析

船舶甲板支撑结构的疲劳载荷主要是波浪载荷，因此，要想提高甲板支撑结构的疲劳寿命评估精度，必须要对波浪载荷建立准确模型^[3]。

采用规则波下产生的波浪载荷谱作为疲劳载荷，规则波是指风速6～8 m/s下的波浪，规则波的波面方程为：

$ \eta {\text{ = }}{\varphi _0}\cos \left( {kx - {w_0}t} \right) \text{，} $

其中， $ {\varphi _0} $ 为波浪的振幅， $ {w_0} $ 为波浪的频率，k为波数。

规则波的速度场方程为：

$ \begin{gathered} u{\text{ = }}\frac{{\text{π}}}{2}{\varphi _0}{\theta ^{kt}}\cos \left( {kx - {w_0}t} \right)，\hfill \\ w = \frac{1}{2}{\varphi _0}{\theta ^{kt}}\sin \left( {kx - {w_0}t} \right) 。\hfill \\ \end{gathered} \text{} $

分别建立波浪的动量方程和能量方程如下：

1）动量方程

$ \frac{{{{\partial}} \left( {\rho {u_j}} \right)}}{{{{\partial}} t}} + \frac{{{{\partial}} \left( {\rho {u_i}{u_i}} \right)}}{{{{\partial}} {x_j}}} = - \frac{{{{\partial}} p}}{{{{\partial}} x}} + \frac{{{{{\partial}}}} }{{{{\partial }}{x_j}}}\left[ {\mu \left( {\frac{{{{\partial}} {u_i}}}{{{{\partial}} {x_j}}} + \frac{{{{\partial}} {u_j}}}{{{\partial }{x_i}}}} \right)} \right] + {F_i} \text{。} $

式中： ${u_i}$ ， ${u_j}$ 分别为流体动量的速度分量； $p$ 为海水密度； ${x_i}$ ， ${x_j}$ 为单位海水坐标分量， ${F_i}$ 为单位水体的惯性力。

2）能量守恒方程

$ \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{\partial} k}}{{{{\partial}} t}} + {{\bar u}_i}\dfrac{{{\partial} k}}{{{\partial} {x_j}}} = \dfrac{{\partial} }{{{\partial} {x_j}}}\left[ {\left( {1 + {\sigma _k}{v_t}} \right)\dfrac{{{\partial} k}}{{{\partial} {x_j}}}} \right] + {P_k} - k\omega }，\\ {\dfrac{{{\partial} \omega }}{{{\partial} t}} + {{\bar u}_j} = \dfrac{{\partial} }{{{\partial} {x_j}}}\left[ {\left( {1 + {\sigma _k}{v_t}} \right)\dfrac{{{\partial} \omega }}{{{\partial} {x_j}}}} \right] + 2(1 - {F_i})\delta } 。\end{array}} \right. \text{} $

式中： ${v_t}$ 为流体的粘性系数； $ {\bar u_i} $ ， $ {\bar u_j} $ 分别为流体平均速度； $ {P_k} $ 为流体压力； $ \delta $ 为粘度系数； $ {\sigma _k} $ 为单位应力。

建立船舶甲板支撑结构受到的波浪弯矩载荷如下式：

$ {M_w} = 0.5h \cdot {K_g} \cdot {A_1} \cdot {A_2} \cdot B{L^2} \times {10^{ - 2}} \text{。} $

其中： $ {M_w} $ 为波浪弯矩； $ h $ 为波高， $h = 1.75 + 3.94(L/ $ $ 100) - 0.30{(L/100)^2} \text{，} $ L为船长； ${K_g}$ 为船体形状影响系数， $ {K_g} = 1.437\alpha \left[ {0.032 + 0.013\left( {{C_b}/\alpha - 0.60} \right)} \right] \text{，}$ $ \alpha $ 为水线长度系数， $ {C_b} $ 为船舶宽度系数； $ {A_1} $ 为船舶航行速度影响系数， ${A_1} = 1 - \left( {3 + 25{F_{nw}}} \right){M_s}/(D) + 1.5{F_{nw}} \text{，}$ $ {F_{nw}} $ 为波浪附加作用力， $ {M_s} $ 为船舶静水弯矩， $ D $ 为船舶排水量； $ {A_2} $ 为动水压力系数， ${A_2} = (1.25)(0.62 - B/L) - 2(T/L - 0.03) $ ，B为船宽。

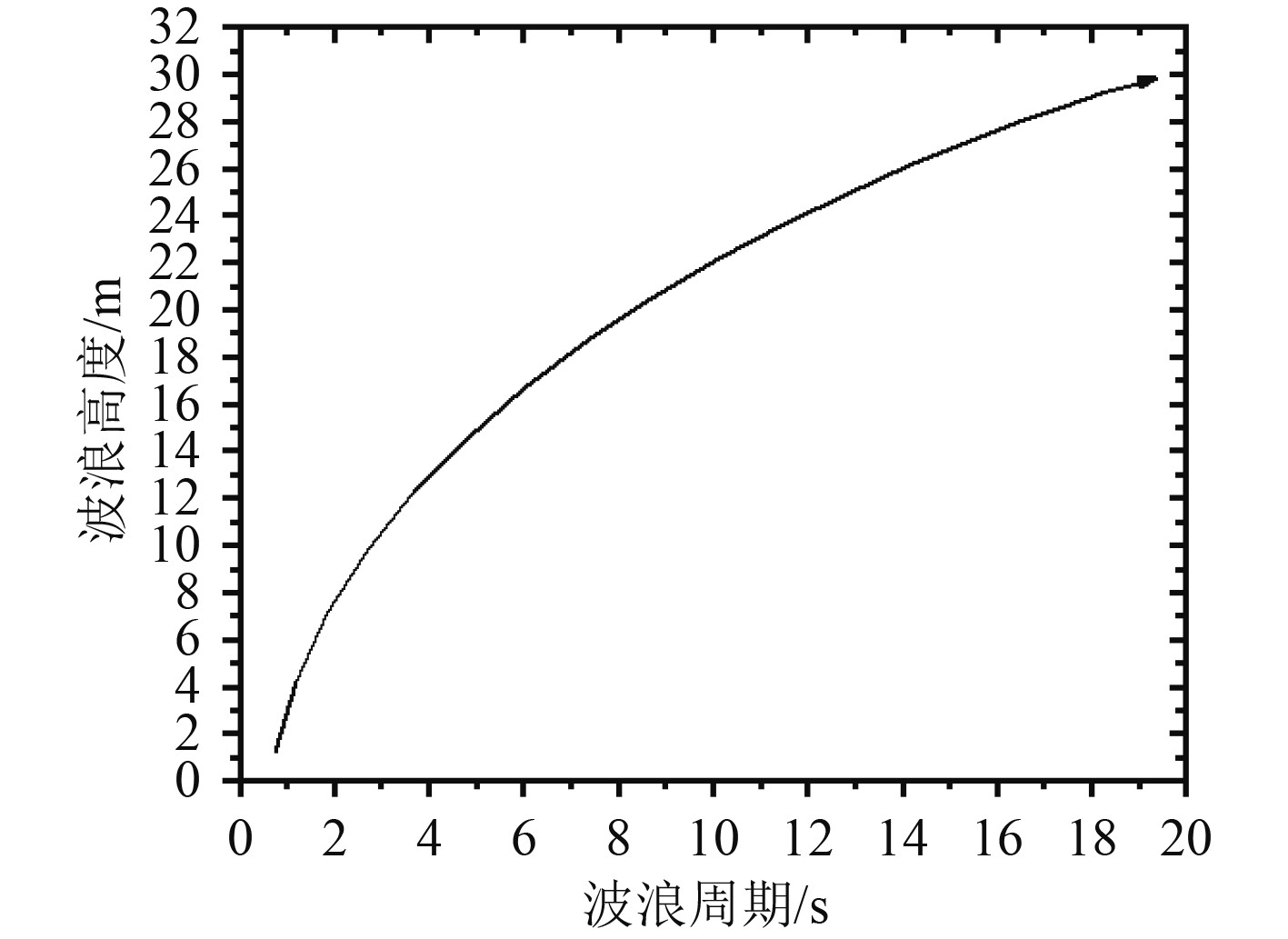
计算疲劳寿命采用的规则波的波高与周期关系曲线如图4所示。

3.2 船舶甲板支撑结构疲劳强度分析的边界条件及有限元模型

结合有限元仿真软件Ansys进行应力分析，然后将应力分析结果作为疲劳载荷的应力幅值进行疲劳特性分析。由于船舶甲板结构的边界载荷通过整体船体传递，因此，在分析船舶甲板结构强度时，需要建立整个船舶的有限元模型。

建立船体模型采用的建模参数如表1所示。

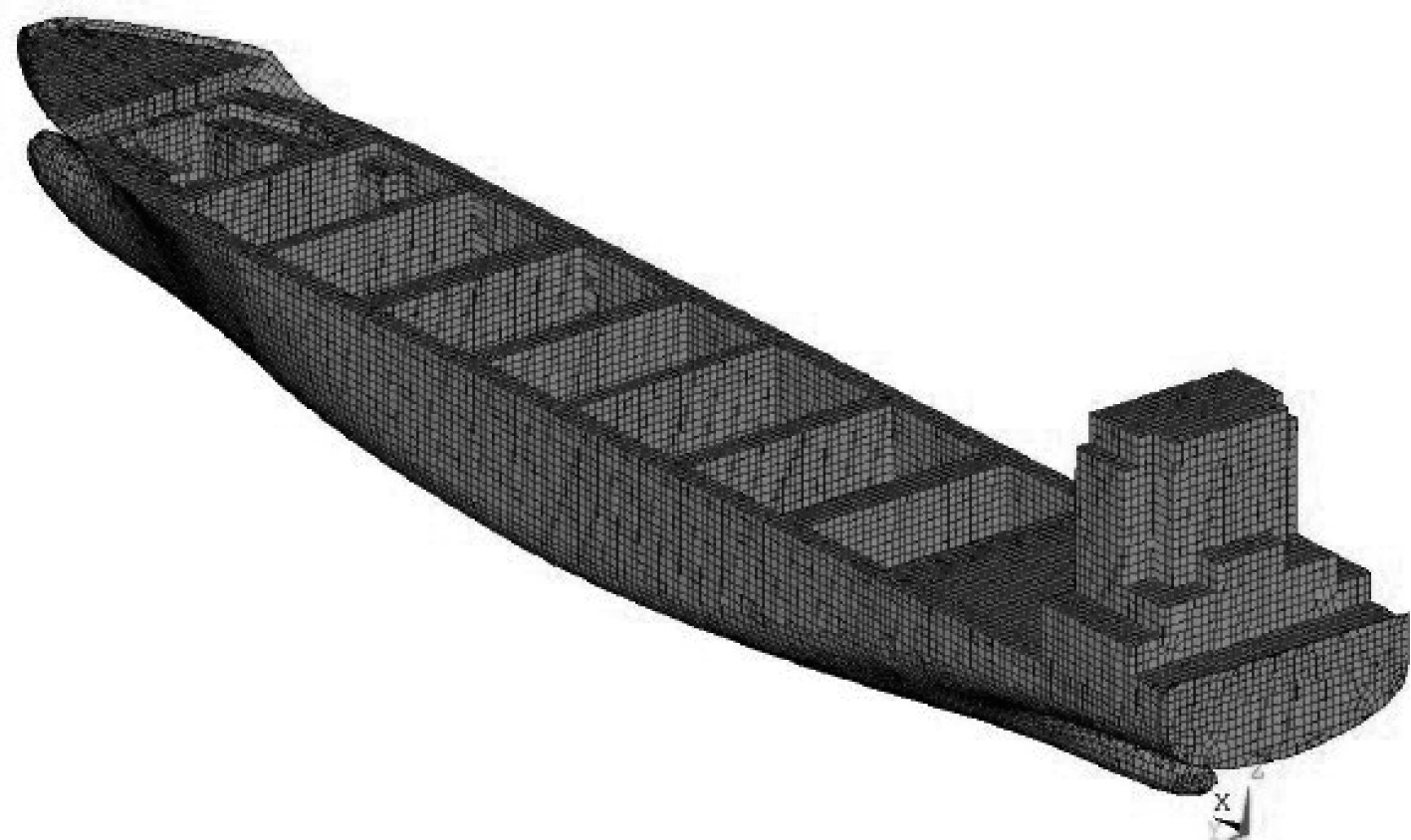
船体有限元模型的材料选用高强度钢，该材料的屈服强度为355 MPa，弹性模量为2.1E10 MPa，泊松比为0.26。整个船体有限元模型如图5所示。

可知，船体有限元模型采用全实体单行进行模拟，有限元模型节点数为45268个，单元数为26846个，采用的单元类型solid 186单元^[4]。

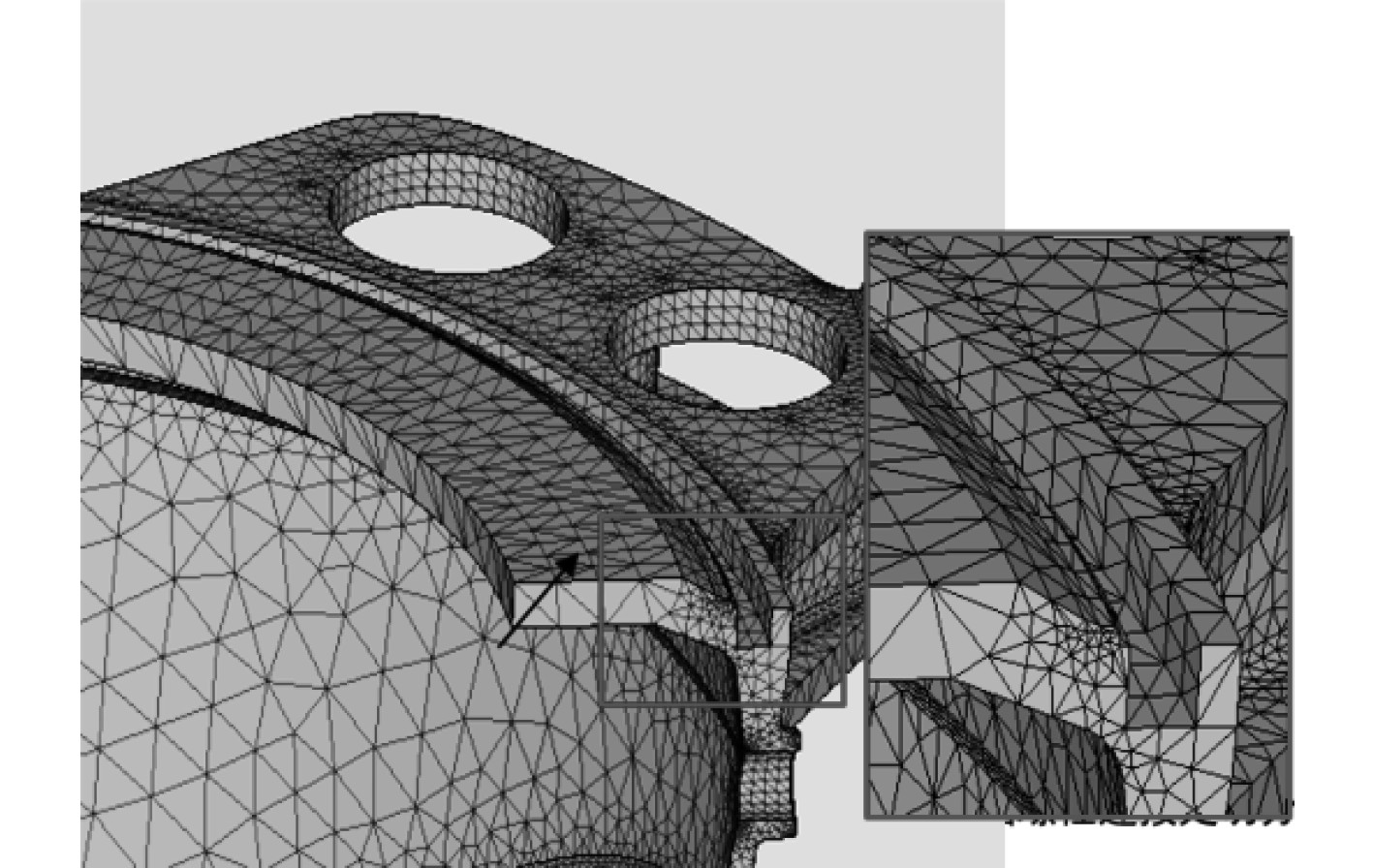
船体甲板支撑结构的局部区域进行了有限元网络的加密，网格大小为60～120 mm，网格类型为四面体网格，如图6所示。

3.3 船舶甲板支撑结构的疲劳强度分析与寿命评估

船舶甲板支撑结构的疲劳强度评估步骤：

1）S-N曲线参数的选择

S-N曲线参数的选择与疲劳强度分析的精度密切相关，在校核船体结构疲劳强度时，基于DNV校核规范，建立S-N曲线的回归公式为：

$ \begin{array}{ll}\mathrm{log}N=12.16-3.0\mathrm{log}S\hfill & t=45， \hfill \\ \mathrm{log}N=12.16-0.75\mathrm{log}\left(\dfrac{t}{32}\right)-3.0\mathrm{log}S\hfill & t\ne 45。 \hfill \end{array} \text{} $

其中，t为结构的厚度，S为应力范围，N为该应力下的循环次数，通过试验，选取S-N曲线为：

$ {S_r}{N_r}^m = 1.06 。$

2）热点应力区域的处理

所谓热点区域，是指容易发生应力集中的位置，通常处于焊接结构的焊脚等位置^[5]，通常，应力最大的点成为热点，该处不论是极限应力还是疲劳应力，都容易出现失效。

将甲板支撑结构的热点应力位置定为h=0.5+0.1a的厚度范围，并按照0.85 mm的厚度将热点应力区域的网格划分层次，如图7所示。

3）进行Ansys有限元计算

将海浪载荷作为船舶甲板支撑结构有限元模型的输入条件，在Ansys中进行结构静强度的计算，并进行应力集中系数的提取。

应力集中系数是指热点应力区域^[6]的热点应力与名义应力之比，如下式：

$ SCF = \frac{{{\sigma _{{\rm{max}}}}}}{{{\sigma _N}}} \text{。} $

式中： ${\sigma _{{\rm{max}}}}$ 为结构的热点应力， $ {\sigma _N} $ 为名义应力。

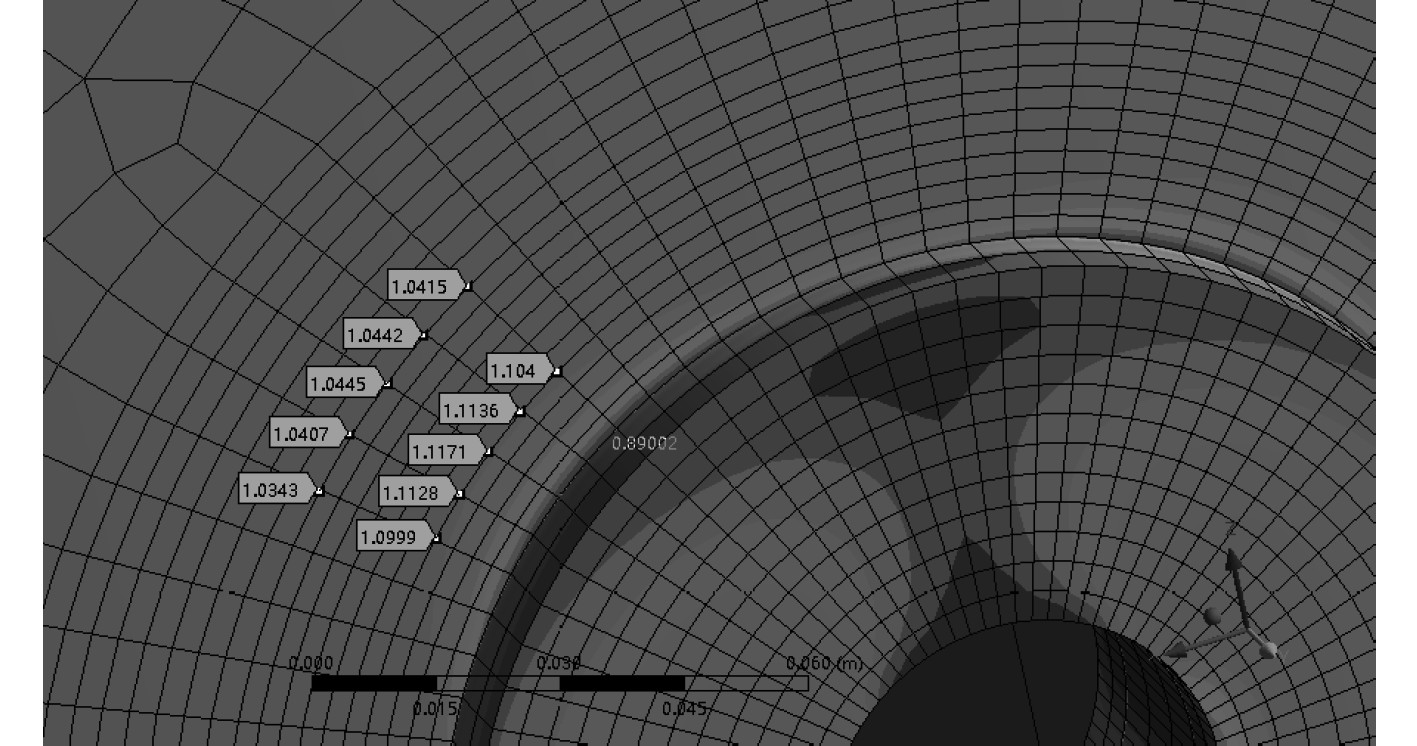
得到有限元仿真结果如图8所示。

4）计算海浪载荷下的支撑结构疲劳累积损伤度

根据S-N曲线，计算波浪载荷不同应力范围单独作用时的循环次数，并按照 $ \dfrac{n}{N} $ 计算应力范围产生的疲劳损伤度，根据Miner疲劳损伤公式计算疲劳寿命。选取编号为1532的节点，计算疲劳寿命为 $L= $ $ \dfrac{20}{0.7356}=28 $ 年。

4 结　语

利用金属材料的S-N曲线疲劳寿命计算方法、Miner疲劳损伤累积计算方法、有限元仿真等技术，对船舶甲板支撑结构的热点区域进行了疲劳寿命计算，对于提升材料的疲劳强度有重要意义。