0 引　言

直翼桨作为一种船用推进装置，具备操纵性能优良、推进效率较高、适用于不同工况等优点，被广泛应用于对稳定性和机动性要求极高的拖船、浮吊和军用舰船等^[1-2]。直翼桨区域的结构加强和受力方式与螺旋桨推进方式相比存在很大区别，其中，直翼桨工作时的激振载荷达到相当量级，易引起共振疲劳。此外，为满足大型化和轻量化的要求，现代船舶广泛使用高强度钢和薄板材，也易引起高应力，疲劳强度问题突显。因此，针对直翼桨区域结构进行交变载荷特性分析，并进一步评估该区域的疲劳损伤具有重要的工程实际意义。

目前，船体疲劳问题研究主要集中在总纵弯曲交变载荷引起的疲劳损伤，疲劳分析也通常在频域内采用谱分析法^[3-4]，各国船级社在规范^[5-6]中对谱分析的计算流程以及计算参数的选取提供了一定的参考，但疲劳时域的分析研究较少，聚焦在船体首部砰击和海洋结构物在风浪联合作用下的疲劳问题^[7-8]。对于主机工作时产生的高频激励和波浪共同作用下的复杂情况，由于2种载荷的频率和振幅存在较大差异，使得疲劳损伤计算较为困难，采用谱分析难以将2种载荷的结构响应耦合，已不能准确评估该区域船体结构的疲劳寿命。

本文结合实船项目，研究直翼桨区域在激振载荷和波浪载荷的时间历程计算方法，分析了在2种载荷作用下的应力–时间响应历程（简称“应力响应时历”），通过雨流计数法对该区域结构节点进行应力范围和循环次数统计，比较了不同载荷对疲劳损伤的贡献。

1 疲劳时域分析方法 1.1 疲劳时域分析方法流程

采用船体直翼桨区域疲劳时域分析方法，首先确定主要激振载荷和波浪载荷的时历曲线，再通过瞬态响应直接计算法得到结构热点应力响应时历，并在时域内进行线性叠加，得到合成应力时历。通过应力循环计数方法，如雨流计数法等，得到应力范围和循环次数。最后基于Miner线性累积损伤理论得到疲劳累积损伤值，流程如图1所示。

1.2 激振载荷时历分析

直翼桨区域结构所受激振载荷主要包括螺旋桨盘内激振力和盘外脉动压力，一般结合水动力性能分析和实测数据研究得到。相比常规船舶尾部螺旋桨，直翼桨的轴频振幅很小，影响可忽略不计。

1）激励力的时域信号拟合公式如下：

$\begin{split} F\left( t \right) = {A_0} + {A_1}\cos (2\text{π} {f_1}t - {\varphi _1}) + {A_2}\cos (2\text{π} {f_2}t - {\varphi _2})。\hfill \\ \end{split} $

(1)

式中： $ {A_0} $ 为平均振幅； $ {A_1} $ 为叶频振幅； $ {f_1} $ 为叶频； $ {\varphi _1} $ 为叶频相位； $ {A_2} $ 为倍叶频振幅； $ {f_2} $ 为倍叶频； $ {\varphi _2} $ 为倍叶频相位。

2）盘外脉动压力拟合公式如下：

$ P\left( t \right) = \sum\limits_{i = 1}^n {{\alpha _i}\cos \left( {{\omega _i}t + {\varepsilon _i}} \right)。} $

(2)

式中： $ {\alpha _i} $ 为第i阶下脉动压力的幅值； $ {\omega _i} $ 为第i阶下脉动压力的圆频率； $ {\varepsilon _i} $ 为第i阶下脉动压力的初相位。

1.3 波浪载荷时历分析

基于三维线性势流理论，海浪是平稳正态过程，假定各成分波随机并独立，组合后也是平稳正态过程^[9]。

波浪载荷的主要问题是求解船舶周围流场的速度势，即

$ \begin{gathered} \varPhi \left( {x,y,z,t} \right) = \left[ { - Ux + {\varPhi _S}\left( {x,y,z} \right)} \right] + \hfill \\ {Re} \left\{ {\left( {{\phi _I}\left( {x,y,z} \right) + {\phi _D}\left( {x,y,z} \right) + {\phi _R}\left( {x,y,z} \right)} \right){e^{i\omega t}}} \right\} 。\hfill \\ \end{gathered} $

(3)

在定航速U下的定常兴波势 $ {\varPhi _S} $ 和入射波势 $ {\phi _I} $ 为已知量，绕射势 $ {\phi _D} $ 和辐射势 $ {\phi _R} $ 需根据质量连续性方程和相关边界条件求得。再由伯努利方程，流场内任意一点压力 $ p\left( {x,y,z,t} \right) $ 可表示为：

$ p - {p_0} = - \rho gz - \rho \frac{{\rm{{\partial}} \Phi }}{{{\partial} t}} - \frac{1}{2}\rho {\left| {\nabla \Phi } \right|^2}。$

(4)

实际海浪环境下的不规则波具有随机性。在工程应用中，一般通过有限数量的规则波叠加模拟不规则波。波浪参数的合理定义直接影响叠加结果，进而影响到波浪载荷的计算精度。对于海况分布图中的每一海况，通过给定的海浪谱推导出其波的时域形式，可选取双参数的Pierson-Moskowitz谱(简称P-M谱)，其表达式为：

$ {G_{\eta \eta }} = \frac{{H_s^2}}{{4\text{π} }}{\left( {\frac{{2\text{π} }}{{{T_z}}}} \right)^4}{\omega ^{ - 5}}\exp \left( {{{ - }}\frac{1}{\text{π} }{{\left( {\frac{{2\text{π} }}{{{T_z}}}} \right)}^4}{\omega ^{{{ - }}4}}} \right)。$

(5)

将频率范围等分为N个区间，叠加后依旧是周期函数，其周期是各自的最小公倍数。设 $ \Delta \omega = ({\omega _{\max }}\~{\omega _{\min }})/N $ ,则所模拟波的周期为 $ 2\text{π} /\Delta \omega $ 。但为表现出不规则波的随机性，将 $ \Delta \omega $ 定义为变量，可通过在 $ \left[ {{\omega _i},{\omega _{i + 1}}} \right] $ 区间内选取随机值 $ \mathop {{\omega _i}}\limits^ \wedge $ 替换 $ {\omega _i} $ ，即

$ \mathop {{\omega _i}}\limits^ \wedge = {\omega _{i - 1}} + ({\omega _i} - {\omega _{i - 1}}) \times {n_{rand}}。$

(6)

式中， $ {n_{rand}} $ 是 [0,1]范围内的随机值。

1.4 疲劳应力响应计算

在激振载荷和波浪载荷诱导的结构热点应力响应叠加时，应计及热点应力方向的影响。疲劳失效一般发生在构件焊缝位置，且导致疲劳失效的热点应力方向多与裂纹萌生方向垂直。因此，提取不同载荷作用下沿焊缝垂直方向的主应力再线性叠加作为结构热点应力的方式较为合理。激振载荷和波浪载荷联合作用下的结构热点应力响应时历可表示为：

$ \sigma \left( t \right) = {\sigma _e}\left( t \right) + {\sigma _w}\left( t \right)。$

(7)

根据静力分析法，计算波幅 $ {a_i} $ ，频率 $ {\omega _i} $ ，初相位 $ {\varepsilon _i} $ 的子波作用下船体单元的应力响应 $ {\sigma _i} $ ，将所有子波线性叠加得到 $ {\sigma _w}\left( t \right) $ ：

$ {\sigma _w}\left( t \right) = \sum\limits_{i = 1}^n {{a_i}{\sigma _{_i}}\cos ({\omega _i}t + {\varepsilon _i})}。$

(8)

1.5 疲劳累计损伤计算

在疲劳研究领域，雨流计数法被认为是一种比较科学的计数方法^[10]。通过雨流计数对结构热点应力响应时历进行处理，得到各级热点应力范围及其循环次数。应力范围结果应考虑平均应力的影响，可采用Goodman公式对其进行修正，其原理是将计算得到的应力范围和应力均值转化为应力比为 $ R = - 1 $ 的标准S-N曲线的等效应力范围^[11]，如下式：

$ {S_{eq}} = \frac{S}{{2\left(1 - \dfrac{{{S_{m} }}}{{{\sigma _b}}}\right)}}。$

(9)

式中： $ {S_{eq}} $ 为修正后的等效应力范围； $ S $ ， $ {S_m} $ 分别为雨流计数得到的应力范围和应力均值； $ {\sigma _b} $ 为所用材料的抗拉极限。

假设时域分析时段 $ T $ 内足以反映船舶寿命期 $ {T_d} $ 内载荷的平均水平，在航率为 $ \delta $ ，典型工况i的时间分配系数为 $ {\alpha _i} $ ，时域分析时段内发生了 $ {n_i} $ 次热点应力循环，应力范围 $ {S_{ij}} $ 的发生概率为 $ {P_{ij}} $ ，则目标船考虑激振载荷和波浪载荷联合作用下的疲劳累积总损伤表示为：

$ D = \frac{\delta }{A}\sum\limits_i {\sum\limits_j {\frac{{{\alpha _i}{T_d}{P_{ij}}}}{T}{n_i}S_{ij}^m} } 。$

(10)

2 直翼桨区域结构疲劳分析算例 2.1 有限元模型

建立船体局部有限元模型，范围以直翼桨所处位置为中心，船长方向延伸至结构强支撑构件上(如舱壁板、桁材、强肋骨、强横梁等)，垂向取主船体范围内的所有构件，并采用全宽模型，避免左右舷结构和航向产生的不对称影响，如图2所示。

在直翼桨整体重心处建立质量点，在直翼桨基座上选择节点与质量点建立MPC关联，将该点作为盘内激振载荷的作用点，如图3所示。为了更大程度上减小MPC带来的结构刚度的增大，直翼桨安装面上的螺栓孔原则上应尽量布置在基座围井支撑结构两侧。

2.2 疲劳热点选取

依据有限元分析结果，目标船直翼桨基座区域的结构产生较大应力，可以作为疲劳强度的校核部位。主要选取以下3类热点位置：直翼桨基座支撑构件翼板与直翼桨基座盘面的焊缝位置、直翼桨基座支撑构件腹板与筒壁以及基座盘面的交点位置和直翼桨基座支撑构件腹板与筒壁以及船底板的交点位置，如表1和图4所示。

2.3 载荷计算

计算时选取高速（16 kn）、中速（14 kn）、低速（8 kn）作为典型工况，其中三者之间的时间分配比例关系为：中速工况占50%，高速工况和低速工况各占25%。

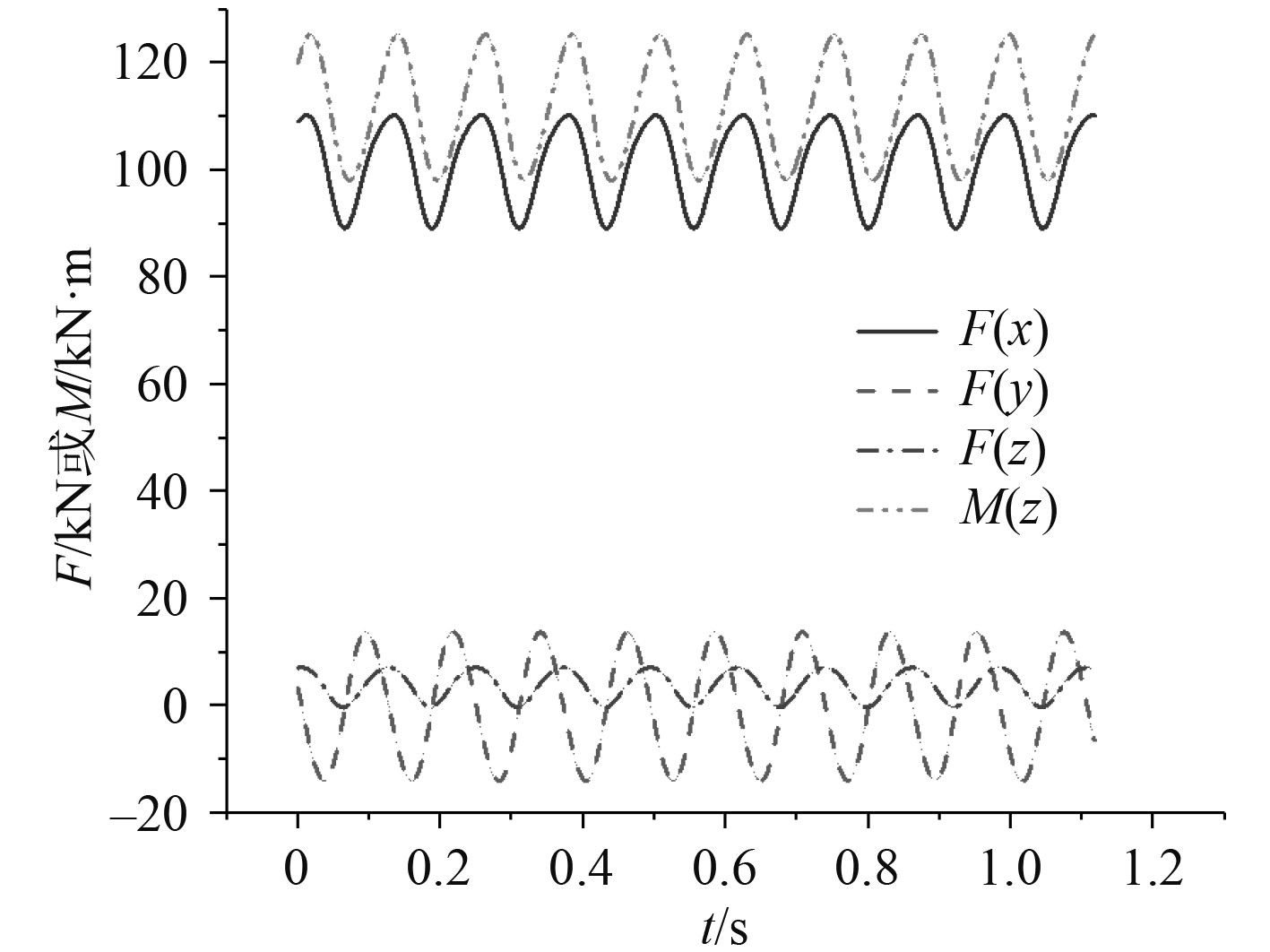
以高速工况为例，首先计算激振力4个分量（即纵向力Fx，横向力Fy，垂向力Fz和基座扭矩My）的时间历程，其中图5为按式（1）计算得到的激振力各载荷分量时历曲线，可以合理描述激振力的作用情况。

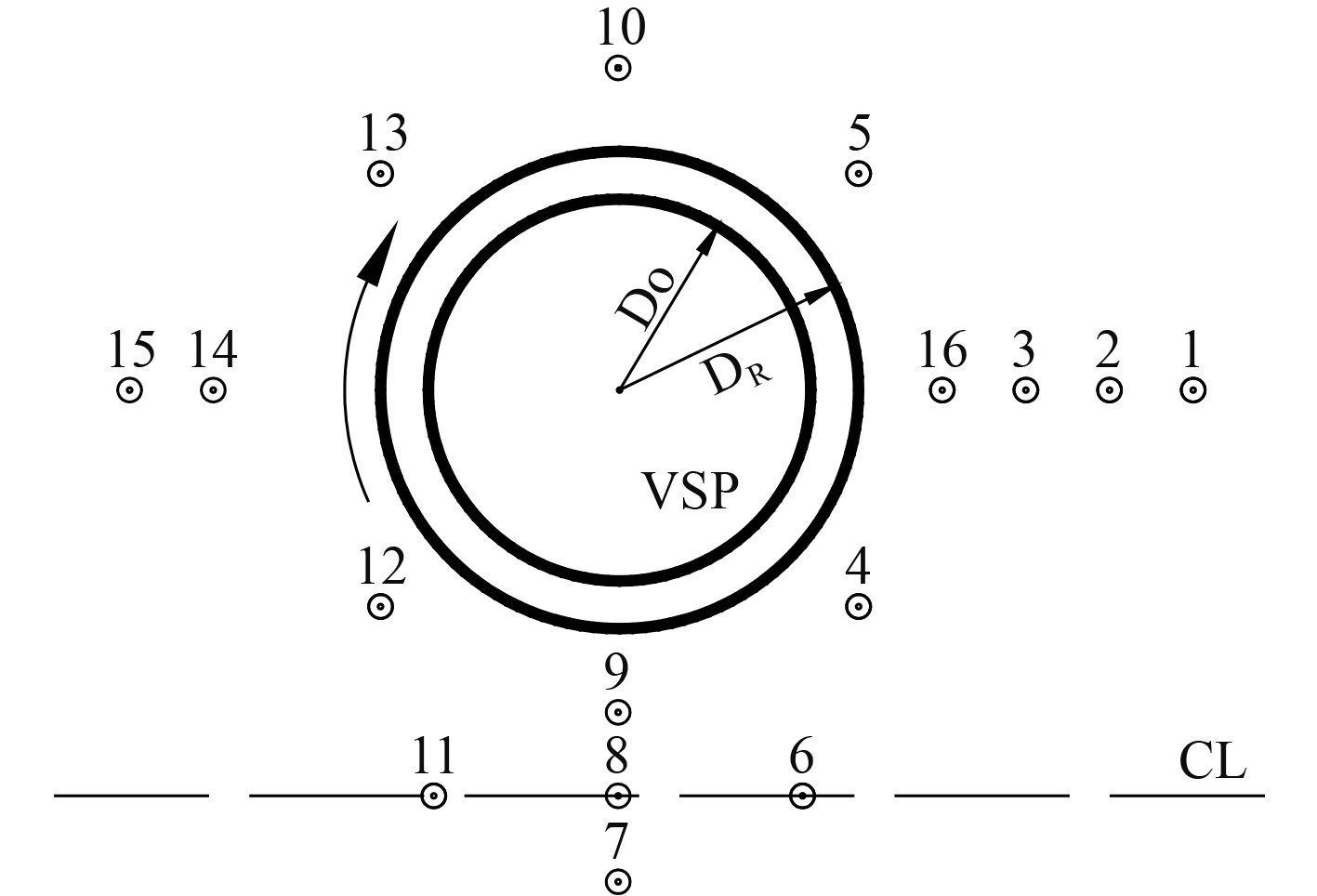
脉动压力以单元加载的形式分布在直翼桨盘外四周，如图6所示，在左右盘外各选取16个测点施加脉动压力。

根据式（2）计算得到高速工况下的脉动压力时历曲线，如图7所示。

船体波浪载荷预报采用载荷计算软件Walcs-Basic进行全船湿表面模型的时域水动力计算，得到的水动力结果通过PCL函数功能投影到结构模型上。

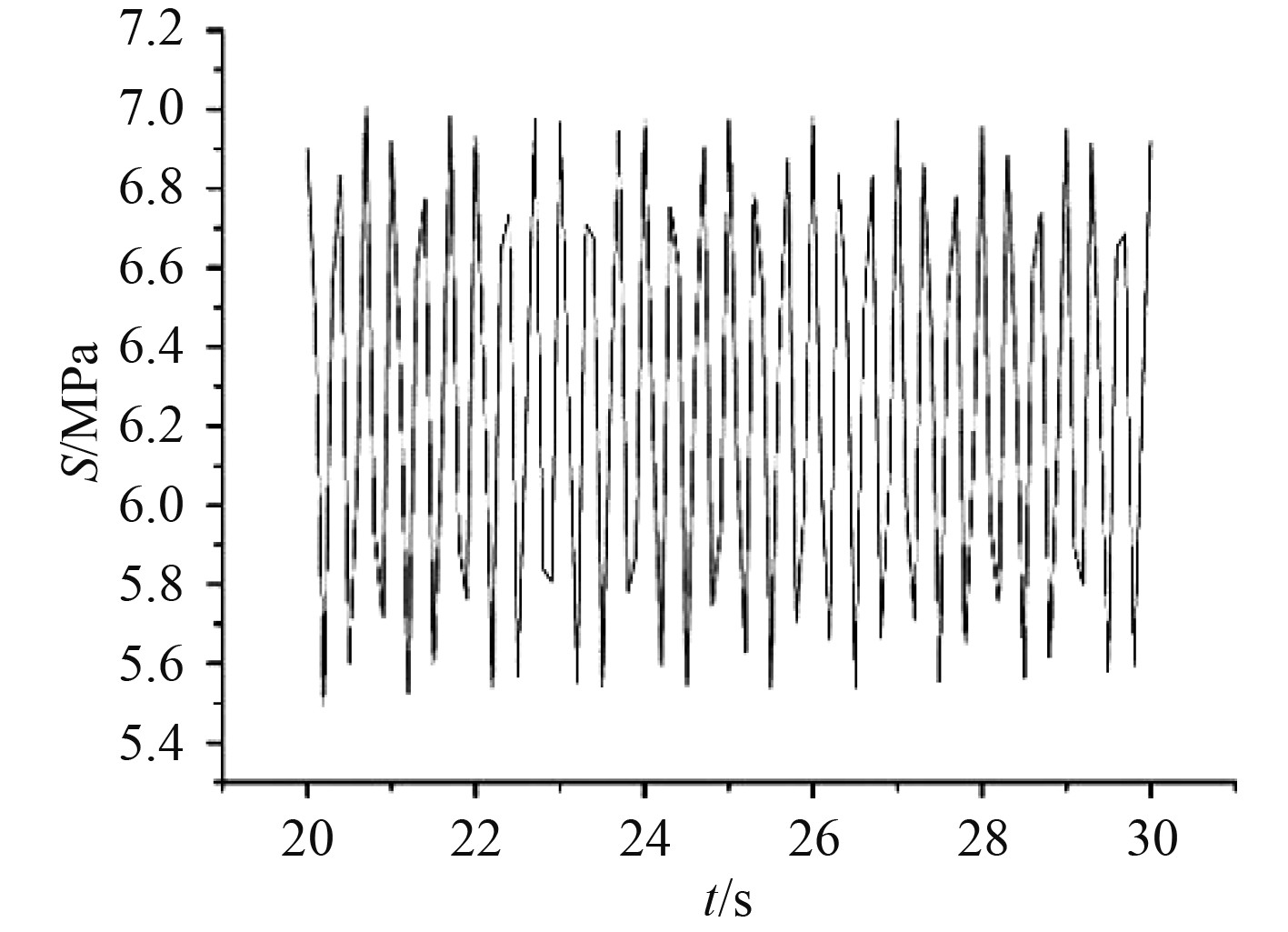
2.4 热点应力计算

采用有限元分析软件分别得到激振载荷和与波浪载荷共同作用下的结构应力响应时历。时长是影响时域分析结果准确性的重要参数之一。为了确保船舶结构计算的可靠性，分析时间历程去除首尾船舶运动不稳定时间，图8为Hotspot03在激振载荷下取稳定段20～30 s内的应力响应时历曲线。

统计选定时间内应力响应的均值、最大值和最小值，如表2所示。

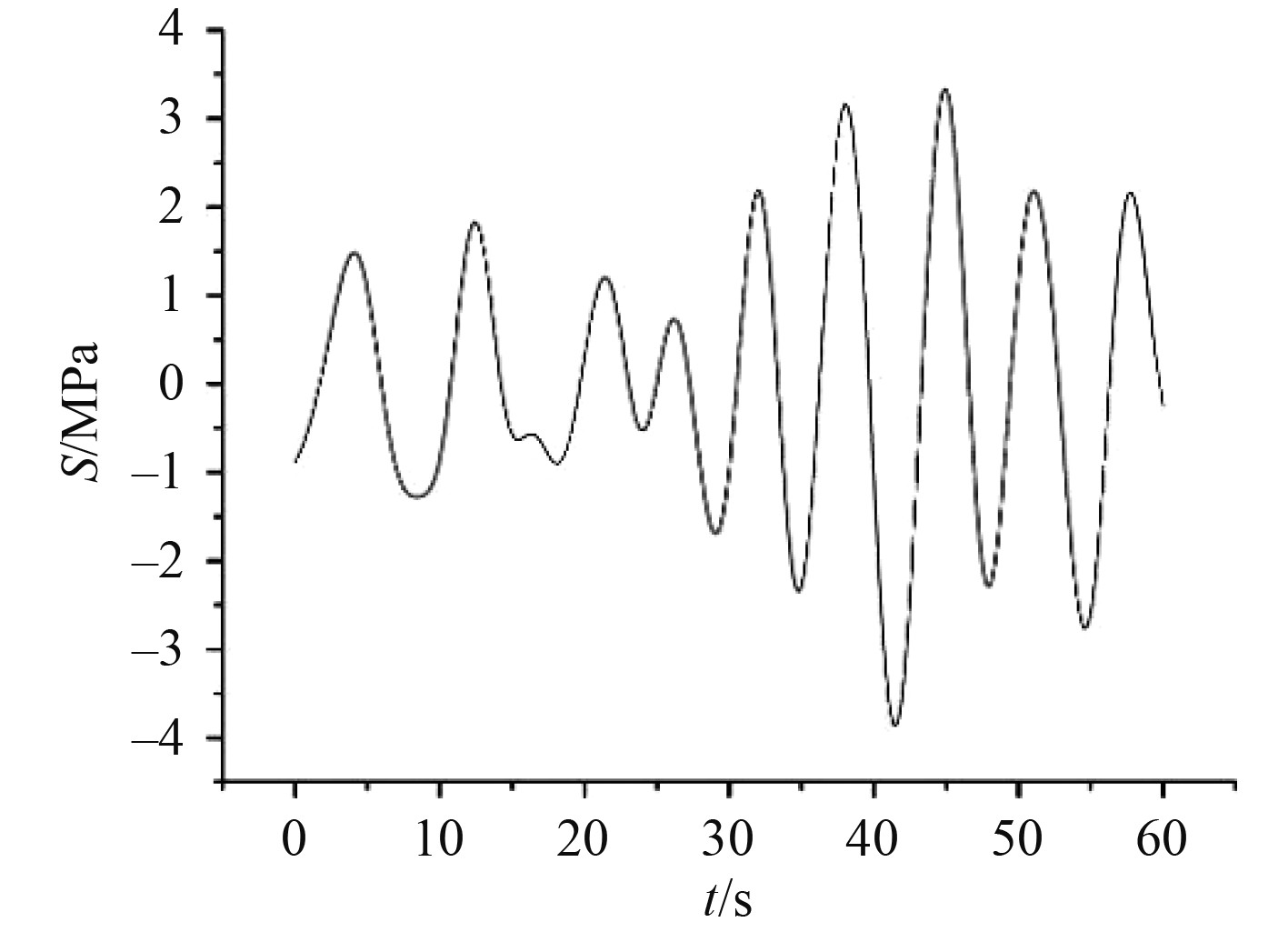
根据复数响应振幅理论，通过波浪载荷作用下插值得到的各个热点应力得到不同频率子波的初相位和应力，并根据P-M谱计算各个子波对应的波幅，叠加得到应力响应时历。图9为Hotspot03在波浪载荷下取稳定段60 s内的应力响应时历曲线。

在得到激振载荷作用下的应力时历和波浪载荷作用下的应力时历的基础上进行线性叠加。图10为Hotspot03计算得到的60 s内的应力响应时历。

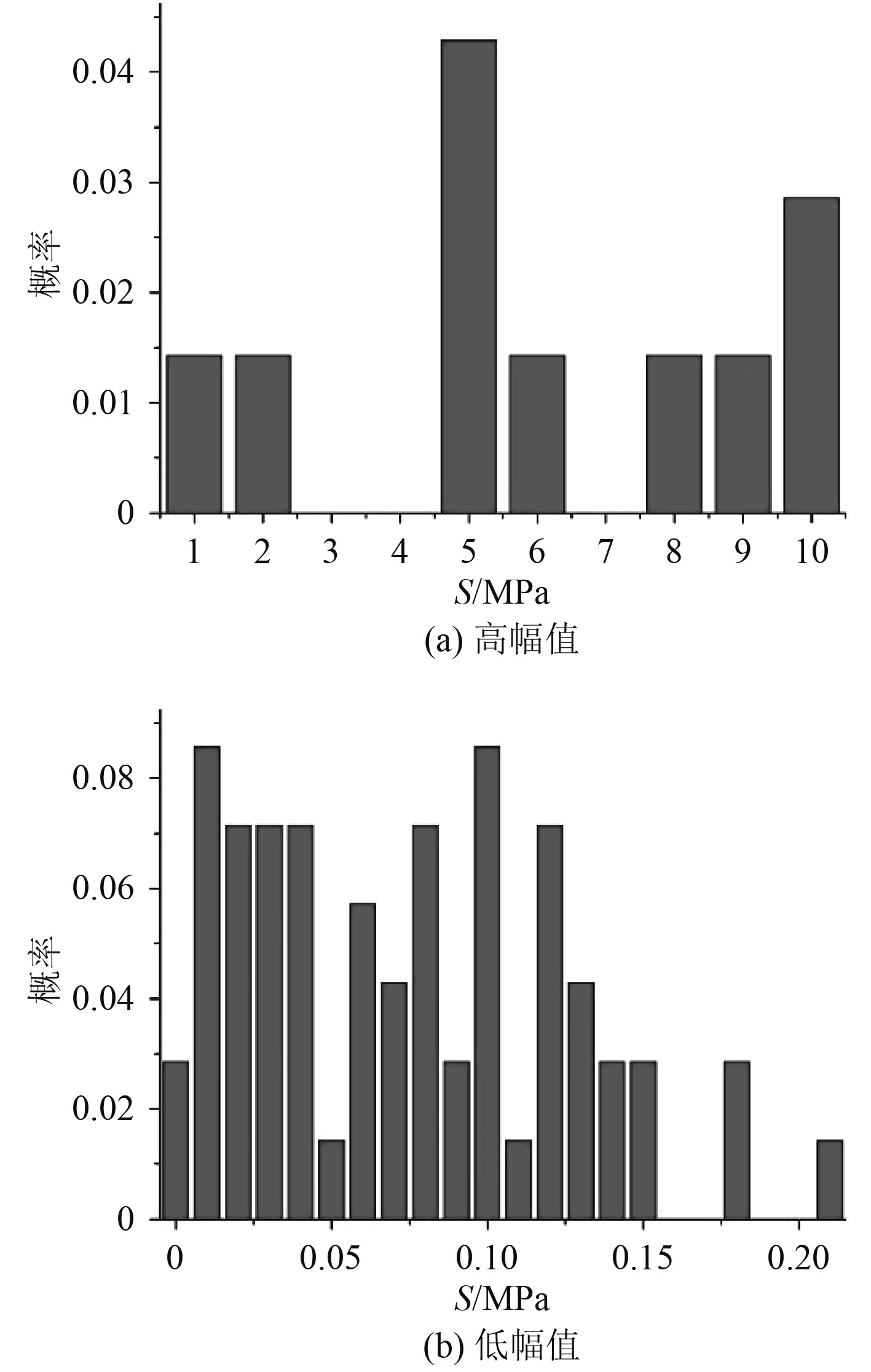
观察所得应力合成时历，发现得到的合成应力都是高频随机信号，不能直接进行疲劳损伤值计算。采用雨流计数法的三点计数程序进行计数处理，得到应力时历下不同应力范围及其概率。由于热点位置处激振载荷产生应力幅值与波浪载荷产生应力幅值相差较大，在计数时可分别考虑低幅值部分与高幅值部分，图11为Hotspot03的应力统计结果。

2.5 疲劳损伤计算结果

分别对上述8个热点进行分析，计算出热点在载荷作用下引起的的损伤值，损伤值情况如表3所示。

从统计结果来看，直翼桨区域结构的疲劳问题较为明显。其中，支撑构件翼板与基座盘面的交缝位置处出现的损伤最大，这是因为此处连接结构出现突变，应力出现集中，易发生疲损伤。其次是支撑构件腹板与筒壁在船底板处的交缝，此处受盘内激振力作用较大，也容易发生疲劳损伤。

3 结　语

1）基于时域分析方法，将激振载荷和波浪载荷下的结构应力响应时历曲线叠加再分析，可以较为合理地模拟直翼桨区域在真实环境下的疲劳损伤情况；

2）激振载荷对直翼桨基座支撑构件翼板与基座盘面焊缝位置处疲劳损伤影响最大，局部位置达到总损伤值的50%，在设计过程中需考虑该位置共振疲劳的影响；

3）在靠近船体中线面的位置，波浪载荷对直翼桨区域结构疲劳影响占主导地位。