混沌现象,特指一种随机不确定且难以找寻规律的现象。20世纪80年代,Fujisaka等对混沌相关理论的探索开启了混沌加密技术的大门。经过专业领域研究人员的不懈努力,混沌理论依托混沌同步电路得以应用于保密通信领域,且获得了不错的效果[1-3]。
在水声通信领域,为避免水声信号被侦获后的信息泄露,水声通信除了可靠性、隐蔽性之外,还要求通信具有较高的保密性。通常使用扩频通信来实现通信的隐蔽和抗干扰能力,而扩频通信中,扩频码的生成是扩频的关键,因此,怎样在满足扩频码基本性能要求的基础上更便捷地产生大量可用扩频码,成为了扩频通信研究中的重要课题[2]。其中,利用混沌离散映射函数产生的具有加密属性的混沌码逐渐引起了人们的注意。
在混沌扩频码应用于水声扩频通信方面,已有单位对其进行研究并开展了海试。王海斌等在提高远程水声通信速率的方法上进行了充分研究,提出利用混沌调频M-ary技术增加通信速率,并研究了改进型Tent混沌映射在水声通信中的应用。在2003年南海海域进行的海试结果简表如表1所示。其中SL为声源级,TL为传播损失,TLR为多径效应下的额外损耗,AN为环境噪声谱级,GT为时间增益,SNR1与SNR2分别为理论与实测的信噪比值。值得注意的是,海试中声信号带宽极小,仅为50 Hz;在通信距离为31 km的条件下,误码率量级为10−3[4-5]。
|
|
表 1 水声通信试验数据 Tab.1 Experimental data of underwater acoustic communication |
另外,申晓红等在基于Logistic混沌映射的水声跳频通信方面进行了理论研究与相关试验。在水深不到100 m的山区湖泊试验中,采用基于Logistic混沌映射的FHSS通信技术,BFSK调制方式和Hamming码达成了16.7 bps的通信速率。试验中收发平台距离3~15 km、布放深度为10~20 m,单基元接收;在中远距离浅水通信中多径效应恶劣的条件下2次实现了误比特率BER为10–7量级的通信试验[4]。
在上述2个混沌水声通信的研究中,试验人员分别采用改进型Tent混沌映射与Logistic混沌映射设计了水声扩频通信的理论及试验方案,综合看来,将混沌码应用于水声扩频通信具有一定可行性。
1 混沌映射加密通信技术混沌保密通信的核心是将混沌信号与目标信息结合,使合成信号具有类噪声性质,不易被发现。当包含有用信息的类噪声信号被目标接收平台侦测到后,由对应的混沌机制提取混沌信号,恢复原始有用信号,这一过程如图1所示。混沌保密通信的加密与解密过程与扩频通信的扩频与解扩过程极其相似,因此,可以在扩频通信基础上设计混沌加密的水声扩频通信系统[5-7]。
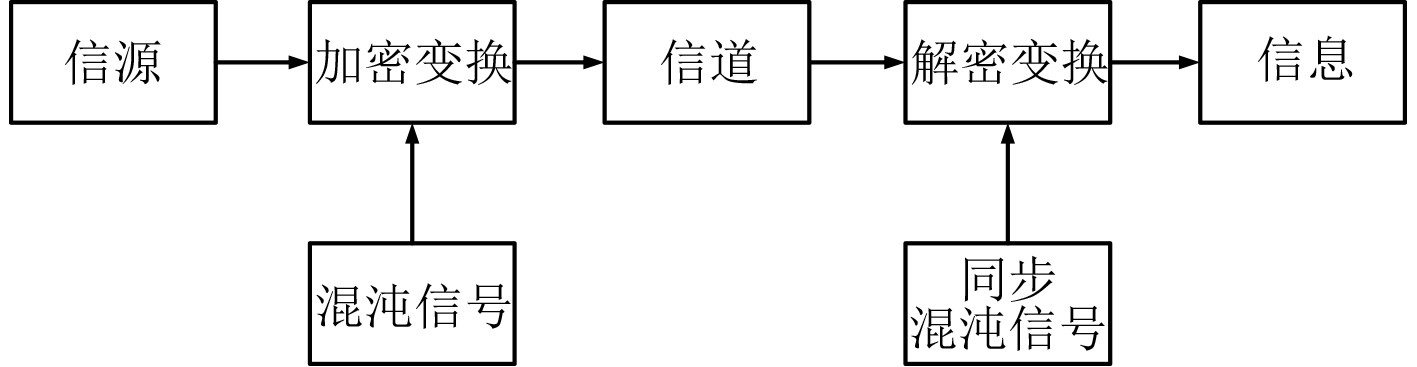
|
图 1 基于混沌同步的保密通信 Fig. 1 Secure communication based on chaotic synchronization |
基于混沌加密的数字通信系统中,使用离散混沌映射函数以及一定初始条件得到的实值混沌序列无法直接应用于通信加密,需要将实值序列依据特定算法转化为二进制序列[5-7]。在混沌扩频通信中,混沌映射可以用于替代伪随机数生成器,生成0~1之间的混沌数,由混沌实值序列得到的二进制序列可作为相应的扩频码。
1)Tent映射
Tent映射属于分段线性混沌映射。在映射函数的迭代规则下,经过有限次数的计算后(迭代次数取决于计算机设备),Tent映射任何一个初值条件都将失去效果,需要重新寻找新的映射函数初值。
| $ {x_{k + 1}} = \left\{ \begin{gathered} {x_k}/\beta ,{\text{ }}{{\text{x}}_k} \in (0,\beta ],\hfill \\ (1 - {x_k})/(1 - \beta ),{\text{ }}{{\text{x}}_k} \in (\beta ,1] 。\end{gathered} \right. $ | (1) |
2)Logistic映射
Logistic混沌离散映射函数,在一个有效初值的迭代计算下就能产生混沌序列。然而Logistic映射的不足之处也非常明显。有资料表明Logistic映射是最简单的混沌映射,且被广泛应用于保密通信中,对其混沌序列的恢复重建方法已引起相当重视,加密效果相对较差;由于Logistic映射不均匀的不变分布,映射函数得到的混沌实值序列在某些情况下会产生失衡,进一步会影响因之得到的二进制序列的平衡性,不符合扩频通信中扩频码的要求;其次只有Logistic方程中
| $ {x_{k + 1}} = \mu {x_k}(1 - {x_k}) ,$ | (2) |
其中,
3)Chebyshev映射
Chebyshev映射方程对初值极为敏感,因而较容易获得大量不同的实值序列。只要满足初值
综上所述,Chebyshev混沌映射相较于Tent映射与Logistic映射有较为明显的优势。从无周期性、序列平衡性、初值敏感性、良好相关函数4个方面仿真评估Chebyshev混沌离散实值序列的性能。
2 Chebyshev混沌序列性能评估1)Chebyshev混沌序列的构造
k阶Chebyshev离散映射方程[8]为:
| $ {x}_{n+1}={\rm{cos}}(k\cdot {\rm{arccos}} {x}_{n})\text{,}{x}_{0}\in [-1,1]。$ | (3) |
式中:
当
2)Chebyshev实值序列性能仿真
通过Matlab软件仿真来验证Chebyshev离散实值序列的无周期性、平衡性、初值敏感性(易于产生大量扩频序列)以及良好相关函数,并进一步研究了k和N取值对序列相关性的影响。
①无周期性
仿真中取映射初值x0=0.45,映射阶数k=24,迭代步数n=999,通过映射函数产生长度N=1000的离散映射实值序列,为了显示直观,列举序列前100位如图2所示。

|
图 2 离散映射实值序列 Fig. 2 Discrete mapping real valued sequence |
②平衡性
为了验证Chebyshev混沌实值序列的平衡性,取映射初值x0=0.45,映射阶数k=24,迭代步数n分别999,1999,2999,3999,4999,5999,通过映射函数将分别产生6个不同长度的离散实值序列。然后分别对序列求平均值,结果如表2所示。可以看出6个序列虽然长度逐渐增大,但均值都非常接近于0且只有小范围上下波动,即验证了Chebyshev混沌实值序列良好的平衡性。
|
|
表 2 序列均值 Tab.2 Sequence mean |
③初值敏感性
为了从仿真图像中直观显示出Chebyshev离散映射对初值的敏感性,取另外一个映射初值y0=0.45001,其他条件不变,通过映射函数产生长度N=1000的离散映射实值序列。图3显示了初值分别为x0和y0时的离散实值序列曲线,同样只各取实值序列前100位作对比,可以看出,即使2个离散映射的初值只相差0.00001,实际映射得到的序列取值差异大且不相关,即显示了Chebyshev离散映射对初值的敏感性。在实际应用中,映射对初值的敏感性利于获得大量可用的扩频码。

|
图 3 初值不同的2个离散实值序列 Fig. 3 Two discrete real valued sequences with different initial values |
④Chebyshev实值序列的相关性分析
对Chebyshev实值序列的自相关性进行分析。这里映射初值x0=0.45,映射阶数k=24,迭代步数n=999,通过Chebyshev映射函数产生长度N=1000的离散映射实值序列,取值区间为(–1,1)。序列自相关性如图4(a)所示,从图中可以看出序列的自相关函数尖锐。又取另一初值y0=0.45001,得到另一序列自相关性如图4(b)所示,也体现出了自相关函数的尖锐性。
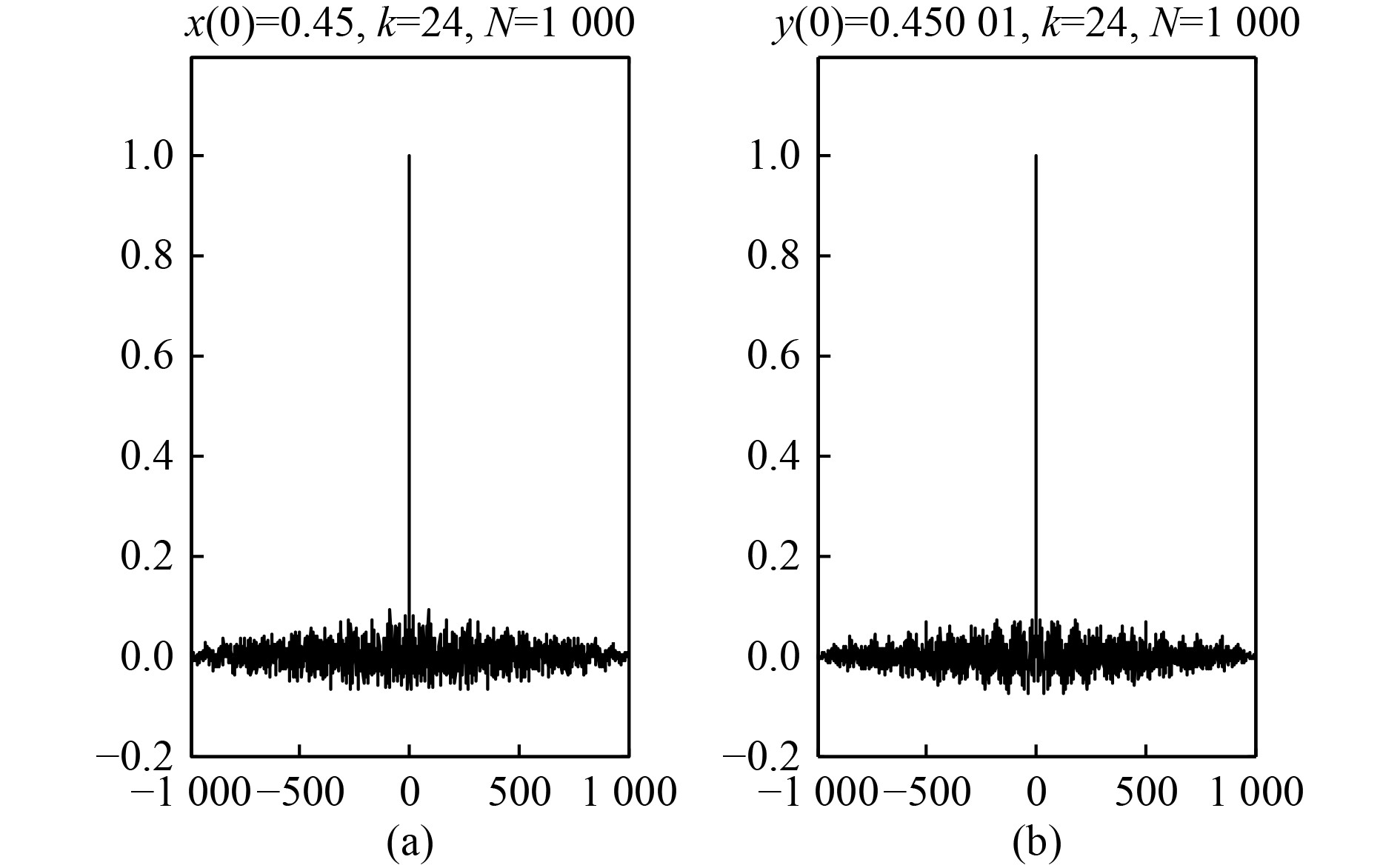
|
图 4 Chebyshev实值序列的自相关性 Fig. 4 Autocorrelation of Chebyshev real valued sequences |
分析Chebyshev实值序列的互相关性。对初值分别为x0=0.45,y0=0.45001(初值极接近)的2个Chebyshev实值序列的互相关性进行分析。如图5所示,初值接近的2个序列的互相关值接近于0,表明Chebyshev实值序列应用为扩频码时互相关性良好。
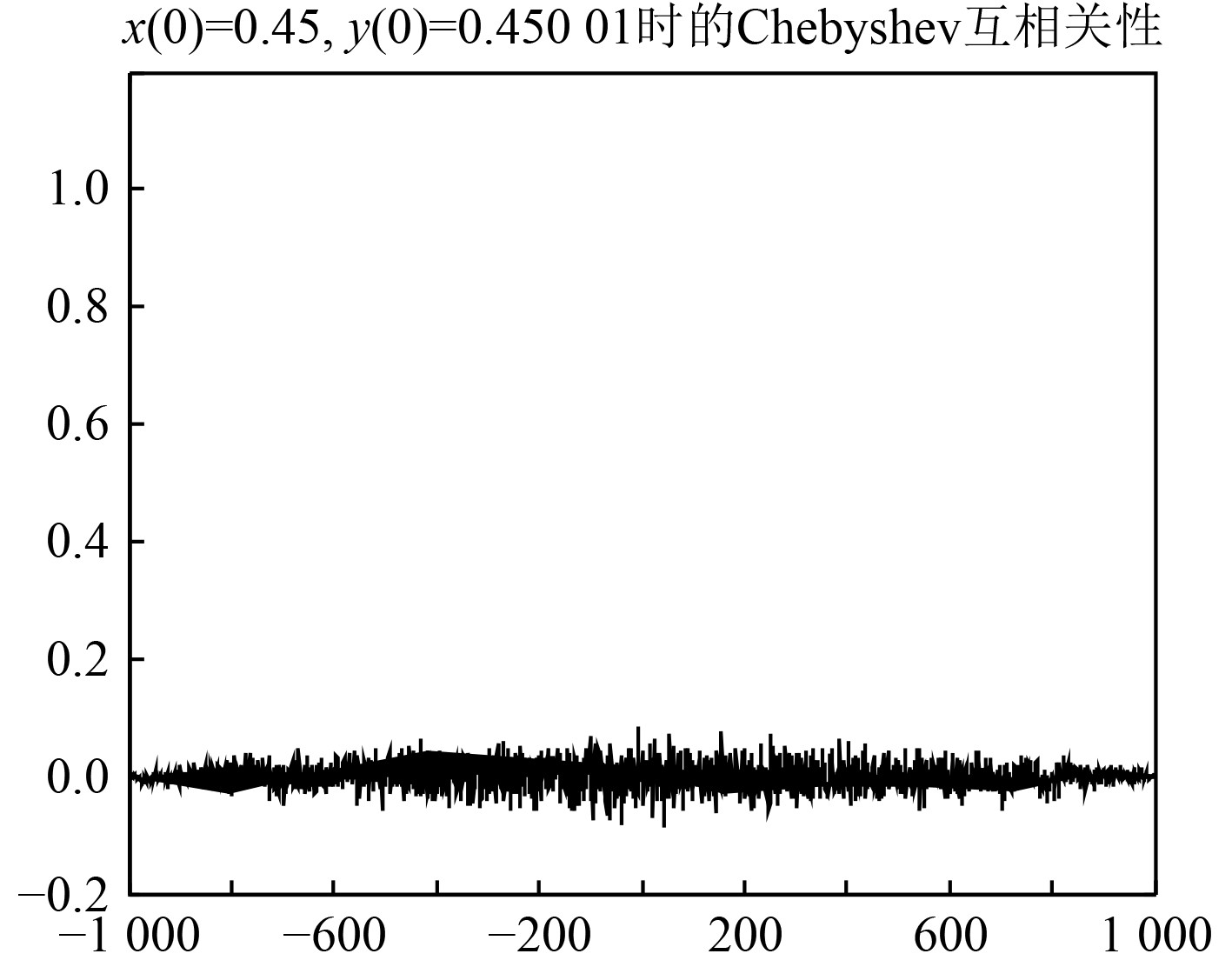
|
图 5 序列的互相关性 Fig. 5 Cross correlation of sequences |
⑤Chebyshev序列相关性与其参数k与N的关系
为了期望得到相关性更好的Chebyshev实值序列,进一步研究序列相关性与映射函数中参数k与N的对应关系,用以指导Chebyshev序列在扩频通信中的应用。具体方法是:使参数k与N值其中一个不变,通过改变另一个参数值得到不同序列的相关性,并进行比较。其中自相关性能参考自相关函数除中央极值以外的最大值,互相关性能则参考互相关极值[7-8](经过离散映射得到Chebyshev序列后,由于序列中有负值,先对序列值进行绝对值处理)。
为了起到对照的效果,取映射初值x0=0.45,y0=0.45001(与相关性验证时的取值相同),序列长度N=1000,k取值范围为[2, 3, ···, 50],得到序列相关性与k的关系如图6所示(自相关结果由x0=0.45得到)。结果表明,随着k值的增大,序列的相关性能变化不明显。
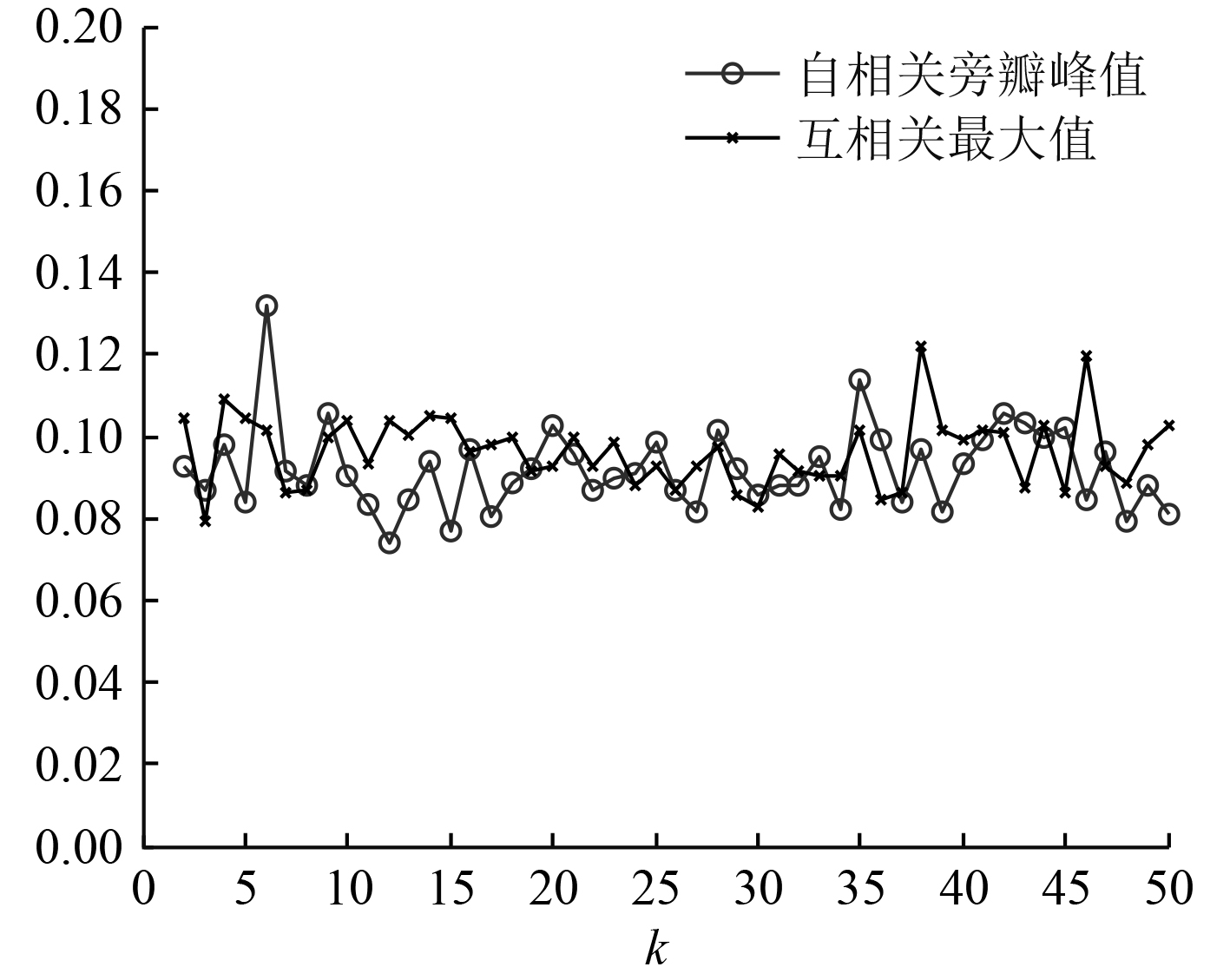
|
图 6 k值对Chebyshev序列相关性的影响 Fig. 6 Influence of k value on Chebyshev sequence correlation |
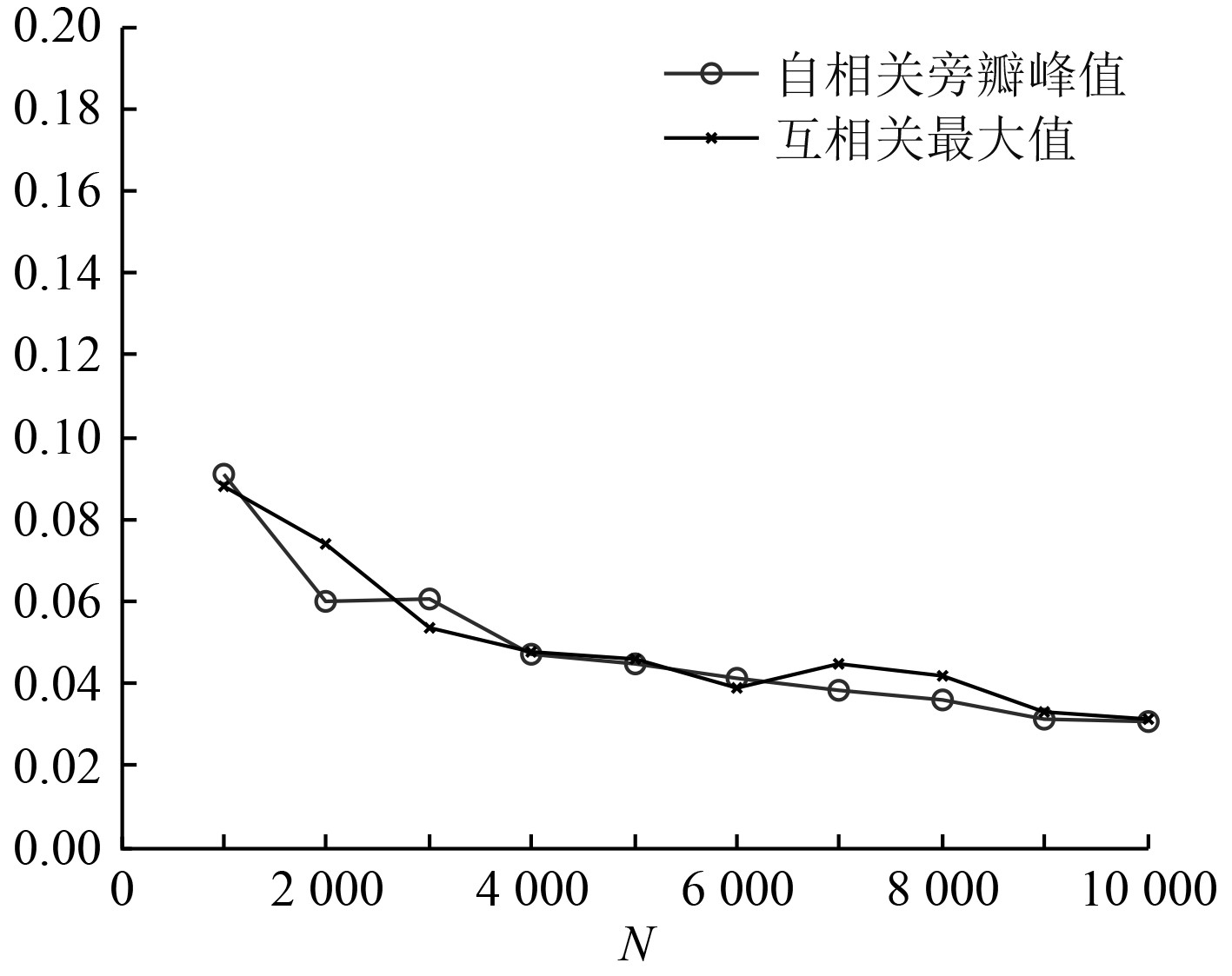
映射初值x0=0.45,y0=0.45001,取k=24,N=[1000,2000,···,10000],序列相关性能如图7所示(自相关结果由x0=0.4得到)。结果表明,Chebyshev混沌实值序列的相关性能是N值的增函数,但也只能获得极有限的提升。
|
图 7 N值对Chebyshev序列相关性的影响 Fig. 7 Influence of N value on Chebyshev sequence correlation |
综上所述,由Chebyshev混沌离散映射得到的实值序列具有无周期、平衡性好、易于大量产生、相关性良好等优点,且经过仿真分析表明,序列的相关性能随着k值的增大变化不明显,随着序列长度N值的增加会有一定限度提高。
3 结 语基于混沌加密技术,利用Chebyshev混沌映射函数的无周期混沌序列,可产生具有加密属性的扩频码用于水声扩频通信,既保证扩频通信隐蔽和抗干扰能力,还提供较强的保密性。通过理论分析和仿真评估,证明具有加密属性的Chebyshev序列的优良特性,可极大增强信息传输的安全性。
| [1] |
陈韵, 王逸林, 蔡平, 等. 基于分数阶Fourier变换的远程水声通信技术研究[J]. 兵工学报, 2011, 32(9): 1159-1164. |
| [2] |
REN H P, BAI C, KONG Q, et al. A chaotic spread spectrum system for underwater acoustic communication[J]. Physica A Statistical Mechanics & Its Applications, 2017, 478. |
| [3] |
吕曜辉, 杜鹏宇, 张宏滔, 等. 基于混沌正交组合序列的M元码分多址水声通信[J]. 声学技术, 2018, 37(1): 32-37. |
| [4] |
周锋, 尹艳玲, 乔钢. 猝发混合扩频水声隐蔽通信技术[J]. 声学学报, 2017, 42(1): 37-47. |
| [5] |
SHU Xiu-jun, WANG Hai-bin, et al. A method of multichannel chaotic phase modulation spread spectrum and its application in underwater acoustic communication[J]. Chinese Journal of Acoustics, 2017, 42(1): 130-144. |
| [6] |
JIANG Z, WANG H, YANG X, et al. Adaptive chaotic probabilistic frequency hopping method for underwater acoustic communication system[J]. Journal of Xian University of Technology, 2012.
|
| [7] |
HUANG F, HUANG H, JUN S U. Short burst underwater acoustic communication method based on chaotic sequence[J]. Ship Electronic Engineering, 2014.
|
| [8] |
Yao-hui L, Peng-YU D U, ZHANG H T, et al. M-ary code division multiple access underwater acoustic communication based on chaotic orthogonal combination sequence[J]. Technical Acoustics, 2018.
|
 2022, Vol. 44
2022, Vol. 44
