2. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074;
3. 内蒙古工业大学 理学院,内蒙古 呼和浩特 010051
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China;
3. College of Sciences, Inner Mongolia University of Technology, Hohhot, 010051
非线性波浪是海洋工程研究的重要领域之一,有许多描述波浪行为的数学模型。浅水波Korteweg-de Vries (KdV)方程是学者们较早关注讨论的方程,由荷兰科学家Kortweg和de Vries于1895年提出[1]。KdV方程也是许多其他物理系统的一个重要非线性数学模型,在晶体非线性振动,等离子体声波传播,非线性光学,无碰撞磁流体波传播等领域中都有非常广泛的应用[2]。KdV方程具有非常典型的可积性,例如无穷多个对称守恒量[3],
由非线性偏微分方程描述的孤立波方程精确解研究是非线性科学中的一个热点问题[10-11],例如Hirota双线性变换法,Painleve分析法,逆散射法,tanh-coth方法,G'/G展开法等。但是,上述解析方法在应用上有着不同的限制。一般来说,没有一个通用的方法可以求解所有非线性偏微分方程。Zabusky等[12]数值研究中发现KdV方程两孤立波互相作用后,除有相位移动外,不改变波形和速度。然后,Gardner等[13]用反散射方法解析证明。关于KdV方程和BBM方程的研究文献有很多,在理论和数值上都得到了很好的研究[14-16]。作为KdV方程的改进,BBM方程允许出现一族孤立波解,但目前还没有类似KdV方程的反向散射方法对其孤立波相互作用进行解析研究。Bona等[17]使用数值方法研究BBM方程孤立波的相互作用,指出BBM方程的两孤立波相互作用后出现小的频散尾巴。研究表明BBM方程不存在两孤立子相互作用的精确解。蔡加祥等[18]给出了BBM方程的拟线性隐式差分格式和非线性隐式差分格式。本文基于质量、动量和能量守恒量对KdV方程和BBM方程两孤立波相互作用特性进行近似解析和数值研究,并进行综合比较分析。
1 数学模型本文研究如下形式的KdV方程和BBM方程[19]:
| $ {u_t} + {u_x} + u{u_x} + {u_{xxx}} = 0 ,$ | (1) |
| $ {u_t} + {u_x} + u{u_x}{\text{ - }}{u_{xxt}} = 0。$ | (2) |
式中:
KdV方程和BBM的孤立波解可以通过应用一般的孤立波形状来求得:
| $ {u_{{\text{KdV}}}} = a{\text{sec}}{{\text{h}}^{\text{2}}}\left[ {\sqrt {\frac{a}{{12}}} \left( {x - ct} \right)} \right], $ | (3) |
| $ {u_{{\text{BBM}}}} = a{\text{sec}}{{\text{h}}^{\text{2}}}\left[ {\sqrt {\frac{a}{{12}}} \frac{{\left( {x - ct} \right)}}{{\sqrt c }}} \right]。$ | (4) |
式中:
KdV方程和BBM方程的质量,动量和能量守恒量[18]可分别用下式计算:
| $ {I_1} = \int_{ - \infty }^{ + \infty } {u{\rm{d}}x}, $ | (5) |
| $ {I_2} = \int_{ - \infty }^{ + \infty } {{u^2}dx} ,{I_2} = \int_{ - \infty }^{ + \infty } {{u^2} + u_x^2{\rm{d}}x}, $ | (6) |
| $ {I_3} = \int_{ - \infty }^{ + \infty } {{u^3}{\text{ - 3}}u_x^2{\rm{d}}x}。$ | (7) |
如果2个波合并,则可以将守恒量增加到另一个波的不变量中,从而得到合并波形的合并质量、动量和能量。这3个量是理解应用守恒量计算波浪合并方法的关键。因为提供了3个已知参数,从中可以找到合并波的良好近似值。对于具有不同振幅
2个输入孤立波的振幅为
|
|
表 1 输入孤立波与完全合并波形 Tab.1 Input solitary wave and merged wave shape |
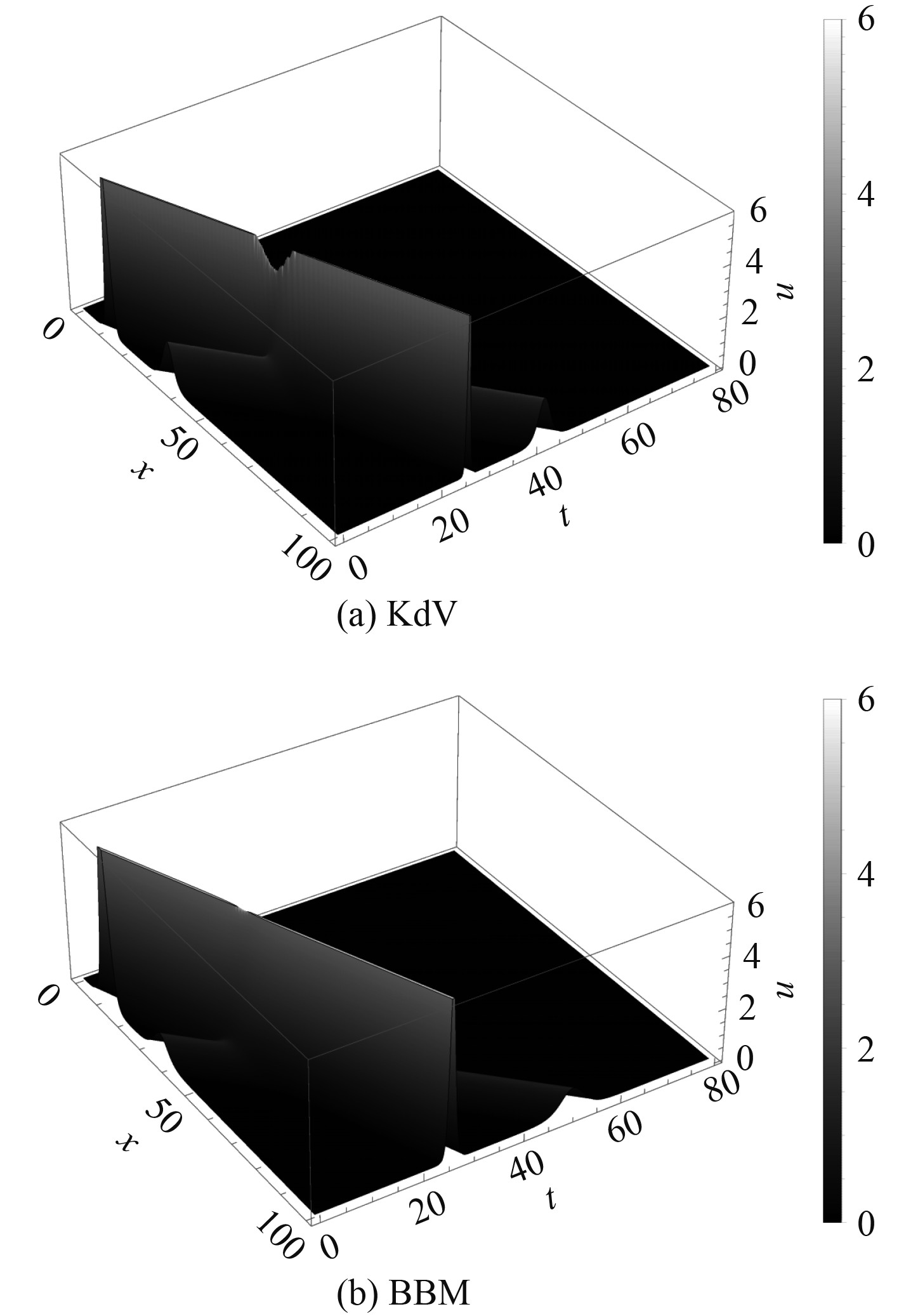
|
图 1
双孤立波完全相互作用三维图
|
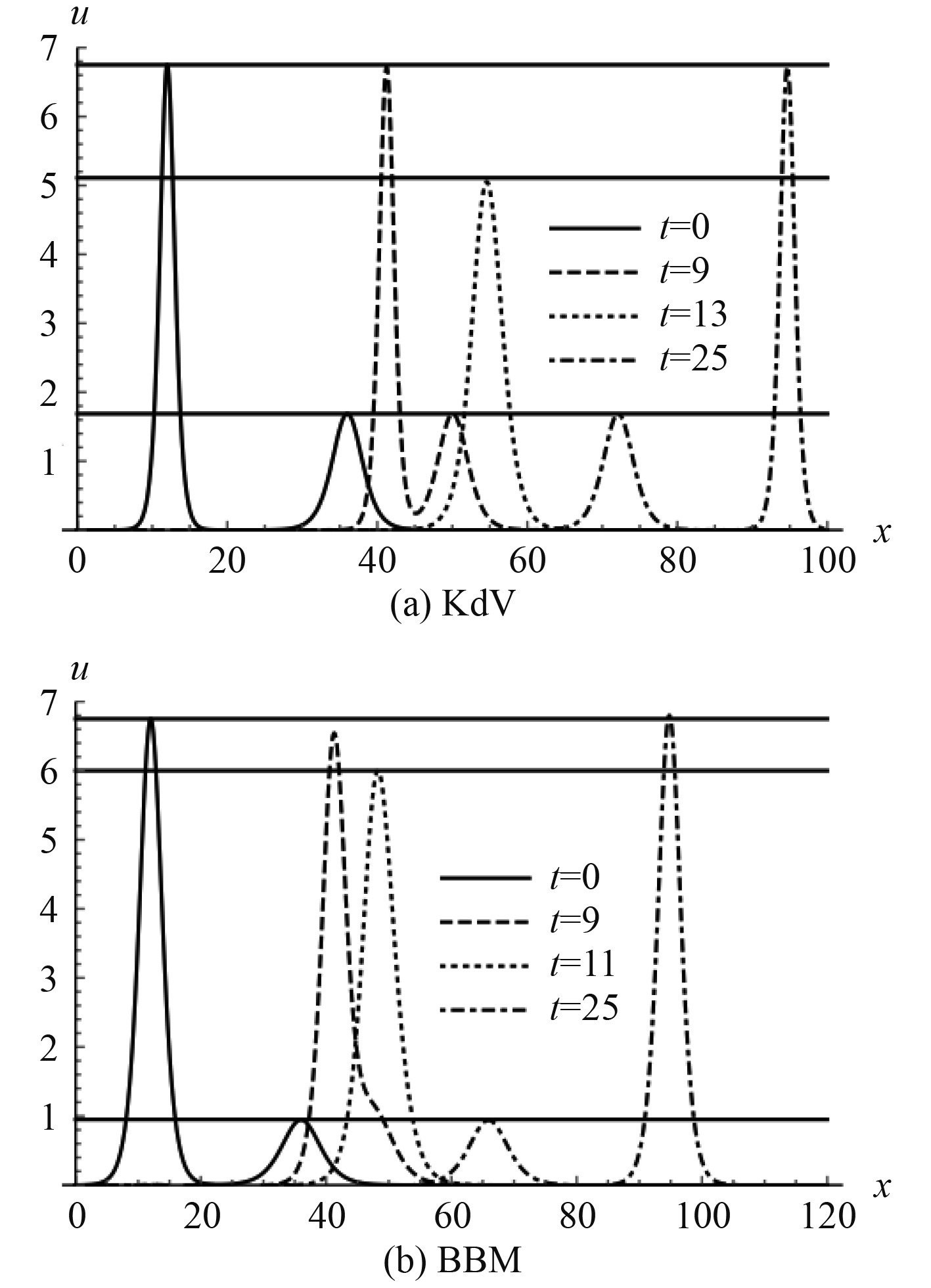
|
图 2
双孤立波完全相互作用的空间剖面
|
| $ U\left( x \right) = A{\text{sec}}{{\text{h}}^{\text{2}}}\left( {Bx} \right) 。$ | (8) |
式中:
| $ {I_{1{\text{KdV}}}} = 4\sqrt 3 \left( {{a_1}^{1/2} + {a_2}^{1/2}} \right) = \frac{{2A}}{B},$ | (9) |
| $ {I_{2{\text{KdV}}}} = \frac{8}{{\sqrt 3 }}\left( {{a_1}^{3/2} + {a_2}^{3/2}} \right) = \frac{{4{A^2}}}{{3B}} ,$ | (10) |
| $ \begin{split}{I_{3{\text{KdV}}}} = & \frac{{8\sqrt 3 }}{5}\left( {{a_1}^{5/2} + {a_2}^{5/2}} \right) =\\& \frac{{16{A^2}\left( {A - 3{B^2}} \right)}}{{15B}}, \end{split}$ | (11) |
| $ {I_{1{\text{BBM}}}} = 4\left( {{a_1}\sqrt {1 + \frac{3}{{{a_1}}}} + {a_2}\sqrt {1 + \frac{3}{{{a_2}}}} } \right) = \frac{{2A}}{B}, $ | (12) |
| $\begin{split} {I_{2{\text{BBM}}}} = &\frac{{16}}{5}\left[ {\frac{{a_1^2\left( {5 + 2{a_1}} \right)}}{{6 + 2{a_1}}}\sqrt {1 + \frac{3}{{{a_1}}}} + \frac{{a_2^2\left( {5 + 2{a_2}} \right)}}{{6 + 2{a_2}}}\sqrt {1 + \frac{3}{{{a_2}}}} } \right] =\\& \frac{{4{A^2}\left( {5 + 4{B^2}} \right)}}{{15B}}, \\[-15pt]\end{split} $ | (13) |
| $\begin{split}{I_{3{\text{BBM}}}} = & \frac{{16}}{{15}}\left[ {\frac{{a_1^3\left( {9 + 4{a_1}} \right)}}{{6 + 2{a_1}}}\sqrt {1 + \frac{3}{{{a_1}}}} + \frac{{a_2^3\left( {9 + 4{a_2}} \right)}}{{6 + 2{a_2}}}\sqrt {1 + \frac{3}{{{a_2}}}} } \right] =\\& \frac{{16{A^2}\left( {A - 3{B^2}} \right)}}{{15B}}。\\[-15pt]\end{split} $ | (14) |
2个输入孤立波的振幅
|
|
表 2 KdV和BBM数值结果和合并拟合误差 Tab.2 Error between two cases of merging fit |
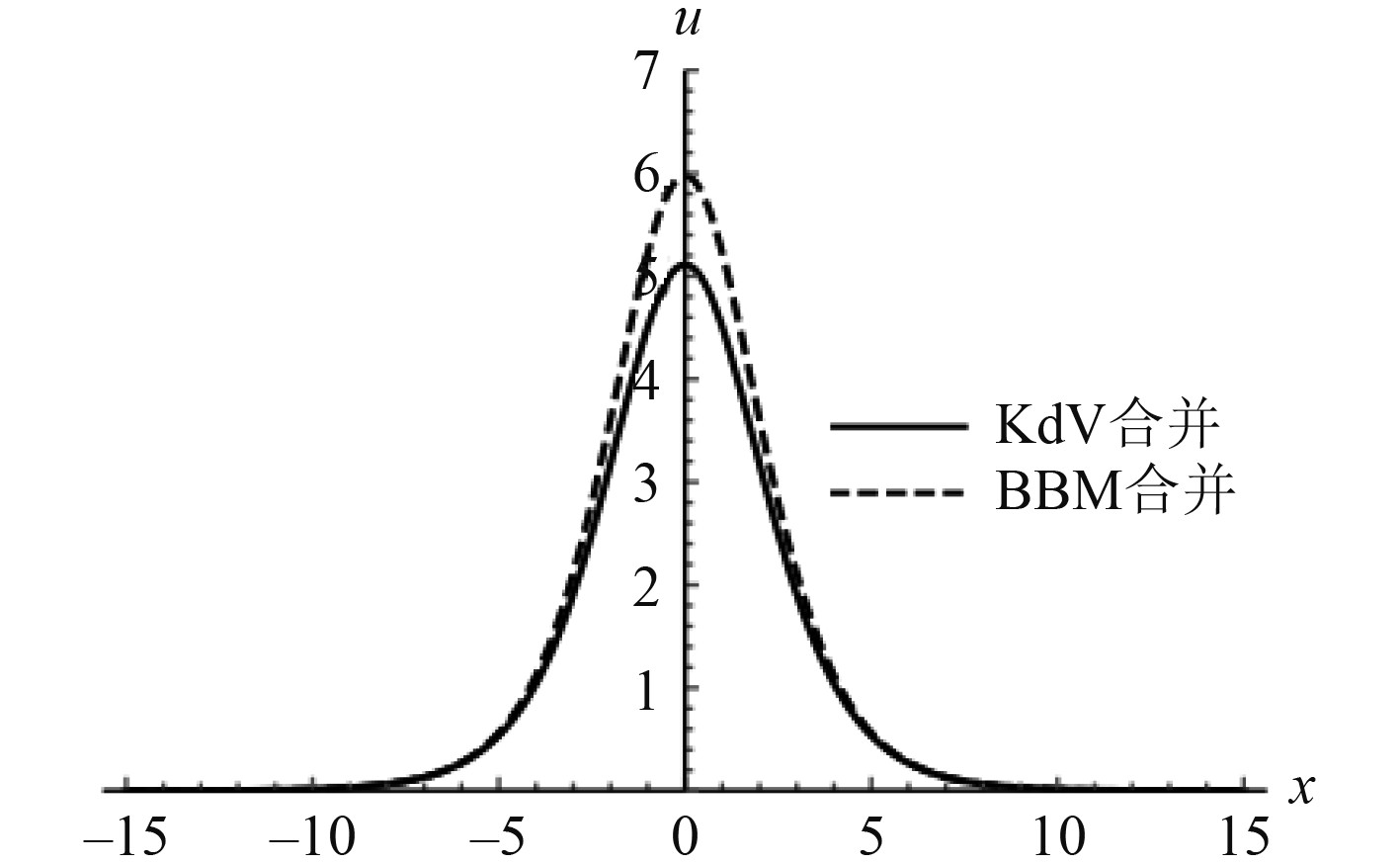
|
图 3
KdV与BBM双孤立波相互作用完全合并波形
|
本文研究了KdV方程和BBM方程2个孤立波的完全相互作用,输入不同组合孤立波在两者最大化合并。应用的守恒量方法不考虑BBM方程分散波小尾部的产生。在KdV方程和BBM方程2个孤立波的完全相互作用过程中,应用守恒量等式计算合并波形,无需求解非线性偏微分方程。综合比较了KdV方程和BBM方程的数值计算结果以及近似合并波形解析结果,认为使用守恒量近似分析方法研究孤立波相互作用,具有良好的近似解析模型,并且具有较小的计算量。
| [1] |
WHITHAM G B. Linear and nonlinear waves[M]. New York: John Wiley, 1974: 454-471.
|
| [2] |
DAUXOIS T, PEYRARD M. Physics of solitons[M]. Cambridge: Cambridge University Press, 2006: 185-211.
|
| [3] |
MIURA R, GARDNER C S, KRUSKAL M. Korteweg-de Vries equation and generalizations. II. existence of conservation laws and constants of motion[J]. Journal of Mathematical Physics, 1968, 9: 1204. DOI:10.1063/1.1664701 |
| [4] |
HIROTA R. An exact solution has been obtained for the Korteweg-de Vries equation for the case of multiple collisions of N solitons with different amplitudes[J]. Physical Review Letters, 1971, 27: 1192. DOI:10.1103/PhysRevLett.27.1192 |
| [5] |
王建勇, 程雪苹, 曾莹, 等. Korteweg-de Vries方程的准孤立子解及其在离子声波中的应用[J] . 物理学报, 2018, 67(11): 110201.
|
| [6] |
KUDRYASHOV N A. Traveling wave reduction of the modified KdV hierarchy: the lax pair and the first integrals[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 73: 472-480. DOI:10.1016/j.cnsns.2019.03.007 |
| [7] |
ZHANG G Q, YAN Z Y. Inverse scattering transforms and soliton solutions of focusing and defocusing nonlocal mKdV equations with non-zero boundary conditions[J]. Physica D:Nonlinear Phenomena, 2020, 402: 132170. DOI:10.1016/j.physd.2019.132170 |
| [8] |
PEREGRINE D H. Calculations of the development of an undularbore[J]. Journal of Fluid Mechanics, 1964, 25(2): 321-330. |
| [9] |
BENJAMIN T B, BONA J L, MAHONY J J. Model Equations for Long Waves in Nonlinear Dispersive Systems[J]. Philosophical Transactions of the Royal Society of London, 1972, 272(1220): 47-78. |
| [10] |
陈旭东, 朱仁庆, 杨帆, 等. 畸形波作用下浮体的载荷与响应研究新方法[J]. 舰船科学技术, 2018, 40(5): 8-14. DOI:10.3404/j.issn.1672-7649.2018.05.002 |
| [11] |
尤翔程, 李世远. 纳米颗粒球形度对倾斜通道中纳米流体反向混合对流传热的影响[J]. 石油科学通报, 2021, 6(4): 604-613. DOI:10.3969/j.issn.2096-1693.2021.04.042 |
| [12] |
ZABUSKY N J, KRUSKAL M D. Interaction of solitons in a collisionless plasma and the recurrence of initial states[J]. Physical Review Letters, 1965, 15: 240-243. |
| [13] |
GARDNER C S, GREENE J M, KRUSKAL M D, et al. Korteweg-de Vries equation and generalization VI. methods for exact solution[J]. Communications on Pure and Applied Mathematics, 1974, 27: 97-133. DOI:10.1002/cpa.3160270108 |
| [14] |
王明亮. BBM方程的孤立波解及其互相作用[J]. 兰州大学学报(自然科学版), 1993, 29(1): 7-13. |
| [15] |
韩海英, 那仁满都拉. KdV孤子与BBM孤子基本特性的比较研究[J]. 内蒙古民族大学学报(自然科学版), 2021, 36(1): 19-24. HAN H Y, Narenmandula. A comparative study of the basic properties of KdV and BBM solitons[J]. Journal of Inner Mongolia University for Nationalities, 2021, 36(1): 19-24. |
| [16] |
包立平, 李瑞翔, 吴立群. 一类KdV-Burgers方程的奇摄动解与孤子解[J]. 应用数学和力学, 2021, 42(9): 948-957. |
| [17] |
BONA J L, PRITCHARD W G, SCOTT L R. Solitary wave interaction[J]. Physics of Fluids, 1980, 23(3): 438-441. DOI:10.1063/1.863011 |
| [18] |
CAI J X, HONG Q, YANG B. Local structure-preserving methods for the generalized Rosenau-RLW-KdV equation with power law nonlinearity[J]. Chinese Physics B, 2017, 26(10): 100202. DOI:10.1088/1674-1056/26/10/100202 |
| [19] |
TAYLOR P H. A simple approach for shallow-water solitary wave interactions[C]//Proceedings of 20th Australasian Fluid Mechanics Conference (AFMC 2016). Perth, Australia, 2016: 1-4.
|
 2022, Vol. 44
2022, Vol. 44
