0 引　言

部分小型水下机器人通常选择以螺旋桨式推进器作为其动力源，其推力的大小直接影响水下机器人的水动性能。因此，如何精确预测水下推进器的推力是提高水下机器人水动性能的关键。水下推进器螺旋桨的静推力是指在水下机器人速度为零时，螺旋桨产生的最大推力。

国内外许多专家学者在原有工况图的基础上利用计算机软件进行螺旋桨的性能计算，实现了对螺旋桨敞水性能的分析计算。王超等^[1]对某型号螺旋桨的水动力性能进行试验测试，利用CFD模拟了该型号螺旋桨的推力系数、转矩系数及螺旋桨叶片表面压力分布，通过试验测试系数对仿真结果进行验证，证明CFD仿真具备可行性。CFD仿真可用作设计参考，但仿真过程繁琐，且需要第三方软件协助，不适应系统化集成计算。

神经网络在螺旋桨性能预测中的应用方兴未艾。孙群等^[2]利用人工神经网络技术，建立螺旋桨数值预测的修正方法，提高了螺旋桨敞水性能预测的精度，其训练数据来自实测数值，精度高的同时数据获取难度较大。翟鑫钰等^[3]基于神经网络的螺旋桨敞水性能预测方法，利用CFD仿真软件进行螺旋桨敞水性能数值计算，将计算数据作为神经网络训练、比对数据，数据来源难度降低，但神经网络规模较简单。基于此，建立一种RBF神经网络敞水性能估计器，对网络规模进行动调整，通过广义逆动态地调整各网络间的连接权重，进行网络参数的优化，构建一种高维优化的神经网络敞水性能估计器。为保证神经网络规模和训练精度，利用多组不同型号螺旋桨敞水性能的仿真数值进行训练，进而构造一种高维度的RBF神经网络敞水性能估计器。借助神经网络敞水性能估计器代替传统的螺旋桨敞水实验，以满足小规模螺旋桨敞水性能快速性、稳定性和准确性的要求。最后，通过螺旋桨CDF仿真值验证该RBF神经网络敞水性能估计器的准确性。

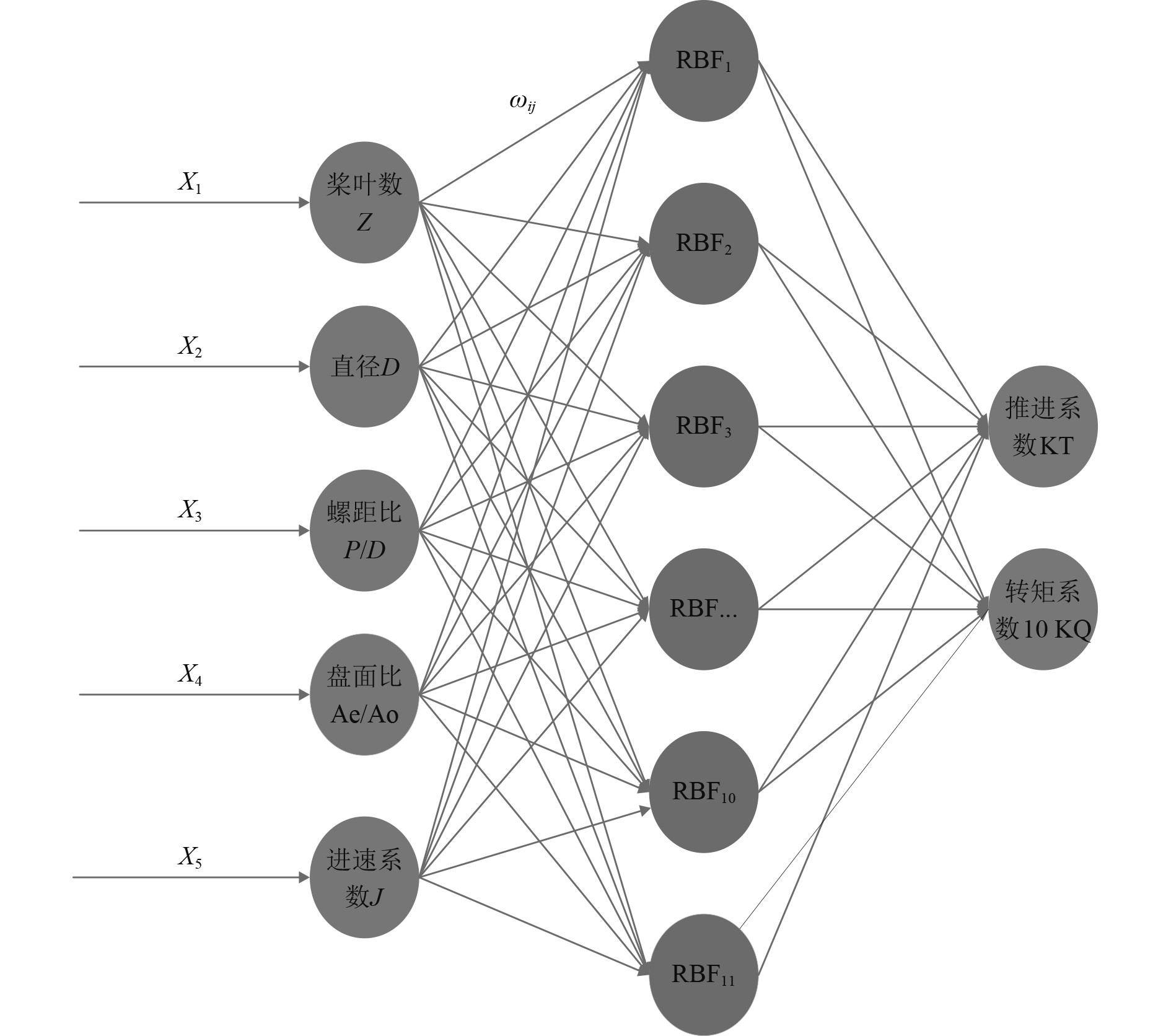
1 RBF神经网络螺旋桨敞水性能估计器模型 1.1 RBF神经网络螺旋桨敞水性能估计器模型的建立

RBF神经网络是一种前反馈式神经网络，主要包括输入层、隐藏层、及输出层3层网格结构^[4]。RBF径向基神经网络的隐节点之间采用中心向量与输入模式之间的距离来作为函数的自变量，并快速使用径向基函数作为一个激活函数。接着对网络规模进行调整，广义逆动态地调整各网络间的连接权重，进行网络参数的优化，进而构建一种高维优化的神经网络估计器，最终达到输出敞水能参数误差小于预先设置的学习精度，或者在达到预先设定的学习次数时，停止整个神经网络的学习训练过程，神经网络结构示意图如图1所示。

影响RBF神经网络螺旋桨敞水性能估计器的因素较多，且各因素之间的影响是相互关联，所以拟合螺旋桨基本参数和RBF神经网络螺旋桨估计器的函数关系较为复杂，故根据工程实践经验，选择螺旋桨的桨叶数Z，螺旋桨直径D，螺距比P/D、盘面比Ae/Ao和进速系数J作为RBF神经网络螺旋桨估计器模型的输入参数^[5-7]。输出层为螺旋桨的推进系数KT和转矩系数10 KQ。确定RBF神经网络螺旋桨估计器输入和输出之后，需要构建网络规模，隐含层取11个节点数，然后对网络规模进行调整，广义逆动态地调整各网络间的连接权重，进行网络参数的优化。具体步骤如下：

1）构建隐含层神经元宽度

进行初始化处理，并保持在迭代过程中不变。

$ {\delta _j} = {\delta _{\min }} + \left( {{\delta _{\max }} - {\delta _{\min }}} \right) \bullet rand\left( {} \right)\;\;j = 1,2, \cdots , \cup , $

(1)

式中： $ {\delta _j} \in \Re $ 表示隐含层第 $j$ 个 ${\rm{RBF}}$ 单元的宽度； $ {\delta _{\min }} $ 和 $ {\delta _{\max }} $ 分别为预定义的宽度的最小值和最大值。

令 ${\boldsymbol{X}} = {\left( {x_1^{\rm{T}},x_2^{\rm{T}}, \cdots ,x_M^{\rm{T}}} \right)^{\rm{T}}} \in {\Re ^{M \times n}}$ 表示训练集的输入集， ${{\boldsymbol{x}}_q} = {\left( {{x_{q1}},{x_{q2}}, \cdots ,{x_{qn}}} \right)^{\rm{T}}} \in {\Re ^{1 \times n}}$ 为输入级的第q个输入样本，M为训练集样本规模；令 $Y \in {\Re ^{M \times 1}}$ 为训练集的期望输出，建立RBF神经网络螺旋桨估计器：

2）构成RBF单元

通过式(2)计算网络规模 $ k_{sise}^i $ ，并从 $ {a_i} $ 中取出前 $ k_{sise}^i $ 的RBF单元的中心向量，即从 $ {a_i} $ 中选择出 $\ \mu _1^i,\mu _2^i, \cdots , $ $ \ \mu _{k_{sise}^i}^i$ ；从宽度向量 $ \delta $ 中选择其前 $ k_{sise}^i $ 与步骤1中选择出来的中心进行一一匹配构成 $ k_{sise}^i $ 个RBF单元：

3）计算输入层X下隐含层的输入H

$ {\phi _j}\left( x \right) = \exp \left( { - \dfrac{{\parallel x - {\mu _j}{\parallel ^2}}}{{2\delta _j^2}}} \right),j = 1,2, \cdots ,k_{sise}^i，$

(2)

$ H = {\left( {\begin{array}{*{20}{c}} {{\phi _{11}}}& \ldots &{{\phi _{1M}}} \\ \vdots & \ddots & \vdots \\ {\phi k{{_{sise}^i}_1}}& \cdots &{{\phi _{k_{sise}^iM}}} \end{array}} \right)^{\rm{T}}}，$

(3)

$ \begin{gathered} {\phi _{jq}} = \exp \left( { - \dfrac{{\parallel {x_q} - \mu _j^i{\parallel ^2}}}{{2\delta _j^2}}} \right),q = 1,2, \cdots ，\hfill \\ M\;and\;j = 1,2, \cdots ,k_{sise}^i。\hfill \\ \end{gathered} $

(4)

4）广义逆计算出各网格之间的连接权重 $ {W_i} $

$ {{\boldsymbol{H}}^ + } = {\left( {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}} + \lambda I} \right)^{ - 1}}{{\boldsymbol{H}}^{\rm{T}}}，$

$ {W_i} = {{\boldsymbol{H}}^ + }Y。$

综上所述，构建一种高维优化的神经网络估计器，设定RBF神经网络螺旋桨敞水性能估计器的网络学习速率为0.6，迭代次数上限设置为10000，学习精度设置为0.01。最终达到输出敞水性数误差小于预先设置的学习精度，或者在达到预先设定的学习次数时，停止整个神经网络的学习训练过程。

1.2 RBF神经网络训练

为提高RBF神经网络螺旋桨估计器模型的精确性，需要代大量的样本进行学习，学习样本要正确地反映神经网络输入和输出层之间的关系，利用多组螺旋桨仿真数据作为训练样本，见表1。

1.3 RBF神经网络螺旋桨敞水性能估计器模型训练结果

将150组样本代入神经网络进行训练，得到RBF神经网络螺旋桨敞水性能估计器模型。所用到的螺旋桨参数见表2，代入RBF神经网络螺旋桨敞水性能估计器模型，得到这种特殊型号螺旋桨的敞水系数，如图2所示。

2 螺旋桨CFD敞水性能仿真计算 2.1 构造螺旋桨几何模型

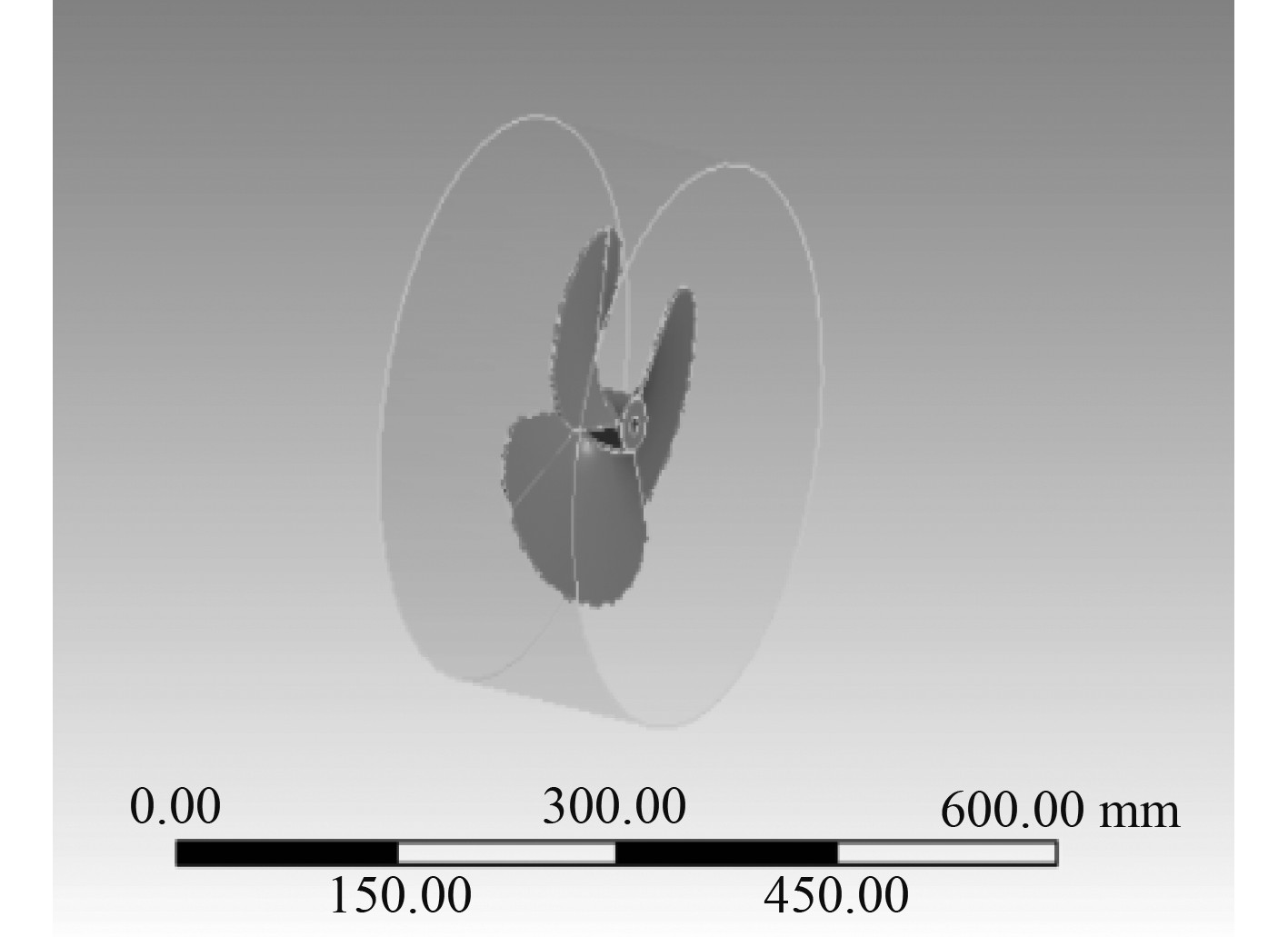
采用Pro/Engineer软件构造螺旋桨三维模型，将三维模型导入软件中，利用建模功能完成螺旋桨的桨毂和导管的三维几何建模，最后利用布尔运算功能将叶片、浆毂以及导管的合并，从而形成导管螺旋经的三维模型，如图3所示。

2.2 控制方程

1）连续性方程

水下推进器系统必须满足基本定律—质量守恒定律。对于推进器系统，概括上述定律如下：单位时间内流体微元体中增加的质量，等于同一时间间隔内流入该微元体的净质量^[8]。

2）动量守恒方程

对于整个水下推进器系统，在考虑流体粘性的基础上，为了简化模型，便于计算，将其视为是粘度系数恒定的牛顿流体，主要做层流流动，但伴随瞬时的湍流运动，水下推进器系统的动量守恒方程见下式^[9]：

$ \left\{ {\begin{array}{*{20}{c}} {\rho \dfrac{{{\rm{d}}u}}{{{\rm{d}}t}} = \rho {f_x} - \dfrac{{\partial p}}{{\partial x}} + \mu {\nabla ^2}u}，\\ {\rho \dfrac{{{\rm{d}}v}}{{{\rm{d}}t}} = \rho {f_y} - \dfrac{{\partial p}}{{\partial y}} + \mu {\nabla ^2}v} ，\\ {\rho \dfrac{{{\rm{d}}w}}{{{\rm{d}}t}} = \rho {f_z} - \dfrac{{\partial p}}{{\partial z}} + \mu {\nabla ^2}w} 。\end{array}} \right. $

(5)

式中： $f$ 控制体的质量力；P表示控制体的表面压力； $u$ 表示流体的动力粘度。

2.3 建立计算域

螺旋桨敞水性能计算基本假设是将螺旋桨放置在无限大的浅水流域，为模拟这一流场并且为了减少边界的影响，建立一个旋转域和一个静止域，如图4所示。静止域长度为10L，直径为6D，旋转域直径为D，长度为L。螺旋桨桨轴中心位于离入口4L、离出口5L的圆面圆心处^[10]。

2.4 网格划分

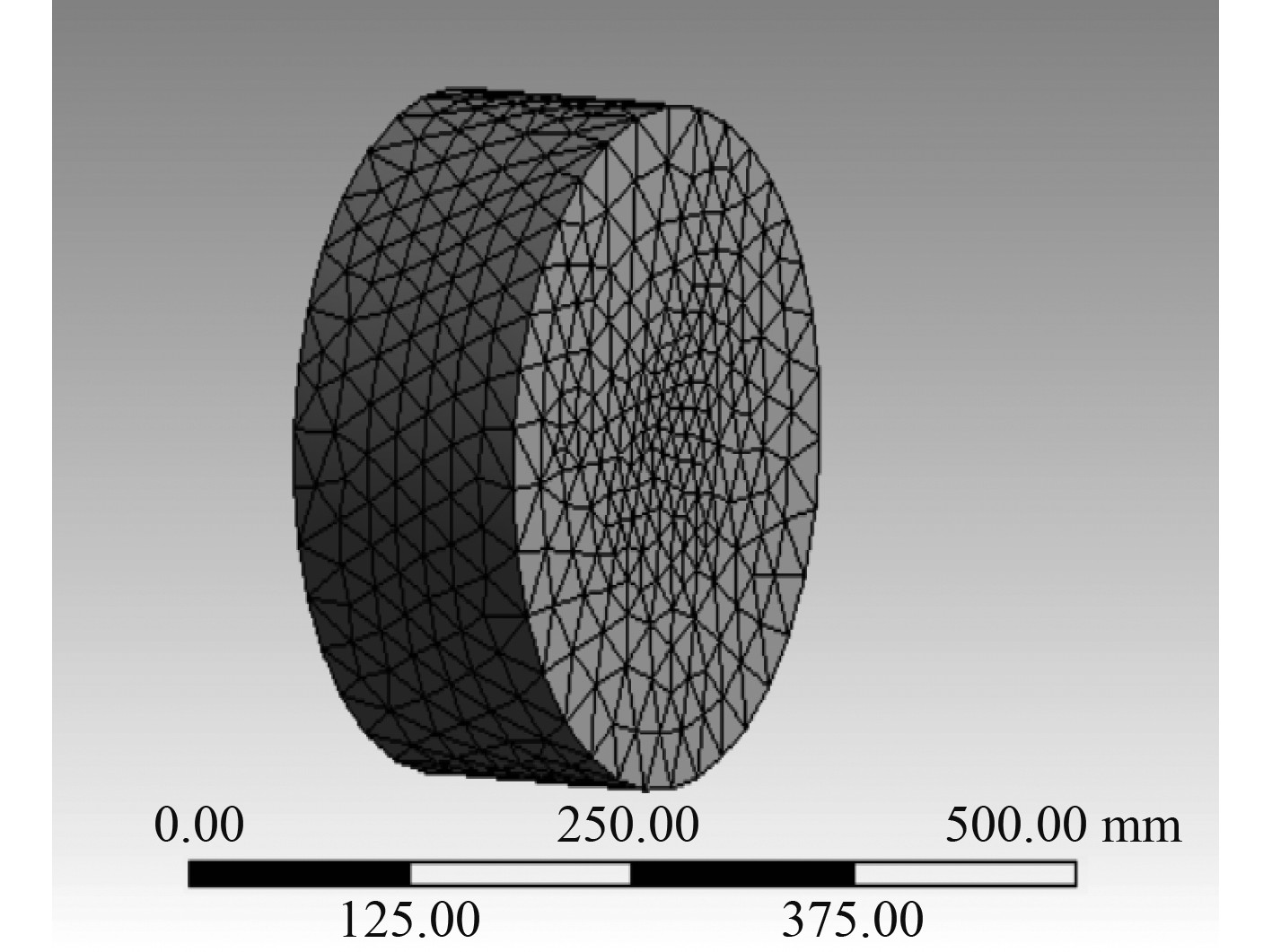
利用Fluent进行自由网格划分处理，然后对螺旋桨桨叶及桨毂进行加密处理。在网格类型上，在螺旋桨的周围区域设置为Tet/Hybrid单元TGrid类型，除此之外，利用Cooper生成体网格。这样设置计算域好处是在螺旋桨复杂的外形周围形成非结构网格，在离桨较远的区域生成结构网格，网格质量可以得到有效的保证，计算较容易收敛。生成的螺旋桨网格和计算域网格如图5和图6所示。

2.5 设置边界条件

进口边界条件为入口速度，入口速度动态变化，与进速系数有关，进速系数取0.1～1.0（间隔0.1）^[11]。转速n取1 600 r/min。周期边界条件选择旋转，设置迭代次数为1000。

$ {V_A} = JnD $

(6)

2.6 计算结果验证

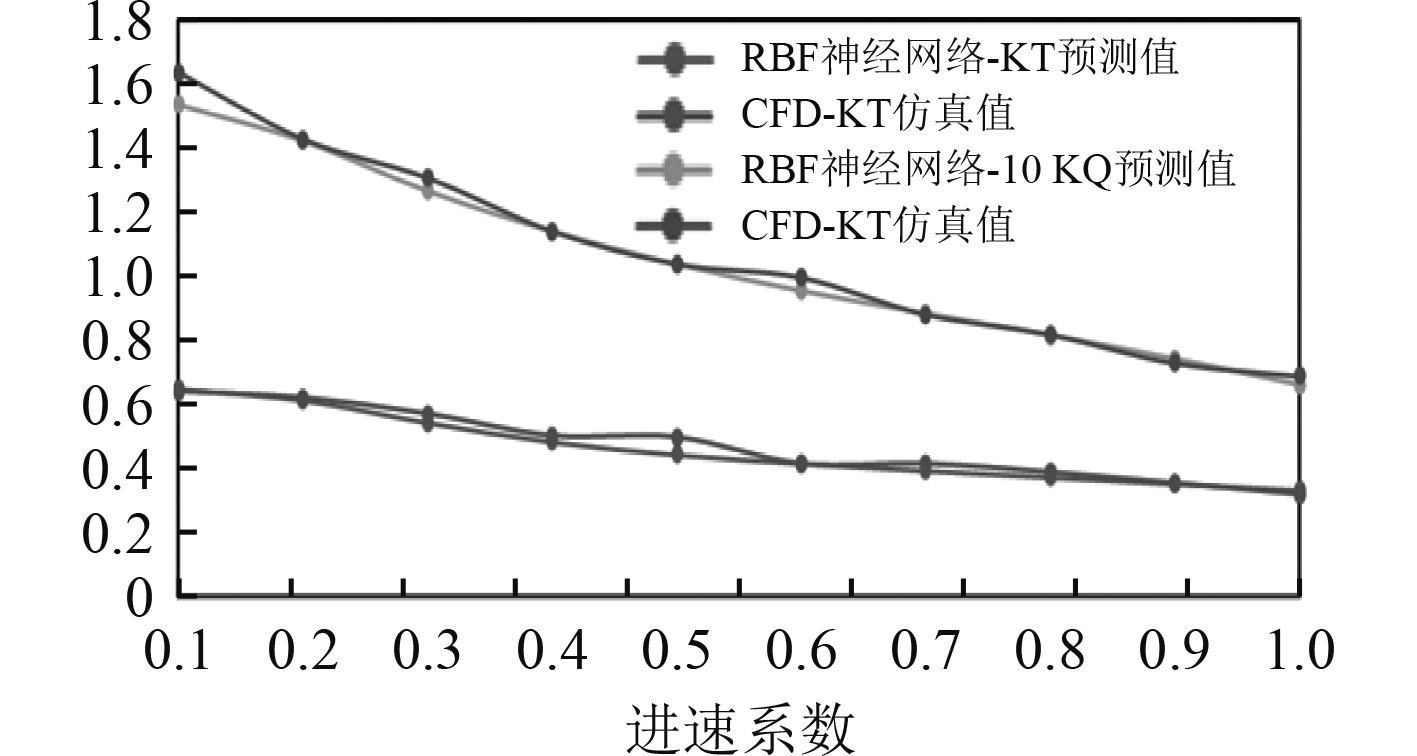
通过CDF仿真软件和利用神经网络得到的螺旋桨推力系数 $K_T$ 和扭矩系数 $10 K_Q$ 。如图7所示，神经网络估计器预测螺旋桨敞水性能系数与CFD仿真结果一致较高，最大相对误差为1.57%，相对误差较小。因此，可以利用RBF神经网络估计器模型对螺旋桨敞水性能进行快速、准确的预测。

3 结　语

构建一种高维优化的RBF神经网络螺旋桨敞水性能估计器，利用多组不同型号的螺旋桨仿真值进行网络训练，通过广义逆动态地调整各网络间的连接权重，进行网络参数的优化，进而对网络规模进行调整，提高了模型精度。该模型预测的同系列螺旋桨参数对应结果与CDF仿真数据对比显示，两者差距较小，误差范围在1.57%范围以内，基于此证明：

高维优化的BDF神经网络螺旋桨敞水性能预测模型能够作为螺旋桨敞水系数的有效预测方式之一，满足集成设计的系统集成以及快速性和准确性的需求。