2. 海军研究院, 北京 100161
2. Naval Research Academy, Beijing 100161, China
目前,对于舰艇舱室结构毁伤效果的研究多集中在装药舱内静止爆炸的情况[1-5]。但在实际情况下,由于舰艇舱室结构多以薄壁板为主,反舰导弹战斗部在侵彻舰艇外板的过程中,速度损耗较小,进入舱室内部后仍有较大的剩余速度,这就导致其内装炸药多在运动状态下爆炸。已有相关研究表明,受装药运动速度的影响,舱内动爆冲击波场的分布特性相较于静爆有较大改变[6]。随着高速、超高速反舰武器的不断发展,高速运动的战斗部舱内爆炸毁伤效果越来越受重视。杜红棉等[7]基于火箭撬试验方法设计进行了导弹动爆情况下对模拟舱室毁伤效果的试验,认为导弹运动正向的反射冲击波超压可达到运动负向反射冲击波的3.5倍。邢存震等[8]基于实弹打靶试验,发现动爆冲击波在舱室结构内存在有明显的“前冲”效应。徐维铮等[9]基于瞬时爆轰假定,对比分析了静止装药和运动装药舱内爆炸载荷特性,认为静止装药在舱内爆炸压力场沿舱室长度方向呈对称分布,装药动爆时的运动速度会破坏这种对称性,导致舱内动爆载荷表现出明显的方向性。对动爆载荷作用下舱室结构毁伤效果开展研究,可更加贴近于真实的毁伤状态,同时也是弹药设计和使用者更加关心的问题。
本研究利用有限元计算软件Autodyn对不同运动速度的球形裸装TNT在典型舱室结构内爆炸过程进行模拟,分析了不同装药当量和装药运动速度对典型舱室结构的不对称毁伤特性,总结出舱室结构在动爆载荷作用下的5种不对称破坏模式。在此基础上,采用量纲分析的方法,推导并给出了动爆载荷作用下舱室结构不对称毁伤模式的无量纲数及各破坏模式的对应区间,实现了舱室结构在动爆载荷下毁伤效果的快速预测及评估。本文研究结论可为舱室结构毁伤效果评估及防抗爆结构设计提供参考和依据。
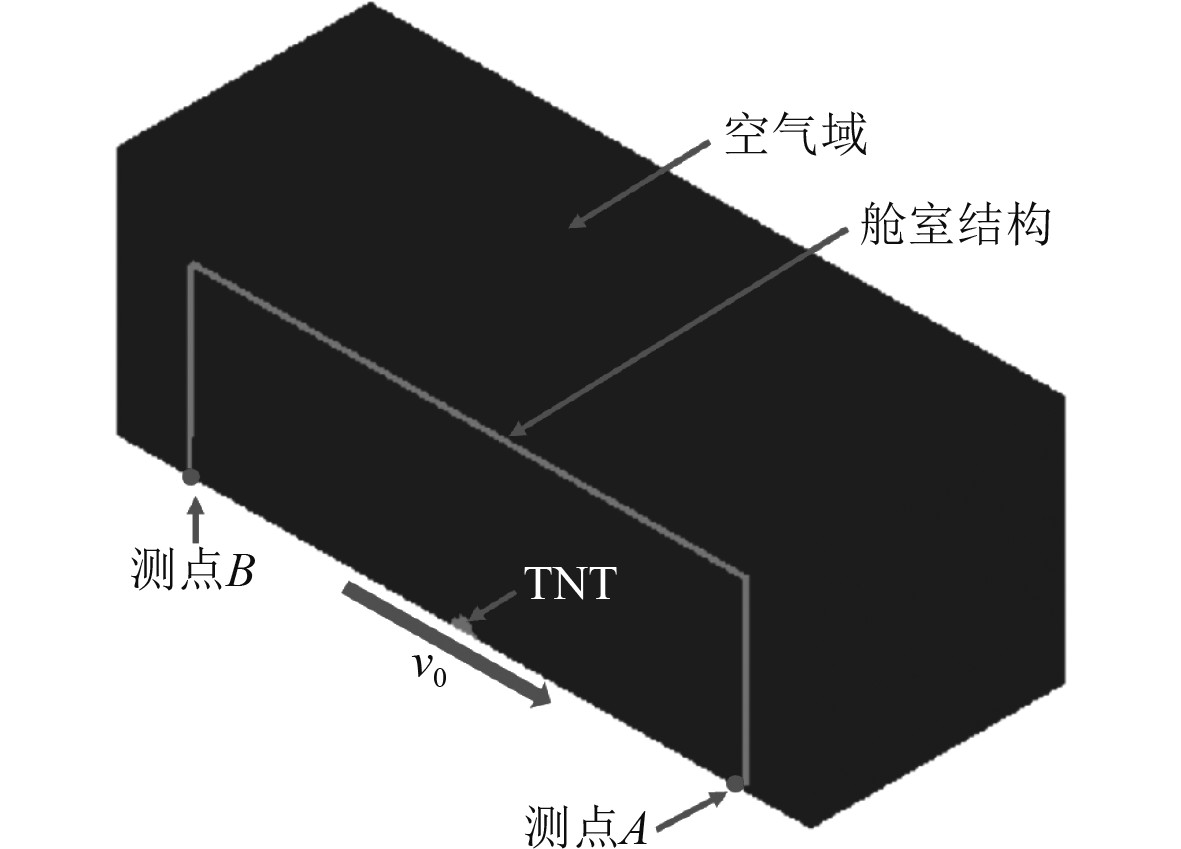
1 数值仿真模型的建立 1.1 有限元模型主要分析装药当量和装药运动速度对典型舱室结构的毁伤效果,因此采用单一舱室模型,其特征尺寸为2.4 m×2.4 m×3.6 m,舱壁厚度为4 mm,材料为Q235B型钢,不设置加强结构。装药当量取用范围为5−50 kg,装药运动速度为v0=0~400 m/s,速度梯度为100 m/s。为提高计算效率,建立1/4对称模型进行简化计算,观察点位置如图1所示。空气域网格尺寸为装药半径的1/5,舱室结构网格尺寸为30 mm。
|
图 1 装药舱内动爆数值仿真计算模型 Fig. 1 Numerical simulation model of dynamic explosion in charge chamber |
由于舱壁厚度远小于舱壁结构尺寸,故舱壁结构选用4节点壳单元,采用Lagrange方程进行描述。空气和炸药均选用8节点体单元,采用多物质Euler进行描述。空气域尺寸足以保证舱室结构在舱内动爆载荷作用下发生大变形或破损后仍完全浸没其中。舱室结构边界位置施加固支约束,以模拟舱室结构的约束情况。空气域外围设置Flow_out边界条件,以模拟无限空气域内舱室结构破损后舱内压力的泻处情况。
1.2 材料模型与参数该仿真计算中,舱室结构材料为Q235B型钢,采用Johnson-Cook状态方程来描述爆炸载荷作用下舱室结构的变形情况,状态方程如下:
| $ \sigma {\text{ = }}\left( {A + B{\varepsilon _p}^n} \right)\left( {1 + C\ln \varepsilon _p^*} \right)\left( {1 - T_H^m} \right)。$ | (1) |
式中:σ为等效应力;εp为有效塑性应变;εp*为标准有效塑性应变率;A,B,n,C,m为材料相关的试验参数;TH=(T-Tr)/(Tm-Tr),Tr为参考温度,Tm为材料熔点温度。具体参数如表1所示。
|
|
表 1 Q235B型钢Johnson-Cook状态方程参数 Tab.1 Johnson-Cook equation of state parameters of Q235B section steel |
空气一般视为理想气体,采用Ideal Gas状态方程,能够准确反应实际气体的物理行为,状态方程如下:
| $ P = \left( {\gamma - 1} \right)\rho e。$ | (2) |
式中:P为压强;γ为绝热指数;ρ为空气密度;e为空气内能。具体参数如表2所示。
|
|
表 2 空气Ideal Gas状态方程参数 Tab.2 Air ideal gas equation of state parameters |
TNT采用JWL状态方程来描述炸药爆轰过程中所产生气体的急剧扩张过程,状态方程如下:
| $ P = A\left( {1 - \frac{\omega }{{{R_1}v}}} \right){e^{ - {R_1}v}} + B\left( {1 - \frac{\omega }{{{R_2}v}}} \right){e^{ - {R_2}v}} + \frac{{\omega e}}{v}。$ | (3) |
式中:A,B,R1,R2,ω为试验拟合参数;e为单位体积爆轰产物的内能;v为爆轰产物的相对比容,且v=ρ0/ρt;ρ0为炸药初始密度;ρt为爆轰后到某一时刻的密度。具体参数如表3所示。
|
|
表 3 TNT JWL状态方程参数 Tab.3 TNT JWL equation of state parameters |
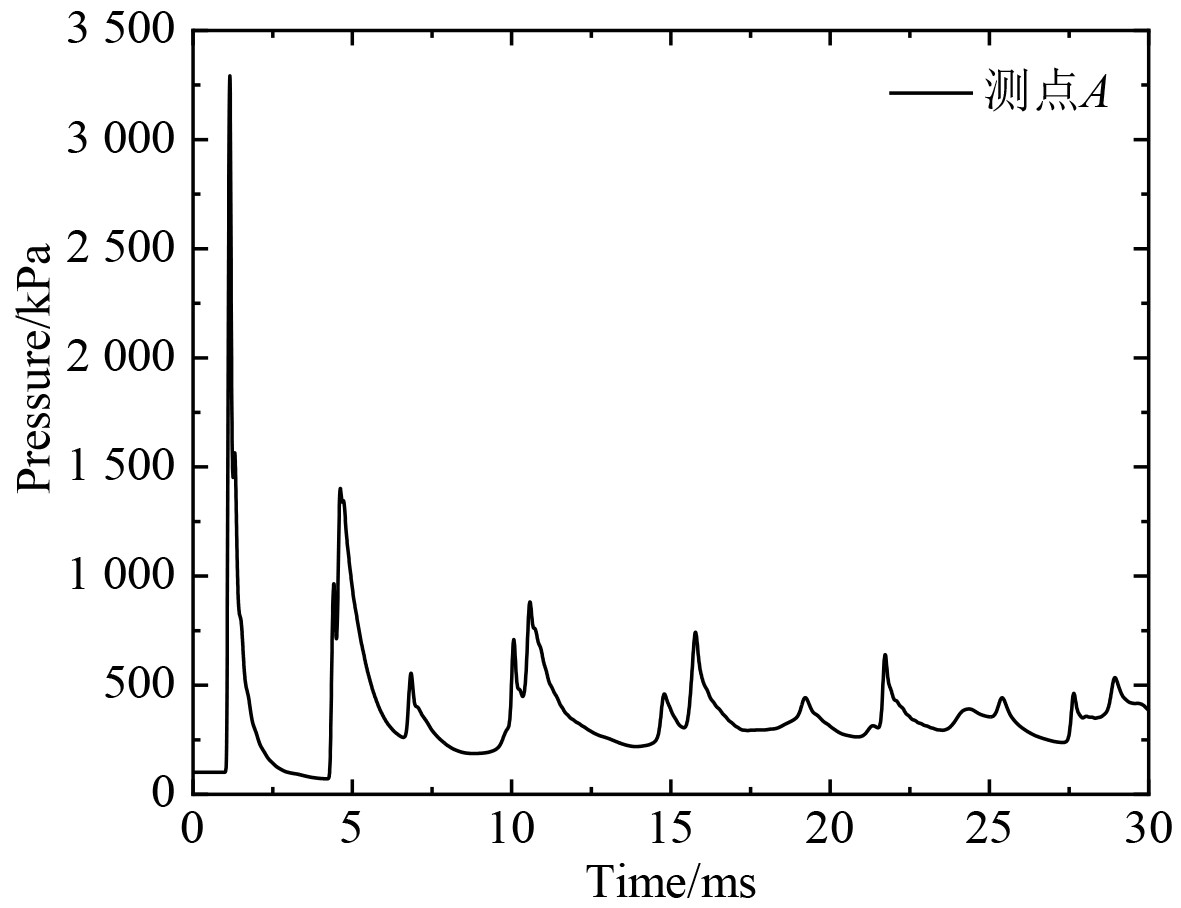
利用5kg TNT球形裸装炸药舱内静爆工况对仿真计算的准确性进行验证,图2为测点A位置处的反射超压时程曲线。
|
图 2 5kg TNT舱内静爆时测点A处反射超压时程曲线 Fig. 2 Time history curve of reflection overpressure at measuring point A during static explosion in 5kg TNT chamber |
由图2可知,A位置处的首次反射冲击超压峰值为3292.11 kPa。由于测点A位置为舱壁中心,舱内爆炸入射超压在此位置发生正反射,故可由静爆冲击波计算公式及正反射计算公式对此位置处的首次反射冲击波超压进行求解[10],即
| $ \Delta {P_m}\left\{ {\begin{array}{*{20}{c}} {\dfrac{{1.40717}}{Z} + \dfrac{{0.55397}}{{{Z^2}}} -}\\ {\dfrac{{0.03572}}{{{Z^3}}} + \dfrac{{0.000625}}{{{Z^4}}}},&{0.05 \leqslant Z \leqslant 0.3},\\ {\dfrac{{0.61938}}{Z} - \dfrac{{0.03262}}{{{Z^2}}} + \dfrac{{0.21324}}{{{Z^3}}}},&{0.3 \leqslant Z \leqslant 1.0},\\ {\dfrac{{0.0662}}{Z} + \dfrac{{0.405}}{{{Z^2}}} + \dfrac{{0.3288}}{{{Z^3}}}},&{1.0 \leqslant Z \leqslant 10} 。\end{array}} \right. $ | (4) |
| $ \Delta {P_f} = 2\Delta {P_m} + \frac{{\left( {\gamma + 1} \right)\Delta {P_m}^2}}{{\left( {\gamma - 1} \right)\Delta {P_m} + 2\gamma {P_0}}}。$ | (5) |
式中:∆Pm为静爆冲击波超压;Z为比例距离,且Z=R·W−1/3,R为爆距,W为装药当量;∆Pf为反射冲击波超压;P0为大气压力,一般取101.33 kPa;γ为空气绝热指数。
基于式(4)和式(5),求得该位置处的正反射冲击波超压为3552.86 kPa,与仿真结果的相对误差为7.34%,该误差在可接受范围内,可认为该仿真计算模型准确可靠。
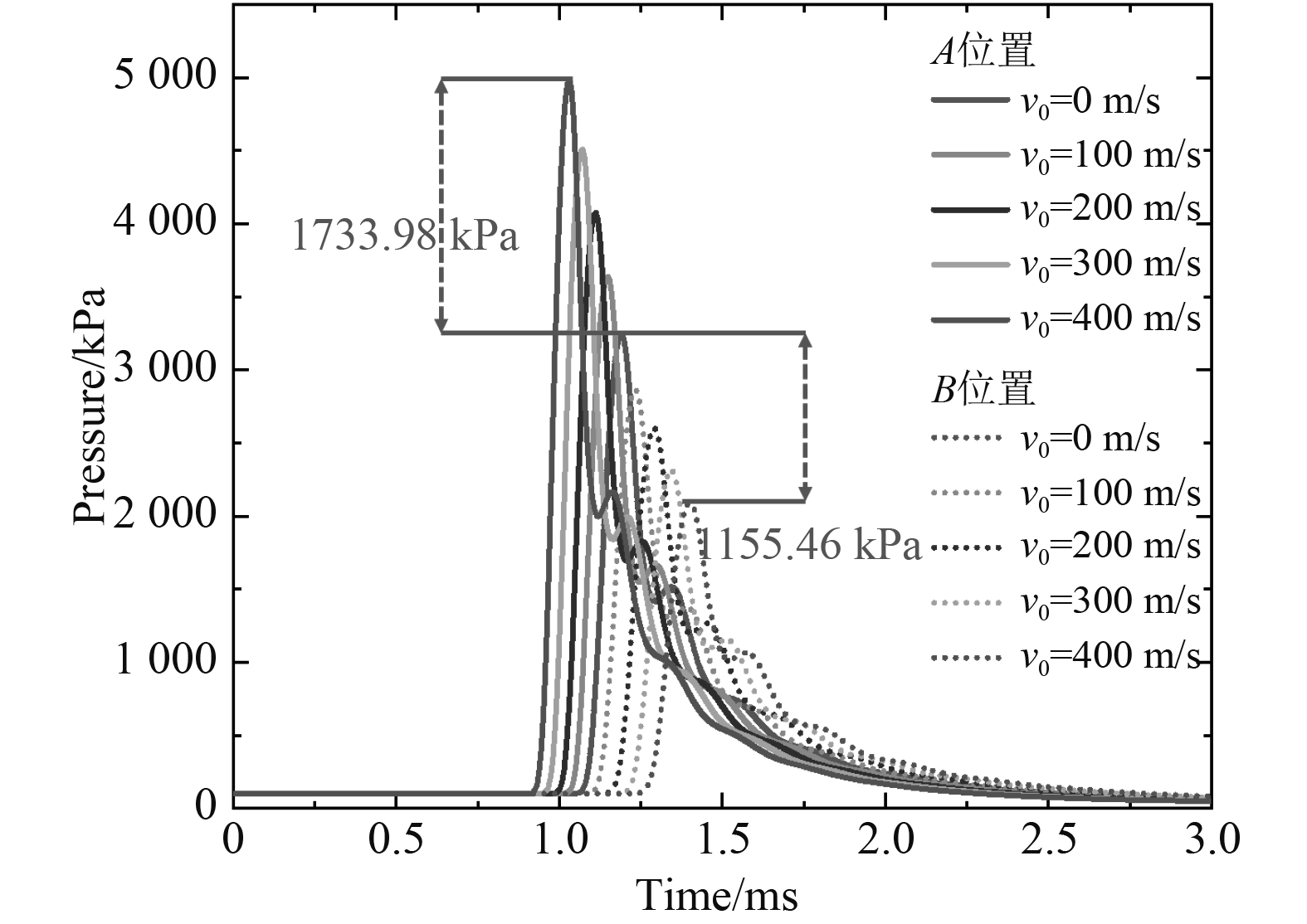
2 舱室毁伤效果研究 2.1 动爆载荷特性分析以5kg TNT球形裸装炸药为例,当装药以不同运动速度舱内动爆时,正、负向舱壁中心位置反射冲击波超压时程曲线如图3所示。为更清晰表示装药运动速度对正、负向舱壁中心位置正反射冲击波超压的影响情况,此处仅展示首次反射超压。
|
图 3 装药各运动速度下舱内爆炸时A,B位置处正反射超压 Fig. 3 Charge chamber exploded under the speed of A and B location is reflection overpressure |
由图3可知,当装药舱内静止状态下爆炸时,A,B位置处的正反射超压峰值及到达时刻一致,表现出了较好的一致性和对称性。当装药由静止提速至400 m/s时,装药运动正向舱壁的正反射超压峰值提升了1733.98 kPa,相较于静爆提升了53.39%;装药运动负向舱壁的正反射超压降低了1155.46 kPa,相较于静爆削弱了35.58%。整体来看,随着装药运动速度的增加,装药运动正向舱壁的正反射超压峰值不断提高,且超压峰值到达时刻不断提前;装药运动负向舱壁的正反射超压峰值不断减弱,且超压峰值的到达时刻不断延迟。相较于装药静爆时正、负向舱壁正反射超压的对称性,动爆超压表现出了明确的方向性,即装药运动速度会对装药运动正向载荷有所增幅、对装药运动负向载荷有所削弱。
2.2 舱壁破坏模式分析舱壁为舱室结构的基础组成部分,在本文舱室结构中,存在有2种尺寸的舱壁。分别为2.4 m×2.4 m的正方形舱壁(装药运动正、负向舱壁)和2.4 m×3.6 m的长方形舱壁(装药运动周向舱壁)。经大量仿真工况计算结果分析,装药运动周向舱壁,即长方形舱壁的毁伤效果对装药运动速度的响应较为迟钝,在各装药运动速度下的毁伤效果与静爆下的毁伤效果无明显差异;而装药运动正、负向舱壁,即正方形舱壁的毁伤效果对装药运动速度较为敏感,装药运动正向舱壁的毁伤效果会随着装药运动速度的增加而提升,装药运动负向舱壁的毁伤效果会随着装药运动速度的增加而削弱。由此可认为,动爆载荷作用下,舱室结构的不对称毁伤效果主要体现在装药运动正、负向舱壁上。
整体来看,由于舱室结构的对称性,装药运动正、负向舱壁在动爆载荷的作用下,均呈现出3种破坏模式,表4给出了舱壁的破坏模式、破坏特征及表现形式。
|
|
表 4 装药运动正、负向舱壁破坏模式及表现形式 Tab.4 The failure modes and manifestations of positive and negative bulkheads in charge movement |
装药运动正、负向舱壁虽存在有相同的破坏模式,但受装药运动速度的影响,正负向舱壁的受载情况及破坏程度并不相同,这就导致动爆载荷作用下,舱室结构的毁伤效果具有不对称性的特点。
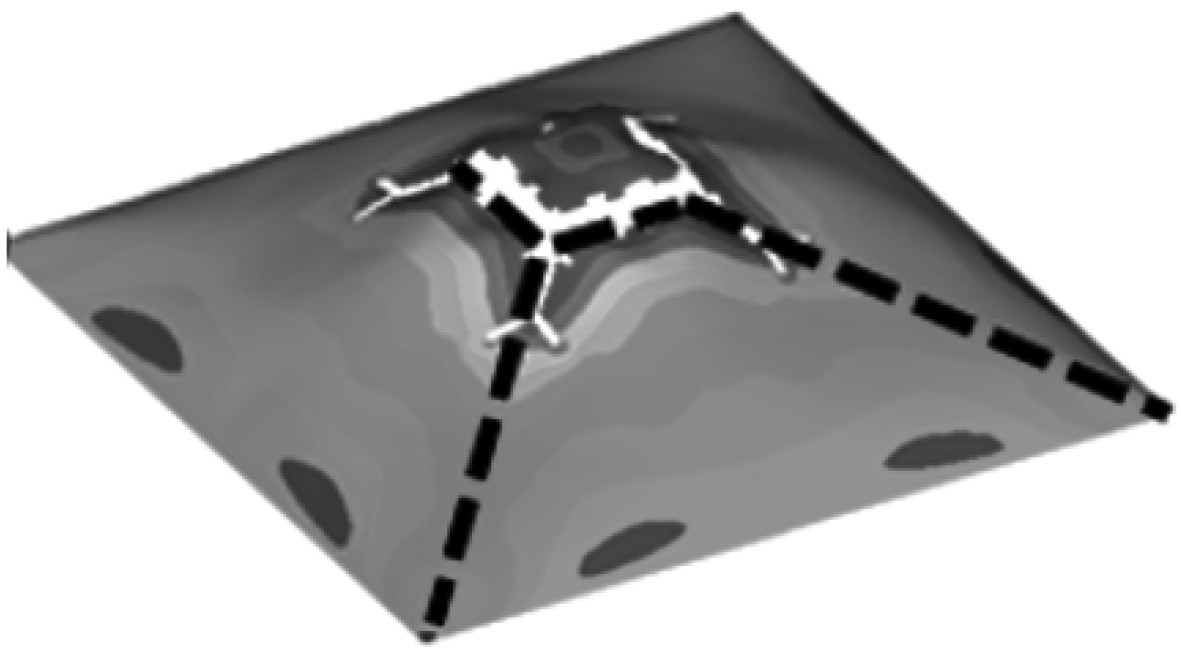
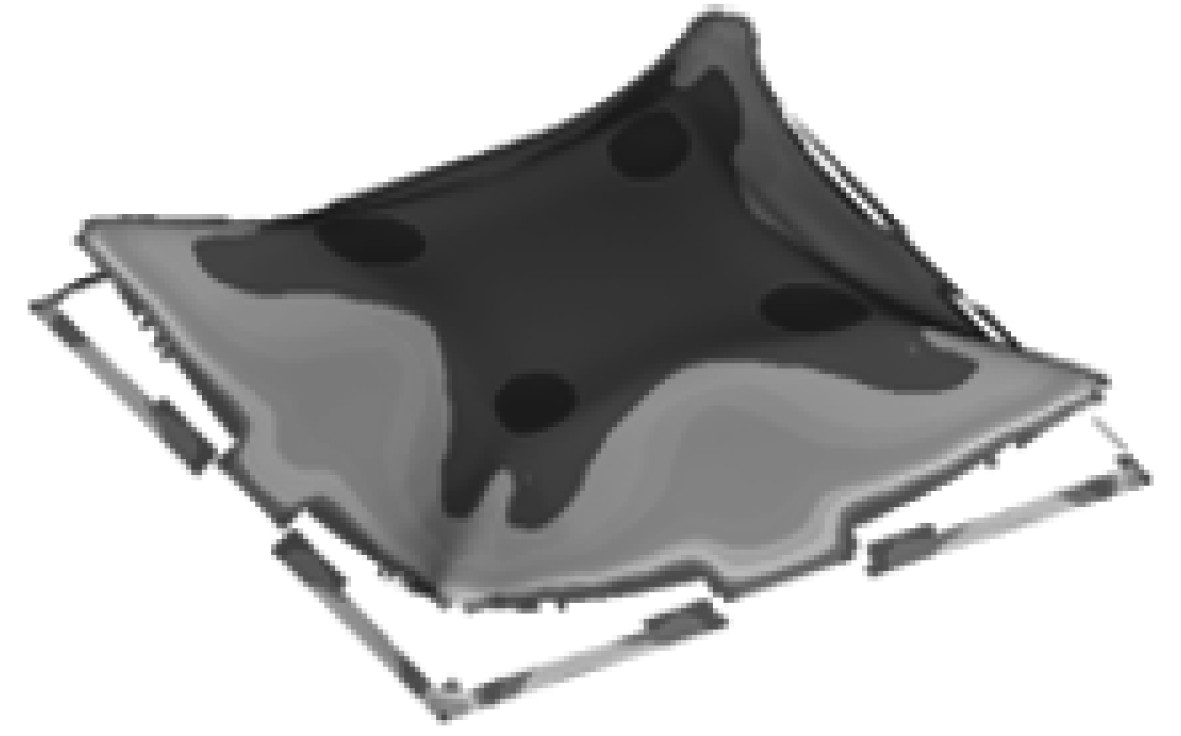
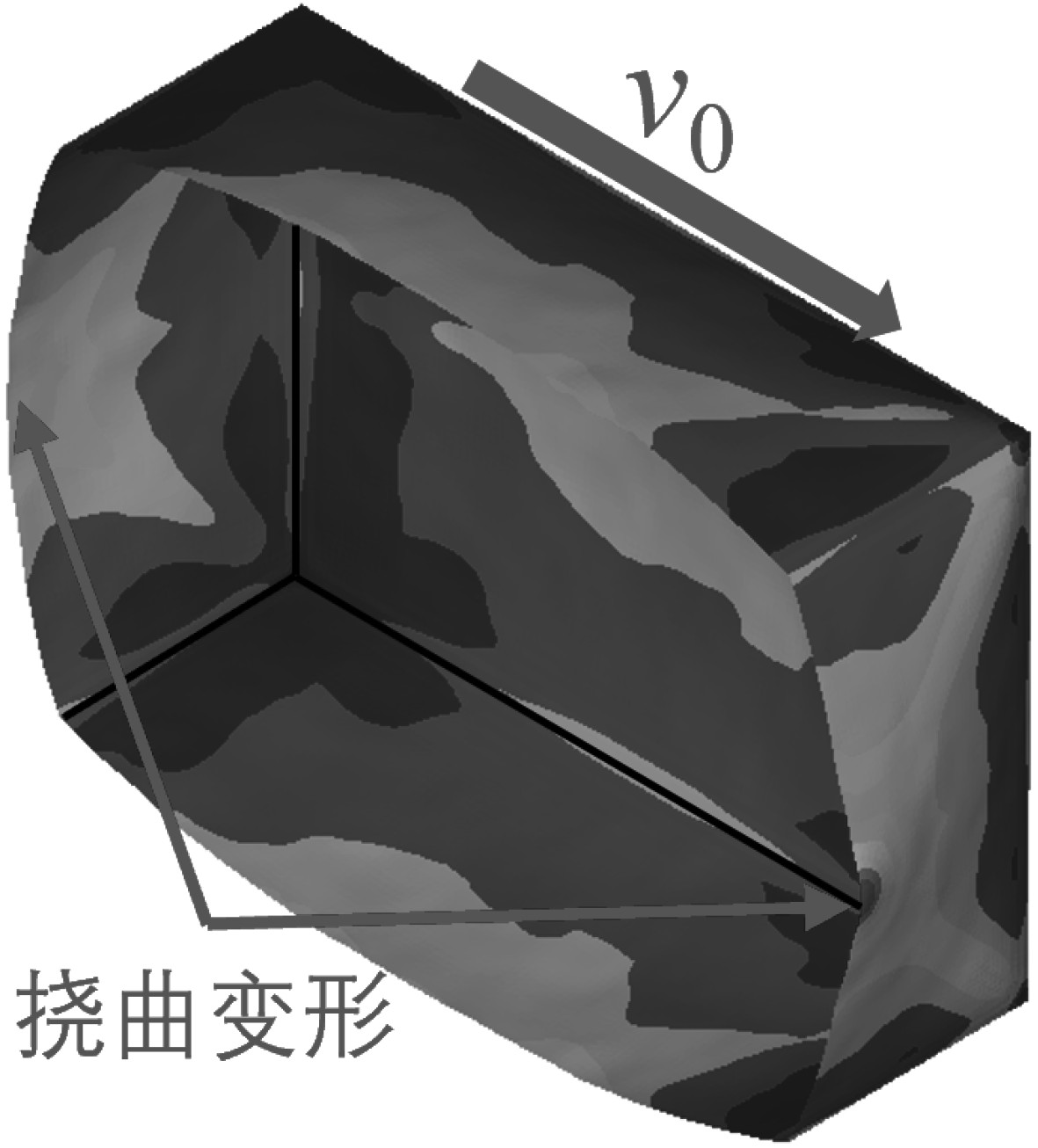
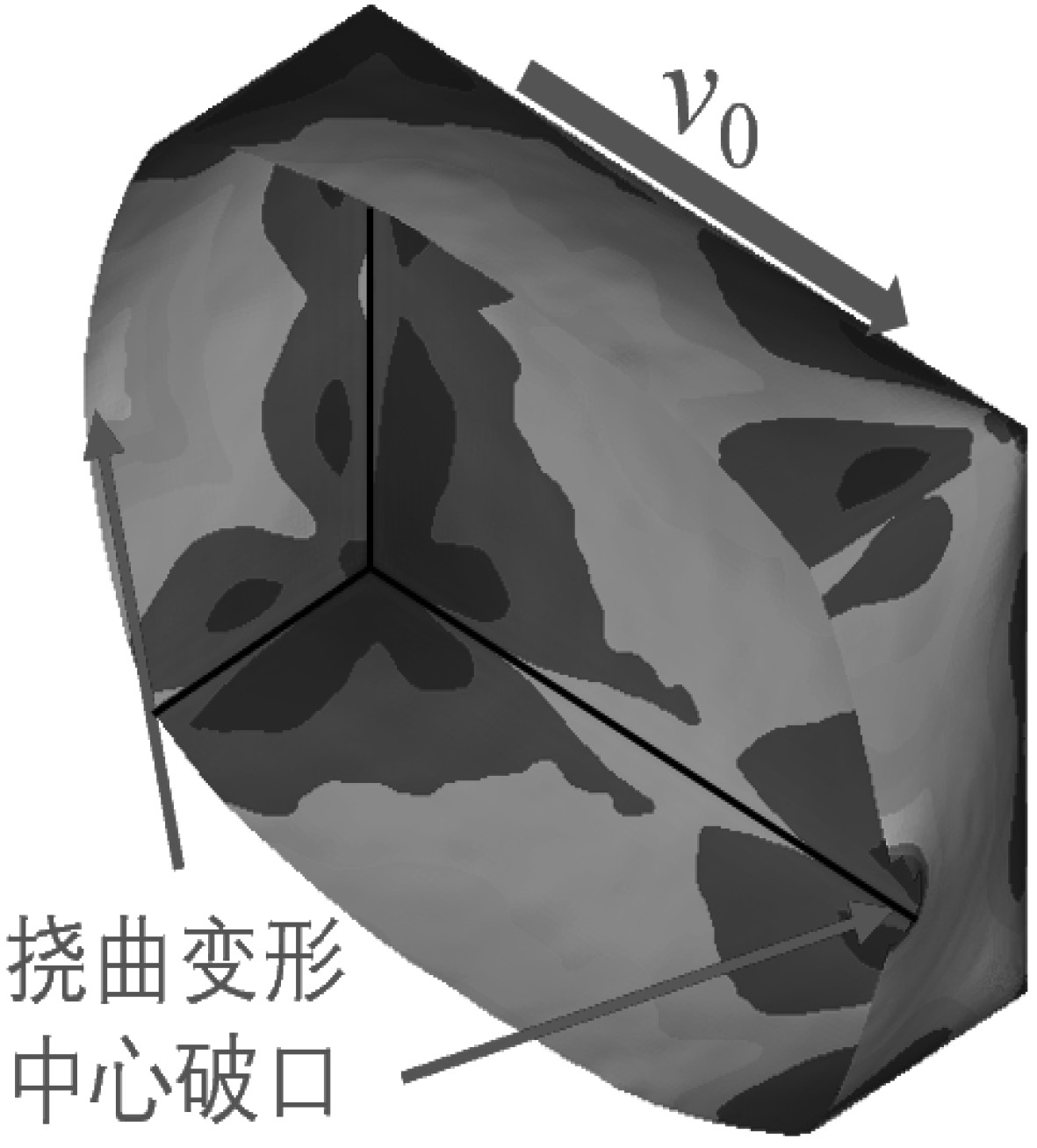
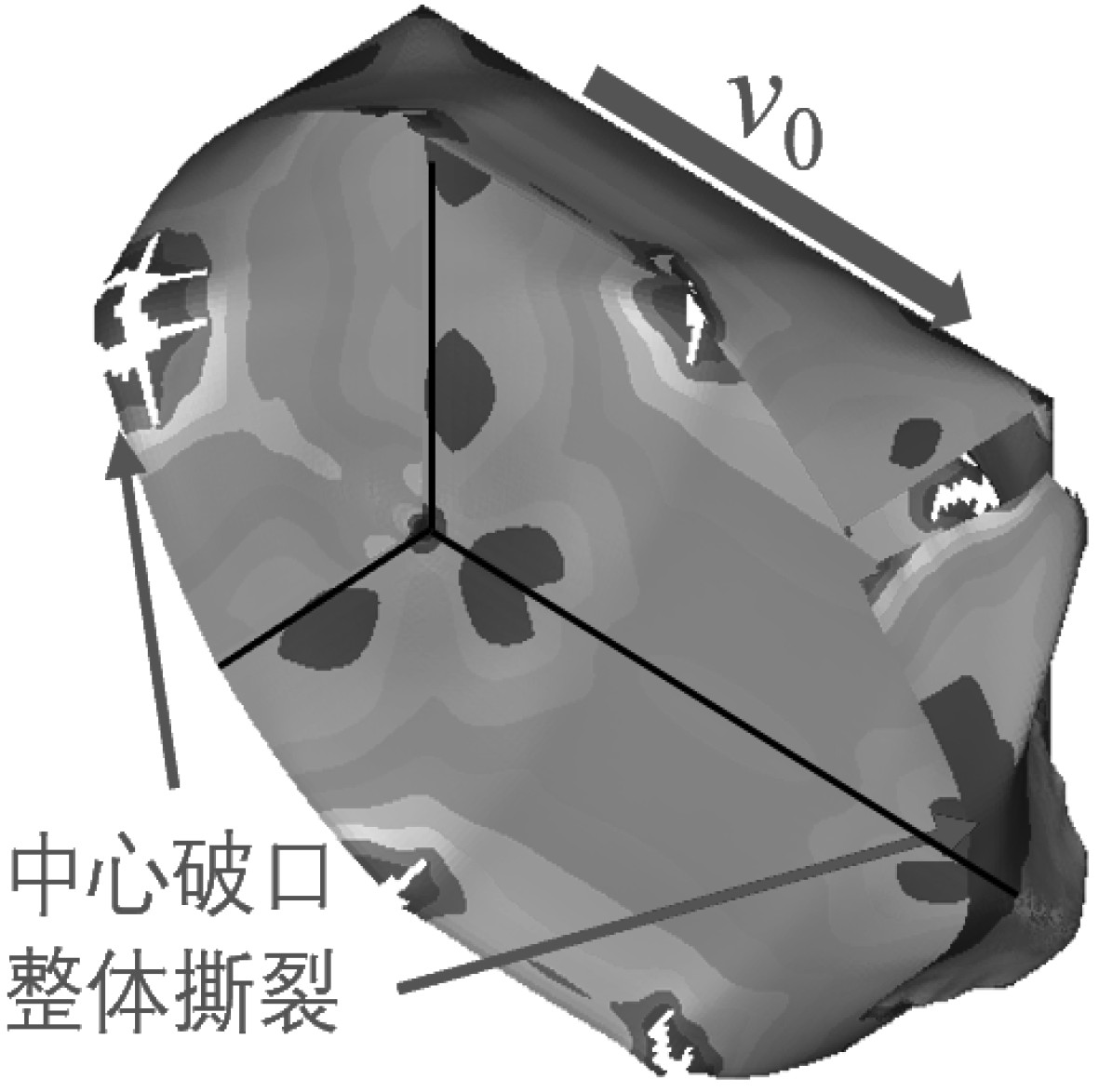
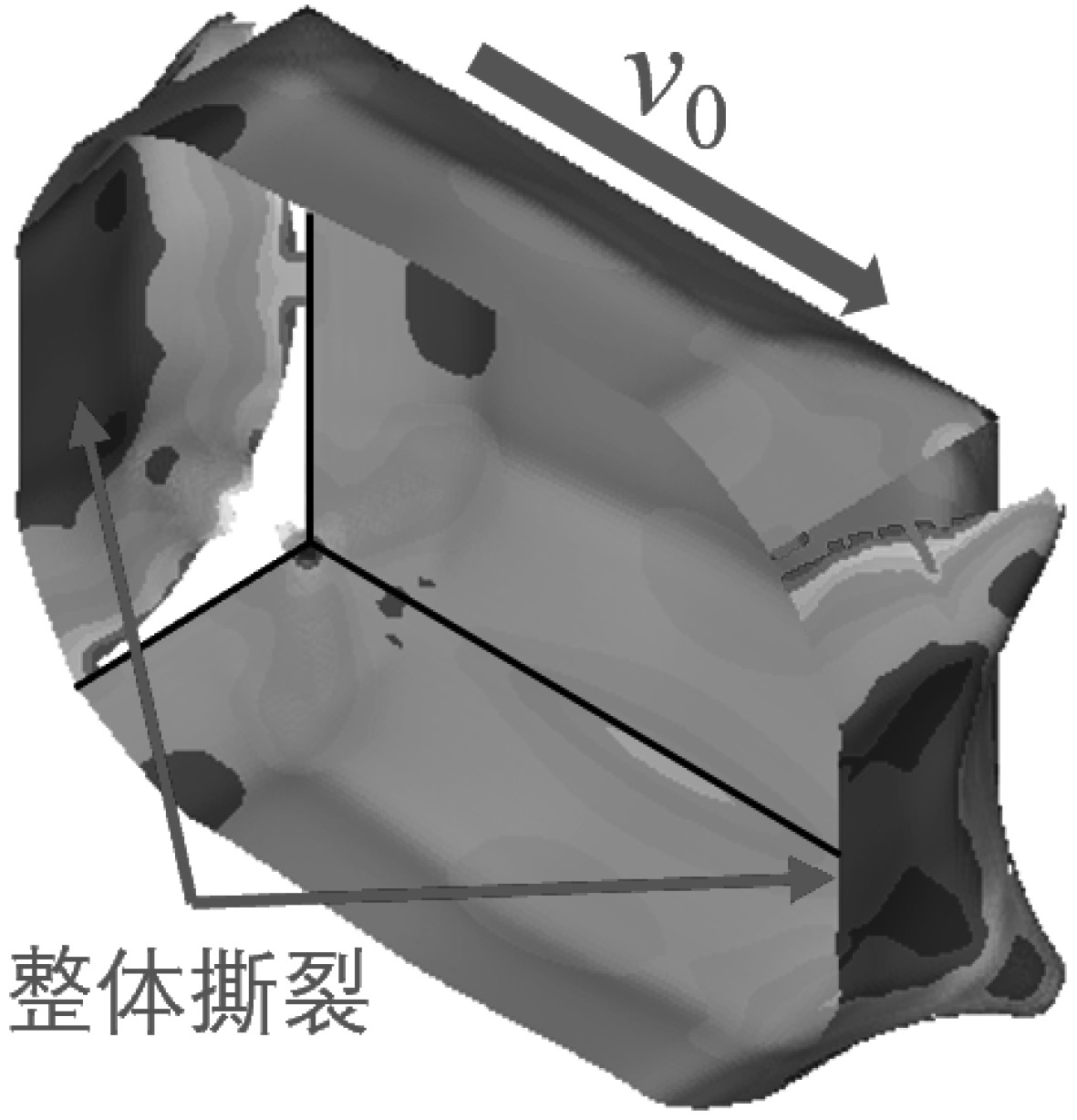
综合各仿真计算工况,将动爆载荷作用下舱室结构的不对称破坏模式总结为5类,表5给出了舱室结构的破坏模式、破坏特征及表现形式。
|
|
表 5 舱室不对称破坏模式及表现形式 Tab.5 Asymmetric failure modes and manifestations of cabin |
利用量纲分析法可以对多影响因素的复杂问题进行分析,找出主要影响因素,因而被广泛运用[11-13]。对于运动装药舱内爆炸载荷作用下舱室结构的不对称破坏模式这一复杂问题,量纲分析法完美地解决了难以利用现有的物理模型或数学模型方程进行描述的难点。
分析可知,装药运动速度会改变舱内爆炸载荷的分布特性,进而影响对舱室结构的毁伤效果。因此,从装药舱内静爆时的对称毁伤模式入手,以装药运动速度为加成量进行舱室结构不对称破坏模式的量纲分析。
3.1 静爆载荷下舱室结构破坏模式分析由于装药舱内静爆时,两正方形舱壁的破坏模式一致,可简化为对舱壁破坏模式的分析。对于正方形舱壁破坏模式的影响因素有:TNT当量m;舱室特征尺寸L1;L2和L3;舱壁厚度H;舱室结构材料密度ρs;材料声速cs;材料屈服强度σ;环境声速c0;环境密度ρ0。本文典型舱室尺寸为2.4 m×2.4 m×3.6 m,可将舱室特征尺寸简化为L1和L2,并引入舱室长细比L2/L1这一无量纲量。
将Dj定义为装药舱内静爆情况下正方形舱壁破坏模式,可将装药舱内静爆毁伤情况表示为:
| $ {D_j} = \left\{ {m,{L_1},{L_2},\frac{{{L_2}}}{{{L_1}}},H,{\rho _S},{c_S},\sigma ,{\rho _0},{c_0}} \right\}。$ | (6) |
装药舱内爆炸发生在理想空气条件下,可将环境声速c0和环境密度ρ0视为定值。对于典型舱室结构内装药爆炸这类特定问题,舱壁材料所选用的Q235B型钢,在爆炸载荷作用下舱室结构产生响应的过程中,舱室结构的材料密度ρs不发生改变,亦可视为定值。经此简化分析后,仅需考虑装药质量m,舱室特征尺寸L1,L2和舱室长细比L2/L1。
根据Π定理对剩余影响因素进行量纲分析,有
| $ {D_j} = F\left( {{\varPi _1},{\varPi _2},{\varPi _3}} \right),$ | (7) |
式中:
| $ {\varPi _{\text{1}}} = \frac{m}{{{H^3}{c_s}^{ - 2}\sigma }} = \frac{{m{c_s}^2}}{{{H^3}\sigma }} ,$ | (8) |
| $ {\varPi _{\text{2}}} = \frac{{{L_{\text{1}}}}}{H} {\varPi _{\text{3}}} = \frac{{{L_{\text{2}}}}}{H} 。$ | (9) |
由于舱室长细比L2/L1为无量纲量,不需要进行处理。因此,装药舱内静爆情况下舱室整体破坏模式的无量纲函数为:
| $ {D_j} = \left\{ {\frac{{m{c_s}^2}}{{{H^3}\sigma }},\frac{{{L_1}}}{H},\frac{{{L_2}}}{H},\frac{{{L_2}}}{{{L_1}}}} \right\}。$ | (10) |
对式(10)中的各无量纲数进行组合后得到:
| $ {D_j} = \frac{{m{c_s}^2}}{{{H^3}\sigma }} \cdot \frac{{{H^3}}}{{{L_1}^3}} \cdot \frac{{{L_2}}}{H} \cdot \frac{{{L_1}}}{{{L_2}}} = \frac{{m{c_s}^2}}{{{L_1}^2H\sigma }} 。$ | (11) |
在该静爆情况下舱室破坏模式无量纲表达式中,包含了装药质量m、舱室结构材料声速cs、舱室特征尺寸L1、舱壁厚度H和舱室结构材料屈服极限σ。符合毁伤效应与内爆载荷、材料性能及作用空间密切相关的特性。
由于舱室整体破坏模式的这3种表现形式相互独立,将正、负向舱壁挠曲破坏定义为舱室整体破坏模式1、中心破口定义为舱室整体破坏模式2、整体撕裂定义为舱室整体破坏模式3。采用上述无量纲表达式对各计算工况进行参数化分析,装药舱内静爆下舱室结构破坏模式分布情况如图4所示。

|
图 4 静爆下舱室结构毁伤模式分布情况 Fig. 4 Distribution of damage mode of cabin structure under static explosion |
由图4可知,随着无量纲毁伤数的增大,装药舱内静爆时对舱室整体的破坏程度逐渐提高。由于装药舱内静爆仿真计算工况较少,暂时能够确定的毁伤模式与无量纲毁伤数之间的关系如表6所示。
|
|
表 6 静爆下舱壁破坏模式对应的无量纲毁伤表达式对应区间 Tab.6 Static detonation bulkhead failure mode under the corresponding dimensionless mutilate expression corresponding interval |
装药舱内动爆时,装药的运动速度破坏了静爆下舱室毁伤效果的对称性,加剧了正向舱壁的破坏程度,削弱了负向舱壁的破坏程度。为此,以静爆毁伤效果无量纲快速预测方法为基础,引入装药运动速度v0,依据量纲一致性原则,有
| $ {\Pi _{\text{4}}}{\text{ = }}\frac{{{v_0}}}{{{c_s}}}。$ | (12) |
由于装药舱内静爆时,对正、负向舱壁的破坏模式及破坏程度对称,装药运动速度仅对其产生增加或削弱的作用。由此可认为装药舱内静爆时对正、负向舱壁的破坏效果为“基础量”,装药舱内动爆时的运动速度为对正、负向舱壁破坏效果的“加成量”。可将装药舱内静爆时的“基础量”假设为1,则对于装药于动正向舱壁的无量纲表达式为:
| $ {D_{d{\text{1}}}} = \frac{{m{c_s}^2}}{{{L_1}^2H\sigma }} \cdot \left( {1 + \frac{{{v_0}}}{{{c_s}}}} \right),$ | (13) |
对于装药运动负向舱壁的无量纲表达式为:
| $ {D_{d{\text{2}}}} = \frac{{m{c_s}^2}}{{{L_1}^2H\sigma }} \cdot \left( {1 - \frac{{{v_0}}}{{{c_s}}}} \right)。$ | (14) |
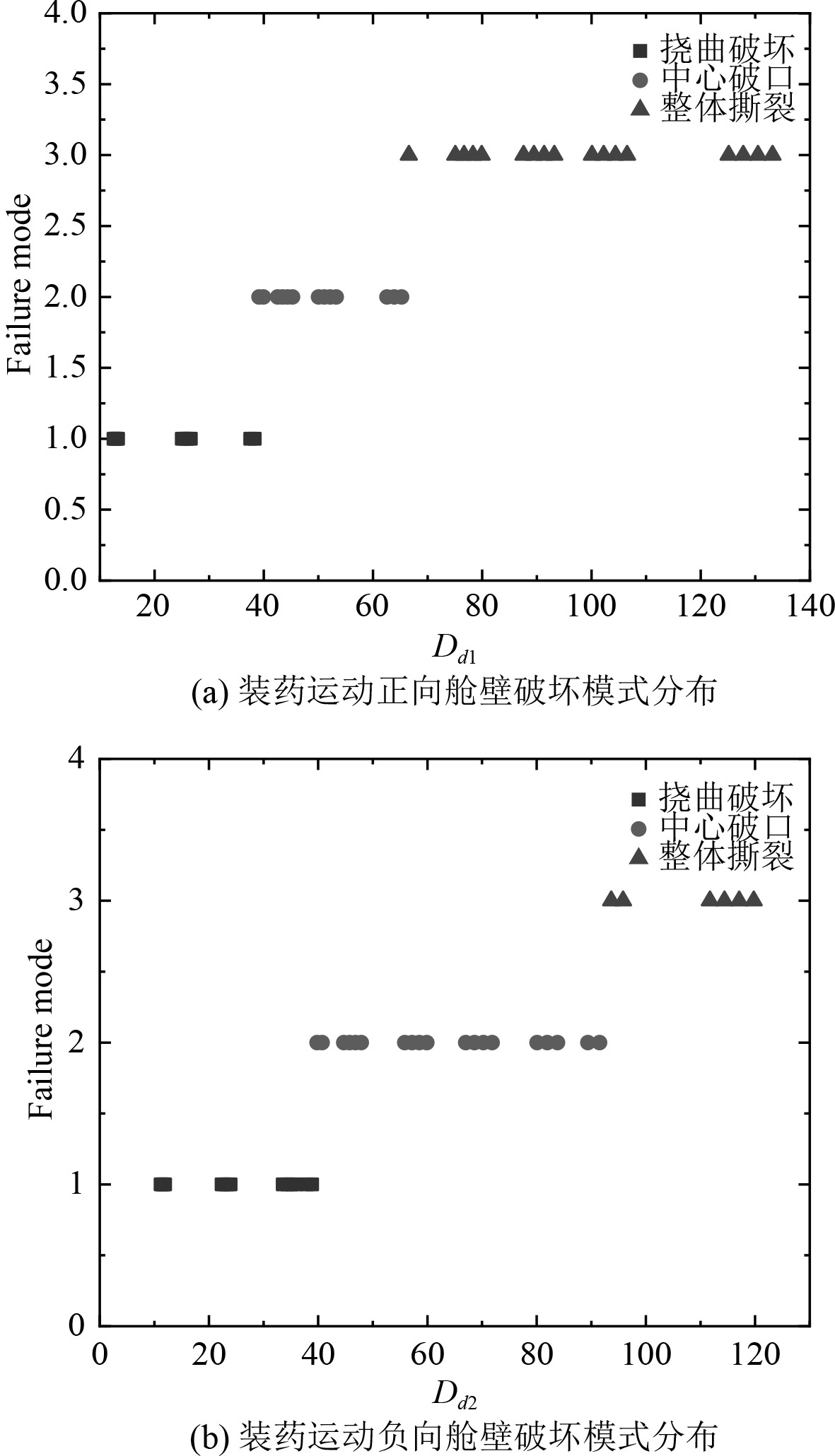
采用上述无量纲数对各计算工况进行参数化分析,装药运动正、负向舱壁破坏模式分布情况如图5所示。
|
图 5 装药运动正、负向舱壁破坏模式分布 Fig. 5 Positive and negative bulkhead failure modes of charge movement are distributed |
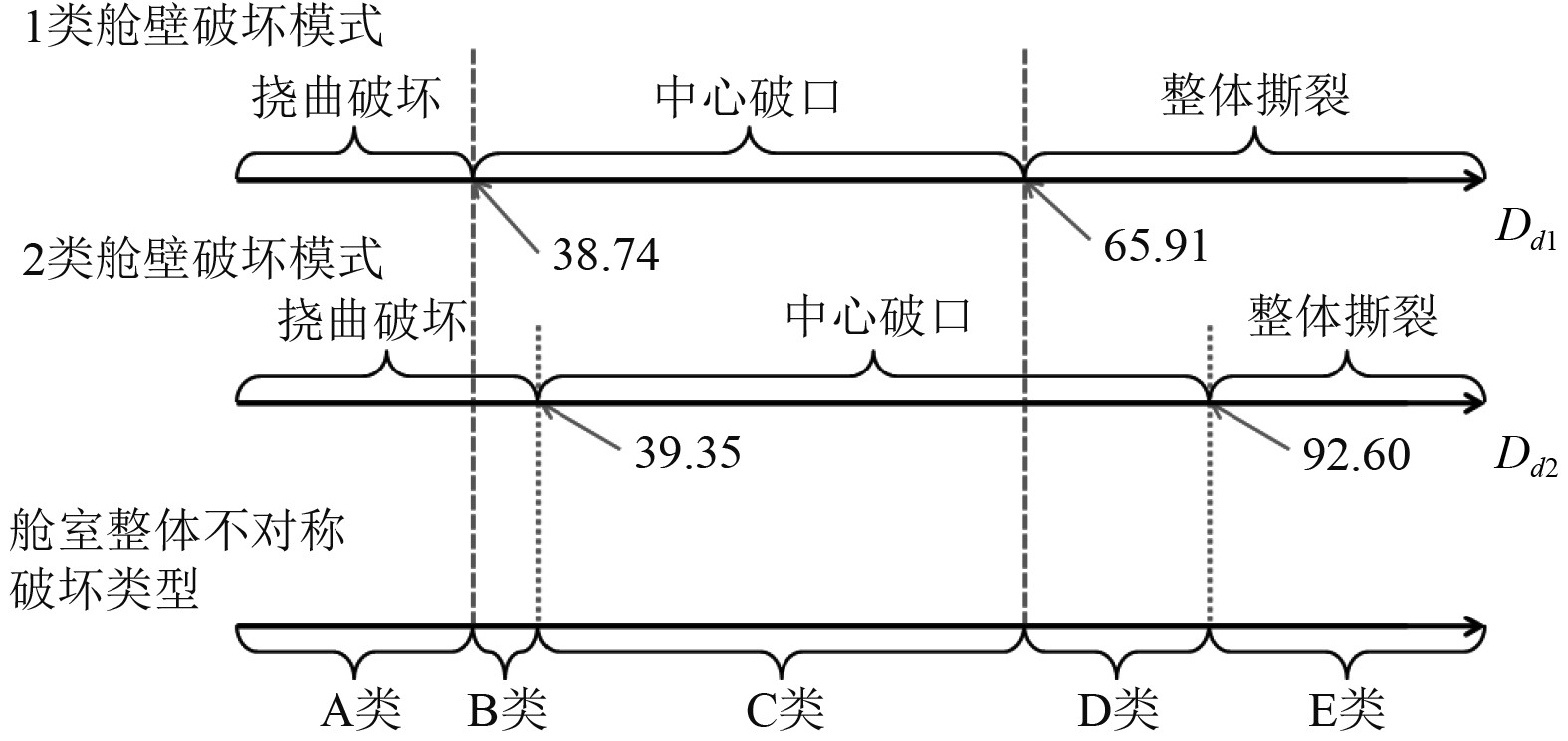
装药舱内动爆对舱室整体破坏的不对称性主要表现在正、负向舱壁的破坏模式及破坏程度不同。结合图5,将正、负向舱壁不同破坏模式的取值区间投影至Dd1和Dd2的坐标轴上,综合正、负向舱壁的破坏模式分区区间,可得到装药舱内动爆情况下,舱室不对称破坏模式无量纲分析下的分区图,如图6所示。图中不同毁伤模式的边界假定为相邻值的中间值。
|
图 6 舱室结构不对称破坏模式无量纲分区图 Fig. 6 The dimensionless zoning diagram of the failure mode of cabin structure asymmetry |
如图6所示,在舱室整体不对称破坏类型坐标轴中,每一区间对应一种不对称破坏模式。故装药舱内动爆条件下舱室整体的不对称破坏模式快速预测总结如下:
| $\begin{array}{c} \left.\begin{array}{c}{D}_{d\text{1}}=\displaystyle\frac{m{c}_{s}{}^{2}}{{L}_{1}{}^{2}H\sigma }\cdot \left(1+\frac{{v}_{0}}{{c}_{s}}\right)\\ {D}_{d\text{2}}= \displaystyle\frac{m{c}_{s}{}^{2}}{{L}_{1}{}^{2}H\sigma }\cdot \left(1-\frac{{v}_{0}}{{c}_{s}}\right)\end{array}\right\}= \\ \left\{\begin{array}{cc}{D}_{d\text{1}},{D}_{d\text{2}}\leqslant \text{38}\text{.74}& \Rightarrow \text{A}{{{\text{类不对称破坏}}}},\\ \text{38}\text{.74}\leqslant {D}_{d\text{1}},{D}_{d\text{2}}\leqslant \text{39}\text{.35}& \Rightarrow \text{B}{{{\text{类不对称破坏}}}},\\ \text{39}\text{.35}\leqslant{D}_{d\text{1}},{D}_{d\text{2}}\leqslant\text{65}\text{.91}& \Rightarrow \text{C}{{{\text{类不对称破坏}}}},\\ 65.91\leqslant {D}_{d\text{1}},{D}_{d\text{2}}\leqslant 92.60& \Rightarrow \text{D}{{{\text{类不对称破坏}}}},\\ 92.60\leqslant{D}_{d\text{1}},{D}_{d\text{2}}& \Rightarrow \text{E}{{{\text{类不对称破坏}}}}。\end{array}\right.\end{array} $ | (15) |
将装药舱内动爆相关工况参数代入式(13)和式(14),分别计算出正、负向舱壁响应的Dd1和Dd2值,利用式(15)定义区间,就可以预测动爆载荷下舱室的不对称破坏模式。
4 结 语本文基于数值仿真分析的方法,研究动爆载荷作用下舱室结构的毁伤效果。运用Autodyn有限元软件,采用流固耦合算法进行了大量仿真计算,总结出了动爆载荷作用下舱室结构的5种不对称破坏模式。
依据量纲分析理论,提出一个适用于静爆载荷作用下舱室结构毁伤效果的无量纲表达式和一组适用于动爆载荷作用下舱室结构毁伤效果的无量纲表达式,并将所得到的无量纲表达式应用到动爆载荷作用下舱室结构不对称破坏模式的分析中。结合大量工况的数值模拟结果,拟合得到了舱室不对称破坏模式分布图及评估区间,实现了动爆载荷对舱室结构毁伤效果的快速预测与评估。
| [1] |
侯海量, 朱锡, 梅志远. 舱内爆炸载荷及舱室板架结构的失效模式分析[J]. 爆炸与冲击, 2007, 27(2): 151-158. HOU H L, ZHU X, MEI Z Y. Study on the blast load and failure mode of ship structure subject to internal explosion[J]. Explosion and Shock Waves, 2007, 27(2): 151-158. DOI:10.3321/j.issn:1001-1455.2007.02.010 |
| [2] |
侯海量, 朱锡, 李伟, 等. 舱内爆炸冲击载荷特性实验研究[J]. 船舶力学, 2010, 14(8): 901−907. HOU H L, ZHU X, LI W, et al Experimental studies on characteristics of blast loading when exploded inside ship cabin[J]. Journal of Ship Mechanics, 2010, 14(8): 901−907. |
| [3] |
朱建方, 王伟力, 曾亮. 舰艇舱室内爆毁伤的建模与仿真分析[J]. 系统仿真学报, 2009, 21(22): 7066-7068+7-72. ZHU J F, WANG W L, ZENG L. Modeling and simulation of damage effect of ship cabin subject to internal explosion[J]. Journal of System Simulation, 2009, 21(22): 7066-7068+7-72. |
| [4] |
孔祥韶, 吴卫国, 李晓彬, 等. 舰船舱室内部爆炸的数值模拟研究[J]. 中国舰船研究, 2009, 4(4): 7-11. KONG X S, WU W G. Numerical simulation of cabin structure under inner explosion[J]. Chinese Journal of Ship Research, 2009, 4(4): 7-11. |
| [5] |
杜志鹏, 张磊, 赵鹏铎. 实尺度舰船舱内炮弹静爆试验方法[J]. 中国舰船研究, 2018, 13(3): 103-109. DU Z P, ZHANG L, ZHAO P D. Test method for static explosion of naval artillery shell in full-scale warship cabin[J]. Chinese Journal of Ship Research, 2018, 13(3): 103-109. |
| [6] |
北京工业学院八系. 爆炸及其作用下册[M]. 北京: 国防工业出版社, 1979: 270−272.
|
| [7] |
杜红棉, 王燕, 祖静, 等. 导弹动爆对模拟船舱毁伤效果试验研究[J]. 高压物理学报, 2011, 25(3): 261-267. DOI:10.11858/gywlxb.2011.03.011 |
| [8] |
邢存震, 唐恩凌, 梁德刚, 等. 密闭空间内爆炸冲击波超压特性试验研究[J]. 沈阳理工大学学报, 2017, 36(1): 33-37. DOI:10.3969/j.issn.1003-1251.2017.01.009 |
| [9] |
徐维铮, 吴卫国. 约束空间内爆超压载荷影响因素二维数值模拟[J]. 中国舰船研究, 2019, 14(2): 91-98. |
| [10] |
姚术健, 张舵, 卢芳云, 等. 多箱室结构内部爆炸损伤特性研究[J]. 兵工学报, 2015, 36(S1): 87-91. |
| [11] |
BAKER, W E. Explosion in air[M]. Austin, Texas, US: University of Texas Press, 1973.
|
| [12] |
YAO S J, ZHANG D, LU F Y. Dimensionless numbers of dynamic response analysis of clamped square plates subjected to blast loading[J]. Archive of Applied Mechanics, 2015, 85(6): 735-744.
|
| [13] |
赵亚溥. 断裂力学中的相似方法[J]. 力学进展, 1998, 28(3): 323-337. ZHAO Y B. Similarity method in fracture mechanics[J]. Advances in Mechanics, 1998, 28(3): 323-337. DOI:10.6052/1000-0992-1998-3-J1998-148 |
 2022, Vol. 44
2022, Vol. 44