船载特种起重机是一类较为特殊的机械设备,它以甲板为载体,由可自由旋转的基座和起重臂组等组成,能够对货物进行吊装运输。船舶在水上作业时,受到风浪等因素的作用产生摆动和摇晃,由此会对起重机的作业稳定性造成不利影响。为避免起重过程中发生安全事故,需要采取有效的控制措施。本文就大型船载特种起重机作业稳定性优化系统展开分析探讨[1-3]。
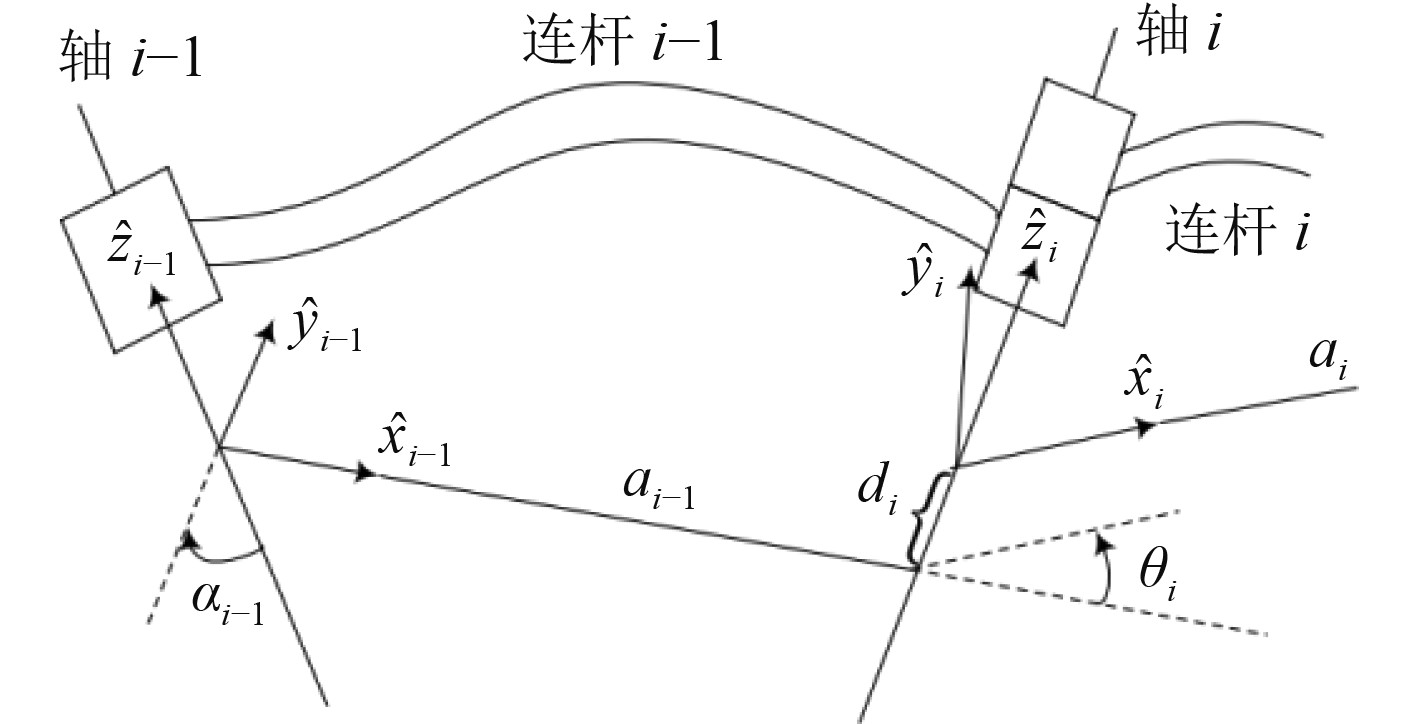
1 大型船载特种起重机建模 1.1 运动模型起重机归属于多刚体系统的范畴,这是一种相对比较复杂的力学系统,在研究该系统时,需要了解起重臂末端的位姿与运动、杆和关节的位姿与运动、杆件的空间关系等。在对连杆的位置关系进行描述时,要为每个连杆定义固连坐标系和命名[4-6]。船载特种起重机的基座要求牢固、稳定,由此使固连在基座上的坐标系具有固定不变的特点,可在运动学问题的研究中,以该坐标系为参考。依据坐标系建立准则构建的连杆坐标系如图1所示。
|
图 1 船载特种起重机连杆坐标系示意图 Fig. 1 Schematic diagram of connecting rod coordinate system of ship borne special crane |
当附体坐标系建立完毕后,为更加清晰描述各个连杆的关系,建立齐次变换矩阵。船载特种起重机上的连杆数量较多,基于这一前提,运动学方程要确定臂梁相对于起重机基座的变换。可在分析船载特种起重机连杆运动的过程中,以连杆坐标系作为参考,每个连杆在任一瞬会产生2种速度,分别为线速度、角速度。为便于研究,以三自由度的船载特种起重机为例,该起重机采用的是链式结构,各个相邻连杆之间均存在关联,可依托起重机的基座坐标系,对各连杆的速度依次计算。在实际应用中,起重机的基座高度与臂组长度全部可忽略不计,为便于分析,可默认2个坐标系的原点处于重合状态。连杆坐标系的角速度用ωm表示,线速度用Vm表示,构成连杆在坐标系中的角速度分量有两个,据此通过推导能够获得雅可比矩阵,该矩阵的行数为起重机操作臂在空间笛卡尔坐标系的自由度数量;矩阵的列数为起重机操作臂的关节数。其中行对应关节的角速度或线速度的分量,列则对应关节产生的角速度或线速度。
1.2 动力模型本文研究的重点是船载特种起重机作业稳定性问题,与之关系最为密切的是稳定性控制,因此在分析动力学建模问题时,仅对与起重机稳定性控制关系最为密切的逆动力学求解进行讨论。船载特种起重机各个关节的位置、速度以及加速度等条件均为已知的前提下,对所需的力矩进行求取即为逆动力学的求解方法。具体步骤如下:先将各个连杆质心的角速度及线加速度求出,按欧拉动力学方程,对作用于质心上的力矩加以计算;接下来写出各个连杆力矩的平衡式,以迭代的方法,计算出关节的力矩,计算过程中要对连杆的重力予以考虑,在此前提下,起重机起重臂组的基座会以加速度的方式向上做运动,这个过程完全是由重力引起。假设船载特种起重机各部分的质量简单分布,各个连杆的质量均集中于最末端,在质量集中的情况下,连杆的质心惯性张量为零矩阵。由于起重机的动力学方程中项数多、耦合性强,故此需要通过Matlab软件对动力学模型编程,在此基础上完成控制仿真。
1.3 船载起重机建模船载特种起重机建模是一项复杂程度相对较高的工作,为使模型的构建过程得以简化,选用ADAMS分析软件,这是一款在机械动力学仿真领域中应用非常广泛的软件,其自带3D模型零件库,能针对复杂机械系统,建立虚拟样机,通过分析和测试模块,研究机械系统的性能[7-8]。本文的船载特种起重机,采用的是当前较为先进的可伸缩折叠式系统,该系统具有强耦合、非线性等特点,系统本身的复杂程度较高,由以下几个部分组成:可旋转式基座、机械臂、传感器等。其中基座与船舶的甲板相连,能够自由转动,基座上是起重臂组,包括主臂和基本臂两部分,以铰接的方式连接,驱动装置为液压油缸和马达,具体结构如图2所示。

|
图 2 船载特种起重机整体结构示意图 Fig. 2 Overall structure diagram of ship borne special crane |
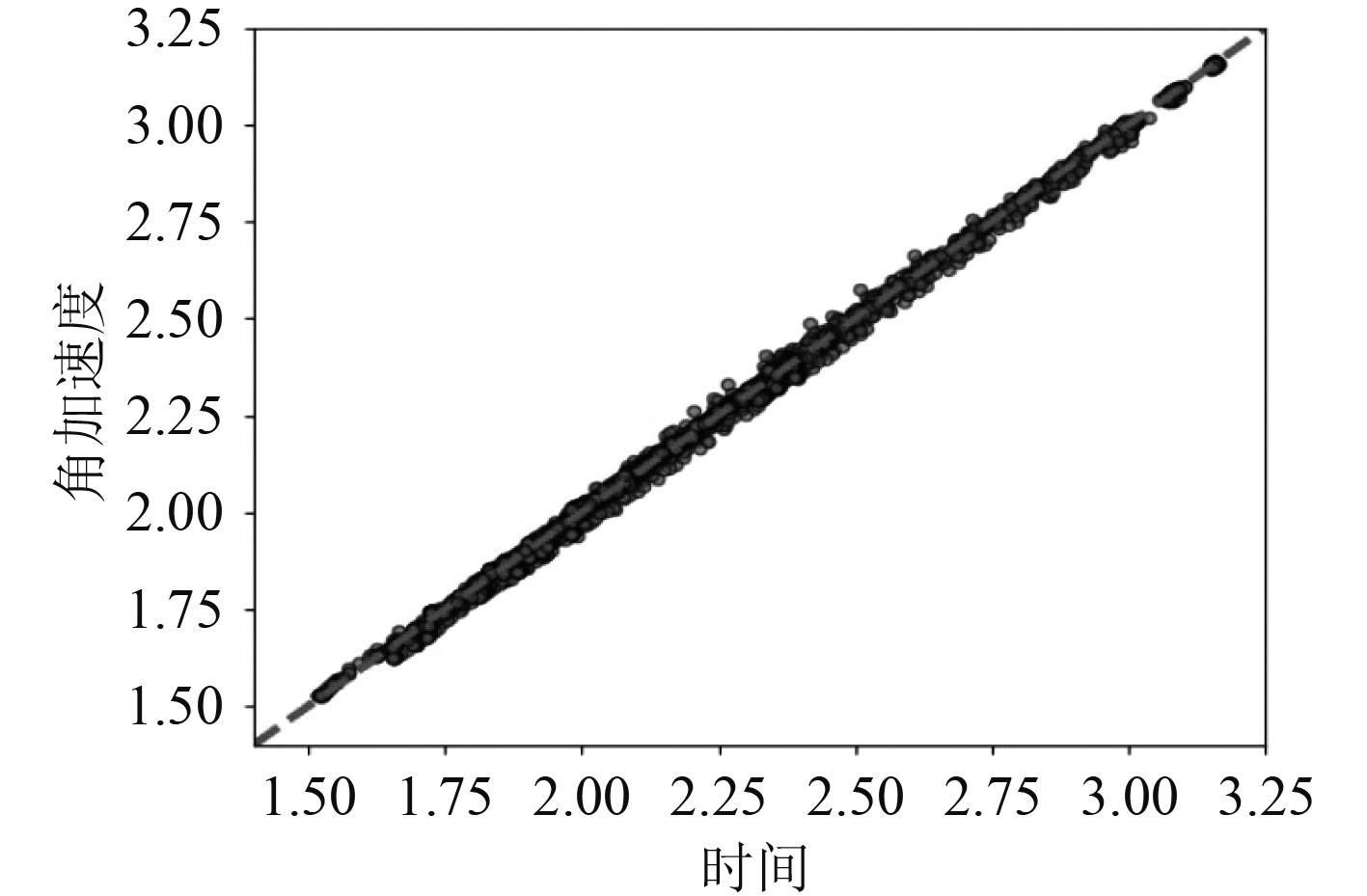
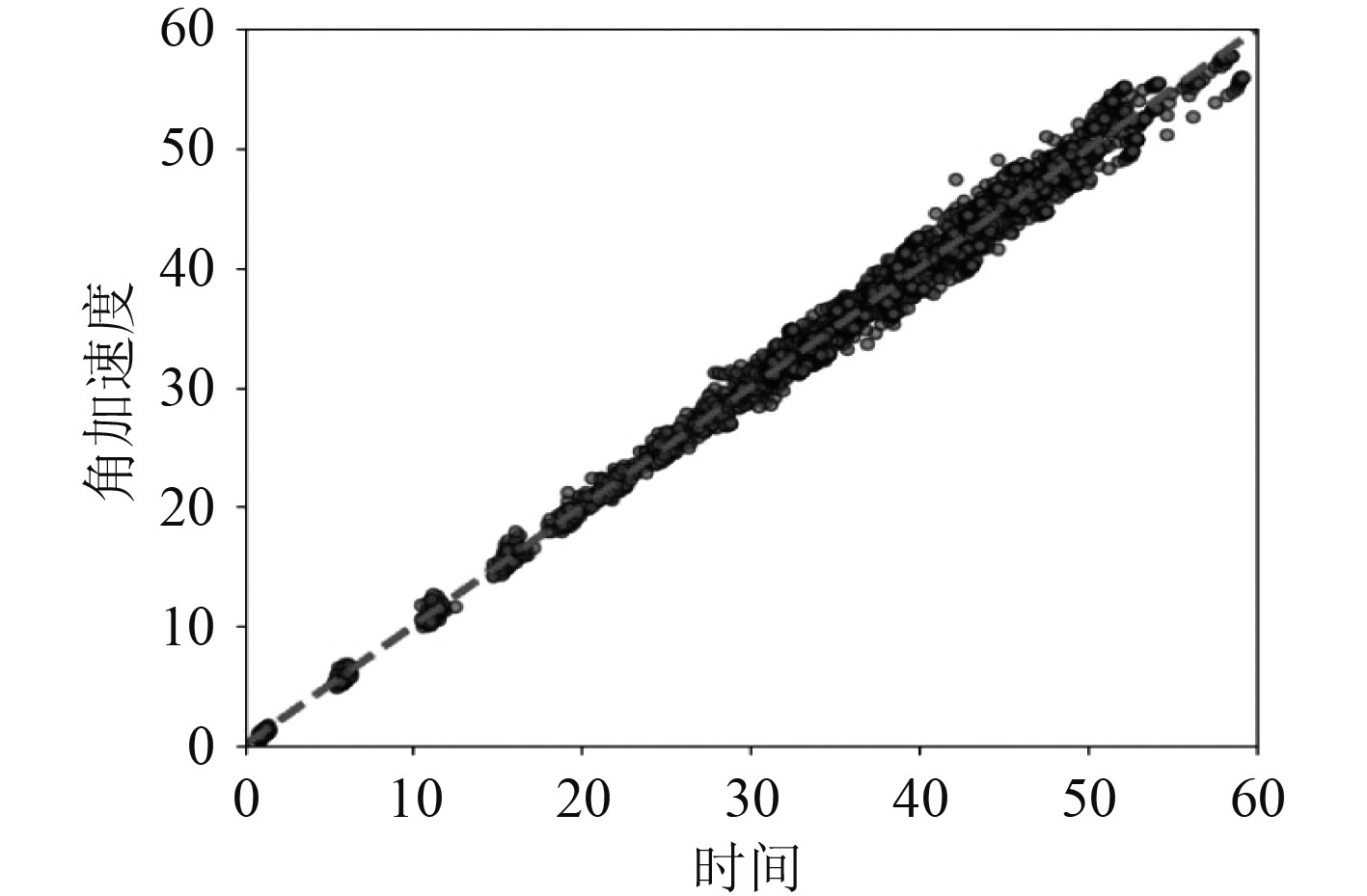
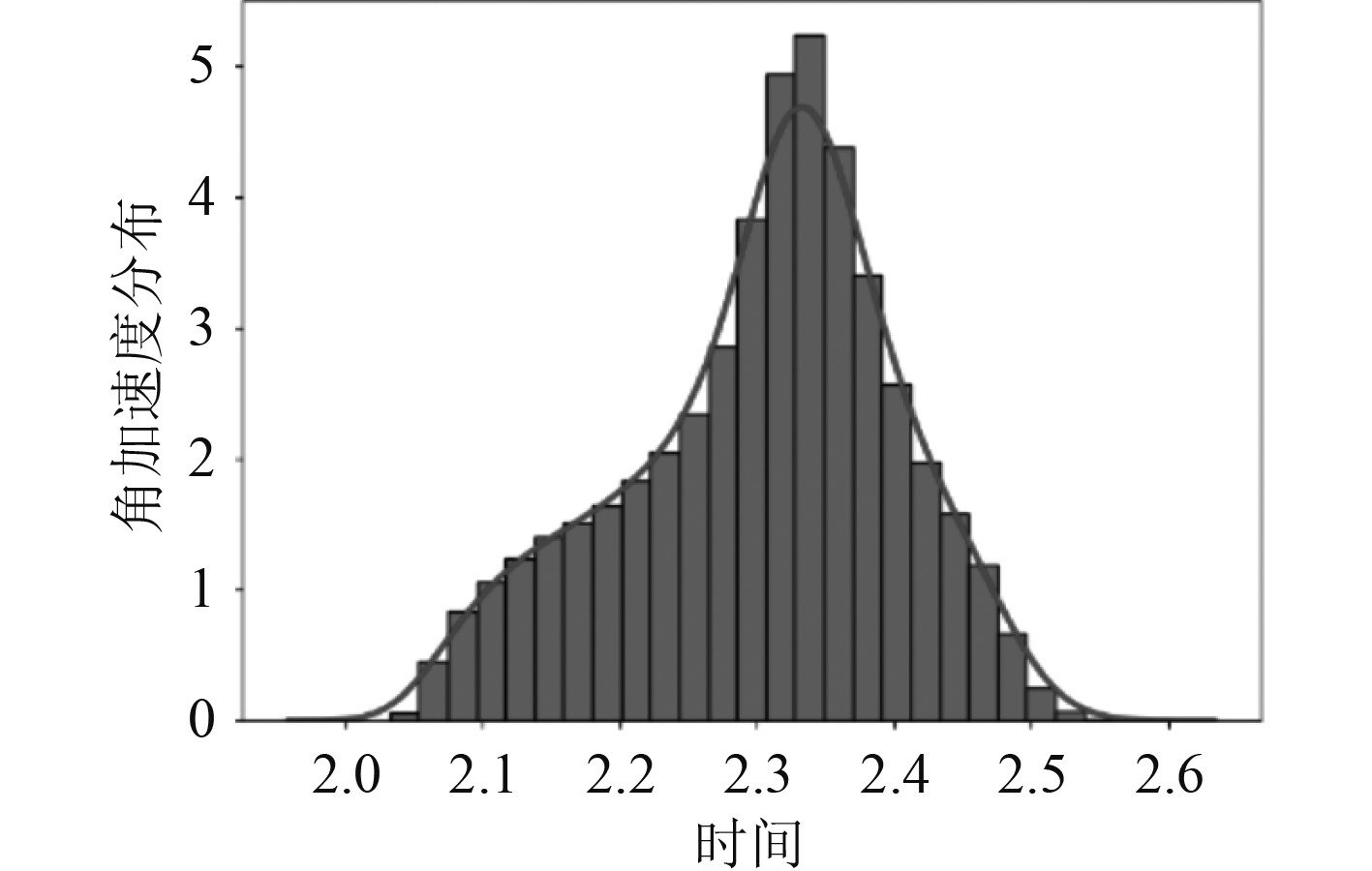
在对船载特种起重机建模的过程中,要先进入ADAMS软件,并设置好网格与单位,随后打开视窗,用工具箱中的零件库搭建模型。该模型的最底端为基座,与基座相连接的是起重臂组,模型为各个部分增加了运动副,如基座为转动副,各关节处也为转动副。在仿真研究中,可将模型的基本参数适当缩小,这样便于后续的计算分析,虽然参数缩小,但却并不会影响动力学仿真与控制。构建的模型要在检验合格后才能使用,ADAMS自带多种检验方式,经过检验能够发现模型中存在的错误,本次研究的重点是起重机作业稳定性的优化控制,检验时,可对各关节施加运动,通过运动仿真检验模型是否正确。以添加数学函数的方法,对模型中的各个关节施加期望的运动,函数可以从函数库中选取,本次检验中施加的函数为正弦函数运动sin,为检验模型的合理性,要测量各关节在不同时刻的角速度及加速度。将仿真时间设定为1 s,步数设置为5000,在这个仿真过程中,动作会变得比较慢,便于观察起重机的运动状况,由系统对各关节的角速度及加速度分别测量,获得的量值经绘图功能处理后,可以得到相应的曲线。图3~图5分别为起重机基座、基本臂和主臂的角加速度情况。
|
图 3 船载特种起重机基座的角加速度曲线 Fig. 3 Angular acceleration curve of base of ship borne special crane |
|
图 4 船载特种起重机基本臂的角加速度曲线 Fig. 4 Angular acceleration curve of basic boom of ship borne special crane |
|
图 5 船载特种起重机主臂的角加速度曲线 Fig. 5 Angular acceleration curve of main boom of ship borne special crane |
采用模糊控制与神经网络相结合的方法进行优化,模糊控制作为一种智能控制方法,优点是推理与归纳能力强,缺点是自适应能力差。CMAC作为神经网络,具有极强的泛化能力,学习速度快,在机器人控制中的应用较为广泛。在应用中发现,CMAC神经网络存在一定的不足,即对于概念或是集合无明确的限定。为实现优化控制的目标,将模糊控制与CMAC结合到一起,形成一个关节控制器,从而使网络模型同时具备模糊控制与CMAC的所有优点,以弥补彼此的缺陷和不足。该控制器自学习能力强,在强耦合、非线性的机械系统中具有良好的控制效果。
2.2 学习算法为使控制器在船载特种起重机作业稳定性优化控制中的作用得以充分发挥,需要对控制器进行训练,具体量值包括联想强度、高斯隶属函数、宽度值等。将控制器的期望输出设定为yq,实际输出为y,则目标误差函数可以用下式表示:
| $ {E}=\frac{1}{2}\left({y}_{{q}}-{y}\right)^{2} \text{。} $ |
神经网络学习时,可以采用误差反向传播算法,控制器对高斯隶属函数及宽度值的调整与神经网络调整块的划分方式基本相同,调整后,空间位置会发生改变。控制器能够以在线的方式调整宽度值,这样一来可以节省大量的存储空间。
2.3 稳定性控制船载特种起重机作为大型、复杂的机械系统,其每个关节的驱动力矩,均可由伺服控制器按期望的轨迹给出。本文研究的起重机是较为特殊的系统,相当于船舶的机械臂,可将其视作为机械人系统,强耦合、非线性是该系统较为突出的特点。由建立的起重机运动、动力以及结构模型可知,在起重机作业过程中,为保持稳定性,需要对以下关节有效控制:基座的旋转关节、基本臂与主臂的俯仰关节。为实现优化控制的目标,要对以上关节的运动轨迹进行跟踪控制,通过仿真的方法,验证控制器的控制效果,使用Matlab软件,在M文件中对控制过程进行仿真。先对起重机的相关参数合理设定,将数据样本的采集周期设为0.0005 s,仿真时间设置为2 s,利用模糊控制与神经网络结合形成的控制器对关节的运动轨迹进行控制。为全面观察控制器的性能,在仿真过程中增加一个脉冲信号,借此来检验控制器的鲁棒性。由仿真结果可知,控制器不但跟踪特性较好,而且鲁棒性也比较强,可通过该控制器,对船载特种起重机各关节的运动轨迹进行跟踪控制,以此来确保作业稳定性。
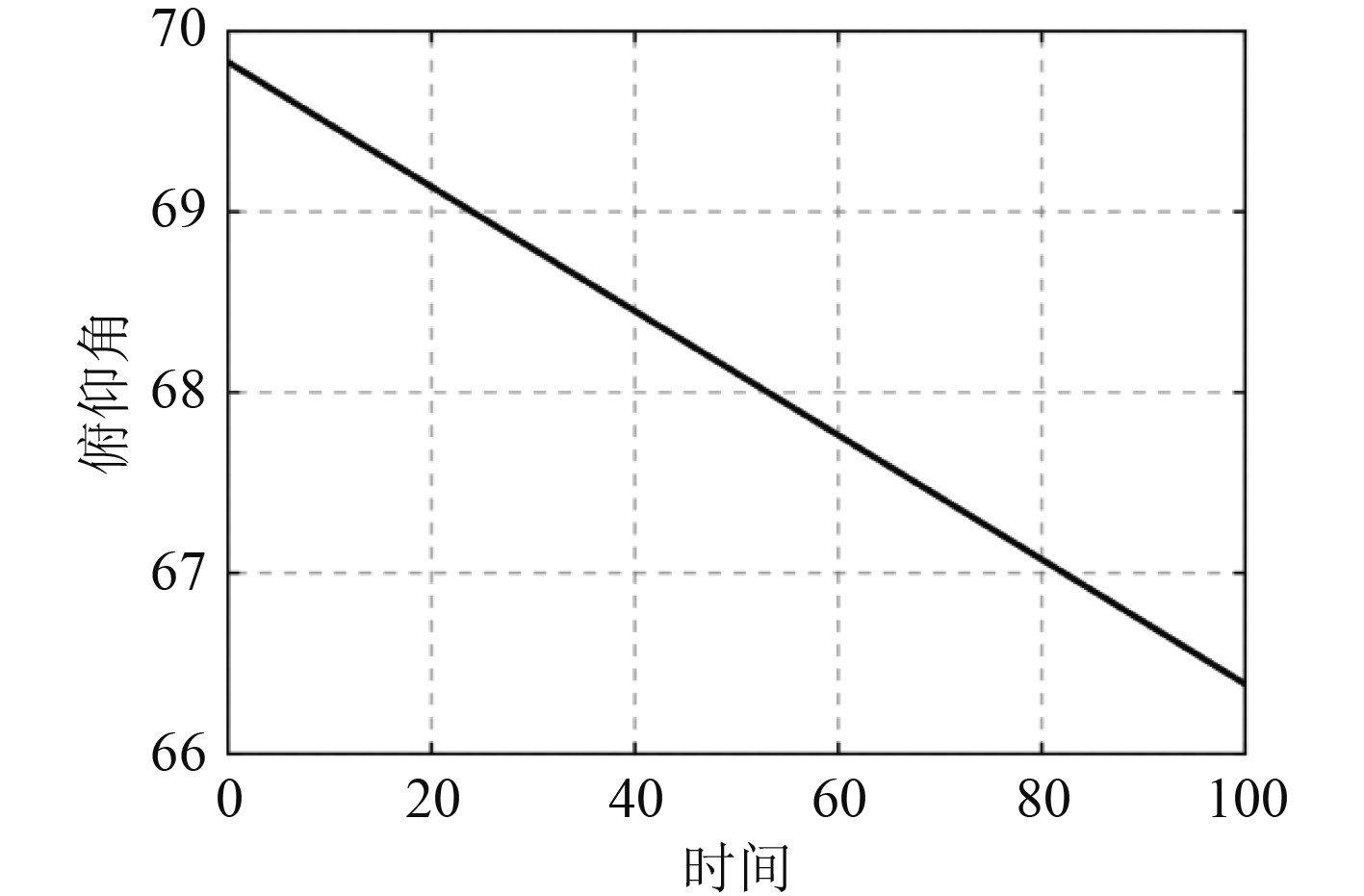
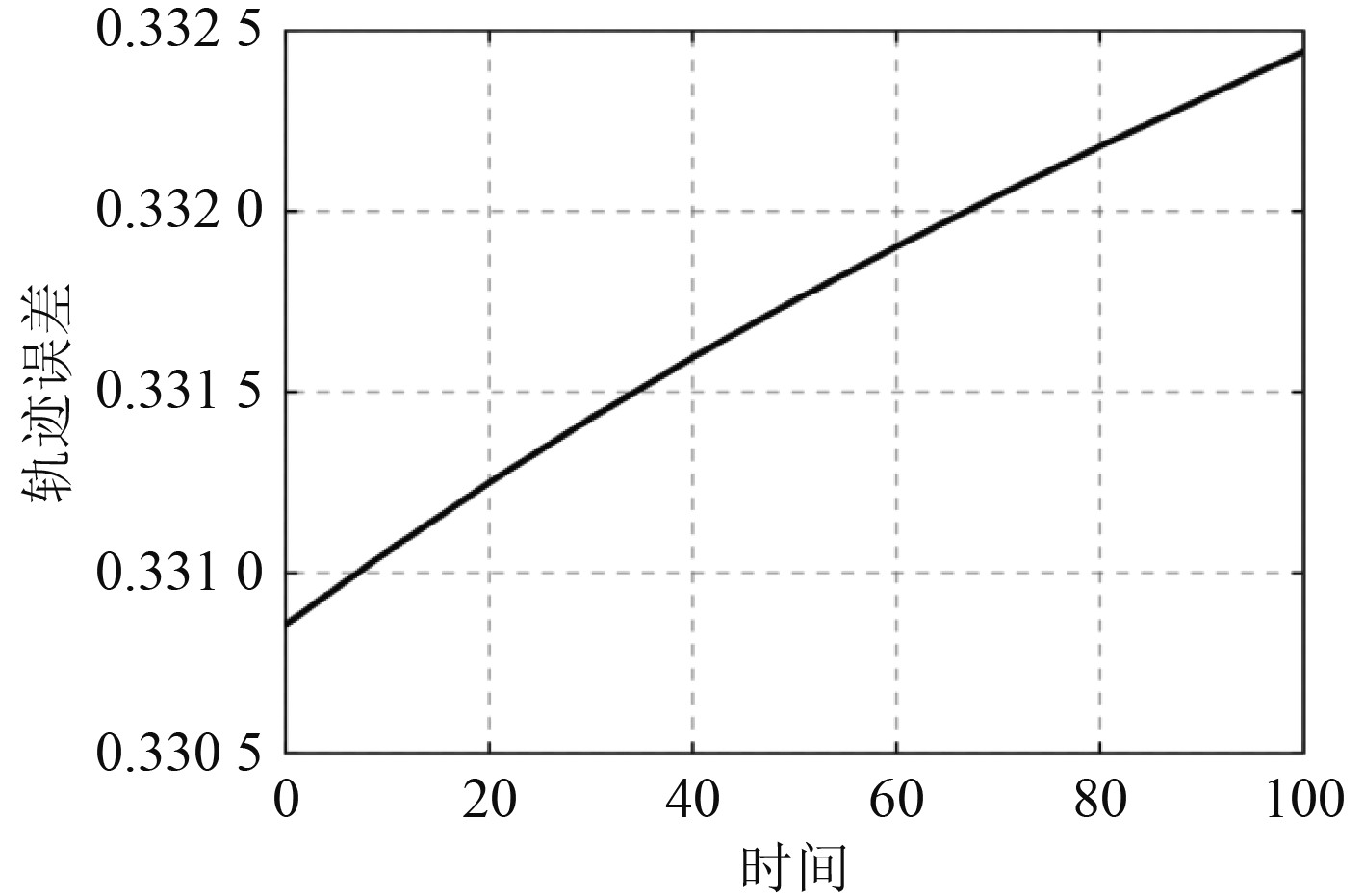
2.4 控制系统仿真在对大型船载特种起重机作业稳定性控制系统设计时,需要先建立一体化的样机模型,整个模型由起重机的机械系统和控制系统两部分组成,从控制系统向机械系统发送控制参数,形成闭环反馈控制,对起重机作业过程实现精确控制,确保作业的稳定性。起重机的旋转基座能够在船舶的甲板上自由旋转,而位于基座上的起重臂组却并不能随意转动,这是因为它的俯仰角度受限,只能在一定范围内做俯仰运动。船载特种起重机基座的轨迹俯仰角变化曲线如图6所示。为使系统仿真更接近真实情况,以船载特种起重机的实际工况为依托,给基座、基本臂和主臂3个关节设定期望轨迹。在控制器中定义高斯模糊隶属函数,联想强度的初值采用随机值。通过仿真得到起重机的轨迹跟踪误差曲线图7所示。
|
图 6 船载特种起重机基座的轨迹俯仰角变化曲线 Fig. 6 Change curve of trajectory pitch angle of shipborne special crane base |
|
图 7 船载特种起重机基座的轨迹误差曲线 Fig. 7 Trajectory tracking error curve of Shipborne special crane base |
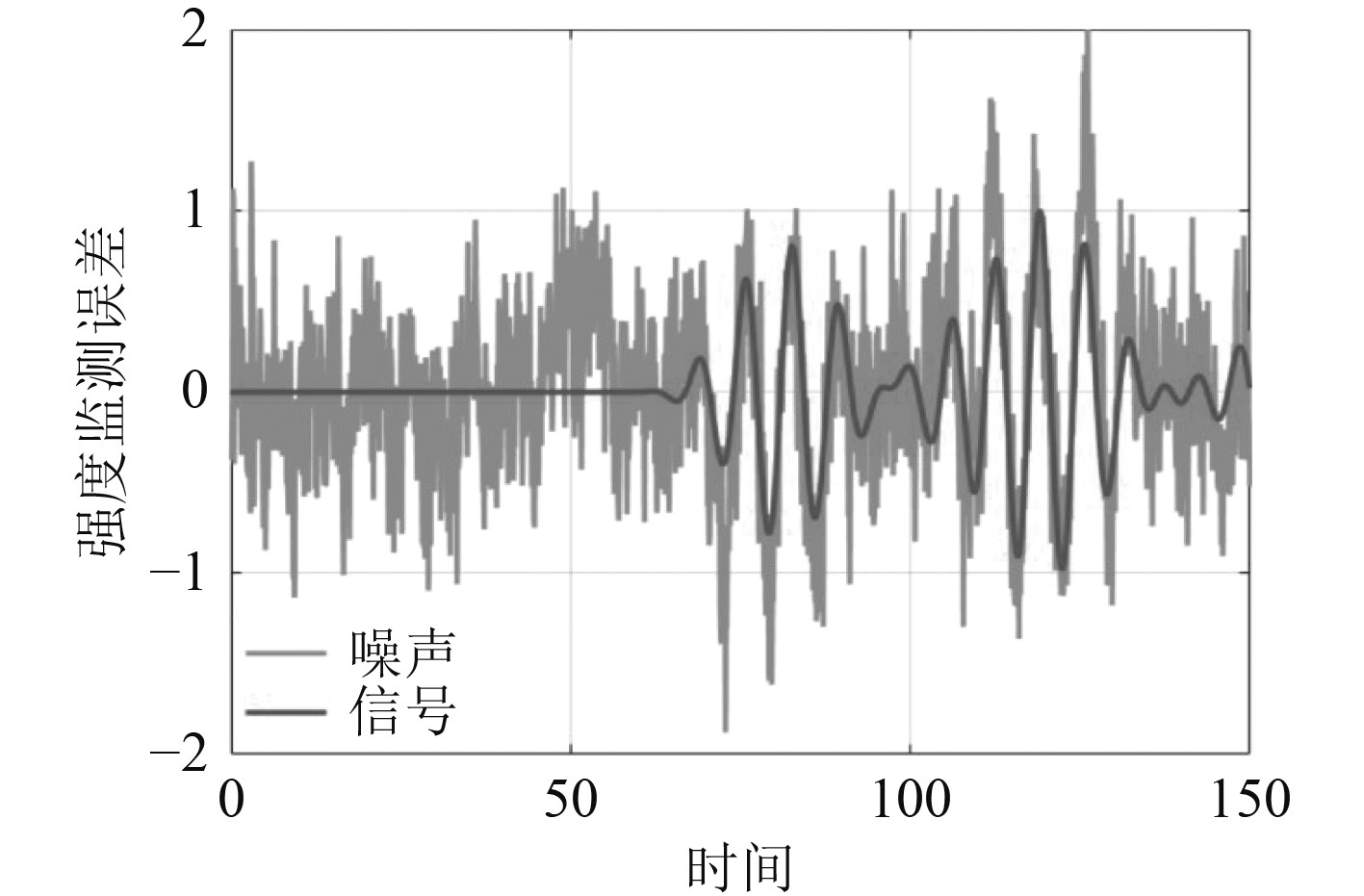
船载起重机受力强度监测误差曲线如图8所示。由仿真结果可知,本次设计的控制器具有良好的跟踪特性,说明模糊控制与神经网络结合的方法合理可行,能够对大型复杂机械系统的稳定性起到优化控制的效果。
|
图 8 船载起重机受力强度监测误差曲线 Fig. 8 Monitoring error curve of force and intensity of shipborne crane |
对大型船载特种起重机进行运动学、动力学以及结构模型的构建,并将模糊控制与神经网络相结合,设计出控制器。经过仿真,验证了控制器的有效性,能够对大型船载特种起重机作业过程进行控制,确保稳定性,避免安全事故的发生。
| [1] |
刘广辉, 仝强, 吕超, 等. 深水半潜式起重铺管船大型起重机整体安装方案[J]. 石油和化工设备, 2021, 24(10): 97-99+102. DOI:10.3969/j.issn.1674-8980.2021.10.026 |
| [2] |
朱亮. 探究超起装置对起重机伸缩臂的稳定性影响[J]. 装备维修技术, 2020(1): 82-82,45. |
| [3] |
姚峰林, 孟文俊, 赵婕, 等. 起重机n阶伸缩臂架稳定性的递推公式及数值解法[J]. 中国机械工程, 2019(21): 2533-2538. DOI:10.3969/j.issn.1004-132X.2019.21.003 |
| [4] |
胡婷. 关于起重机抗倾覆稳定性的分析[J]. 中国设备工程, 2019(4): 120-121. |
| [5] |
孟瑞艳, 李纲. 大柔度起重机整体稳定性缩比实验及高等非线性分析[J]. 建设机械技术与管理, 2018(11): 64-66. |
| [6] |
韩运才, 沈刚. 流动式起重机的稳定性与起重量特性探讨[J]. 特种设备安全技术, 2017(6): 32-34. DOI:10.3969/j.issn.1674-1390.2017.06.013 |
| [7] |
韩雪岩, 许冬, 兰玉华. 起重机用新型PMSM转子设计及稳定性研究[J]. 电机与控制学报, 2017(4): 75-82. |
| [8] |
赵君龙, 覃刚, 王强. SOC(特种)型海事起重机桁架式臂架强度与稳定性分析[J]. 船海工程, 2017(1): 122-125. DOI:10.3963/j.issn.1671-7953.2017.01.030 |
 2022, Vol. 44
2022, Vol. 44
