伴随着电子信息技术、人工智能技术以及大数据技术的飞速发展,船舶的推进系统也得到了长足的进步[1]。推进系统是一种十分复杂的电力系统,作为船舶最重要的部件,推进系统的可靠性对船舶的稳定性具有决定作用。由于船舶需要长时间在海上航行,一旦出现异常情况无法得到及时的救援,因此船舶推进系统的运行情况,会直接影响整个船舶的运营[2]。船舶推进系统的工作环境十分恶劣,由于船舶自身震动以及海浪产生的颠簸都会对船舶的推进系统的稳定性产生影响,因此针对船舶的推进系统进行工作状态的监督、故障的诊断以及故障的预测十分重要,这样可以避免一部分恶性事件的产生[3]。船舶推进系统的正常与否直接影响到船舶的运行以及战斗情况,因此如何才能对船舶的推进系统的故障问题进行迅速且精准的定位,成为船舶日常维护的重要工作之一[4]。故障诊断及预测技术是一种既可以降低维护成本又可以提高经济效益的技术,因此诊断技术及预测技术被各行各业广泛使用,但是在船舶推进系统中,该技术的应用还不是十分成熟,国内外的研究都比较少,因此对船舶推进系统的诊断技术进行研究,有着十分重要的作用[5]。
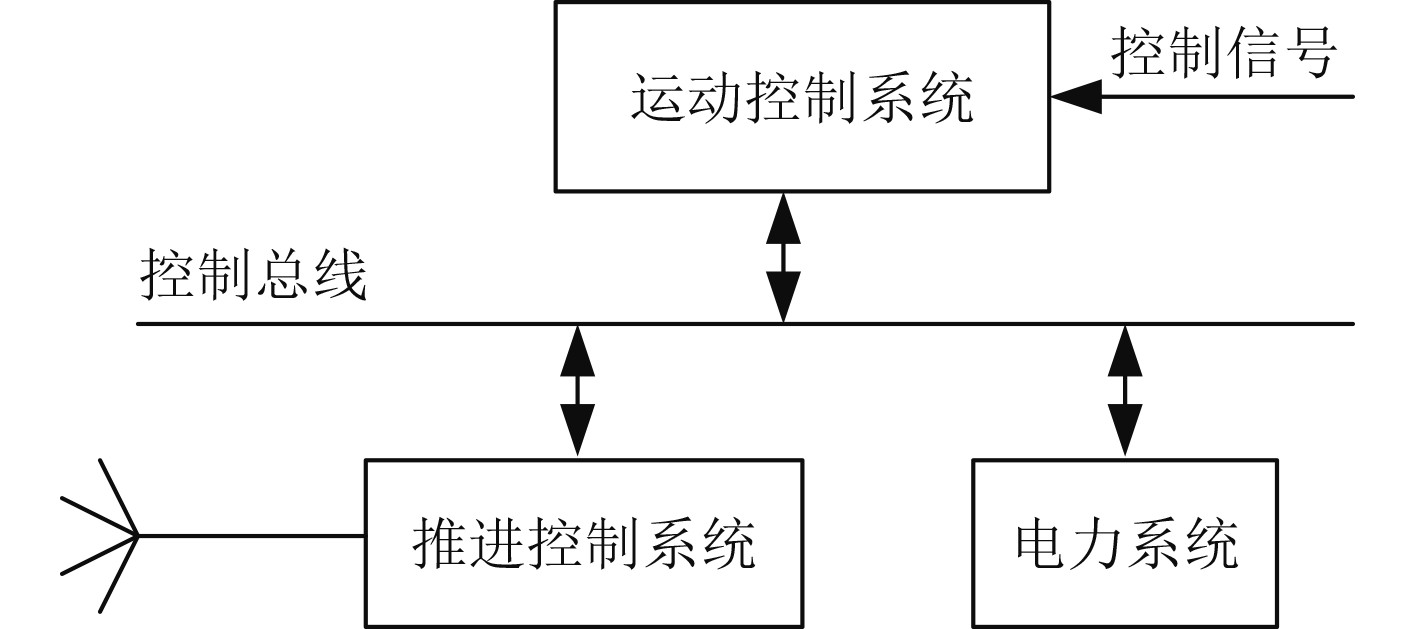
1 船舶推进系统 1.1 船舶推进系统的基本结构从船舶推进系统的结构来看,船舶推进系统是一种复杂系统,一般可以将船舶的推进系统分成运动控制系统、推进控制系统以及电力系统3部分,如图1所示。
|
图 1 船舶推进系统基本结构 Fig. 1 Basic structure of ship propulsion system |
船舶的运动控制系统在驾驶室的控制台中,所以控制台又被称作驾控台,操控人员可以通过驾驶室的控制台发送出船舶的速度、航向等运动命令,船舶的运动控制系统根据收到的命令进行控制方案的选择,最终达到控制航行姿态的目的。船舶推进系统的电力由电力系统提供,船舶推进速度调控是由推进控制系统负责的,根据相应的舵角进行航向的调控[6]。
在一个典型的船舶推进系统中,运动控制系统由含有发令车钟能力的操控台进行远程控制,船舶上的电力系统由发电机组成,船舶上的配电盘可以根据船舶负载量对电力系统中的发电机进行控制,最终通过变压器、开关和相关的电线将电力传输给耗电负载。船舶的推进系统主要包括控制台、电压器、电机、变流器。船舶推进控制系统主要任务就是根据船舶控制台发出的控制命令调节船舶电机的转速,以达到控制船速的目的。船舶的监控系统用来对相关信号进行检测与采集,实现船舶安全维护、异常状态监控、事故报警等功能。
1.2 船舶推进系统分类船舶电机驱动螺旋桨是船舶的主要推进方法,根据不同船舶对推进功率的不同需求,可以选择单台电机驱动或者多台电机驱动2种方案,多台电机驱动又可以分为串联推进驱动和并联推进驱动2种模型。
船舶推进系统中使用单个螺旋桨进行船舶驱动的属于单轴推进系统,有2种方式可以增加电机功率,一种是将2台电机进行串联,增加船舶推进系统的功率;另一种是通过齿轮箱将2台驱动电机进行并联。由于这种方法提高了船舶推进系统的故障冗余以及容错能力,因此被广泛使用。船舶推进系统中使用2个螺旋桨进行船舶驱动的属于双轴推进系统,在双轴推进系统中根据2台电机互联方式不同,又可以分为双桨双机串联和双桨双机并联2种模式,由于优秀的故障冗余以及容错能力,双桨双机并联模式得到了广泛使用。随着吊舱式推进设备技术的突破,多轴推进系统得到了快速发展,由于多轴系统中包含了多个推进器,因此多轴推进系统有着灵活的操作性、很好的故障冗余以及容错能力,但是因为推进器数量的增加,各个推进器之间的协调难度加大,增加了系统的控制复杂度[7]。
1.3 船舶推进系统核心部件船舶推进系统的核心部件包括推进器、逆变器、电机、变压器,这些部件也是实现船舶推进的重要技术。电机是船舶的重要负载之一,船舶的电机是直接或者通过齿轮给船舶提供直推或者侧推的动力,常用的船舶推进电机可以分成直流推进电机和交流推进电机。直流推进电机的优点在于电机的调速以及控制性比较好,因此广泛地应用于渡船、拖车等对机动性要求比较高的船舶上。直流推进电机的短处在于换向器以及电刷结构,并且直流推进电机在工作的过程中产生的机械摩擦对电机的精度以及可靠性有很大的影响,直流推进电机的机械换向严重限制了电机的最大功率。随着电机容量的增大,电机的体积也会增大,因此电刷极其容易出现故障,所以直流推进电机一般用在小型船舶上[8]。交流推进电机的优点在于结构简单,缺点在于调速性能差,因此交流推进电机可以在大型的补给船以及潜艇等船舶上使用。船舶运行的驱动装置一般采用螺旋桨推进器,根据调速的方式,螺旋桨可以分为定速电机变距螺旋桨和变速电机定距螺旋桨。螺旋桨的功能主要是将电机的驱动力转换成船舶前进的动力,是用来吸收电力的,电机驱动螺旋桨比传动轴驱动螺旋桨有着更高的灵活性。
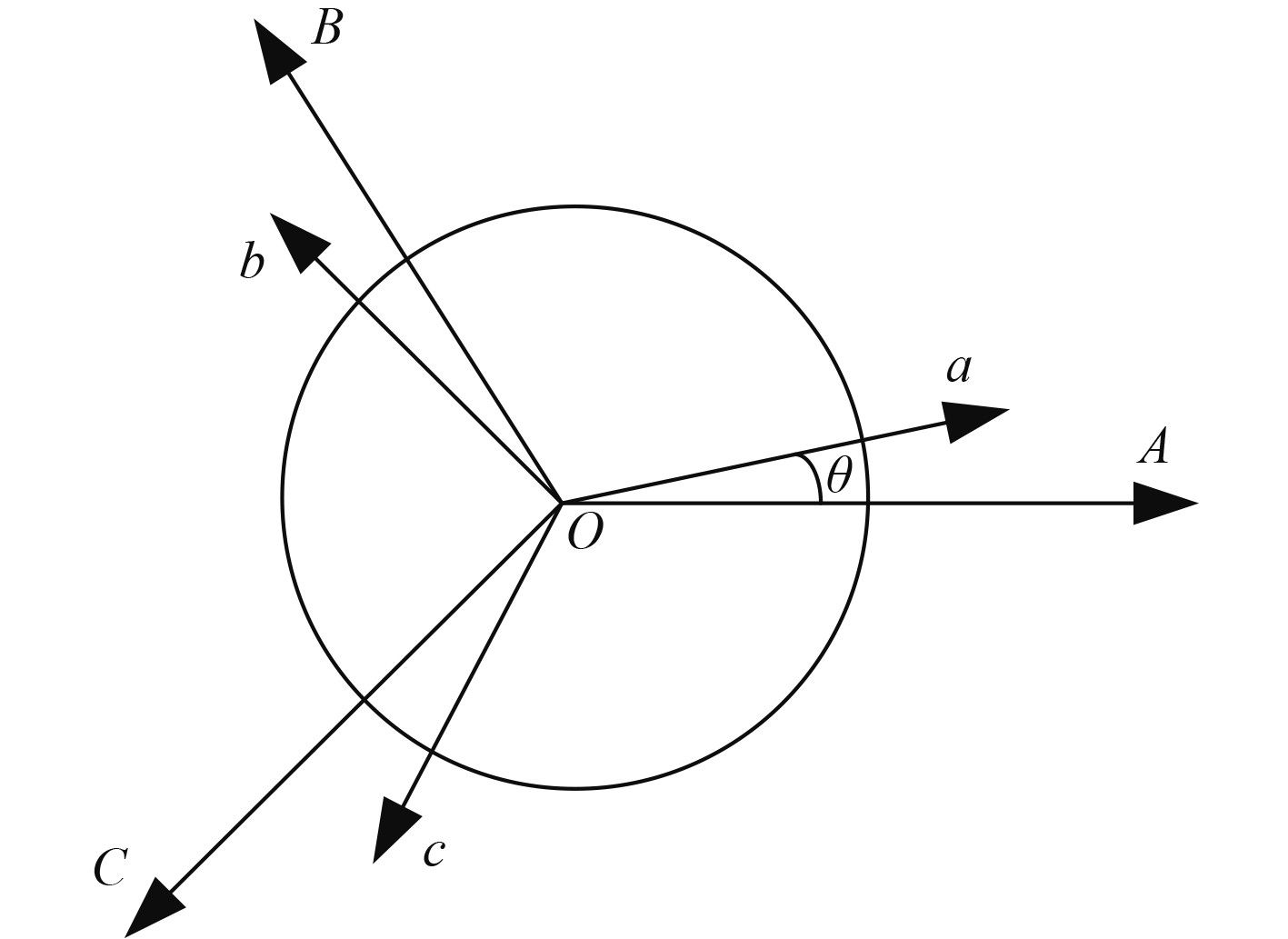
2 船舶推进系统数学模型 2.1 推进电机模型由于船舶的推进电机模型比较复杂,所以传统的静态电机模型不能用来表示船舶推进电机的高性能调控,因此船舶推进电机的模型应该考虑电能、磁能、机械能等多种因素,建立电机的动态模型。推进电机绕组模型可以由图2中的绕组模型表示。
|
图 2 等效绕组模型 Fig. 2 Equivalent winding model |
从图2可以看出,在船舶推进电机的等效绕组模型中,以定子的A相绕组轴线作为参考,并结合B轴和C轴,构成了OABC坐标系,OABC坐标系在空间上是静止状态。以转子a相绕组轴线为参考并结合bc两个轴线,共同构成了oabc坐标系,oabc坐标系在空间上是随着转子转动而转动的,OABC坐标系和oabc坐标系之间的夹角是θ,以该等效绕组模型为基础,可以使用电压、磁链以及运动方程来描述船舶推进系统的数学模型。
| $ \left[ {\begin{array}{*{20}{c}} {{U_{ABC}}} \\ {{U_{abc}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_s}}&0 \\ 0&{{R_r}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_{ABC}}} \\ {{I_{abc}}} \end{array}} \right] + p\left[ {\begin{array}{*{20}{c}} {{\varPsi _{ABC}}} \\ {{\varPsi _{abc}}} \end{array}} \right]\text{,} $ | (1) |
式(1)为电压方程,其中UABC=[uA uB uC]T,Uabc=[ua ub uc]T,Rs=[Rs Rs Rs],Rr=[Rr Rr Rr],s为定子,r为转子;p=d/dt为微分算子。
磁链方程如下式:
| $ \left[ {\begin{array}{*{20}{c}} {{\varPsi _{ABC}}} \\ {{\varPsi _{abc}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_s}}&{{L_{sr}}} \\ {{L_{sr}}}&{{L_r}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_{ABC}}} \\ {{I_{abc}}} \end{array}} \right]\text{,} $ | (2) |
式中:ΨABC=[ΨA ΨB ΨC]T,Ψabc=[Ψa Ψb Ψc]T。
运动方程如下式:
| $ J\frac{{{\rm{d}}{w_r}}}{{{\rm{d}}t}} = {T_{em}} - {T_1}\text{。} $ | (3) |
式中,J为转动惯量。
2.2 推进器模型以螺旋桨环流、动量以及叶元体等理论为基础,结合螺旋桨敞水特性实验,就可以得到螺旋桨图谱,螺旋桨图谱很好的展现了螺旋桨的效率、进速、推力系数以及转矩系数之间的关系。根据螺旋桨特性曲线,螺旋桨的转矩公式如下:
| $ Q = {K_Q}\rho {n^2}{D^5}\text{,} $ | (4) |
螺旋桨的推力式如下:
| $ T = {K_T}\rho {n^2}{D^4}\text{。} $ | (5) |
由于螺旋桨在船尾流场中旋转,这就导致船舶的船首和船尾的水流速度不一样,最终在船首和船尾之间产生了压力差,该压力差阻碍了船舶前进,船尾的水流速度的加大也增加了船体和周围水流之间的摩擦阻力,这2种阻力属于螺旋桨推力的减额,螺旋桨推力的减额一般用推力的减额和推力的比值表示,因此考虑螺旋桨推力减额的推力公式可以用下式表示:
| $ {T_{ef}} = T - \Delta T = T\left( {1 - \frac{{\Delta T}}{T}} \right) = T\left( {1 - t} \right)\text{。} $ | (6) |
式中,t为推力减额和推力的比值。
螺旋桨的推力除了受到推力减额的影响,还会受到伴流的影响。伴流对螺旋桨的影响一般体现在降低螺旋桨的进速,伴流一般使用船舶的进速与船舶的速度之间的差值和船舶的速度的比ω来表示,如下式:
| $ \omega = \frac{u}{{{V_S}}} = \frac{{{V_S} - {V_A}}}{{{V_S}}} = 1 - \frac{{{V_A}}}{{{V_S}}}\text{,} $ | (7) |
船舶螺旋桨的进速可以用下式(10)表示:
| $ {V_A} = \left( {1 - \omega } \right){V_S} \text{。} $ | (8) |
船舶的阻力是船体阻力以及附加阻力一起构成的合力,船体阻力又可以细分成摩擦和剩余2种阻力,附加阻力是指水、空气、风浪等对船舶产生的阻力。
船舶的摩擦阻力和船体长度、速度、湿表面积有关,用下式表示:
| $ {C_r} = \frac{{{R_f}}}{{\dfrac{1}{2}\rho V_s^2S}} \text{。} $ | (9) |
其中Cr计算可以采用下式:
| $ {C_r} = \frac{{0.075}}{{{{\left( {\log {Re} - 2} \right)}^2}}}\text{。} $ | (10) |
式中:Re为雷诺数,计算式如下:
| $ {Re} = \frac{{{V_s}{L_{WT}}}}{\upsilon }\text{。} $ | (11) |
船舶的湿表面积计算如下:
| $ S = {L_{WT}}\left[ {2d + 1.37\left( {{C_B} - 0.274} \right)B} \right]\text{。} $ | (13) |
船舶的剩余阻力计算式如下:
| $ {R_{res}} = {C_r}\frac{1}{2}\rho V_s^2S\text{。} $ | (13) |
船舶的附加阻力主要是附体阻力和空气阻力,计算式如下:
| $ \Delta {R_A} = {K_A}R\text{,} $ | (14) |
| $ {A_x} = C\frac{1}{2}{\rho _A}{v_A}{S_y}\text{。} $ | (15) |
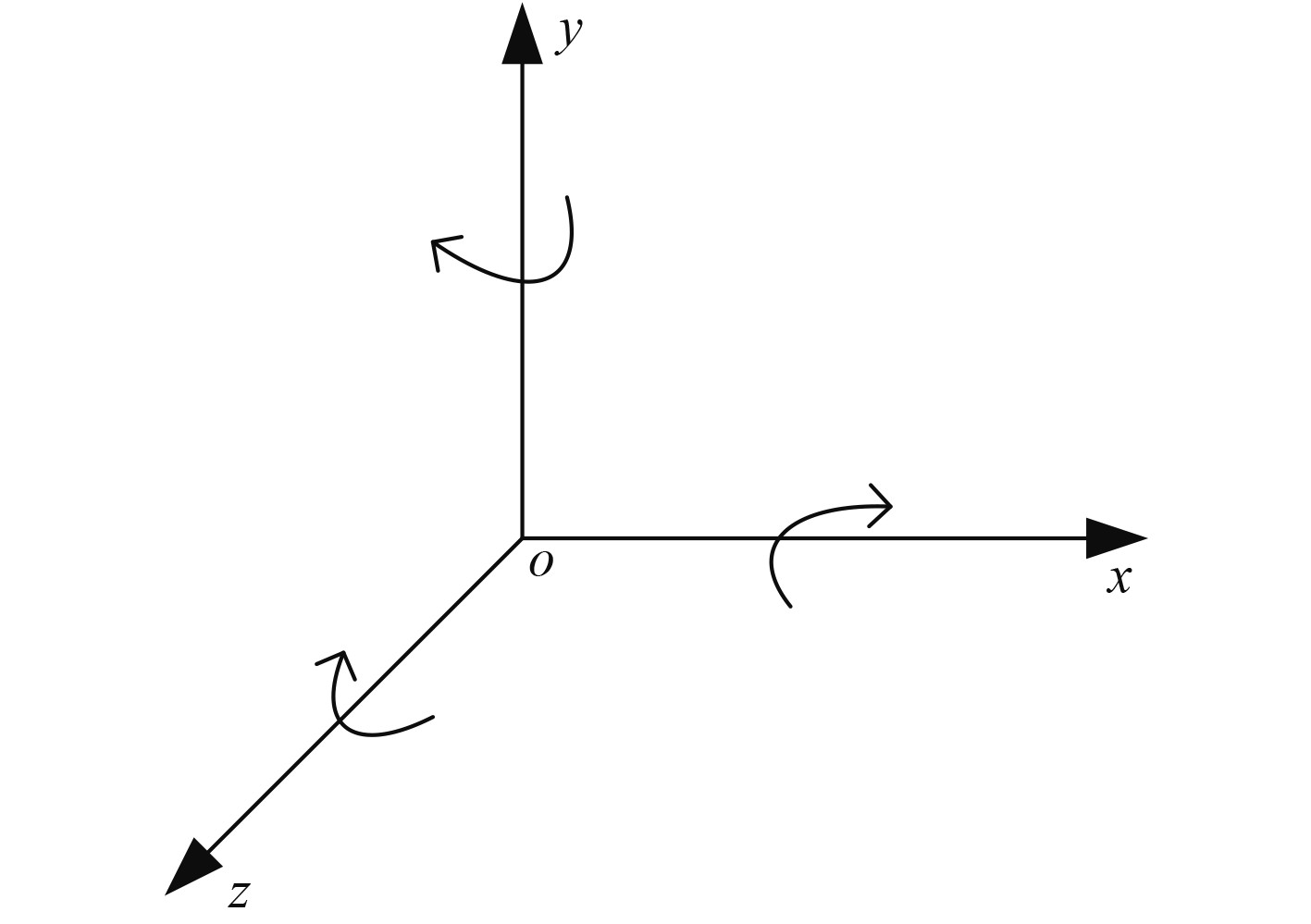
船舶的航行运动是一种十分复杂的运行,因为船舶是漂浮在水面上的,因此船舶具备前后、上下、横漂、横移、纵荡、垂荡6个自由度(见图3),再结合船舶在航行过程中会受到风、流、浪等因素的阻力,极大地增加了船舶运行的分析难度。
|
图 3 船舶六自由度模型 Fig. 3 Ship six degree of freedom model |
从图3可以看出船舶在空间的3个方向上均包含直线和旋转2种运动,因此船舶在海面上航行拥有6个自由度,船舶在海平面上的航行运动可以用下式表示:
| $ \left( {m + \Delta m} \right)\frac{{{\rm{d}}{V_s}}}{{{\rm{d}}t}} = {T_{ef}} - R \text{。} $ | (16) |
式中:m为船体重量;∆m为船体附加重量;R为船体航行过程中遭遇的阻力。
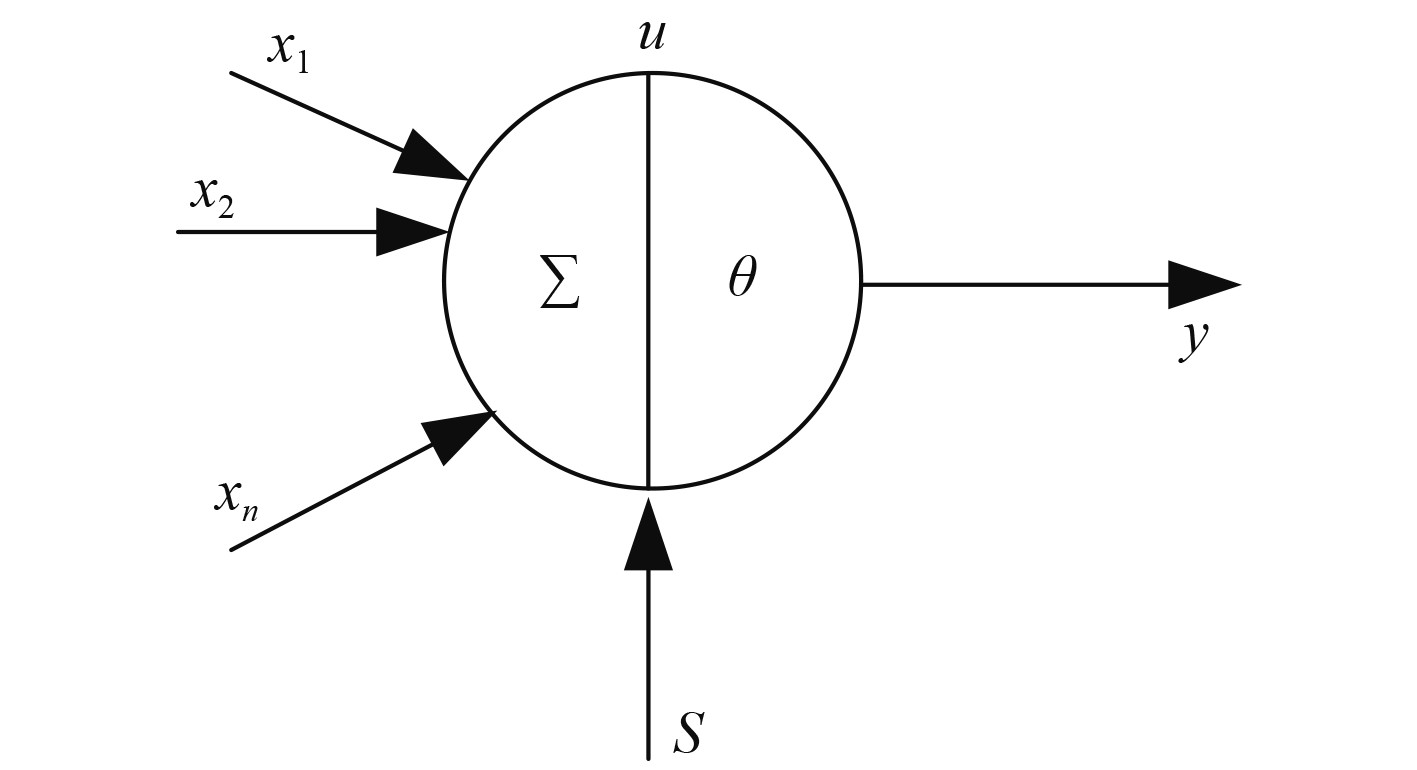
3 船舶推进系统故障诊断和预测 3.1 基于神经网络的故障诊断和预测作为一种自适应类型的识别模式,神经网络无需提前给出相关知识或者函数,因为神经网络的决策机制是通过自己的学习机制自动学习得到的。网络拓扑结构、神经元特点以及训练机制共同决定了神经网络的特性。神经网络因为这些特点,广泛地应用于故障诊断和预测领域。神经网络中包含了大量的神经元,因此神经元是神经网络的基础结构,神经元属于多输入、单输出的结构,其基本结构如图4所示。图中u是神经元内部状态,θ是阈值,x作为神经元的输入,s属于神经元控制命令,y是输出信号。
|
图 4 神经元结构模型 Fig. 4 Neuron structure model |
神经元模型一般可以使用一阶微分方程来表示,如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {\tau \dfrac{{{\rm{d}}{u_i}}}{{{\rm{d}}t}} = - {u_i}\left( t \right) + \displaystyle\sum {{w_{ij}}{x_j}\left( t \right) - {\theta _i}} } ,\\ {{y_i}\left( t \right) = f\left[ {{u_i}\left( t \right)} \right]} 。\end{array}} \right. $ | (18) |
支持向量机可以分成线性支持向量机和非线性支持向量机。二叉树分类是一种线性支持向量机,该方法是将多分类问题转变成多个二分类问题之后,再对二分类问题进行处理。以二分类理论为基础,二叉树分类法可以根据K个类构建出k-1个分类器,其中构建的第m个二分类器是将第m类的样本归为同一类,用ym=+1来表示,除了m类之外的类划分成另一类,用ym=−1来表示,按照以上方法,第m个分类器的输出表达式可以用下式表示:
| $ {f^m}\left( x \right) = {{\rm{sgn}}} \left\{ {\sum {\alpha _1^my_1^mK\left( {{x_i},x} \right) + {b^m}} } \right\}\text{。} $ | (19) |
船舶推进系统作为船舶的重要系统之一,迅速并且精准地对船舶推进系统的相关故障进行诊断和预测是船舶日常维护的重要内容。船舶的故障诊断技术是一种可以扩大船舶经济效益、降低船舶损失的一种技术,因此对船舶的故障诊断和预测技术进行研究十分重要。本文介绍了船舶推进系统、船舶推进系统相关的数学模型,基于神经网络和支持向量机研究了船舶的故障诊断和预测技术。
| [1] |
赖永发, 徐合力, 高岚. 基于LDA_GA_SVM的船舶电力推进系统故障诊断[J]. 中国船修, 2020(33): 33-39. |
| [2] |
白桂银. 船舶电力推进系统故障诊断技术[J]. 舰船科学技术, 2019(41): 91-93. |
| [3] |
胡燕. 虚拟现实技术在船舶推进系统故障诊断中的应用[J]. 舰船科学技术, 2018(40): 58-60. |
| [4] |
廖丽, 唐仁奎. T-S模糊模型在船舶推进系统故障诊断中的研究[J]. 舰船科学技术, 2016(38): 154-156. |
| [5] |
罗黎. 神经网络在船舶电力推进系统故障诊断中的应用[J]. 舰船科学技术, 2016(38): 97-99. |
| [6] |
陈郭, 张刚, 佘道明. 基于T-S模糊模型的船舶推进系统故障诊断研究[J]. 船舶工程, 2015(37): 59-63. |
| [7] |
梁树甜, 孟德东. 支持向量机在船舶电力推进系统故障诊断中的应用[J]. 船电技术, 2014(34): 50-54. |
| [8] |
黄辉, 褚建新, 沈爱递. 基于小波分析的船舶螺旋桨故障诊断[J]. 船舶工程, 2014(36): 45-48. |
 2022, Vol. 44
2022, Vol. 44
