2. 船舶动力工程技术交通行业重点实验室, 湖北 武汉 430063;
3. 国家水运安全工程技术研究中心, 湖北 武汉 430063;
4. 武汉理工大学 物流工程学院, 湖北 武汉 430063
2. Key Laboratory of Marine Power Engineering and Technology (Ministry of Communications), Wuhan 430063, China;
3. National Engineering Research Center for Water Transport Safety, Wuhan 430063, China;
4. School of Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China
吊舱推进是20世纪90年代发展起来的一种船舶电力推进系统,直接将螺旋桨连接到电机上是其革命性的构思[1]。吊舱推进器将推进系统设计成一个整体悬挂在船体尾部的舱室,可以360°旋转产生任意方向的推力,因此搭载吊舱推进器的船舶具有较高的操纵性[2]。由于吊舱推进器整体布置于水下,进流更均匀,且没有尾轴,螺旋桨的水动力性能得到提升,空泡效应减少,因此振动与噪声水平均有所下降[3]。随着国家开始重视邮轮旅游产业的发展和国际主要邮轮公司将投资重点转向我国,国内的邮轮旅游业正处于蓬勃发展阶段[4],也开展了一些邮轮的自主建造项目。邮轮因其特殊的用途,需要较频繁的在海上转向、进出狭窄水道和出入港,因此对操纵性和机动性有很高的要求[5]。除此之外对舒适性的要求也较高,这主要是对振动和噪声的控制,现代邮轮客舱的噪声标准达到了45~49 dB[6]。搭载吊舱推进器的邮轮通常轴系较短,但同样需要较高的操纵性,如将吊舱推进器推广至军用,轴系的振动会传递到吊舱舱体并引起水下声辐射,从而降低军舰的隐蔽性,这都对吊舱推进器的各项性能提出了更高的要求。目前吊舱推进技术在国外已趋于成熟,数个公司先后推出了不同系列的吊舱推进器, 例如Azipod,Mermaid,Dolphin,SSP等。国内近年来虽然也承建了一些搭载吊舱推进器的电力推进船舶,但其吊舱推进设备大多依赖国外进口[7], 同时也开展了一些吊舱推进技术的理论研究,为吊舱推进器的国产化奠定了基础。各种型号的吊舱推进器在不同工况下的水动力特性引起了很多学者的重视[8-10],吊舱推进电机控制系统也是研究较多的领域[11-12]。此外,张旭等[13]给出了吊舱支撑结构的设计和校核方案。郑建等[14]进行了吊舱推进器温升实验,为冷却系统的设计提供了参考。刘洁等[15]基于Matlab平台构建了搭载吊舱推进器船舶的模型,验证了吊舱推进船舶良好的操纵性,刘洪梅等[16]采用实验法得到了相似的结论。张少明等[17]基于 PLC 技术设计了双吊舱式的电力推进回转系统。赵鹏飞等[18]分析了吊舱推进器与船体的耦合振动效应。
目前关于吊舱推进器轴系的研究还比较少。虽然对于船舶轴系振动特性的研究由来已久,但大多针对的是传统柴油机-螺旋桨驱动方式的轴系。从Prohl将传统的Holzer法改进成传递矩阵法,并推广应用到船舶轴系横向振动的研究中[19],之后很多学者都用这种方法研究了推进轴系的自由振动和强迫振动特性[20-22]。随着计算器运算能力的提升,有限元等数值方法被广泛运用到船舶轴系振动特性的分析中。秦丽[23]建立了集装箱船推进轴系的有限元模型,分析了轴系在螺旋桨激励力、惯性载荷等条件下的振动特性。李全超等[24]借助有限元软件分析了不同支撑参数下的轴系振动特性。Zou等[25]采用有限元/边界元方法建立了螺旋桨-轴流体动力学模型,分析了桨叶弹性对轴系振动特性的影响。与数值法相比,解析法具有计算时间较短、物理意义明确等优点,也有一些学者将解析法运用到船舶推进轴系的振动分析中,田哲等[26]给出了轴的振动方程,研究了船体变形激励下轴的振动特性,Zhang等[27]建立了包括螺旋桨的轴系解析模型,分析了轴的固有振动特性。这些研究通常将轴系简化为均质等截面梁,但吊舱推进器轴系各段之间材料、直径等相差较大。本文将相关方法推广应用到了吊舱推进器的轴系振动特性研究中,并将轴系视为非均质变截面梁。轴系的振动会沿着轴承传递到舱体,并引起水下声辐射,降低舰船的隐蔽性,由于吊舱推进器轴系径向轴承比推力轴承数量多,横向振动的传递作用更显著,因此本文以横向振动为例,对吊舱推进器轴系的振动特性进行分析。在已有文献基础上,将吊舱推进器轴系简化为非均质变截面梁,提出吊舱推进器轴系振动的解析算法,构建动力学模型,给出轴系各段之间的连续条件和边界条件,形成有效的振动特性解析方法,研究吊舱推进器轴系在螺旋桨激励和舱体变形激励下的强迫振动特性。
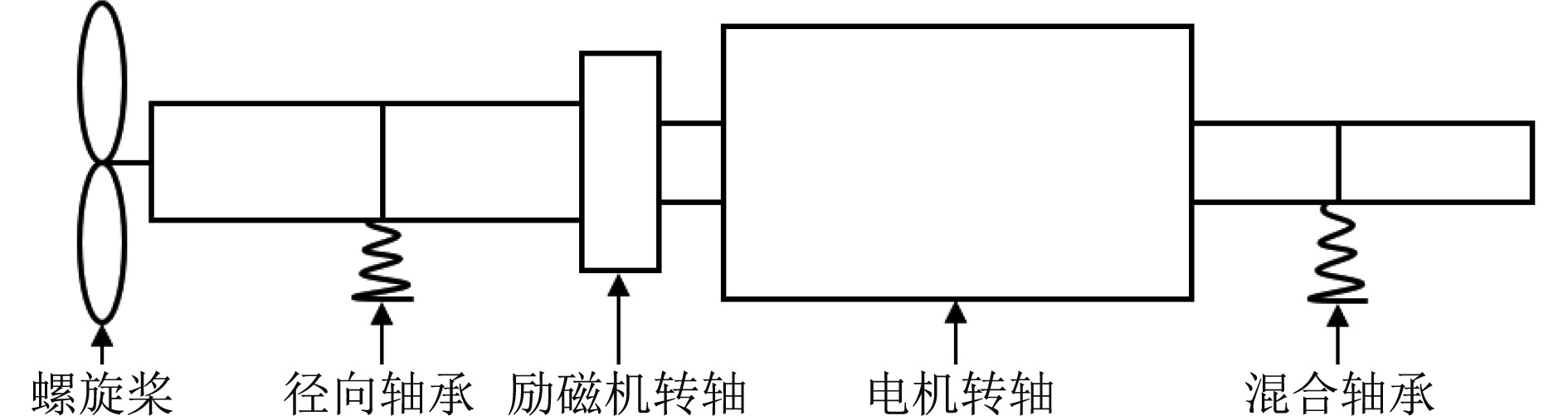
1 吊舱推进器轴系振动理论推导 1.1 系统模型如图1所示,吊舱推进器轴系是由螺旋桨、推力轴、电机转轴、励磁机转轴、驱动端径向轴承和非驱动端混合轴承等组成的结构。由于吊舱推进器轴系与传统的柴油机轴系相比,长度较短,各段直径相差较大,电机转轴、励磁机转轴与其他轴段材料也不相同,不能直接简化为均质等截面梁。在对其进行建模和计算方法研究时,将螺旋桨简化为带有转动惯量的集中质量,轴承简化为弹簧结构。
|
图 1 吊舱推进器轴系结构示意图 Fig. 1 Schematic diagram of the pod propeller shafting |
在轴系的弯曲振动计算中,不考虑轴的剪切变形和截面绕中性轴转动对弯曲振动的影响,轴即简化为欧拉-伯努利梁。将未变形时轴的轴线取作
| $ \frac{{\partial }^{2}}{\partial {x}^{2}}\left[E\left(x\right)I\left(x\right)\frac{{\partial }^{2}y\left(x,t\right)}{\partial {x}^{2}}\right]+\rho \left(x\right)A\left(x\right)\frac{{\partial }^{2}y\left(x,t\right)}{\partial {t}^{2}}=0 ,$ | (1) |
将方程的解分离变量
| $ y\left(x,t\right)=\varphi \left(x\right)q\left(t\right), $ | (2) |
代入振动方程,得到
| $ \frac{\ddot{q}\left(t\right)}{q\left(t\right)}=-\frac{{\left[E\right(x\left)I\right(x\left){\varphi }^{\text{'}\text{'}}\left(x\right)\right]}^{\text{'}\text{'}}}{\rho \left(x\right)A\left(x\right)\varphi \left(x\right)}, $ | (3) |
其中用“
| $ \ddot{q}\left(t\right)+{\omega }^{2}q\left(t\right)=0 ,$ | (4) |
| $ {\varphi }^{\left(4\right)}\left(x\right)-{\alpha }^{4}\varphi \left(x\right)=0。$ | (5) |
其中:
| $ \alpha =\sqrt[4]{\frac{\rho \left(x\right)A\left(x\right)}{E\left(x\right)I\left(x\right)}{\omega }^{2}}{\text{。}} $ | (6) |
方程(5)的解确定轴弯曲振动的模态函数,其通解形式为:
| $ \varphi \left(x\right)={C}_{1}\mathrm{cos}\left(\alpha x\right)+{C}_{2}\mathrm{sin}\left(\alpha x\right)+{C}_{3}\mathrm{ch}\left(\alpha x\right)+{C}_{4}\mathrm{sh}\left(\alpha x\right)。$ | (7) |
其中积分常数
由图1所示,吊舱推进器轴系各段之间因直径、材料不同及轴承的支撑作用共分为数段,各轴段之间在位移、转角、弯矩、剪力等方面存在连续性,可据此建立其连续条件。
| $ {y}_{i}\left({l}_{i},t\right)={y}_{i+1}\left(0,t\right), $ | (8) |
| $ \frac{\partial {y}_{i}\left({l}_{i},t\right)}{\partial x}=\frac{\partial {y}_{i+1}\left(0,t\right)}{\partial x}, $ | (9) |
| $ E\left(x\right)I\left(x\right)\frac{{\partial }^{2}{y}_{i}\left({l}_{i},t\right)}{\partial {x}^{2}}=E\left(x\right)I\left(x\right)\frac{{\partial }^{2}{y}_{i+1}\left(0,t\right)}{\partial {x}^{2}}, $ | (10) |
| $ E\left(x\right)I\left(x\right)\frac{{\partial }^{3}{y}_{i}\left({l}_{i},t\right)}{\partial {x}^{3}}=E\left(x\right)I\left(x\right)\frac{{\partial }^{3}{y}_{i+1}\left(0,t\right)}{\partial {x}^{3}}。$ | (11) |
当轴的两段之间因支撑轴承分段时,式(11)变为[27]:
| $ E\left(x\right)I\left(x\right)\frac{{\partial }^{3}{y}_{i}\left({l}_{i},t\right)}{\partial {x}^{3}}=E\left(x\right)I\left(x\right)\frac{{\partial }^{3}{y}_{i+1}\left(0,t\right)}{\partial {x}^{3}}+{S}_{i}{y}_{i+1}\left(0,t\right) ,$ | (12) |
其中
对于吊舱推进器轴系的非驱动端,有边界条件
| $ E\left(x\right)I\left(x\right)\frac{{\partial }^{2}y\left(l,t\right)}{\partial {x}^{2}}=0 ,$ | (13) |
| $ E\left(x\right)I\left(x\right)\frac{{\partial }^{3}y\left(l,t\right)}{\partial {x}^{3}}=0 ,$ | (14) |
而在轴的驱动端,螺旋桨可视为集中质量,边界条件变为[27]:
| $ E\left(x\right)I\left(x\right)\frac{{\partial }^{2}y\left(0,t\right)}{\partial {x}^{2}}={-\omega }^{2}\frac{\partial y\left(0,t\right)}{\partial x}j ,$ | (15) |
| $ E\left(x\right)I\left(x\right)\frac{{\partial }^{3}y\left(0,t\right)}{\partial {x}^{3}}={-\omega }^{2}\partial y\left(0,t\right){m}_{1}。$ | (16) |
其中:
| $ {m}^{\text{'}}=\left[\chi \left(1+1.66\frac{H}{D}\right)+0.083\frac{H}{D}\right]\frac{7.85-\tau }{4.85}m 。$ | (17) |
其中:
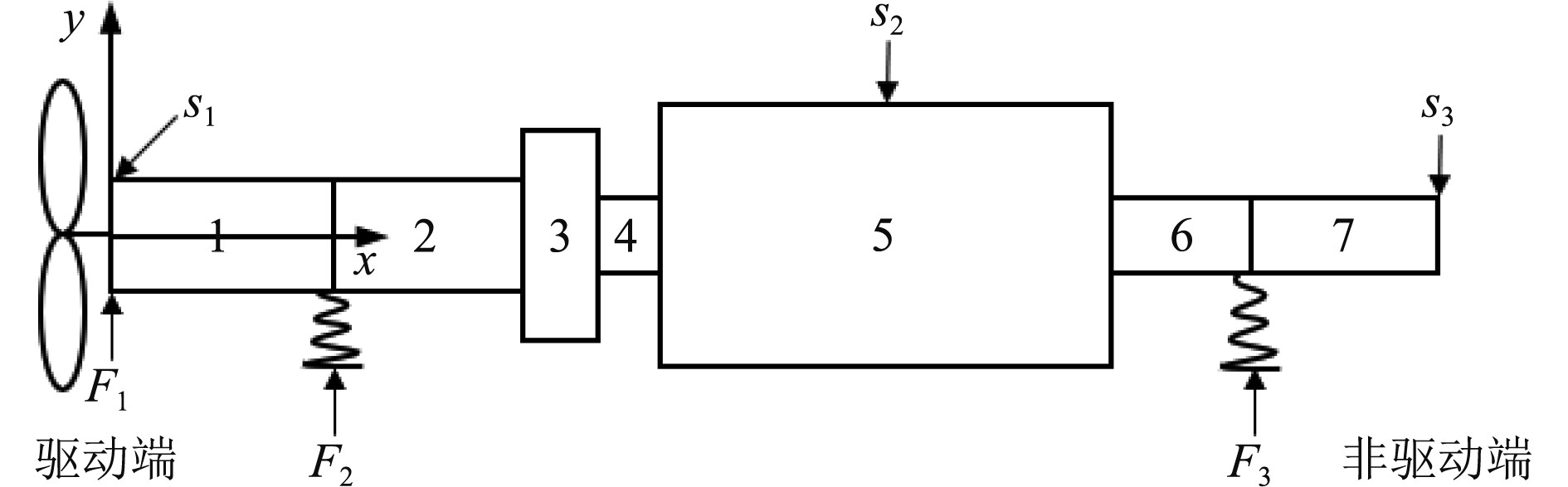
采用某型号吊舱推进器轴系作为计算模型,如图2所示。轴系从左至右共分为7段,各段参数如表1所示。吊舱推进器轴系在驱动端布置有径向滚子轴承,非驱动端布置有混合轴承,混合轴承包括径向滚子轴承和滑动推力轴承。其中驱动端径向轴承的刚度为
|
图 2 吊舱推进轴系计算模型 Fig. 2 Calculation model of the pod propulsion shafting |
|
|
表 1 吊舱推进器轴系各段参数表 Tab.1 Parameters of each section of the pod propeller shafting |
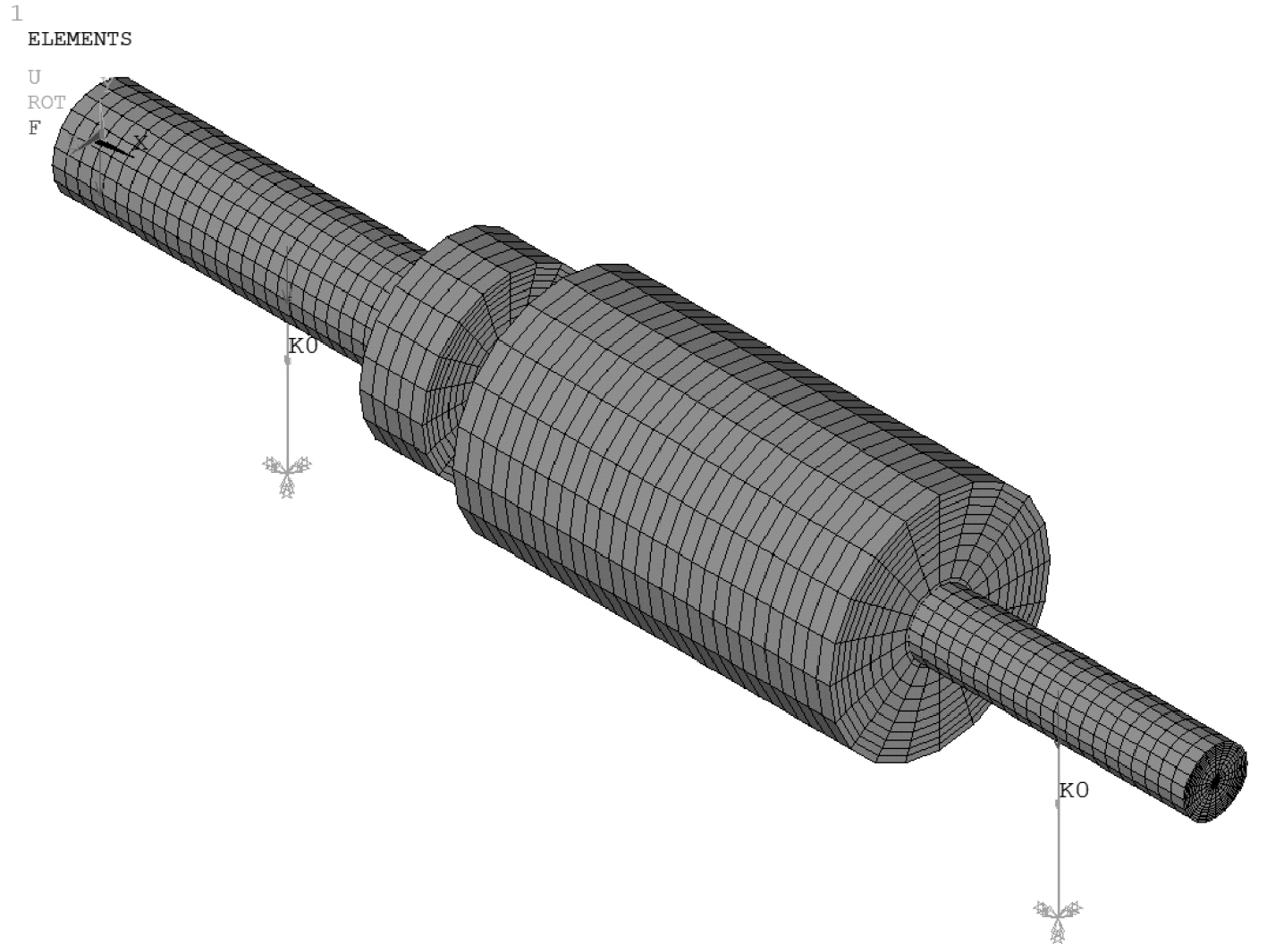
为验证本文解析法的正确性,采用Ansys有限元软件建立吊舱推进器轴系模型,如图3所示。其中轴采用beam188单元建模,螺旋桨采用mass21单元模拟, 轴承采用combin14单元模拟, 下端设置为全约束,即将轴承与舱体视为刚性连接。在
|
图 3 吊舱推进器轴系有限元模型 Fig. 3 Finite element model of pod propeller shafting |

|
图 4 解析法与数值法振动响应对比 Fig. 4 Comparison of analytical method and numerical method of vibration response |
计算模型与上一节相同,分析轴承刚度、激励点位置、电机转轴尺寸对吊舱推进器轴系振动特性的影响。
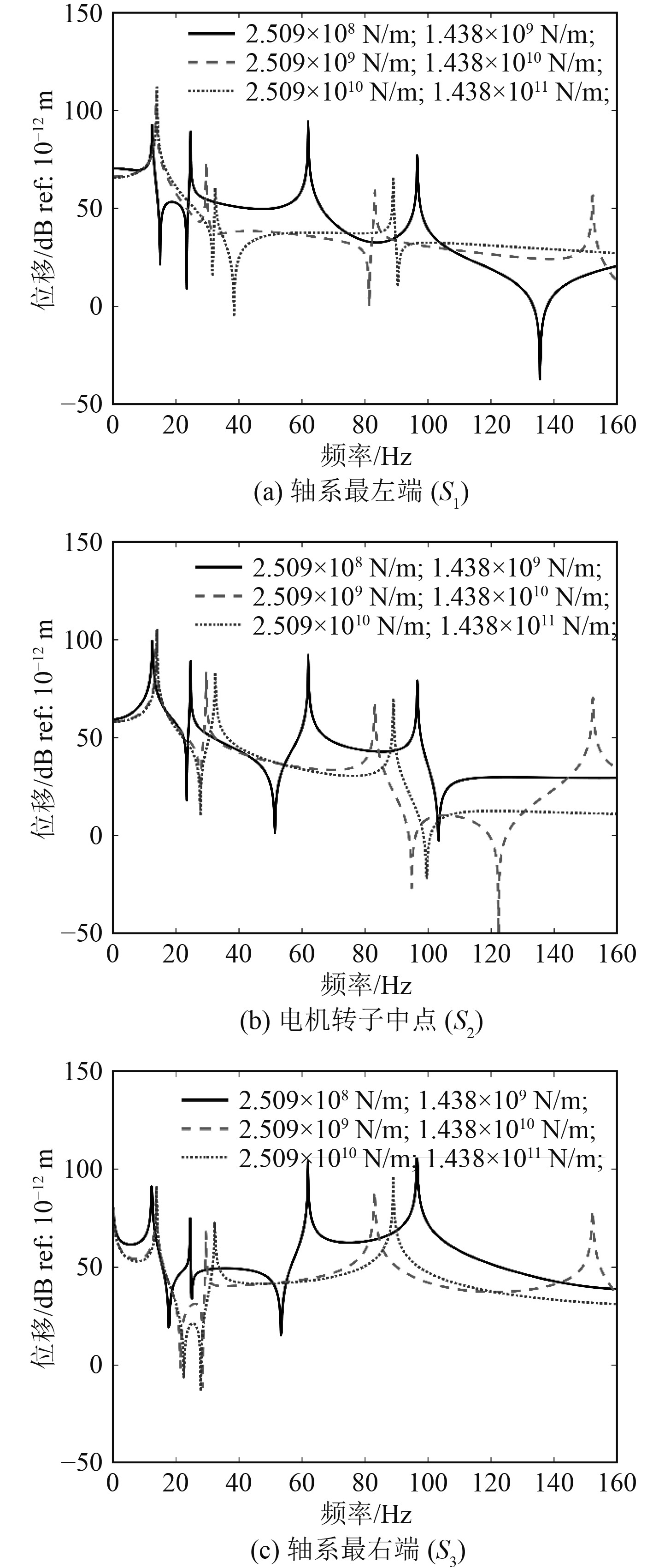
3.1 轴承刚度对轴系振动特性影响讨论轴承刚度对于轴系振动特性的影响。吊舱推进器轴系上布置有径向刚度分别为
|
图 5 不同轴承刚度下轴系振动响应 Fig. 5 Vibration response of shafting under different bearing stiffness |
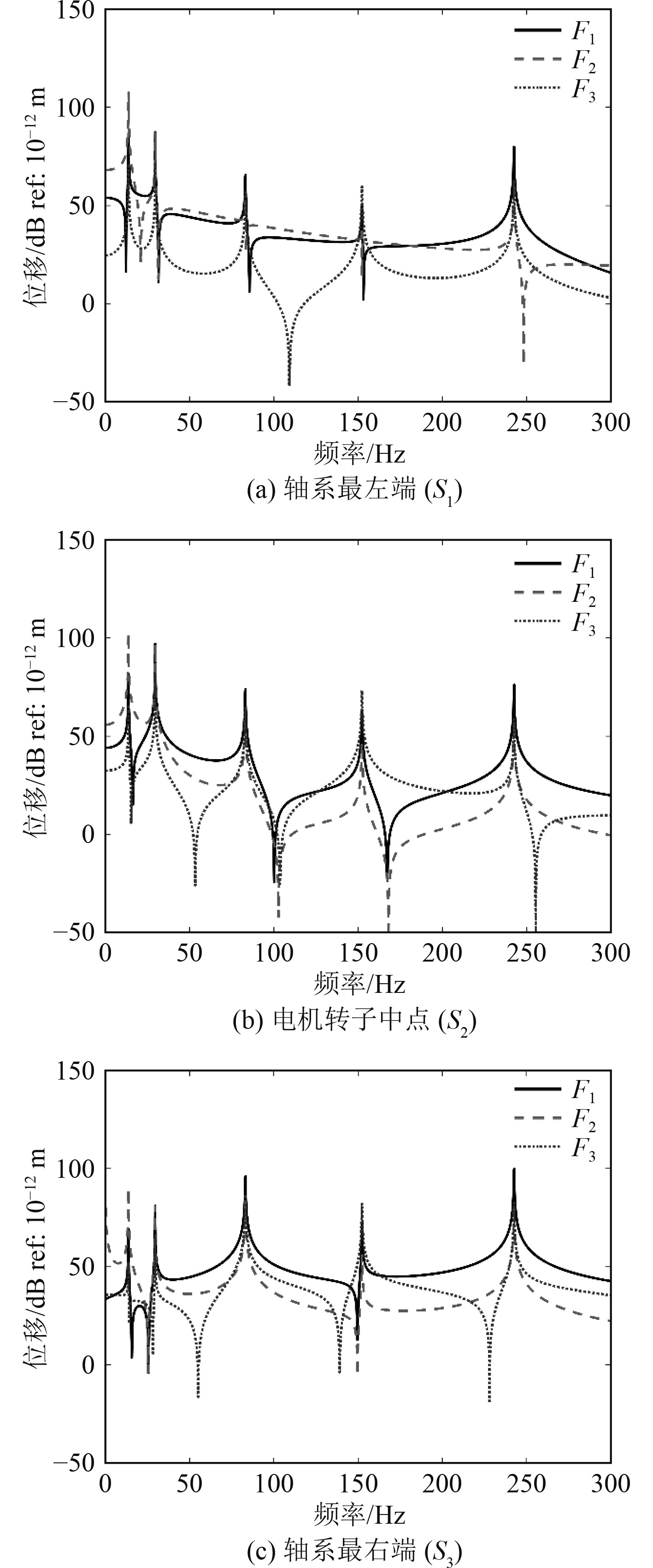
本节讨论激励点的位置对吊舱推进器轴系振动特性的影响,分别在螺旋桨处(
|
图 6 不同激励点位置下轴系振动响应 Fig. 6 Vibration response of shafting under different excitation point positions |
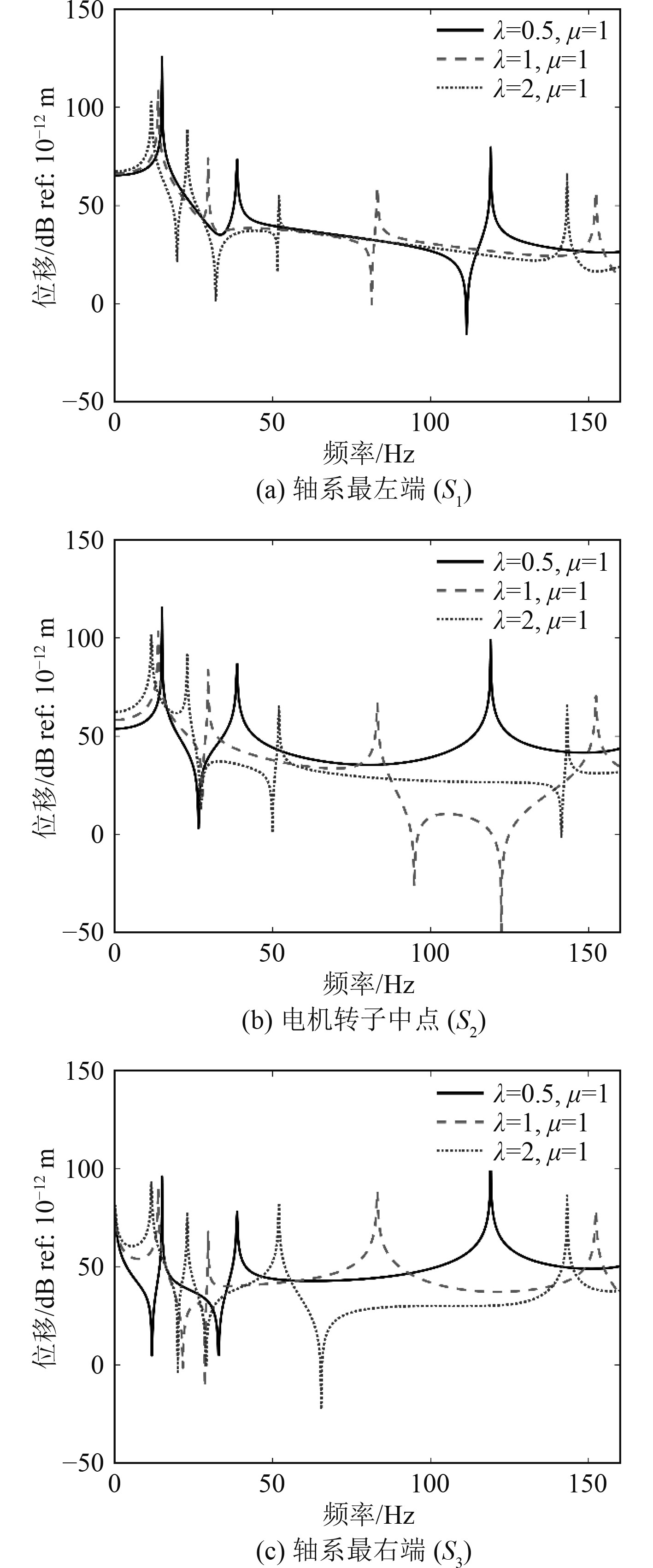
轴系第5段为电机转轴,讨论电机转轴尺寸对整体轴系振动特性的影响。以转轴原始长度
|
图 7 不同电机转轴长度下轴系振动响应 Fig. 7 Vibration response of shafting under different motor shaft lengths |
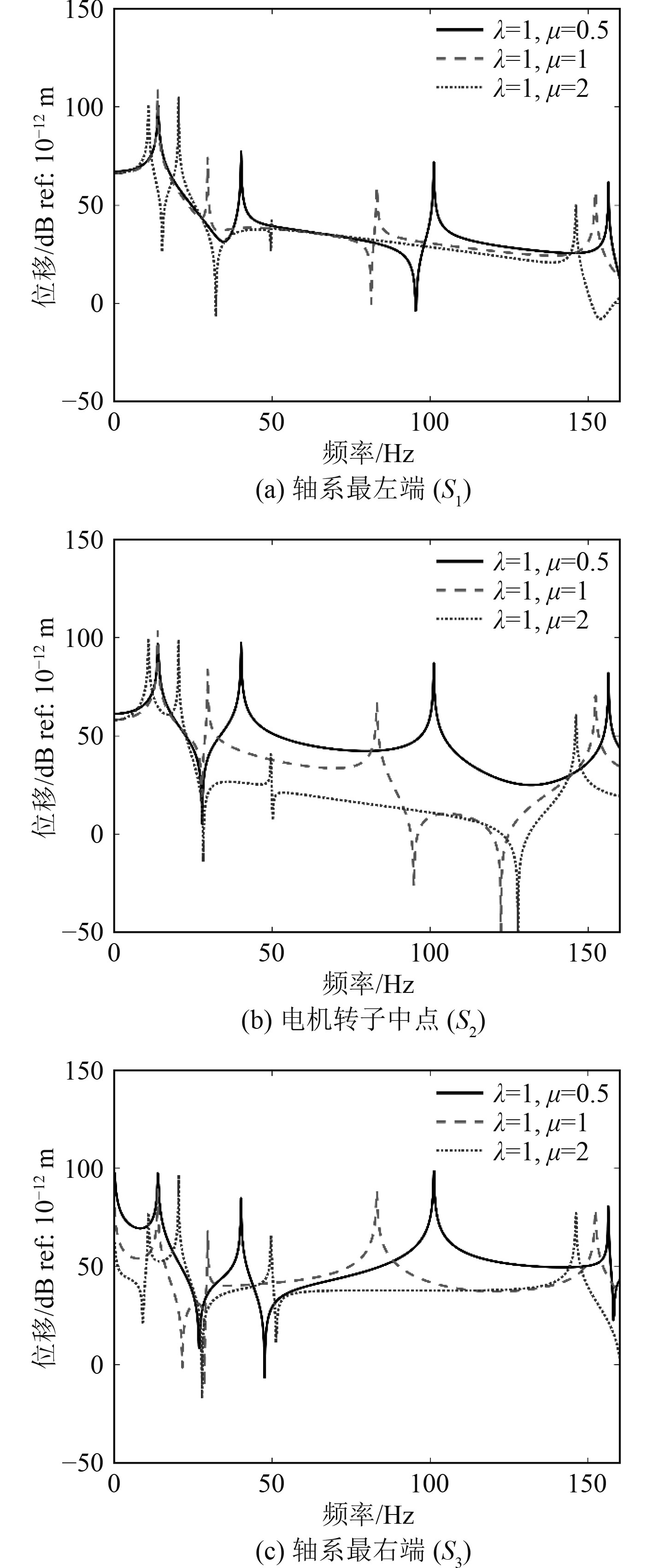
|
图 8 不同电机转轴直径下轴系振动响应 Fig. 8 Vibration response of shafting under different motor shaft diameters |
本文提出将吊舱推进器轴系视为非均质变截面梁的解析算法,在轴系各段之间建立了连续条件,并分别给出了螺旋桨端和自由端的边界条件,分析了吊舱推进器轴系的振动特性,结论如下:
1)轴承刚度的增大使得吊舱推进器轴系中高阶共振峰的频率增大,整体幅值减小;
2)螺旋桨激励与其他激励相比在低频段占主导作用;
3)电机转轴长度越长、与相邻轴段直径相差越大时整体轴系越容易发生低频振动。电机转轴直径减小使得该轴段振幅增大。
| [1] |
唐文彪, 张聪, 欧阳武, 等. 大型船舶吊舱推进器发展现状[J]. 舰船科学技术, 2020, 42(7): 8-12. |
| [2] |
郑安宾, 田忠殿, 胡举喜, 等. 吊舱推进器的发展及应用前景[J]. 液压气动与密封, 2019, 39(6): 1-3+7. DOI:10.3969/j.issn.1008-0813.2019.06.001 |
| [3] |
高宜朋, 曾凡明, 张晓锋. 吊舱推进器在舰船推进系统中的发展现状及关键技术分析[J]. 中国舰船研究, 2011, 6(1): 90-96. DOI:10.3969/j.issn.1673-3185.2011.01.018 |
| [4] |
王占坤, 赵鹏, 郭越. 国际邮轮发展现状及对中国启示[J]. 海洋经济, 2012, 2(6): 15-19. |
| [5] |
杨刚, 孙瑞红, 叶欣梁. 豪华邮轮转向推进系统的技术探讨[J]. 物流科技, 2019, 42(12): 47-49. DOI:10.3969/j.issn.1002-3100.2019.12.013 |
| [6] |
李兰美, 黄斐, 陈明铭. 豪华邮轮建造特点初步分析[J]. 造船技术, 2014(2): 10-13+26. DOI:10.3969/j.issn.1000-3878.2014.02.003 |
| [7] |
高海波, 高孝洪, 陈辉, 等. 吊舱式电力推进装置的发展及应用[J]. 武汉理工大学学报(交通科学与工程版), 2006(1): 77-80. DOI:10.3963/j.issn.2095-3844.2006.01.021 |
| [8] |
姚震球, 徐植融, 凌宏杰, 等. 拖式吊舱推进器的水动力特性分析[J]. 舰船科学技术, 2020, 42(9): 44-49. YAO Zhen-qiu, XU Zhi-rong, LING Hong-jie, et al. Analysis of hydrodynamic characteristics of pull podded thruster[J]. Ship Science and Technology, 2020, 42(9): 44-49. |
| [9] |
盛立, 熊鹰, 杨勇. 吊舱式CRP推进器水动力性能数值模拟[J]. 舰船科学技术, 2012, 34(10): 9-16. SHENG Li, XIONG Ying, YANG Yong. Experimental investigation and numberical simulation on the open-water performance of poded contra-rotating propulsor[J]. Ship Science and Technology, 2012, 34(10): 9-16. DOI:10.3404/j.issn.1672-7649.2012.10.002 |
| [10] |
徐佩, 郭春雨, 王超, 等. 冰几何尺寸对吊舱推进器水动力性能的影响[J]. 哈尔滨工程大学学报, 2020, 41(11): 1642-1650. |
| [11] |
姜星星. 吊舱式船舶电力推进控制的研究分析[D]. 镇江: 江苏科技大学, 2013.
|
| [12] |
姚文龙, 涂志平, 池荣虎, 等. 船舶吊舱推进电机控制策略发展综述[J]. 舰船科学技术, 2017, 39(19): 1-6. YAO Wen-long, TU Zhi-ping, CHI Rong-hu, et al. Development of the control strategy for ship podded propulsion motor[J]. Ship Science and Technology, 2017, 39(19): 1-6. |
| [13] |
张旭, 骆伟, 张艳, 等. 吊舱式推进器支撑结构设计与校核[J]. 广东造船, 2019, 38(6): 34-37. DOI:10.3969/j.issn.2095-6622.2019.06.012 |
| [14] |
郑建, 田忠殿, 王平, 等. 吊舱推进器温升试验方法设计研究[J]. 船舶工程, 2020, 42(S1): 189-191. |
| [15] |
刘洁, 李彦. 吊舱推进船舶操纵性仿真研究[J]. 科学技术与工程, 2011, 11(3): 507-512. DOI:10.3969/j.issn.1671-1815.2011.03.017 |
| [16] |
刘洪梅, 许文兵, 陈雄, 等. 吊舱推进与传统推进船舶操纵性能对比分析[J]. 船舶力学, 2011, 15(5): 463-467. LIU Hong-mei, XU Wen-bing, CHEN Xiong, et al. Maneuvering performance comparison between POD and conventional ships[J]. Journal of Ship Mechanics, 2011, 15(5): 463-467. DOI:10.3969/j.issn.1007-7294.2011.05.003 |
| [17] |
张少明, 崔浩, 蒋祖星. 基于PLC技术的双吊舱式电力推进回转系统设计[J]. 舰船科学技术, 2018, 40(22): 121-123. |
| [18] |
赵鹏飞, 夏利娟, 张鑫. 邮轮推进器舱与吊舱推进器耦合振动分析[J]. 舰船科学技术, 2019, 41(11): 66-70. |
| [19] |
PROHL M A. A method for calculating vibration frequency and stress of a banded group of turbine buckets[J]. Trans. ASME, 1958, 169-180. |
| [20] |
蔡双利, 曾凡明, 唐成. 某电力推进轴系横向振动影响因素分析[J]. 船海工程, 2013, 42(1): 118-120+125. |
| [21] |
唐天国. 基于传递矩阵法的船舶推进轴振动特性研究[J]. 舰船科学技术, 2017, 39(8): 31-33. TANG Tian-guo. Study on vibration characteristics of ship propulsion shaft based on transfer matrix method[J]. Ship Science and Technology, 2017, 39(8): 31-33. |
| [22] |
YANG Yong, CHE Chidong, TANG Wenyong. Shafting coupled vibration research based on wave approach[J]. Journal of Shanghai Jiaotong University Science, 2014, 19(3): 325−336.
|
| [23] |
秦丽. 大型船舶推进轴系功率流分析理论与方法研究[D]. 武汉: 武汉理工大学, 2014.
|
| [24] |
李全超, 俞强, 刘伟. 支撑参数对船舶轴系-轴承-基座系统振动特性影响研究[J]. 舰船科学技术, 2016, 38(11): 101-104. LI Quan-chao, YU Qiang, LIU Wei. Effect of supporting parameters on marine shaft vibration characteristics[J]. Ship Science and Technology, 2016, 38(11): 101-104. |
| [25] |
ZOU Donglin, ZHANG Jianbo, TA Na, et al. Study on the axial exciting force characteristics of marine propellers considered the effect of the shaft and blade elasticity[J]. Applied Ocean Research, 2019, 89: 141−153.
|
| [26] |
田哲, 张聪, 严新平, 等. 计入船体变形激励的大型船舶推进轴系振动性能研究[J]. 船舶力学, 2015, 19(11): 1368-1376. TIAN Zhe, ZHANG Cong, YAN Xin-ping, et al. Vibration characteristic study of large vessel’s shaft system taking into account the ship hull deformation excitations[J]. Journal of Ship Mechanics, 2015, 19(11): 1368-1376. |
| [27] |
ZHANG Cong, TIAN Zhe, YAN Xinping. Analytical analysis of the vibration of propulsion shaft under hull deformation excitations[J]. Journal of V: bioengineering, 2016, 18(1): 44−55.
|
| [28] |
刘延柱, 陈文良, 陈立群. 振动力学[M]. 北京: 高等教育出版社, 2011.
|
| [29] |
罗晨. 水面舰船轴系—尾部结构耦合振动及水声特性研究[D]. 北京: 中国舰船研究院, 2014.
|
 2022, Vol. 44
2022, Vol. 44
