对于无破冰能力的极区船舶,航行于北极航道的碎冰区域时,需要考虑碎冰对船舶的影响。极地船舶碎冰载荷的研究直接关系到船舶能否安全、高效的航行于碎冰区。
北极航道内的碎冰表现出很强的离散特性,针对这一问题,专家学者运用离散元法,发展出多种海冰离散元模型。Loset[1]利用二维离散圆盘对浮冰冰区中的浮碎冰进行了动力学的数值模拟。Hanse[2]采用二维离散元对浮碎冰区中系泊船舶的运动响应进行数值模拟。近十年来,国内的学者在冰载荷领域的研究出现大幅增加。季顺迎等[3]采用三维圆盘,球体模型,块体模型对浮碎冰及平整冰与直立结构,船舶结构等相互作用进行了数值模拟。童波等[4]基于voronoi图参照真实冰区测量信息,利用遗传算法对浮冰尺度概率分布展开了优化研究,并用有限元法对船舶在浮冰区航行阻力平均值进行了数值计算。研究发现,大多数学者侧重于碎冰数值模型的改进,很少注重海冰材料参数的变化对碎冰载荷的讨论。
本文基于极区船舶航行于碎冰区的理想化假设,结合理论研究,建立碎冰二维圆盘粘弹性模型,引入包括流体阻力、螺旋桨推力与舵力、欧拉力、碎冰载荷的三自由度船舶运动方程,模拟船舶航行于浮碎冰区域,得到船舶航行过程中的碎冰载荷时历曲线,并研究在不同的海冰特性参数情况下,船舶纵向碎冰载荷的变化。
1 碎冰间的接触假设单个碎冰用圆形盘表示,碎冰间接触力作用于水平面,并以弹簧弹性、阻尼器粘性、滑块摩擦为特征表示。在碎冰-碎冰和碎冰-船舶碰撞中,变形表示为重叠。
1.1 碎冰运动运用直角坐标系,2个接触的圆盘被标记为
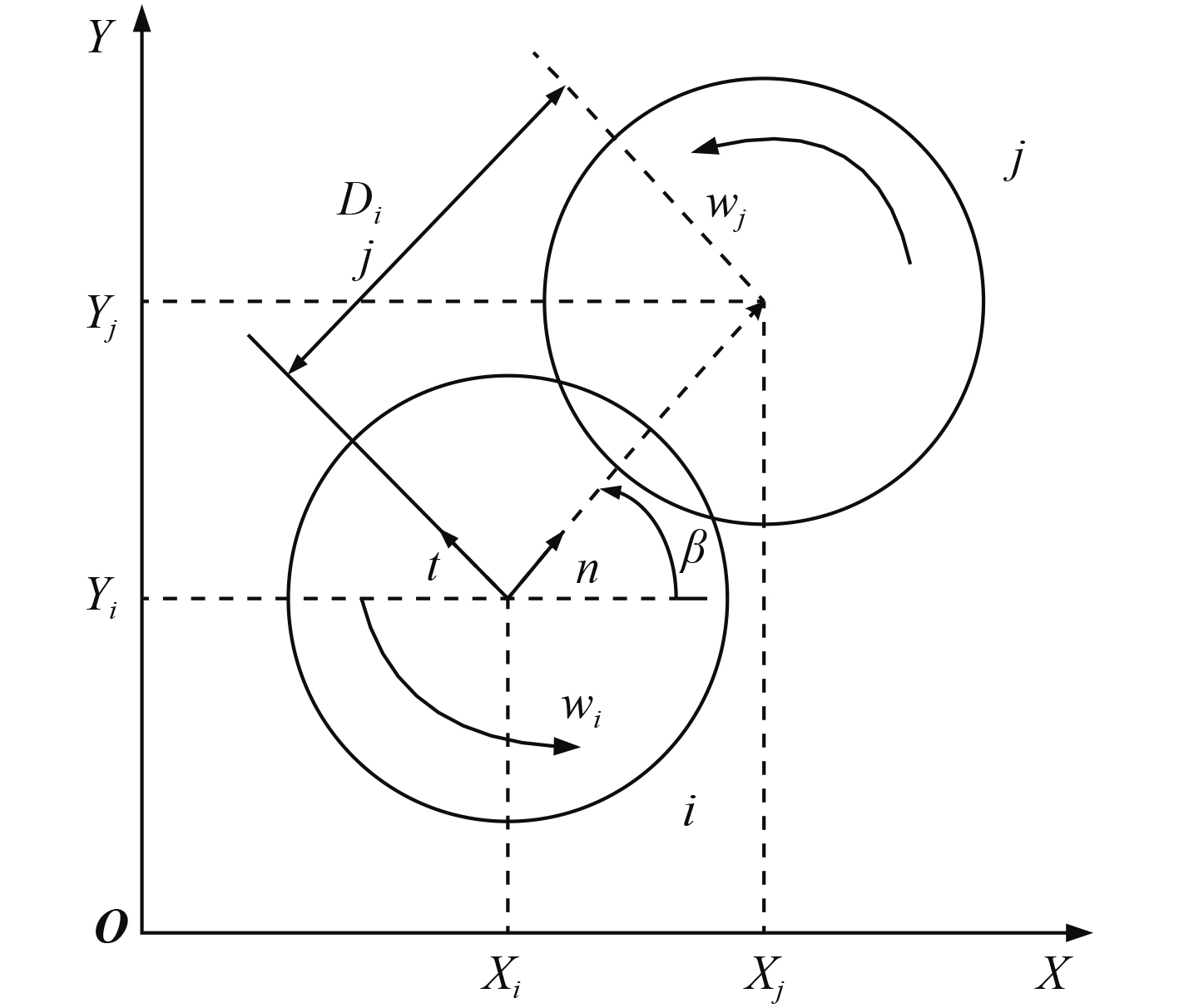
|
图 1 圆盘i与j之间接触示意图 Fig. 1 Sketch showing contact between discs i andj. |
| $ {{n}} = \frac{{{{{X}}_j} - {{{X}}_i}}}{{{D_{ij}}}} = (\cos \beta ,\sin \beta ),$ | (1) |
| $ {{t}} = ( - \sin \beta ,\cos \beta )。$ | (2) |
式中:
接触深度为:
| $ \delta = ({R_i} + {R_j}) - {D_{ij}} ,$ | (3) |
接触点(接触深度的中点)的相对速度为:
| $ {{{\dot X}}_{ij}} = {{{\dot X}}_i} - {{{\dot X}}_j} + ({R_i}{\dot \omega _i} + {R_j}{\dot \omega _j}){{t}},$ | (4) |
在法向和切向上的相对速度
| $ {\dot \delta _n} = {{{\dot X}}_{ij}} \cdot {{n}},$ | (5) |
| $ {\dot \delta _t} = {{{\dot X}}_{ij}} \cdot {{t}}。$ | (6) |
碎冰-碎冰相互碰撞通过“软粒子”方法建模,如图2所示。其中法向为弹簧与阻尼器并联,称为Kelvin模型。在
| $ F_{ni}^t = - {k_{ne}}{\delta ^t} - {k_{nv}}\dot \delta _{ni}^t ,$ | (7) |
式中:
切向为弹塑模型(非滑动)与摩擦块(滑动),
| $ F_{ti}^t = \min \left\{ {\left( {F_{ti}^{t - 1} - {k_{te}}(\Delta t)\dot \delta _{ti}^t} \right)} \right.,\left. {\mu F_{ni}^t} \right\} 。$ | (8) |
式中:
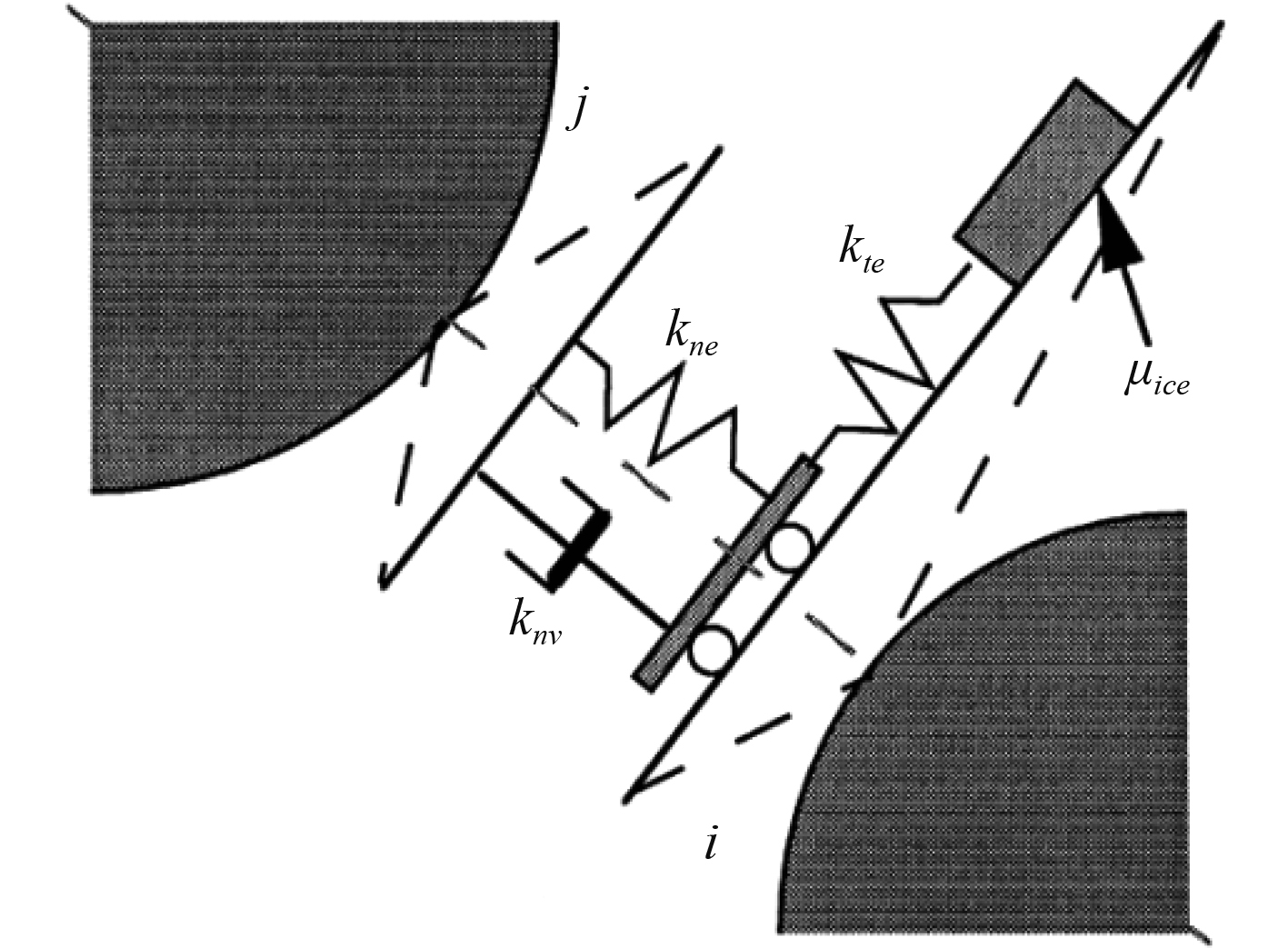
|
图 2 圆盘间相互接触力模型[6] Fig. 2 Disc interaction force model. |
由于海流的作用,碎冰受到海流的拖曳力,以及碎冰加速运动时,考虑到碎冰的附加质量。季顺迎[19]等描述了这部分的详细计算。计算出作用在每个圆盘上的所有合力和力矩后,采用中心差分法用于运动方程的数值积分,得到所有圆盘的新的速度和位置。
1.3 碎冰间的接触判断对于大量的圆盘,离散元法需要一个高效的计算方法[7]。通过使用一组单元格结构来识别相邻的圆盘,如图3所示。每个单元格是正方形的,整体单元格的边缘与大地坐标系
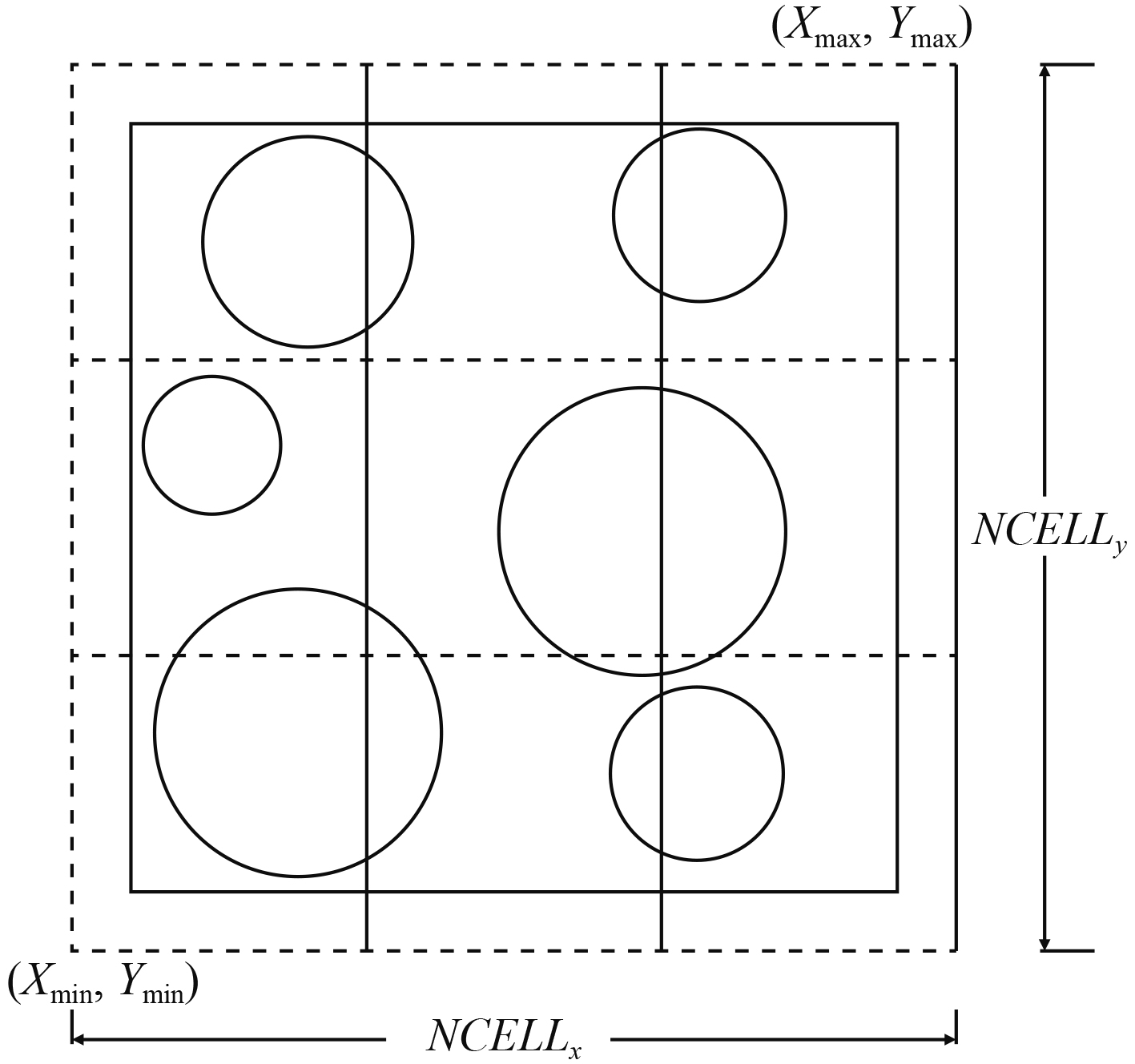
|
图 3 碎冰域与单元格 Fig. 3 Broken ice domain and cells structure. |
| $ {I_x} = NCEL{L_x} * {{\rm{int}}} \left[ {\left( {{X_i} - {X_{\min }}} \right)/\left( {{X_{\max }} - {X_{\min }}} \right)} \right] + 1 ,$ | (9) |
| $ {I_y} = NCEL{L_y} * {{\rm{int}}} \left[ {\left( {{Y_i} - {Y_{\min }}} \right)/\left( {{Y_{\max }} - {Y_{\min }}} \right)} \right] + 1 。$ | (10) |
式中:
| $ ICELL = ({I_y} - 1) * NCEL{L_x} + {I_x}。$ | (11) |
单元格尺寸和圆盘大小比率约为0.01。通过这个比率,每个单元格只包含几个圆盘,当识别可能的圆盘接触时,只需扫描圆盘当前单元格的8个相邻单元就足够了。
2 船舶运动方程极区船舶在碎冰区中航行是一个复杂的运动过程,船体主要受到碎冰载荷、螺旋桨推力和舵力、流体阻力、假想欧拉力。本文模拟了船舶在碎冰域直航过程中的纵荡、横荡和首摇运动,用Newmark迭代法解决了船舶运动与外载荷的耦合问题。
2.1 运动方程的建立引入大地坐标系和随船坐标系,如图4所示。大地坐标系
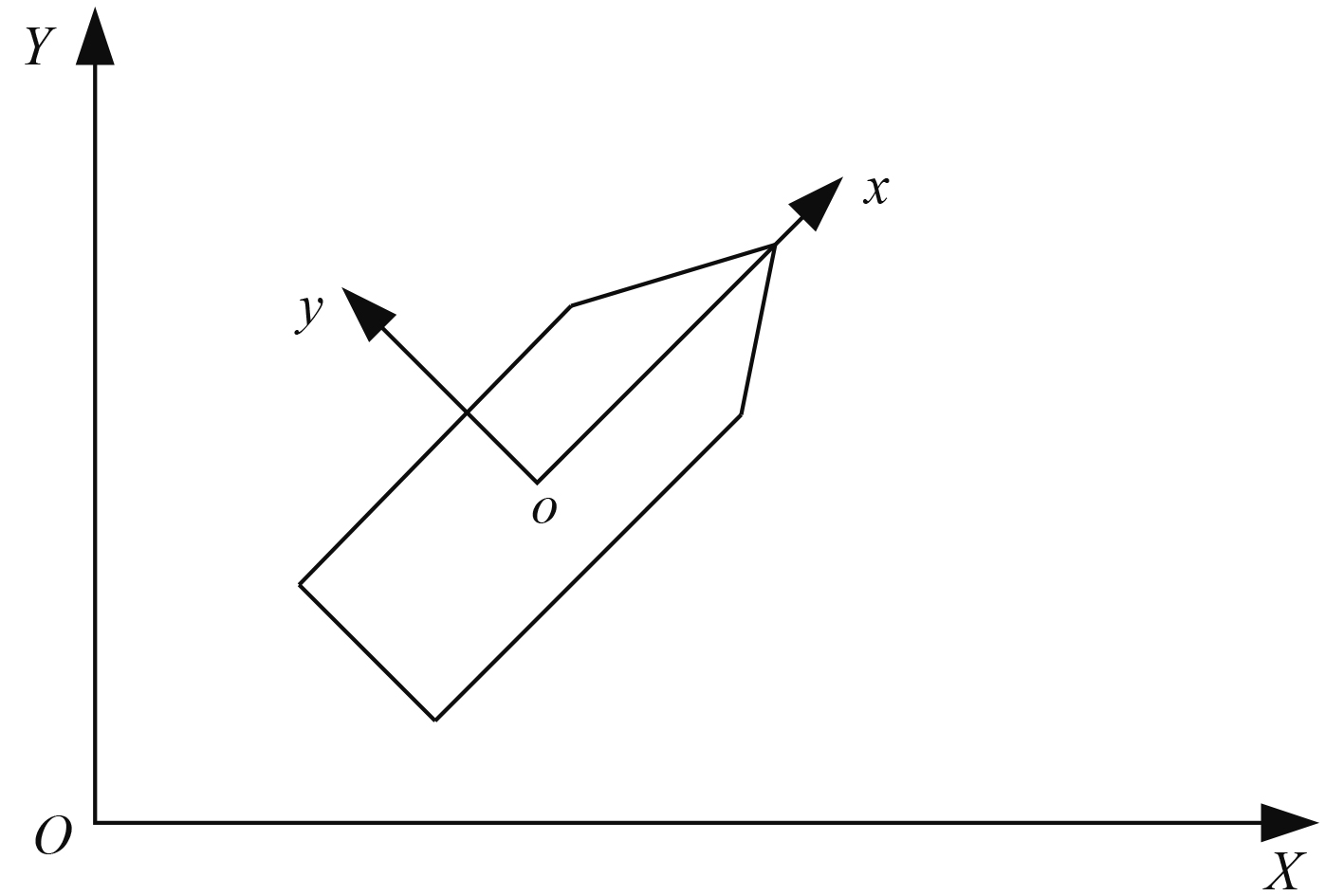
|
图 4 大地坐标系和随船坐标系 Fig. 4 Earth-fixed/ship-fixed coordinate system |
极区船舶在碎冰域航行三自由度非线性耦合运动微分方程为:
| $ ({\boldsymbol{M}} + {\boldsymbol{A}}){{\ddot {\boldsymbol{r}}}}(t) + {{{\boldsymbol{B}}\dot {\boldsymbol{r}}}}(t) + {{{\boldsymbol{Cr}}}}(t) = {{{\boldsymbol{F}}}}(t)。$ | (12) |
式中:
| $ {\boldsymbol{M}} = {\rm{diag}}({M_1},{M_2},{I_6}),$ | (13) |
由船舶几何模型计算得出;
| $ {\boldsymbol{A }}= {\rm{diag}}({A_{11}},{A_{22}},{A_{66}}),$ | (14) |
由周昭明[8]经验公式计算得出;
在冰载荷的早期计算中,用于克服冰阻力的净推力为:
| $ {T_{net}} = {T_B}\left( {1 - \frac{1}{3}\frac{u}{{{v_{ow}}}} - \frac{2}{3}{{\left( {\frac{u}{{{v_{ow}}}}} \right)}^2}} \right)。$ | (15) |
式中:
| $ F_1^p(t) = {T_{net}} - \frac{1}{2}{C_D}{\rho _w}v_w^2{A_r} ,$ | (16) |
| $ F_2^p(t) = \frac{1}{2}{C_L}{\rho _w}v_w^2{A_r} ,$ | (17) |
| $ F_6^p(t) = \frac{1}{2}{C_L}{\rho _w}v_w^2{A_r} \cdot {x_r} 。$ | (18) |
式中:
考虑到船舶相对于水的运动所产生的水动力,假设周围的水完全被冰覆盖,忽略波浪的影响[10]:
| $ F_1^c(t) = \frac{{0.075}}{{{{({{\log }_{10}}Rn - 2)}^2}}}\frac{1}{2}{\rho _w}{S_w}u\left| u \right| ,$ | (19) |
| $ F_2^c(t) = \frac{1}{2}{\rho _w}\int_L {{C_d}} (x)D(x)v(x)\left| {v(x)} \right|{\rm{d}}x,$ | (20) |
| $ F_6^c(t) = \frac{1}{2}{\rho _w}\int_L {{C_d}} (x)D(x)v(x)\left| {v(x)} \right|x{\rm{d}}x。$ | (21) |
式中:
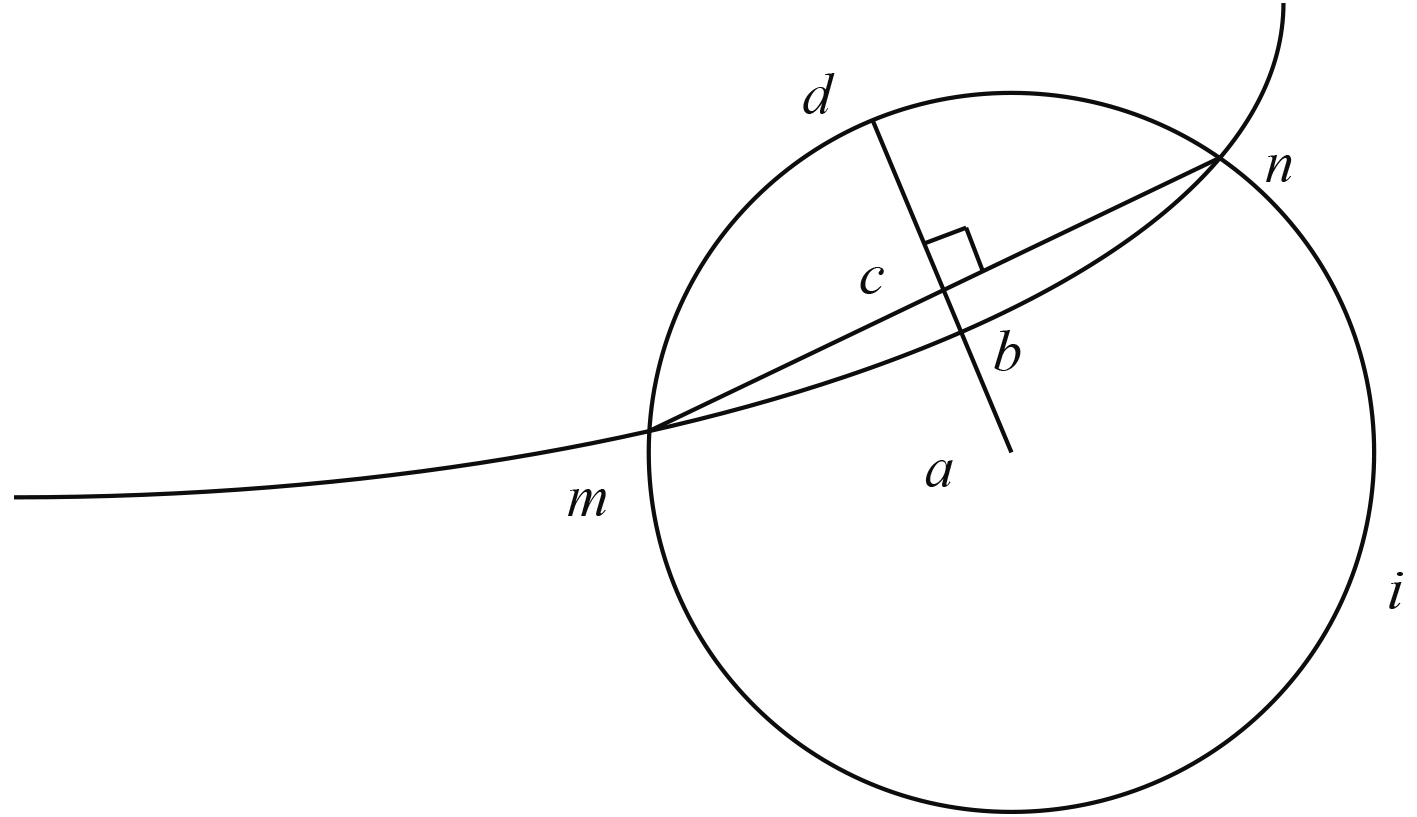
碎冰与船体型线接触的其中一种形式,如图5所示。其中,点
|
图 5 船体型线与圆盘接触示意图 Fig. 5 Sketch showing contact between hull lines and disks |
| $ \delta = {R_i} - ab = bd 。$ | (22) |
船体型线与圆盘相交,两者间的法线方向和切线方向等与圆盘-圆盘相交(碎冰间的作用)一致。其中海冰特性参数,本文假设船-冰与冰-冰之间相等,并在后续的参数分析中进行相同的参数变换。3个自由度的碎冰载荷为:
| $ F_1^s(t) = F_{ni}^t(\cos \beta ) + F_{ti}^t( - \sin \beta ),$ | (23) |
| $ F_2^s(t) = F_{ni}^t(\sin \beta ) + F_{ti}^t(\cos \beta ),$ | (24) |
| $ F_6^s(t) = F_1^s(t) \cdot {{L + }}F_2^s(t) \cdot {{L}} 。$ | (25) |
式中:
因此,在3个自由度下,船体外载荷为:
| $ {F_1}(t) = F_1^p(t) + F_1^c(t) + F_1^s(t) + mvr,$ | (26) |
| $ {F_2}(t) = F_2^p(t) + F_2^c(t) + F_2^s(t) - mur ,$ | (27) |
| $ {F_6}(t) = F_6^p(t) + F_6^c(t) + F_6^s(t)。$ | (28) |
式中:最后一项为欧拉力,由于随船坐标系相对于固地坐标系的非定常旋转,所以考虑假想欧拉力。其中,
本文采用Newmark方法求解船舶运动方程,一般积分方程为:
| $ {{\dot r}}({t_{k + 1}}) = {{\dot r}}({t_k}) + \frac{1}{2}{{\ddot r}}({t_k})\Delta t + \frac{1}{2}{{\ddot r}}({t_{k + 1}})\Delta t ,$ | (29) |
| $ {{r}}({t_{k + 1}}) = {{r}}({t_k}) + {{\dot r}}({t_k})\Delta t + \frac{1}{3}{{\ddot r}}({t_k})\Delta {t^2} + \frac{1}{6}{{\ddot r}}({t_{k + 1}})\Delta {t^2} 。$ | (30) |
其中:
| $ {{\ddot r}}({t_{k + 1}}) = {({{M}} + {{A}})^{ - 1}}({{F}}({t_{k + 1}}) - {{B\dot r}}({t_{k + 1}}) - {{Cr}}({t_{k + 1}})) 。$ | (31) |
将式(31)代入式(30)得到:
| $ \begin{split} {{r}}({t_{k + 1}}) = &{\left( {\frac{6}{{\Delta {t^2}}}({{M}} + {{A}}) + \frac{3}{{\Delta t}}{{B}} + {{C}}} \right)^{ - 1}}({{F}}({t_{k + 1}}) +\\ & ({{M}} + {{A}}){\text{z}}_k^1 + B{\text{z}}_k^2)。\end{split} $ | (32) |
其中:
| $ {{z}}_k^1 = \frac{6}{{\Delta t}}{{r}}({t_k}) + \frac{6}{{\Delta t}}{{\dot r}}({t_k}) + 2{{\ddot r}}({t_k}),$ | (33) |
| $ {{z}}_k^2 = \frac{3}{{\Delta t}}{{r}}({t_k}) + 2{{\dot r}}({t_k}) + \frac{1}{2}{{\ddot r}}({t_k})\Delta t 。$ | (34) |
在每个时间步内外载荷要进行迭代,直到精度可以满足要求为止。收敛准则基于外载荷从一个迭代到下一个迭代的变化,可以表示为:
| $ \frac{{\sqrt {(F_1^{i + 1} - F_1^i) + (F_2^{i + 1} - F_2^i) + (F_6^{i + 1} - F_6^i)} }}{{\sqrt {{{(F_1^i)}^2} + {{(F_2^i)}^2} + {{(F_6^i)}^2}} }} < \varepsilon 。$ | (35) |
式中:
碎冰场域中,海冰特性参数
上述模型描述中,弹簧系数分为法向弹簧系数和切向弹簧系数。Savage[11]发现当使用Hertzian接触公式时,2个同等大小圆盘之间碰撞时法向弹簧系数
切向弹簧系数的计算为:
| $ {k_{te}} = \frac{{{k_{ne}}}}{{2(1 - \nu )}} 。$ | (36) |
Wang[13]对柱状海冰泊松比进行了测量,泊松比范围分别为0.8~1.2和0~0.2。当泊松比为0.2时,大约
海冰粘性系数
| $ {\zeta _n} = \frac{{ - \ln e}}{{\sqrt {({\text{(π} ^2} + {{\ln }^2}e)} }}。$ | (37) |
粘性系数
| $ {k_{nv}} = 2{\zeta _n}\sqrt {m{k_{ne}}}。$ | (38) |
式中:
切向上的碎冰力在摩擦极限(非滑动接触)下为弹塑性,在摩擦极限(滑动接触)处为摩擦。摩擦系数
根据上述数值计算方法,运用Matlab软件进行程序编写。以碎冰和船舶特性为输入(见表1和表2),以三自由度瞬时碎冰载荷和船舶运动为输出,对某极区航行船舶在碎冰域的航行进行数值模拟。然后,参考季顺迎等[19]“雪龙”号在三维圆盘碎冰区域进行船舶冰载荷模拟,以验证数值方法的正确性。最后,验证海冰特性参数的改变,对碎冰载荷的影响。
|
|
表 1 船体主要参数 Tab.1 Main parameters of ships |
|
|
表 2 碎冰主要参数 Tab.2 Main parameters of broken ice |
建立一个长度
图6为船舶航行于碎冰域中0,70,140 s时船舶与碎冰相互作用的运动状态图。从图中可以看出,船舶在碎冰域航行中留下清晰的航行线路。由于碎冰域的四周边界设置的是周期性边界,所以没有明显碎冰尾迹现象。

|
图 6 船体与碎冰相互作用示意图 Fig. 6 Snapshots of the interaction between ship hull and ice floes |
图7为船舶在碎冰域中航行140 s所受到的碎冰载荷纵向、横向、首摇3个自由度上的时历曲线。可以看出,3个自由度的碎冰载荷的随机性较高。横向碎冰载荷与首摇碎冰载荷的波动曲线相似,是由于碎冰块与船舶相互耦合运动所致。其中,纵向碎冰载荷最小值为−1 043 kN,平均碎冰载荷为−431 kN;横向碎冰载荷最大值为377 kN,最小值为−315 kN,平均碎冰载荷为1.89 kN;首摇碎冰载荷最大值为2 428 kN,最小值为−1 954 kN,平均载荷为−37.25 kN。相较于纵向平均碎冰载荷,横向与首摇平均碎冰载荷的值较小。在碎冰大小在4.6~6.6 m之间,密集度在60%的情况下,不着重讨论碎冰载荷对于船舶横向和首摇的影响。

|
图 7 三个自由度碎冰载荷时历曲线 Fig. 7 Three degrees of freedom ice crushing load time history curve |
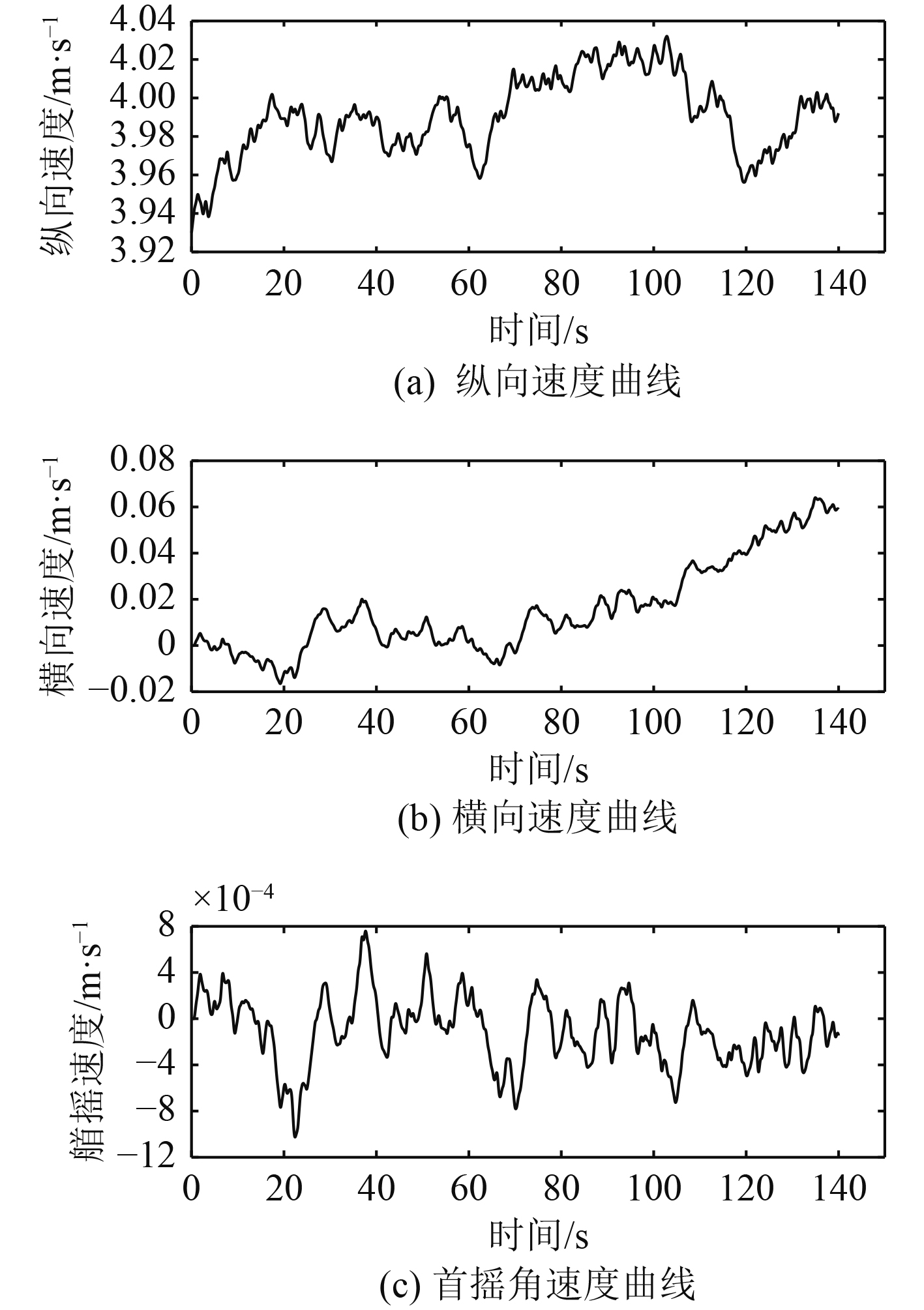
图8为船舶纵向、横向、首摇3个自由度的速度—时间曲线。在纵向速度,船舶行驶到20 s左右时,速度达到动态稳定,稳定速度大约为3.98 s。在横向速度,速度始终波动的上行趋势,是由于碎冰随机分布引起的。在数值模拟中也出现过横向速度波动向下的情况,但这不影响纵向速度趋于动态稳定。在首摇速度,首摇速度在0值附近上下波动。
|
图 8 三个自由度速度—时间曲线 Fig. 8 Three degrees of freedom speed - time curve |
通过对比季顺迎等[19]数值模拟,“雪龙”号以4 m/s速度在密集度为60%的三维碎冰圆盘域中航行,纵向载荷最大值为1 479 kN,平均载荷为440 kN。对比可知,纵向最大载荷相差29.1%,平均载荷相差0.02%。“雪龙”号长167 m,宽22.6 m,吃水9 m、首柱倾角52°,本文所用船舶长150 m,宽21.5 m,吃水9.5 m,首柱倾角30°。水线面形状的不同可能是造成最大碎冰载荷相差较大的一个原因。另外由于本文是二维平面模型,并没有考虑到三维碎冰中的翻转、堆积、滑移,这也是最大碎冰载荷较大差异的原因之一。综上所述,编写的二维碎冰离散元计算模型基本满足运算要求。
4.2 海冰特性参数分析在主机功率不变,并且表2中各项主要参数不变的情况下,本文分别对法向弹簧系数
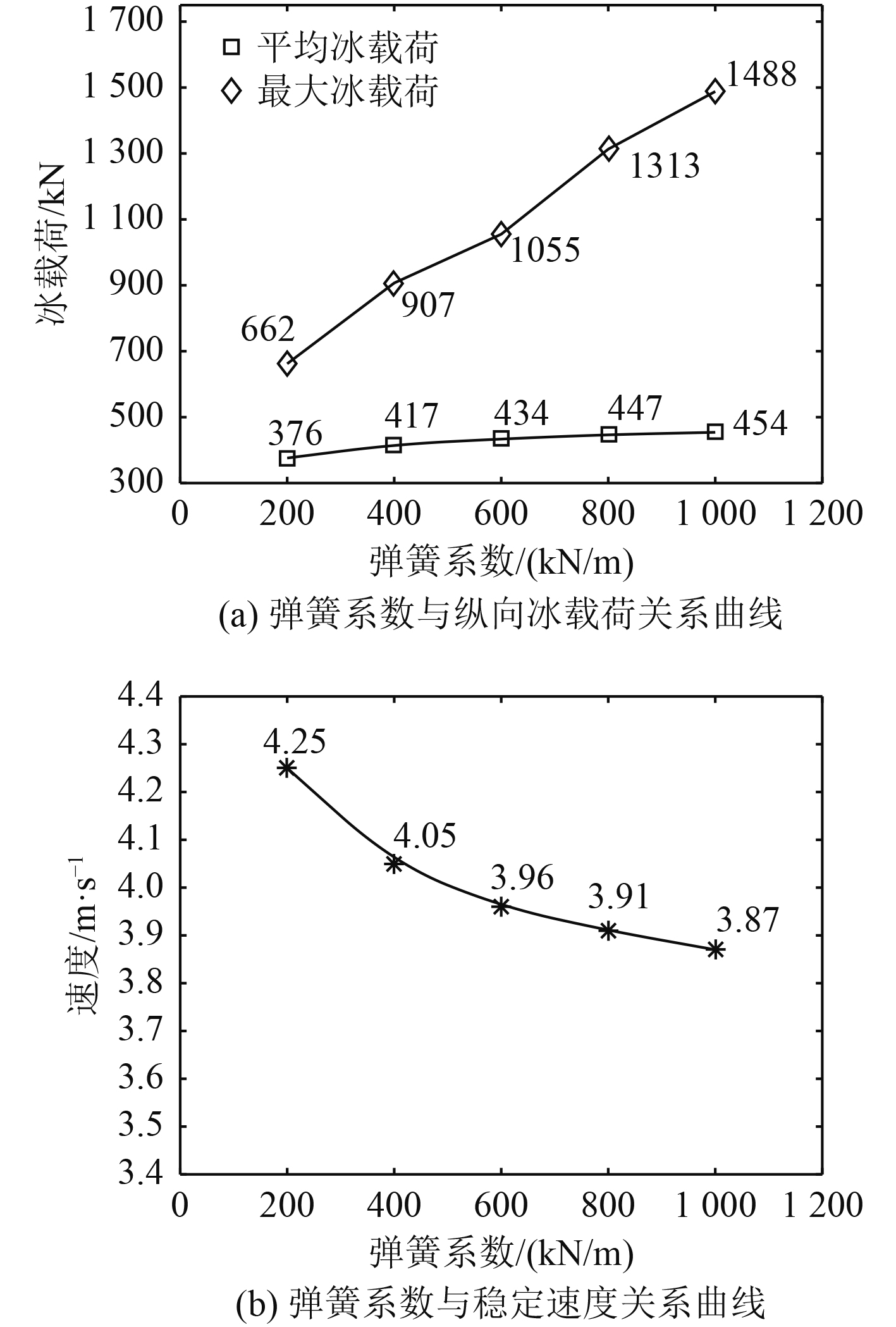
为分析弹簧系数对船舶碎冰载荷的影响,在不同的弹簧系数下对碎冰与船舶的相互作用进行分析。计算的主要参数选用表1和表2中所列数值。弹簧系数分别选取200 kN/m,400 kN/m,600 kN/m,800 kN/m和1 000 kN/m。考虑到碎冰载荷主要作用于船舶前进方向,因此主要分析纵向碎冰载荷受到的影响。图9分别为不同的弹簧系数下,弹簧系数对纵向碎冰载荷影响的曲线图和弹簧系数—稳定速度关系曲线。
|
图 9 不同弹簧系数对碎冰载荷的影响 Fig. 9 Effects of different spring coefficients on ice crushing load |
随着弹簧系数的增大,稳定速度越来越小,而碎冰载荷平均值越来越大。通过文献[1,19]可知,平均碎冰载荷与船速的关系成正比,所以本组模拟中弹簧系数对于平均碎冰载荷的影响远大于船速。对于海冰材料,弹簧系数主要在整体运动系统中,起到动量传递作用。弹簧系数越大,在能量传递过程中动量损失越小,船舶受到冰块的冲击就越大,所以平均碎冰载荷越来越大。平均碎冰载荷随着弹簧系数的增大而增大并不是呈线性增加的,而是弹簧系数到达某一值时,对平均碎冰载荷影响较小。进一步说明,碎冰在某一不易发生形变能力的范围内,对平均碎冰载荷影响不大。随着弹簧系数的增加,最大碎冰载荷变化范围较大,说明碎冰块对船体的最大瞬时冲击随着碎冰的刚度增加作用显著。
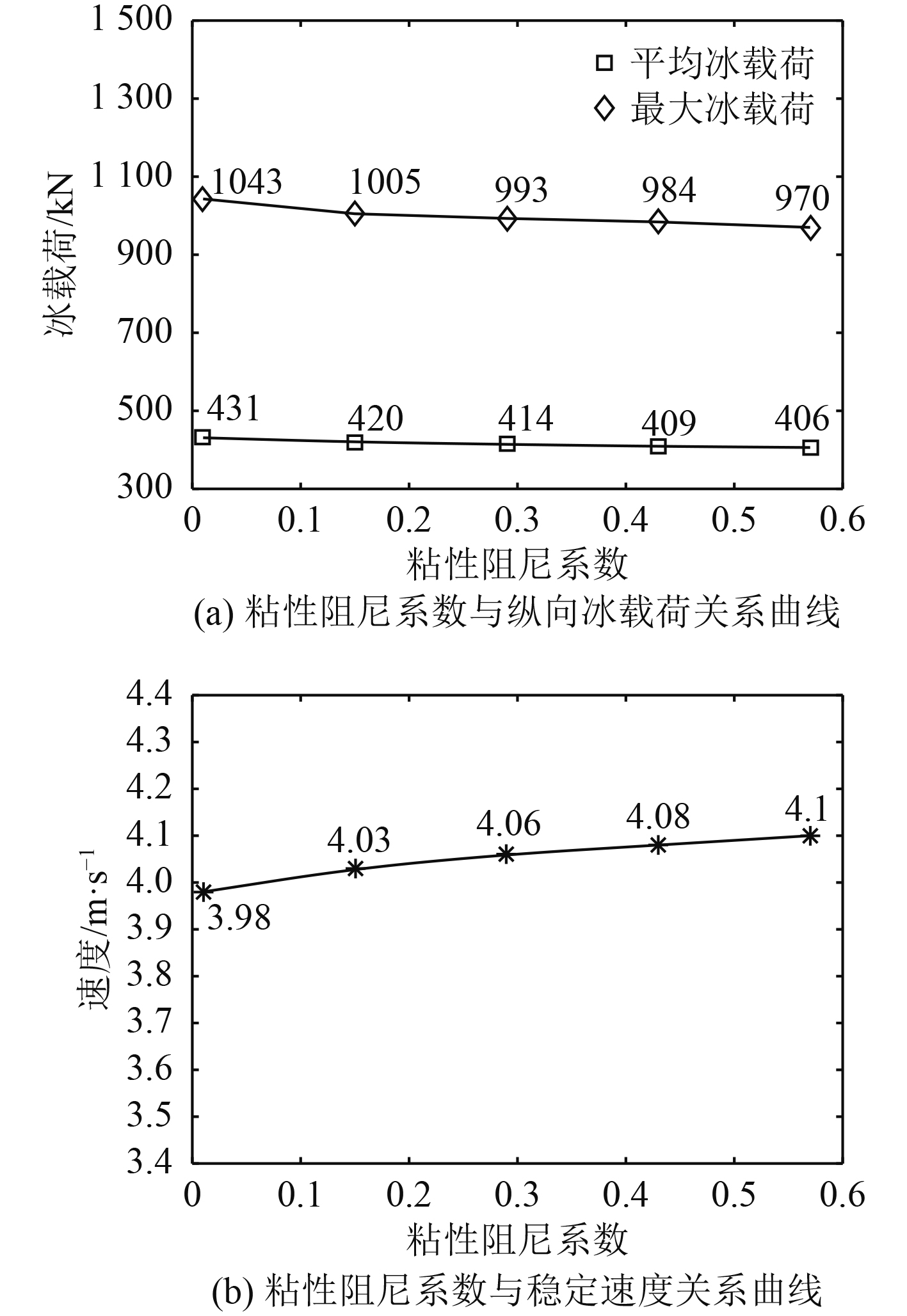
图10为粘性阻尼系数分别选取0.01,0.15,0.29,0.43和0.57时,粘性阻尼系数对纵向碎冰载荷影响曲线图和粘性阻尼系数—稳定速度关系曲线。图10(a)中平均碎冰载荷随着粘性阻尼系数的增大而减小;图10(b)中,稳定速度随着粘性阻尼系数的增大而增大。与弹簧系数一样,粘性阻尼系数对平均碎冰载荷的影响大于船速。因为Kelvin模型的“滞弹性”性质,粘性起到动量损失的作用。但这种动量损失作用于海冰材料内部,从整体运动系统来看,表现为“弹簧系数减小”,动量减小,所以平均碎冰载荷随着粘性阻尼系数的增加而减小,而且相邻两者之间的差值越来越小,趋近于某一值。粘性阻尼系数在0.01时与0.57时的平均碎冰载荷相比较,差值仅为25kN,与弹簧系数及摩擦系数对平均碎冰载荷影响相差很多。粘性阻尼系数对最大碎冰载荷影响也比较小。
|
图 10 不同粘性阻尼系数对碎冰载荷的影响 Fig. 10 Effects of different viscous damping coefficients on ice crushing load |
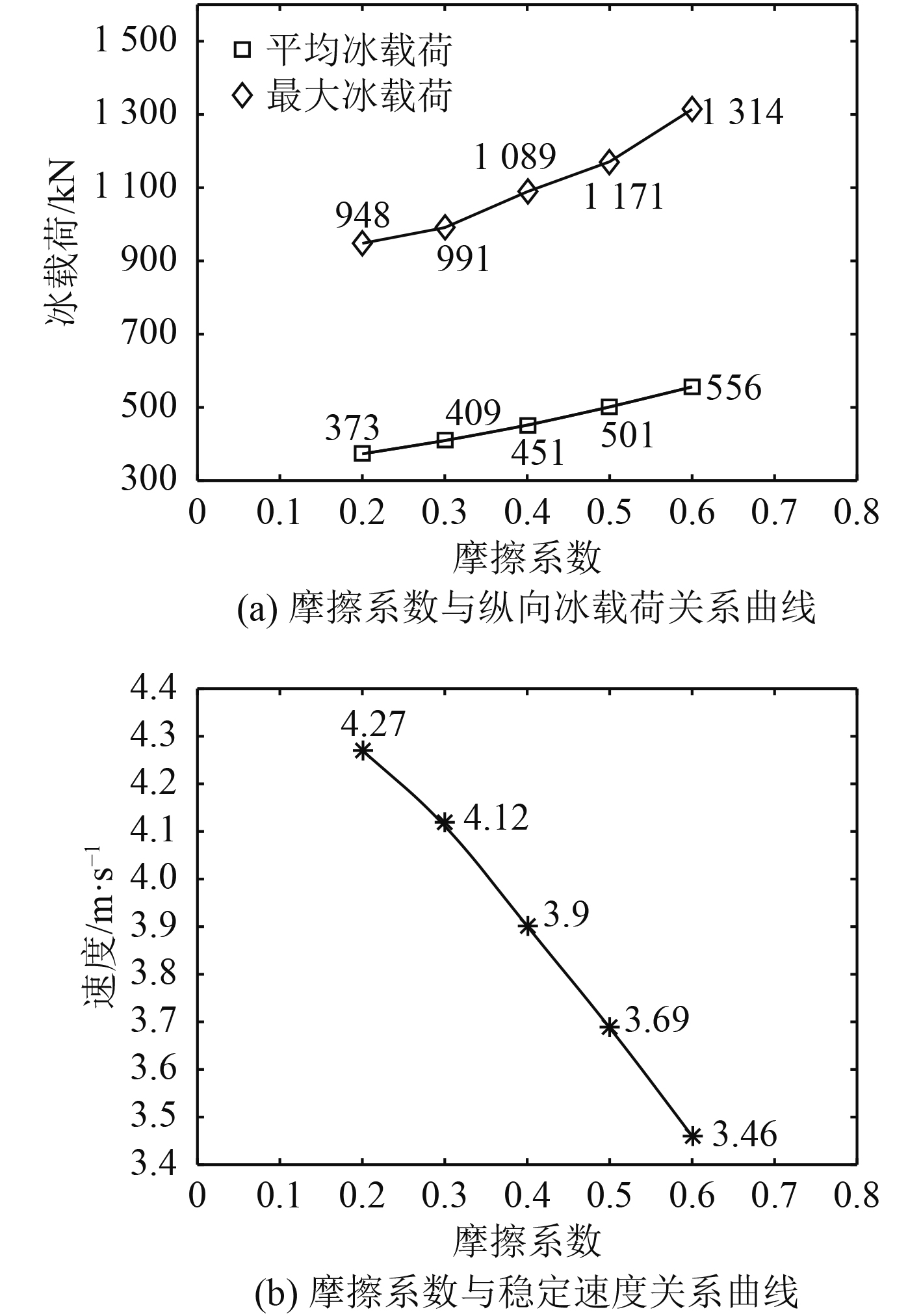
图11为摩擦系数分别选取0.2,0.3,0.4,0.5和0.6时,摩擦系数对纵向碎冰载荷影响曲线图和摩擦系数—稳定速度关系曲线。与弹簧系数、粘性阻尼系数一样,船速对于平均碎冰载荷的影响远不及摩擦系数。由于摩擦系数的增大,摩擦阻力增大,整体运动系统的能量损失增大,所以平均碎冰载荷增大,同时也增强了碎冰块对船体的瞬时摩擦阻力。
|
图 11 不同摩擦系数对碎冰载荷的影响 Fig. 11 Effects of different friction coefficients on ice crushing load |
本文主要讨论了极区航行船舶在碎冰域航行中,碎冰对船舶的运动响应分析以及海冰特性参数对碎冰载荷敏感性分析,主要得出以下结论:
1)运用碎冰基本的力学行为和物理特性,结合船舶操纵性的相关知识,完成二维碎冰离散元程序的编写,通过与相关文献数值模拟结果的对比,证明了碎冰计算程序的适用性和精确性,可用于极地船舶在碎冰区的运动响应分析。
2)通过对弹簧系数
3)通过对碎冰载荷的海冰特性参数敏感性分析,建议在数值模拟和船模实验中,结合实际海冰特性参数,选择合理的海冰弹粘性系数和摩擦系数,确保船舶运动响应预报精度,为极地船舶设计与航行安全提供参考。
值得注意的是,本文建立的碎冰离散元模型仅限于二维,未考虑碎冰翻转、滑动、堆积等三维运动现象,因此,需对船舶与碎冰的三维作用模型开展进一步研究。
| [1] |
SVEINUNG L. Discrete element modelling of a broken ice field — Part II: simulation of ice loads on a boom[J]. Cold Regions Science and Technology, 1994, 22(4): 349-360. DOI:10.1016/0165-232X(94)90020-5 |
| [2] |
HANSEN E H, SVEINUNG L. Modelling floating offshore units moored in broken ice: comparing simulations with ice tank tests[J]. Cold Regions Science and Technology, 1999, 29(2): 107-119. DOI:10.1016/S0165-232X(99)00017-8 |
| [3] |
季顺迎, 王帅霖, 刘璐 极区船舶及海洋结构冰荷载的离散元分析[J]. 科技导报, 2017, 35(3): 72−80. JI Shunying, WANG Shuailin, LIU Lu. Analysis of ice load on ship and offshore structure in polar region with discrete element method[J]. Science and Technology Review. 2017, 35(3): 72−80. |
| [4] |
童波, 涂勋程, 谷家扬, 等. 基于参数化设计的浮冰区船舶冰阻力研究[J]. 船舶力学, 2019, 23(7): 755−762. TONG Bo, TU Xun-cheng, GU Jia-yang, et al. Study on ship ice resistance based on parametric design of brash ice zone[J]. Journal of Ship Mechanics. 2019, 23(7): 755−762. |
| [5] |
SVEINUNG L. Discrete element modelling of a broken ice field — Part I: model development[J]. Cold Regions Science and Technology, 1994, 22(4): 339-347. DOI:10.1016/0165-232X(94)90019-1 |
| [6] |
HANSEN E H, SVEINUNG L. Modelling floating offshore units moored in broken ice: Model description[J]. Cold Regions Science and Technology, 1999, 29(2): 97-106. DOI:10.1016/S0165-232X(99)00023-3 |
| [7] |
BELYTSCHKO T, LIN J I. A three-dimensional impact-penetration algorithm with erosion[J]. Computers and Structures, 1987, 25(1): 95-104. DOI:10.1016/0045-7949(87)90220-3 |
| [8] |
周昭明, 盛子寅, 冯悟时. 多用途货船的操纵性预报计算[J]. 船舶工程, 1983(6): 21−29. ZHOU Zhaoming, SHENG Ziyin, FENG Wushi. On maneuverability prediction for multipurpose cargo ship[J]. Strip Engineering 1983(6): 21−29. |
| [9] |
SU B, RISKA K, MOAN T. A numerical method for the prediction of ship performance in level ice[J]. Cold Regions Science and Technology, 2010, 60(3): 177-188. |
| [10] |
FALTINSEN O. M. Sea Loads on Ships and Offshore Structures[C]// UK: Cambridge University Press, Cambridge, 1990.
|
| [11] |
SAVAGE S B. Marginal Ice Zone Dynamics Modelled by Computer Simulations Involving Floe Collisions[C]// Report prepared for Institute for Mechanical Engineering, National Research Council Canada, Ottawa, 1992.
|
| [12] |
SAYED M, DALEY C. Experiments of Crushing Interaction Between Ice Foes[J]. Gene Therapy, 1992, 12(7): 607-616. |
| [13] |
WANG Y S. Uniaxial compression testing of Arctic sea ice[C]// Proceedings of the Sixth International Conference POAC. 1981: 346−355.
|
| [14] |
HOPKINS M A. On the mesoscale interaction of lead ice and floes[J]. Journal of Geophysical Research Oceans, 1996, 101(C8): 18315-18326. DOI:10.1029/96JC01689 |
| [15] |
BABIC M. Discrete particle numerical simulation of granular material behavior[C]// New York: Department of Civil and Environmental Engineering, Clarkson University, Potsdam, 1988: 88−11
|
| [16] |
BABIC M, SHEN H H, SHEN H T, et al. The stress tensor in granular shear flows of uniform, deformable disks at high solids concentrations[J]. Journal of Fluid Mechanics, 1990, 219(1): 81-118. DOI:10.1017/S0022112090002877 |
| [17] |
LU Q, LARSEN J, TRYDE P, et al. On the role of ice interaction due to floe collisions in marginal ice zone dynamics[J]. Journal of Geophysical Research, 1989, 14525-14537. |
| [18] |
BARKER A, TIMCO G W. The friction coefficient of a large ice block on a sand/gravel beach[C]// Canada: Proceedings 12th Workshop on the Hydraulics of Ice Covered Rivers, CRIPE'03, Edmonton, 2003.
|
| [19] |
JI Shunying, LI Zilin, LI Chunhua, et al. Discrete element modeling of ice loads on ship hulls in broken ice fields[J]. Acta Oceanologica Sinica, 2013(11): 50−58.
|
 2022, Vol. 44
2022, Vol. 44
