在实际工程中,流体的流动状态是复杂多变的,不稳定流体状态经常出现,在管系中,当稳定流动的水流突然被阻拦,某一界面上的流速急剧变化,引起整个管路系统中的流体压力和密度激烈交替的现象,称为水锤,也称为水击[1]。水锤发生时,压力冲击将使管壁受力产生噪声。水锤是一种典型的非稳态的流动现象,也称为瞬时变化流动现象,流场中各流动参量,如密度、流速、加速度、压强等,不仅会随空间位置的不同变化而变化,还会随着时间而不断变化。
管路系统的阀门启闭[2-4]或事故停泵工况[5-6]相对来说比较容易导致管路压力交替变化,剧烈升高和降低,从而形成水锤,给实际工程带来严重损失。但当泵主要是提供沿程水力损失的补偿压力,同时流速不快,并且泵前管路较短,有可能断电停泵也没有多大影响,所以本文运用AFT Impulse建立通用型FPSO压载水系统模型,研究系统的关阀水锤,得出不同关阀工况下水锤仿真结果。通过多次仿真对结果进行比较,得到相对合理的关阀方案,确保管路系统的安全。
AFT Impulse是一款复杂的水锤建模与分析软件,采用特征线法进行管路系统的水锤分析[7],相对于Flowmaster这款基于对系统模拟仿真运算时间较长的软件来说,AFT Impulse则更加侧重于流体分析的开发理念,可以简单快速进行仿真,更加适用于工程设计。使用AFT Impulse可以对大部分管道系统进行瞬态分析模拟。了解管道系统瞬态压力极限,在必要时,通过增加抑制水锤压力设备,确保系统安分析全运行。
1 水锤微分方程刚性水锤理论和弹性水锤理论是水锤的2种基本理论[8]。刚性水锤理论是根据水是不可压缩的这一假设条件成立的,弹性水锤理论不仅考虑了水的可压缩性而且考虑了管壁的弹性。
在实际应用中,由于刚性水锤理论计算结果的误差较大,因此一般采用弹性水锤理论进行计算。水锤的基本微分方程由动量方程和连续性方程组成,这是水锤计算和瞬态流动研究的理论基础[9]。水锤基本微分方程的推导基于以下3个假设:
1)水流为流速分布均匀,流体各点密度相同的一维流动;
2) 在任何时刻管内充满着连续流体,且不包括水柱拉断情况;
3)在瞬变流中采用与稳定流相同的摩擦阻力。
根据弹性理论将基本微分方程分为2个方程式。
动量方程:
| $ \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + \frac{{\partial v}}{{\partial t}} + g\sin \alpha + \frac{{fv\left| v \right|}}{{2D}} = 0 。$ | (1) |
式中:
连续性方程:
| $ \frac{{{a^2}}}{g}\frac{{\partial v}}{{\partial x}} + \frac{{\partial P}}{{\partial t}} = 0 。$ | (2) |
水击的动量方程 (1)和连续性方程(2)组成了双曲线微分方程。其中变量为速度和水力坡度线,2个变量根据时间和管段长度变化而变化。
计算水锤的方法主要有图解法、解析法和特征线法。其中,基于特征线法的电气算法随着计算机技术的快速发展得到了越来越广泛的应用,现已成为水锤计算的主要方法。可以用特征线法写成4个常微分方程,将变换后的运动方程和连续性方程分别用
| $ \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + \frac{{\partial v}}{{\partial t}} + g\sin \alpha + \frac{{fv\left| v \right|}}{{2D}} = {L_{\text{1}}} ,$ | (3) |
| $ \frac{1}{\rho }\frac{{\partial P}}{{\partial t}} + {a^2}\frac{{\partial v}}{{\partial x}} = {L_2}。$ | (4) |
对
| $ {L_1} + \lambda {L_2} = 0 ,$ | (5) |
| $ \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + \frac{{\partial v}}{{\partial t}} + g\sin \alpha + \frac{{fv\left| v \right|}}{{2D}} + \lambda \left( {\frac{1}{\rho }\frac{{\partial P}}{{\partial t}} + {a^2}\frac{{\partial v}}{{\partial x}}} \right) = 0。$ | (6) |
将上式重新排列组合:
| $ \frac{\lambda }{\rho }\left( {\frac{{\partial P}}{{\partial t}}{\text{ + }}\frac{1}{\lambda }\frac{{\partial P}}{{\partial x}}} \right){\text{ + }}\left( {\frac{{\partial v}}{{\partial t}}{\text{ + }}\lambda {a^2}\frac{{\partial v}}{{\partial x}}} \right){\text{ + }}\frac{{fv\left| v \right|}}{{2D}}{\text{ + }}g\sin \alpha = 0 ,$ | (7) |
令
| $ \pm \frac{1}{{a\rho }}\left( {\frac{{\partial P}}{{\partial t}} + \frac{{{\rm{d}}x}}{{{\rm{d}}t}}\frac{{\partial P}}{{\partial x}}} \right) + \left( {\frac{{\partial v}}{{\partial t}} + \frac{{{\rm{d}}x}}{{{\rm{d}}t}}\frac{{\partial v}}{{\partial x}}} \right) + \frac{{fv\left| v \right|}}{{2D}} + g\sin \alpha = 0 ,$ | (8) |
括号中代表
通过微分原则以进一步简化:
| $ \frac{{{\rm{d}}P}}{{{\rm{d}}t}} = \frac{{\partial P}}{{\partial x}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + \frac{{\partial P}}{{\partial t}} ,$ | (9) |
| $ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \frac{{\partial v}}{{\partial x}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + \frac{{\partial v}}{{\partial t}}。$ | (10) |
这代表了4个特征方程,即2对正(
| $ \left. \begin{gathered} \frac{1}{{a\rho }}\frac{{{\rm{d}}P}}{{{\rm{d}}t}} + \frac{{{\rm{d}}V}}{{{\rm{d}}t}} + \frac{{fv\left| v \right|}}{{2D}} + g\sin \alpha = 0 \hfill \\ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = + a \hfill \\ \end{gathered} \right\}{C^ + } ,$ | (11) |
| $ \left. \begin{gathered} - \frac{{\text{1}}}{{a\rho }}\frac{{{\rm{d}}P}}{{{\rm{d}}t}} + \frac{{{\rm{d}}V}}{{{\rm{d}}t}} + \frac{{fv\left| v \right|}}{{2D}}{\text{ + }}g\sin \alpha = 0 \hfill \\ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = - a \hfill \\ \end{gathered} \right\}{C^ - } 。$ | (12) |
将方程式进一步简化为便于仿真的形式。对于正特性,将顶部方程乘以
| $ \frac{1}{\rho }{\rm{d}}P + a{\rm{d}}v + \frac{{fv\left| v \right|}}{{2D}}{\rm{d}}x + g\sin \alpha {\rm{d}}x = 0 ,$ | (13) |
由于
| $ \frac{1}{\rho }{\rm{d}}P + a{\rm{d}}v + \frac{{fv\left| v \right|}}{{2D}}{\rm{d}}x + gdz = 0 ,$ | (14) |
使用质量流代替速度,并同乘以
| $ {\rm{d}}P + \frac{a}{A}{\rm{d}}m + \frac{{fm\left| m \right|}}{{2D\rho {A^2}}}{\rm{d}}x + \rho g{\rm{d}}z = 0。$ | (15) |
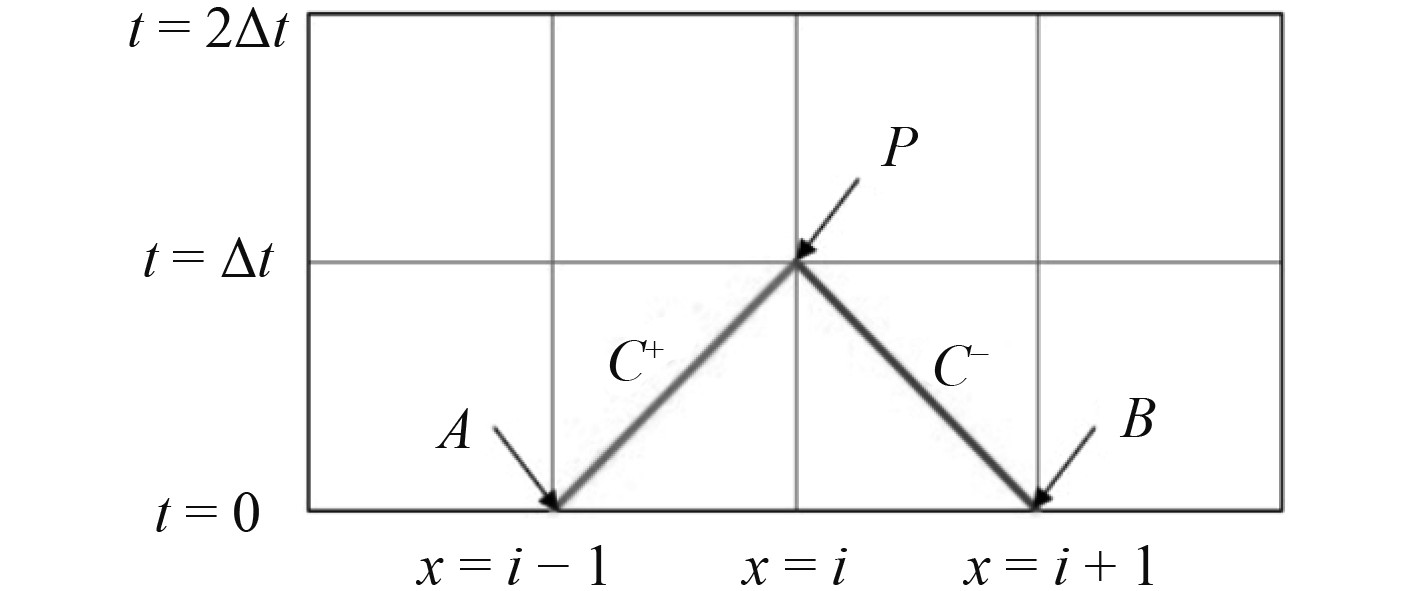
该方程可以沿正特性积分。通过特征网格(见图1)可以更加直观进行观察。在一段时间
|
图 1 特征网格 Fig. 1 Characteristic grid |
| $ \int_{{P_A}}^{{P_P}} {{\rm{d}}P} + \frac{a}{A}\int_{{m_A}}^{{m_P}} {{\rm{d}}m} + \frac{f}{{2D\rho {A^2}}}\int_{{x_A}}^{{x_P}} {m\left| m \right|{\rm{d}}x} + \rho g\int_{{Z_A}}^{{Z_P}} {{\rm{d}}z} = 0。$ | (16) |
式中:
| $\begin{split} &({P}_{P}-{P}_{A})+\frac{a}{A}\left({m}_{P}-{m}_{A}\right)+\\ &\quad \frac{f}{2D\rho {A}^{2}}\left[{m}_{P}\left|{m}_{A}\right|\left({x}_{P}-{x}_{A}\right)\right]+\rho g\left({z}_{P}-{z}_{A}\right)=0 。\end{split}$ | (17) |
定义阻抗和阻力:
| $ \begin{gathered} B = \frac{a}{A},\hfill \\ R = \frac{{f\Delta x}}{{2D\rho {A^2}}} 。\hfill\\ \end{gathered} $ |
代入对P点压力进行描述,式(18)为正特性,式(19)为负特性。
| $ {P_P}{\text{ = }}{P_A} - B\left( {{m_P} - {m_A}} \right) - R{m_P}\left| {{m_A}} \right| - \rho g\left( {{z_P} - {z_A}} \right) = 0 ,$ | (18) |
| $ {P_P}{\text{ = }}{P_B} + B\left( {{m_P} - {m_B}} \right) + R{m_P}\left| {{m_B}} \right| + \rho g\left( {{z_P} - {z_B}} \right) = 0 。$ | (19) |
最终得到一个由2个方程组成的系统,只有2个未知数:在点P处的质量流量和压力。联合边界条件方程,进行计算机求解可以快速准确得到管道中各节点处随时间的压力波动。
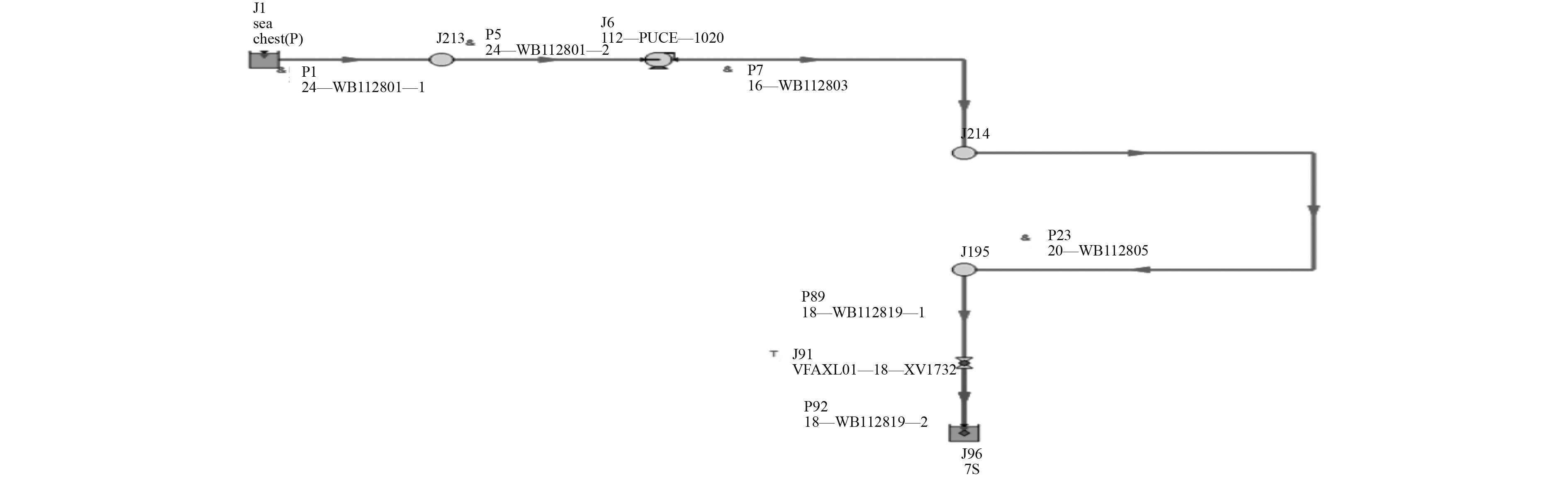
2 实例分析 2.1 模型分析本文分析的是国内某船厂的深水通用型FPSO压载水系统,根据管路系统的布局,此案列中选取从海底门进水到右舷7舱室的水锤压力分析。
|
图 2 从海底门到右舷7舱室的模型 Fig. 2 Model of 7 cabins from undersea door to starboard side |
|
|
表 1 海底门右舷7舱室管系 Tab.1 Piping system of No.7 cabin on starboard side of submarine gate |
泵的参数设置如下;额定流量2 400 m3/h,额定扬程65 m,额定转速1 402 r/min
管路采用玻璃管,参数设置如下:波速1 015 m/s,绝对粗糙度0.053 mm
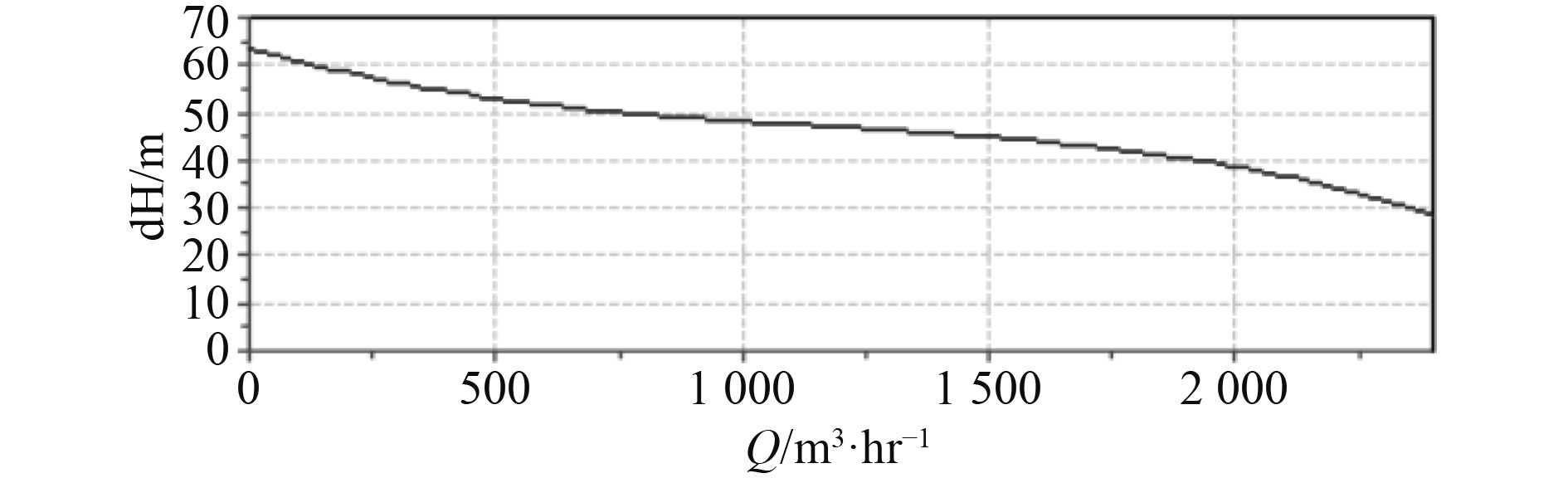
在压载水管系建模过程中,选取离心泵作为管系的泵,泵特性曲线参数如表2和图3所示。
|
|
表 2 离心泵的曲线数据 Tab.2 Curve data of centrifugal pump |
|
图 3 泵的曲线图 Fig. 3 Curve of pump |
一般来说,若在离心泵停止前阀门完全关闭,则水锤最大压力会在阀门的入口处。其次,由于管路两端的压力不平衡,也会产生最大水锤压力,在长度相对比较长的管路中,管路两端的压力差会更加明显,更容易出现两端压力不平衡现象。在本文研究中,引起水锤压力的管路发生在管路最长的20—WB112805和阀门入口处的18—WB112819-1的管路上。
目前对于水锤压力的设计校核是根据美国标准[10-12]ASME B31.3-2012作为参考的,要求有以下几点:
1)刚性管的最大压力值不能超过管系设计承载压力值的1.33倍,且超压值持续时间要满足2个要求:无论什么时候都不能超过10 h,每年累计时间不能超过100 h。
2)刚性管的最大压力值不能超过管系设计承载压力值的1.2倍,且超压值持续时间要满足2个要求:无论什么时候都不能超过50 h,每年累计时间不能超过500 h。
在深水通用型FPSO工程中,一般取1.33倍管道系统的设计压力作为校核条件。此实例中压载水系统的设计压力为8.5 bar,所以管路系统中最大允许水锤压力值为11.305 bar。
因此,比较了几种不同关闭阀门的方案下的水锤压力变化,阀门运用直线闭阀和两阶段闭阀的方式,两阶段关闭时,80%快关,后面20%缓慢闭阀,关闭方案如表3所示。
|
|
表 3 关阀工况 Tab.3 Valve closing conditions |
根据上述模型,对直线关闭,在不同线性关阀时间工况进行瞬态分析。
正常情况工作时,管路各压力值如表4所示,各管路中最大水锤压力值为4.975 bar。
|
|
表 4 正常情况各管路压力 Tab.4 Pressure of each pipeline under normal conditions |
表5~表7分别为管路直线关闭情况下的管路的压力情况,分别为10 s,15 s和25 s的线性关闭。当直线关阀时间为10 s时,管路内最大水锤压力值为34.980 bar,关阀时间为15 s时,最大水锤压力值为32.028 bar,关阀时间为25 s时,最大水锤压力值为25.321 bar,这些压力值均大于压载水系统的设计压力11.305 bar。
|
|
表 5 直接关闭,总闭阀时间10 s Tab.5 direct closing, total closing time 10 s |
|
|
表 6 直线关闭,总闭阀时间15 s Tab.6 linear closing, total valve closing time 15 s |
|
|
表 7 直线关闭,总闭阀时间25 s Tab.7 linear closing, total valve closing time 25 s |
由直线关闭不同关阀时间系统水锤分析可知:
1) 在系统阀门突然关闭时,管路内存在非常明显的水锤现象,使管路中的水锤压力值超过正常工作压力的数倍,会对管路系统造成危害;
2) 较长管路和在阀门入口处的管路中极易产生水锤现象;
3) 延长关阀时间可有效降低管路中最大水锤压力值,即延长关阀时间是一种相对有效的抑制水锤的方式。
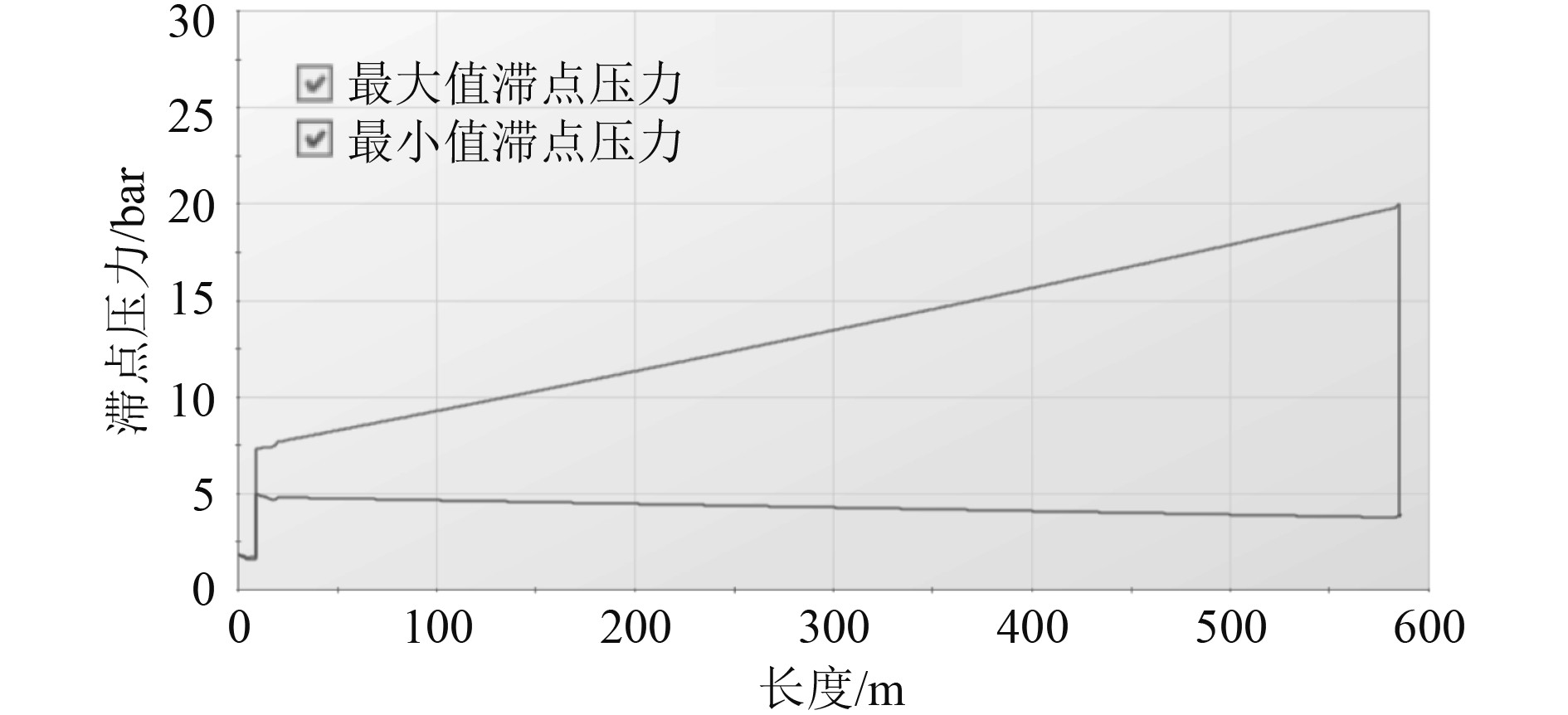
3.2 两阶段关阀水锤分析在进一步研究抑制水锤效果的过程中,经过多次模拟,优化了阀门关闭曲线,由直线关阀改为两阶段关阀两阶段关闭时,前面80%快关,后面20%缓慢闭阀。为了方便与直线关阀做对比,选取两阶段闭阀总时间依旧为10 s和15 s,不同关阀曲线下水锤分析如表8和表9、图4和图5所示。
|
|
表 8 两阶段关闭,快关3 s,缓慢关闭7 s Tab.8 Two-stage shutdown, fast closing 3 s, slow closing 7 s |
|
|
表 9 两阶段关闭,快关3 s,缓慢关闭12 s Tab.9 Two-stage shutdown, fast closing 3 s, slow closing 12 s |
|
图 4 两阶段关闭,快关3 s,缓慢关闭7 s Fig. 4 Two-stage shutdown, fast closing 3 s, slow closing 7 s |
|
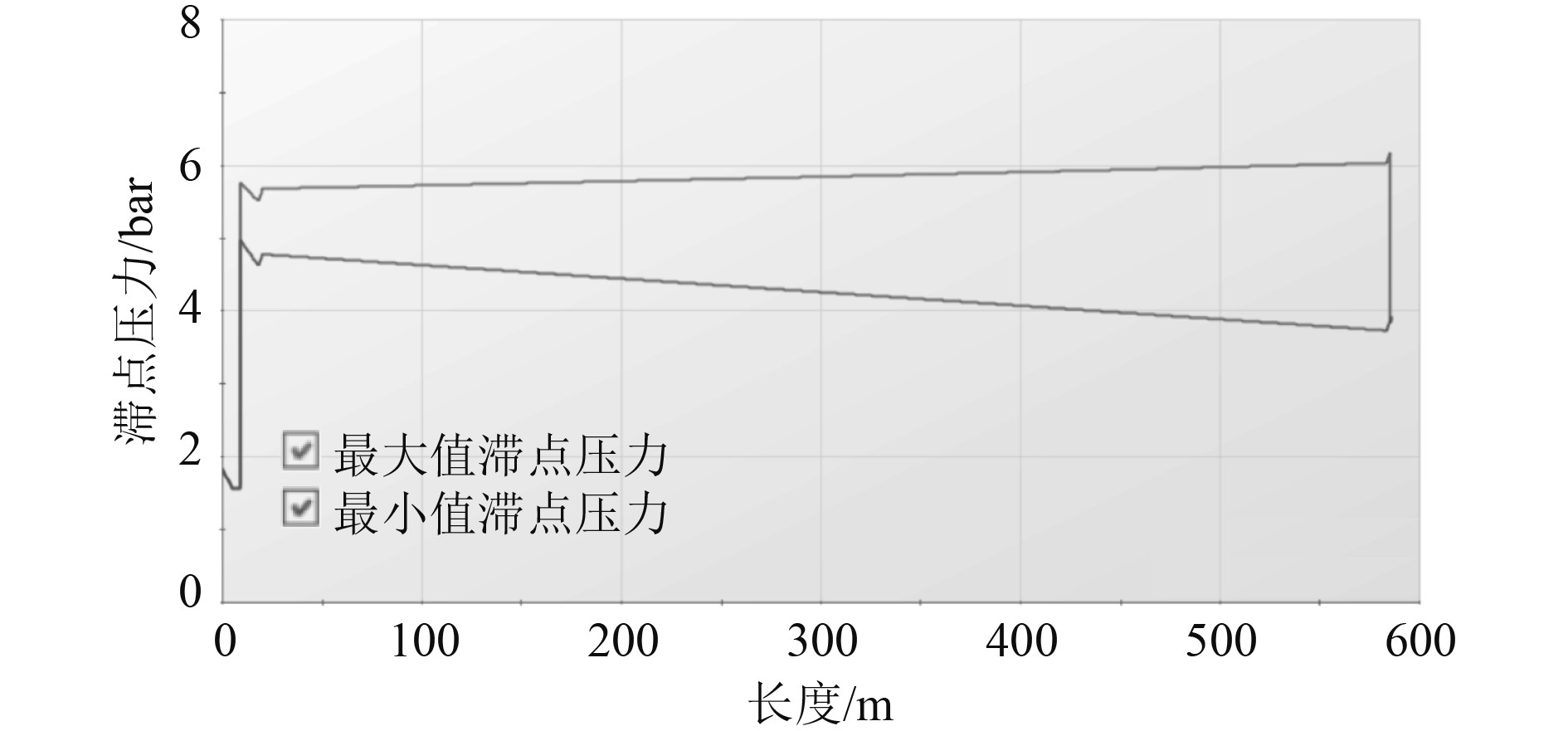
图 5 两阶段关闭,快关3 s,缓慢关闭12 s Fig. 5 Two-stage shutdown, fast closing 3 s, slow closing 12 s |
由表8和表9所知,在10 s直线关阀时,管路内最大水锤压力值为34.980 bar,在优化阀关闭曲线,改为10 s两阶段关阀,管路内最大水锤压力值为20.007 bar,在15 s直线关阀时,管路内最大水锤压力值为32.028 bar,优化关阀曲线,两阶段关阀后,管路中最大水锤压力值为6.177 bar,小于压载水管路系统中最大允许水锤压力值为11.305 bar,进一步对管路系统起到了防护作用。
由图4和图5更能直观感受到在优化关阀曲线后,总时间相同的情况下,相对于直线关阀,两阶段关阀更能有效减小管路内水锤的压力值,使管路内水锤压力达到系统允许范围之内,进而对管路系统起到更有效的保护作用。因此在通用型FPSO关键管网系统中采用两阶段闭阀更能有效对水锤产生抑制效果,从而缩短总关阀时间。
3.3 系统水锤其他抑制措施在管路系统中也可以通过增加水锤抑制装置来对管路中压力水锤进行有效的抑制,由于船舶系统中需要考虑其安装空间,采用在阀前增加缓气罐的方法进行水锤研究。
缓气罐可用于减小管路中流量的不均匀度,消除水锤起到稳压卸荷的作用,如表10和表11、图6和图7所示。
|
|
表 10 直线关阀10 s关阀,阀前加入缓气罐 Tab.10 Close the valve in a straight line for 10 s, and add a buffer tank in front of the valve |
|
|
表 11 两阶段关阀10 s关阀,阀前加入缓气罐 Tab.11 Close the valve in two stages for 10 s, and add a buffer tank in front of the valve |
|
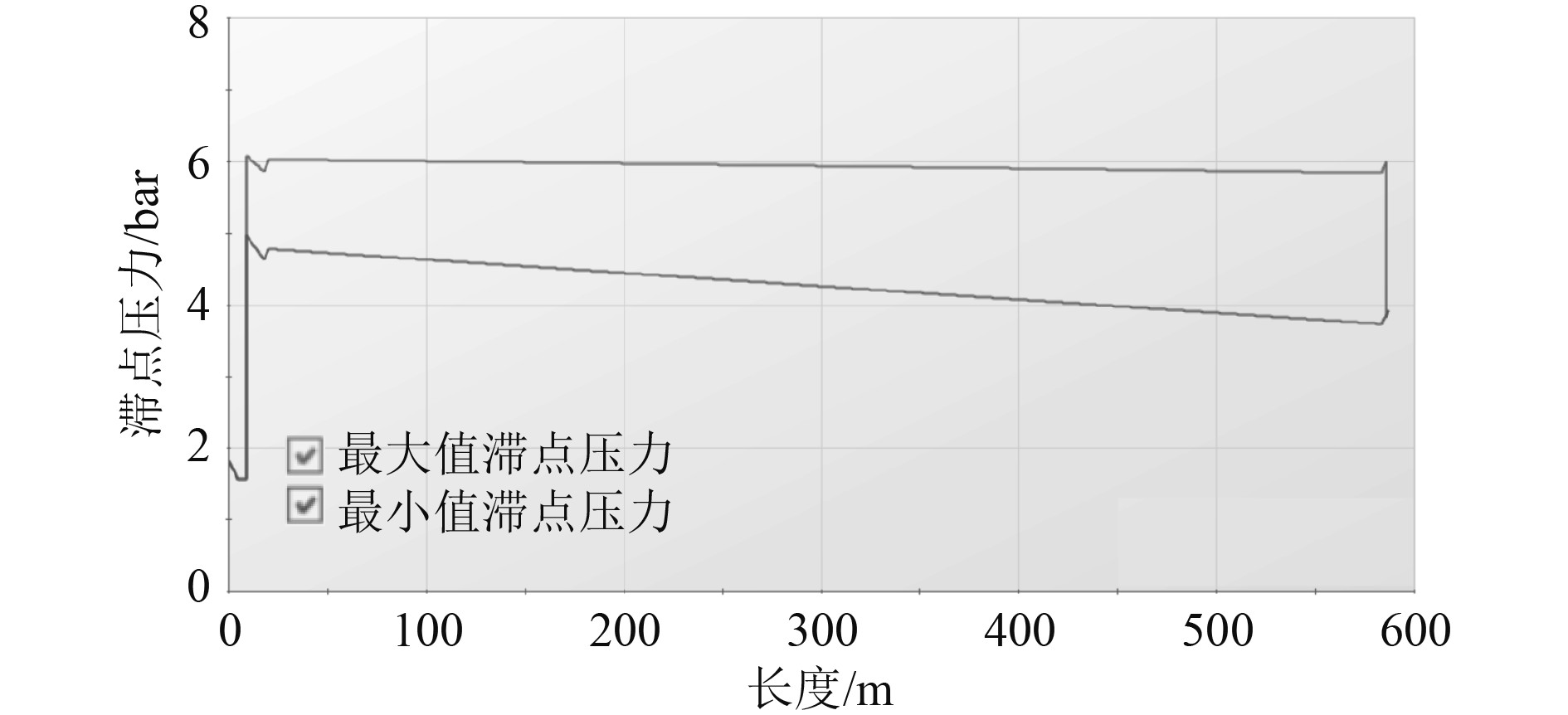
图 6 直线关阀10 s关阀,阀前加入缓气罐 Fig. 6 Close the valve in a straight line for 10 s, and add a buffer tank in front of the valve |
|
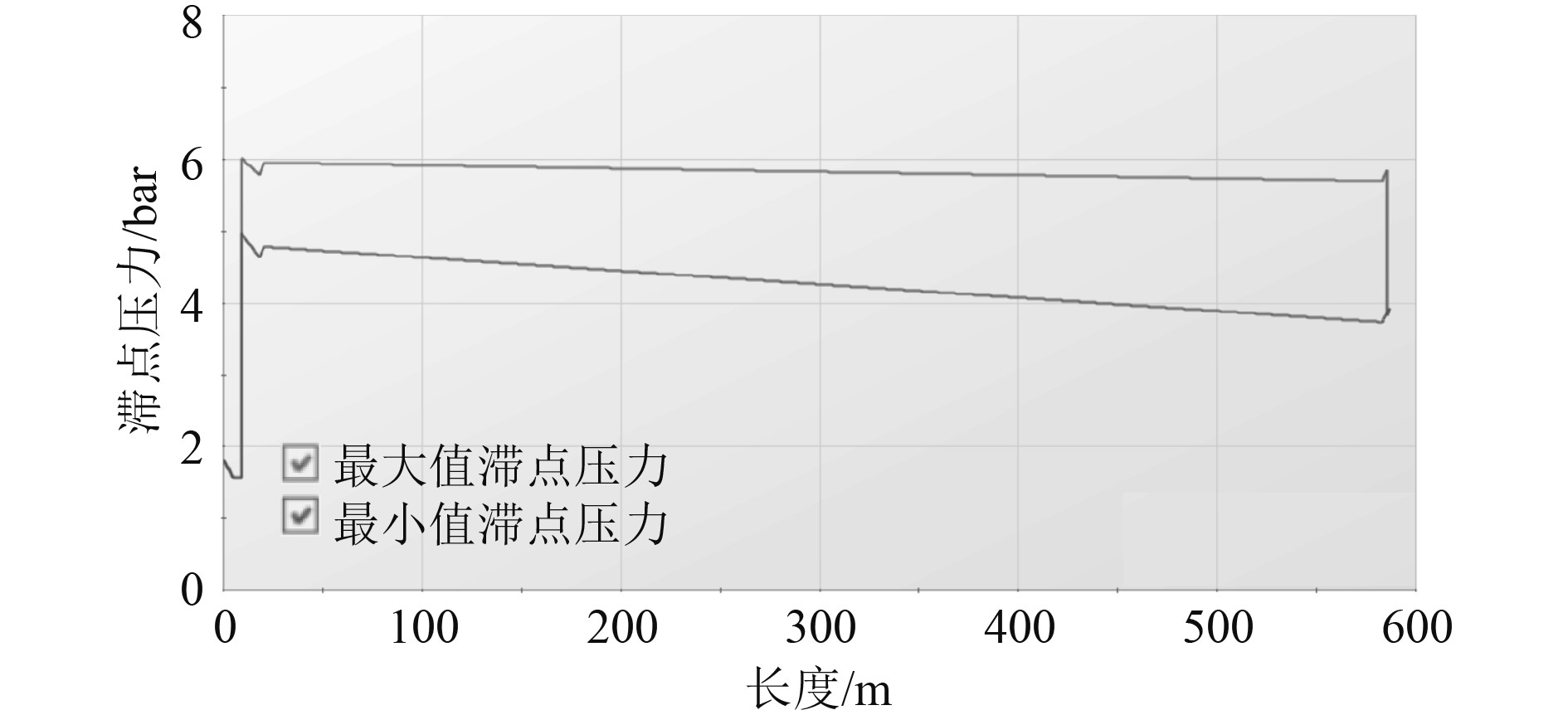
图 7 两阶段关阀10 s关阀,阀前加入缓气罐 Fig. 7 Close the valve in two stages for 10 s, and add a buffer tank in front of the valve |
由表10可知,在10 s直线关阀时,管路内最大水锤压力值为34.980 bar,远远大于压载水管路系统中最大允许水锤压力为11.305 bar。在增加缓气罐后,管路中最大水锤压力值为6.092 bar,符合管路中允许的最大压力值。由表11可知,在10 s采用两阶段关阀时,管路内最大水锤压力值为20.007 bar,增加缓气罐后,管路中最大水锤压力值为6.024 bar,符合管路中允许的最大压力值。
由图6和图7所知,在阀前加入缓气罐后能有效的抑制水锤的产生,使管路中最大水锤压力值趋于稳定状态。因此在阀前增加缓气罐也是一种有效抑制水锤产生的方法,但同时也增加了成本。
4 结 语本文介绍了水锤压力的产生原理及其危害,通过对从海底门进水到右舷7舱室的模型及各关阀工况设置进行水锤压力分析得出,在深水通用型FPSO工程中,压载水系统在紧急关阀时会出现水锤现象,水锤压力大小与关阀工况密切相关。采用两阶段关阀(第1阶段快速关闭,第2阶段缓慢关闭)相对于直线关闭的情况下,在总关闭时间相同时,对于降低最大水锤压力效果比较明显,并进一步缩短了总关阀时间,可以有效保护压载水管路系统。
| [1] |
李志鹏, 朱慈东, 等. 输水系统空气阀结构特性与水锤防护[M]. 北京: 中国水利水电出版社, 2018.
|
| [2] |
杨晓蕾, 沈来新, 等. 重力流输水管道关阀水锤模拟研究[J], 水利水电技术, 2017(5): 95−96.
|
| [3] |
黄源, 赵明, 等. 输配水管网系统中关阀水锤的优化控制研究[J]. 给水排水, 2017, 43(2): 123-127. DOI:10.3969/j.issn.1002-8471.2017.02.028 |
| [4] |
董茹, 杨玉思, 等. 关阀程序对分支线重力流输水系统水锤升压影响[J]. 中国给水排水, 2016, 32(11): 50−54.
|
| [5] |
缪军. 浅谈大管径并联冷却循环水停泵水锤现象的消除解决[J]. 中国设备工程, 2017(9): 111-113. DOI:10.3969/j.issn.1671-0711.2017.09.058 |
| [6] |
刘亚萌, 蒋劲, 等. 基于多目标粒子群算法的停泵水锤防护优化[J]. 中国农村水利水电, 2017(6): 162-167. DOI:10.3969/j.issn.1007-2284.2017.06.034 |
| [7] |
万德民, 舟山LNG接收站装船管路系统典型工况水锤分析[D]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [8] |
乔丁, 高扬程多起伏长距离压力输水管道水锤防护技术研究[D]. 西安: 长安大学, 2013.
|
| [9] |
张健丽, 水锤计算模型对管道水力过渡计算结果的影响研究[D]. 西安: 长安大学, 2012.
|
| [10] |
Metallic industrial piping-design and calculation[S]. BS EN 13480-3-2012, 2012.
|
| [11] |
The American Society of Mechnical Engineerings. ASME CODE for power piping B31.1-2012[S]. 2013.
|
| [12] |
The American Society of Mechnical Engineerings. ASME CODE for process piping B31.3-2012[S]. 2013.
|
 2022, Vol. 44
2022, Vol. 44
