FPSO是集生产、储油、卸油于一体的海上浮式生产储卸油装置,具有抗风浪能力强、适应水深范围广、机动灵活、储卸油能力大等优点,为当前海工结构开发的热点。FPSO依靠特殊的系泊系统锚固在海上,在FPSO所采用的各种系泊系统中,内转塔式单点系泊系统的应用最为广泛,是影响FPSO安全性的关键技术所在。
内转塔式单点系泊系统具有两大基本功能:一是通过特殊连接方式将FPSO系泊于海上系泊点,使其随风浪流作用进行360°全方位自由旋转,形成风向标效应,大大降低FPSO在海上作业时的环境载荷;二是内转塔系统是FPSO与海上井口平台连接的唯一通道,通过海底管道及通信电缆实现FPSO与海底井口平台之间不间断的油气输送和信息传输。内转塔系统是单点式FPSO的核心设备,一旦发生油气泄漏爆炸将对FPSO油气生产系统造成毁灭性打击,因此对爆炸载荷作用下FPSO月池结构的过压分析具有重要意义[1-5]。
本文对FPSO月池结构在爆炸过压载荷作用下的结构响应进行研究。1)采用非线性静力分析方法,考虑材料弹塑性影响,确定月池结构在增量加载至爆炸载荷极值过程中的应力应变响应;2)采用非线性动力分析方法,考虑不同爆炸载荷作用过程(脉冲时间和脉冲峰值),研究月池结构在爆炸载荷作用下的时历变形、应变及能量吸收关系。对比2种计算方法,总结爆炸载荷作用下月池结构的应力应变响应规律。
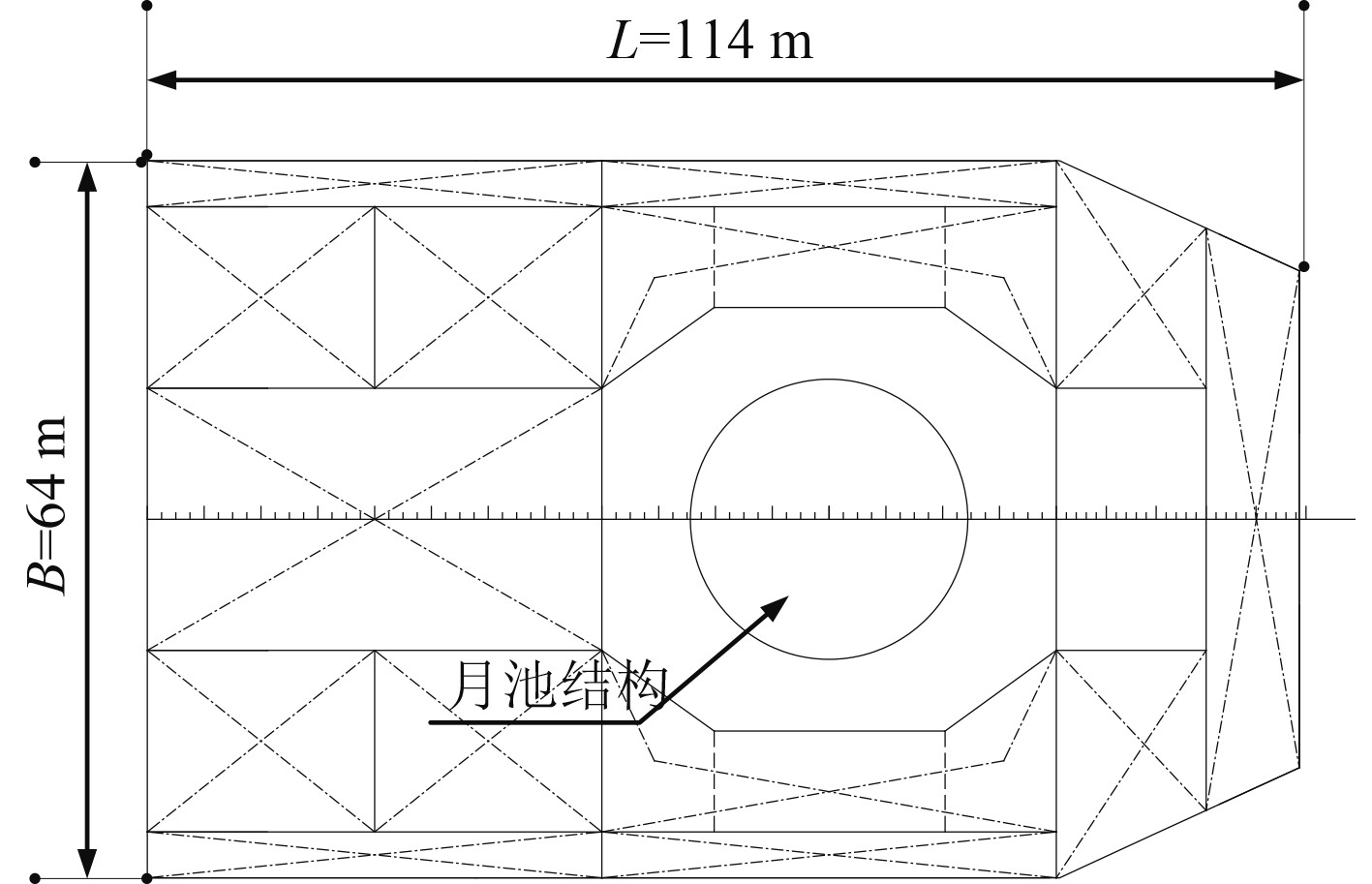
1 月池结构介绍以某内转塔式单点系泊FPSO首部单点舱月池结构作为研究对象,建立包括第1货油舱、单点舱、首尖舱的三舱段结构模型,舱段总长L=114 m,宽B=64 m,高H=33 m,如图1所示。月池结构材料为高强钢AH32,屈服应力315 MPa,极限拉伸强度505 MPa,断裂应变0.153,月池筒形结构壁厚35 mm。
|
图 1 月池结构几何尺寸示意图 Fig. 1 Geometry parameter of moonpool structure |
非线性静力分析方法通常采用牛顿迭代或者改进的牛顿迭代法,通过对结构平衡方程中的刚度矩阵转置进行迭代求解获得收敛的计算结果。该方法不考虑时间效应、惯性载荷影响,通过对结构施加单调递增载荷使结构达到给定位移或应变状态,结合材料本构模型的弹塑性特征,获得载荷变化过程中结构的非线性响应。
尽管非线性静力分析方法不考虑阻尼、惯性效应,但是对于不考虑外载荷时历变化影响的弹塑性分析,其计算精度处于工程应用可接受范围内。对于本文内转塔式FPSO月池结构过压分析,采用非线性静力分析能够得到合理的求解结果。相比于动力分析方法,非线性静力分析方法的另一个计算优势是能够通过细致的载荷步加载得到结构的极限承载载荷,便于评估结构的极限过压载荷,而采用动力分析方法则需要多次的迭代试算才能实现该目的,非常费时费力。
2.2 非线性静力分析仿真根据图1所示月池结构几何尺寸示意图,使用Ansys软件建立非线性静力分析有限元模型,如图2所示。

|
图 2 有限元模型 Fig. 2 Finite element model |
为准确模拟结构弹塑性性能,使用Shell181,Beam188单元建模,其中第1货油舱和艏尖舱网格尺寸按肋骨间距建模,包括甲板、外板、横框架、纵桁等,单点舱采用细网格尺寸(50 mm×50 mm)建模,以准确捕捉单元失效,在爆炸区域-月池筒壁及相邻扶强材结构的网格尺寸设置最密,并逐渐向外部过渡,爆炸区域全部采用板单元模拟,其他粗网格区域则采用板梁单元组合模拟。
材料模型采用多线性随动强化模型,通过定义多线性的应力-应变曲线模拟随动强化效应,该模型适用于服从Mises屈服准则的小应变塑性分析,一般钢材等金属材料均适用,当实际应变值超过输入曲线终点时,按理想塑性材料行为模拟。其本构关系如下:
| ${\sigma _{yk}} = \frac{1}{{2\left( {1 + v} \right)}}\left( {3E{\varepsilon _k} - \left( {1 - 2v} \right){\sigma _k}} \right)\text{。}$ | (1) |
式中:
|
|
表 1 材料曲线数据点 Tab.1 Material curve data |
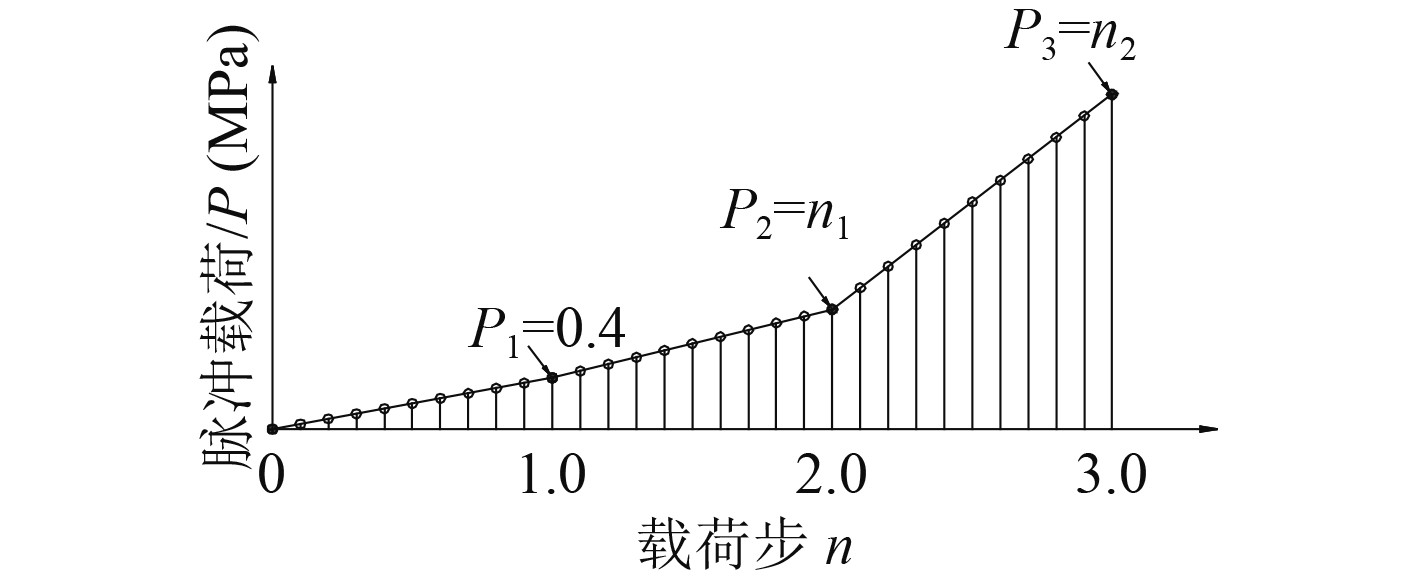
在FPSO舱段模型尾部端面节点上施加刚性约束,对月池筒体区域(水线至主甲板面区域)施加均布面压力模拟爆炸载荷,根据船级社规范规定[6],封闭的内转塔式月池结构爆炸压力载荷的脉动压力峰值为0.4 MPa,因此以0.04 MPa间隔单调递增加载至0.4 MPa,得到月池结构的弹塑性响应结果,并继续单调递增(改为自动载荷步)加载载荷至结构失效,以获取月池结构的最大过压载荷值,载荷步加载示意如图3所示。
|
图 3 非线性静力分析载荷步加载示意图 Fig. 3 Load step of nonlinear static analysis |
图4为脉动压力峰值为0.4 MPa时的月池结构应力、应变响应云图。此时FPSO舱段模型的最大应力单元出现在月池筒壁结构环形加强框架上,最大等效应力为117 MPa,最大等效应变为557E-6,月池内部筒壁结构最大等效应力93 MPa,最大等效应变为541E-6,结构未发生塑性变形。

|
图 4 非线性静力分析-0.4 MPa脉动压力 Fig. 4 Nonlinear static analysis-0.4 MPa impulse load |
随着爆炸载荷的继续增量加载,脉动压力峰值为3.89 MPa时,最大等效应力为505 MPa,最大等效应变为0.153,材料单元发生塑性失效,月池结构达到最大过压载荷值,如图5所示。

|
图 5 非线性静力分析-3.89 MPa脉动压力 Fig. 5 Nonlinear static analysis-3.89 MPa impulse load |
与非线性静力分析不同,动力分析能够考虑载荷随时间变化时结构的力学时历过程,算法上可以考虑阻尼和惯性载荷,对于爆炸、冲击类问题尤为适用。为考察内转塔式FPSO月池结构在过压爆炸载荷作用下的时历响应,采用显式动力分析方法对该过程进行模拟,对比非线性静力分析求解结果,并研究不同脉冲时间对月池结构响应的影响。
3.1 显式动力分析方法基于显式动力分析理论研究FPSO月池结构在过压爆炸载荷作用下的动力响应,适于处理瞬态、大变形问题。其动力平衡方程如下:
| ${{{M}}u_n{''} + {{C}}u_n' + F_n^{int} = F_n^{ext}{\text{。}}}$ | (2) |
式中:
由式(2)计算可得,节点加速度矢量为:
| $u_n{''} = {{{M}}^{ - 1}}\left( {F_n^{ext} - F_n^{int} - Cu_n'} \right)\text{,}$ | (3) |
采用中心差分法计算节点速度矢量与位移矢量为:
| $u_{n + \frac{{\Delta n}}{2}}' = u_{n - \frac{{\Delta n}}{2}}' + u_n{''}\left( {\Delta {t_{n + \frac{{\Delta n}}{2}}} + \Delta {t_{n - \frac{{\Delta n}}{2}}}} \right)/2\text{,}$ | (4) |
| ${u_{n + \Delta n}} = u_n' + u_{n + \frac{{\Delta n}}{2}}'\Delta {t_{n + \frac{{\Delta n}}{2}}\text{。}}$ | (5) |
对于动力分析问题,显式算法非常适用于大矩阵方程的求解,由于显式算法不需要进行矩阵转置与迭代,其所有非线性均包含在内力矢量中,因此在同一时间步内,显式算法较隐式算法的计算效率更高。
3.2 显式动力分析仿真采用Ansys-Lsdyna软件进行显式动力分析求解,有限元模型如图2所示。使用Ansys-Lsdyna隐式-显式转换功能建立显式动力分析模型,需转换模型单元类型由Shell181,Beam188单元转换为Shell163,Beam161单元,并重新进行显式单元属性和材料定义,有限元模型纯网格尺寸保持不变。
FPSO舱段模型采用分段线性塑性模型,该模型可直接定义与应变率相关的应力-应变曲线。本构模型中采用Cowper-Symonds模型考虑应变率影响,本构关系如下:
| ${\sigma _y}\left( {\varepsilon _{eff}^p,{\varepsilon '}_{eff}^p} \right) = {\sigma _y}\left( {\varepsilon _{eff}^p} \right)\left[ {1 + {{\left( {\frac{{{\varepsilon '}_{eff}^p}}{c}} \right)}^{\frac{1}{p}}}} \right]\text{。}$ | (6) |
式中:
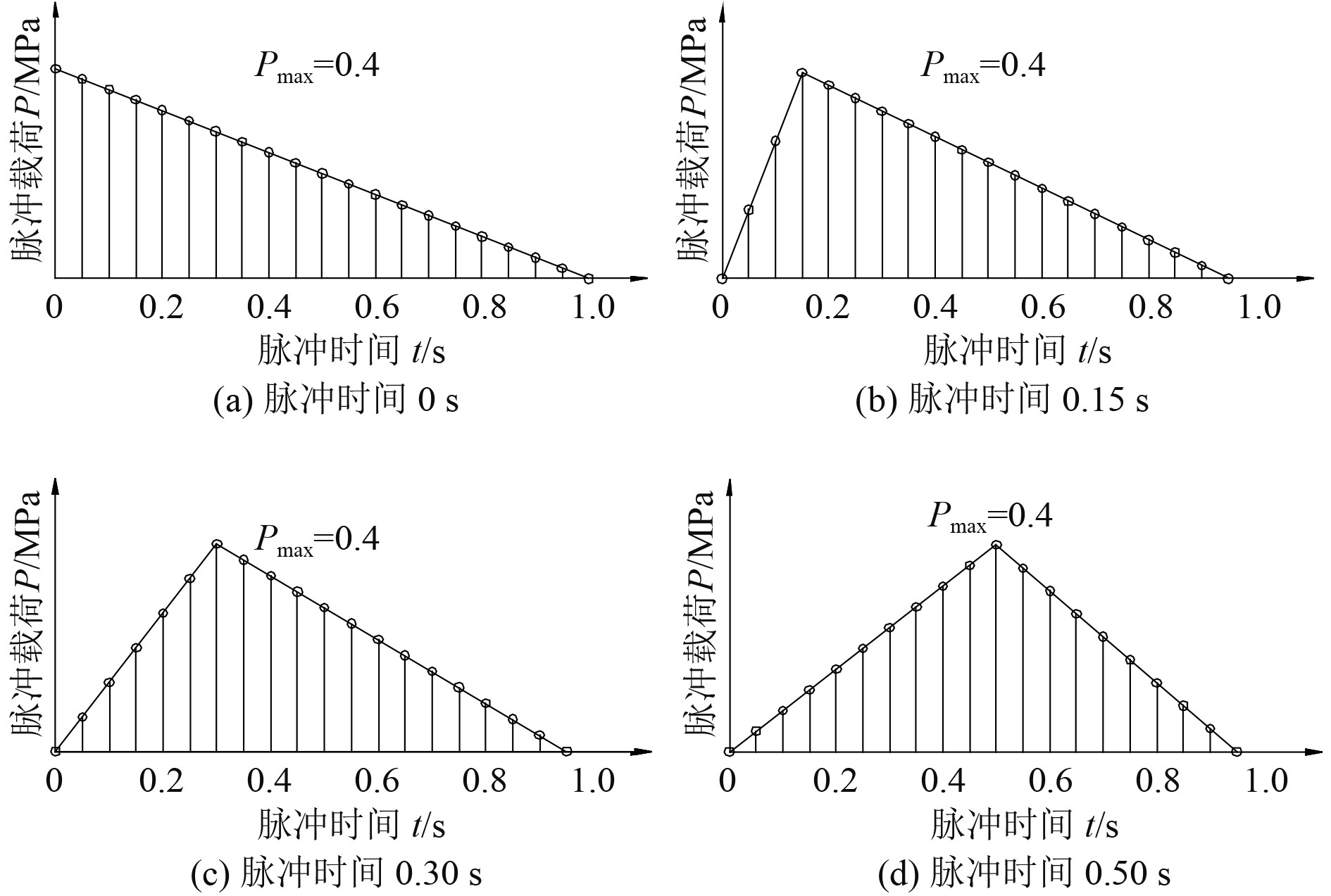
爆炸载荷由时间和空间因素共同定义,在爆炸空间场所(水线至主甲板面区域)基本确定后,决定爆炸载荷大小的主要是压力上升时间、最大脉冲峰值及脉冲周期。基于船级社规范的简化确定方法,假定爆炸压力随时间变化的形状函数为三角形脉冲载荷,脉动压力峰值为0.4 MPa,脉冲周期为1 s,压力上升时间取0 s/0.15 s/0.30 s/0.50 s,研究压力上升时间对结构响应的影响,如图6所示。
|
图 6 三角形载荷-压力上升时间 Fig. 6 Triangular shape load-overpressure load raising time |
以压力上升时间0.5 s爆炸载荷工况为例,图7为爆炸压力载荷在t=0.5 s时刻的等效应力和等效应变云图,此时FPSO舱段模型最大等效应力115 MPa,最大等效应变为714E-6,月池内部筒壁结构最大等效应力88 MPa,最大等效应变为546E-6,结构未发生塑性变形。

|
图 7 压力上升时间0.50 s爆炸载荷工况 Fig. 7 Blast condition with raising time=0.50 s |
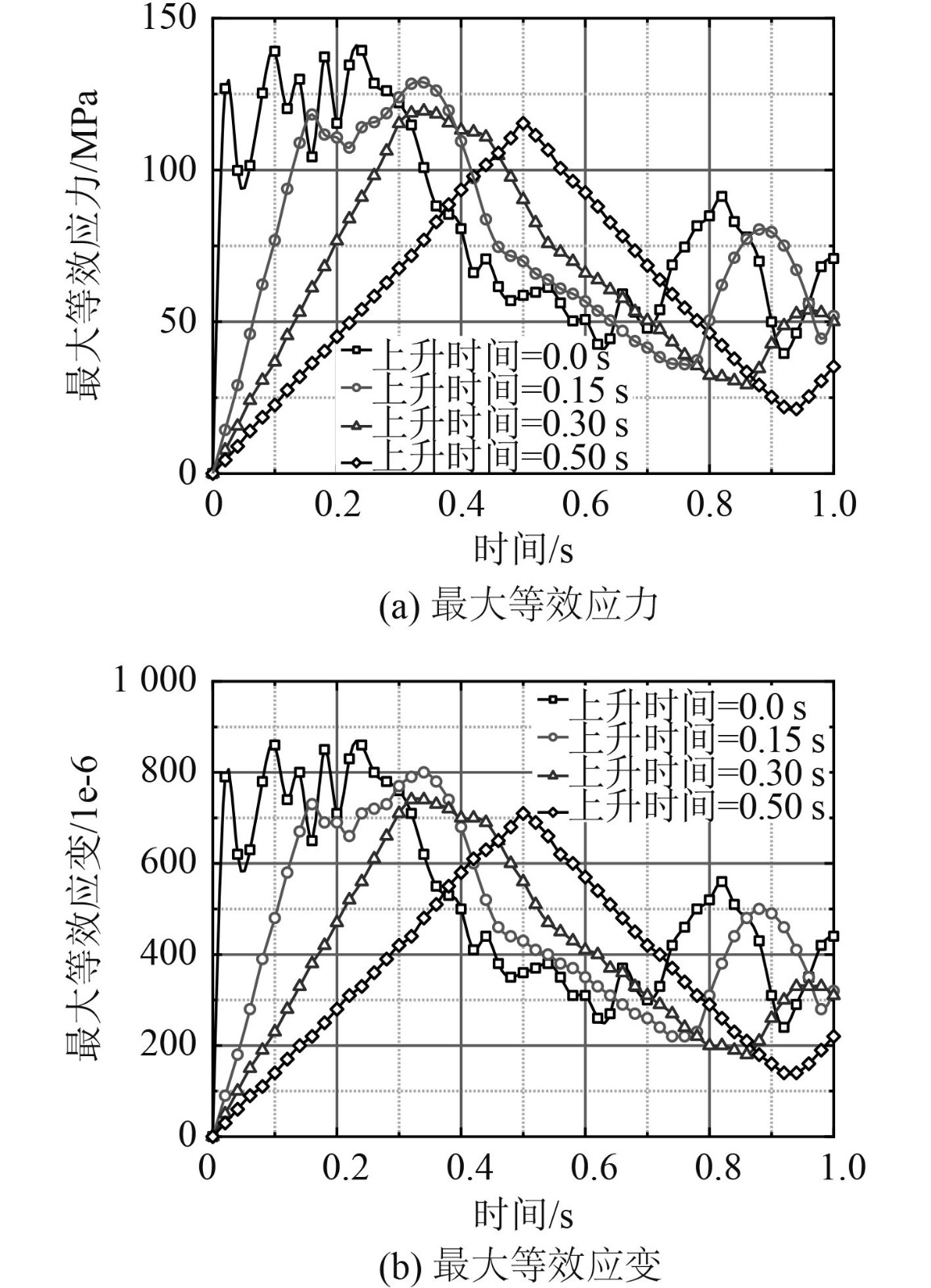
分析压力上升时间0 s,0.15 s,0.30 s,0.50 s爆炸载荷工况下的计算结果,在4个工况下最大等效应力位置均出现于月池筒壁结构环形加强框架上。图8为4个工况下最大等效应力和最大等效应变随载荷时间变化情况,随着压力上升时间的增长,最大等效应力和等效应变随之下降。
|
图 8 压力上升时间0 s/0.15 s/0.30 s/0.50 s Fig. 8 Raising time 0 s/0.15 s/0.30 s/0.50 s |
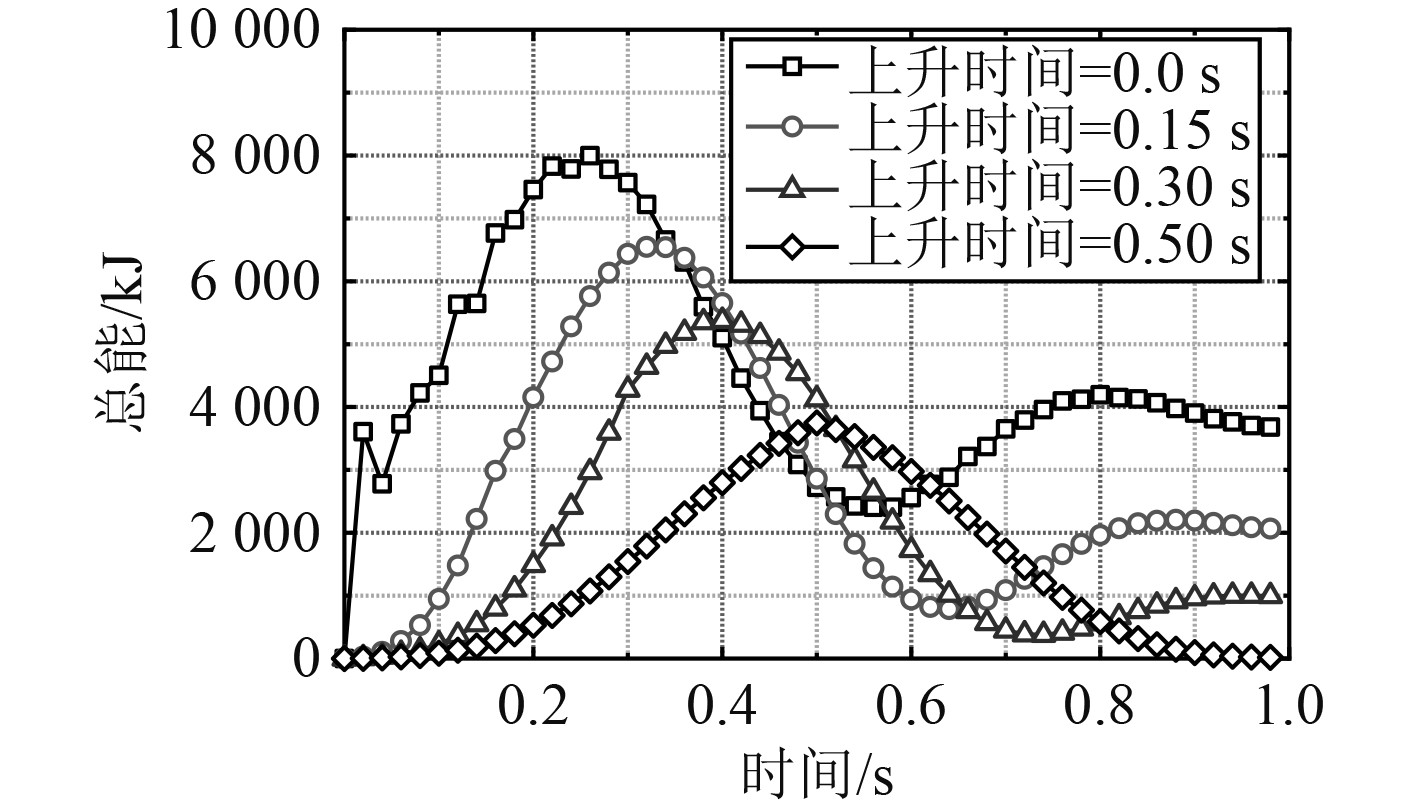
压力上升时间0 s,0.15 s,0.30 s,0.50 s典型爆炸载荷工况下总能量(包括内能、动能、摩擦能、沙漏能,其中摩擦能和沙漏能量级太小可忽略)变化关系如图9所示。结果表明,最大爆炸能量与脉冲压力变化相似但最大峰值稍微滞后,压力上升时间越短产生的爆炸能量越大,其中压力上升时间0 s工况的最大爆炸能量值为8000 kJ。
|
图 9 压力上升时间0 s,0.15 s,0.30 s,0.50 s:总能量变化曲线 Fig. 9 Raising time 0 s, 0.15 s, 0.30 s, 0.50 s: global energy curve |
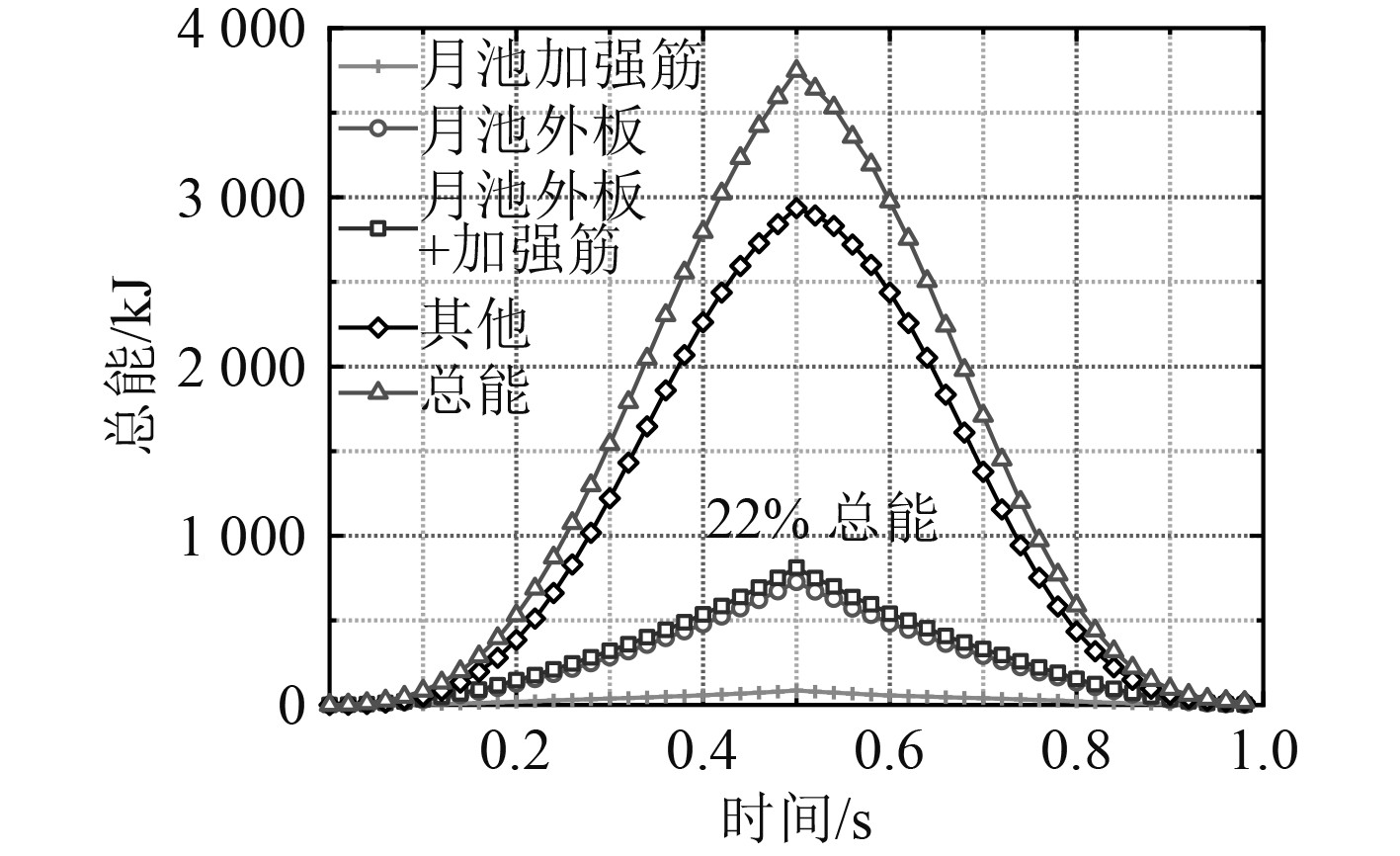
图10为压力上升时间0.50 s爆炸载荷工况下FPSO舱段各结构能量吸收情况,由于直接承受爆炸过压载荷,月池筒壁结构能量吸收较大,约为总能量的22%,其中筒壁外板吸收能量最多,加强筋对能量吸收较小,提高月池筒壁外板板厚能较好的提高月池结构防爆能力。
|
图 10 压力上升时间0.50 s:各构件能量吸收曲线 Fig. 10 Raising time 0.50 s: energy absorbing curve for different components |
以某内转塔单点式FPSO首部月池结构为研究对象,通过采用非线性静力和动力分析2种计算方法,研究月池结构在爆炸过压载荷作用下的结构响应变化规律,参数化研究不同压力上升时间变化时爆炸脉冲载荷对结构响应的影响,对比2种分析方法计算结果的区别,得到如下结论:
1)基于规范确定内转塔式FPSO月池结构爆炸过压载荷的基本数据,脉冲压力峰值0.4 MPa,脉冲时间1 s,采用非线性静力分析方法能够获得满足工程应用的计算结果。
2)非线性静力分析方法不考虑时间、惯性效应,适用于不考虑载荷历程影响的弹塑性分析,较非线性动力分析方法具有一个显著优势是可以通过细致的载荷步增量加载计算得到结构的极限载荷。经计算,研究目标的结构极限过压载荷为3.89 MPa。
3)非线性动力分析方法能够考虑更多设计因素:阻尼、惯性等影响,计算精度高。通过对压力上升时间的参数化研究发现,压力上升时间越短,产生的爆炸能量越大,相应的最大等效应力和最大等效应变也越大。在爆炸过压载荷作用下,结构响应与脉冲载荷变化规律相似但最大峰值稍微滞后。
4)在爆炸过压载荷作用下,直接承受爆炸载荷的月池筒壁结构吸收较大部分爆炸能量,对月池筒壁进行板厚加强并在筒壁周围设置适当加强结构能够有效提高月池结构防爆能力。
| [1] |
刘志刚, 何炎平. FPSO转塔系泊系统的技术特征及发展趋势[J]. 中国海洋平台, 2006, 21(5): 1-6. DOI:10.3969/j.issn.1001-4500.2006.05.001 |
| [2] |
赵耕贤. FPSO结构设计特点[M]. 船舶, 2002, (1): 38-41.
|
| [3] |
单连政, 董本京, 刘猛. FPSO技术现状及发展趋势[J]. 石油矿场机械, 2008, 37(10): 26-30. DOI:10.3969/j.issn.1001-3482.2008.10.007 |
| [4] |
赵耕贤. 船舶与海洋工程结构设计技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2014.9.
|
| [5] |
吴家鸣. FPSO的特点与现状[J]. 船舶工程, 2012, 34(2): 1-4. DOI:10.3969/j.issn.1000-6982.2012.02.001 |
| [6] |
DNVGL. DNVGL-OS-A101: Safety principles and arrangements [M]. 2015.
|
| [7] |
DNV. DNV-RP-C208: Determination of structural capacity by non-linear FE analysis methods [M]. 2013.
|
| [8] |
DNV. DNV-RP-C204: Design against accidental loads [M]. 2010.
|
 2020, Vol. 42
2020, Vol. 42
