顺应全球面临的环境污染问题及节能减排趋势,IMO组织对于船舶EEDI指数及最小功率要求提出了严苛要求。其中关乎EEDI指数的试航航速修正方法及最小功率计算中的波浪增阻计算方法,两大国际指南《ISO15016:2015测速试验标准》[1],《2013恶劣海况下维持船舶操纵性的最小推进功率临时导则》[2]采用的是推荐性的经验公式或者水池试验。经验公式对于不同船型的适用性及精确性需要大量的数据验证,水池试验结果具有较高的准确性,但试验周期长、价格昂贵,且只可针对特定的试验船型。因此,前期研究时为快速准确的获得波浪增阻结果研究人员多采用数值模拟。
波浪增阻的数值计算,目前主要有基于二维切片理论、基于三维势流理论和基于黏流理论的3种数值方法[3]。黏流理论的数值方法主要是基于雷诺平均N-S方程的离散,与基于势流理论的数值方法相比,能处理非线性流动现象,因此也是目前较为流行的一种方法,目前较为流行的计算模型主要包括RANS,LES以及DNS,可根据具体情况进行选择。于海等[4]利用NUMECS/FineMarine对某中型豪华游船波浪增阻进行数值模拟,发现基于粘流数据计算得到的波浪增阻RAO曲线与模型试验结果吻合很好,较常用的势流方法更准确稳定。李纳等[5]以1艘50 m围网渔船船模为研究对象,采用STAR-CCM软件计算研究其约束运动模型在静水和迎浪情况下的阻力及相关性能,计算结果与试验吻合性较好。但是该类方法对计算性能要求很高,且计算速度较慢。尤其对于VLCC这类超大型船舶,RANS模型会将重要涡结构抹去,结果准确度降低;LES以及DNS模型对网格要求很高,大雷诺数下边界层变薄导致计算网格大量增加,计算效率较低[6]。基于三维势流理论准确性与计算效率都较高,Jinpeng Hu等[7]基于Ansys-Aqwa对不同种类浮标的水动力性能进行模拟,发现球形浮标各项水动力性能较优。但这类方法在涉及船舶阻力计算时很少使用,主要原因有两点:一是无法考虑黏性效应,对船舶的粘性阻力及粘压阻力无法准确评估;二是无法处理自由液面非线性流动现象如波浪破碎、甲板上浪等等。然而在计算VLCC这类超大型船舶的波浪增阻时这2个问题可以得到很好的解决,对于VLCC这类超大型结构物在计算波浪增阻时应主要考虑结构物上的绕射力与质量力,黏性力不显著[8]。并且,波浪也可以按照线性波处理,非线性现象都可被忽略。因此,本文以32万吨VLCC为例,利用Aqwa软件分别计算其在静水及波浪环境下受到阻力大小,两者相减得到波浪增阻。通过与模型试验结果相比较,分析这一方法可靠性,为此类大型船舶波浪增阻计算提供参考。
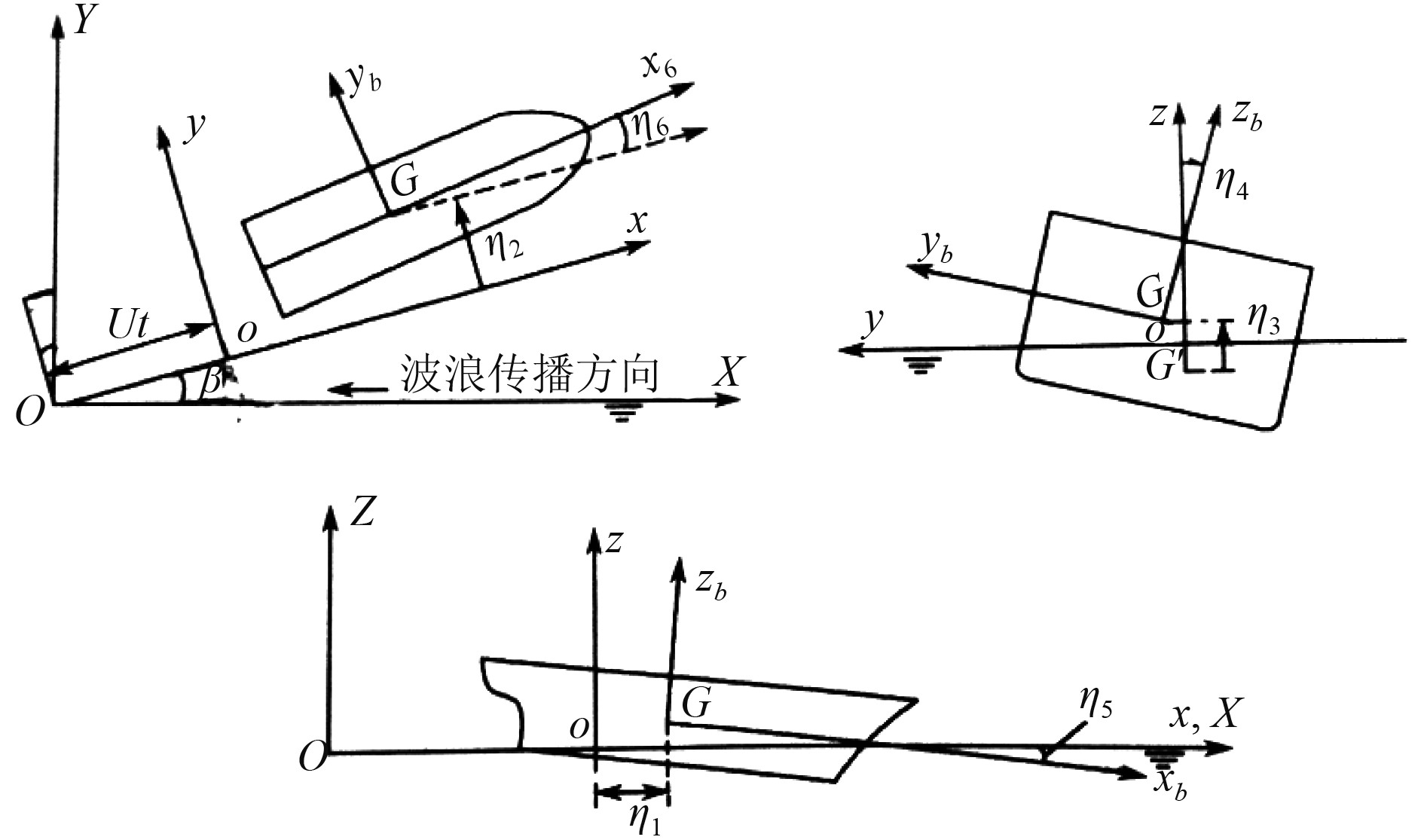
1 计算方法为了便于描述波浪、船舶运动以及流场速度势三者之间的关系,本文引入3个右手坐标系:空间固定坐标系O-XYZ;随船平动坐标系o-xyz;固连于船舶的坐标系G-xbybzb。
3种坐标系相互关系如图1所示。
|
图 1 描述船体运动的3个坐标系 Fig. 1 Three coordinate system for describing the movement of the ship |
在大地坐标系中求解时域解的定解问题时,流场中各点速度势必应满足下列各式:
拉普拉斯方程
| ${\nabla ^2}\phi = \frac{{{\partial ^2}\phi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {z^2}}} = 0 \;{\text{,}}$ | (1) |
底面条件
| $\frac{{\partial \phi }}{{\partial z}} = 0,z = - d\;{\text{,}}$ | (2) |
物面条件
| $\frac{{\partial \phi }}{{\partial n}} = {V_n}\;{\text{,}}$ | (3) |
物面条件
| $\frac{{\partial \eta }}{{\partial t}} + u\frac{{\partial \eta }}{{\partial x}} + v\frac{{\partial \eta }}{{\partial y}} - \frac{{\partial \phi }}{{\partial z}} = 0,z = \eta (x,y,t)\;{\text{。}}$ | (4) |
通过Bernoulli方程可求出流体压力、水动力和力矩,由于微幅波作用下VLCC作微幅振荡运动,瞬时湿表面积S近似相等于平均湿表面积或船体静止时的湿面积S0。因此,本文只需将1阶压力沿平均湿表面积分即可。
各点压力:
| $p = - \rho \frac{{\partial \phi }}{{\partial t}}\;{\text{,}}$ | (5) |
水动力:
| ${F_i}\left( t \right) = - \iint\limits_{{S_0}} {pn{\rm{d}}S} = - \iint\limits_{{S_0}} {\rho \frac{{\partial \phi }}{{\partial t}}{n_i}}{\rm{d}}s\;{\text{,}}$ | (6) |
力矩:
| ${{F}_{i}}\left( t \right)=-\iint\limits_{{{S}_{0}}}{p\left( r\cdot n \right){\rm{d}}S}=-\iint\limits_{{{S}_{0}}}{\rho \frac{\partial \phi }{\partial t}(r\cdot {{n}_{i}})}{\rm{d}}s\;{\text{。}}$ | (7) |
式中:ρ为流体密度;
模型试验在Maritime Research Institute Netherlands(MARIN)进行,试验对象为320 000 DWT VLCC船,船舶主尺度如表1所示。试验目的在于评估最小装机功率,测量规定航速下不同频率入射波引起的波浪增阻大小。
|
|
表 1 主尺度参数 Tab.1 Main particulars |
船体模型由木材构成,如图2所示。根据相关要求,在试验准备阶段按照要求调整好船模重量、重心以及纵向转动惯量,模型及入射波浪各项参数如表2所示(前3列)。模型试验在Depressurised Wave Basin完成,水池尺寸为240 m×18 m×8 m,试验过程由高速摄像机拍摄,船体纵摇、升沉以及航速等试验数据由相关设备记录。

|
图 2 船体模型 Fig. 2 Ship modle |
|
|
表 2 波浪增阻试验结果 Tab.2 Testing Results of the Added Resistance |
综合考虑推进系统尺寸要求船体模型缩尺比选取为35。模型垂线间长为9.26 m,为方便记录分析沿纵向划分21个站位,沿垂向设置10道水线。为贴合实际情况,试验过程中不限制模型深沉与纵摇,仅对横摇、首摇及横荡加以限制,试验过程中主要测量模型受到阻力及各自由度运动响应。
2.3 试验工况及结果试验主要测量本船在满足规范要求的最小安全航速下迎浪时波浪增阻大小。
保持船舶安全航行要求的最小前进航速VS(kn),按下面公式计算:
| ${V_{{S}}} = \max \left( {4{\rm{kn}},{V_{{\rm{kn}}}} = {V_{{\rm{ref}}}} - 10.0 \times \left( {{A_{\rm{R}}}\% - 0.9\% } \right)} \right)\;{\text{,}}$ | (8) |
| ${A_{\rm{R}}}\% = {A_{\rm{R}}}/{A_{{\rm{LS,COR}}}} \cdot 100\% \;{\text{,}}$ | (9) |
| ${A_{{\rm{LS,COR}}}} = {L_{{\rm{PP}}}}{T_{\rm{m}}}(1.0 + 25.0 \times {({B_{{\rm{WL}}}}/{L_{{\rm{PP}}}})^2})\;{\text{。}}$ | (10) |
式中:Vkn为最小航向稳定航速,kn;Vref为相对航行稳定航速,kn,按MEPC.232(65)附录3.7中规定取值;AR为实际舵面积,m2;LPP为两柱间长,m;Tm为船中部吃水,m;BWL为船水线宽,m。
本船VS=5.7 kn。
入射波频率及波高如表2所示。试验中分别测得船舶静水与波浪中阻力大小,通过两者相减得到对应工况下波浪增阻大小并除以波高的平方即可得到波浪增阻2阶传递函数。
3 数值计算 3.1 模型建立船体计算模型如图3所示。网格数为7 893,坐标系原点建立在船体中纵剖面与水线面的交线尾部。为贴合试验减少计算误差,阻力计算时采用拖航方案,通过缆绳连接船舶与移动质点(相当于拖轮,质量足够大,防止速度减小过快),质点以固定航速(5.27 kn)移动,带动船舶。通过分析连接缆绳的张力时程变化情况得出船舶阻力。

|
图 3 船体网格模型 Fig. 3 Ship mesh model |
根据经验公式,纵摇惯性半径选取0.25 L。分别模拟得到船舶静水与波浪中阻力大小,通过两者相减得到对应工况下波浪增阻大小。通过数据处理得到波浪增阻2阶传递函数如表3所示。
|
|
表 3 波浪增阻数值模拟结果 Tab.3 Numerical Simulation Results of the Added Resistance |
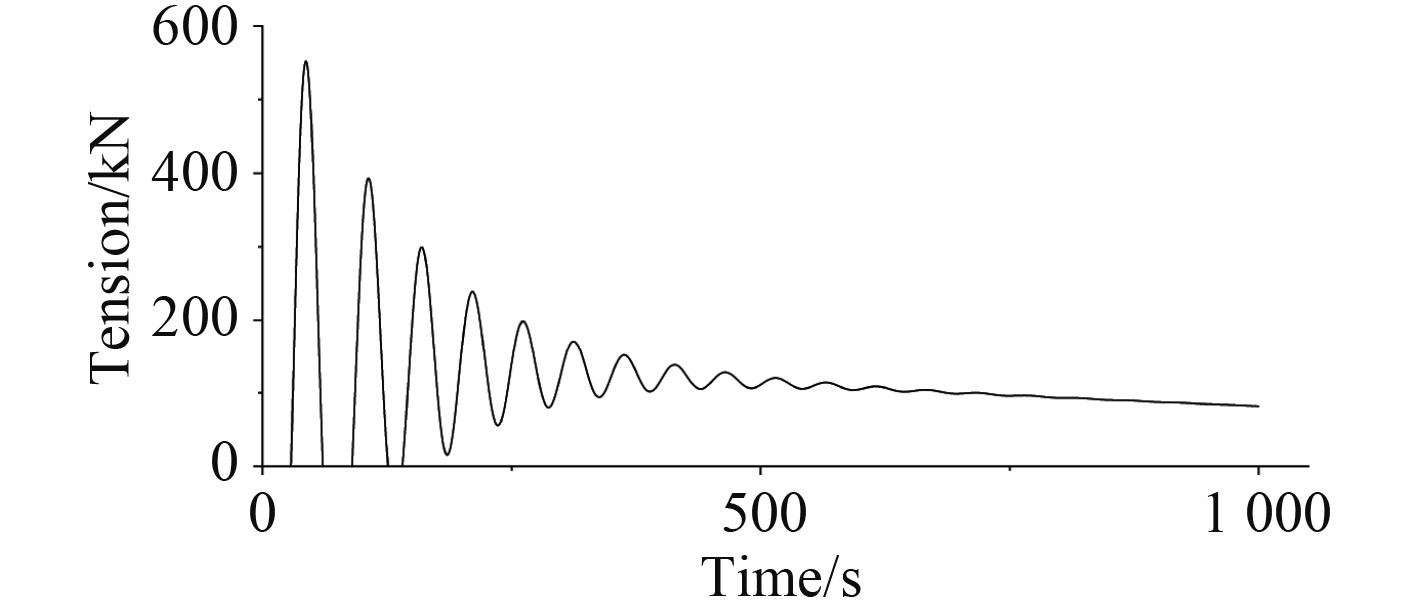
以入射波频率为0.9 rad/s为例,采用Ansys-Aqwa分别模拟船舶在静水及波浪环境下运动状态,分析拖缆张力时程曲线,如图4和图5所示。
|
图 4 静水条件下拖缆张力时程曲线 Fig. 4 Time history of towline tension in calm water |
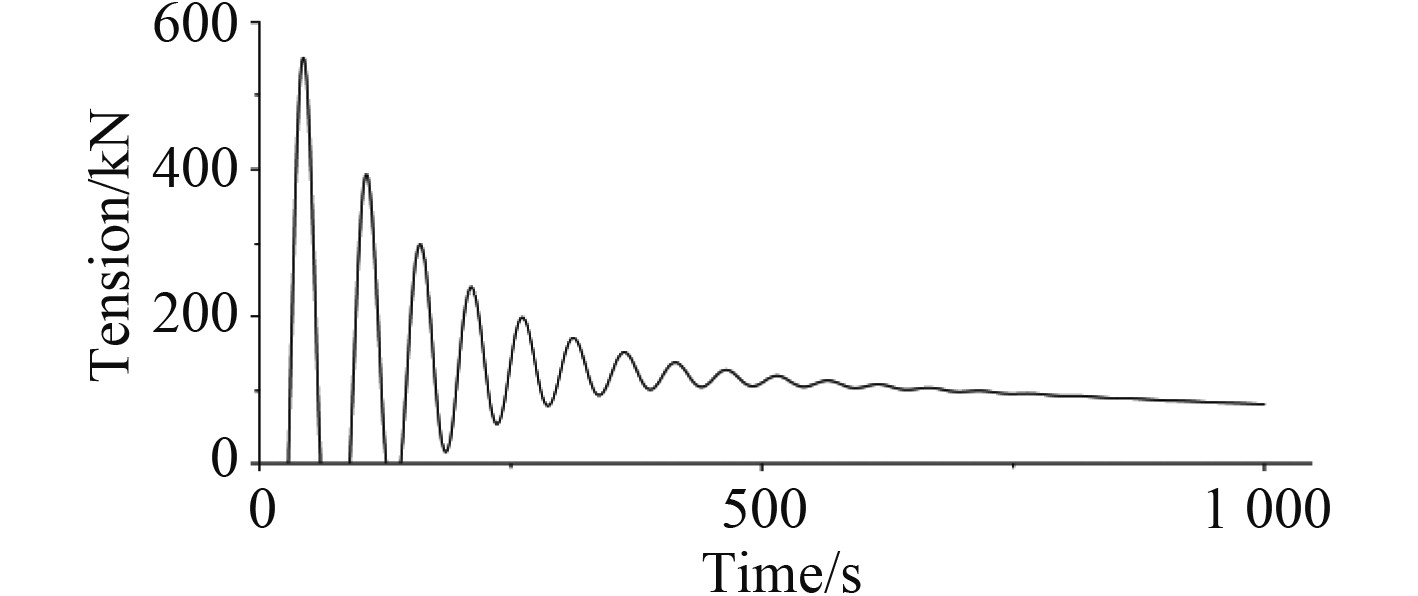
|
图 5 波浪条件下拖缆张力时程曲线(ω=0.9) Fig. 5 Time history of towline tension in wave |
图4和图5分别为静水与波浪条件下拖缆张力时程曲线,初始状态时由于船舶与移动质点速度相差较大,揽绳张力会出现较大波动,不宜作为分析依据。船速基本稳定时缆绳张力波动较小,取此段区间张力的平均值作为船舶阻力值,通过波浪阻力与静水阻力相减得到各入射波频下波浪增阻。以入射波频为0.9 rad/s时为例,静水条件下稳定段取250~1 000 s,波浪条件下稳定段取350~1 000 s,分析得静水阻力为181 kN,波浪阻力为311 kN,波浪增阻即为130 kN。
3.3 计算结果根据以上设置及分析方法计算8种工况(ω=0.35~0.9)的波浪增阻大小,并计算各工况下静水阻力及波浪载荷作用下总阻力,通过两者相减得波浪增阻,计算结果见表3。
各工况下波浪增阻由总阻力R减去Rs得到,用Rw表示。计算结果表明入射波频率在0.4~0.45范围内时总阻力较大,最大值达到432 kN。这主要是由于此段波频区间对应的波长与船长最为接近,容易引起较大的纵摇与垂荡运动。由此亦可见引起波浪增阻最主要的因素为船舶运动引起阻力的增加。
另外,注意到数值模拟得到的静水阻力为181 kN,这与模型试验换算结果324.1 kN相比相差较大,主要原因是数值计算过程中忽略了流体粘性作用,无法算得摩擦及粘压阻力。故这一方法无法准确算得的水阻力大小,单独计算静水阻力或波浪总阻力时不建议采取。
4 数值计算与试验结果对比采用基于三维势流理论计算得到的波浪增阻与模型试验结果对比如图6所示。两图均为波浪增阻2阶传递函数曲线,横坐标和纵坐标分别为入射波频率和波浪增阻传递函数。

|
图 6 数值模拟与模型试验结果对比 Fig. 6 Results Comparision between Numerical Simulation and Model Test |
通过对比发现:1)计算结果较试验结果整体偏大,频率大于0.4 rad/s时误差较小,最大不超过10%,但在低频0.35 rad/s时误差较大,误差达到28%;2)计算结果与模型试验结果的规律性一致,随着波长与船长比的增加,波浪增阻均呈现先增大后减小的趋势,均在入射波频率为0.43时达到最大,此时入射波长与船长最为接近。
5 结 语本文利用三维势流软件Aqwa对VLCC这类超大型船舶进行波浪增阻预报并与模型试验结果进行比较,具体结论如下:
1)采用三维势流理论预报波浪增阻计算效率高且与模型试验得到的结果规律性一致,整体误差较小。因此,这一计算方法可作为此类大型船舶波浪增阻预报的有效手段。
2)虽然波浪增阻数值误差较小,但这一理论计算得出的静水或波浪中航行阻力与试验值相比误差较大,主要原因是未能考虑到摩擦阻力及粘压阻力,因此单独计算静水阻力或波浪总阻力时不建议采用这一方法。
3)试验仅考虑了航速5.27 kn的波浪增阻,能够满足船厂开发初期用于预估航速及验证满足最小功率要求。但当航速增加时非线性效应必然越发明显,占阻力比重也会增加。因此,这一方法是否适用于计算高Frude数时的波浪增阻计算还需进一步验证。
| [1] |
International organization for standardization. Ship and marine technology — guidelines for the assessment of speed and power performance by analysis of speed trial data[S]. 2015.
|
| [2] |
MEPC. 232 (65), 2013. Interim guidelines for determining minimum propulsion power to maintain the manoeuvrability of ship in adverse conditions[S].
|
| [3] |
魏锦芳, 陈京普, 王杉, 等. 船舶全浪向波浪增阻数值计算与模型试验验证[J]. 中国造船, 2017, 58(4): 24-30. DOI:10.3969/j.issn.1000-4882.2017.04.003 |
| [4] |
于海, 封培元, 熊小青, 等. 中型豪华游船波浪增阻数值模拟分析[J]. 船舶, 2019, 30(1): 99-104. DOI:10.3969/j.issn.1001-9855.2019.01.018 |
| [5] |
李纳, 谌志新. 50 m围网渔船波浪增阻数值模拟[J]. 船舶工程, 2019, 41(4): 7-12. |
| [6] |
尹崇宏, 吴建威, 万德成. 基于IDDES方法的模型尺度和实尺度VLCC阻力预报与流场分析[J]. A辑, 2016, 31(3): 259-268. |
| [7] |
HU Jinpeng, ZHU Ling, LIU Shihui. Analysis and optimization on the flow ability of wave buoy based on AQWA[J]. IOP Conference Series: Earth and Environmental Science, 2018, 171(1). |
| [8] |
FALTINSEN. O. M. 船舶与海洋工程环境荷载[M]. 上海: 上海交通大学出版社, 2008: 8-9.
|
| [9] |
吴思莹. LNG-FSRU船舶在波浪中的运动与液舱内流体晃荡的耦合数值分析[D]. 镇江: 江苏科技大学, 2016.
|
 2020, Vol. 42
2020, Vol. 42
