由于化石燃料的大量使用,大气和海洋环境污染越来越严重。LNG作为下一代可替代的清洁燃料被大量开采利用,需求量不断攀升的背景下,运输LNG的船舶和储存设备也相应普及。天然气为了便于储存运输被要求冷却至–162 ℃低温下,由气态变为液态的天然气密度更大,粘性很小。当在海上输运时,船舶的晃荡将带动LNG一起晃荡,对于LNG动力燃料舱等特殊设备,随着槽罐内液位的不断下降,诱发自由液位的波动将更加剧烈,LNG液体对槽罐壁面的拍打而产生更大的冲击力。低温下的LNG与外界环境的巨大温差,使漏热会更加容易侵入被吸收,LNG受热相变产生BOG,加之液体的晃荡,槽罐内的热动响应会更加不稳定和难以预测。基于计算传热学理论[5],研究其中的内在机理和晃荡产生的影响,为今后设计防范设备及理论指导做好充足的准备。
国内外学者对于LNG技术的研究也做了大量的工作。LEE.D.H等[4]通过数值模拟研究了不同参数的敏感性对于LNG罐体所受载荷的影响,测试了不同密度、粘度和湍流模型,主要分析的是压力和水位的变化,数值模型并没有考虑低温液体和外界漏热等。Roh S等[1]运用数值模拟理论计算了LNG储罐中气相区压力增大时的瞬态自然对流现象,得出气相区加压对LNG蒸发的影响等,确定LNG气相区压力的变化对LNG相变会有一定的影响。在针对本文晃荡的工况下,气相区的压力变化也加以考虑,考虑液相和气相同时出现压力波动的案例。LEE.H.B等[2]分析了LNG从储存舱室中泄漏到多孔保温棉后的蒸发相变过程等。Liu Zhan等[3]考虑不同振幅下低温液氧储罐的水动力特性,该案例进行了一系列数值模拟,晃荡的过程是非绝热过程,伴随有气体的冷凝过程等。何晓聪等[6]运用数值模拟分析了不同晃荡工况下船用LNG储罐所受的冲击力和防波板的作用效果等。储运LNG船舶在航行中受外界环境影响,储槽内LNG液体出现晃荡,以及储槽维护结构的漏热,使得储罐内温度和压力变化,LNG出现相变,导致LNG的耗损及安全隐患有待进一步深入分析。针对在晃荡和外界漏热影响下船舶LNG储槽热质传递过程,利用气-液两相VOF模型,建立描述LNG储槽热动响应的数学模型,分析在不同外部漏热、晃荡幅度和储槽内LNG液位高度下,储槽内LNG损耗及其热质传递特性,以及 LNG储槽内自由液面波动。
1 物理模型针对船舶储存LNG槽所建立的物理模型如图1所示。储槽长3.7 m,直径为1.2 m,前端和后端都是半圆形封头。除分析液面高度的影响外,储槽LNG液面高度选取为0.6 m为研究对象。图1为数值计算使用的二维截面图。忽略储槽外部和内部布置的一些特别设备,主要集中分析晃荡下储罐内部LNG热动响应特性。
|
图 1 船用LNG储槽二维示意图 Fig. 1 Two-dimensional schematic diagram of a marine LNG storage tank |
为了更好地分析流体的状态,在储槽内部布置了一些压力检测点,来监测一些位置的压力变化,计算了壁面上和内部液体液面的波动情况和壁面上所受到的冲击力和力矩。晃荡中心位于原点,初始液位高度是0.6 m占总体积的一半,外部的环境压力和温度分别是101 325 Pa和300 K。
2 数值模型 2.1 控制方程LNG储槽内部自由液面受到外部的摇晃会发生移动变化,储槽内存在液相和气相区,利用描述气-液两相流动的VOF模型,分析在晃荡和外界漏热影响下船舶LNG储槽热质传递过程,建立LNG气液相的热动响应及气液界面变化的数学方程如下:
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \left( {\rho \vec v} \right) = {S_{{m}}}\;{\text{,}}$ | (1) |
| ${\alpha _l} + {\alpha _v} = 1\;{\text{。}}$ | (2) |
式中:αl和αv分别为气相和液相的体积分数;Sm为质量源相,考虑到LNG达到饱和温度之后会发生相变,实际过程中包含了蒸发和冷凝,源相作用于整个流体区域,相变的影响同时作用于气液交界面和储槽的内壁面上。该相变模型采用的是LEE Model,如下式:
| ${s_m} = \left\{ {\begin{array}{*{20}{c}} {{r_l}{\alpha _l}{\rho _l}\left( {{T_l} - {T_{sat}}} \right) / {T_{sat}},{T_l} \geqslant {T_{sat}}} {\text{,}}\\ {{r_v}{\alpha _v}{\rho _v}\left( {{T_v} - {T_{sat}}} \right)/{T_{sat}},{T_v} < {T_{sat}}} {\text{。}} \end{array}} \right.$ | (3) |
式中,rl和rv分别为传质强度因子,具体数值按不同的实验值来对照,本文选取0.1。
由于考虑了静压力的影响,LNG饱和温度也会发生响应的变化,其中的变化关系式,LNG饱和温度和饱和压力的拟合函数关系是如下:
| ${T_{sat}} = 0.3709{{\rm{e}}^{ - 15}}{p^3} - 3.8013{{\rm{e}}^{ - 10}}{p^2} + 17.956{{\rm{e}}^{ - 5}}p + 96.859{\text{,}}$ |
方程中加入了重力项和外部激励项,具体的表达式如下:
| $\begin{split} \frac{\partial }{{\partial t}}\left( {\rho \vec v} \right) + \nabla \left( {\rho \vec v\vec v} \right) =\; & - \nabla p + \nabla \left[ {\mu \left( {\nabla \vec v + \nabla {{\vec v}^{\rm{T}}}} \right)} \right] + \rho g -\\ &\rho ({{\dot \omega }} \times {{r}} + {{\omega }} \times {{\omega }} \times {{r}} + 2{{\omega }} \times {{V}})\;{\text{。}}\end{split}$ | (4) |
能量方程:
| $\frac{\partial }{{\partial t}}\left( {\rho E} \right) + \nabla \left( {\vec v(\rho E + p)} \right) = \nabla (\lambda \nabla T) + {S_h}\;{\text{。}}$ | (5) |
能量源相等于总的传质量乘以汽化潜热:
| ${S_h} = {S_m}{h_{fg}}\;{\text{。}}$ | (6) |
船舶在海上受到波浪的摇晃转化为储罐壁面上的外部激励。用简谐函数表示为:
| $y = A\sin \left( {\frac{{2{\text{π}}}}{T}t} \right)\;{\text{,}}$ | (7) |
| $v = y' = A\frac{{2{\text{π}}}}{T}\cos \left( {\frac{{2{\text{π}}}}{T}t} \right)\;{\text{,}}$ | (8) |
| ${{a}} = y'' = - {{A}}\frac{{4{{\text{π}}^2}}}{{{T^2}}}\sin \left( {\frac{{2{\text{π}}}}{{{T}}}{{t}}} \right)\;{\text{。}}$ | (9) |
式中:A为晃荡的幅度;T为周期;t为晃荡时间。旋转中心位于储槽的中心上,旋转轴是Y轴,该晃荡激励方程通过自定义函数接口导入到模型中。
四周壁面的受热边界条件为:
| $ {\rm{\lambda }}\frac{{\partial {{T}}}}{{\partial {{x}}}} = {{h}}\left( {{T_a} - {T_w}} \right)\;{\text{。}} $ | (10) |
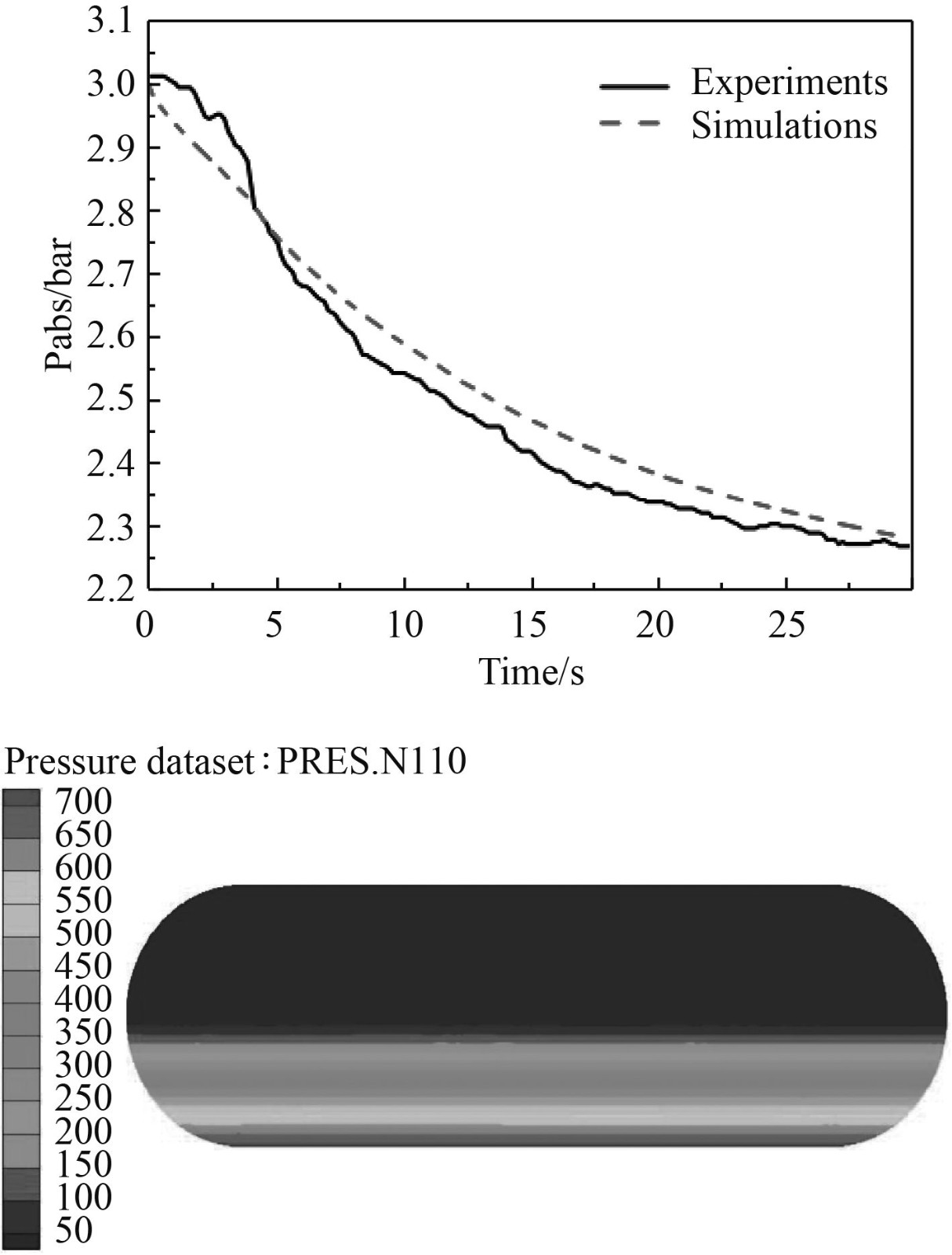
与文献[7]试验所测量的压力值变化相对照,计算气相区压力随时间的变化曲线。可以看出液位在一定时,数值分析结果与试验趋于一致,储罐中划分的网格数为32 740,图2为液相区的静压力云图,最大的静压力结果为724 Pa,与理论上的静压力734 Pa偏差1.4%。由数值计算结果与试验对照可见,本文所建立的数学模型和数值分析方法正确,其结果是可信的。本文VOF模型、相变传质模型(LEE Model)和k-ϵ湍流模型,离散的格式采用的是2阶精度的离散格式,保证计算结果的精度,动量项和能量项都采用2阶迎风格式,压力速度耦合算法采用SIMPLEC算法,残差值低于10–6。
|
图 2 晃荡条储槽内LNG压力计算结果与试验对照[7] Fig. 2 Calculation result of LNG pressure in sloshing tank and comparison with test |
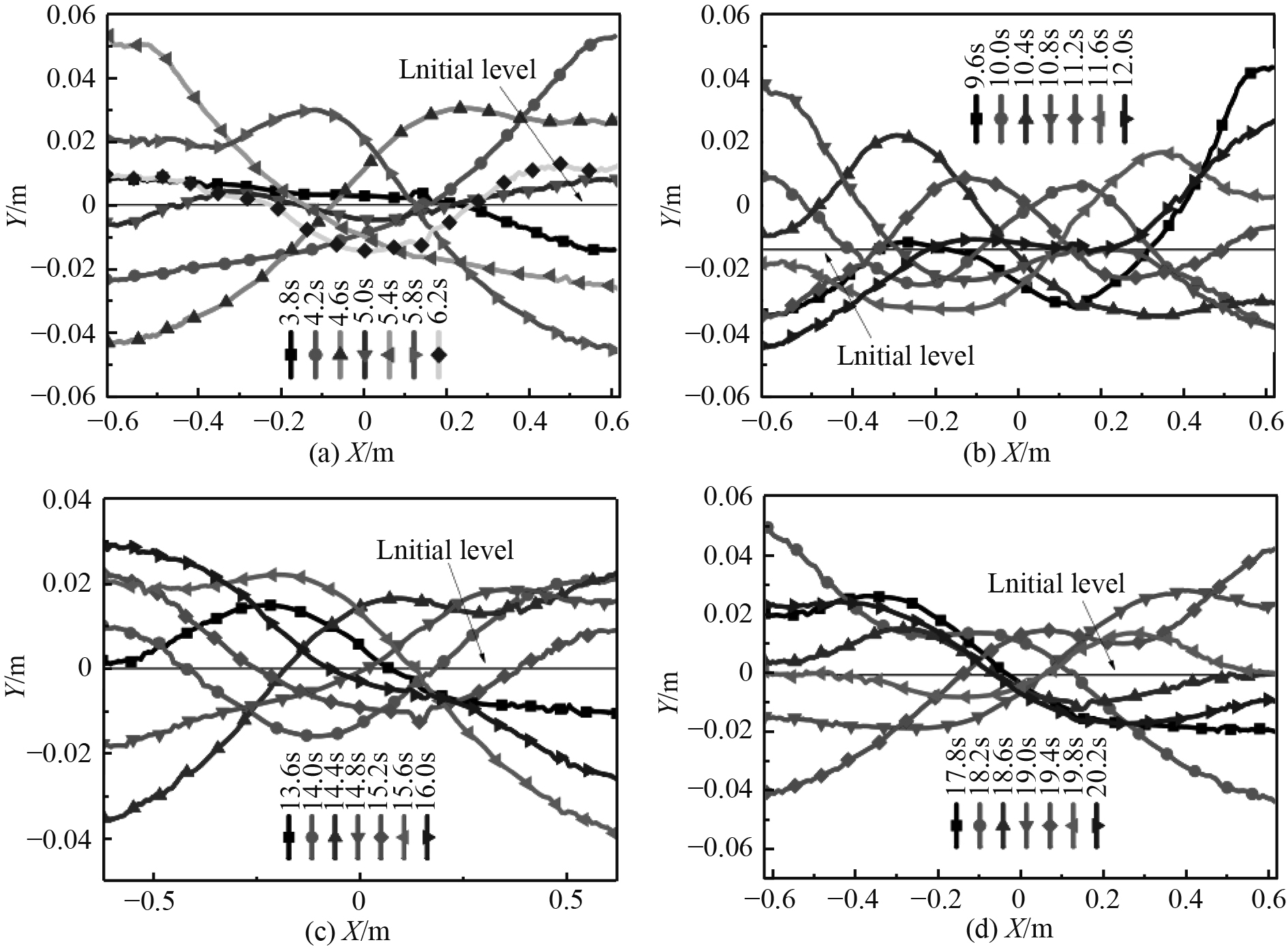
LNG储槽存在气体空间时发生晃荡工况,低温液体与气相区的内界面会诱发连续的波动,本文采取VOF算法计算并捕捉液体表面的形状,为了深入分析波动的变化规律,实验中以气液分界面即整个变化的自由液面为检测面,得出图3中4幅(每幅代表一个晃荡周期)液面抬升的变化曲线图。自由液面的晃荡波动曲线形状在初始液位来回上下变化,左壁面上液位抬升峰值达到0.05 m。从图3(a)可以发现,在–0.2~0 m和0~0.2 m处都出现一个波峰,是由于晃荡动能的传递产生的,从4.2~4.6 s,动态监测点在右侧最高,随着时间的推移,波峰向左侧移动。当波峰到达左侧时,又随着晃荡向右侧推动,自由液面在第1个周期如此往复来回运动。从图3(b)可知,在第2个周期中,自由液面即存在波峰,有出现了波谷。随着晃动能量传递,带动了液体更多的颠簸起伏。图3(c)和图3(d)中所示,内界面中的变化又与第1个周期中的类似,可知液体液体吸收了晃动能量之后逐渐趋向稳定了。
|
图 3 在晃荡条件下储槽内LNG不同时间的液面高度 Fig. 3 Liquid level of LNG in storage tank at different times under sloshing conditions |
原因是刚开始储槽晃荡带动液体时,液体处于静止状态,没有动能,液体存在一定的惯性。当LNG各部分液体全部吸收完外部的晃荡能量后,液体在初始液面上下波动呈现有规律的周期性变化。从液面的抬升曲线可以发现,越靠近中间,液体的波动峰值就越小,是因为一部分液体吸收晃动能被晃动到罐子壁面的两侧。
图4分别检测的是LNG储槽内气相区和液相区温度随时间变化的过程,气相区的初始温度为134 K,液相区的初始温度为112 K,液体的过冷度为25 ℃左右,气相区的绝对压力是0.5 MPa,气相区为饱和的天然气,液相区为过冷的液化天然气,由于受到外部晃荡环境的作用,自由液面向左向右不断波动,气态的天然气温度从0 ~18 s不断下降,下降到115 K左右,最终将接近液体的温度。由于液体的扰动将带动气相区的混乱,一开始在气液交界面处不断从气相区吸收热量,随着液位在左右两侧上下抬升,左右两侧气液之间的热交换明显大于中部的液体。气相区的温度从灌顶到自由液面处自上而下不断下降,液体中的冷量从自由分界面逐渐扩散到顶部,最终达到温度均匀。从图4 可知,液相区中自由表面附近的液体由于吸收了气相区中的热量,温度略有回升,大概在1°左右。由于外部的激励,储槽中的LNG从静止突然变为运动,会存在惯性作用。经过一定时间之后,LNG储槽内的物理量变化将达到稳定。温度气相区的温度从134 K经过18 s降到112 K,下降速率为1.2 K/s。基于上述的分析描述,LNG储槽内液体在海上的晃荡过程是随时间动态变化的,实际过程中远比本案例中的要更加复杂多变。通过本文的调查研究,可以为实际工程问题提供一些有价值的理论指导。

|
图 4 不同时刻下的温度云图 Fig. 4 Temperature contours at different times |
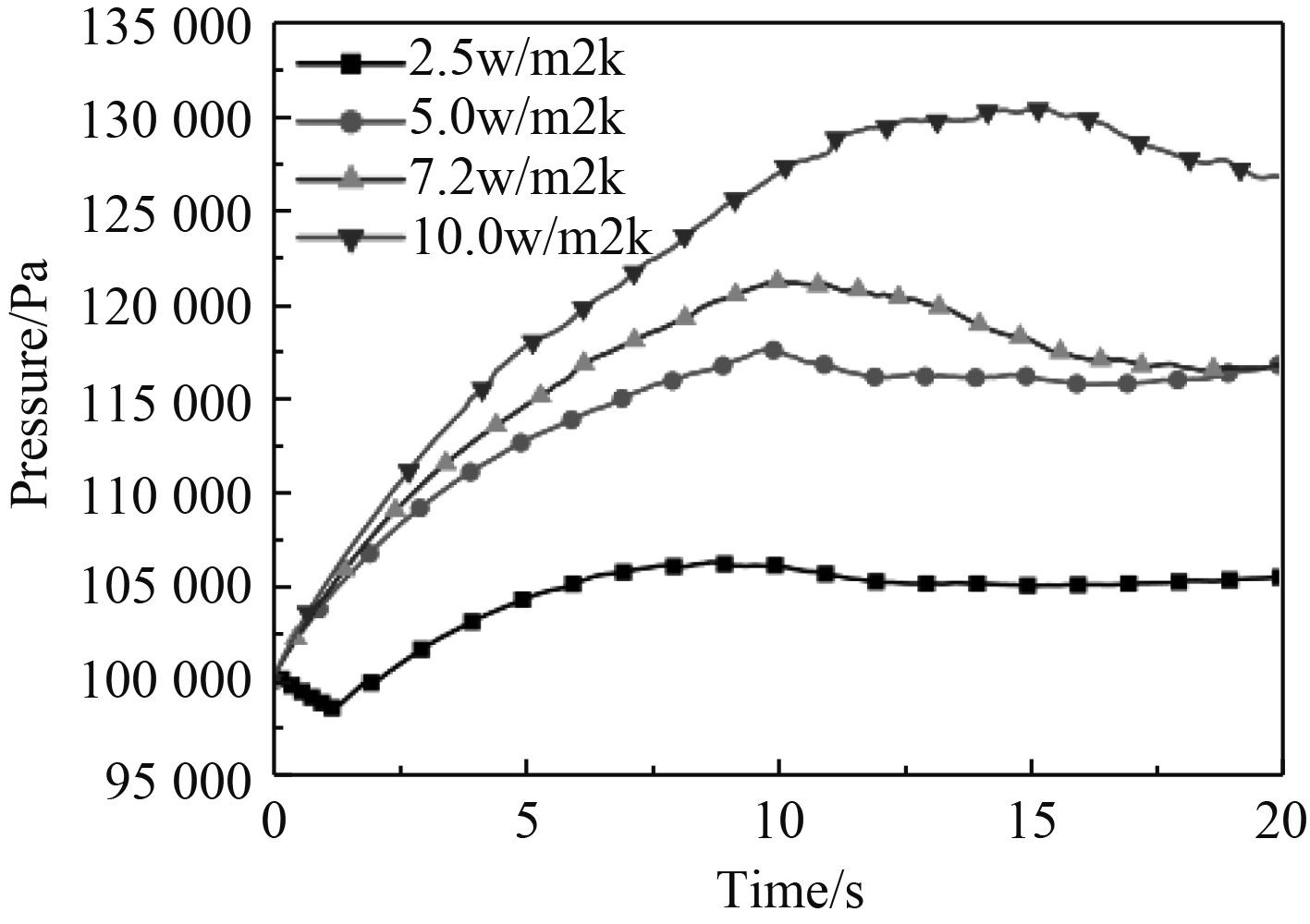
海上船舶LNG燃料储存舱由于操作失误、恶劣的海况或舱壁材料受损等原因,受到外部热量侵入的影响,而且要考虑LNG储槽受到连续晃荡的情况。为了便于研究,假设外界不同量的漏热传递给LNG,近似表示成在不同的对流换热系数作为舱壁的边界条件。储槽晃荡的振幅1°,周期为2.5 s,充液量为50%,数值模拟了在2.5 w/km2,5.0 w/km2,7.0 w/km2及10.0 w/km2条件下,LNG汽化成BOG后气相区压力随时间的变化,如图5所示。经过20 s之后,蒸发量在前10 s会逐渐上升后趋于平稳,气相区压力也随之稳定。晃荡的LNG储存舱所受到的外部漏热越大,相同时间内气相区的压力上升速度和最终压力也越大,导致的蒸发损耗量也越大。
|
图 5 不同对流换热系数下气相区压力随时间的变化 Fig. 5 Variation of pressure in the gas-phase region over time with different convective heat transfer coefficients |
在外部漏热作用下,低温储槽罐体内部流体温度,压力会逐渐升高,气液界面也会随之发生传热传质现象,考虑到气液界面间的热质传递主要为热对流引起的,相变模型采用软件中的LEE Model。当气液界面发生质量转移的时候,能量也随之转移,其转移总能量为传质率乘以汽化潜热。
晃荡过程中低温LNG储罐的压力增加对比,观察压力增速变化,不难发现,由于外部漏热加热波动的液相,用于使其消除过冷度上升,对压力增加作用不大,所以气相区受外部漏热更加敏感。另外,对于罐体内部产生相变的情况,刚开始的时间,罐体的压力增加主要来源于外部漏热对气相区的直接加热。压力上升曲线并不是完全线性的,可看出罐体压增速率是变化的,主要由于外部漏热导入罐体内后的分布不均所致,外部漏热进入罐体后,一部分热量会用来加热液相区或气相区,贡献给压力增加,另一部分热量会被转移到气液界面用于产生气液相变。罐体气液界面蒸发量仅占罐内液体初始质量的一小部分,所以说在刚开始的阶段,由相变量带来的压力增加极其微弱,罐体压增主要还是由于外部漏热直接加热所致。
罐体内LNG受到静压力的影响,表面的液体压力小对应的饱和温度小,底部的液体压力大对应的饱和温度大,整个计算域初始温度设置成表面的饱和温度111.6 K,LNG表面先达到相变点,底部液体还存在一定的过冷度。当船舶在海上发生左右摇摆时,考虑到晃荡效应的不稳定性,LNG燃料储存舱中的液体液面也会随之移动变化,内部液体会强迫对流,加快了液体内部的热交换。
4.3 在不同的晃动幅度下储槽内LNG热动响应特性在双燃料船舶中,以LNG燃料动力储槽为研究对象,同时考虑晃荡效应和温差效应,在两效应耦合的作用下,探究LNG储存舱中相变率的变化情况和流动状况。
船舶在海上航行时会受到不同振幅的波浪影响,LNG燃料动力储槽也会引起不同振幅的晃荡,从图6发现,在晃荡情况下,随着振幅的增加,LNG自由液面变化越明显,波动也越剧烈,很不稳定。在0~20 s之间,随着振幅的增加,冷凝量和气相区的冷却会增加,气相区压力降增加,不同振幅之间区分得越明显,而随着时间的增加,曲线越来越趋于稳定。船舶在静止或晃动很轻微时,LNG燃料储存舱中,受到外部漏热的作用,导热和自然对流占主导,而船舶存在晃荡效应后,不仅存在导热和自然对流,而且还有强迫对流。在这种混合效果下,内部液体中的显热会加快吸收,使内部流体的热量更加均匀,储存舱中LNG的相变量会随着晃荡强度上升表现出不稳定的特性,尤其在前期0~20 s之间,当外部的热量全部传化为LNG的汽化潜热时,LNG的气化量逐渐稳定。

|
图 6 压力分别在A=0.5°(a),A=1°(b),A=2°(c)下不同时刻的压力云图 Fig. 6 Pressure cloud diagrams at different moments of pressure at A = 0.5 °(a),A = 1 °(b) and A = 2°(c) |
从图7可知,船舶晃荡幅度越大,LNG储槽内冷凝量就大,LNG的气相区压力下降也越明显,晃荡幅度为2°时,持续20 s时间,LNG气相区压力从500 kPa减少到150.7 kPa,减少了349.3 Pa,平均的气相区压力下降为17 465 Pa/s,而振幅1°时,平均的气相区压力下降为16 190 Pa/s,振幅0.5°时,平均的气相区压力下降为14 960 Pa/s。从图7也可以发现,晃荡的振幅会加强LNG储罐中气相区和液相区的换热效果从而增加蒸发速率。

|
图 7 不同振幅下气相区压力和平均温度随时间的变化 Fig. 7 Variations of pressure and average temperature in the gas phase region with time at different amplitudes |
考虑到在实际工况下,LNG燃料会随时被消耗,储槽会存在不同的载液量,本文设置了3种不同的液相体积分数,分别为25%,50%和75%。在外部晃荡激励条件和散热条件不变的情况下,图8为不同LNG体积分数下,晃荡的储罐中气相区压力随时间的变化曲线。初始时储罐中的压力为500 kPa,液体的温度为112 K,液体存在25 K左右的初始过冷度。随着外部激励施加在罐壁面后,罐中的液体会左右摇动,发生晃荡。罐中的气液交界面倾斜后相较于静止时的交界面,过冷液体和过热气体接触的面积更大,这将导致高温的气相区会得到很大的冷量而被冷却。从图8所示3种不同罐中液位水平,气相区监测点的压力变化,可以很容易发现在不同的充液水平下气相区压力随时间近似线性的下降。而且,对于一个更高的液位工况,更多的冷量被储存在液体中,因此气相区别冷却的更加明显。在相同的初始气相区压力中,液位越高,气相区压力下降的越多。对于本研究,25%的充液工况下气相区压力从500 kPa下降到219.8 kPa,压力下降率为14010 Pa/s。50%的充液工况下气相区压力从500 kPa下降到176.2 kPa,压力下降率为16190 Pa/s。75%的充液工况下气相区压力从500 kPa下降到109 kPa,压力下降率为19550 Pa/s。
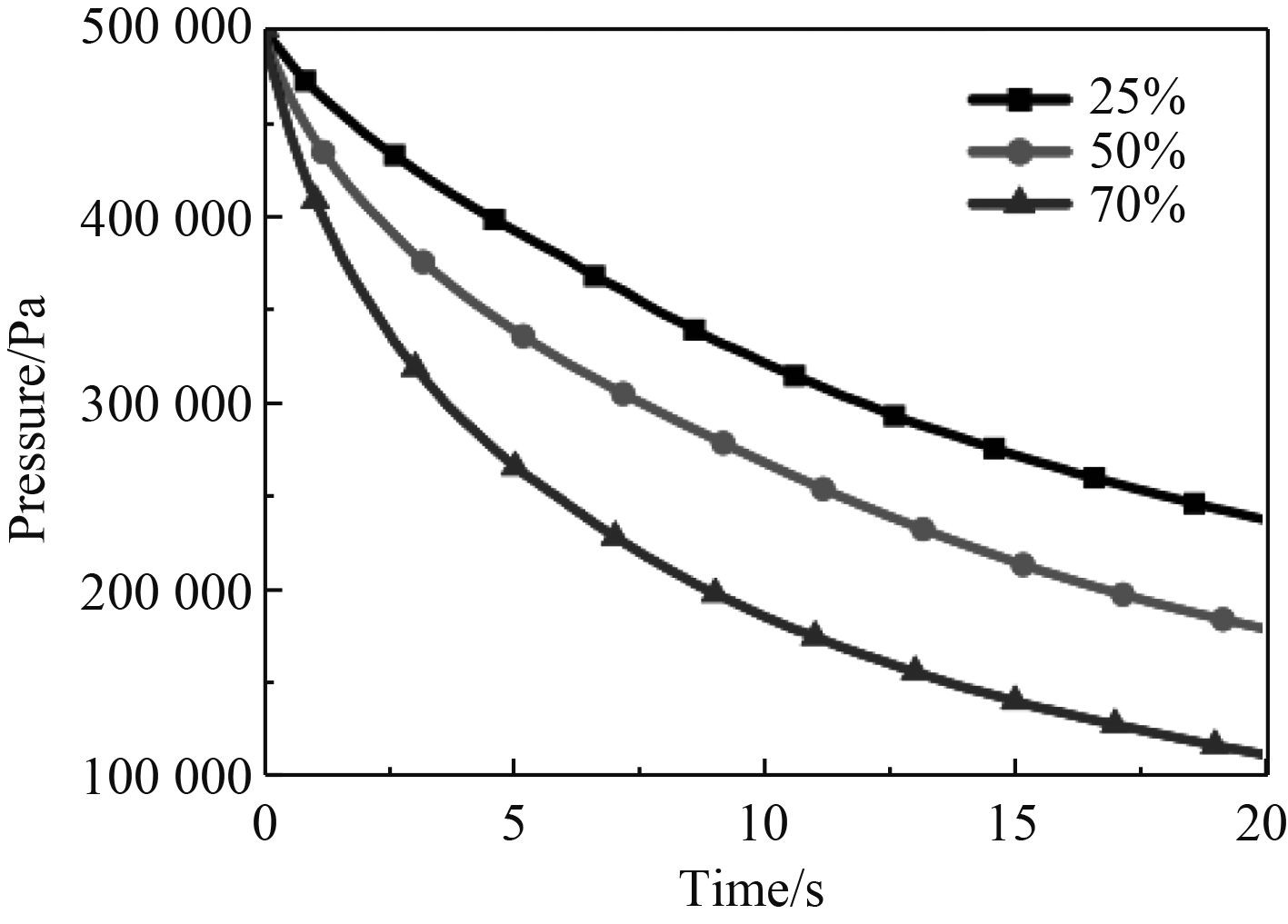
|
图 8 不同充液量下气相区压力变化 Fig. 8 Pressure change in the gas phase region under different filling volumes |
本文运用数值模拟LNG动力船燃料储罐受到晃荡20 s过程中的瞬态效应,得出LNG储罐气相区压力和温度随不同对流换热系数、充液量和振幅的变化特点。在这20 s瞬态的过程中,LNG最终的蒸发量很低,分析了液相区静压力的影响,液相区底部存在一定过冷度,蕴含的冷量比较多,再加上储槽的晃荡效应,加速了底部的冷能掺混到顶部,使得LNG蒸发量减少,并出现了气相区BOG的冷凝。
由液相区液体在自身重力作用下产生的静压力,得出了气相区和液相区之间的物理量之间变化特性。因为晃荡的高度非线性和随机性,引起储罐中LNG热动响应的不稳定,出现不同程度的振幅波动。以上分析研究,为海上船舶实际状况下,LNG燃料储罐的操作和维护提供一定的理论参考。
| [1] |
ROH S, SON G, SONG G, et al. Numerical study of transient natural convection in a pressurized LNG storage tank[J]. Applied Thermal Engineering, 2013, 52(1): 209-220. DOI:10.1016/j.applthermaleng.2012.11.021 |
| [2] |
LEE H B, PARK B J, RHEE S H, et al. Liquefied natural gas flow in the insulation wall of a cargo containment system and its evaporation[J]. Applied Thermal Engineering, 2011, 31(14-15): 2605-2615. DOI:10.1016/j.applthermaleng.2011.04.028 |
| [3] |
LIU Zhan, FENG, Yuyang, LEI, Gang, et al. (2018). Sloshing hydrodynamic performance in cryogenic liquid oxygen tanks under different amplitudes. Applied Thermal Engineering. 150. 10.1016/j.applthermaleng.2018.12.145.
|
| [4] |
LEE D H, KIM M H, KWON S H, et al. A parametric sensitivity study on LNG tank sloshing loads by numerical simulations[J]. Ocean Engineering, 2007, 34(1): 3-9. DOI:10.1016/j.oceaneng.2006.03.014 |
| [5] |
陶文铨. 数值传热学-第2版[M]. 西安: 西安交通大学出版社, 2001.
|
| [6] |
何晓聪, 何荣. 船用LNG储罐的液体晃荡数值分析[J]. 船海工程, 2016, 45(3). DOI:10.3963/j.issn.1671-7953.2016.03.040 |
| [7] |
GROTLE E, VILMAR Æsøy. Numerical Simulations of Sloshing and the Thermodynamic Response Due to Mixing[J]. Energies, 2017, 10(9). |
| [8] |
李娟. 基于三维参数的船舶稳性设计与优化研究[J]. 舰船科学技术, 2019, 41(02): 14-16. DOI:10.3404/j.issn.1672-7649.2019.02.003 |
 2020, Vol. 42
2020, Vol. 42
