船舶在航行过程中不可避免会受到风浪等因素干扰,产生不同的运动。尤其是船舶的横摇运动,会对船舶的正常航行、使用寿命、人员舒适度产生很大的影响,严重情况下还会造成船毁人亡的巨大经济损失[1]。对于军舰来说,横摇运动还会严重影响武器的使用性能,很大程度上降低武器打击精度与船舶作战效能[2],对战争胜负起到不可忽视的作用。
减摇装置经过了漫长的发展历程,到目前主要的减摇装置有舭龙骨、减摇水舱、减摇鳍、舵减摇等[3-4],而其中减摇鳍、舵减摇、以及舵鳍联合减摇领域的研究与应用最为热烈、最为广泛,舵减摇的探索与研究更是方兴未艾。与其他减摇技术相比,舵减摇技术凭借结构简单,费用低,效果好,灵敏性高等一系列优点,备受各国学者的追捧。
由于船舶舵的作用重心和船舶重心不在同一高度,在通过摆舵进行首摇控制的同时也会产生横摇力矩。舵减横摇就是利用操舵产生的横摇力矩来抵消船舶受海浪等外界条件干扰产生的横摇力矩。因此操舵能产生多大的横摇效果,在理论上就可能具有多大的舵减横摇潜力。因此对船舶进行不同操舵,观察船舶产生的横摇效果,从而分析船舶的舵减摇潜力。
为探究某新型船舶的舵减摇潜力,将该船舶的实际船体参数引入到船舶运动模型中,通过建立的Matlab仿真平台进行模拟仿真,观察船舶在不考虑海浪等环境干扰情况下,不同摆舵幅度和操舵频率对船舶横摇角的影响。根据横摇角的变化设计实验方案,探究该新型船舶在舵速限制下能产生的最大横摇角,分析船舶具备的舵减摇潜力。
1 船舶运动四自由度模型的建立船舶在海上航行时受到船舶螺旋桨推力、操舵产生力矩、水的阻力、海风海浪干扰力以及各力之间的耦合作用等会呈现出不同的运动状态。一般用以下6个自由度表示船舶运动:纵荡、横荡、升沉、首摇、横摇、纵摇[5]。在研究船舶舵减横摇中,升沉和纵摇一般较小,同时耦合作用影响不大,所以描述舵减横摇过程一般采用横荡、纵荡、首摇和横摇4个自由度。其中
假设船舶是在不可压缩,无粘性且无限的理想流体中运动。作用于船体的惯性类流体力及力矩的数值与船舶加速度成正比,可等效为附加质量或附加惯性矩的计算。建立四自由度的船舶运动方程如下[7]:
| $ \left\{\begin{aligned} &\left(m+{m}_{11}\right)\dot{u}={X}_{HH}+{X}_{HR}+{X}_{HP}+\left(m+{m}_{22}\right){\text{,}}\\ &\left(m+{m}_{22}\right)\dot{v}={Y}_{H}-(m+{m}_{11})ur{\text{,}}\\ &({I}_{x}+{m}_{44})\dot{p}={K}_{H}+{K}_{\varphi }+{K}_{\dot{\dot{\varphi }}}{\text{,}}\\ &\left({I}_{Z}+{m}_{66}\right)\dot{r}={N}_{H}{\text{。}}\end{aligned}\right. $ | (1) |
其中:m为船舶质量;
又由刚体运动学推得:
| $ \left\{\begin{aligned} &\dot{{{x}}_{0}}={\rm{{u}cos}}\varPsi -{\rm{{v}sin}}\psi{\text{,}}\\ &\dot{{r{y}}_{0}}={\rm{{u}sin}}\psi +{\rm{{v}cos}}\psi{\text{,}} \\ &\dot\psi=r{\text{,}}\\ &\dot{{\varPhi }}=p{\text{。}}\end{aligned}\right. $ | (2) |
其中,
1)对方程右侧的船舶受力进行分析[7]
水的粘性流体动力
| $ {X_{HH}} = - \left( {13\;747.99{{u - 638}}{\rm{.1}}{{{u}}^{\rm{2}}}{\rm{ + 313}}{\rm{.8}}{{{u}}^3}} \right){\text{。}} $ | (3) |
螺旋桨推力在X轴方向上的力
| $\left\{ \begin{aligned} &{{{{X}}_{{{HP}}}} = \left( {1 - {{t}}} \right)*2}{\text{,}}\\ &{T = {{{K}}_{{T}}}\rho {{\rm{n}}^2}{{D}}_{{P}}^4}{\text{,}}\\ &{{{{K}}_{{T}}} = 0.752\;4 - 0.558\;2{{J}} + 0.010\;34{{{J}}^2}}{\text{,}}\\ &{{{J}} = \frac{{\left( {1 - {{{W}}_{{{p}}0}}} \right){\rm{u}}}}{{{{n}}{{{D}}_{{p}}}}}} {\text{。}}\end{aligned} \right.$ | (4) |
其中,
操舵对船舶X轴方向上的力
| $ \left\{ \begin{aligned} &{{{{X}}_{{\rm{HR}}}} = {{{F}}_{\rm{N}}}\sin{\rm{\delta}} }{\text{,}}\\ &{{{{F}}_{{\rm{N}} = \left( {{{{C}}_{{\rm{NS}}}} + {{{C}}_{{\rm{NP}}}}} \right)\frac{1}{2}{\rm{\rho }}{{{V}}^2}{{{A}}_{{R}}}}}}{\text{,}}\\ &{{{{C}}_{{\rm{NS}}}} = {{\rm{\alpha }}_1}\left[ {{\rm{\delta }} + {{\rm{\alpha }}_2}\left( {{{v}} + {{{I}}_{\rm{R}}}{{r}}} \right)} \right]} {\text{。}}\end{aligned} \right.$ | (5) |
其中:
船舶所受横向力
船舶所受横摇水动力矩由
| $ {K_\phi } =m{\rm{ghsin}}{\rm{\phi}} {\text{。}} $ | (6) |
| $\left\{ \begin{aligned} &{{K_{\dot \phi }} = - 2{{{N}}_{\dot {\rm{\phi}} }}p}{\text{,}}\\ &{{{{N}}_{\dot {\rm{\phi}} }} = {{\rm{u}}_{\dot {\rm{\phi}} }}\sqrt {{{{I}}_{{\rm{xl}}}}{{{{m}}gh}}} }{\text{,}}\\ &{{{{I}}_{{\rm{xl}}}} = {{I}_{\rm{x}}} + {m_{44}}}{\text{,}}\\ &{{{{u}}_{\dot {\rm{\phi}} }} = {{{u}}_{\dot {\rm{\phi }}}}\left( 0 \right)\left( {1 + 3.3{{{F}}_{{r}}}} \right)}{\text{,}}\\ &{{{{u}}_{\dot {\rm{\phi}} }}\left( 0 \right) = \frac{1}{2}\frac{{0.057{{L}}{{{B}}^4}}}{{{{W}}\left( {{{{B}}^2} + {{{D}}^4}} \right)}}{{\rm{\phi}} _{\rm{m}}}}{\text{。}} \end{aligned} \right. $ | (7) |
其中:
| $ \begin{split} {K_H} =\;& ({{K}}_{{v}}'{{v'}} + {{K}}_{{r}}'{m{r'}} + {{K}}_{{\delta }}'{{\delta '}} + {{K}}_{{{vvv}}}'{{{{v'}}}^3} + \\ &{{K}}_{{{rrr}}}'{{{{r'}}}^3} + {{K}}_{{{\delta \delta \delta }}}'{{{{\delta '}}}^3} + {{K}}_{{m{vvr}}}'{{{m{v'}}}^2}{{r'}} + {{K}}_{{{vrr}}}'{{{{r'}}}^2}{{v'}} + \\ &{{K}}_{{{v\delta \delta }}}'{{{{\delta '}}}^2}{{v'}} + {{K}}_{{{\delta \delta r}}}'{{{\rm{\delta '}}}^2}{m{r'}} + {{K}}_{{{v\delta r}}}'{{v'\delta '}}{{{r}}'})\frac{1}{2}{{\rho }}{{{v}}^2}{{{L}}^3} {\text{。}}\end{split} $ | (8) |
其中:
2)附加质量的计算
本文选用周昭明等回归公式对船的附加质量及附加惯性矩进行估算[8]。
2 船舶横摇角变化规律在建立的船舶运动模型基础上对该舰船横摇角变化规律进行仿真研究。通过改变船舶的摆舵幅度、摆舵频率,探究在不同条件下船舶摆舵产生的横摇角规律。
2.1 摆舵频率对横摇的影响规律实验中,在航速18 kn、摆舵幅度为20°时,运用不同摆舵频率进行模拟,比较分析船舶在摆舵幅度不变时,摆舵频率对船舶横摇的影响。仿真结果如图1~图4所示。
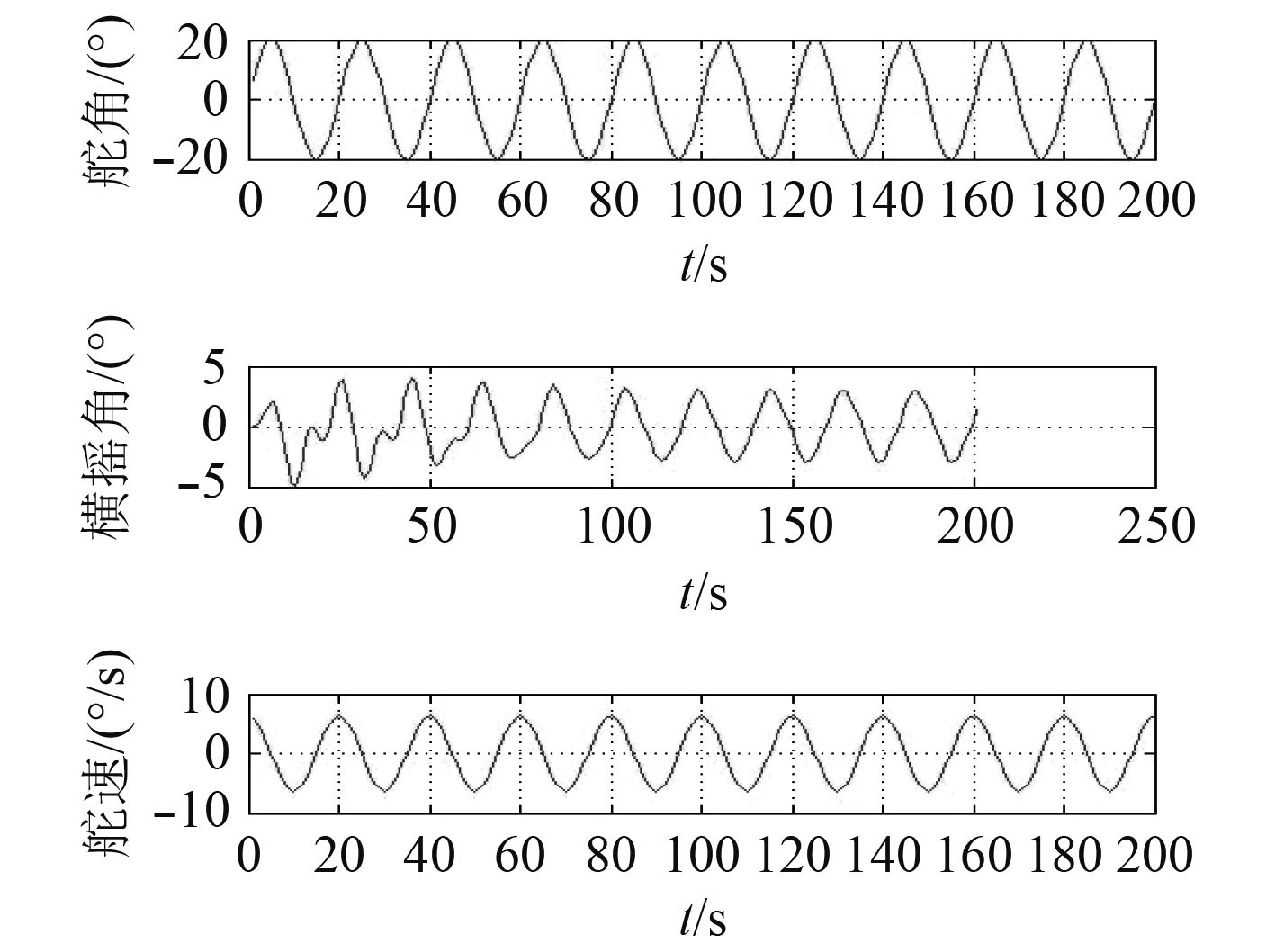
|
图 1 航速为18 kn,摆舵幅度为20°,频率为0.314 Hz下船舶舵角、横摇角、舵速的变化 Fig. 1 The ship’s rudder angle, roll angle and rudder speed change at a speed of 18 kn, a rudder amplitude of 20° and a rudder frequency of 0.314 Hz. |
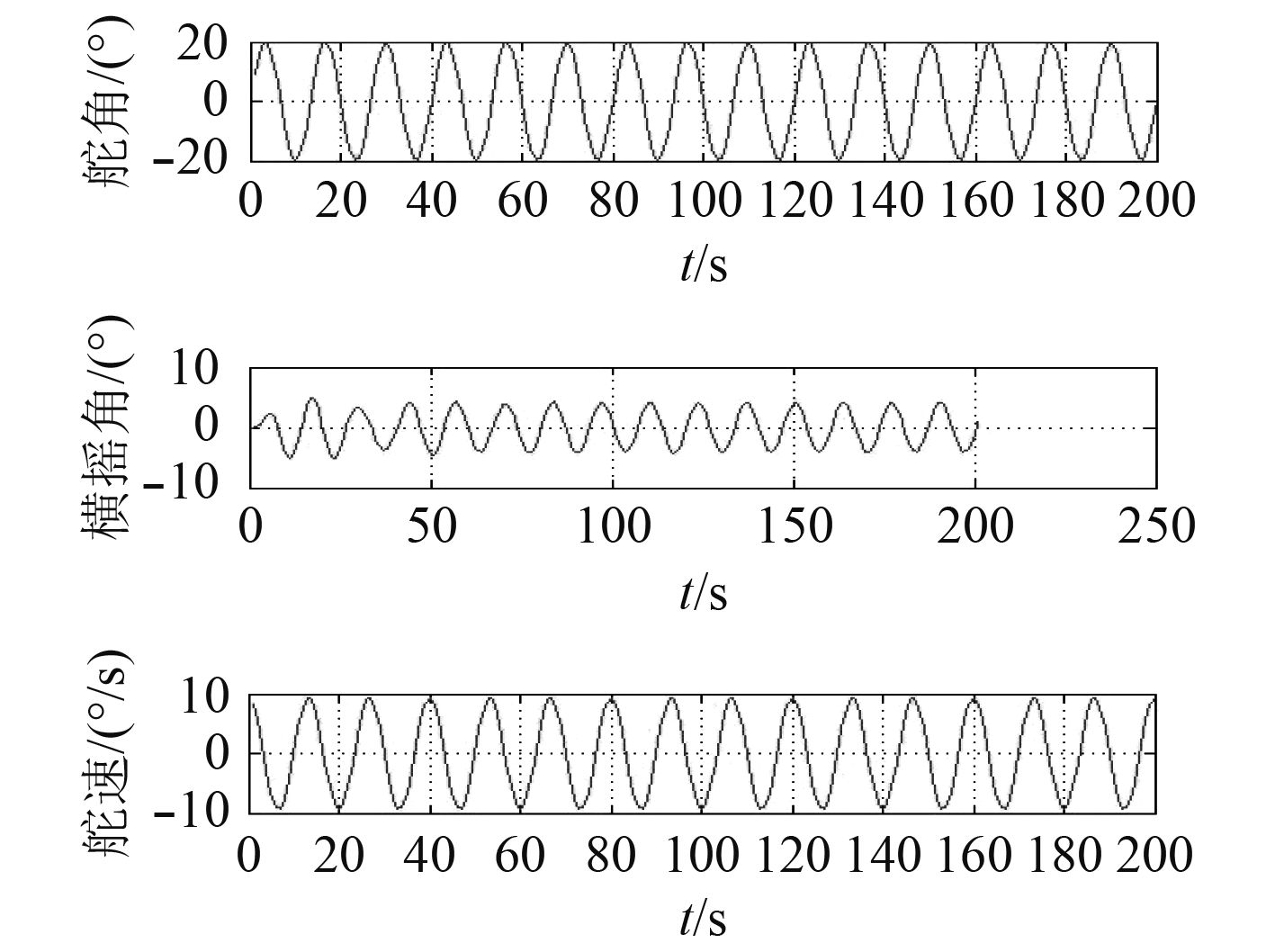
|
图 2 航速为18 kn,摆舵幅度为20°,频率为0.471 Hz下船舶舵角、横摇角、舵速的变化 Fig. 2 The ship’s rudder angle, roll angle and rudder speed change at a speed of 18 kn, a rudder amplitude of 20° and a rudder frequency of 0.471 Hz. |
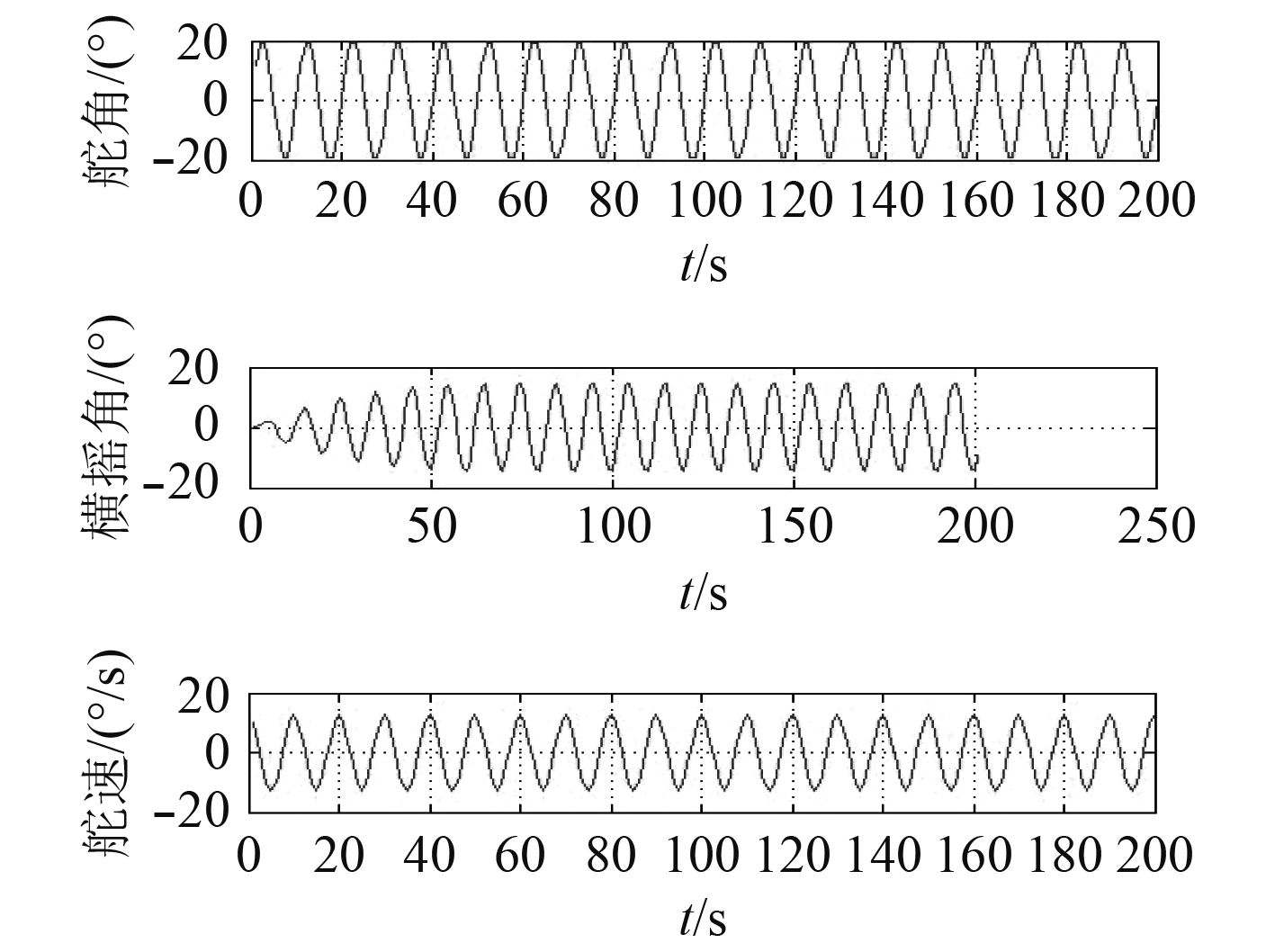
|
图 3 航速为18 kn,摆舵幅度为20°,频率为0.628 Hz下船舶舵角、横摇角、舵速的变化 Fig. 3 The ship’s rudder angle, roll angle and rudder speed change at a speed of 18 kn, a rudder amplitude of 20° and a rudder frequency of 0.628 Hz. |
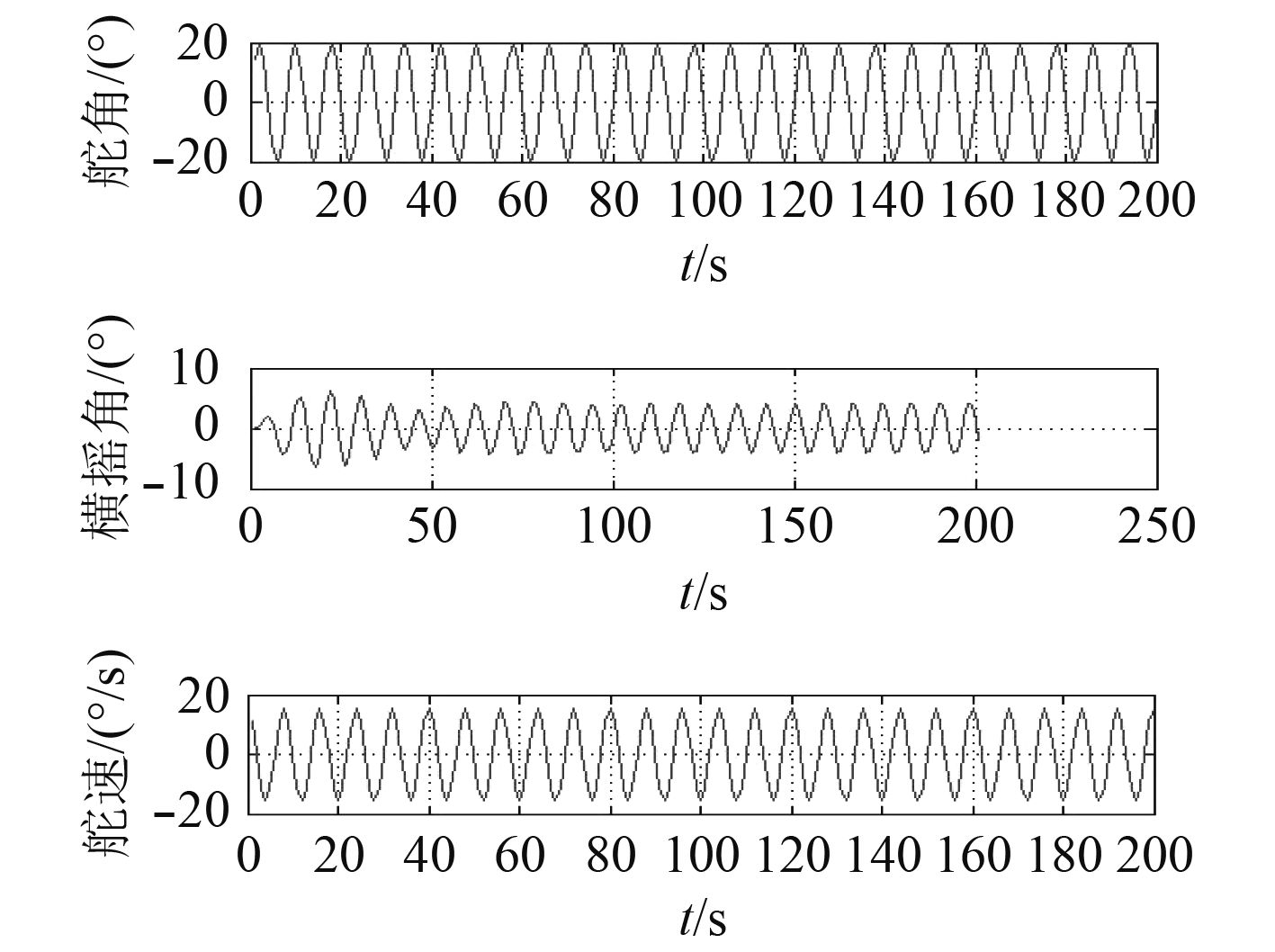
|
图 4 航速为18 kn,摆舵幅度为20°,频率为0.78 5 Hz下船舶舵角、横摇角、舵速的变化 Fig. 4 The ship’s rudder angle, roll angle and rudder speed change at a speed of 18 knots, a rudder amplitude of 20° and a rudder frequency of 0.785 Hz. |
根据实验可得,在航速18 kn,保持船舶摆舵幅度20°不变,船舶最大横摇角随摆舵频率的变化规律如表1所示。
|
|
表 1 航速18kn,摆舵幅度20°情况下,最大横摇角随摆舵频率变化 Tab.1 Maximum roll angle with the rudder frequency at 18 kn and 20° yaw amplitude |
1)对比图1~图4并结合表1可以发现,在船舶航速不变,摆舵幅度相同的情况下,摆舵产生的横摇角会随着摆舵频率出现先上升后下降的趋势。相应的船速、摆舵幅度下会对应一个摆舵频率使船舶产生横摇角呈现最大值:航速18 kn情况下,摆舵幅度为20°时,最大的横摇角出现在摆舵频率为0.653 Hz附近。
同样,经过实验得到,摆舵幅度为10°时,最大的横摇角出现在摆舵频率为0.659 Hz附近;摆舵幅度为35°时,最大的横摇角出现在摆舵频率为0.647 Hz附近(此时超出船舶最大舵速)。在不同摆舵幅度下船舶最大横摇角数值如表2所示。
|
|
表 2 18 kn航速下,船舶在不同摆舵幅度下最大横摇角对应的摆舵频率 Tab.2 The yaw frequency corresponding to the maximum roll angle of the ship at different yaw amplitudes at 18 kn |
2)经过实验分析,船舶在摆舵幅度不变时,横摇角会随摆舵频率增大出现先增后减的变化并且有峰值的存在。其原因是船舶摆舵频率过小,产生的横摇力矩很小,不足以使船摆动;船舶摆舵频率过高,由于船舶惯性,船舶横摇反应滞后导致来不及响应,因此船舶横摇角也小。
2.2 摆舵幅度对横摇的影响规律根据上文结论可知,在摆舵幅度不变时,横摇角随摆舵频率增加,出现先增加后减小的趋势,即每个摆舵幅度下都存在一个摆舵频率使横摇角达到最大。因此探究摆舵幅度对横摇角的影响,应该选取该摆舵幅度下存在的最大横摇角。
实验在保持船速18 kn,选取摆舵幅度10°,20°和35°的情况进行仿真分析,探究船舶摆舵产生最大横摇角随摆舵幅度的变化规律。根据表2,选取合适摆舵频率对不同摆舵幅度下进行仿真。
在18 kn航速不变情况下,实验摆舵幅度10°,20°和35°,得到对于摆舵幅度下的最大横摇角如表3所示。
|
|
表 3 18 kn航速下,在不同摆舵幅度下船舶的最大横摇角 Tab.3 Maximum roll angle of the ship at different yaw amplitudes at 18 kn |
对比图5~图7结合表3可以发现,在船舶航速18 kn不变时,操舵产生的最大横摇角随船舶操舵幅度增大而增大。
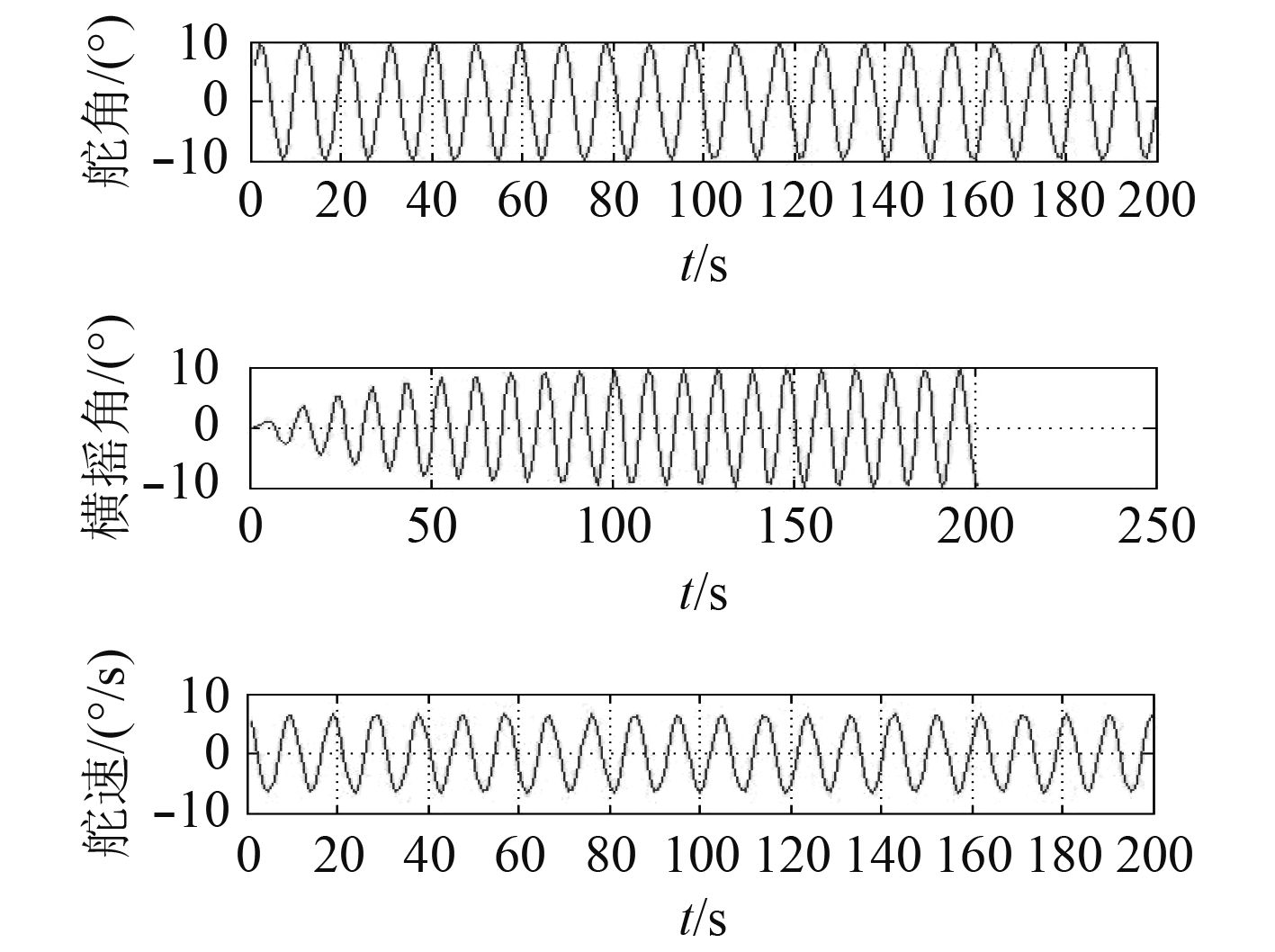
|
图 5 航速18 kn,摆舵幅度10°下船舶舵角、最大横摇角、舵速的变化 Fig. 5 Changes in ship rudder angle, maximum roll angle and rudder speed at 18 kn and 10° yaw amplitude |
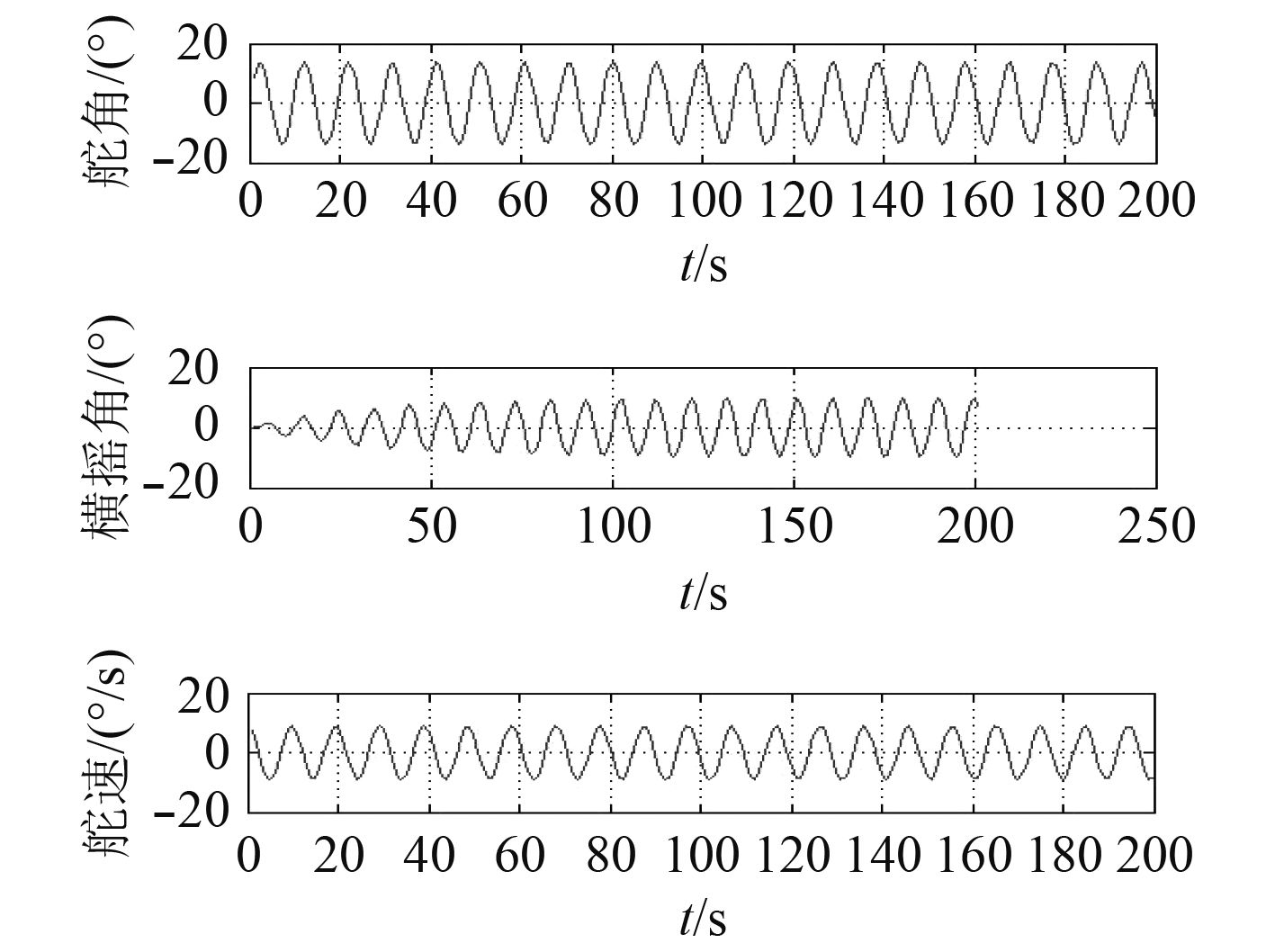
|
图 6 航速为18 kn,摆舵幅度20°下船舶舵角、最大横摇角、舵速的变化 Fig. 6 Changes in ship rudder angle, maximum roll angle and rudder speed at 18 kn and 20° yaw amplitude |
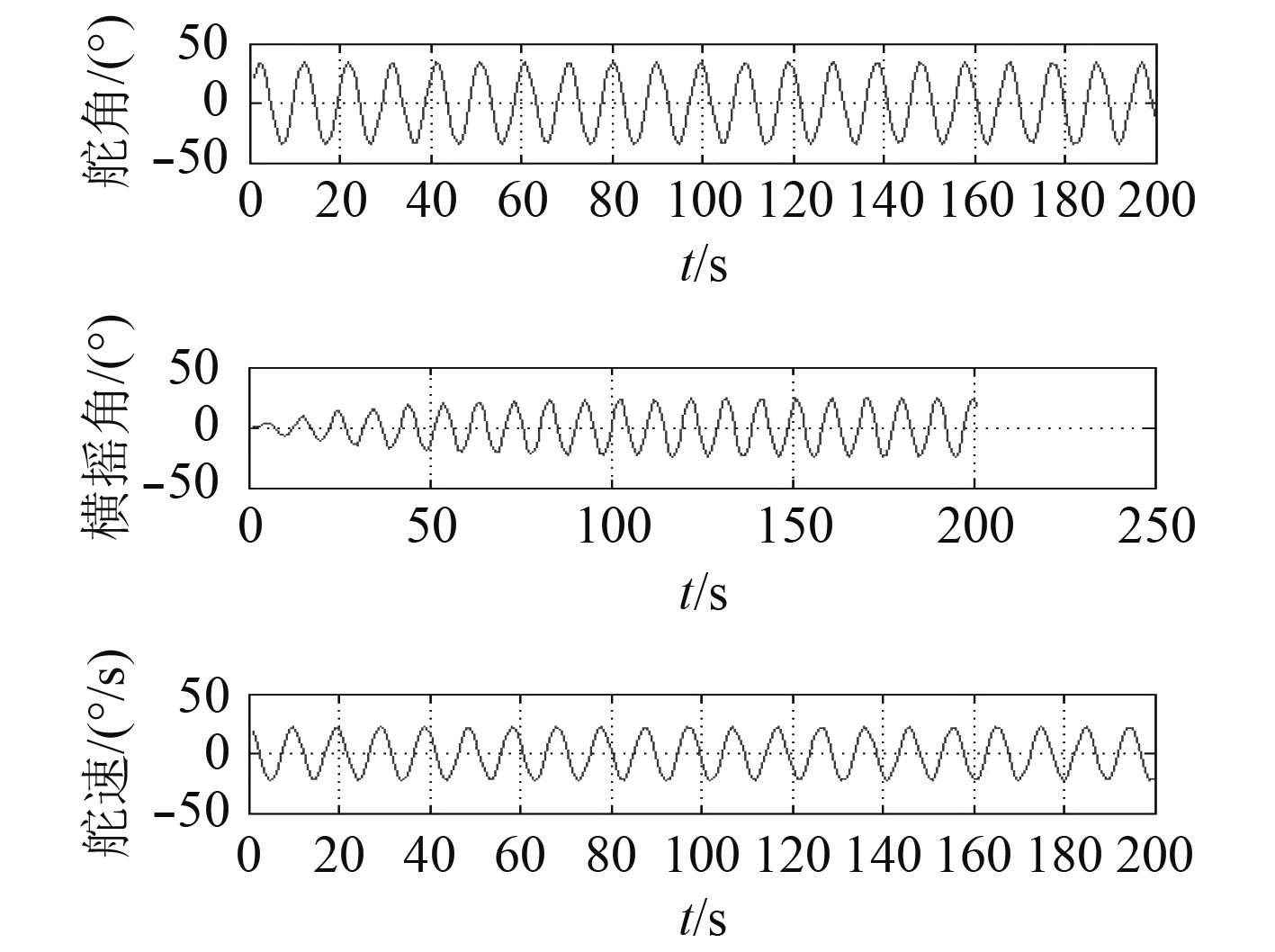
|
图 7 航速为18 kn,摆舵幅度35°下船舶舵角、最大横摇角、舵速的变化 Fig. 7 Changes in ship rudder angle, maximum roll angle and rudder speed at 18 kn and 35° yaw amplitude |
对比在航速18 kn,摆舵幅度在10°,20°,35°变化时船舶产生的最大横摇角可以看出,在航速一定下,随着摆舵幅度增加,船舶操舵产生的最大横摇角增大。并且,由于随着摆舵幅度的增加,其产生横摇角峰值对应的舵速增大。因此在船舶舵速允许下,可以考虑通过加大摆舵幅度来提高舵减摇潜力。
2.3 船速对横摇角的影响规律船速本身并不能影响船舶的横摇,但是在操舵过程中,相同的操舵方式对于不同航速下的船舶,产生的横摇角也不同。本文就该船舶在相同的摆舵幅度和摆舵频率下,取航速18 kn和27 kn,探究的船舶横摇角的变化规律。
在摆舵幅度10°、摆舵频率0.659 Hz下,在船舶航速18 kn和27 kn下,仿真探究船舶横摇角的变化,如图8所示。
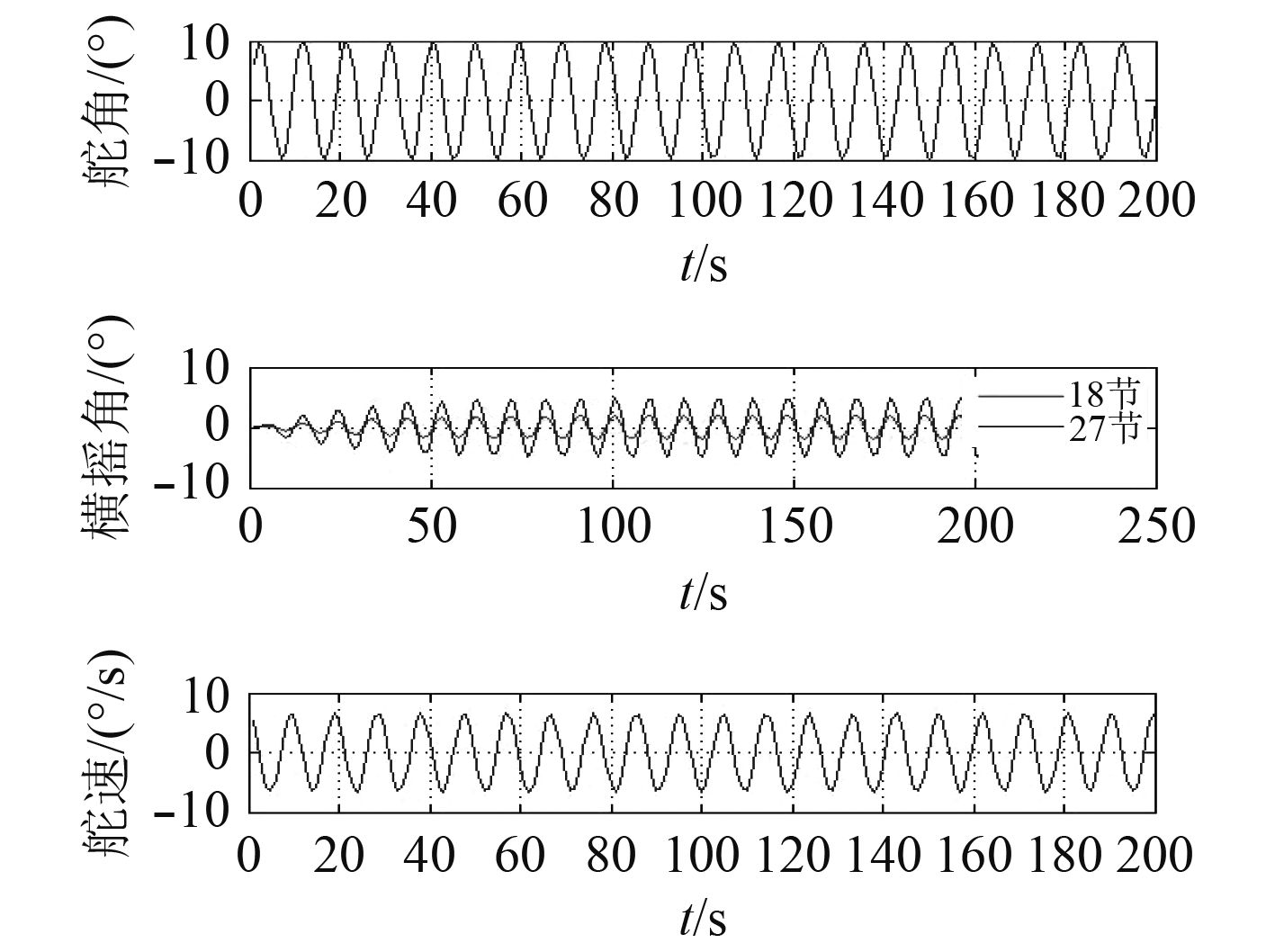
|
图 8 保持船舶摆舵幅度10°、摆舵频率0.659 Hz不变,不同航速下船舶横摇角变化 Fig. 8 Keeping the ship’s rudder amplitude 10°, the rudder frequency 0.659 Hz unchanged at different speeds |
根据图8可得,在船舶摆舵幅度和摆舵频率相同时,船舶横摇角随船舶航速的增加而增大。这与船舶舵减摇在低速时舵效较差的实际情况符合。
3 在舵速限制下所具备的舵减摇潜力分析根据上文结论,船舶的横摇角不能随意增大,会受到船舶硬件尤其是摆舵幅度和舵速的影响。针对该船舶舵速最大为10°/s的前提条件,通过上文得到的操舵方式对船舶横摇角的影响规律,设计实验分析该船舶通过升摇能够产生最大的横摇运动,揭示该船舶的舵减摇潜力。由于船舶最大航速为30 kn,船舶不可能一直处于最高航速航行,且27 kn已经贴近最大航速,本文利用27 kn的数据进行计算。
1)在船舶航速27 kn、摆舵幅度为10°时,对于最大横摇角24.28°时,最大舵速为6.60°/s,符合船舶舵速要求;
2)在船舶航速27 kn、摆舵幅度为15°时,对于最大横摇角34.43°时,最大舵速为9.79°/s,符合船舶舵速要求;
3)在船舶航速27 kn、摆舵幅度为20°时,对于最大横摇角时,最大舵速为13.03°/s,超出船舶舵速要求。根据上述实验可知,船舶在最大舵速增大到13.03°/s的过程中,横摇角随舵速递增,因此实验在摆舵幅度20°,最大舵速为10°/s情况下,最大横摇角为13.13°/s。
根据实验结果,船舶在27 kn,舵速最大为10°/s的限制下,不同摆舵幅度能够产生最大的横摇角如表4所示。
|
|
表 4 航速27 kn,最大舵速为10°/s下,船舶不同摆舵幅度对应的最大横摇角 Tab.4 Maximum roll angle corresponding to different yaw amplitudes of ships with a speed of 27 kn and a maximum rudder speed of 10° per second |
根据以上实验得到的船舶横摇角变化规律,结合表4可以看出,考虑船舶舵速最高为10°/s的限制,船舶在27 kn航行、摆舵幅度为15°、摆舵频率为0.653 Hz时,船舶能够产生最大的横摇角约为34.4°。经分析,合理的操舵策略使该船舶具备良好的舵减摇潜力,单靠船舶的操舵进行减摇理论上对该船舶来说具有可行性。
4 结 语1)本文将实际的船舶参数代入建立的船舶四自由度运动模型中,利用Matlab仿真平台进行仿真。发现船舶的操舵影响船舶横摇,且横摇角的大小与船舶摆舵幅度、摆舵频率以及进行操舵时船舶的航速有关。
2)船舶在静水条件下的升摇能力即代表船舶在海中航行时的舵减摇潜力。根据实验得到船舶横摇角变化规律:船舶横摇角随摆舵频率的增加,出现先增后减趋势,每个摆舵幅度下存在一个摆舵频率使横摇角达到峰值;船舶摆舵幅度越大,其能够产生的最大横摇角也越大,对应的舵速要求也越高;船舶航速越大,相同摆舵幅度和摆舵频率产生的横摇角越大。
为提高船舶舵减摇潜力,可以采取合理的操舵策略。船舶的摆舵幅度和频率并不是越大越好,在考虑船舶摆舵幅度和舵速的器件可行性基础上,选取合理的操舵策略使舵升摇效果达到最好。
3)对本船来说,在航速27 kn情况下船舶通过摆舵产生的最大横摇角可达30°以上,具备较好的舵减摇潜力。
本文采用实际船舶参数、针对具体船舶进行模拟仿真,具有很大的针对性、现实性。同时,在该新型船舶的舵升摇能力探究的过程,掌握了船舶横摇角变化规律。利用横摇角变化规律结合船舶本身硬件要求尤其是舵速要求,可以设计出船舶达到横摇运动最大效果的方案,分析该船舶舵减摇潜力,证明了该船舶具备较好的舵减摇潜力。
| [1] |
马亮. 船舶舵鳍联合减摇控制策略研究[D]. 大连: 大连海事大学, 2012. MA Liang. Research on ship rudder fin joint anti-rolling control strategy[D]. Dalian: Dalian Maritime University, 2012. |
| [2] |
CROSSLAND P. The effect of roll stabilization controllers on warship operational performance[J]. Control Engineering Practice, 2003, 114(11): 423-431. |
| [3] |
郭大勇, 梁利华, 赖志昌, 等. 新型主动式减摇装置的仿真研究[J]. 自动化技术及应用, 2001(3): 20-22. GUO Da-yong, LIANG Li-hua, LAI Zhi-chang, et al. Simulation study of a new type of active anti-rolling device[J]. Automation Technology and Applications, 2001(3): 20-22. |
| [4] |
邹令辉. 基于最优控制的舵鳍联合减摇性能指标函数的分析研究[J]. 舰船科学技术, 2018(4): 40-4. ZOU Ling-hui. Analysis of the performance index function of rudder fin combined anti-rolling based on optimal control[J]. Ship Science and Technology, 2018(4): 40-4. |
| [5] |
袁远, 成志军, 金咸定. 船舶在波浪中运动的六自由度非线性耦合方程[J]. 上海交通大学学报, 2001, 35(4): 541-543. YUAN Yuan, CHENG Zhi-jun, JIN Xian-ding. Six-degree-of-freedom nonlinear coupled equation for ship motion in waves[J]. Journal of Shanghai Jiaotong University, 2001, 35(4): 541-543. DOI:10.3321/j.issn:1006-2467.2001.04.014 |
| [6] |
贾欣乐, 杨盐生. 船舶运动数学模型[M]. 大连: 大连海事大学出版社, 2003.
|
| [7] |
Sarch M G.. Fin stabilizers as maneuver control surfaces[D]. Monterey: Naval Postgraduate School, 2003.
|
| [8] |
周昭明, 盛子寅, 冯悟时. 多用途货船的操纵性预报计算[J]. 船舶工程, 1983(6): 21-29. ZHOU Zhao-ming, SHENG Zi-kai, FENG Wu-shi. Maneuverability forecast calculation of multipurpose cargo ships[J]. Ship Engineering, 1983(6): 21-29. |
 2020, Vol. 42
2020, Vol. 42
