海洋发展战略重要性日益显著,有关水下声波探测及深潜器结构声性能研究日益增多。水下复杂结构受声波激励后,会产生包含复杂结构几何形状、内部结构、材料等信息的散射声场,此类水下复杂结构声散射研究在当今水下结构声性能研究中尤为重要,相应的计算方法也较为丰富。
目前,声散射问题的计算方法包括了近似解法和数值解法,多应用于严格理论解较难解决的复杂结构中。汤渭霖[1-2]使用Kirchhoff近似的物理声学方法,将其推广到非硬表面的情况,解决了附加吸声覆盖层的目标强度计算问题;范威[3]使用简正波Kirchhoff近似混合方法,实现对大尺寸复杂目标在浅海波导中的散射声场计算。T矩阵方法是在半解析方法基础上的数值方法,所求单一T矩阵适用于各入射方向,能够精确解决中、高频散射问题,广泛应用于复杂结构目标声散射计算[4-5],但无法计算表面有棱角模型,例如两端平面的圆柱壳。王朔中[6]提出应用于水下结构声散射的时域有限差分方法,此方法可有效用于复杂结构声散射计算,但需同时考虑内外空间,导致在求解远场问题时,外部网格量较大,计算量大大增加。有限元计算方法由于其对复杂结构及多频段的可用性,被广泛用于研究水下复杂目标声散射[7-9],Rajabi等[10]使用三维有限元方法计算了多层复合材料圆柱壳的声散射特性。虽然三维有限元计算方法精度高、模型构建要求低,但是其效率较差是显而易见的。为了提高计算效率,二维轴对称计算方法需大力推广。目前对于二维轴对称运用计算方法研究较少,Mario Zampolli等[11]提出了求解轴对称目标声散射的方法,胡珍、张培珍等[12-13]利用二维有限元方法分别研究了水下掩埋目标及水中局部填充带球冠柱体的声散射特性。
本文研究对象为双层周期加筋圆柱壳模型,该模型大范围运用在水下鱼雷、深潜器等结构中,具有极大的工程价值。而这类模型在数值计算的过程中,随体积和频率增多的网格量,导致需要庞大的计算量来满足计算精度。为了解决这一问题,本文利用有限元方法,推导出适用于二维轴对称模型的公式,结合仿真软件,计算了双层周期加筋圆柱壳模型在平面波作用下的回波特性,并将三维与二维的计算结果和效率进行对比,说明二维轴对称有限元方法在水下复杂目标声散射计算中具有较高计算精度与计算效率。
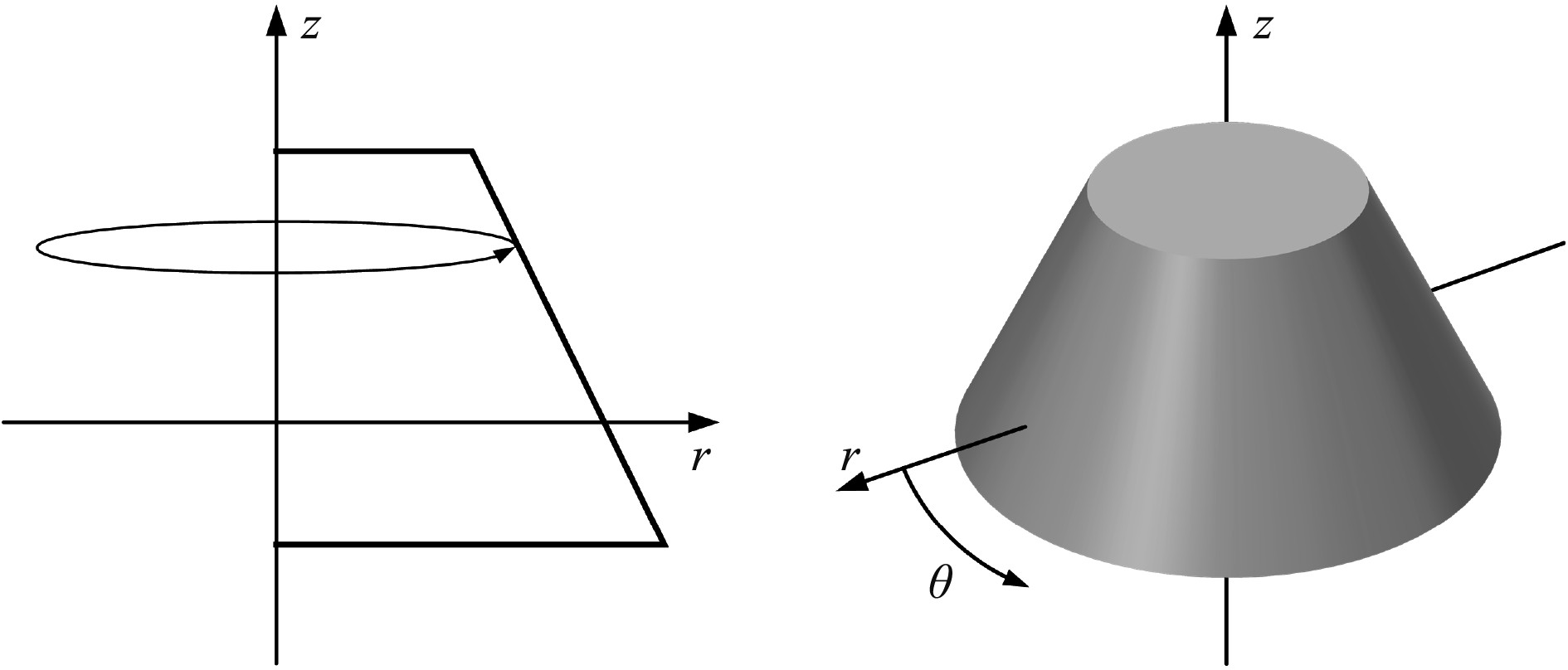
1 基本理论本文研究的轴对称目标如图1所示。采用非轴对称激励的平面波入射,选用柱坐标r,θ,z。这种情况,通过二维有限元方法计算,既能保证计算精度,也能大大提高计算效率。本节介绍柱坐标下的入射平面波展开公式,远场声目标强度计算公式,以及此种情况下弹性域与声场域的变分方程。随后基于变分方程,将三维有限元问题转化为了二维有限元问题,并在商用有限元软件COMSOL中构建二维轴对称结构声散射计算模型。
|
图 1 旋转结构图 Fig. 1 Rotating structure |
一般柱坐标入射声场pinc可以通过Fourier级数形式按照m阶展开得到:
| $ {p^{{\rm{inc}}}}(r,\theta ,z) = p_m^{{\rm{inc}}}(r,z){e^{im\theta }}, - \infty < m < + \infty {\text{,}} $ | (1) |
其中,
根据式(1),对入射平面波展开,它的波数向量k平行于rz平面,并与r轴形成一个角度
| $ p_m^{{\rm{inc}}}(r,z) = {i^m}{e^{(ikz\sin \phi )}}{J_m}(kr\cos \phi ){\text{,}} $ | (2) |
其中,
在柱坐标系中,距原点距离为r处,远场声目标强度公式为:
| $ TS({{r}}) = 20{\log _{10}}\frac{{{{r}}\left| {{p^{{\rm{scat }} ,\infty }}({{r}})} \right|}}{{\left| {{p^{{\rm{inc }}}}} \right|}}{\text{,}} $ | (3) |
其中,
根据弹性域与声场域变分方程,可以在COMSOL中构建水下轴对称目标非轴对称激励计算模型。相应变分方程可表示为:
| $ \begin{split} & \int_{{\varOmega _s}} {\left[ {\begin{array}{*{20}{l}} { - {\omega ^2}{\rho _s}\left( {\left( {{u_m}\delta {u_m} + {w_m}\delta {w_m}} \right)\left\{ {\begin{array}{*{20}{l}} {2{\text π} } \\ {\text π} \end{array}} \right\} + {v_m}\delta {v_m}\left\{ {\begin{array}{*{20}{l}} 0 \\ {\text π} \end{array}} \right\}} \right) + } \\ {\left. {(\sigma _r^m\delta \left( {\varepsilon _r^m} \right) + \sigma _\theta ^m\delta \left( {\varepsilon _\theta ^m} \right) + \sigma _z^m\delta \left( {\varepsilon _z^m} \right)} \right)\left\{ {\begin{array}{*{20}{l}} {2{\text π} } \\ {\text π} \end{array}} \right\} + } \\ {\left( {2\sigma _{r\theta }^m\delta \left( {\varepsilon _{r\theta }^m} \right) + 2\sigma _{\theta z}^m\delta \left( {\varepsilon _{\theta z}^m} \right)} \right)\left\{ {\begin{array}{*{20}{l}} 0 \\ {\text π} \end{array}} \right\} + 2\sigma _{{r_2}}^m\delta \left( {\varepsilon _{rs}^m} \right) \times \left\{ {\begin{array}{*{20}{l}} {2{\text π} } \\ {\text π} \end{array}} \right\}} \end{array}} \right]} \times \hfill \\ & rdrdz + {I_{\partial {\Omega _s}}} = 0 \hfill {\text{,}}\\[-10pt] \end{split} $ | (4) |
| $ \begin{split} \int_{{\varOmega _f}} & \left[ {\begin{array}{*{20}{l}} { - \frac{1}{{{\omega ^2}{\rho _f}}}\left( {\frac{{\partial p_m^{{{\rm scat}}}}}{{\partial r}}\delta \left( {\frac{{\partial p_m^{{{\rm scat}}}}}{{\partial r}}} \right)\left\{ {\begin{array}{*{20}{l}} {2{\text π} } \\ {\text π} \end{array}} \right\} + \frac{{{m^2}}}{{{r^2}}}p_m^{{{\rm scat}}}\delta \left( {p_m^{{{\rm scat}}}} \right) \times } \right.} \\ {\left. {\left\{ {\begin{array}{*{20}{l}} 0 \\ {\text π} \end{array}} \right\} + \frac{{\partial p_m^{{{\rm scat}}}}}{{\partial z}}\delta \left( {\frac{{\partial p_m^{{{\rm scat}}}}}{{\partial z}}} \right)\left\{ {\begin{array}{*{20}{l}} {2{\text π} } \\ {\text π} \end{array}} \right\}} \right) + \frac{1}{{{\rho _f}c_f^2}}p_m^{{{\rm scat}}}\delta \left( {p_m^{{{\rm scat}}}} \right)\left\{ {\begin{array}{*{20}{l}} {2{\text π} } \\ {\text π} \end{array}} \right\}} \end{array}} \right] \times \hfill \\ & r{{\rm d}}r{{\rm d}}z + {I_{\partial {\Omega _f}}} = 0 {\text{。}}\hfill \\[-10pt] \end{split} $ | (5) |
其中:
| $ {{I_{\partial {\varOmega _s}}} = \int_{{\Gamma _{fsi}}} {\left( {p_m^{scat} + p_m^{inc}} \right)} \left( {{n_r}\delta {u_m} + {n_z}\delta {w_m}} \right)\left\{ {\begin{array}{*{20}{c}} {2{\text{π}} }\\ {\text{π}} \end{array}} \right\}r{\rm{d}}\ell }{\text{,}} $ | (6) |
| $ \begin{split} & {I_{\delta {\varOmega _f}}} = \int_{{\Gamma _{fsi}}} {\left[ {{u_m}{n_r} + {u_z}{n_z} - \frac{1}{{{\omega ^2}{\rho _f}}}\left( {\frac{{\partial p_m^{inc}}}{{\partial r}}{n_r} + \frac{{\partial p_m^{inc}}}{{\partial z}}{n_z}} \right)} \right]} \times \hfill \\ & \quad \quad \quad \left\{ {\begin{array}{*{20}{l}} {2{\text π} } \\ {\text π} \end{array}} \right\}\delta p_m^{s{\text{cat}}}r{\rm{d}}\ell {\text{。}} \hfill \\[-20pt] \end{split} $ | (7) |
式(4)~式(7)中:大括号内取值,根据周向模数m取值而定,当
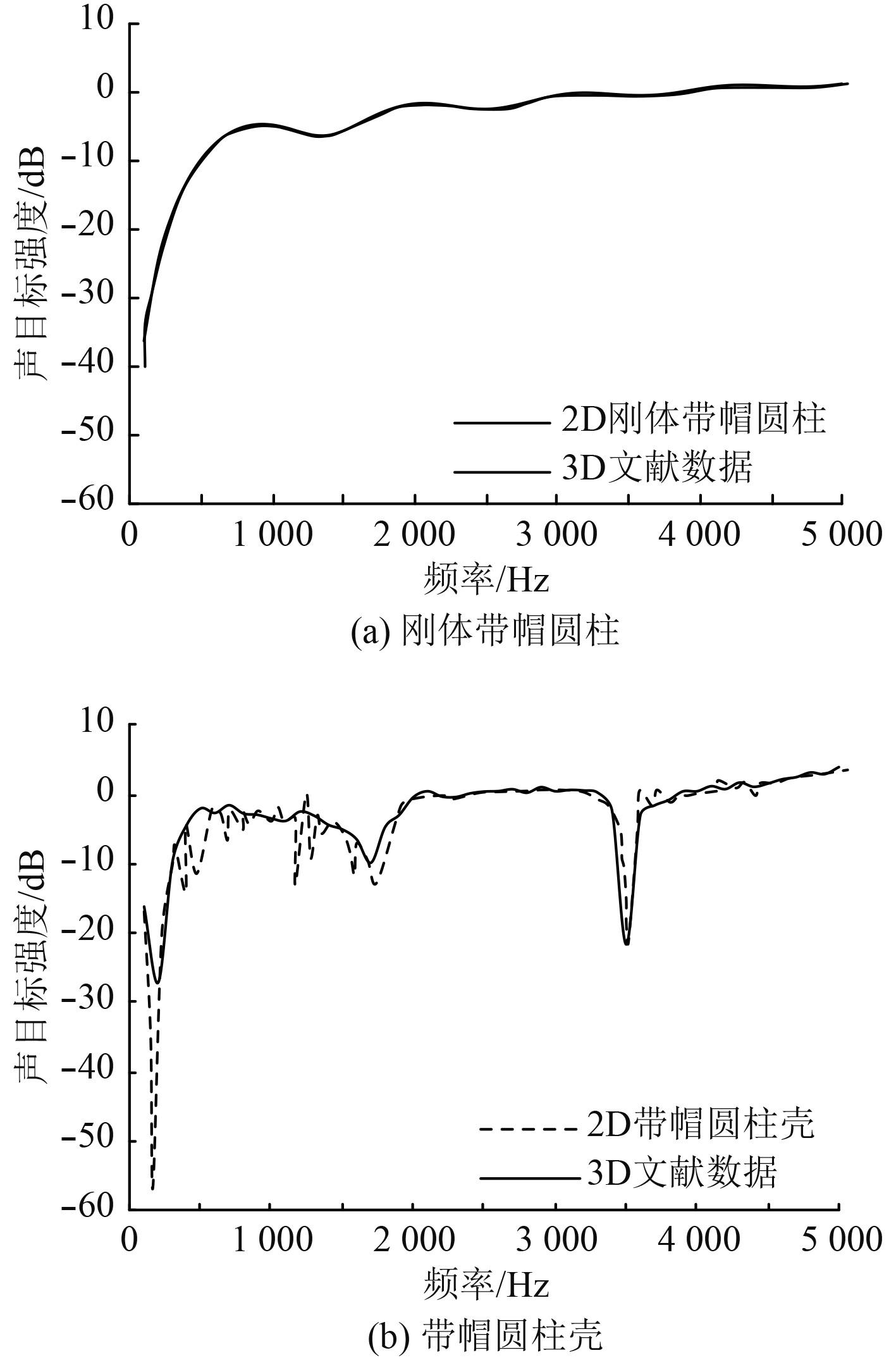
利用文献[11]中长度200 cm,半径25 cm,壳厚1 cm带帽圆柱的刚体与真空壳结构进行方法验证。对比计算中入射平面波为正横方向,材料横波波速1400 m/s,纵波波速3500 m/s,密度3000 kg/m3。通过刚体带帽圆柱与带帽圆柱壳的声目标强度TS计算结果对比可知,利用COMSOL构建的二维轴对称声散射计算模型的计算结果与参考文献结果吻合度非常高,如图2所示。可以证明所使用二维轴对称有限元法具有较高的准确性,完全适用于轴对称壳体结构声散射这一类问题的计算。
|
图 2 声目标强度TS对比 Fig. 2 Comparison of acoustic target intensity TS |
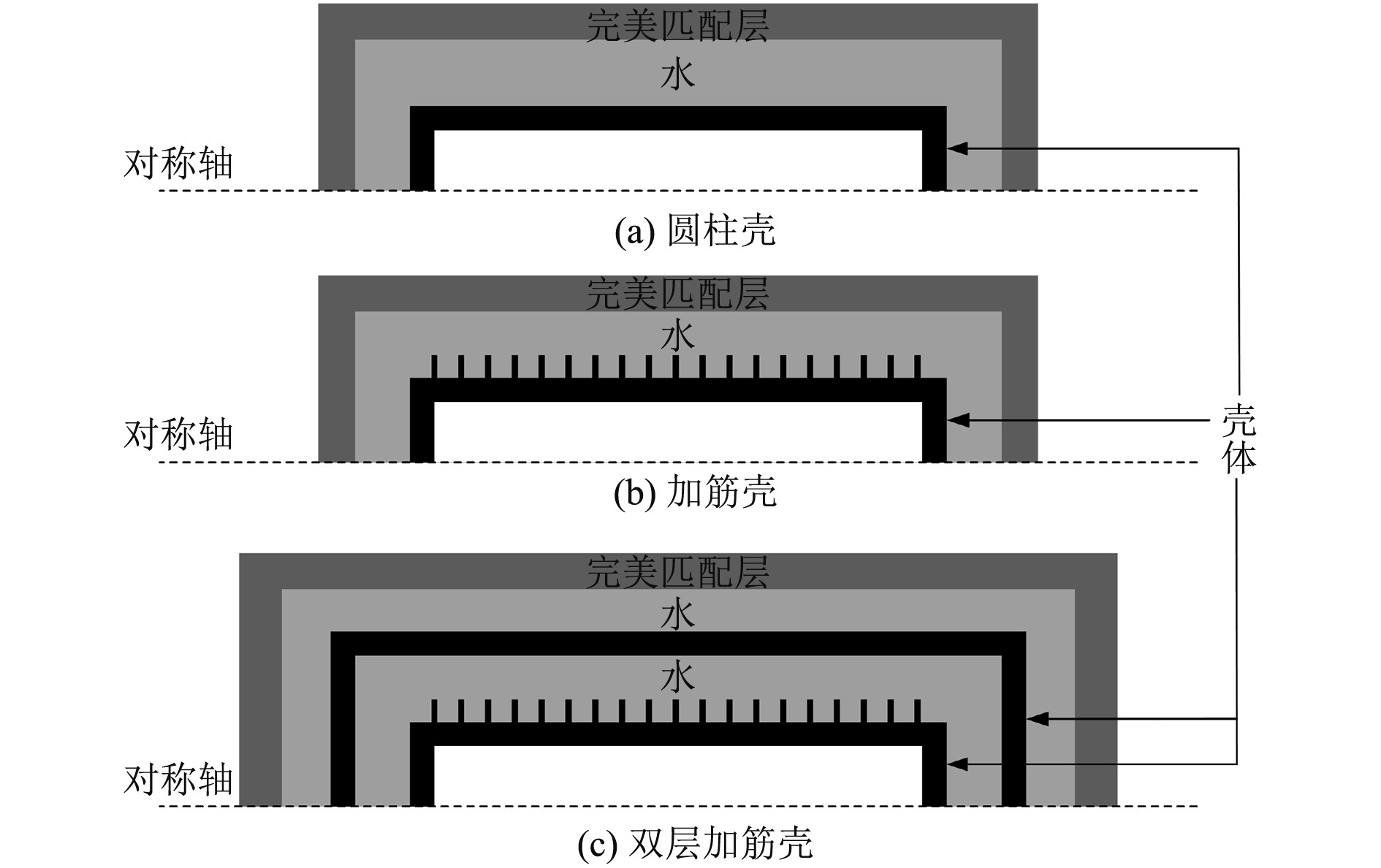
为了验证计算方法在不同物理结构中的有效性,构建纯圆柱壳、加筋圆柱壳和双层加筋圆柱壳的二维轴对称仿真模型,如图3所示。模型由水包围,入射平面波为正横入射,采用收发合置方式计算散射声场,计算频带为100~5000 Hz,步长为10 Hz。相关模型几何尺寸与材料参数见表1和表2。
|
|
表 1 几何参数 Tab.1 Geometric parameters |
|
|
表 2 材料参数 Tab.2 Material parameters |
|
图 3 二维轴对称模型 Fig. 3 Two-dimensional axisymmetric model |
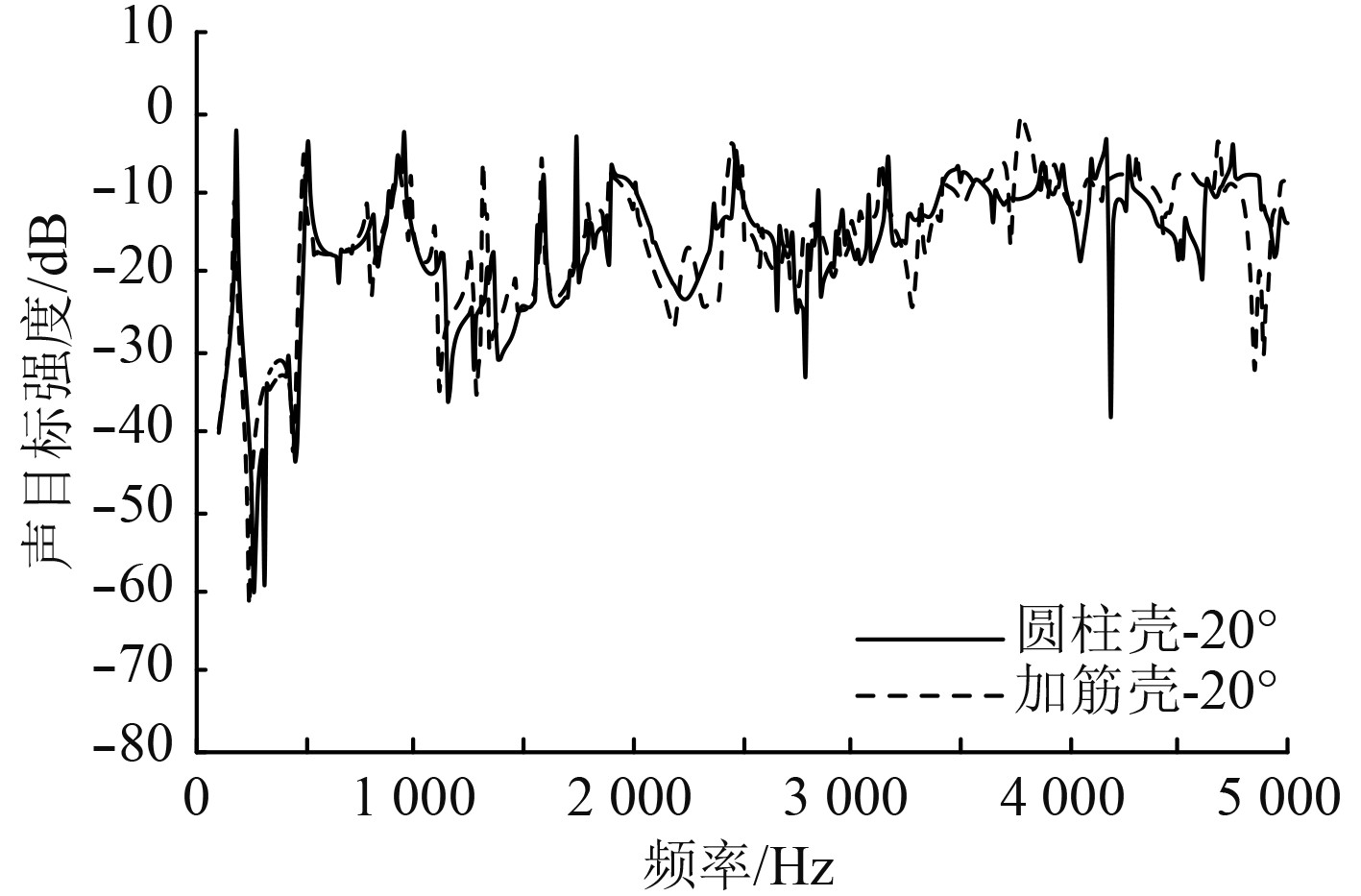
图4~图6为单一圆柱壳与加筋圆柱壳在不同入射方向(包括0°,20°,40°入射)下的声目标强度TS对比曲线,其中入射角度为入射波与模型正横方向的夹角,0°即为正横。对比单一圆柱壳与加筋圆柱壳,随着入射波频率的增大,入射波波长减小,环形加强筋对声目标强度的影响逐渐明显。

|
图 4 圆柱壳与加筋壳声目标强度(0°) Fig. 4 Acoustic target intensity of cylindrical shell and stiffened shell(0°) |
|
图 5 圆柱壳与加筋壳声目标强度(20°) Fig. 5 Acoustic target intensity of cylindrical shell and stiffened shell(20°) |

|
图 6 圆柱壳与加筋壳声目标强度(40°) Fig. 6 Acoustic target intensity of cylindrical shell and stiffened shell(40°) |
当入射角为0°时,加筋壳声目标强度与圆柱壳在低频范围内基本吻合,仅在高频段3500~5000 Hz的3600 Hz与4500 Hz附近存在较大差异;当入射角为20°时,加筋壳在3400Hz,3800 Hz,4250 Hz附近以及4500~5000 Hz范围内与圆柱壳TS存在差异;当入射角为40°时,加筋壳TS与圆柱壳差异愈加明显,从1750 Hz开始出现较多小的偏差点,无法达到小角度入射时低频范围内的吻合程度。上述现象都说明随着入射角度的增大,加筋壳在高频段的影响相较单一圆柱壳会逐渐增大。
2.3 双层加筋圆柱壳对比分析图7~图9为加筋圆柱壳与双层加筋圆柱壳在0°,20°,40°入射平面波作用下的声目标强度TS对比曲线。

|
图 7 加筋壳与双层加筋壳声目标强度(0°) Fig. 7 Acoustic target intensity of stiffened shell and double layer stiffened shell(0°) |
|
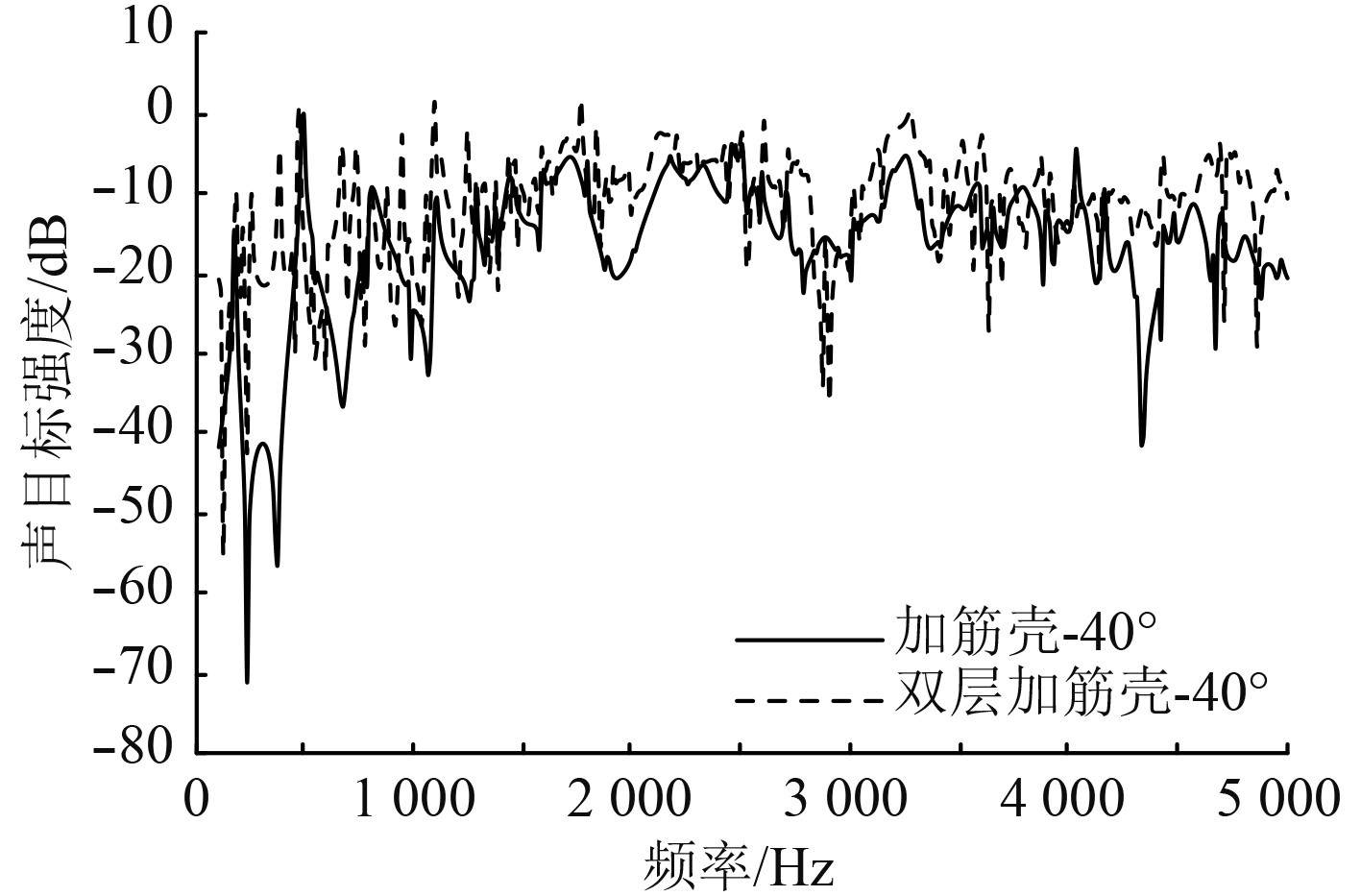
图 9 加筋壳与双层加筋壳声目标强度(40°) Fig. 9 Acoustic target intensity of stiffened shell and double layer stiffened shell(40°) |
对于双层加筋圆柱壳,为表明外壳对声散射特性的影响,在图7中增加了单一圆柱外壳在正横入射时的声目标强度曲线。对比加筋圆柱壳与双层加筋圆柱壳,由图7可见,对于正横入射而言,其双层结构TS更多是由外部壳体所贡献的,相较内部加筋柱壳来说,外部壳体的计算结果普遍较高一点。特别是在3000 Hz之后,双层加筋圆柱壳TS与单一圆柱外壳吻合程度进一步增加。

|
图 8 加筋壳与双层加筋壳声目标强度(20°) Fig. 8 Acoustic target intensity of stiffened shell and double layer stiffened shell(20°) |
当入射角度为20°时,圆柱外壳对声散射特性的影响减弱,只在1400~2500 Hz内,圆柱外壳的影响较大,而在1400以下、2500 Hz以上,双层结构与内部加筋柱壳结果相近。当入射角度为40°时,双层结构与内部加筋柱壳结果则更为相近。总之,随着入射角度增大,外部壳体影响逐渐缩小,内部加筋结构影响增强,双层加筋结构与单层加筋结构声目标强度逐渐吻合。
2.4 计算效率对比分析表3与图10显示了各结构模型3D与2D的计算效率,结果均由装载Intel(R)Xeon(R)E5-2686v4@2.3GHz芯片工作站计算所得,操作系统为64位Windows 10专业版。
|
|
表 3 各模型3D与2D计算效率对比 Tab.3 Comparison of 3D and 2D calculation efficiency of each model |
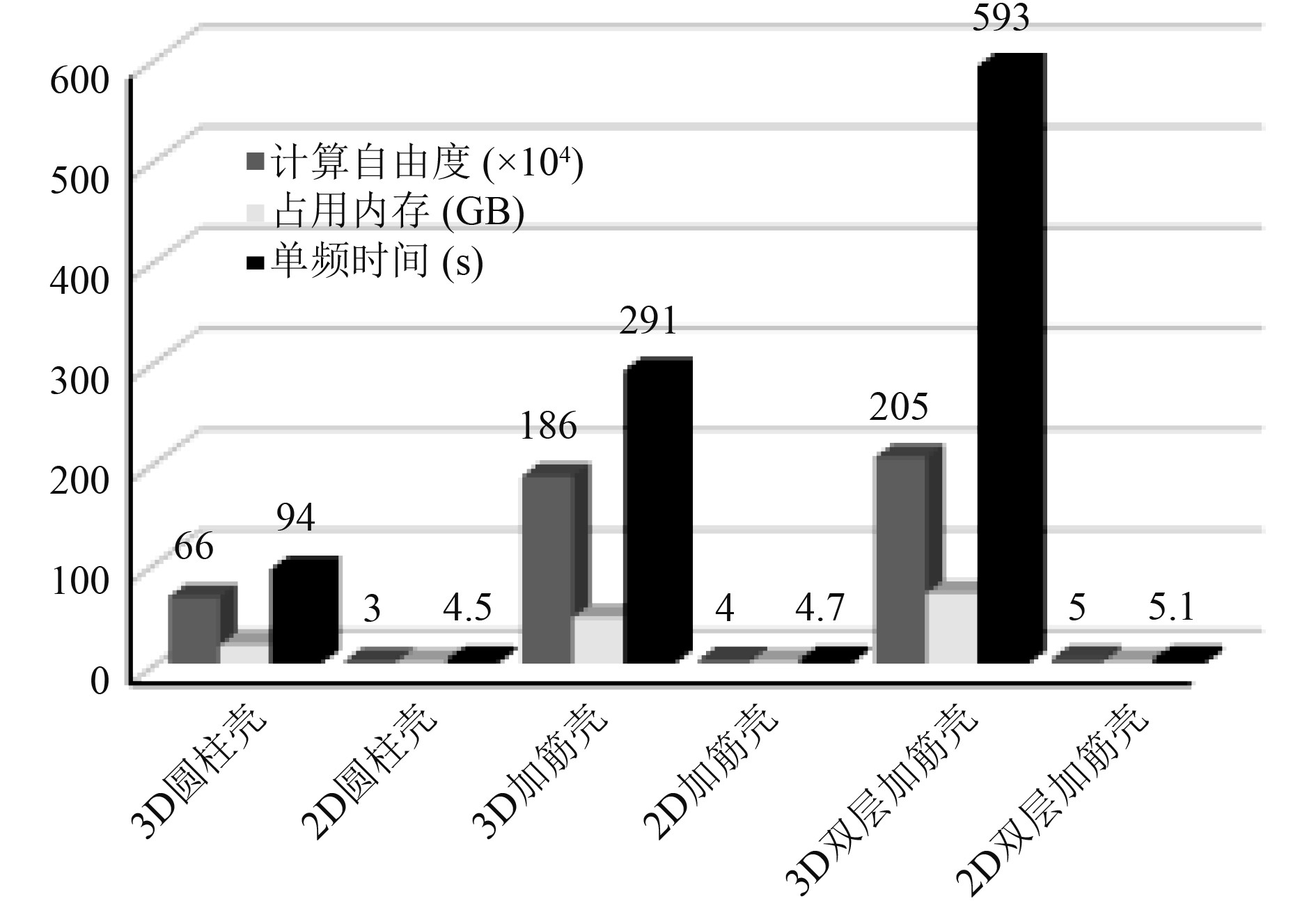
|
图 10 各模型3D与2D计算效率对比 Fig. 10 Comparison of 3D and 2D calculation efficiency of each model |
由图11对比3D与2D模型的计算效率可得:
1)在最大网格尺寸不超过入射波波长1/6情况下,三维模型的计算自由度是二维模型的30~40倍;
2)二维模型运行内存占用基本稳定在2GB左右,三维模型运行内存占用随着结构复杂度升高,所需内存成倍增加;
3)计算时间上,二维模型平均单频点所需时间与三维模型相差20~100倍,远低于三维模型。如果考虑周向模数m,对于本文模型m=10已能满足计算精度,每个频点计算10次后,计算时间也与三维模型相差甚远。
3 结 语针对水下复杂结构声散射分析精度较低且耗时较大的问题,本文基于轴对称结构在非轴对称激励情况下的变分理论,在有限元仿真软件中实现了对旋转柱壳结构的声散射特性分析。通过与相关文献三维模型声目标强度计算结果的对比,验证了该方法的准确性;通过仿真分析圆柱壳、加筋壳、双层加筋壳等不同复杂结构的声散射特性,进一步说明了该方法的高效性。基于本文提出的方法,后续可在水下目标声辐射方面开展研究,拓宽应用范围。
| [1] |
汤渭霖. 用物理声学方法计算非硬表面的声散射[J]. 声学学报, 1993(1): 45-53. |
| [2] |
汤渭霖. 用物理声学方法计算界面附近目标的回波[J]. 声学学报, 1999(1): 1-5. |
| [3] |
范威, 范军, 陈燕. 浅海波导中目标散射的简正波-Kirchhoff近似混合方法[J]. 声学学报, 2012(05): 13-21. |
| [4] |
NUMRICH, S. K. Scattering of acoustic waves by a finite elastic cylinder immersed in water[J]. The Journal of the Acoustical Society of America, 1981, 70(5): 1407-1411. DOI:10.1121/1.387131 |
| [5] |
MACKOWSKI D W, MISHCHENKO M I. Calculation of the T matrix and the scattering matrix for ensembles of spheres[J]. Journal of the Optical Society of America A, 1996, 13(11): 2266-2278. DOI:10.1364/JOSAA.13.002266 |
| [6] |
WANG, Shuozhong. Finite-difference time-domain approach to underwater acoustic scattering problems[J]. The Journal of the Acoustical Society of America, 1996, 99(4): 1924-1931. DOI:10.1121/1.415375 |
| [7] |
TEZAUR R, MACEDO A, FARHAT C, et al. Three-dimensional finite element calculations in acoustic scattering using arbitrarily shaped convex artificial boundaries[J]. International Journal for Numerical Methods in Engineering, 2002, 53(6): 1461-1476. DOI:10.1002/nme.346 |
| [8] |
ISAKSON M J, CHOTIROS N P. Finite element modeling of acoustic scattering from fluid and elastic rough interfaces[J]. IEEE Journal of Oceanic Engineering, 2015, 40(2): 475-484. DOI:10.1109/JOE.2014.2313060 |
| [9] |
ESPANA A L, WILLIAMS K L, PLOTNICK D S, et al. Acoustic scattering from a water-filled cylindrical shell: Measurements, modeling, and interpretation[J]. The Journal of the Acoustical Society of America, 2014, 136(1): 109-121. DOI:10.1121/1.4881923 |
| [10] |
RAJABI M, AHMADIAN M T, JAMALI J. Acoustic scattering from submerged laminated composite cylindrical shells[J]. Composite Structures, 2015, 128: 395-405. DOI:10.1016/j.compstruct.2015.03.017 |
| [11] |
ZAMPOLLI M, TESEI A, JENSEN F B, et al. A computationally efficient finite element model with perfectly matched layers applied to scattering from axially symmetric objects[J]. The Journal of the Acoustical Society of America, 2007, 122(3): 1472-1485. DOI:10.1121/1.2764471 |
| [12] |
胡珍, 范军, 张培珍, 等. 水下掩埋目标的散射声场计算与实验[J]. 物理学报, 2015, 65(6). |
| [13] |
张培珍, 李秀坤, 范军, 等. 局部固体填充的水中复杂目标声散射计算与实验[J]. 物理学报, 2016, 65(18): 273-281. |
 2020, Vol. 42
2020, Vol. 42
