0 引　言

在舰船上，由于转子不平衡等原因，泵类旋转机械存在轴频、叶频等十分突出的低频振动线谱，通过基座、管路等通道向外传递^[1-2]。动力吸振器（DVA）是被动控制振动线谱的有效手段，已经在汽车、船舶、建筑等领域广泛应用。在设计和应用动力吸振器时，往往将控制对象简化为质点或多自由度系统，根据等效质量和刚度来确定吸振频率。舰船管路系统跨径比大、自身固有频率低、边界条件复杂，对吸振频率和控制效果有较大影响，在开展管路系统吸振设计时，管路已不适合简化为质点或多自由度系统。因此，有必要针对舰船管路系统的特点，开展管路吸振器的振动特性研究。

吴崇建等^[3]用弯曲波法建立了多点支撑欧拉梁的运动方程，研究了用动力吸振器抑制梁共振的特性。Park等^[4]建立了悬臂梁上集中质量块的频率方程，与前人的研究成果吻合较好。尹志勇^[5]等根据梁的能量传递理论设计了三向管路动力吸振器，并在试验台架上验证了控制效果。梁建等^[6]以附加阻尼吸振器的固支梁作为分析模型，定性研究阻尼吸振器对电路板共振响应的抑制作用，分析了等效质量比、固有频率比和损失因子等对吸振器控制效果的影响规律。刘天彦等^[7]针对管路系统设计了动力吸振器，并通过台架试验验证了吸振器对特征频率的抑制效果。虽然上述学者针对管路吸振器已开展了一些理论和试验研究，但是在建模、设计时均未考虑支撑刚度、激励及吸振器的相对位置等因素对吸振效果的影响。舰船上空间有限，管路支撑方式多样，研究如何在复杂环境中合理布置管路吸振器，提升控制效果，具有重要的工程意义。

本文以欧拉梁振动理论为基础，建立任意横向激励下，不同边界下管路—吸振器系统的横向振动模型，用有限元方法验证模型的准确性，研究了吸振器安装部位、控制对象和支撑刚度等对控制效果的影响规律。

1 管路吸振器系统振动模型 1.1 管路—吸振器系统振动模型

在两端弹性支撑的管路上加装管路吸振器，当管路长度远大于管径时，管路可简化为欧拉-伯努利梁，吸振器可简化为质量-弹簧系统。在任意横向激励作用下，管路—吸振器的振动模型如图1所示。

管路—吸振器的弯曲运动方程如下：

$ \rho \frac{{\partial }^{2}y}{\partial {t}^{2}}+EI\frac{{\partial }^{4}y}{\partial {x}^{4}}={d}_{j}\delta \left(x-{x}_{j}\right)+{f}_{i}\delta \left(x-{x}_{i}\right){\text{，}} $

(1)

$ {f}_{i}=c\left(\frac{\partial {y}_{id}}{\partial t}-\frac{\partial {y}_{i}}{\partial t}\right)+k({y}_{id}-{y}_{i}) {\text{，}}$

(2)

$ {f}_{i}=-m\frac{{\partial }^{2}{y}_{id}}{\partial {t}^{2}} {\text{。}}$

(3)

其中： $ {d}_{j} $ 为激励力； $ {x}_{j} $ 为激励的x坐标； $ {x}_{i} $ 为吸振器安装部位的x坐标； $ {y}_{i} $ 为吸振器在梁上安装部位的y向位移； $ {y}_{id} $ 为质量块的y向位移； $ m $ 为质量块质量； $ c $ ， $ k $ 为吸振器的阻尼和刚度； $ E $ 为梁的弹性模量； $ I $ 为梁的惯性矩。

根据振动理论^[8]，梁的挠度可用振型函数和广义坐标表示:

$ {y}_{i}\left(x,t\right)=\sum\nolimits_{n=1}^{\infty }{W}_{n}\left(x\right){q}_{n}\left(t\right) {\text{，}}$

(4)

其中 $ {q}_{n}\left(t\right) $ 为广义坐标， $ {W}_{n}\left(x\right) $ 为梁的第n阶固有振型函数，且满足：

$ EI\frac{{d}^{4}{W}_{n}\left(x\right)}{d{x}^{4}}-{\omega }_{n}^{2}\rho A{W}_{n}\left(x\right)=0 {\text{。}}$

(5)

将式（4）代入式（1），然后代入式（5），可得：

$ \begin{split} &\sum\nolimits_{n=1}^{\infty }{W}_{n}\left(x\right)\frac{{d}^{2}{q}_{n}\left(t\right)}{d{t}^{2}}+\sum\nolimits_{n=1}^{\infty }{\omega }_{n}^{2}{{q}_{n}\left(t\right)W}_{n}\left(x\right)=\\& \frac{{d}_{j}\delta \left(x-{x}_{j}\right)+{f}_{i}\delta \left(x-{x}_{i}\right)}{\rho A}{\text{，}} \end{split}$

(6)

式中，右边第1项为激励源，第2项为弹簧质量系统作用在梁上的力。两边分别乘以 $ {W}_{n}\left(x\right) $ ，在[0，L]上积分，利用振型函数的正交性和归一性，可得：

$ \frac{{{\rm{d}}}^{2}{q}_{n}\left(t\right)}{{\rm{d}}{t}^{2}}+{\omega }_{n}^{2}{q}_{n}\left(t\right)=\frac{{{W}_{n}\left({x}_{j}\right)d}_{j}+{W}_{n}\left({x}_{i}\right){f}_{i}}{\rho A} {\text{。}}$

(7)

对式（7）进行傅里叶变换，可得：

$ -{\omega }^{2}{q}_{n}\left(\omega \right)+{\omega }_{n}^{2}{q}_{n}\left(\omega \right)=\frac{{{W}_{n}\left({x}_{j}\right)d}_{j}\left(\omega \right)+{W}_{n}\left({x}_{i}\right){f}_{i}\left(\omega \right)}{\rho A} {\text{。}}$

(8)

即

$ {q}_{n}\left(\omega \right)=\frac{{{W}_{n}\left({x}_{j}\right)d}_{j}\left(\omega \right)+{W}_{n}\left({x}_{i}\right){f}_{i}\left(\omega \right)}{\rho A\left({\omega }_{n}^{2}-{\omega }^{2}\right)} {\text{。}}$

(9)

与此同时，对式（2）~式（4）进行傅里叶变换，可得：

$ {y}_{i}\left(\omega \right)=\sum\nolimits_{n=1}^{\infty }{W}_{n}\left({x}_{i}\right){q}_{n}\left(\omega \right) {\text{，}}$

(10)

$ jc\omega \left[{y}_{id}\left(\omega \right)-{y}_{i}\left(\omega \right)\right]+k\left[{y}_{id}\left(\omega \right)-{y}_{i}\left(\omega \right)\right]=m{\omega }^{2}{y}_{id}\left(\omega \right) {\text{。}}$

(11)

由式（9）～式（11）可以建立梁上任意一点位置 $ {x}_{k} $ 的响应 $ {y}_{k}\left(\omega \right) $ 与激励力 $ {d}_{j}\left(\omega \right) $ 之间的关系：

$ {y}_{k}\left(\omega \right)=C{d}_{j}\left(\omega \right)+\frac{AD}{1-B}{d}_{j}\left(\omega \right) {\text{，}}$

(12)

其中：

$ \begin{split} &A=\sum\limits_{n=1}^{\infty }{W}_{n}\left({x}_{i}\right)\frac{{W}_{n}\left({x}_{j}\right)}{\rho A\left({\omega }_{n}^{2}-{\omega }^{2}\right)} \text{，}\\&B=\frac{m{\omega }^{2}\left(jc\omega +k\right)}{jc\omega +k-m{\omega }^{2}}\sum\limits_{n=1}^{\infty }\frac{{W}_{n}^{2}\left({x}_{i}\right)}{\rho A\left({\omega }_{n}^{2}-{\omega }^{2}\right)}{\text{，}} \end{split}$

$ \begin{split} &C=\sum\nolimits_{n=1}^{\infty }{W}_{n}\left({x}_{k}\right)\frac{{W}_{n}\left({x}_{j}\right)}{\rho A\left({\omega }_{n}^{2}-{\omega }^{2}\right)} {\text{，}}\\&{{D}}=\frac{m{\omega }^{2}\left(jc\omega +k\right)}{jc\omega +k-m{\omega }^{2}}\bullet \sum\nolimits_{n=1}^{\infty }\frac{{W}_{n}\left({x}_{k}\right){W}_{n}\left({x}_{i}\right)}{\rho A\left({\omega }_{n}^{2}-{\omega }^{2}\right)}{\text{。}}\end{split}$

由式（12）可知，若 $ m=0 $ ，则 $ D=0 $ ，此时式（12）也可表示未安装吸振器时梁的响应特性。

1.2 弹性支撑边界下欧拉梁的振动方程

方程（5）解的形式为：

$ W\left(x\right)={c}_{1}{e}^{\beta x}+{c}_{2}{e}^{-\beta x}+{c}_{3}{e}^{i\beta x}+{c}_{4}{e}^{-i\beta x} {\text{，}}$

(13)

对于两端均为弹性支撑的梁，假设管路左端的支撑刚度为 $ {K}_{1} $ ，管路右端的支撑刚度为 $ {K}_{2} $ 。在两端边界，分别满足以下方程：

在x=0处， ${{\partial }^{2}W}/{\partial {x}^{2}}=0$ ， ${\partial \left({EI\partial }^{2}W\right)}/{\partial {x}^{3}}= -{K}_{1}W$ ，即

$ {c}_{1}+{c}_{2}-{c}_{3}-{c}_{4}=0 {\text{，}}$

(14)

$ EI{\beta }^{3}\left({c}_{1}-{c}_{2}-{ic}_{3}+i{c}_{4}\right)+{K}_{1}\left({c}_{1}+{c}_{2}+{c}_{3}+{c}_{4}\right)=0 {\text{。}}$

(15)

在x=L处， ${{\partial }^{2}W}/{\partial {x}^{2}}=0$ ， ${\partial \left({EI\partial }^{2}W\right)}/{\partial {x}^{3}}={K}_{2}W$ ，即

$ {c}_{1}{e}^{\beta L}+{c}_{2}{e}^{-\beta L}-{c}_{3}{e}^{i\beta L}-{c}_{4}{e}^{-i\beta L}=0 {\text{，}}$

(16)

$ \begin{split}& EI{\beta }^{3}\left({c}_{1}{e}^{\beta L}-{c}_{2}{e}^{-\beta L}-{ic}_{3}{e}^{i\beta L}+i{c}_{4}{e}^{-i\beta L}\right)-\\&{K}_{2}\left({c}_{1}{e}^{\beta L}+{c}_{2}{e}^{-\beta L}+{c}_{3}{e}^{i\beta L}+{c}_{4}{e}^{-i\beta L}\right)=0{\text{。}} \end{split}$

(17)

式（14）～式（17）若有非零解，则系数的行列式应为0。经过计算，可得：

$ \begin{split}&\left[\left(1-{T}_{1}-{T}_{2}\right)cos\beta L+\left({T}_{1}+{T}_{2}-2{T}_{1}{T}_{2}\right)sin\beta L\right]{e}^{\beta L}+\\&\left[\left(1+{T}_{1}+{T}_{2}\right)cos\beta L+\left({T}_{1}+{T}_{2}+2{T}_{1}{T}_{2}\right)sin\beta L\right]{e}^{-\beta L}-2=0{\text{。}} \end{split}$

(18)

式（18）即为管路两端均在弹性支撑状态下，梁的振动频率方程。其中， ${{T}}_{1}={{K}_{1}}/{EI{\beta }^{3}}$ ， ${{T}}_{2}={{K}_{2}}/{EI{\beta }^{3}}$ 分别为管路两端支撑的弹性影响因素。

在刚性支撑条件下，管路两端支撑刚度 $ K\to \infty $ ，频率方程变为 $ sin\beta L=0 $ ；若管路两端为自由边界，支撑刚度 $ K\to 0 $ ，则频率方程变为 $ cos\beta L{e}^{\beta L}+ cos\beta L{e}^{-\beta L}-2=0 $ 。

根据频率方程及边界条件，可求出振型函数 $ W\left(x\right) $ 。再结合式（12），可求得梁上任意点在给定激励下的振动响应。

2 计算模型数值验证

选取一种舰船常用的管路，用有限元方法验证本文提出计算方法的准确性。管路规格为外径D=57 mm，内径d=50 mm，长度L=2000 mm，材料为钢材，弹性模量为2.1E¹¹Pa，密度为7850 kg/m³，泊松比为0.3。用有限元软件和本文提出的模型，分别计算管路两端分别为刚性支撑、自由和弹性支撑时，管路的前4阶固有频率和振型图。在有限元建模时，管路采用的beam4单元，用combin14模拟弹性支撑边界条件。3种边界条件下，管路的固有频率计算结果如表1所示。

由表1可知，在刚性支撑、自由和弹性支撑等3种边界条件下，本模型计算得到的前4阶固有频率计算结果与有限元计算结果差别在1.6%以内。

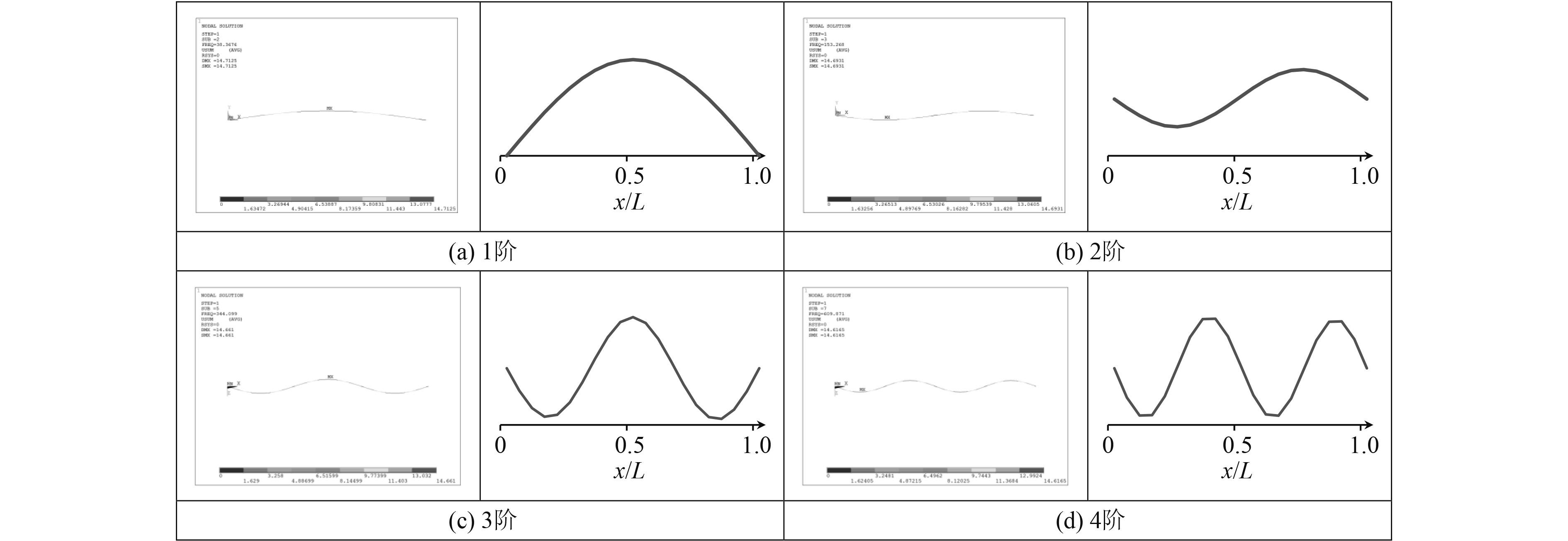
管路两端分别为刚性支撑、自由和弹性支撑时，用有限元和本文提出的模型计算得到的管路前4阶振型图分别如图2～图4所示。

可以看出，在3种边界条件下，本文计算得到的管路振型图与有限元计算结果基本一致。综合固有频率和振型图的计算结果来看，本文提出计算模型的准确性得到了验证。

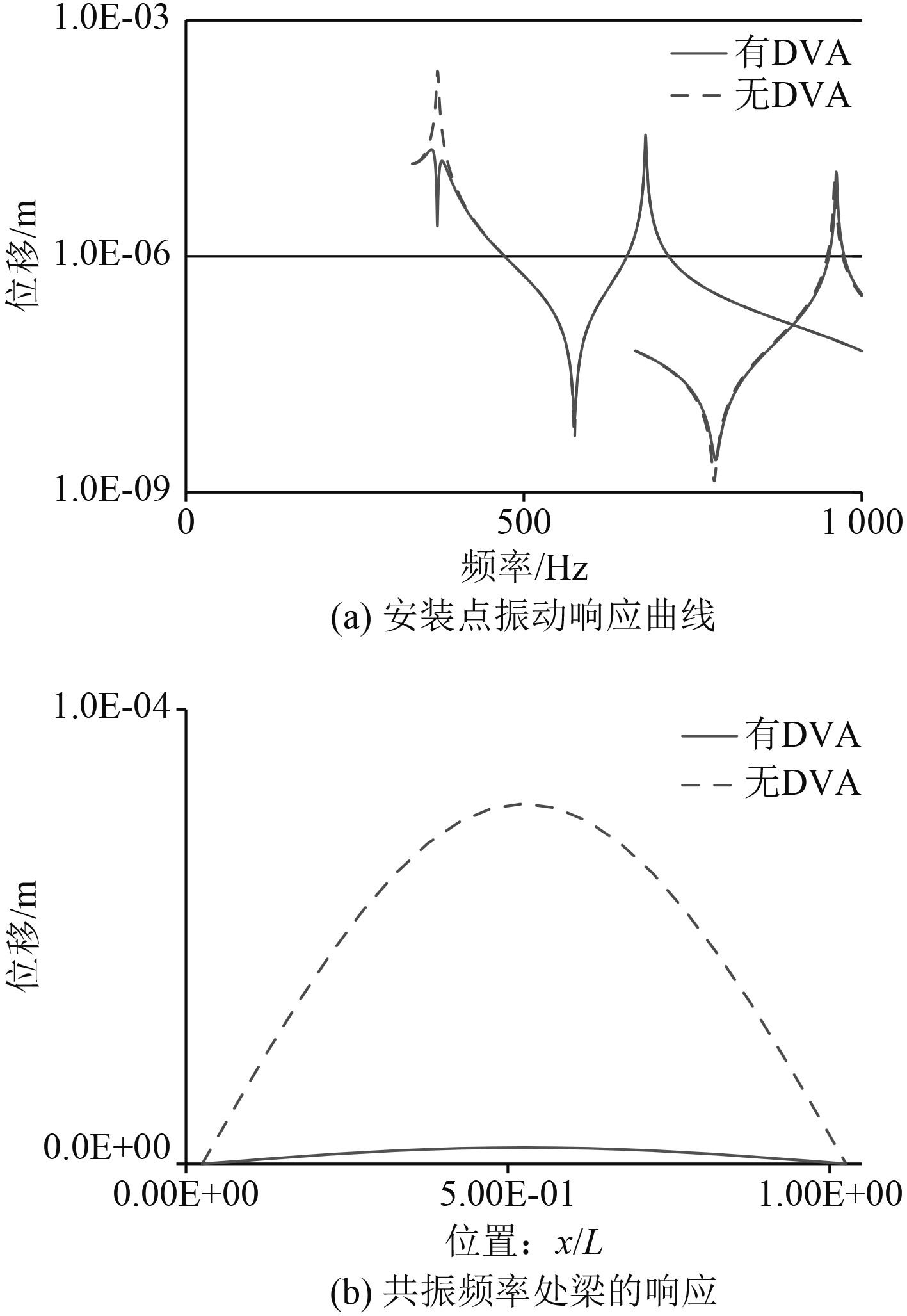
3 管路吸振器控制效果分析 3.1 管路吸振器参数设计

根据上一节计算结果，可知在上述刚性和弹性支撑边界下，管路的一阶固有频率分别为为38 Hz和35 Hz，由此可以确定管路吸振器的特征频率。按照设计经验，吸振器与管路的质量比初步取为0.02，吸振器的刚度根据吸振频率及自身质量可确定。图6为在管路两端刚性支撑和弹性支撑的边界条件下，在管路中间x/L=0.5处加装动力吸振器前后，在安装部位施加单位激励后管路的振动响应曲线。

可以看出，在2种边界条件下，针对特定模态在管路加装动力吸振器后，在单位激励下，该阶线谱的振动响应得到明显抑制，而其他频段基本不受影响。在共振频率处，不仅在安装部位，管路整体的振动都得到了有效控制。

3.2 吸振器控制效果影响因素分析

a）吸振器与激励力位置关系

舰船上空间紧张，管路支撑和吸振器的安装位置都受到一定约束。因此，合理选择管路吸振器和激励力的布置位置，对于提高控制效果具有重要意义。图7为管路吸振器的控制频率为管路的1阶固有频率（35 Hz），管路分别在刚性和弹性支撑状态下，受单位激励作用管路的振动响应。

由图7可以看出，针对特定管路模态，不论管路两端为刚性还是弹性支撑，激励力及吸振器的位置均对管路的振动响应有重要影响。针对控制频率，激励越靠近振动模态的位移极值点，管路整体的振动越大；吸振器布置越靠近振动模态的位移极值点，管路整体的控制效果越好；如果管路两端为刚性支撑边界，不论吸振器及激励的位置如何变化，总有较好的控制效果；若管路两端为弹性支撑，如果激励的位置不在位移极值点，那么吸振器离激励位置越远，控制效果越差。在图7（a）中，当DVA的位置与激励距离△=0.75L时，加装吸振器后管路最大位移与加装前的比值为0.65，加装DVA对管路振动控制效果较差。

b）非共振频率控制效果

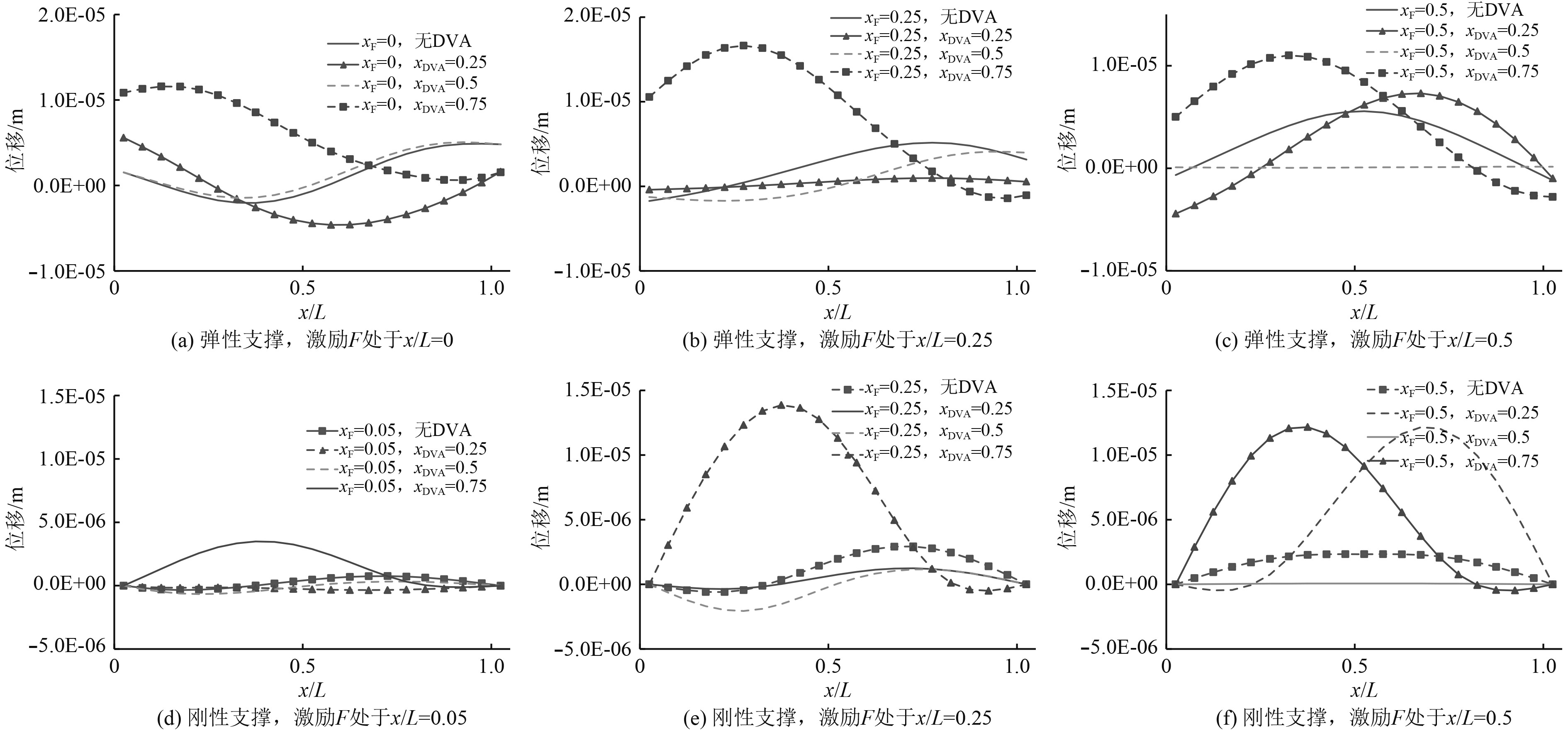
舰船上管路系统的振动响应线谱除了来自于系统自身固有频率，也包含来自设备的轴频、叶频等线谱激励，后者在很多时候是管路振动响应线谱的主要来源。因此，针对线谱激励的控制具有重要的实际意义。同样受限于空间，合理选择吸振器的布置位置，对于控制效果也具有重要意义。以舰船上常见的100 Hz振动激励为对象，设计控制频率为100 Hz的吸振器。图8为管路分别在刚性和弹性支撑状态下，在100 Hz频率处，激励位置与吸振器位置的变化对管路振动响应的影响规律。

由图8可以看出，针对特定激励，不论管路两端为刚性还是弹性支撑，激励力及吸振器的位置均对管路的振动响应有重要影响。针对控制频率，如果吸振器的安装位置与激励的位置重合，那么管路整体的振动会受到良好抑制，如果激励和吸振器均处于振动模态的位移极值点，抑振效果更加显著；如果吸振器的安装位置与激励位置不重合，不论管路两端是刚性还是弹性支撑，随着二者之间距离的增大，控制效果越来越差；当吸振器与激励的距离大于一定值时，会产生严重的负面效果，显著放大管路的振动。在图8（b）和图8（e）中，激励的位置处于x/L=0.25，若吸振器的位置加在x/L=0.75处，那么加装DVA后，管路的振动反而被放大，加装吸振器后管路上最大位移幅值与加装前的比值分别为3.22和4.79。

综上，在针对特定模态频率和针对特定激励应用吸振器时，管路系统的振动特性存在较大差异，后者对激励及吸振器位置更为敏感。因此，以特定激励为管路系统振动控制对象时，吸振器的布置应尽量靠近激励位置。

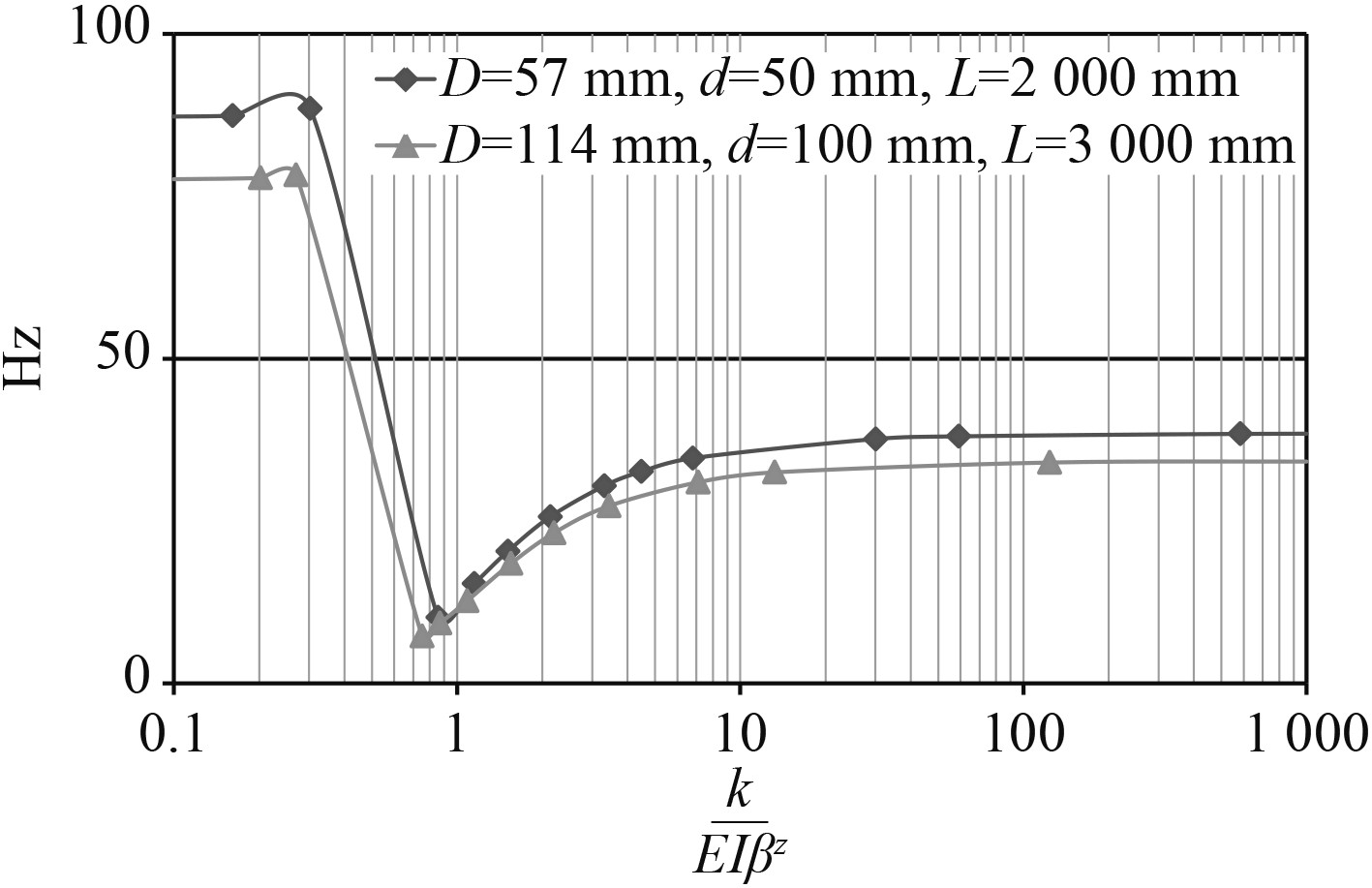
3）管路支撑刚度

由管路的频率方程可知，管路的振动特性不仅取决于自身，也取决于管路两端的支撑刚度。综合而言，管路支撑的弹性影响因素 $ T={k}/{EI{\beta }^{3}} $ 对管路的振动特性影响最大。图9为2种规格管路的1阶固有频率随弹性影响因素的变化情况。管路规格分别为D=57 mm，d=50 mm，L=2000 mm和D=114 mm，d=100 mm，L=3000 mm。

由图9可知，对于2种不同规格的管路，管路1阶固有频率在 $ T\in \left[0.1,10\right] $ 区间内变化较为显著。当 $ T $ 大于10时，随着刚度的增大，管路两端类似刚性支撑，支撑刚度的增大对1阶固有频率的影响在10%以内；当 $ T $ 小于0.1时，管路两端类似自由状态，支撑刚度的减小对1阶固有频率的影响小于1%。因此，以管路振动模态频率为控制对象设计吸振器时，需要重视管路两端支撑刚度的影响。

4 结　语

通过本文的研究工作，可以得出以下结论：

1）本文提出的一种管路吸振器的振动特性计算方法，在刚性支撑、自由支撑和弹性支撑等不同类型的边界条件下，管路的前4阶固有频率与有限元计算结果偏差在1.6%以内，振型的计算结果基本一致。

2）针对特定模态频率，如果激励的位置不在振动极值点，那么吸振器离激励位置越远，控制效果越差，甚至没有控制效果；吸振器及激励的位置对管路刚性支撑条件的影响要小于弹性支撑。针对特定频率的激励，吸振器与激励位置重合时有良好的控制效果，如果吸振器的安装位置与激励位置不重合，不论管路两端是刚性还是弹性支撑，那么随着二者之间距离的增大，控制效果越来越差，在某些条件下管路振动甚至放大超过3倍。因此，在应用管路吸振器时，应区分控制对象为特定模态频率还是特定激励；以特定激励为管路系统振动控制对象时，高度重视吸振器的布置位置，尽力使其靠近激励。

3）若弹性影响因素特定区间内，管路1阶固有频率对支撑刚度十分敏感。当 $ T $ 大于10时，管路两端类似刚性支撑，支撑刚度的增大对1阶固有频率的影响在10%以内；当 $ T $ 小于0.1时，管路两端类似自由状态，支撑刚度的减小对1阶固有频率的影响在1%以内。因此，以管路振动模态频率为控制对象设计吸振器时，需要重视管路两端支撑刚度的影响。