2. 中国船舶集团公司第七一三研究所,河南 郑州 450015
2. The 713 Research Institute of CSSC, Zhengzhou 450015, China
电磁轨道炮用一体化弹丸(Integration Launch Projectile, ILP)作为电磁发射武器的载体已经逐渐成熟,正在走向工程化应用阶段[1]。一体化弹丸主要由电枢、弹丸组件(弹体)和弹托[2]等组成。一体化弹丸在膛内发射运动时,电枢与通电导轨形成回路产生电磁力,推动一体化弹丸加速运动。弹托用于支撑和保护弹体弹丸组件的作用。一体化弹丸以很高的炮口初速度(大于2000 m/s)出膛后 [3],电枢、弹托与弹体在膛口处受到外力的作用而分开,弹丸飞向目标,完成打击目标的任务。一体化弹丸炮口弹体与弹托分离发生初始弹道阶段,该阶段的弹道特性的好坏直接影响弹体的整个外弹道。为保证一体化弹丸有较好的初始弹道参数,需要通过结构设计来保证弹体、弹托具有良好的分离特性。
一体化弹丸同传统的次口径位移稳定脱壳穿甲弹(APFSDS)具有结构的相似性,古刚将传统的脱壳动力学理论用于对一体化弹丸的脱壳机理分析。李鸿志等[4-7]通过风动试验方法,高速摄像捕捉了脱壳穿甲弹脱壳过程,研究了脱壳机理,并对弹托表压以及分离弹道进行了理论计算。黄振贵等[8-10]利用CFD仿真技术对脱壳弹进行了脱壳过程的仿真,并同试验高速摄影对比分析,结果验证了通过CFD仿真技术研究脱壳过程是有效的途径。Takeuchi等[11]利用动态层网格技术整体脱落式的尾翼稳定脱壳穿甲弹在坑道内发射和弹托分离过程进行了二维对称无粘性数值模拟。赵润祥等[12]依据风动试验的出来的试验数据,建立微分方程模型,对APSFDS弹托分离轨迹进行分析计算,得出的分离规律与相关文献基本吻合。张学伟等[13]研究了不同攻角情况对脱壳穿甲弹脱壳过程的影响,结果显示存在攻角不利于脱壳的进行。李湘平等[14]采用动网格技术建立弹托分离模型,并以尾翼稳定脱壳穿甲弹为例,探讨了不同马赫数下弹托、弹体气动参数在分离过程中的变化情况。
本文结合脱壳动力学和流体动力学原理,建立一体化弹丸弹托分离二维模型,采用动网格技术并耦合六自由度方程,对膛口弹体和弹托分离过程进行模拟仿真,获得弹体和弹托分离流场云图及相关的运动参数。本文认为分离过程中电枢形成的流场和机械干扰对弹体影响较小,仿真模型未将电枢考虑在内。
1 计算方法与数值模型 1.1 仿真思路与控制方程采用文献[15-16]控制方程和计算方法,弹体和弹托分离过程中需要仿真出不同时刻的流场分布以及在流场中求解弹体、弹托六自由度空间运动姿态,该过程主要涉及到流动方程组的解算、弹体和弹托的六自由度(6DOF)刚体运动解算(假设整个过程中无变形发生),同时由于弹体和弹托相对位置的变化而引起的网格更新。具体仿真思路为:分离初始时刻通过输入边界条件(初速、坐标位置)以及求解对象的质量转动惯量等参数求解非定常Euler方程,求解该时刻弹体和弹体周围流场的分布(包括压力场、速度场和密度场),然后通过积分求解处弹体和弹托的受力状态,并将该值作为6DOF运动方程组求解参数输入条件的一部分,求解下一时刻弹体、弹托的空间位置和运动学参数,之后由动网格技术中的弹簧光顺法和局部网格重构法根据新的边界值自动计算出弹体、弹托移动后网格节点位置。如此不断地重复上一循环直到弹体弹托各自的流场完全不在耦合认为分离结束。求解过程如图1所示。
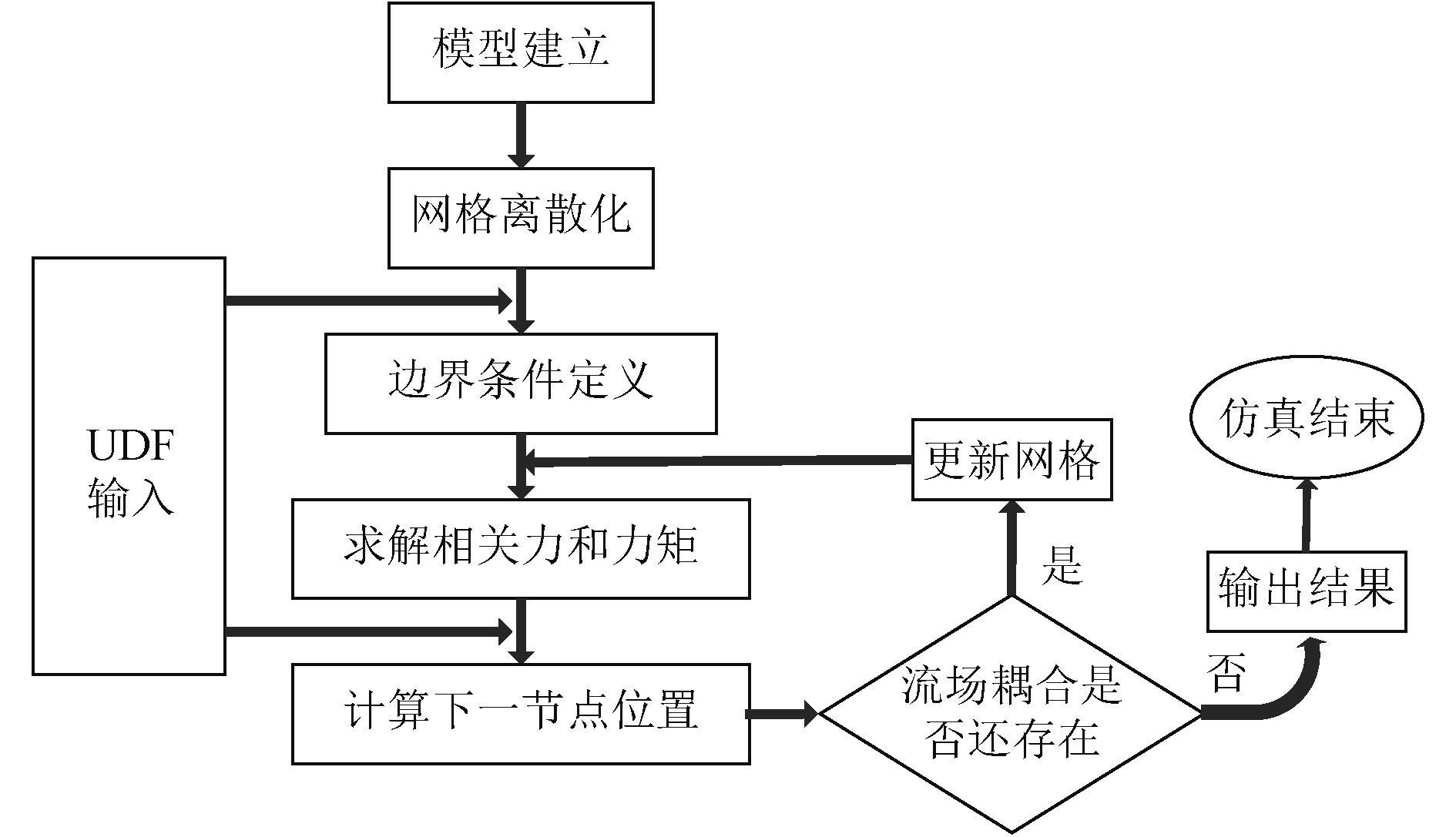
|
图 1 仿真流程示意图 Fig. 1 The process of simulation |
流体参数计算采用二维N-S粘性非定常流动控制方程[17]如下:
| $\frac{{\partial U}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial U}}{{\partial y}} = 0{\text{。}}$ | (1) |
式中:
式中:
| $E = \frac{p}{{(\gamma - 1)\rho }} + \frac{{{u^2} + {\upsilon ^2}}}{2}{\text{,}}$ | (2) |
压强由理想气体状态方程确定:
| $p = \rho RT{\text{。}}$ | (3) |
求解上述方程要得到唯一解需要添条件方程,可以通过雷诺应力模型(RSM),或者引入湍流模型(Turbulence Model),考虑到一体化弹丸在无限大的空气场中完成脱壳,可以认为该流动完全是湍流流动,同时忽略空气分子的粘性影响,考虑采用标准
| $\rho \frac{{{\rm{D}}k}}{{{\rm{D}}t}} = \frac{\partial }{{\partial {x_i}}}[(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {x_i}}}] + {G_k} + {G_b} - \rho \varepsilon - {Y_M}{\text{,}}$ | (4) |
| $\rho \frac{{{\rm{D}}\varepsilon }}{{{\rm{D}}t}} = \frac{\partial }{{\partial {x_i}}}[(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}})\frac{{\partial \varepsilon }}{{\partial {x_i}}}] + {C_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} + {C_{3\varepsilon }}{G_b}) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}{\text{。}}$ | (5) |
式中:
| $ \mu = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }{\text{。}} $ | (6) |
六自由度运动方程用于求解弹体和弹托刚体在运动过程中的相关变量参数,分为动力学和运动学方程,质心运动标量形式的动力学方程,由于该仿真仅涉及二维运动,故只考虑X,Y方向的运动以及绕心转动,计算仿真为下列方程组的一种特殊情况。
| $\begin{aligned} & {m\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = P\cos \alpha \cos \beta - X - mg\sin \theta }{\text{,}} \\ & mV\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = P(\sin \alpha \cos {\gamma _V} + \cos \alpha \sin \beta \sin {\gamma _V}){\text{ + }} \hfill \\ & \quad \quad \quad Y\cos {\gamma _V} - Z\sin {\gamma _V} - mg\cos \theta \hfill {\text{,}}\\ \\ & - mV\cos \frac{{{\rm{d}}{\psi _V}}}{{{\rm{d}}t}} = P(\sin \alpha \sin {\gamma _V} - \cos \alpha \sin \beta \cos {\gamma _V}) + \hfill\\ & \quad \quad \quad Y\sin {\gamma _V} + Z\cos {\gamma _V} {\text{;}} \end{aligned}$ | (7) |
绕心转动标量形式的动力学方程:
| $\begin{aligned} & {J_{{x_1}}}\frac{{{\rm{d}}{\omega _{{x_1}}}}}{{{\rm{d}}t}} + ({J_{{z_1}}} - {J_{{y_1}}}){\omega _{{z_1}}}{\omega _{{y_1}}} = {M_{{x_1}}}{\text{,}} \\ & {J_{{y_1}}}\frac{{{\rm{d}}{\omega _{{y_1}}}}}{{{\rm{d}}t}} + ({J_{{x_1}}} - {J_{{y_1}}}){\omega _{{x_1}}}{\omega _{{z_1}}} = {M_{{y_1}}} {\text{,}} \\ & {J_{{z_1}}}\frac{{{\rm{d}}{\omega _{{z_1}}}}}{{{\rm{d}}t}} + ({J_{{y_1}}} - {J_{{x_1}}}){\omega _{{y_1}}}{\omega _{{x_1}}} = {M_{{z_1}}} {\text{;}} \\ \end{aligned} $ | (8) |
质心运动的运动学方程:
| $\begin{aligned} & \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = V\cos \theta \cos {\psi _V} {\text{,}} \\ & \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = V\sin \theta {\text{,}} \\ & \frac{{{\rm{d}}z}}{{{\rm{d}}t}} = - V\cos \theta \sin {\psi _V}{\text{;}} \\ \end{aligned} $ | (9) |
刚体绕质心转动的运动学方程:
| $ \begin{aligned} & \frac{{{\rm{d}}\vartheta }}{{{\rm{d}}t}} = {\omega _{{y_1}}}\sin \gamma + {\omega _{{z_1}}}\cos \gamma {\text{,}} \\ & \frac{{{\rm{d}}\psi }}{{{\rm{d}}t}} = ({\omega _{{y_1}}}\cos \gamma - {\omega _{{z_1}}}\sin \gamma )/\cos \vartheta {\text{,}} \\ & \frac{{{\rm{d}}\gamma }}{{{\rm{d}}t}} = {\omega _{{x_1}}} - \tan \vartheta ({\omega _{{y_1}}}\cos \gamma - {\omega _{{z_1}}}\sin \gamma ){\text{。}} \\ \end{aligned} $ | (10) |
随着脱壳的进行,弹体和弹托的空间位置发生变化,计算域中上一时刻的网格出现拉伸或压缩的情况,若不更新重新划分网格,可能会出现畸变的情况,导致计算误差过大甚至计算发散而终止,因此为保证计算的顺利进行,需要在下一时刻计算前采用动网格技术更新网格,以适应新的空间位置。采用局部重构和弹簧光顺法更新网格,控制体积
| $\begin{split}\frac{{\rm{d}}}{{{\rm{d}}t}}&\int_V {\rho \phi {\rm{d}}V} + \int_{\partial V} {\rho \phi (u - {u_g}){\rm{d}}A = }\\ & \int_{\partial V} {\varGamma \nabla \phi {\rm{d}}A} + \int_V {{S_\phi }{\rm{d}}V}{\text{。}} \end{split}$ | (11) |
式中:
在分离过程中电枢一直处于弹体、弹托后方,速度衰减很快,随着时间的推移不断远离弹体,认为其对弹体飞行干扰可以忽略,并忽略内部卡销的飞散影响。为了网格离散化和计算方便,仅仅将弹体和弹作为整体的构成部分,并忽略四瓣弹托加工的差异性。经过简化后得到由四瓣托包裹弹丸的三维造型如图2所示。

|
图 2 简化后一体化弹丸模型 Fig. 2 Simplified model of ILP |
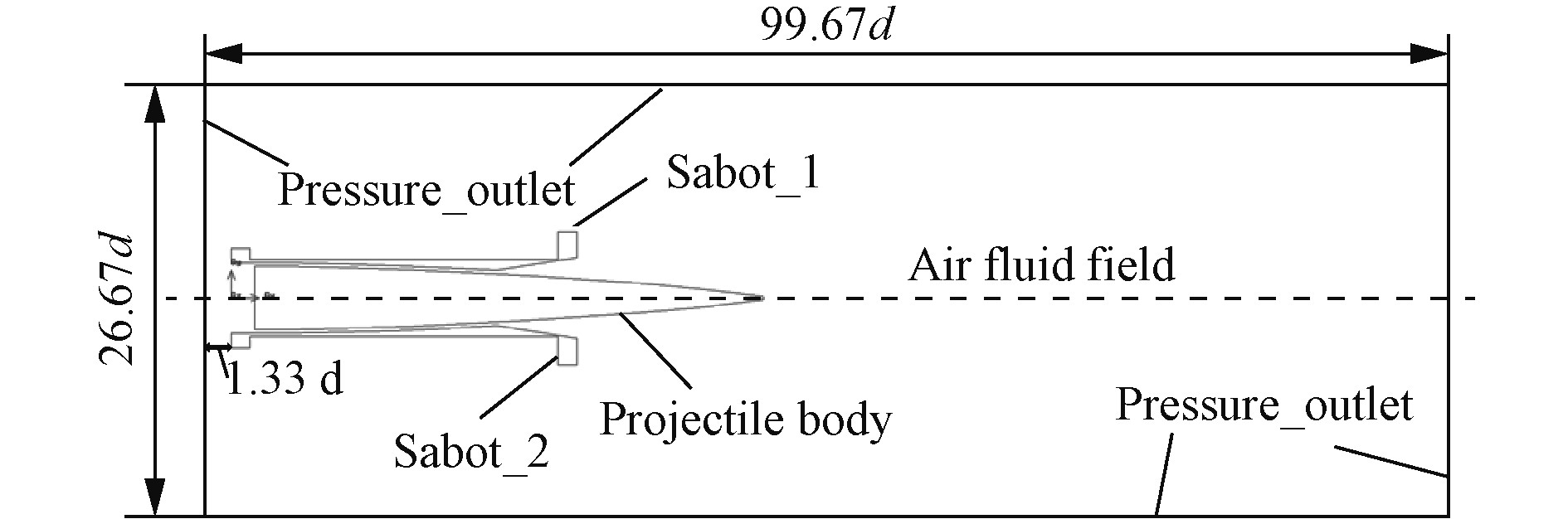
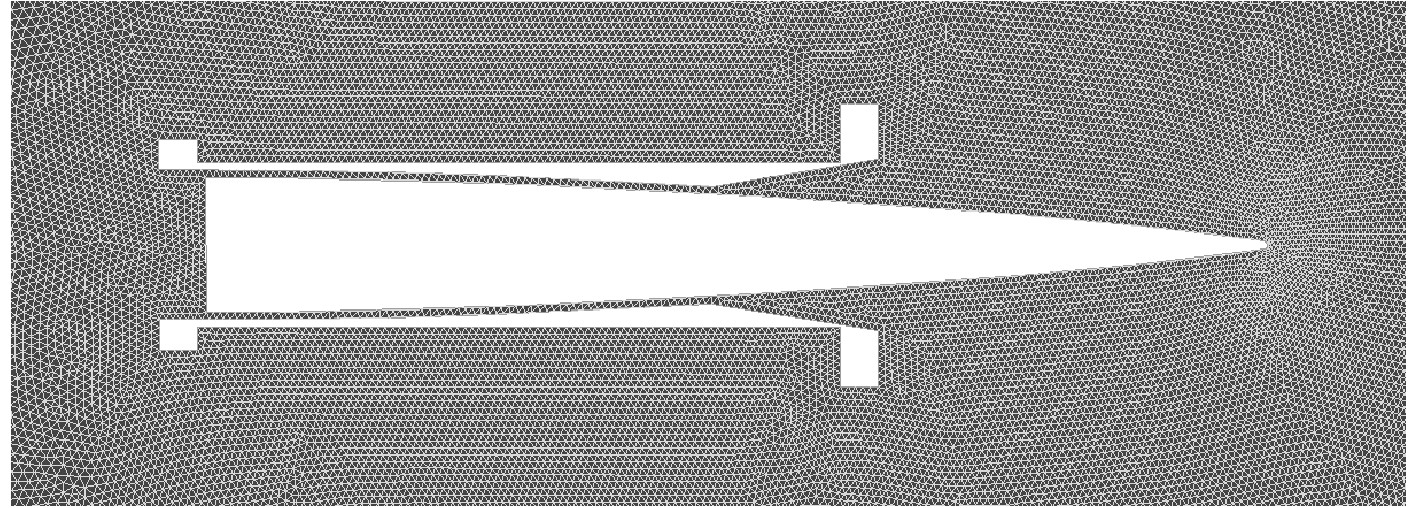
建立二维流场模型,通过多次试算,选取空间区域长度为99.67倍弹体直径、宽度为26.67倍弹体直径的矩形的区域内,一体化弹丸置于矩形区域中心轴上,尾部距离左端边界1.33倍弹体,如图3所示。弹托和弹体之间留出空隙以便于后期网格的划分建立和动网格区域更新。整个计算区域采用非结构化网格进行划分。其附近网格划分较密如图4所示,目的是减少仿真过程中气动压力、密度等参数的误差,
|
图 3 二维流场模型示意图 Fig. 3 Two-dimensional flow field model |
|
图 4 一体化弹丸附近网格分布图 Fig. 4 Grid distribution of ILP nearby |
计算区域采用动网格(弹簧光顺法和局部重构)来更新计算区域,通过写入UDF标定弹体、弹托的质量和转动惯量属性,选择6DOF来计算弹托弹体在脱壳过程中不同位置的运动参数,将坐标系位于一体化弹丸对称轴上的最尾端,并设定弹托和弹体的质心坐标、初速等参数如表1所示。图3中外围边界设置为压力出口(Pressure-out),为一个标准压值(101325 Pa),计算时将重力及地面相关空气参数(密度、粘性系数)考虑在内,在初始时刻,仅考虑射角为零的情况。考虑到初速很高,在计算初期,为避免计算不稳定的情况,时间上采用基于隐式向后时间差分形式对流动方程进行离散,空间上基于有限元体积法的方式离散,选用迎风格式中2阶隐式AUSM格式。
|
|
表 1 弹体、弹托初始位置及速度设定值 Tab.1 Initial position and velocity of projectile body and sabot |
图5显示了在整个过程中几个时刻弹体弹托分离流场从生成到耦合再到两者流场完全分离的过程,从这几个时刻研究整个分离的特性。
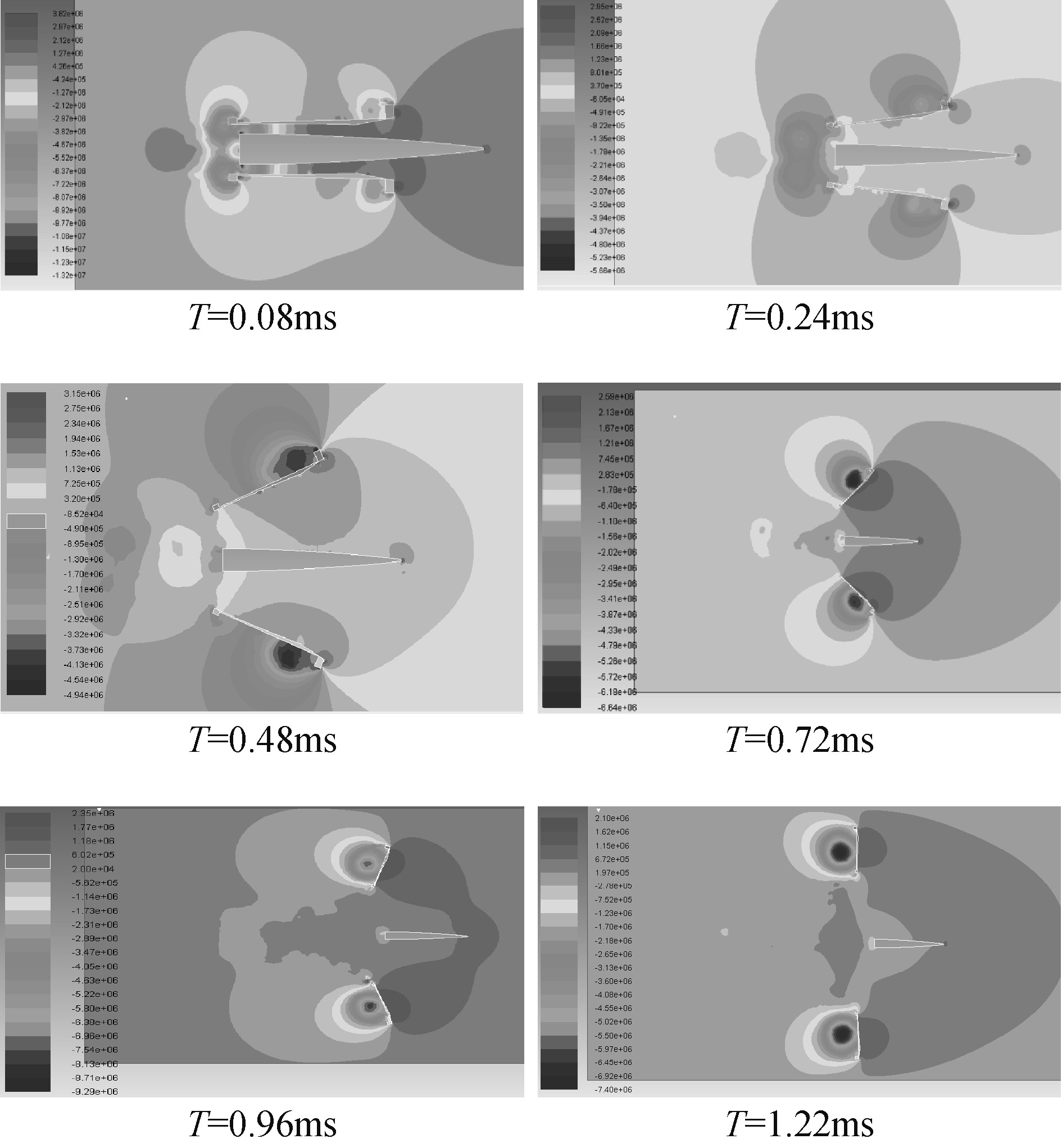
|
图 5 一体化弹丸脱壳时不同时刻x-y压力云图 Fig. 5 x-y stress nephogram ofILP, separation at different time |
在刚开始分离时刻(如T=0.05 ms时刻),气流相对于弹体和弹托高超速流动,在弹头部和弹托边缘迅速形成强激波并耦合,前腔体内高压迅速形成,但腔体内缝隙较小,无法满足高压气体顺畅流通,在整个空间内造成壅塞的现象,并沿着X反方向递减分布。弹托尾部气流流动速度为此时刻整个流场最大值,气流沿着弹体弹托之间的缝隙高速流动,形成有梯度的压力差,并在弹托尾部形成对称的涡流区。
在T=0.24 ms时刻弹体弹托远离加剧,内部泄压完成,对称的低压涡流区脱离弹托尾部后移,并蔓延至两弹托另一侧同尾部流场耦合形成一个拓展的低压流场区。弹托沿着轴线方向形成一定的倾角,其内表面开始逐渐成为迎风面。弹托内外表面分别出现高低压区,在分界处形成了脱体激波。弹托的压差形成了很强的翻转力矩,但相对于上下弹托的耦合流场相对于弹体而言是对称的,弹体可以沿着原先的弹道飞行。
T=0.48 ms时刻弹体弹托的耦合流场继续加强,弹体被整个流场完全包裹。对比整个过程发现,在此时间段,弹体受到弹托不对称性的干扰最大,最容易失稳。上下弹托前沿处收到的气动压力达到28个标准大气压值(见图6),之后该处值迅速下降。在T=0.72 ms弹体表面压力值由于激波区耦合作用的减弱而降低,同时弹托后沿区域低压区压力值达到最大,之后耦合流场逐渐分离,在T=0.96 ms时刻耦合基本结束。
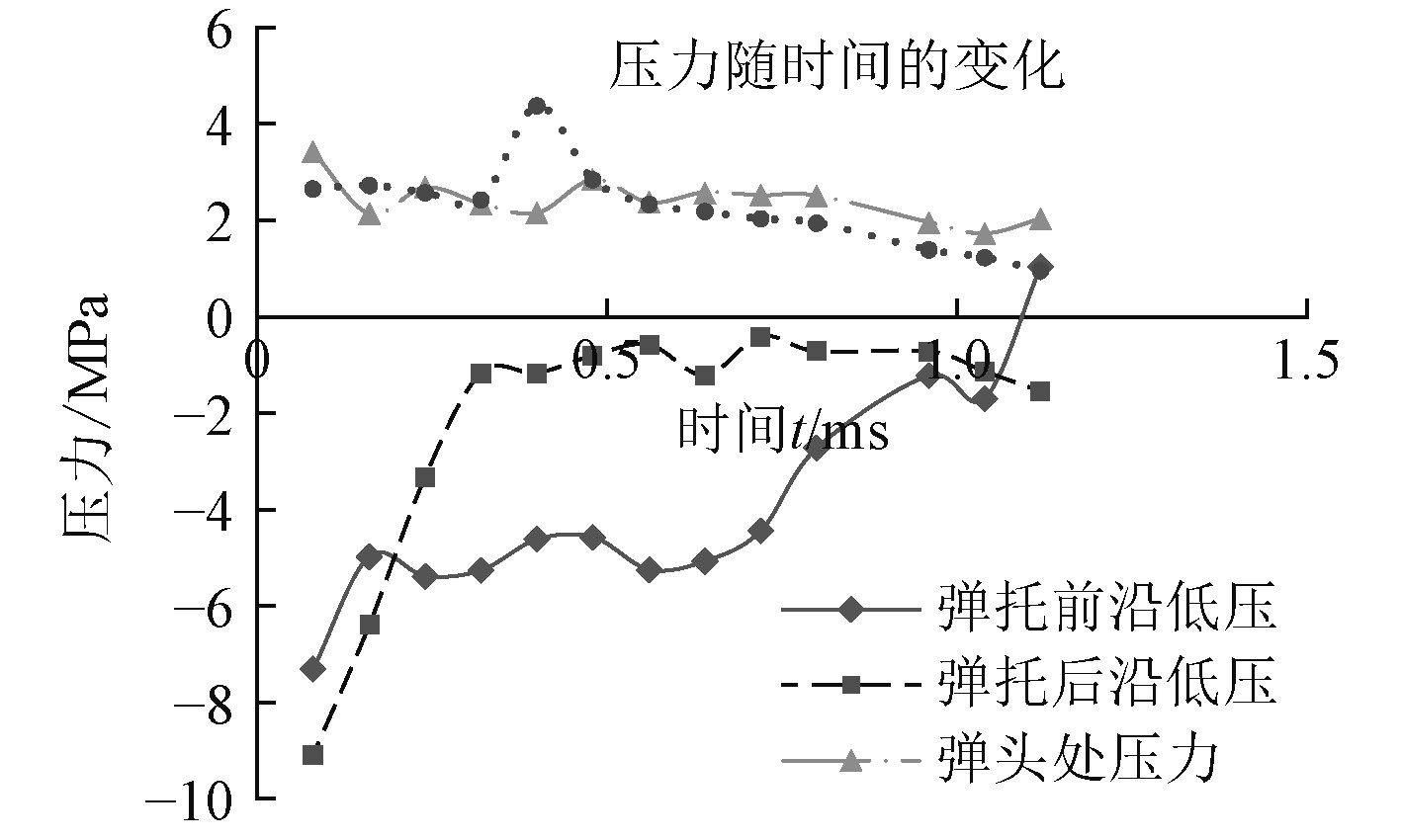
|
图 6 压力随时间的变化 Fig. 6 Changes of pressure with time |
在T=1.22 ms一体化弹丸脱壳基本结束,弹托和弹托各自流场完全分离。但弹托流场形成的弱余波反射在弹体的头部的上方和尾翼的下方,该弱余波对弹体而言形成了偏转力矩,对弹体飞行稳定性可能造成一定的影响。图6显示在分离结束后期,弹托前沿低压区达到了最大值。
2.2 弹托6DOF运动结果与分析为直观看到一体化弹丸动态分离过程,提取不同时刻弹托相对于弹体相对位置的速度矢量云图,如图7所示。可以看出,弹托前沿总是先于弹托后沿原理弹体,并随着时间的推移该原理越来明显,弹托倾角加大,说明在分离过程中,气动阻力为主要的脱壳动力来源,属于风阻型脱壳[18]。
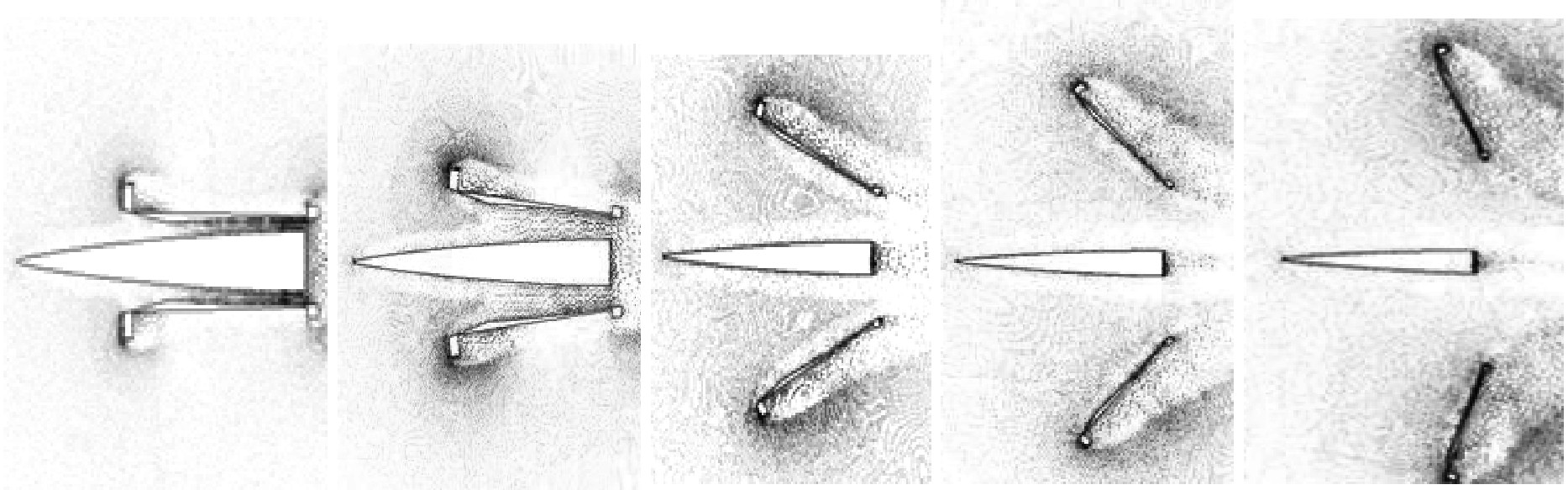
|
图 7 试验同模拟仿真弹托不同时刻分离状态对比 Fig. 7 Comparisom between test and simulation of ILP,separation state at different time |
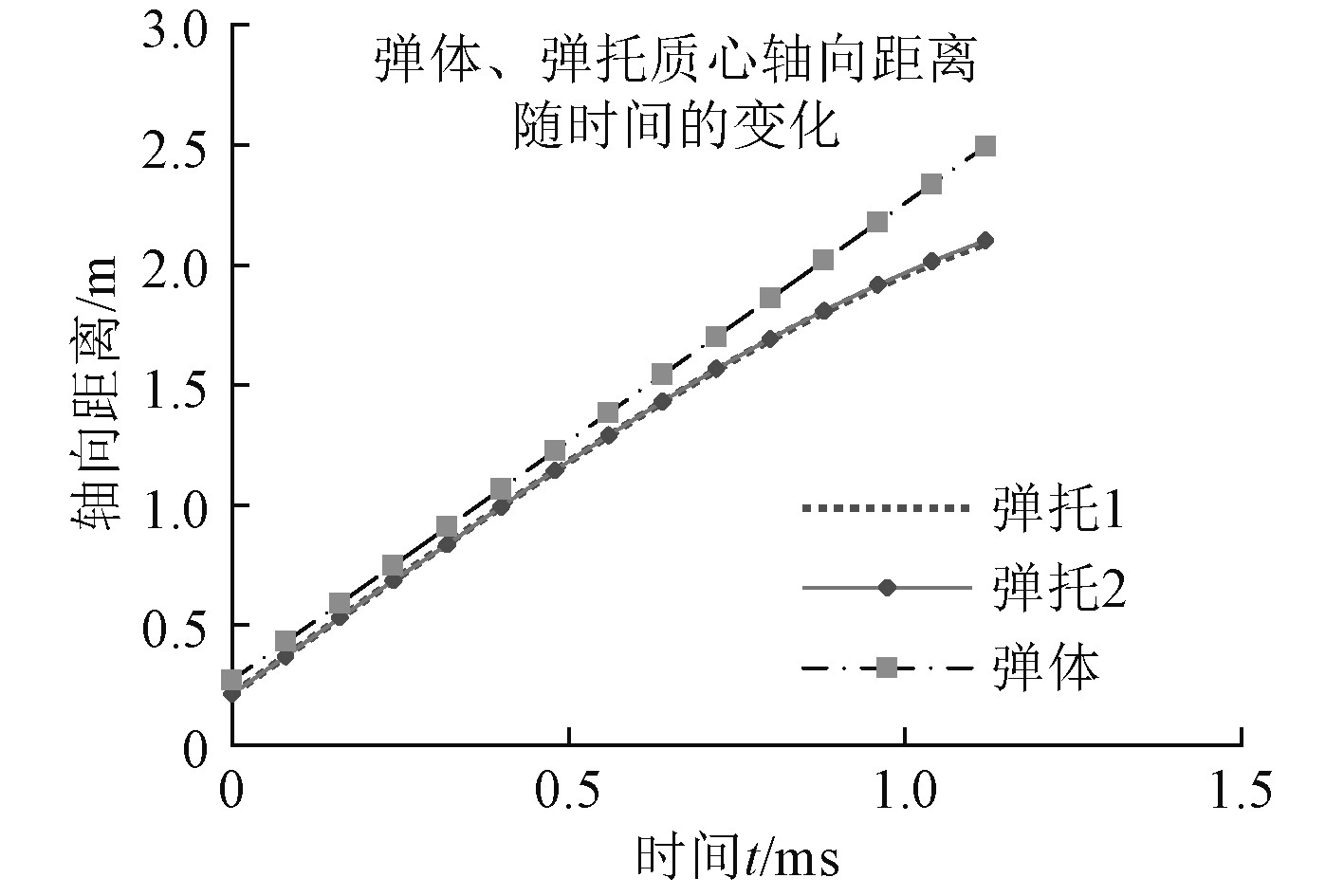
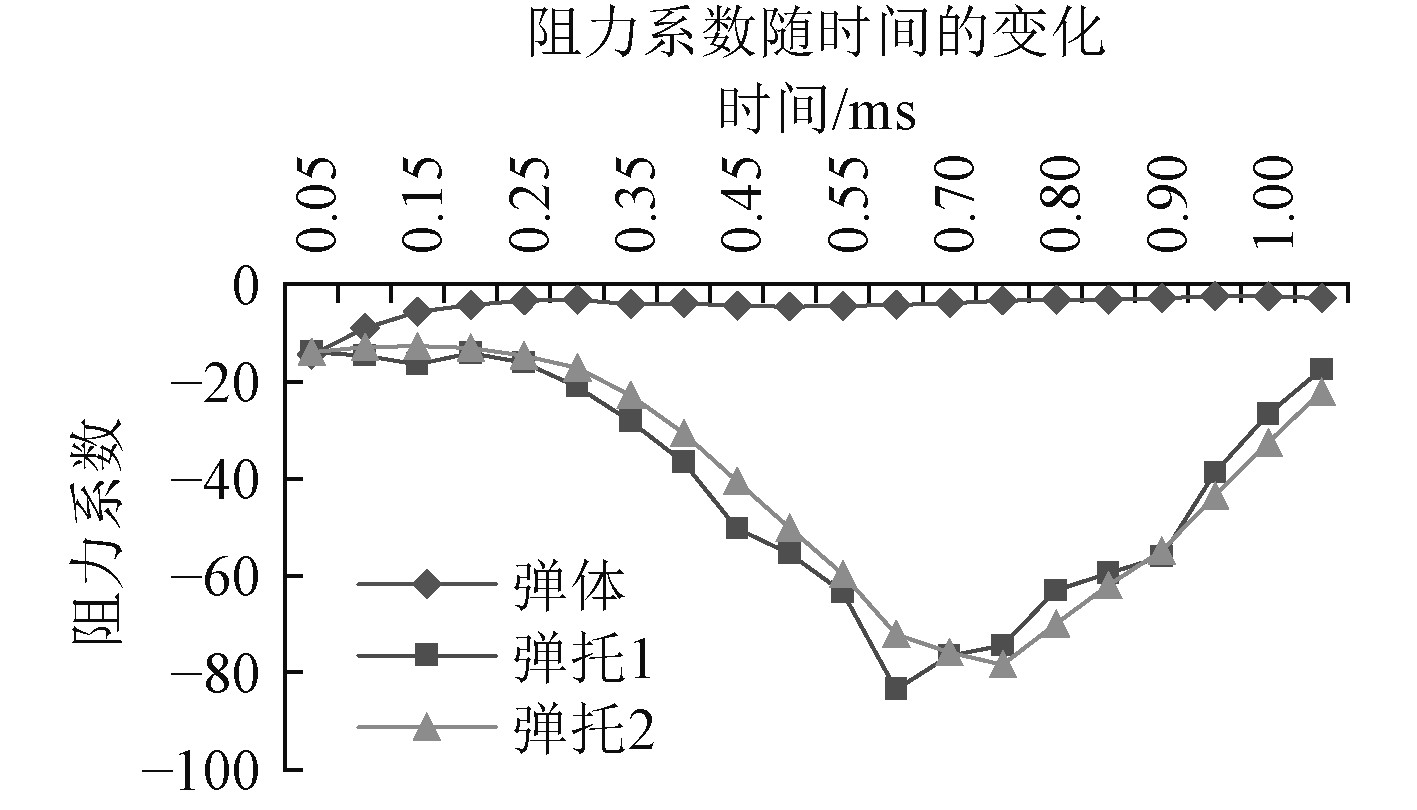
以弹托分离时,在轴向和径向距离为重点分析弹托在重力和空气动力的作用下刚体的运动情况。图8显示上下弹托随着时间的推移逐渐加速向后远离弹体,说明在分离过程中弹托飞行不仅滞后弹体,同时加速同弹体脱离。图9中显示两弹托的阻力系数总体上先增大后减小,这是因为弹托在做俯仰运动的过程中,一方面迎风面增大,风阻加强,同时受到耦合流场的波阻干扰,阻力系数增大,在分离后期,虽然迎风面继续增大,风阻加强,但耦合流场的波阻消失,使得阻力系数减小。说明耦合流场的波阻对弹托的分离状态起到主要作用。弹体的阻力系数在整个分离过程中都保持基本不变状态,说明弹体受到耦合流场的影响较小。
|
图 8 弹体、弹托质心轴向距离随时间变化 Fig. 8 Changes of projectile body and sabot,barycenter at axial direction with time |
|
图 9 阻力系数随时间的变化 Fig. 9 Changes of drag coefficient with time |
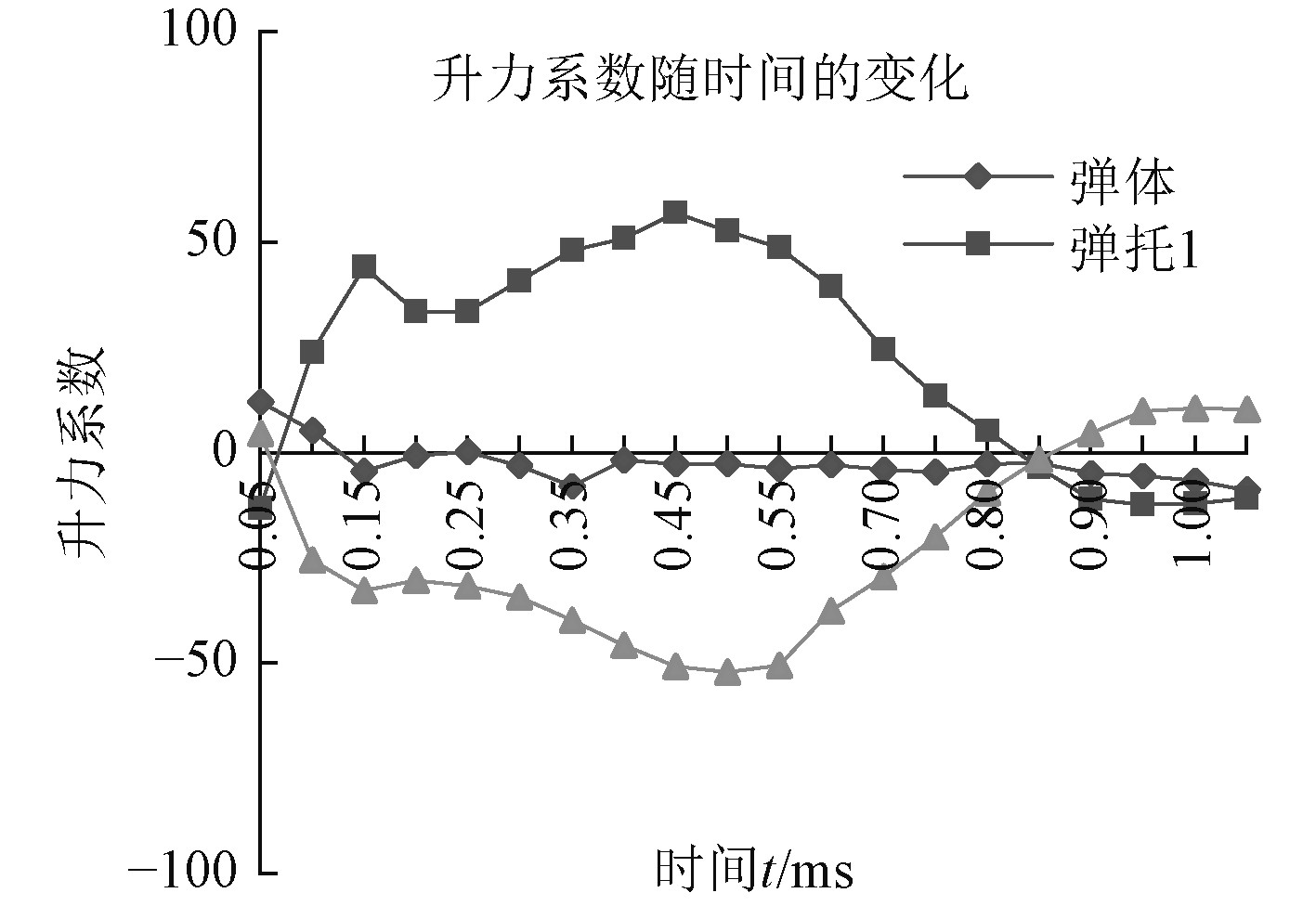
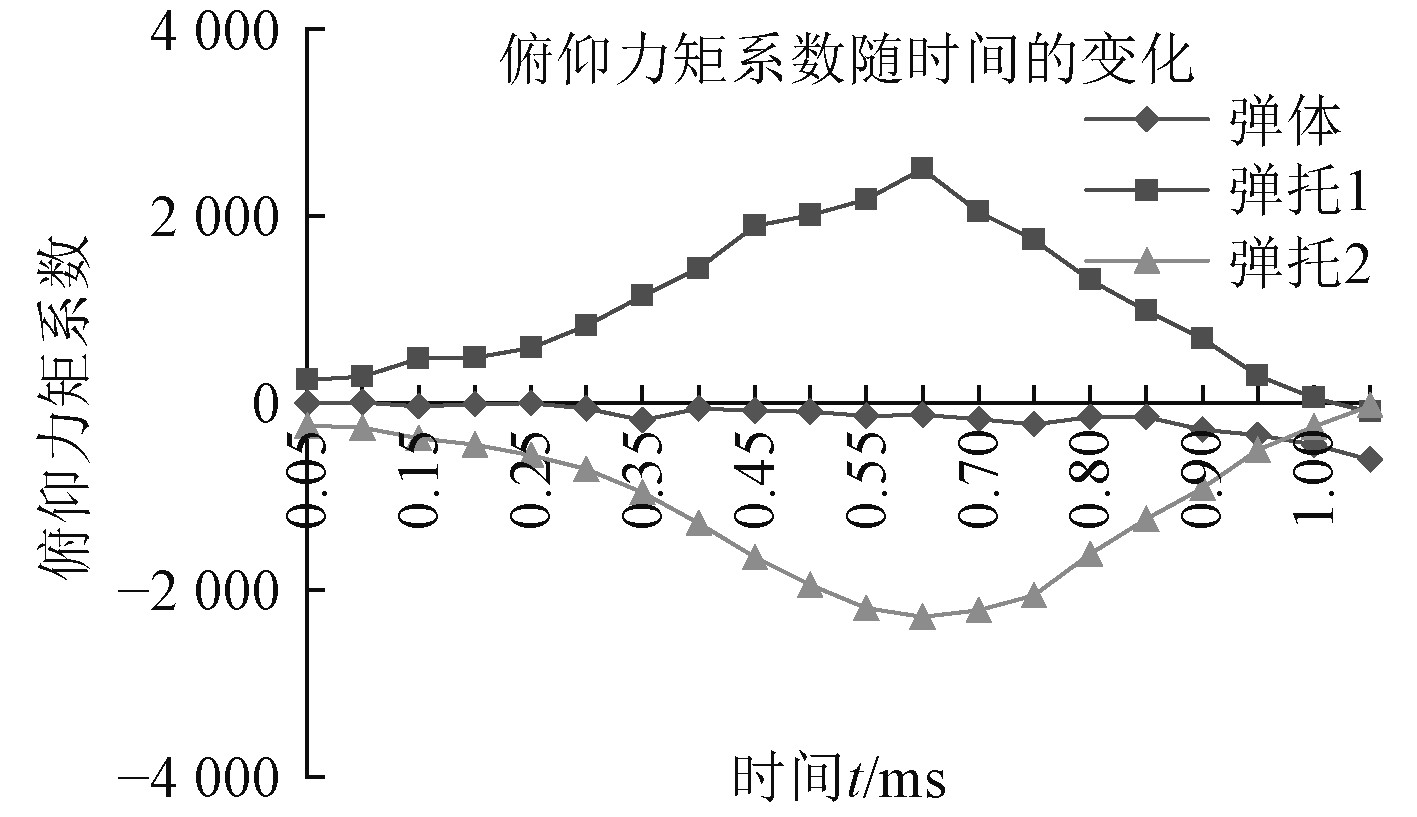
图10 显示弹托的升力系数随着时间的推移处于不断起伏的状态,主要是由于在分离过程中受到复杂的空气动力作用的原因,但整体上呈现先增大之后稳定,最后急剧下降的趋势。该变化规律同流场的生成、耦合、分离相互对应。图11显示弹托的俯仰力矩变化规律同升力系数的变化类似,但俯仰力矩系数的最大值出现时刻滞后于升力系数出现的最大时刻,说明弹托后期的速度急剧减小,阻力对俯仰力矩的贡献比重加大。弹体分离过程中,弹体由于流场的对称性基本维持稳定不变的状态,但在终了阶段升力系数和俯仰力矩系数均有增大的趋势,说明弹体有开始偏离原来的轨迹趋势,弹道性能变差,该参数的变化同图5T=1.22 ms时刻的云图状态相对应。
|
图 10 升力系数随时间的变化 Fig. 10 Changes of lift coefficient with time |
|
图 11 俯仰力矩系数随时间的变化 Fig. 11 Changes of pitching moment coefficient with time |
本文基于Navier-Stokes控制方程和6DOF外弹道控制方程,采动网格技术(光顺法和局部重构法),对一体化弹丸出膛后弹体、弹托分离流场进行数值研究,数值模拟结果直观反映出弹托、弹丸流场耦合作用下连续分离的过程,并得到相关的气动参数,仿真结果同相应的试验结果基本一致。
1)研究结果表明,一体化弹的分离过程属于风阻型脱壳,在分离过程中弹体、弹托分离流场呈现激波生成、耦合和分离的复杂过程。耦合流场的波阻对弹托分离起到最主要的作用,弹体由于流场的对称性受耦合流场的影响较小。
2)分离终了时期,弹托分离流场的反射余波使得弹体前后方分别产生了高低压区,该区域产生的不平衡力(矩)有可能使弹体出现失稳的情况,需要进一步研究。
| [1] |
杜传通, 雷彬, 金文龙, 等. 电磁轨道炮电枢技术研究进展[J]. 火炮发射与控制学报, 2017, 38(2): 94-99. |
| [2] |
古刚, 向阳. 国际电磁发射技术研究现状[J]. 舰船科学技术, 2007, 29(1): 156-158. GU Gang, XIANG Yang. The overview of the international electromagnetic launch technology research[J]. Ship Science and Technology, 2007, 29(1): 156-158. |
| [3] |
ZUO Peng , LI Jun , SONG Xiangqian, Jetal, Characteristics of current distribution in rails and armature with different section sharp rails [J], IEEE Transactions on Plasma Science, 2013 41(5): 1488-1492
|
| [4] |
李鸿志, 崔东明, 何正求, 等. 尾翼脱壳穿甲弹近炮口区飞行姿态的显示[J]. 工学报, 1992, 13(1): 66-69. LI Hong zhi, CUI Dong ming, HE Zheng qiu, et al. Visualization of flight attitude of a fin- stabilized sabot discard projectile near the muzzle[J]. Acta Armamentarii, 1992, 13(1): 66-69. |
| [5] |
崔东明, 何正求, 李鸿志. 高速脱壳穿甲弹的中间弹道研究[J]. 华东工学院学报, 1991, 60(4): 89-93. CUI Dong- ming, HE Zheng-qiu, LI Hong- zhi. Intermediate ballistic research of high speed armour- piercing sabot discard projectile[J]. Journal of East China Institute of Technology, 1991, 60(4): 89-93. |
| [6] |
SCHMIDT E M, SHEAR D D. Aerodynamic interference during sabot discard[J]. Journal of Spacecraft and Rockets, 1978, 15(3): 162-167. DOI:10.2514/3.57301 |
| [7] |
SIEGELMAN D, CRIMI P, SCHMIDT E. Projectile/sabot discard aero-dynamics[C]∥6th Atmospheric Flight Mechanics Conference. Danvers, Massachusetts, US: AIAA, 1980.
|
| [8] |
黄振贵, 陈志华, 郭玉洁. 尾翼稳定脱壳穿甲弹脱壳动力学过程的三维数值模拟[J]. 兵工学报, 2014, 35(1): 10-17. HUANG Zhen-gui, CHEN Zhi-hua, GUO Yu-jie. Numerical Simulation on three-dimensional dynamic process of sabot discarding of APFSDS[J]. Journal of China Ordnance, 2014, 35(1): 10-17. DOI:10.3969/j.issn.1673-6524.2014.01.003 |
| [9] |
GUILLOT M J, REINECKE W G. A numerical and experimental investigation of sabot separation dynamics[C]∥AIAA 34th AerospceSciences Meeting and Exhibit.Reno, NV: AIAA, 1996: 455
|
| [10] |
武频, 赵润祥, 郭锡福, 等. APFSDS弹托分离干扰三维流场数值模拟[J]. 空气动力学学报, 2005, 23(1): 1-4. WU Pin, ZHAO Run-xiang, GUO Xi-fu. Two dimension numerical simulation of APFSDS sabots discarding[J]. Journal of Projectiles, 2005, 23(1): 1-4. DOI:10.3969/j.issn.0258-1825.2005.01.001 |
| [11] |
TAKEUCHI F, MATSUO A.Numerical investigation of sabot separation process in a ballistic range using moving overlapped grid method[C]∥51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Grapevine, Texas, US: AIAA, 2013
|
| [12] |
赵润祥, 武频, 王福华, 等. 弹托风洞测力试验及其分离规律计算[J]. 南京理工大学学报: 自然科学版, 2001, 25(6): 579-583. ZHAO Run- xiang, WU Pin, WANG Fu- hua etal. Force measurement experiment of sabots with wind tunnel and the calculation of its discarding rules[J]. Journal of Nanjing University of Science and Technology: Natural Science, 2001, 25(6): 579-583. |
| [13] |
张学伟, 李强, 高斌, 等. 不同攻角对尾翼稳定脱壳穿甲弹脱壳过程影响分析[J]. 弹箭与制导学报, 2016, 36(3): 28-34. ZHANG Xuewei, LI Qiang, GAO Bing. Analysis on influence of different AOA on discarding process for APFSDS[J]. Journal of Projectiles, Rocket, Missiles and Guidance, 2016, 36(3): 28-34. |
| [14] |
李湘平, 鲁军勇, 冯军红, 等. 采用动网格技术的弹托分离仿真模型[J]. 国防科学技术大学学报, 2018, 40(5): 9-13. LI Xiangping, LU Junyong, FENG Junhong, etal. Simulation model for sabot discard using dynamic mesh technique[J]. Journal of National University of Deffnse Technology, 2018, 40(5): 9-13. |
| [15] |
SNYDER DO, KOUTSAVDIS E K, ANTTONEN JSR.Transonic store separation using unstructured CFD with dynamic meshing[C]∥33rd AIAA Fluid Dynamics Conference and Exhibit. Orlando, Florida: AIAA, 2003: 2013-3919
|
| [16] |
PANAGIOTOPOULOS E E, KYPARISSIS SD. CFD transonic store separation trajectory predictions with comparison to wind tunnel investigations[J]. International Journal of Engineering, 2010, 3(6): 538-553. |
| [17] |
Jhon D. ANDERSON(著), 吴颂, 刘赵淼(译). 计算流体力学基础及其应用[M]. 北京: 机械工业出版社, 2000.
|
| [18] |
杨启仁, 徐直军. 脱壳动力学[M]. 北京: 国防工业出版社.1996
|
 2020, Vol. 42
2020, Vol. 42
