0 引　言

波达方向^[1]（Direction Of Arrival，DOA）估计被广泛应用于各个领域，如无线电通信、雷达、声呐超分辨、导航、地震探测和医学等。而水下目标DOA估计^[2]也有着极其重要的作用，如军事侦察中通过被动声呐系统，利用跟踪目标的波达方向，捕获诸如舰船和潜艇的辐射噪声信息，从而获得目标信息。

目前，空间谱估计算法的研究大多数基于均匀线性阵列上进行。最早提出的DOA估计算法是基于阵列的，即常规波束形成（Conventional Beamforming，CBF）法^[3]，但其方位估计精度较低，且在一个波束宽度内无法分辨不同的空间信号。子空间分解类算法中最具代表性的是多重信号分类（Multiple Signal Classification，MUSIC）算法^{[4, 5]}，由于阵列接收数据的信号子空间与噪声子空间相互正交，从而能构造空间谱函数，实现了超分辨DOA估计。但是这类算法要实现DOA估计，需要利用空间平滑等方法，严重地损失了阵列孔径，算法的估计精度极大地降低，持续采样耗时也较长。子空间拟合算法较典型的是极大似然^[6-7]（Maximum Likelihood，ML）算法，这种算法不会损失阵列孔径，由于这类算法本质上是寻找非线性函数最优解的过程，因而需要进行多维搜索，导致巨大的运算量及较长的估计时间。

在上述传统的基于均匀线阵的DOA估计方法中，要达到扩展阵列孔径、提高算法的空间测角分辨力的目的，只能增加阵元数，但是这会导致工程成本的急剧增加。此外，在实际环境中要实现每个相邻阵元之间的间隔完全相等，具有一定的难度。而非均匀线阵^{[8 – 9]}（Non-uniform Linear Array，NLA）能充分扩展阵列孔径，但其并不增加阵元数。在进行水声传感器排布时，它的结构特点使得排布方式具有很大的灵活性。因此研究非均匀水声阵列及其处理方法具有极大的实际意义。

压缩感知^[10-12]（Compressive Sensing，CS）理论是信息论和信号处理领域的一项新兴技术。与传统奈圭斯特采样定理相比较，它的优点在于只要信号是可压缩的或在某个变换域是稀疏的，那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上。再通过求解一个优化问题，然后以高概率从这些少量的投影中重构出原始信号。这种方法的主要优势在于阵元分布形式、接收信号的相干性都不会对DOA估计性能造成影响，而且其有比较低的快拍数要求，从而较好地重构信号。

现阶段，压缩感知DOA估计的研究大都以均匀线阵为基础进行。最早将稀疏性的思想与阵列DOA估计相结合的是Malioutov等^[13]，所提出的阵列模型是阵元数目一定、阵元间隔相等的一个均匀线阵，然后通过对空间角度的离散化建立稀疏重构模型；A. R. Kulaib等^[14]提出均匀圆阵DOA估计的方法，将圆阵转换为虚拟均匀线阵，由此得到的虚拟线阵进行压缩感知DOA估计的方法与普通的均匀线阵一样，但是这种方法计算量明显增加；此后又有学者提出利用方型阵来实现DOA估计，但是方型阵结构复杂，需要硬件资源较多；Jian-Feng Gu等^[15]提出由2个均匀线阵组成的L型阵列进行二维DOA估计，其具有较高的估计精度，但计算复杂度较大。为了解决阵元数对阵列孔径的限制这一问题，众多学者又提出了非均匀线阵的压缩感知DOA估计方法。Piya pal等^[16]提出一种基于累积量的非均匀线阵波达方向估计方法，但其计算量较大；文献[17]提出一种快速求根的MUSIC方法，根据小角度范围内的导向矢量有着可以利用低阶多项式很好近似的特性，该方法将非均匀线阵DOA估计问题转化为组低阶实多项式求根问题。虽然在工程应用中适用，但还是存在高计算量的问题。

为了提高DOA测向精度，均匀阵列需要增加阵元数目，从而扩大阵列孔径，但其增加了工程成本；传统非均匀阵列DOA估计则存在高计算量的问题。针对上述问题，本文提出了一种特殊的非均匀水声阵列稀疏重构方法，通过改进非均匀阵列的形成方式，以2个均匀线性子阵组成一个非均匀线阵，再利用压缩感知稀疏重构的方法进行方向波达角估计。在相同条件下，该方法可以利用更少的阵元识别更多的目标；在低先验知识、低信噪比条件下，能够提高水声阵列的测向精度。

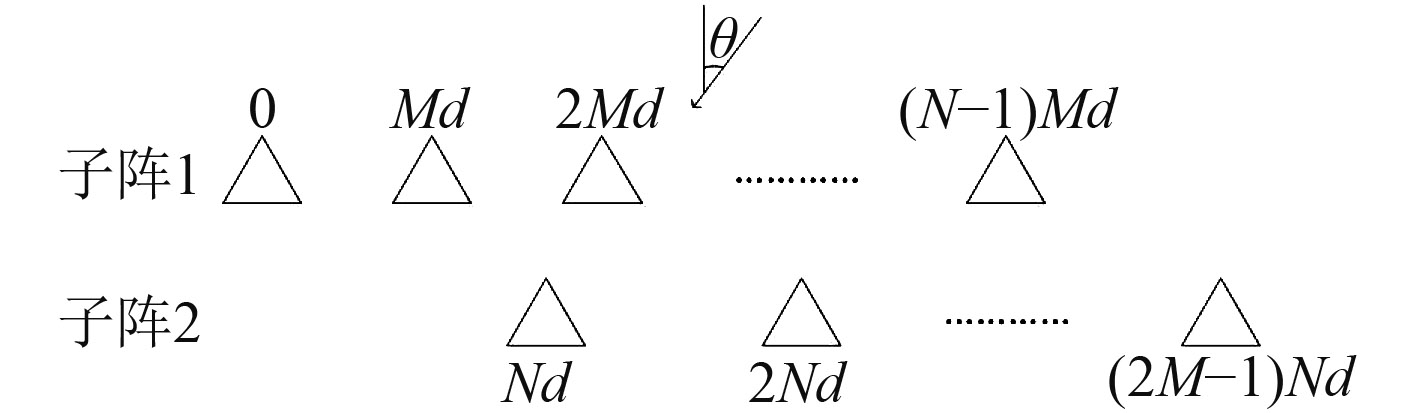
1 阵列信号模型

图1是2个位于同一水平线上的均匀子线阵，这2个子线阵互相穿插形成一个非均匀线阵^{[18 – 20]}，如图2所示。其中子阵1的阵元个数为N，阵元间距为Md₀，这N个阵元的位置集合为 $\{ Mnd,0 \leqslant n \leqslant N - 1\} $ ；子阵2的阵元个数为2M–1，阵元间距为Nd₀，这2M–1个阵元的位置集合为 $\{ Nmd,0 \leqslant m \leqslant 2M - 1\} $ 。因为这2个阵列在0位置共用一个阵元，所以得到的非均匀线阵为2M+N–1个阵元。M和N是满足互质关系的2个整数，且M<N。单位间隔d₀为入射信号的半波长。

假设有K个远场信号 ${s_1}\left( t \right),{s_2}\left( t \right),\; \cdots ,{s_K}\left( t \right)$ ，分别以方位角 ${\theta _1},{\theta _2},\; \cdots ,{\theta _K}$ 入射到非均匀阵列，且满足 ${{ - }}{90^\circ } < {\theta _k} < {90^\circ }$ ，1<k<K。t时刻阵列接收的信号可以表示为

$x\left( t \right) = \sum\limits_{k = 1}^K {a\left( {{\theta _k}} \right)} {s_k}\left( t \right) + n\left( t \right) = {{A}}\left( \theta \right)s\left( t \right) + n\left( t \right)\text{。}$

(1)

其中， $x\left( t \right) = {[{x_1}\left( t \right),{x_2}\left( t \right),\; \cdots ,{x_{N + 2M - 1}}\left( t \right)]^{ T}}$ 表示所有阵元在采样时刻t的输出信号； ${[ \bullet ]^{ T}}$ 表示转置运算； ${{A}} = [a\left( {{\theta _1}} \right),\; \cdots ,a\left( {{\theta _K}} \right)]$ 表示所有入射信号DOA对应的阵列流型矩阵； $a\left( \theta \right) = {[{e^{ - j{d_1}2\pi \sin \theta /\lambda }},\; \cdots ,{e^{ - j{d_{N + 2M - 1}}2\pi \sin \theta /\lambda }}]^{ T}}$ 表示θ对应的导向矢量；λ为入射信号的波长；阵元位置集合为 $S = \{ Mn{d_0},0 \leqslant n \leqslant N - 1\} \cup \{ Nm{d_0},0 \leqslant m \leqslant 2M - 1\} $ ；假设 $D = {[{d_1},\; \cdots ,{d_{N + 2M - 1}}]^{ T}}$ ， $n\left( t \right) = [{n_1}\left( t \right),{n_2}\left( t \right),\; \cdots , $ $ {n_{N + 2M - 1}}\left( t \right)]^{ T} $ 表示均值为0，方差为σ²的加性高斯白噪声向量。 $s\left( t \right) = {[{s_1}\left( t \right)\;{s_2}\left( t \right)\; \cdots \;{s_K}\left( t \right)]^{ T}}$ 为入射角为θ_k的阵列流型矢量。

2 稀疏重构模型

由压缩感知理论和式（1）可得，稀疏表示的水声目标DOA估计问题可以表示为：

$y\left( t \right) = \varPhi x\left( t \right) = \varPhi {{A}}\left( \theta \right)s\left( t \right) + \varPhi n\left( t \right)\text{，}$

(2)

式中：Φ为M×N的高斯随机测量矩阵； $y\left( t \right)$ 为阵列的稀疏表示。从式（2）可以看出，阵列输出 $y\left( t \right)$ 是一个M×1矢量，由于M<N，所以 $y\left( t \right)$ 比传统阵列输出的值要小的多，从而减少了阵列输出的数据量。这也就降低了对阵列硬件的要求和减小了数据处理的计算量。

为了保证估计的精度，需要多次采样快拍，那么式（2）可以重写为

$Y = \varPhi X = \varPhi {{A}}S + N,$

(3)

式中： $Y \!=\! [y\left( 1 \right),y\left( 2 \right),\; \cdots ,y\left( L \right)]$ ； $S \!=\! [s\left( 1 \right),s\left( 2 \right),\; \cdots ,s\left( L \right)]$ ； $N = [n\left( 1 \right),n\left( 2 \right),\; \cdots ,n\left( L \right)]$ ，L为采样快拍数。对于式（3）多次测量问题的解优化过程如（4）所示：

$\min {\left\| S \right\|_{{l_1}}},\;{ s.t}\;{\left\| {Y - \Phi AS} \right\|_{{l_2}}} \leqslant \varepsilon \text{。}$

(4)

3 特殊的非均匀水声阵列稀疏重构方法 3.1 特殊的非均匀阵列分析

根据以上信号模型及假设条件，非均匀线阵的阵元间距可以大于信号半波长，但当阵元位置设置不良时将会导致栅瓣效应，使DOA估计出现模糊。本文的非均匀阵列在进行水声信号DOA估计时，对水下空域目标信号采样，把阵列的输出信号转换成虚拟阵列接收矢量，选择无冗余的虚拟接收信号。

由阵元位置集合 $ S = \{ Mn{d_0},0 \leqslant n \leqslant N - 1\} \cup \{ Nm{d_0},0 \leqslant $ $ m \leqslant 2M - 1\} $ 计算虚拟阵元位置集合。首先，从非均匀线阵的第1个阵元开始，如果在单位间隔d₀的整数倍处存在阵元，则记录阵元信息为1，否则为0，由此将非均匀线阵位置信息转换成实际阵列的位置矢量v。对实际阵列的位置矢量进行 $v*{v^ - }$ 的数学变换，得到虚拟阵元集合w。对虚拟阵元进行左右平移后互与运算，然后根据虚拟阵元位置信息将阵列输出信号进行协方差计算，从而得到虚拟阵元接收数据y_r，如式（5）所示：

$\begin{split}& {y_r} = E[{x_p}\left( t \right){x_q}^H\left( t \right)] = \sum\limits_{k = 1}^K {\sigma _k^2} {a_p}\left( {{\theta _k}} \right){a_p}^H\left( {{\theta _k}} \right) +\\& \sigma _n^2I = {{A}}P{{{A}}^{ H}} + \sigma _n^2I\text{。}\end{split}$

(5)

其中：p，q由虚拟阵元位置信息经过数学运算后得到。

根据实际应用，对y_r进一步改进，得

$\widehat {{y_r}} = \frac{1}{L}\sum\limits_{l = 1}^L {{x_p}} \left( t \right){x_q}\left( t \right)\text{。}$

(6)

3.2 特殊的非均匀阵列稀疏重构方法

将式（6）进行矢量化得

$z = vec\left( {\widehat y} \right) = \widetilde A{ b} + \sigma _n^2\widetilde i\text{。}$

(7)

其中，b表示水声信号空域稀疏向量。

本文以压缩感知理论为基础，提出用稀疏重构的方法求解式（7）。式（7）转换为约束最小值问题：

$\widehat b = \arg \min {\left\| b \right\|_0}\text{，}\;\;{{subject}}\;{{to}}\;\;{\left\| {z - \widetilde Ab - \sigma _n^2\widetilde i} \right\|_2} < \varepsilon \text{。}$

(8)

其中，ε为特殊规定的边界值。定义 $B = \left[ {\widetilde A,\widetilde i} \right]$ ， $r = {\left[ {{b^{ T}} \cdot \sigma _n^2} \right]^{ T}} = \left[ {\sigma _1^2,\; \cdots ,\sigma _D^2,\sigma _n^2} \right]$ ，则式（8）变换为

$\widehat r = \arg \;\mathop {\min }\limits_r {\left\| b \right\|_0}\text{，}\;\;{ subject \;to}\;\;{\left\| {z - Br} \right\|_2} < \varepsilon \text{。}$

(9)

根据入射信号源具有的空域稀疏特性，本文按如下方法构造B：将信号入射空域进行离散采样，可将整个水下观测空域 $\left[ { - {{90}^ \circ },{{90}^ \circ }} \right]$ 离散为Q个角度， $\theta = [{\theta _1},{\theta _2},\; \cdots ,{\theta _Q}]$ ， $B\left( \theta \right)$ 如式（10）所示：

$B\left( \theta \right) = \left[ {a\left( {{\theta _1}} \right),a\left( {{\theta _2}} \right),\; \cdots ,a\left( {{\theta _Q}} \right)} \right]\text{。}$

(10)

其中： $a\left( {{\theta _Q}} \right) = {\left[ {{e^{j{w_1}2\pi d\sin \theta /\lambda }},\; \cdots ,{e^{j{w_n}2\pi d\sin \theta /\lambda }}} \right]^{ T}}$ ，n为虚拟阵列w的长度。

求解式（9）属于凸优化问题，可以利用CVX工具箱解决。CVX可以使上述规划问题转化为特殊的形式，使得上述复杂的规划问题得到简化，从而可以利用凸优化工具箱有效解决问题。

根据重构得到的信号矩阵b中，不为0元素所在向量的位置与水域空间方位角度的对应关系，可以估计出每个信号的角度。

4 仿真结果与分析

在上述理论基础上，信号为远场窄带信号时，利用Matlab仿真。

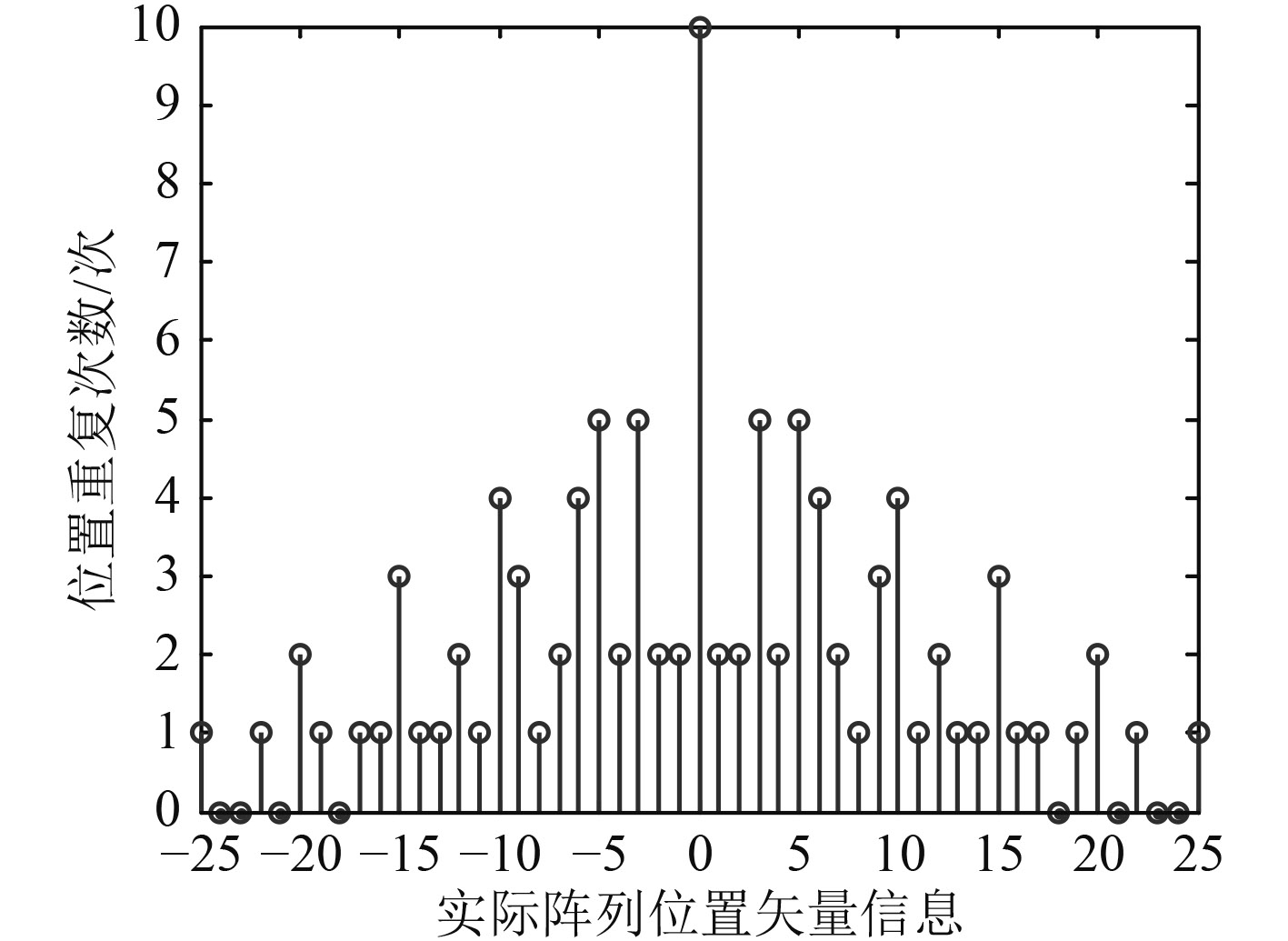
仿真1：设2个均匀子阵线阵1、线阵2的阵元数分别为3，5，则非均匀阵列的阵元位置集合为S = $ \{ 3n{d_0},0 \leqslant n \leqslant 4\} \cup \{ 5m{d_0},0 \leqslant m \leqslant 5\} $ 。仿真得到实际阵列位置矢量v如图3所示，从而得到虚拟阵元位置集合。

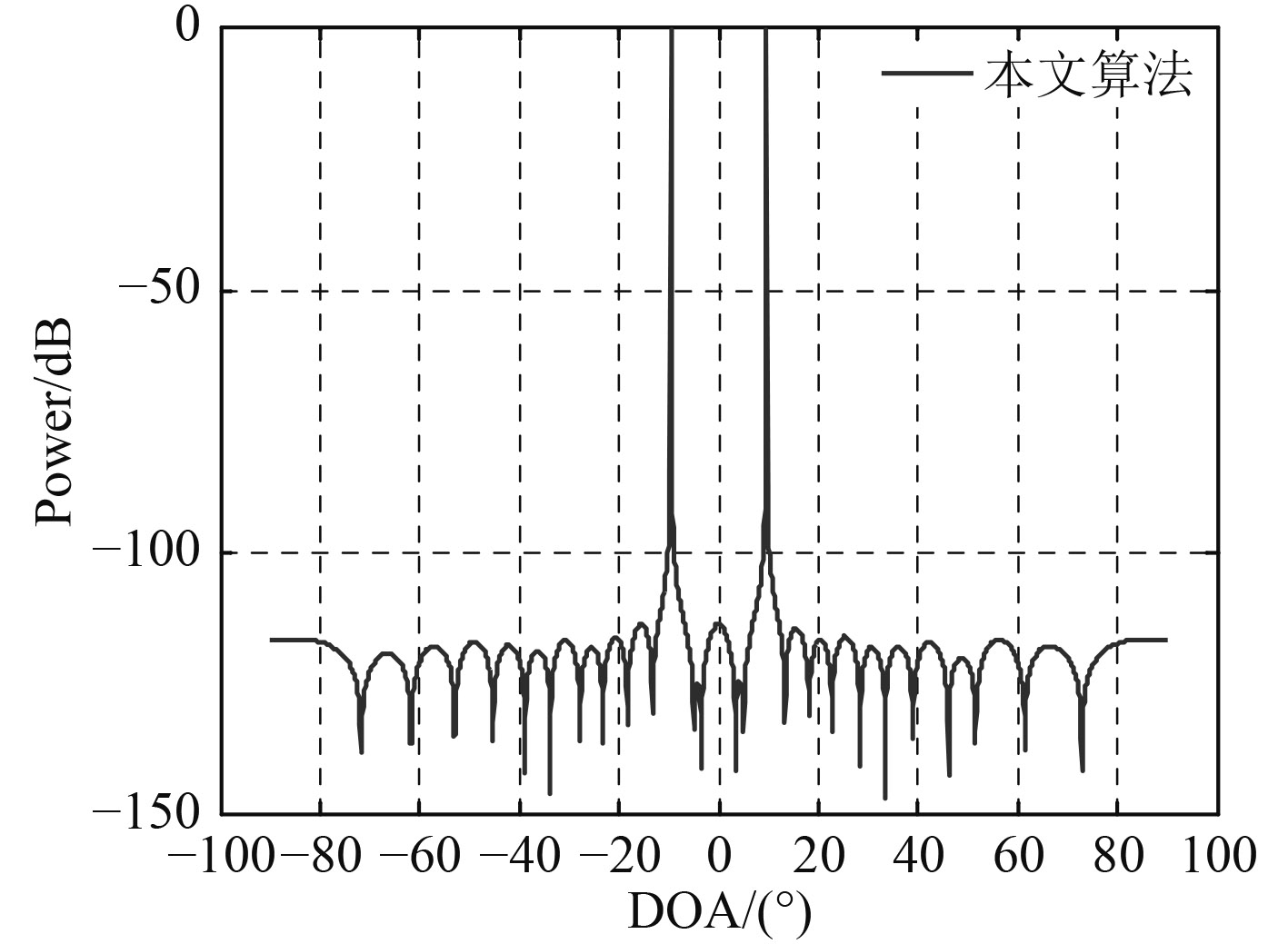
仿真2：设2个均匀子阵的阵元数分别为3和4，阵元总数为9，单位间隔d₀为入射信号波长的一半。水下空域2个非相干窄带信号分别以 ${\theta _1} = - {10^ \circ }$ 和 ${\theta _2} = {10^ \circ }$ 方向入射，信噪比为3 dB，快拍数N=1 000，图4给出了本文算法的归一化空间谱图。从图4可以看出：利用水声信号源的空域稀疏性，得到稀疏解中大系数对应的角度即为水声信号源的波达方向角。

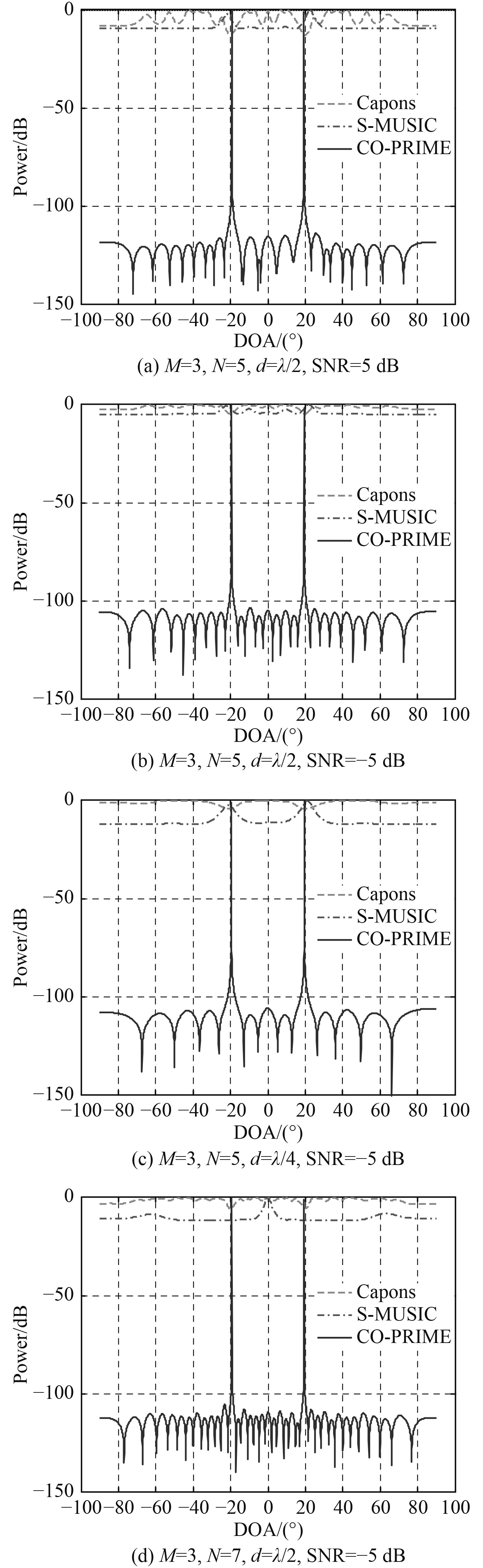
仿真3：为了方便分析Capons算法、平滑MUSIC算法以及本文算法的综合性能，分别改变阵元数、信噪比、阵元最小间距，对3种方法进行性能比较，结果如图5所示。

图5（a）将本文方法与传统的Capons算法和平滑MUSIC方法在M=3，N=5， ${d_0} = \lambda /2$ ，SNR=5 dB条件下进行估计性能比较，从仿真结果可以直观看出，传统的Capons算法估计误差比较大，平滑MUSIC算法和本文算法均能有效估计出目标角度，并且本文所提方法的DOA估计分辨能力更为精确；图5（b）只是改变信噪比参数条件，从图中可以看出，Capons算法不能有效地估计出目标角度，平滑MUSIC算法估计性能下降，本文算法仍能有效估计出目标角度，所以本文所提方法相对于其他传统方法更适用于低信噪比的应用场合。图5（c）只是改变最小阵元间距参数条件，从图中可以看出，最小阵元间距变小时，Capons算法完全失效，平滑MUSIC算法和本文所提的方法能精确估计出目标角度，但本文方法估计得更为精确；图5（d）增加了阵元数，并且在低信噪比条件下，可以看出传统的方法均不能估计出目标角度，而阵元数目的改变对本文算法性能没有太大影响。

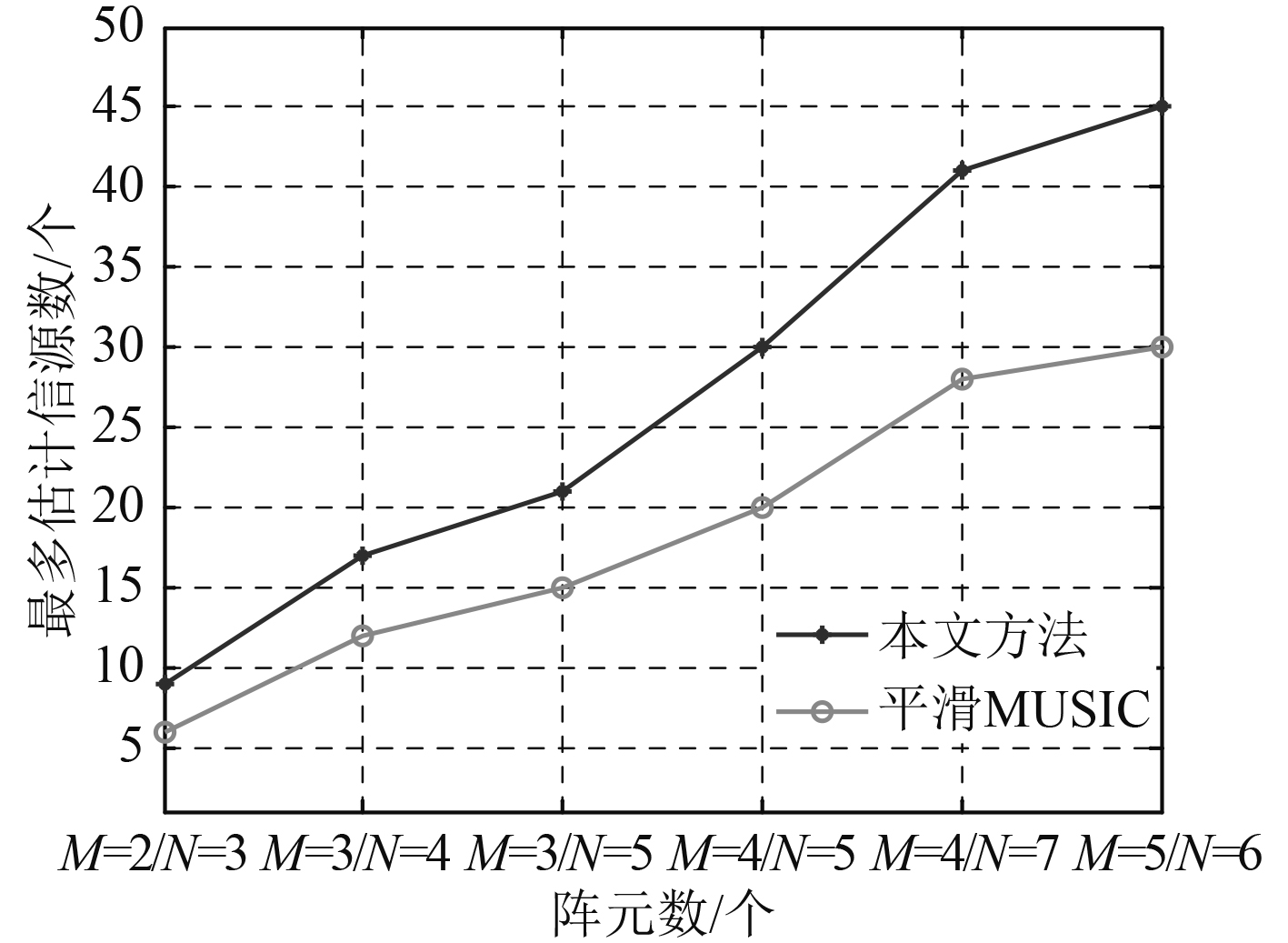
仿真4：在最小阵元间距、信噪比一定时，仿真了阵元数量相同的情况下本文算法和平滑MUSIC方法可以估计的最多信源数，如图6所示。从图中可以看出随着阵元数量的增加，相对于平滑MUSIC算法，本文算法可以估计的最多信源数更可观。

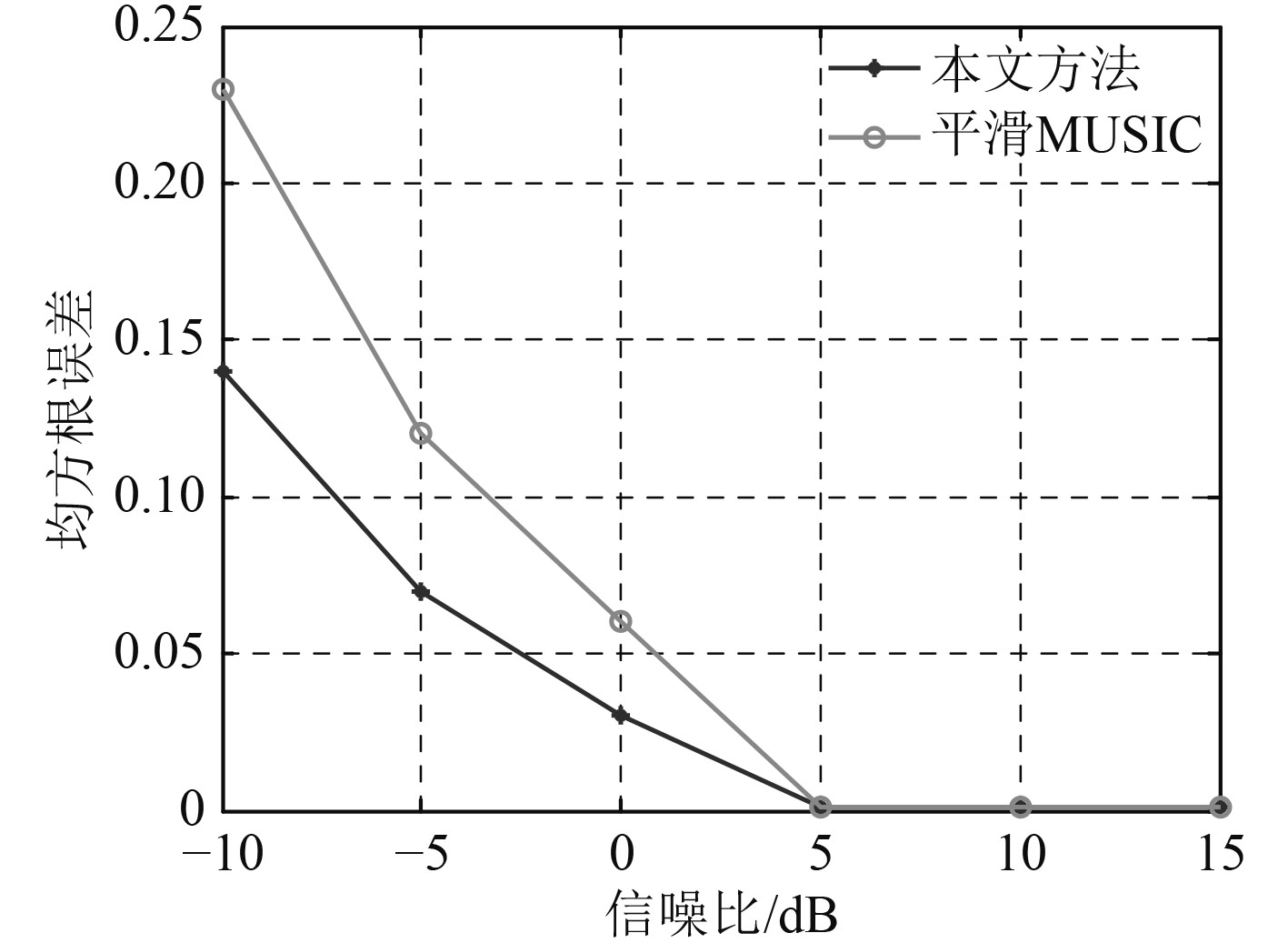
仿真5：由2个阵元数分别为3，5的均匀线性子阵组成的非均匀阵列，单位间隔d₀为入射信号波长的一半，快拍数N=500，图7为在不同信噪比时的目标角度均方根误差。从图中可以看出，低信噪比时，平滑MUSIC方法误差较大，本文算法误差较小，随着信噪比的提高，2种算法的估计误差均趋于平缓，但本文算法的估计误差一直低于平滑MUSIC算法。另外，平滑MUSIC算法的目标角度均方根误差随着信噪比的变化起伏较大，而本文提出的方法变化则比较平缓。

5 结　语

本文在传统非均匀阵列研究基础上，提出了一种水下空域环境中特殊的非均匀阵列DOA估计方法。该方法以2个均匀线阵形成接收阵列，且这2个子阵阵元数满足互质关系。对接收的水声信号进行分析处理，利用虚拟阵列接收的水声信号进行DOA估计。仿真结果表明，与传统的Capons算法和平滑MUSIC算法相比，该算法具有估计精度高、抗噪能力强的特点，且对阵列尺寸要求低，在阵元数目相同的情况下，该算法能测量更多的信号源，能够降低估计的误差，缓解了传统方法在实际应用中所出现的精度低或失效的问题，为水下定位技术问题提供了一种参考。