自沉浮式剖面探测浮标是一种海洋观测平台,其首先应用在国际Argo计划,故又称之为Argo浮标,专用于海洋次表层温、盐、深剖面测量。国际Argo计划自2000年启动实施以来,有35个国家和地区在全球海洋中陆续投放了约11 000个Argo剖面浮标,目前在海上正常运作的浮标总数约在3 800个左右,已经成为全球海洋观测系统的重要支柱[1]。我国虽自“十五”计划开始,就已着手国产剖面浮标关键技术的开发工作,先后研制出了多种型号的自持式剖面漂流浮标,并采用北斗卫星导航系统定位和数据传输,进行了多次海上布放试验,但至今尚未得到国际Argo计划认可,用于全球Argo实时海洋观测网建设中[1]。
本课题组在近期的研究项目中,提出了一种浮标与滑翔机结合的新型剖面探测浮标,本文将基于该浮标的外形结构,结合由美国华盛顿大学海洋学院Stephen C. Riser教授介绍的一种通过加装蓄能器来增大浮标浮力调节范围的方式,对算例浮标的上浮运动进行计算仿真分析。
1 剖面探测浮标结构 1.1 国外浮标简介美国Webb公司研究和开发了APEX型浮标,法国Ifremer研究所1990年研制Marvor型剖面浮标,后与加拿大Metocean公司合作开发PROVOR(海王星)剖面浮标,该类型浮标采用柱塞泵和皮囊实现浮标标的上升和下沉:由柱塞泵向皮囊中注入压力油,增大皮囊的体积从而使浮标体积增大,达到上升的目的;将压力油从皮囊中抽回,使皮囊的体积减小从而减小浮标的体积,实现浮标的下沉工作[1 – 3]。
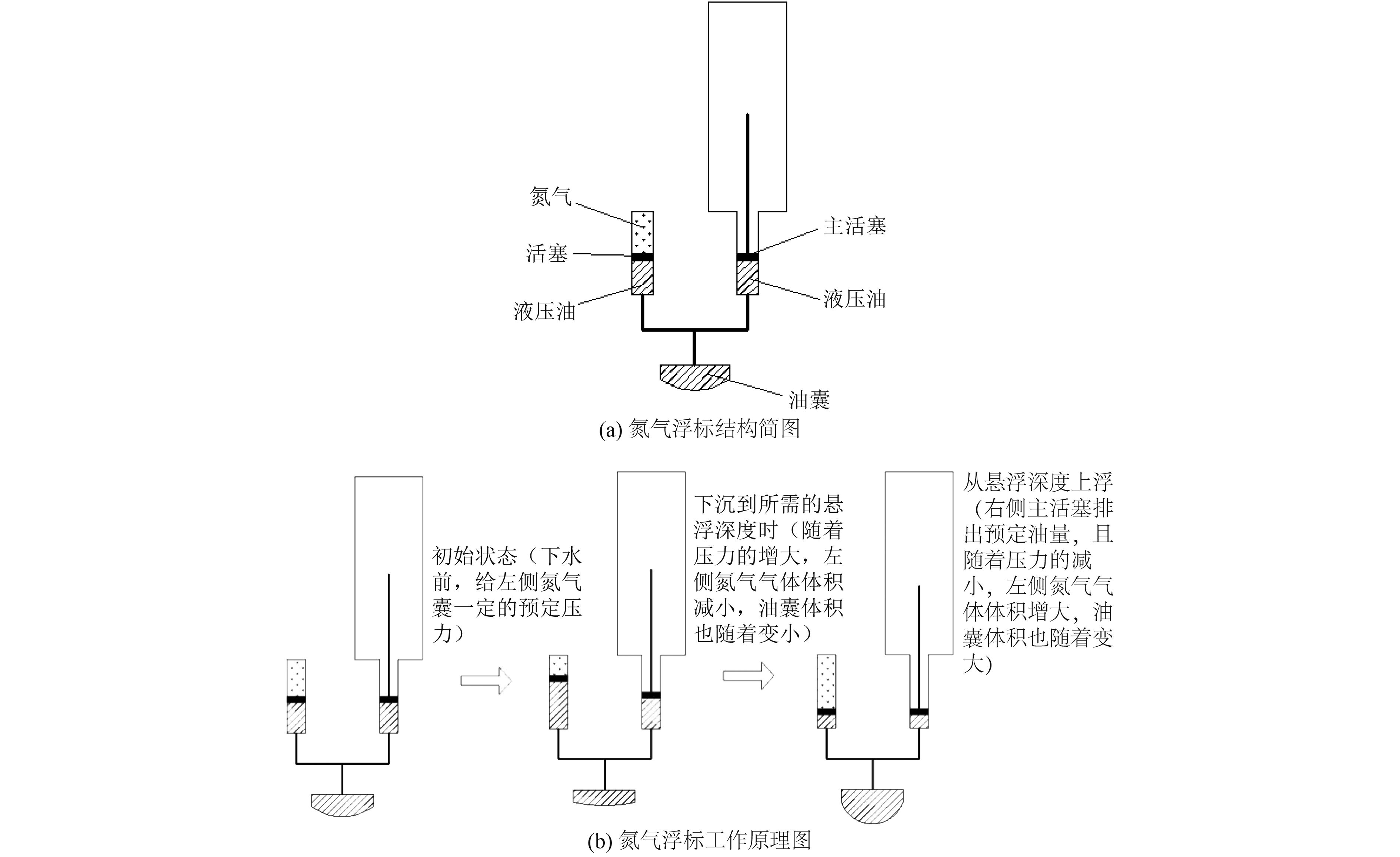
1.2 算例浮标结构组成介绍该浮标的浮力调节机构按照美国华盛顿大学海洋学院Stephen C. Riser教授介绍的氮气浮标的理论[3],结构如图1所示。其中,右侧为主浮力泵,左侧为氮气罐,该氮气罐工作原理与蓄能器相同。在浮标工作过程中,随着主活塞的回缩,浮标开始下沉,在到达预压力深度之前,氮气浮标跟普通浮标一样。随着浮标的继续下沉,海水的压力超过氮气罐内部的压力,氮气罐的活塞就向里移动,压缩氮气罐内的氮气,直到浮标下沉到设定的悬浮深度。浮标上浮时,通过主活塞向外部的油囊注满油而开始上浮的过程,其额外浮力来自气囊中的活塞运动。在本算例浮标中,氮气罐阀门保持常开状态,假定主活塞向外部油囊注油的过程为瞬时过程,随着浮标逐渐上浮,为了使氮气罐内的气体压力和四周海水压力保持平衡,氮气罐中活塞会缓缓向下推动,使蓄能器中的液油推入外部油囊中,从而增大浮标上浮的浮力。
|
图 1 氮气浮标结构简图及工作原理 Fig. 1 The sketch of the structure and thefundamental diagram of N2 float |
算例浮标的基本参数如表1所示。
|
|
表 1 浮标基本参数 Tab.1 The basic parameters of the float |
算例浮标的外形为带机翼的浮标结构,其阻力性能和普通浮标会有略微不同。在进行蓄能器对浮标上浮运动的影响的研究之前,将算例浮标在Fluent中进行仿真计算得到不同速度下匀速直航时的受力情况,再根据水动力系数的计算公式得到相关水动力系数。
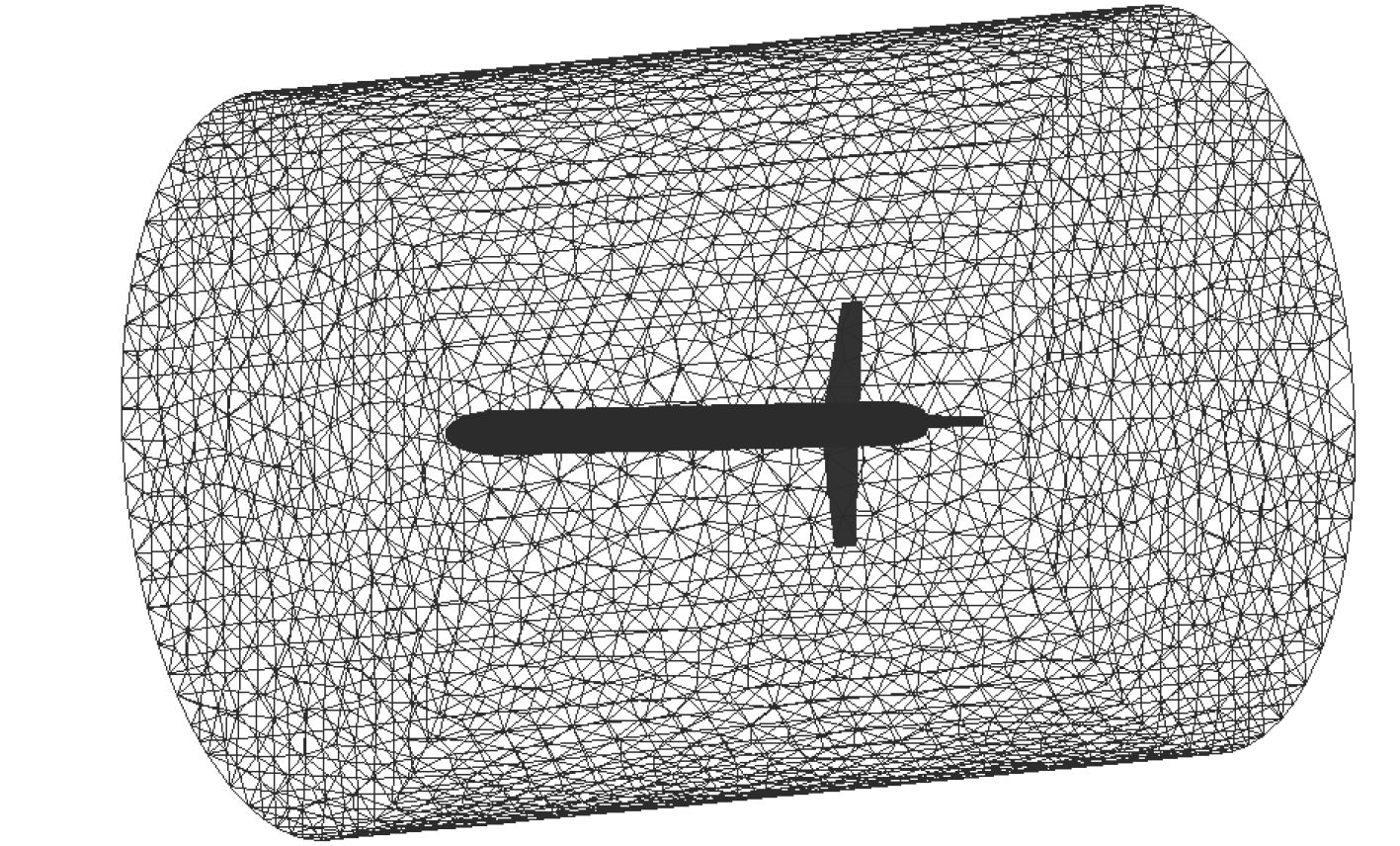
对浮标模型进行网格划分时,采用2种网格划分格式,首先利用O型切分法建立外计算域,其形状如图2所示,在图中所示的小圆柱中用非结构网格建立内计算域,包裹整个浮标模型,如图3所示。计算的湍流模型采用标准k-e湍流模型[4 – 6]。

|
图 2 外域网格 Fig. 2 The mesh of external area |
|
图 3 内域网格 Fig. 3 The mesh of internal area |
取速度为0.2 m/s,0.3 m/s,0.4 m/s和0.5 m/s进行仿真计算后得到各个速度下的阻力及阻力系数如表2所示。
|
|
表 2 浮标阻力和阻力系数 Tab.2 The drag force and drag force coefficient of the float |
已知对于很长的圆柱或两端夹在2个平行壁之间的圆柱体,其阻力系数可按式(1)进行估算[7]:
| $c = \frac{{8\pi }}{{Re\left( {2 - \ln Re} \right)}},$ | (1) |
对于有限长的圆柱体,它的阻力要比无限长圆柱体的阻力小得多。同有限平板一样,阻力减少的原因在于,对于有限长的主柱体,由于气流可以绕过圆柱体的两端使柱体后面的涡旋区得到充气,因而物体后面压力的降低要比无充气时小。实验数据如表3所示。
|
|
表 3 圆柱体阻力系数实验数据 Tab.3 Experimental data of cylinder drag force coefficient |
若将算例浮标简化为细长的圆柱体,结合其基本参数和所取的速度范围,得到相应速度下的雷诺数如表4所示。
|
|
表 4 浮标简化雷诺数 Tab.4 Simplified Reynolds number of the float |
由上述数据可知,算例浮标的雷诺数在6.15×105~1.54×106之间,在此区间有限圆柱的阻力系数为0.37~0.75,因此可以认为CFD仿真计算得到的阻力系数的值有效。
3 浮标运动过程研究 3.1 浮标上浮的基本方程已知进入稳定状态匀速上浮的浮标受力如下式:
| ${F_D} + mg = \rho g{V_{{\text{浮}}}},$ | (2) |
由于
| ${F_D} = {C_D}\frac{\rho }{2}{u_0}^2A,$ | (3) |
则式(2)可表示为
| ${C_D}\frac{\rho }{2}{u_0}^2A + mg = \rho g{V_{{\text{浮}}}}{\text{。}}$ | (4) |
式中:FD为浮标受到的绕流阻力;CD为绕流阻力因素;u0为浮标速度;A为浮标的迎流投影面积;m为浮标质量;V浮为浮标体积;ρ为海水密度;g为重力加速度。
根据式(4)可得要达到速度u0匀速上升,所需要的浮标体积为
| ${V_{{\text{浮}}}} = \frac{{{C_D}\frac{\rho }{2}{u_0}^2A + 2mg}}{{\rho g}}{\text{。}}$ | (5) |
将表2~表4中的参数代入式(5)中得到浮标在不同速度下匀速上浮所需要的体积如表5所示。
|
|
表 5 浮标不同上浮速度下的体积 Tab.5 The volume of the float at different velocity |
已知浮标由海底上浮的过程是一个变加速度的过程,假设浮力保持不变,则浮标上浮过程的动平衡方程可表示为[8]:
| ${{m}}\frac{{{ d}u}}{{{ d}t}} = \rho g{V_{{\text{浮}}}} - mg - {C_D}\frac{\rho }{2}{u^2}A,$ | (6) |
则浮标上浮的瞬时加速度可表示为:
| $\frac{{{ d}u}}{{{ d}t}} = \frac{\rho }{m}g{V_{{\text{浮}}}} - g - {C_D}\frac{\rho }{{2m}}{u^2}A{\text{。}}$ | (7) |
根据式(7)可得:
| $\!\!\! \frac{m}{{\sqrt 2 \left( {\rho g{V_{{\text{浮}}}} \!-\! mg} \right){C_D}\rho A}} \cdot \ln \left| {\left. {\frac{{u \!-\! \sqrt {2\left( {\frac{{\rho g{V_{{\text{浮}}}} \!-\! mg}}{{{C_D}\rho A}}} \right)} }}{{u \!+\! \sqrt {2\left( {\frac{{\rho g{V_{{\text{浮}}}} \!-\! mg}}{{{C_D}\rho A}}} \right)} }}} \right|} \right. \!=\! t \!+\! C{\text{。}}\!\!\!\!\!$ | (8) |
实际中,油囊体积的变化主要由2部分构成,一部分为蓄能器造成的油囊体积改变,另一部分为浮力泵造成的油囊体积的改变,假定浮力泵对油囊体积的改变是瞬时的,但蓄能器压力受浮标所在海水深度的影响,因此蓄能器造成的油囊体积的改变也随深度在时刻变化着。
在蓄能器部分,由于气体蓄能器是以波义耳定律PVn=nRT为基础,假定蓄能器压力为P,气体体积为V,则
| $V = \frac{{nRT}}{P},$ | (9) |
式中:n为N2物质的量;R为气体常量;T为绝对温度。
由于压力P为随深度变化的函数,以4 000 m深度处的位置为坐标原点,设浮标上浮的距离为y,则浮标在4 000 m以上某一深度处所受的海水压力为
| ${P_{{\text{海}}}} = \rho g\left( {4\ 000 - y} \right),$ | (10) |
假定蓄能器在原点处的压力为P0,此时的氮气体积为V0,即
| ${P_0} = {\left. {{P_{{\text{海}}}}} \right|_{y = 0}},$ | (11) |
| ${V_0} = \frac{{nRT}}{{{P_0}}}{\text{。}}$ | (12) |
假定在某一深度处氮气体积为V1,则油囊体积的变化即为蓄能器中氮气体积的变化,即
| ${V_1} - {V_0} = \frac{{nRT}}{{\rho g\left( {4\ 000 - y} \right)}} - {V_0}{\text{。}}$ | (13) |
又浮标上浮速度为上浮距离关于时间的导数,则浮标上浮的瞬时加速度表示为:
| $\frac{{{{ d}^2}y}}{{{ d}{t^2}}}\! =\! \frac{\rho }{m}g\left( {\frac{{nRT}}{{\rho g\left( {4\ 000 \!-\! y} \right)}} \!-\! {V_0} \!+\! {V_{{\text{浮}}}}} \right) \!-\! g \!-\! {C_D}\frac{\rho }{{2m}}{u^2}A{\text{。}}$ | (14) |
式中:V浮为无蓄能器时为使浮标以某一预定速度匀速上浮所需的浮标体积,即假定浮标在水深4 000 m处准备上浮时,主浮力泵向油囊排油的过程是瞬时的。
3.5 浮标上浮过程能源效率分析为了便于更直观地得出算例浮标加装蓄能器后其性能的提升程度,现给定一个确定的上浮时间,通过比较在这一段时间内浮标无蓄能器和有蓄能器时上浮的功率来得出结论。假定2种状态下浮标上浮t秒,其中无蓄能器时上浮高度为y1,有蓄能器时浮标上浮高度为y2,不考虑海水密度随浮标上浮高度变化的影响,算例浮标在上浮过程中所做的功主要由浮力和重力产生。
无蓄能器时,浮标上浮过程所做的功表示为:
| ${W_1} = \left( {{{\rho g}}{V_{{\text{浮}}}} - mg} \right){y_1}{\text{。}}$ | (15) |
式中:W1为浮标不带蓄能器时上浮运动所做的总功;V浮为无蓄能器时为使浮标以某一预定速度匀速上浮所需的浮标体积。
此状态下的功率为:
| ${P_1} = \frac{{{W_1}}}{t}{\text{。}}$ | (16) |
浮标加装蓄能器之后,考虑蓄能器排出的油量,浮标总体积会产生变化,此时浮标上浮运动所做的功表示为:
| ${W_2} = \left( {{{\rho g}}\left( {\frac{{nRT}}{{\rho g\left( {4000 - {y_2}} \right)}} - {V_0} + {V_{{\text{浮}}}}} \right) - mg} \right){y_2},$ | (17) |
此状态下的功率为:
| ${P_2} = \frac{{{W_2}}}{t}{\text{。}}$ | (18) |
式(14)为一维二阶非线性方程,其精确解难以得出,因此采用Dormand-Prince提出的显示龙格-库塔(4,5)算法对该方程进行数值求解,该算法在Matlab中有特定的命令名称为ode45,以下简称ode45算法。
ode45算法的求解思路为用4阶方法提供候选解,用5阶方法控制误差,它是单步解算命令,常用于求解非刚性中等精度的问题。考虑式(14),将龙格-库塔方法的一般形式表示如下[9]:
| ${y_{n + 1}} = {y_n} + h\varphi \left( {{t_n},{y_n},h} \right),$ | (19) |
其中:
| $\varphi \left( {{t_n},{y_n},h} \right) = \mathop \sum \limits_{i = 1}^r {c_i}{K_i},$ | (20) |
| ${K_1} = f\left( {{t_n},{y_n}} \right),$ | (21) |
| ${K_i} = f({t_n} + {\lambda _i}h,{y_n} + h\mathop \sum \limits_{j = 1}^{i - 1} {\mu _{ij}}{K_j}),\;i = 2, \ldots ,r{\text{。}}$ | (22) |
式中:ci,λi,μij均为常数。一般来说,点数r越多,精度越高,经过复杂的数学演算,4阶龙格-库塔公式可表示为:
| $\left\{ \begin{array}{l}{y_{n + 1}} = {y_n} + \frac{h}{6}\left( {{K_1} + 2{K_2} + 2{K_3} + {K_4}} \right),\\{K_1} = f\left( {{t_n},{y_n}} \right),\\{K_2} = f\left( {{t_n} + \frac{h}{2},{y_n} + \frac{h}{2}{K_1}} \right),\\{K_3} = f\left( {{t_n} + \frac{h}{2},{y_n}\frac{h}{2}{K_2}} \right),\\{K_4} = f\left( {{t_n} + h,{y_n} + h{K_3}} \right){\text{。}}\end{array} \right.$ | (23) |
若采用变步长的方法,考虑式(23)的局部截断误差为O(h5),从节点(tn)出发,先以h为步长求出一个近似值,记为
| $y\left( {{t_{n + 1}}} \right) - y_{n + 1}^{\left( h \right)} \approx c{h^5},$ | (24) |
然后将步长折半,即取
| $y\left( {{t_{n + 1}}} \right) - y_{n + 1}^{\left( {\frac{h}{2}} \right)} \approx 2c{\left( {\frac{h}{2}} \right)^5}{\text{。}}$ | (25) |
比较式(24)和式(25),步长折半后误差大约减小到1/16,由此易推得事后估计式为:
| $y\left( {{t_{n + 1}}} \right) - y_{n + 1}^{\left( {\frac{h}{2}} \right)} \approx \frac{1}{{15}}\left[ {y_{n + 1}^{\left( {\frac{h}{2}} \right)} - y_{n + 1}^{\left( h \right)}} \right]{\text{。}}$ | (26) |
在Matlab中对式(7)和式(14)求数值解,采用ode45算法[10],分别计算无蓄能器和有蓄能器时的速度时间关系,得到一系列结果如图2所示。
|
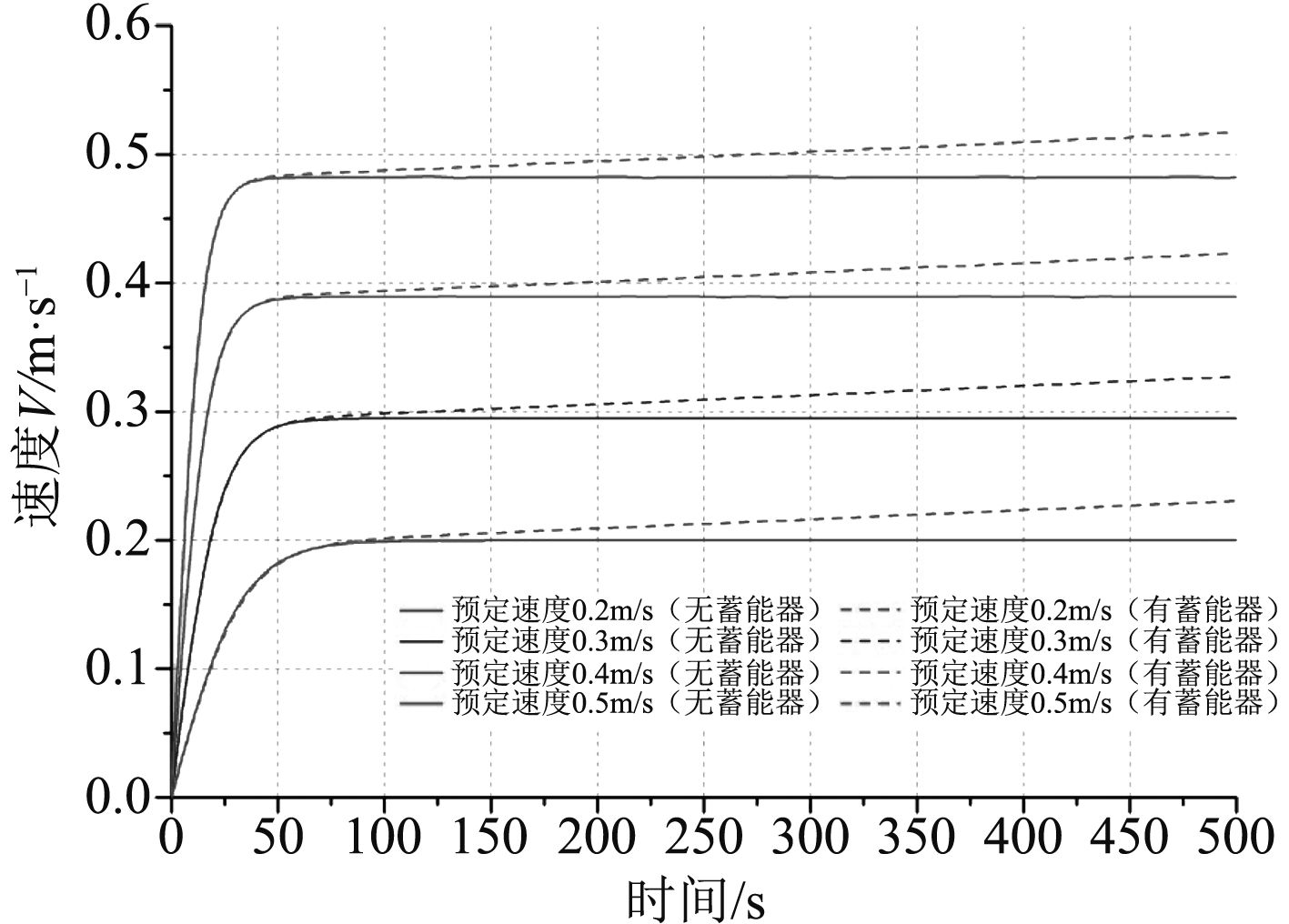
图 4 有无蓄能器时速度随时间变化曲线 Fig. 4 The presence of speed changing over time with/without accumulator |
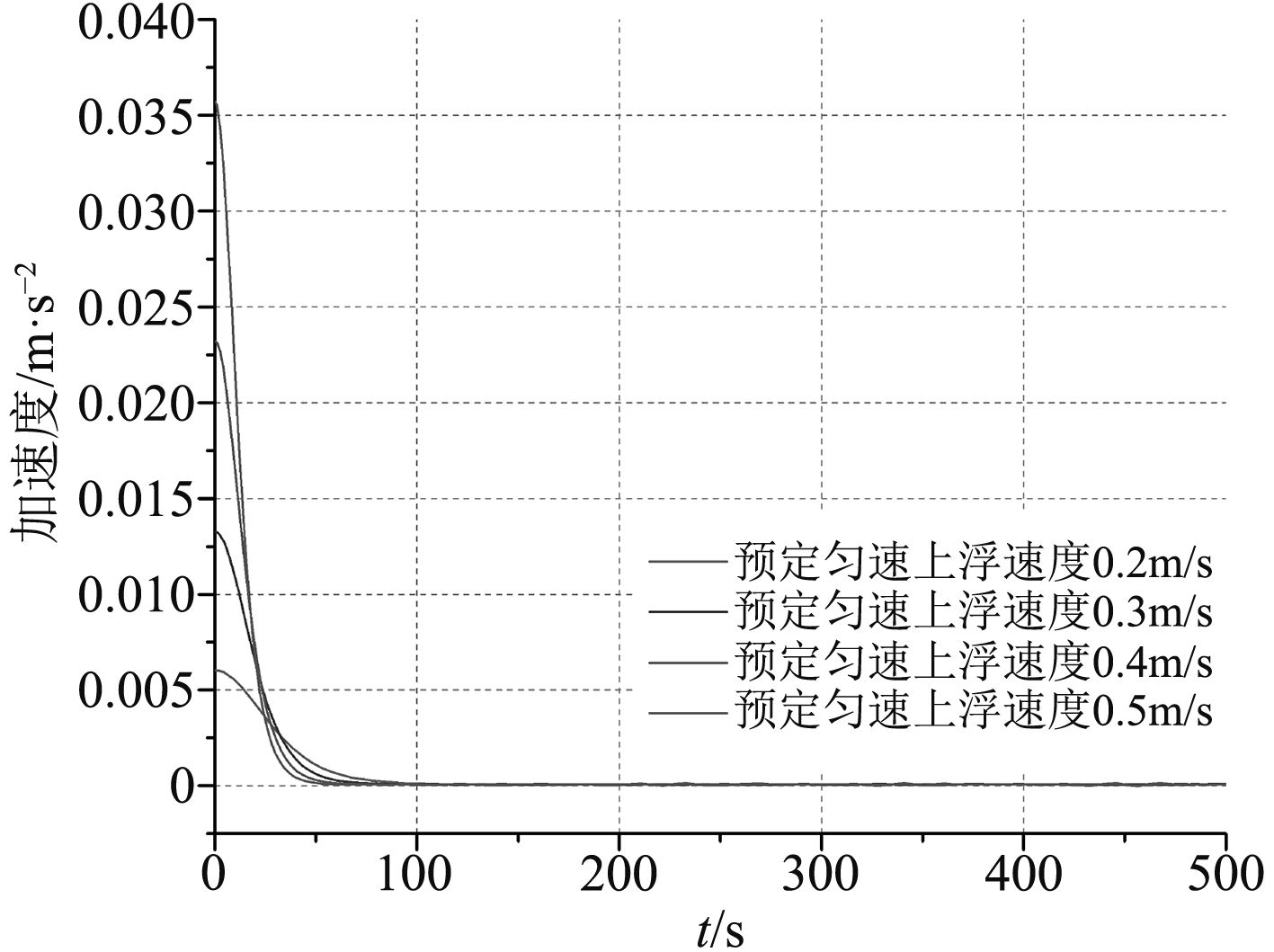
在图4中,只选取了浮标从4 000 m海底开始上浮500 s时间内的速度变化,实线为无蓄能器时浮标上浮速度随时间的变化,由于在无蓄能器的情况下是以假定浮标最后以某一速度匀速上浮为前提来进行计算分析的,因此图中的实线从下往上依次为最终达到的上浮速度分别为0.2~0.5 m/s时的速度随时间的变化曲线。
从图中可以看出,浮标在达到预定速度后速度随时间呈线性增大,通过进一步的计算和数据处理可得到浮标在有无蓄能器2种情况下上浮的加速度随时间的变化如图5~图6所示。
|
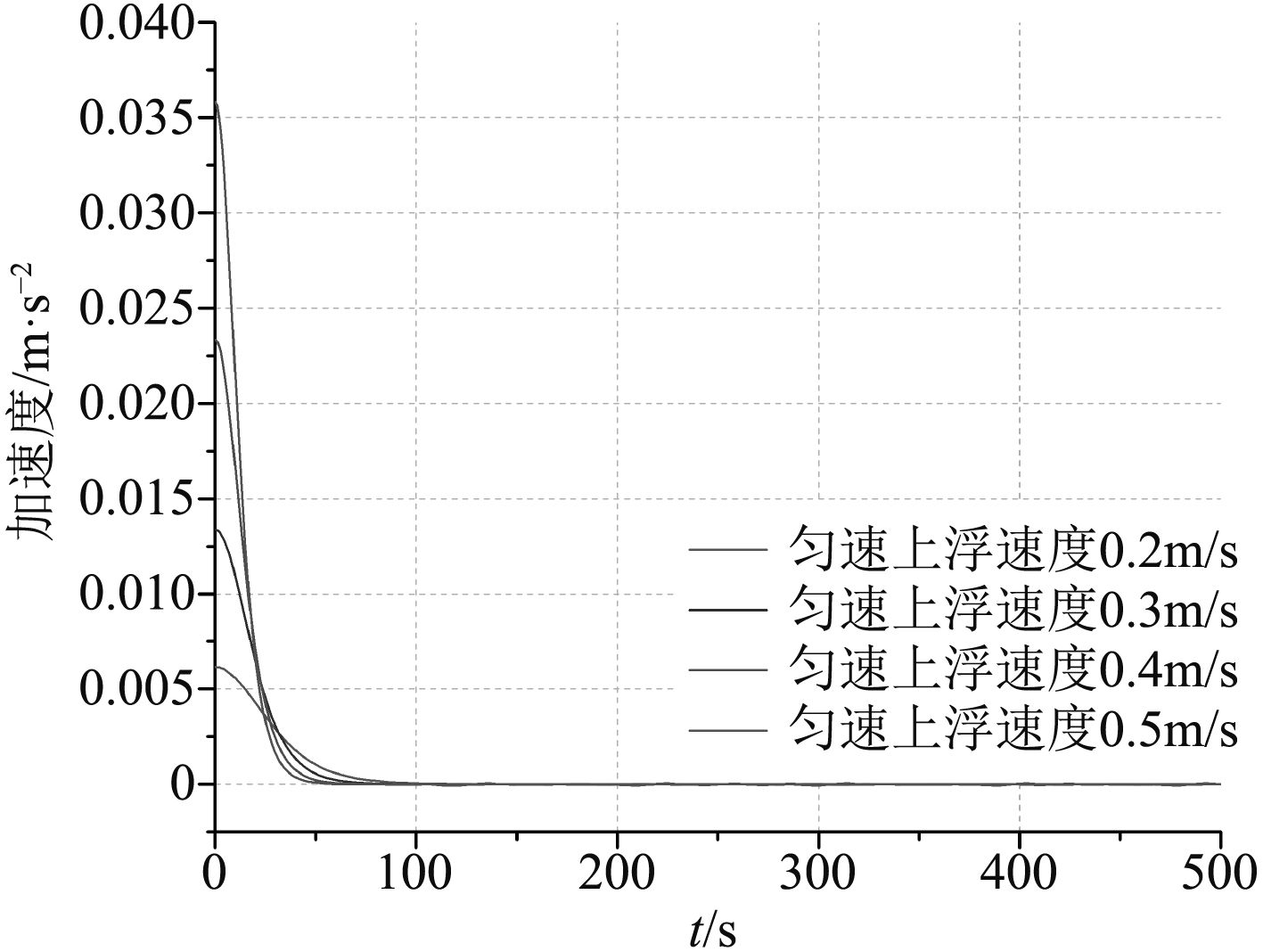
图 5 无蓄能器时加速度随时间变化图 Fig. 5 The presence of accelerated speed changing over time without accumulator |
|
图 6 有蓄能器时加速度随时间变化图 Fig. 6 The presence of accelerated speed changing over time with accumulator |
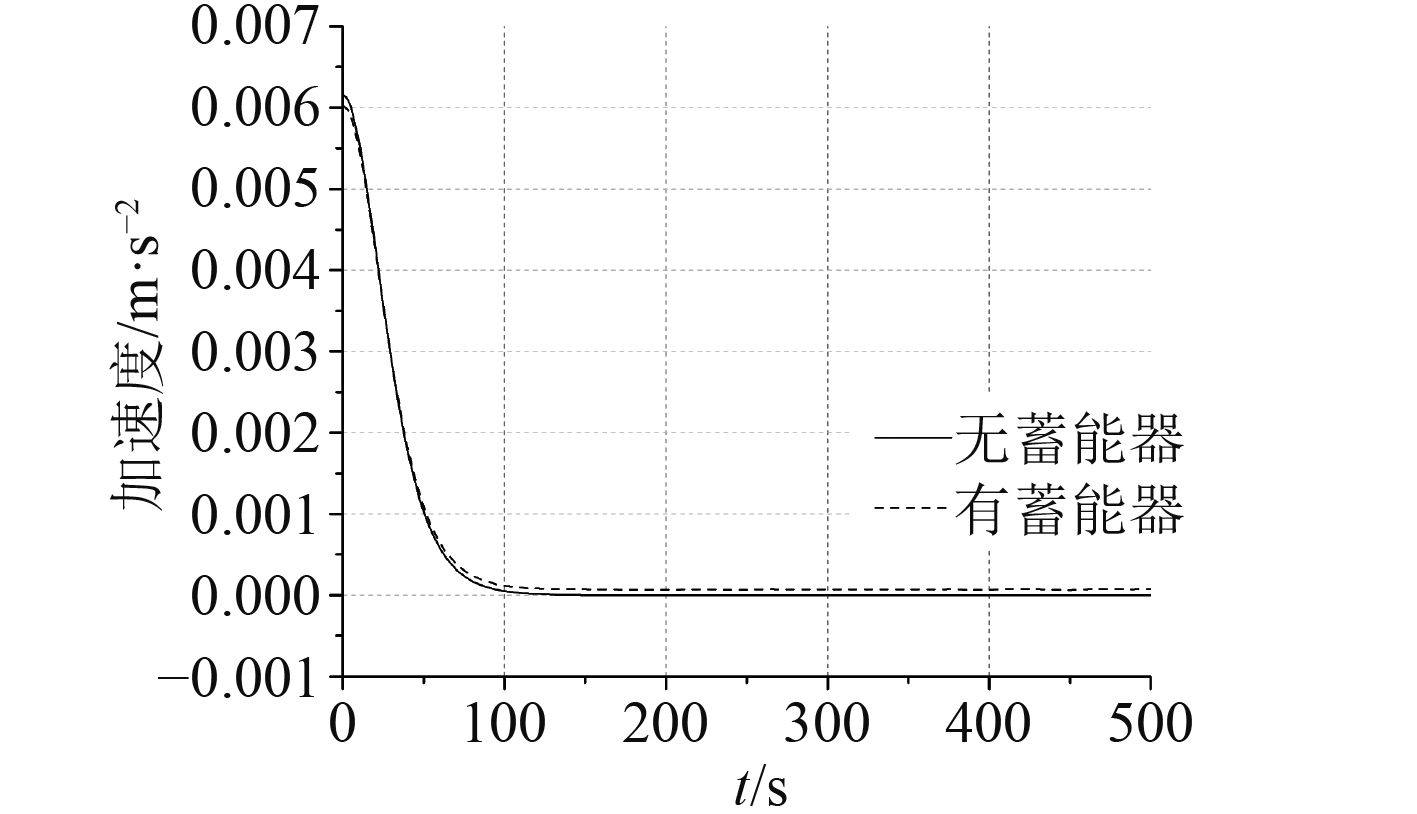
从图5和图6可以看出,有无蓄能器时,其加速度随时间的变化趋势大致相同,在无蓄能器时,由于假定最终匀速上浮,因此在4种不同的预定速度下,最后加速度都会变为0。由于在图4中看出有蓄能器时,浮标在达到预定的上浮的速度后,还会在蓄能器的影响下加速上浮,因此在达到预定速度后加速度应大于0,现对比各个预定速度下有无蓄能器时浮标上浮加速度随时间变化的曲线如图7~图10所示。
|
图 7 预定速度0.2 m/s时加速度比较 Fig. 7 The comparation of accelerated speed at the priming speed 0.2 m/s with/without accumulator |
|
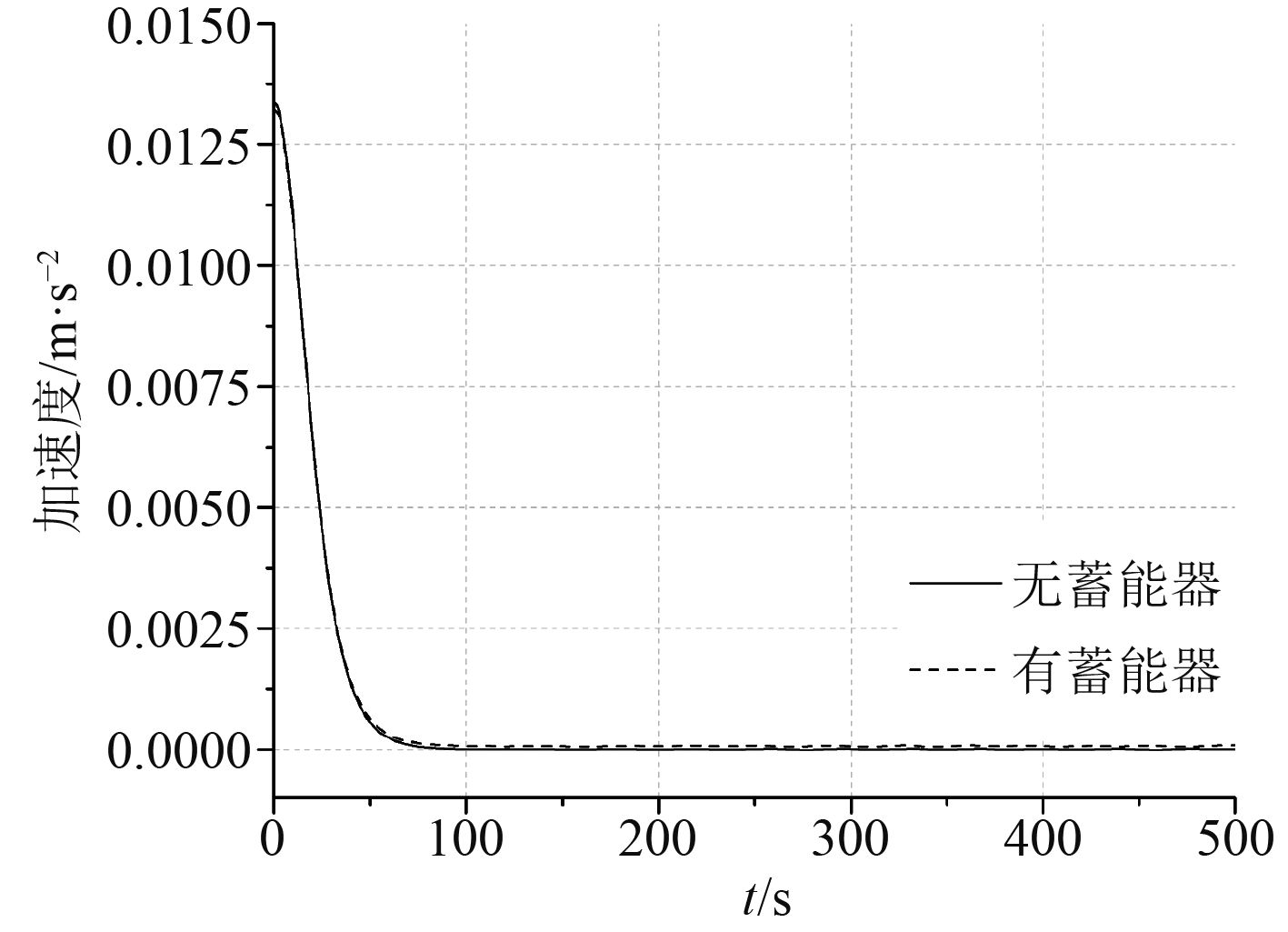
图 8 预定速度0.3 m/s时加速度比较 Fig. 8 The comparation of accelerated speed at the priming speed 0.3 m/s with/without accumulator |
|
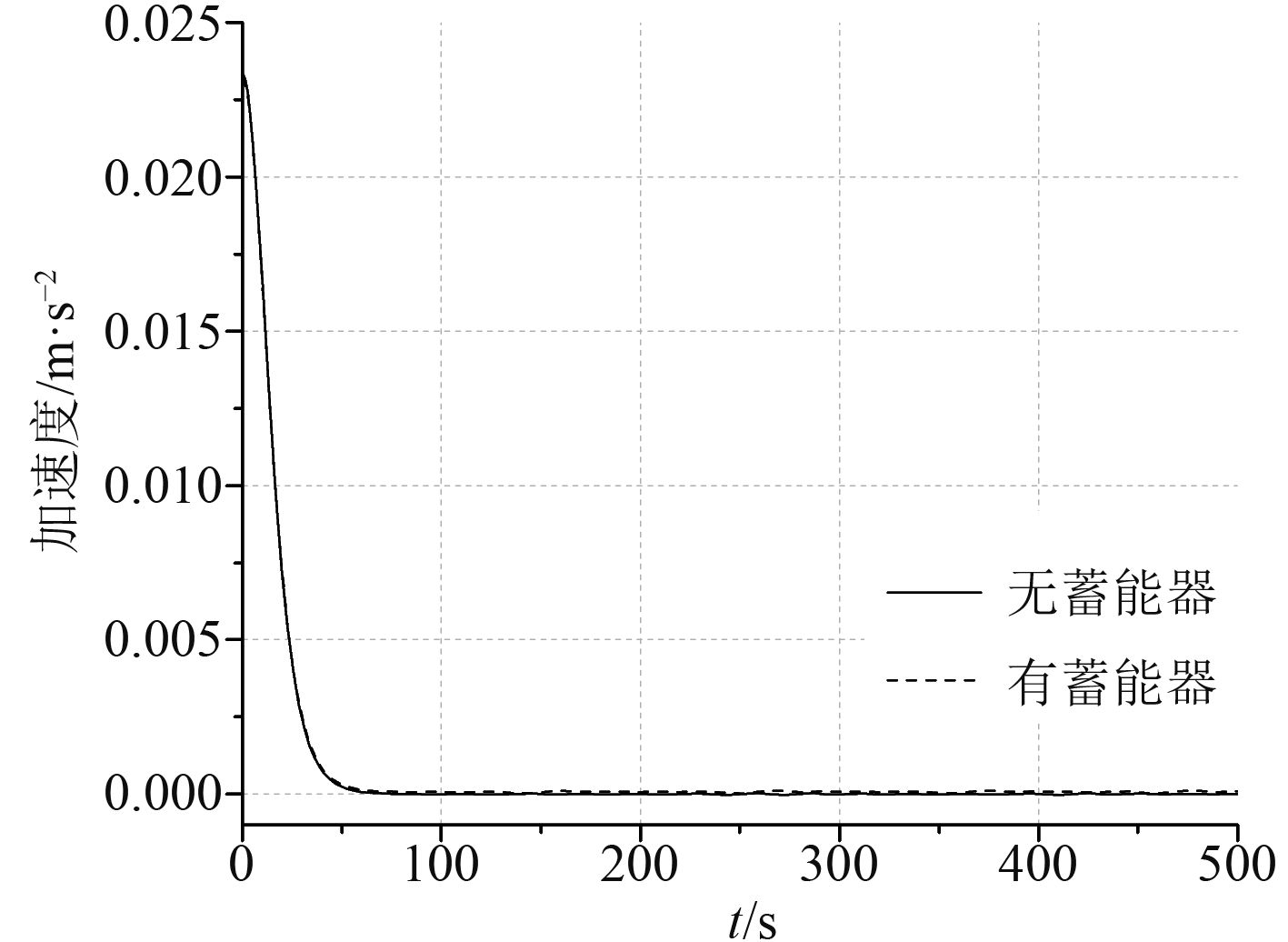
图 9 预定速度0.4 m/s时加速度比较 Fig. 9 The comparation of accelerated speed at the priming speed 0.4 m/s with/without accumulator |
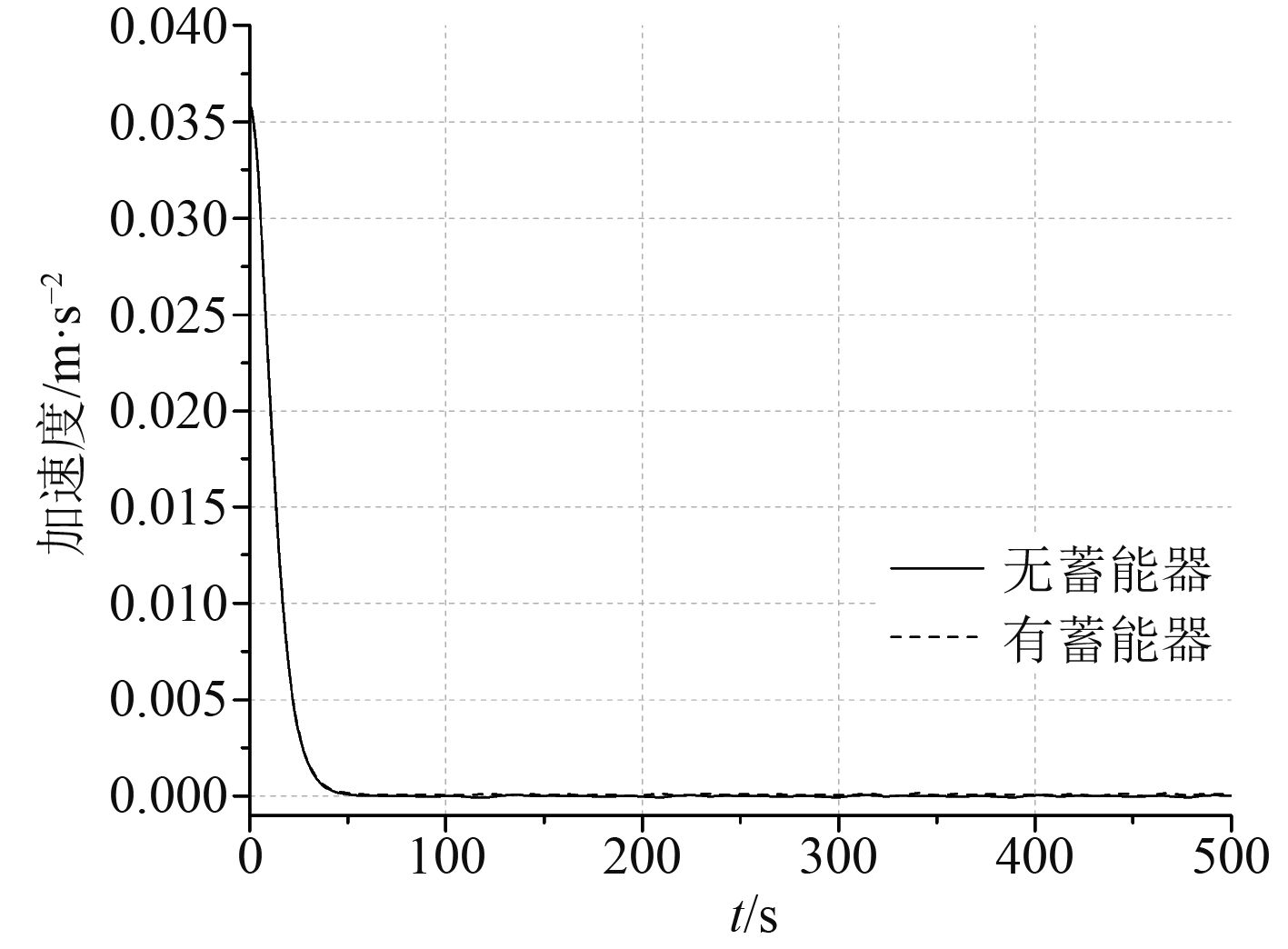
|
图 10 预定速度0.5 m/s时加速度比较 Fig. 10 The comparation of accelerated speed at the priming speed 0.5 m/s with/without accumulator |
由于无蓄能器时理论上最终加速度应为0,但考虑到数值计算的精度问题,上述系列曲线中无蓄能器时的加速度最终在零值附近有轻微的震荡,为了减小Matlab数值计算系统中的误差,并且更加明显的看到有蓄能器时加速度相比于无蓄能器时的变化情况,将图7~图10各图中有蓄能器时的加速度曲线与无蓄能器时的加速度曲线进行抵消相减得到图11~图14,则图11~图14中所反映出来的震荡可看作为完全由蓄能器引起的。
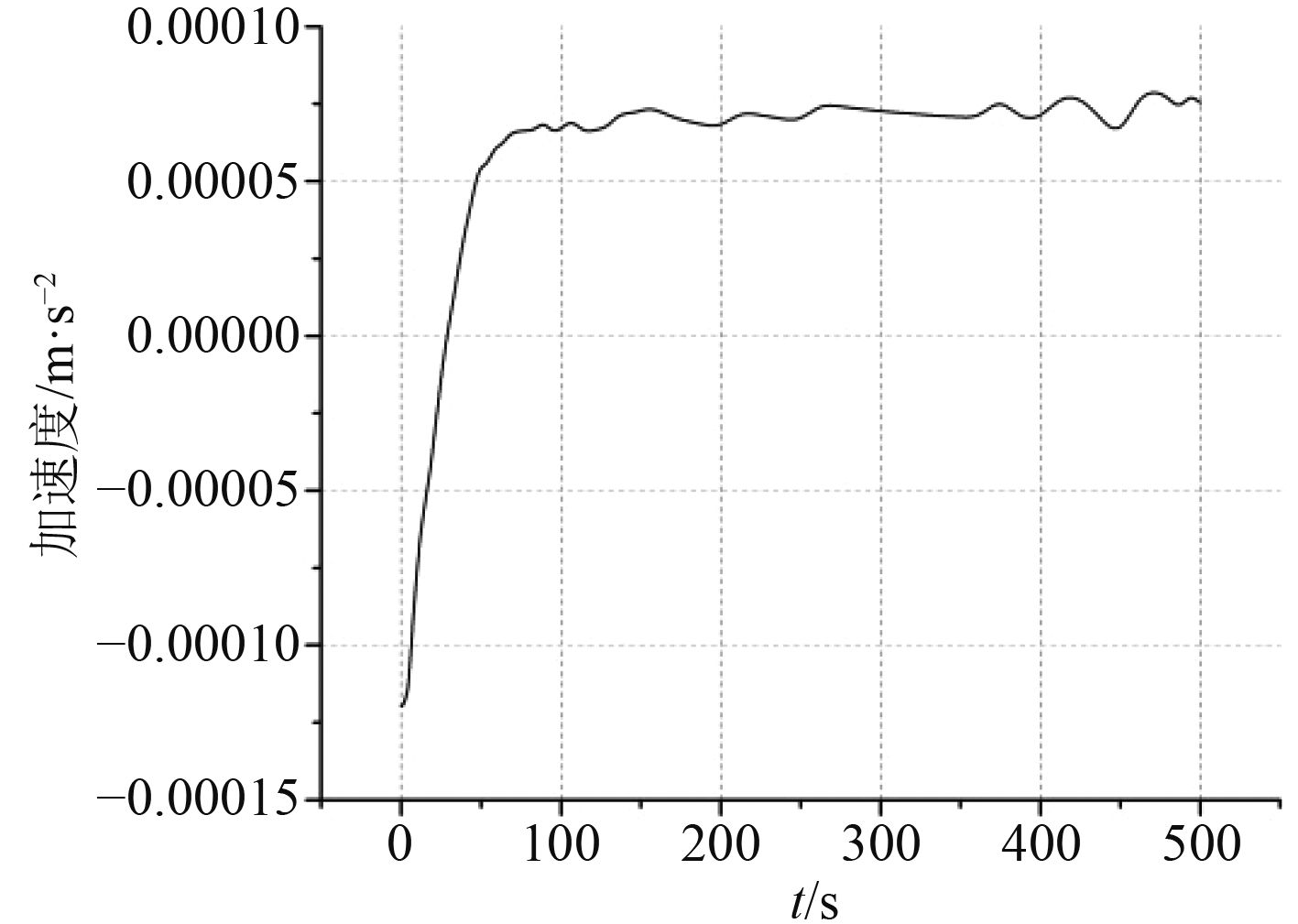
|
图 11 预定速度0.2 m/s时加速度差 Fig. 11 The velocity contrast at the priming speed 0.2 m/s |
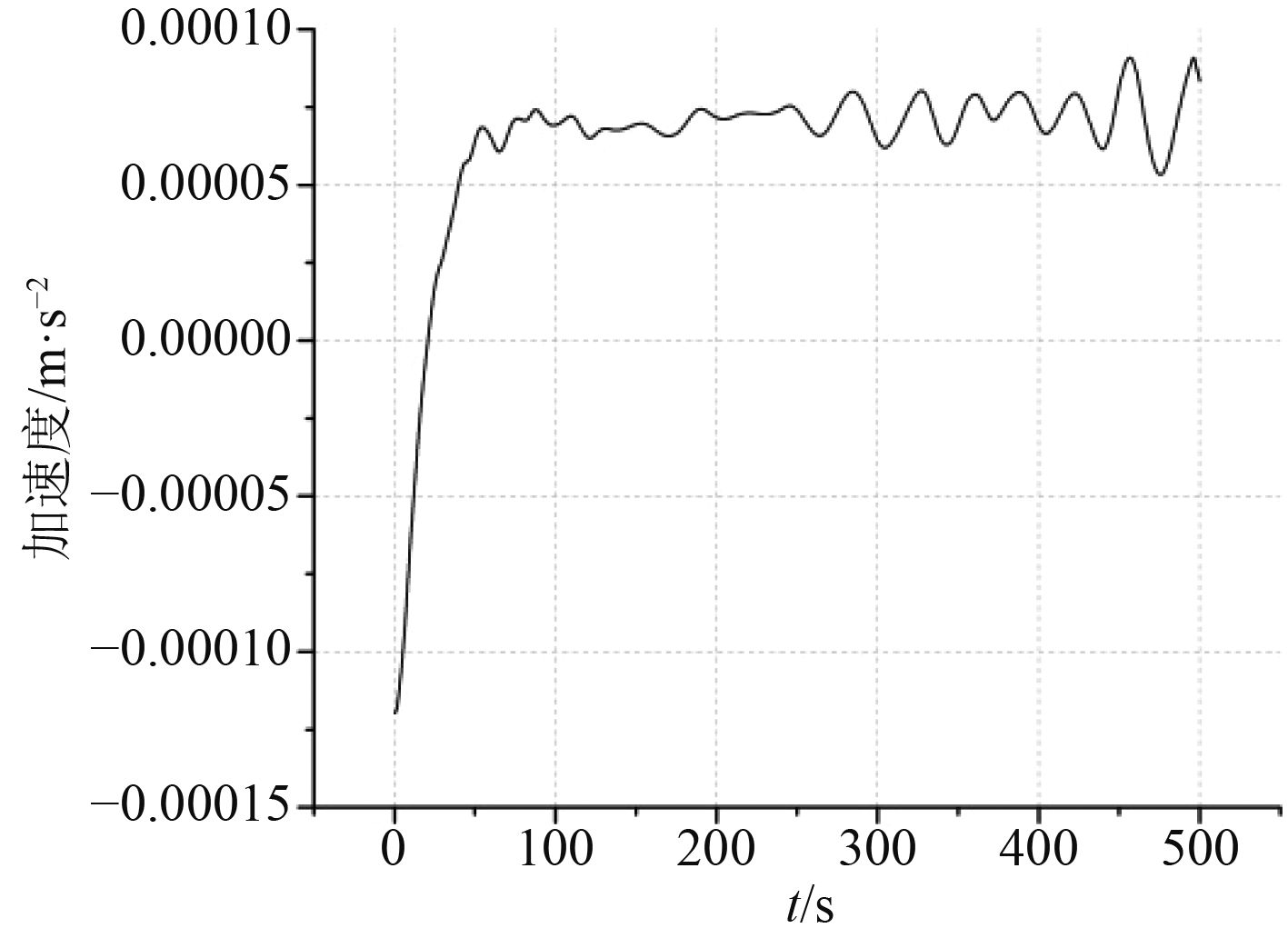
|
图 12 预定速度0.3 m/s时加速度差 Fig. 12 The velocity contrast at the priming speed 0.3 m/s |
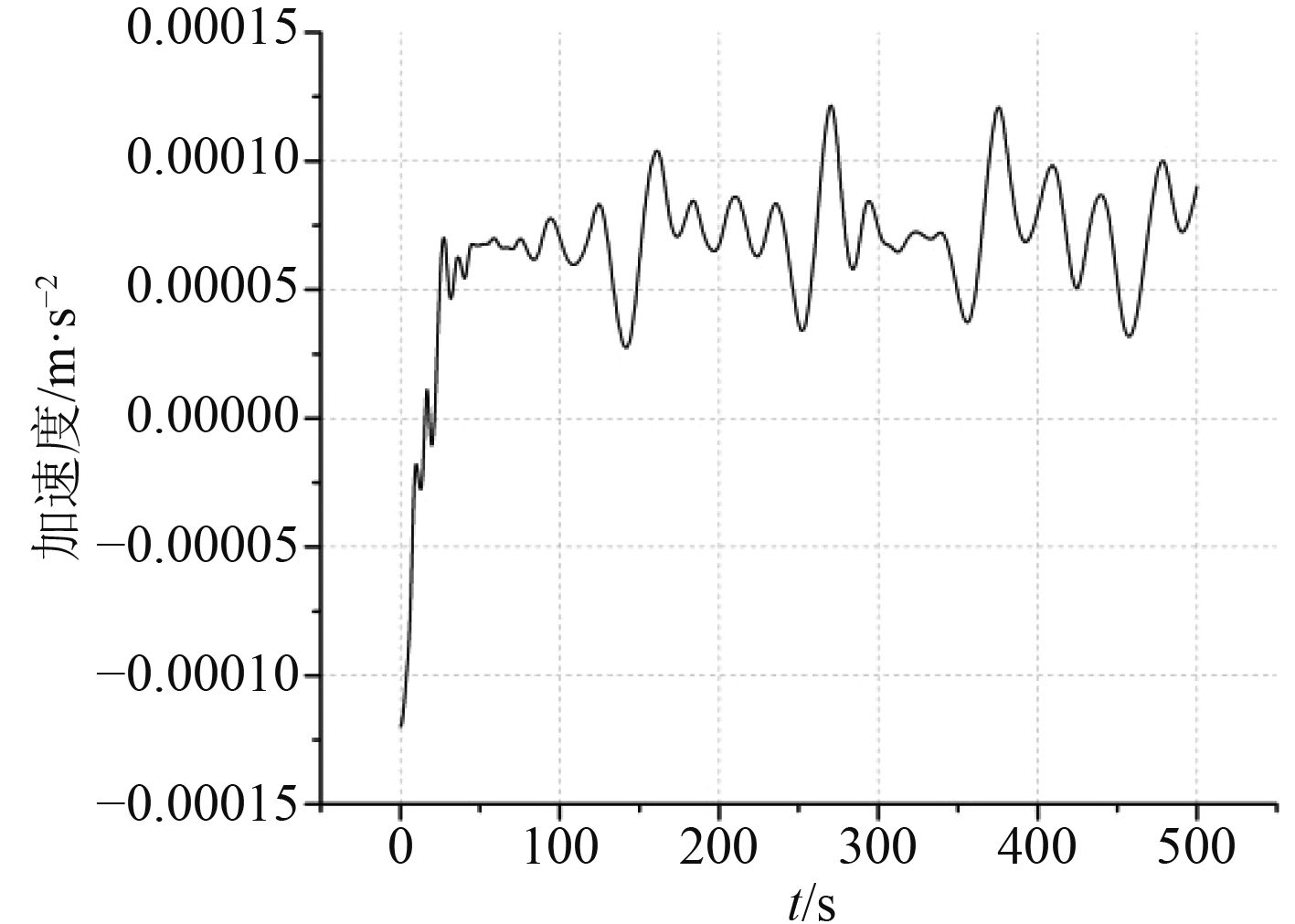
|
图 13 预定速度0.4 m/s时加速度差 Fig. 13 The velocity contrast at the priming speed 0.4 m/s |
|
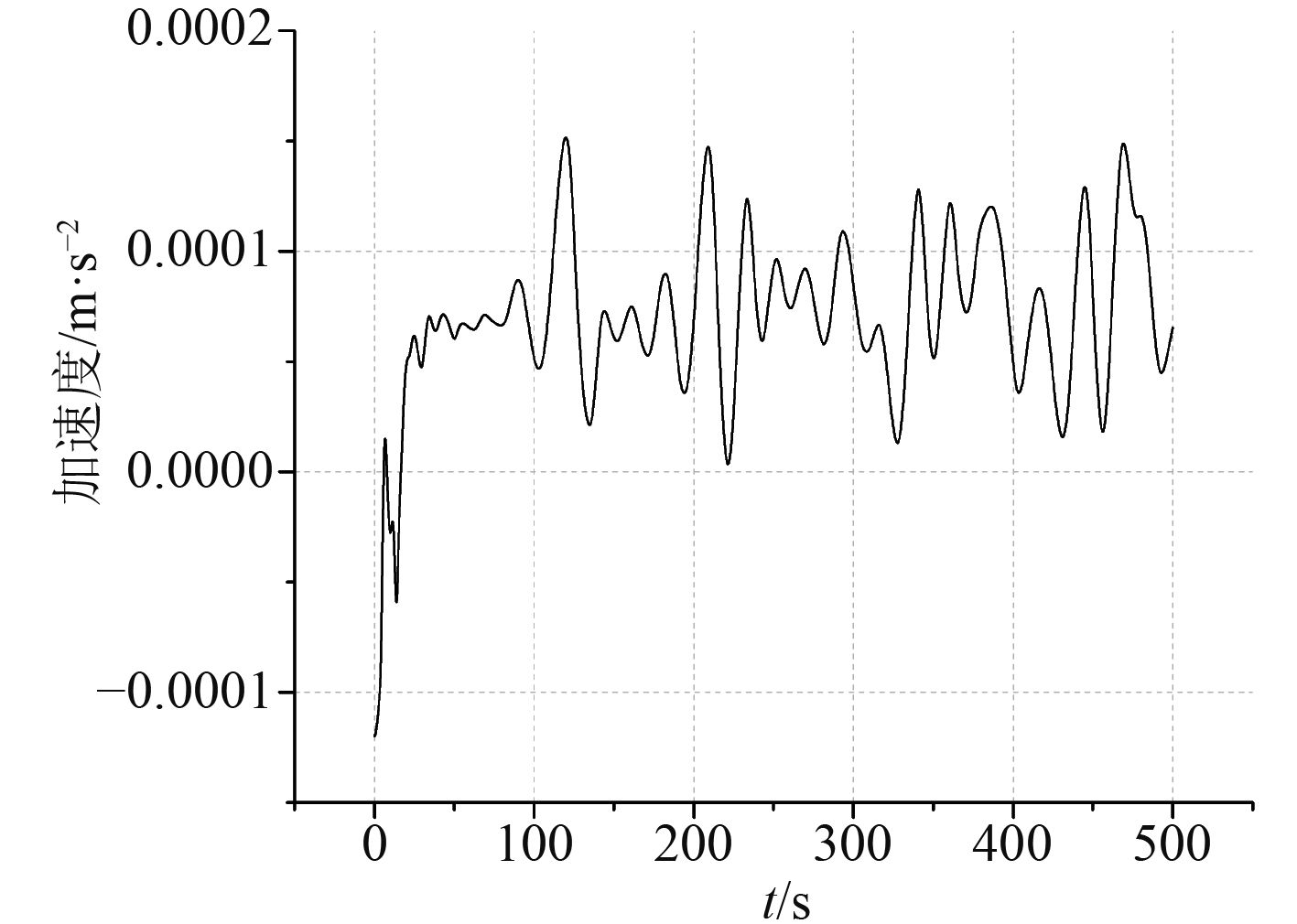
图 14 预定速度0.5 m/s时加速度比较 Fig. 14 The velocity contrast at the priming speed 0.5 m/s |
从图11~图14可以看出,有蓄能器时浮标在达到预定的上浮速度之后其加速度随着时间呈无规律的震荡变化,且随着无蓄能器时预定要达到的匀速上浮的速度的提高,即随着仅靠油泵推出的油量的增大,其震荡得越来越剧烈。除此之外,在浮标上浮的初期,有蓄能器时的加速度小于无蓄能器时的加速度,这是因为有蓄能器时,在浮标上浮之前的运动过程,即浮标下沉的运动过程中,氮气罐中的气体受环境压力影响被压缩时抽出了少量液压油。
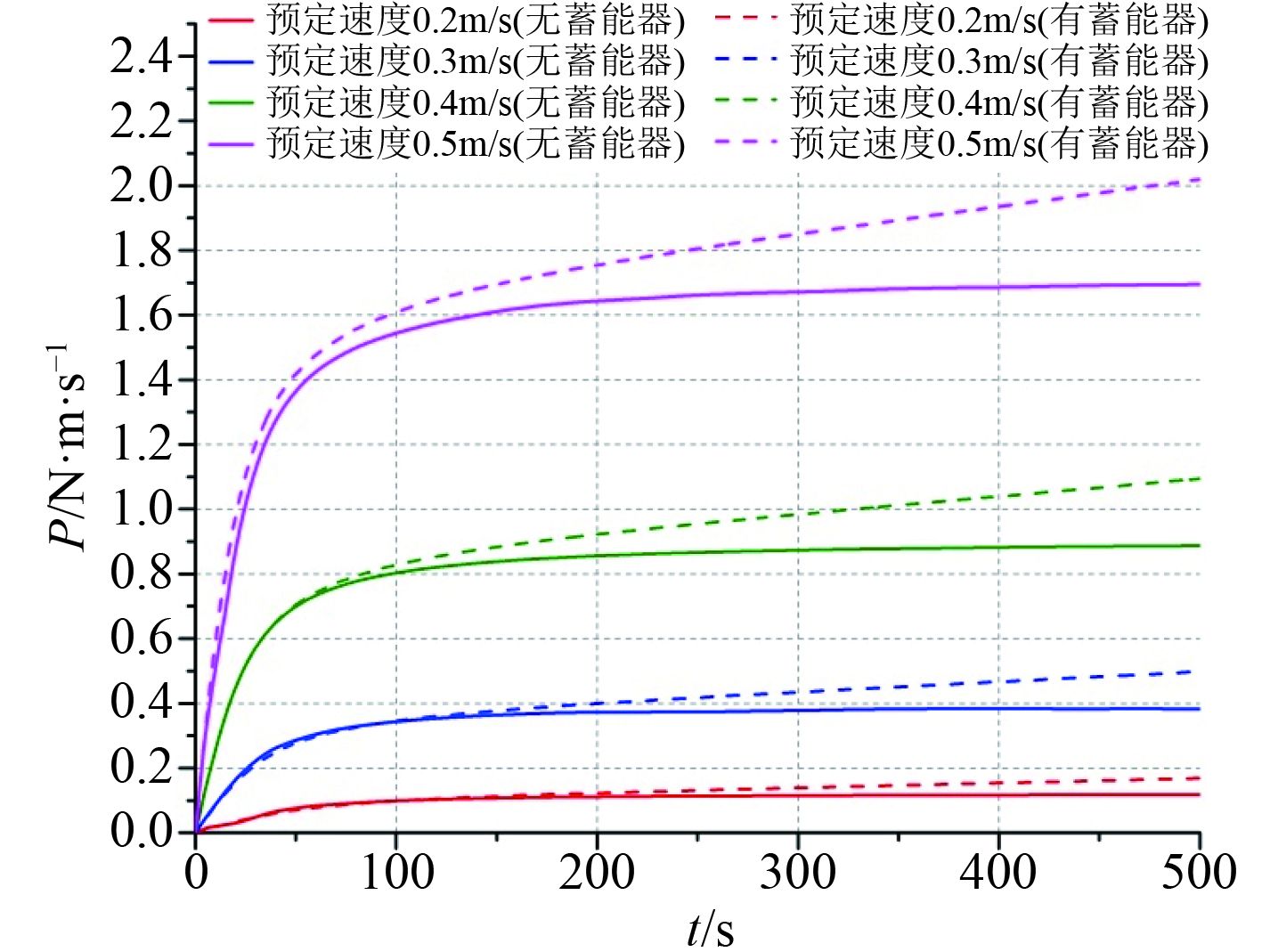
基于上述计算结果,结合式(15)~式(18),得出浮标分别在有无蓄能器时在某一定时间内的功率如图15所示。
从图15可以看出,当浮标未安装蓄能器时,其功率在一段时间后维持稳定,因为此状态下的浮标最终保持匀速上浮,且上浮速度越大其功率越大。当浮标安装蓄能器后,在相同时间内其上浮运动的功率比未安装蓄能器时要大,且预定速度约大其功率增大得越明显。因此可以认为,安装蓄能器对提高浮标上浮功率有一定的作用。
|
图 15 有无蓄能器时功率随时间的变化 Fig. 15 The presence of power changing over time with/without accumulator |
1)基于一种不同于普通浮标的上浮下沉的结构方法,即在传统的通过主浮力泵向外置油囊抽排油的基础上加装氮气蓄能器装置,通过因氮气罐内气体压力随海水压力的变化所储存的能量转变为额外浮力使浮标加速上浮,对这种新型浮标进行其性能的数值仿真计算;
2)用Fluent计算出浮标在各速度下匀速上浮的阻力系数,用力学分析的方法得到浮标在有蓄能器的情况下加速度的表达式并计算出浮标上浮所需要的最小体积;
3)用Matlab进行数值求解得到各种状况下的速度-时间曲线和加速度-时间曲线,并分析得到蓄能器对浮标上浮速度有一定影响;
4)用Matlab进行数值求解得到各种状况下功率-时间曲线,并分析得到安装蓄能器对提高浮标上浮功率有一定的作用。
| [1] |
卢少磊, 孙朝辉, 刘增宏, 等. COPEX和HM2000与APEX型剖面浮标比测试验及资料质量评价[J]. 海洋技术学报, 2016, (1): 84–92.
LU Shao-lei, SUN Chao-hui, LIU Zeng-hong, et al. Comparative testing and data quality evaluation for COPEX, HM2000 and APEX profiling buoys[J]. Journal of Ocean Technology, 2016, (1): 84–92. https://mall.cnki.net/qikan-HYJS201601014.html |
| [2] | 李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学, 2012, 7: 829–837. |
| [3] | 曾庆礼, 张宇文, 赵加鹏. 水下滑翔机总体设计与运动分析[J]. 计算机仿真, 2010, 1: 1–5, 16. http://www.doc88.com/p-98867793476.html |
| [4] | 朱伯康, 刘仁清, 许建平. 一种专门用于低纬度洋区观测的Argo剖面浮标[J]. 海洋技术, 2009, 4: 123–125. |
| [5] |
黄昆仑, 庞永杰, 苏玉民, 等. 潜器线性水动力系数计算方法研究[J]. 船舶力学, 2008, 5: 697–703.
HUANG Kun-lun, PANG Yong-jie, SU Yu-ming, et al. Research on linearity hydrodynamic coefficients calculation method of submergible vehicle[J]. Journal of Ship Mechanics, 2008, 5: 697–703. |
| [6] | 赵宝强, 王晓浩, 姚宝恒, 等. 水下滑翔机三维定常运动建模与分析[J]. 海洋技术学报, 2014, 1: 11–18. http://edu.wanfangdata.com.cn/Periodical/Detail/hyjs201401003 |
| [7] | ZHANG Shao-wei, YU Jian-cheng, ZHANG Ai-qun, et al. Spiraling motion of underwater gliders: Modeling, analysis, and experimental results[J]. Ocean Engineering, 2013, 60(3): 1–13. |
| [8] | L. 普朗特, K. 奥斯瓦提奇, K. 维格哈特著,. 郭永怀, 陆士嘉, 译. 流体力学概论(1版)[M]. 北京: 科学出版社, 1981. |
| [9] |
王世明, 吴爱平, 马利娜. 剖面探测浮标上浮运动研究[J]. 船舶工程, 2010, 6: 57–59, 81.
WANG Shi-ming, WU Ai-ping, MA Li-na. Study on buoy with floating movement by section detection[J]. Ship Engineering, 2010, 6: 57–59, 81. |
| [10] | 李庆扬, 王能超, 易大义. 数值分析(5版)[M]. 北京: 清华大学出版社, 2008. |
| [11] | Clever B. Moler. MATLAB数值计算[M]. 张志涌. 修订版: 北京航空航天大学出版社, 2013. |
| [12] | VERBRUGGHE T, KORTENHAUS A, DE ROUCK J. Numerical modelling of control strategies and accumulator effect of a hydraulic power take-off system[C]// OCEANS 2015 - Genova, Genoa, 2015, 1–10. |
 2018, Vol. 40
2018, Vol. 40
