在现代海上作战平台及攻防体系中,水面舰艇已成为重要一环,随着反舰导弹制导技术的提高,大型水面舰艇面临的威胁与日俱增[1]。作为大型水面舰船最后一道防线的被动防护结构,即舷侧防护舱是舰艇抗爆结构设计的关键。
对于薄板在爆炸冲击载荷作用下的动态响应首先从圆形薄板开始。Wierzbiki和Florence[2]对受冲击波作用的固支圆板进行了实验研究和理论研究,计入了应变率效应。为了对板壳在爆炸冲击载荷作用下的塑性变形进行定量预测,基于Jones的理论研究,Rajendran[3]提出了单自由度(SDOF)下空气中的用于预测塑性中心偏转严重爆炸的经验方法。Hu Gangyi等[4]运用RAVS(Reflected-afterflow-virtual-source)方法来近似计算流体-结构相互作用,并预测爆轰波冲击下双层柱形壳体的瞬态运动。孔祥韶等[5]采用多欧拉域流固一般快速耦合算法,研究舱壁开孔对冲击波压力在舱室角隅汇集和舱室破坏的影响。郑成等[6]利用弹塑性方法研究了爆炸载荷下矩形板的弹塑性响应,并开展了舱室内不同厚度板的爆响应试验。
王芳等[7]对四边约束方形靶板,在爆炸冲击波作用下的塑性大变形响应情况,进行了理论分析与试验研究,在考虑靶板边界影响的前提下根据霍普金森爆炸相似率对靶板的变形挠度与入射比冲量之间的关系给出了修正关系式。
Richard Villavicencio等[8]研究了边界滑移对横向固支的梁受冲击载荷作用时的响应有十分明显的影响,并用数值模拟方法研究了两边固支的矩形板在冲击载荷作用下的塑性变形情况[9]。
本文应用AUTODYN软件,采用三维多欧拉域流固耦合算法,模拟了舱室内舷侧薄板在爆炸冲击载荷作用下的变形以及损伤情况,研究不同边界尺寸对薄板变形挠度的影响。
1 理论分析对一几何尺寸为2X×2Y×δ的矩形薄板,根据矩形板在爆炸冲击波作用下的实际变形形状,可以给出矩形板的位移方程为:
| $\left. {\begin{array}{*{20}{c}}{u = {u_0}\sin \displaystyle\frac{{\pi x}}{X}\cos \frac{{\pi y}}{{2Y}}}\\[8pt]{v = {v_0}\cos \displaystyle\frac{{\pi x}}{{2X}}\sin \frac{{\pi y}}{Y}}\\[8pt]{w = {w_0}\cos \displaystyle\frac{{\pi x}}{{2X}}\cos \frac{{\pi y}}{{2Y}}}\end{array}} \right\}$ |
式中:u,v和w分别为x,y和z方向上的位移;u0和v0分别为x和y方向上的最大位移;w0为板中心点在z方向上的挠度。
在爆炸冲击波载荷作用下,四周约束的矩形板会在极短的时间内发生大挠度塑性变形(远远大于板厚),且在边界处会形成明显的塑性铰线。当薄板发生大挠度变形后的总势能包括:板的弹塑性弯曲变形能Ub,中面应变能Um(中面膜力引起)和四边固定边界处的塑性铰线弯曲变形能U1。
弯曲变形能Ub的计算公式如下:
| $\begin{split}{U_b} =& \frac{{E{\delta ^3}}}{{24\left( {1 - {\upsilon ^2}} \right)}}\int_0^X {\int_0^Y {\left[ {{{\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right)}^2} + {{\left( {\frac{{{\partial ^2}w}}{{\partial {y^2}}}} \right)}^2} + } \right.} } \\& \left. {2\upsilon \frac{{{\partial ^2}w}}{{\partial {x^2}}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} + 2\left( {1 - \upsilon } \right){{\left( {\frac{{{\partial ^2}w}}{{\partial x\partial y}}} \right)}^2}} \right]{ d}x{ d}y\text{。}\end{split}$ |
弹性变形情况下,中面应变能Ume的计算公式如下:
| ${U_{me}} \!=\! \frac{{E\delta }}{{2\left( {1 - {\upsilon ^2}} \right)}}\int_0^X {\int_0^Y {\left[ {\varepsilon _x^2 + \varepsilon _y^2 + 2\upsilon {\varepsilon _x}{\varepsilon _y} + \frac{1}{2}\left( {1 - \upsilon } \right)\gamma _{xy}^2} \right]} } { d}x{ d}y\text{。}$ |
上式仅适用于计算线弹性响应阶段板的中面应变能。
当矩形板从弹性阶段进入塑性响应阶段,相应的应变值ε>εp时,塑性变形过程中,中面应变能Ump的计算公式如下:
| $\begin{align}{U_{mp}} =& \int_0^X {\int_0^Y {\int_0^\delta {\left[ {_0{\varepsilon _x} + {\sigma _0}{\varepsilon _y} + } \right.} } } \\& \left. {\sigma {\tau _p}{\gamma _{xy}} - \frac{1}{2}\left( {{\sigma _0}{\varepsilon _p} + {\sigma _0}{\varepsilon _p} + {\tau _p}{\gamma _p}} \right)} \right]{ d}x{ d}y{ d}z\text{。}\end{align}$ |
四边固定边界处塑性绞线的弯曲变形能,可由下式计算得到:
| ${U_1} = \int_0^Y {{M_p}} {\theta _1}{ d}y + \int_0^X {{M_p}} {\theta _2}{ d}x\text{。}$ |
式中:U1为边界塑性铰线的转动塑性能;θ1,θ2分别为2个边界区域的转动角度;Mp为单位长度板的塑性转动弯矩。
| ${M_p} = 2\int_0^{\frac{\delta }{2}} {{\sigma _0}z{ d}z = } \frac{1}{4}{\sigma _0}{\delta ^2}\text{,}$ |
式中:σ0是材料的屈服应力。
| $\begin{align}{\left. {{\theta _1} = \frac{{\partial \omega }}{{\partial x}}} \right|_{x = X}} = {\omega _0}\frac{\pi }{{2X}}\cos \frac{{\pi y}}{{2Y}},\\{\left. {{\theta _2} = \frac{{\partial \omega }}{{\partial Y}}} \right|_{y = Y}} = {\omega _0}\frac{\pi }{{2Y}}\cos \frac{{\pi x}}{{2X}}\text{。}\end{align}$ |
爆炸冲击波对矩形薄板的作用与作用时间tm密切相关,若tm远小于薄板的振动周期T,则爆炸冲击波对矩形薄板的破坏作用主要取决于冲击波的冲量i,因此可以用动量定理求解矩形钢板的初始动能。
空中爆炸时,若tm远远小于振动周期T,则有矩形板的初始动能为:
| $W = \int_0^X {\int_0^Y {{ d}\left( {\frac{1}{2}m{V_0}^2} \right)} } \text{。}$ |
式中:m为单位面积的钢板质量,m=ρh;ρ为矩形钢板材料的质量密度。
由文献[10]可知,冲击波的作用时间远小于结构响应特征周期,其作用可以看作是一个冲量,因此可采用动量定理求出板的初始动能,即[10]
| $W = \frac{{8XYA_i^2}}{{\rho \delta {H^2}}} \cdot {m_{ef}}^{4/3}\text{。}$ |
根据能量守恒定理,当初始动能全部转化为薄板的势能时,薄板达到最大变形,此时有
| $W = {U_b} + {U_m} + {U_1}\text{,}$ |
将以上变量代入能量方程中,得到
| $\begin{align}& \frac{{{\pi ^4}\left( {1 - 2\upsilon } \right)E{\delta ^3}}}{{384\left( {1 - {\upsilon ^2}} \right)}} \cdot \frac{{w_0^2}}{{{a^2}}} + \frac{{{\pi ^4}E\delta }}{{4096\left( {1 - {\upsilon ^2}} \right)}} \cdot \frac{{w_0^4}}{{{a^2}}} + \\& \frac{{\left( {4\sqrt 3 + 3{\pi ^2}} \right)\delta {\sigma _0}}}{{48}} \cdot w_0^2 - \frac{{\left( {4 + \upsilon } \right)\delta \sigma _0^2}}{{3E}} \cdot {a^2} + \\& {\frac{{4{\sigma _0}{\delta ^2}}}{{\sqrt 3 }}{w_0} - \frac{{8A_i^2m_e^{4/3}}}{{\rho \delta {H^2}}} \cdot {a^2} = 0}\text{。}\end{align}$ |
为求得特定边界尺寸a时的薄板中心挠度w0,在Matlab软件上使用Newton法对上述非线性方程进行迭代求得数值解。
2 数值模拟为了与文献[7]中的实验进行对比,建立5组仿真计算模型。其中薄板边界尺寸为500 mm×500 mm,薄板厚度分别按文献中实验对应设置,试件厚度等参数如表1所示。由于薄板是薄壁结构,其厚度方向尺寸远小于另外2个方向,若使用标准Lagrange算法或Euler算法都将造成过小的时间步长。假设薄板沿厚度方向为零应变,在厚度方向上没有波的传播,同时不传递剪切和旋转力矩,因此使用Shell单元对板结构进行模拟。为优化计算过程并缩短计算时间,建立1/4有限元计算模型进行计算。
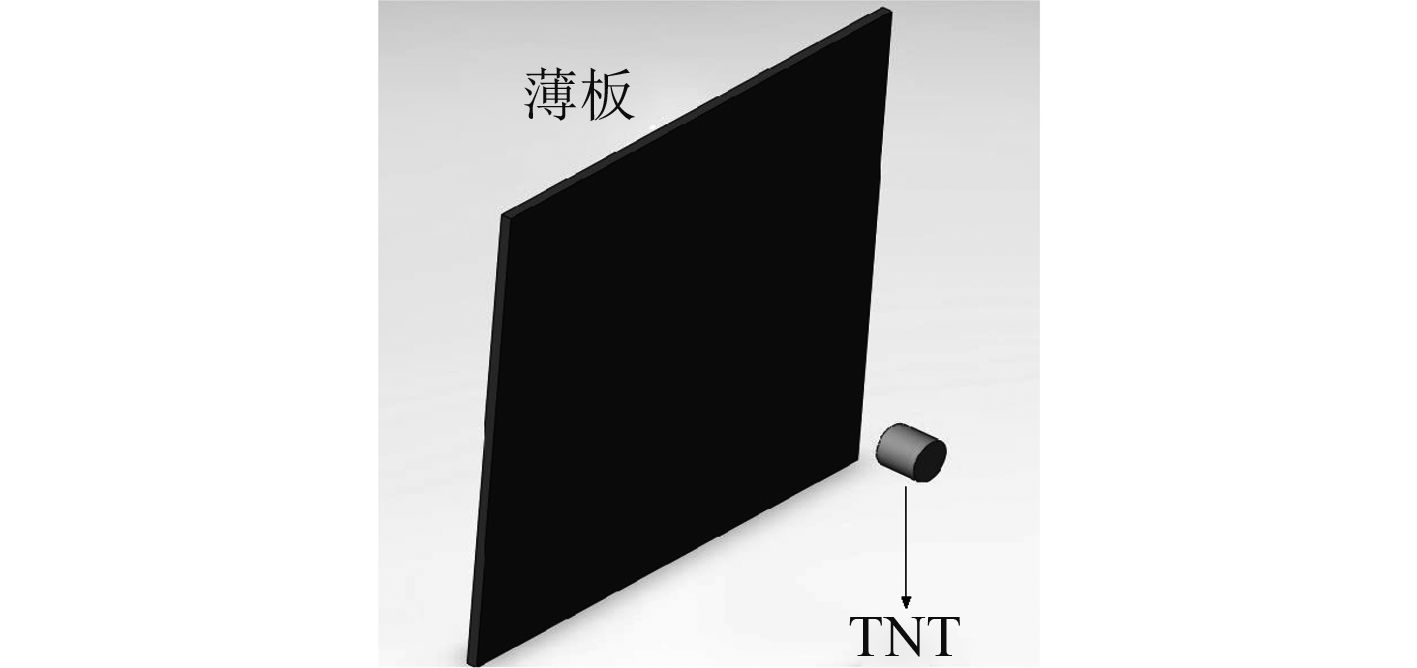
|
图 1 数值模拟计算模型 Fig. 1 Simulation calculation model |
|
|
表 1 仿真算例参数 Tab.1 Parameters of simulation study |
计算中薄板均采用Q235钢,考虑到该材料为一种应变率敏感材料,因此采用Johnson-Cook强度模型,其本构模型是一种粘塑性本构关系。采用Von Mises等效应力与材料的等效塑性应变、等效塑性应变率及温度有关[11],并由此确定其动态屈服应力,即
| ${\sigma _d} = \left( {A + B \times {\varepsilon ^n}} \right) \cdot \left( {1 + c \times \ln {{\dot \varepsilon }^ * }} \right) \cdot \left( {1 - {T^{ * m}}} \right)\text{。}$ |
式中:σd为动态屈服应力;A为静态屈服应力;B和n为材料硬化系数;c为应变率强化参数;m为材料热软化参数;ε*为塑性应变率;T*为无量纲的温度。且
| ${T^ * } = \left( {T - T{}_r} \right)/\left( {{T_m} - T} \right){\text{。}}$ |
式中:T为环境温度;Tr为室温;Tm为材料熔点。
图2显示了薄板在受冲击载荷作用下的Mises等效应力变化情况,数值计算结果如表2所示。
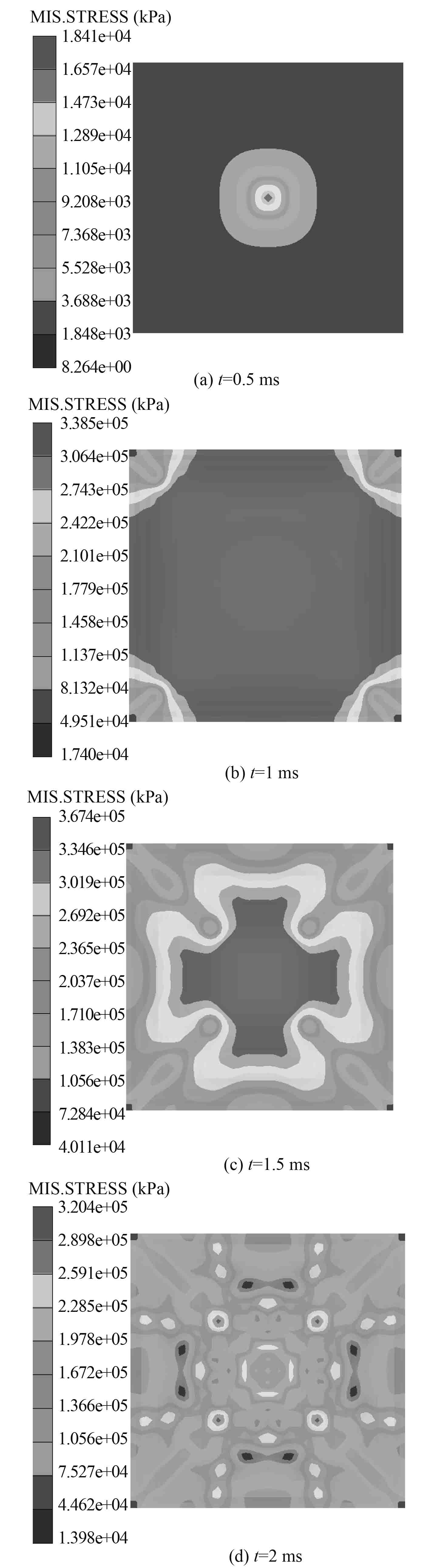
|
图 2 薄板Mises等效应力变化情况 Fig. 2 Process of Mises equivalent stress of the thin plate |
|
|
表 2 试验值分别与数值仿真计算值和理论值对比 Tab.2 Comparison of experiment values,simulation values and theoretical values |
文献[7]中考虑靶板实际受到的载荷为反射冲击波载荷,因此假定反射比冲量的反射系数在一定范围内与反射超压的反射系数相似,同时考虑药量变化对靶板变形挠度的影响,即在相同比冲量作用下,大药量比小药量产生的靶板变形要大,可根据霍普金森爆炸相似率来考虑药量变化的影响,将靶板的变形挠度与入射比冲量之间的关系式作了修正。
将试验值与仿真计算结果与试验结果对比可知,5组数值仿真计算值与试验值相对偏差均小于4%,吻合较好。可以看出,本文所用的流固耦合算法具有良好的可靠性和精确性;而将理论计算值与实验结果相比,两者相差均在10%~15%范围内,其主要原因在于理论计算中并未考虑材料的应变率效应,而是而Q235钢是一种应变率敏感材料,因此实际薄板挠度变形大于理论计算值。
3 边界尺寸影响及分析由第1节的理论分析可知,薄板边界尺寸对于其在爆炸冲击波载荷作用下的挠度变化响应有着重要影响,因此本文采用第2章的流固耦合数值计算方法对建立多组模型不同边界尺寸的影响进行仿真研究,仿真计算模型参数如表3所示。
|
|
表 3 数值计算模型部分参数 Tab.3 Parameters of simulation model |
使用分段三次Hermit插值法将数值模拟计算值与理论计算值绘制成曲线进行对比,如图3所示。
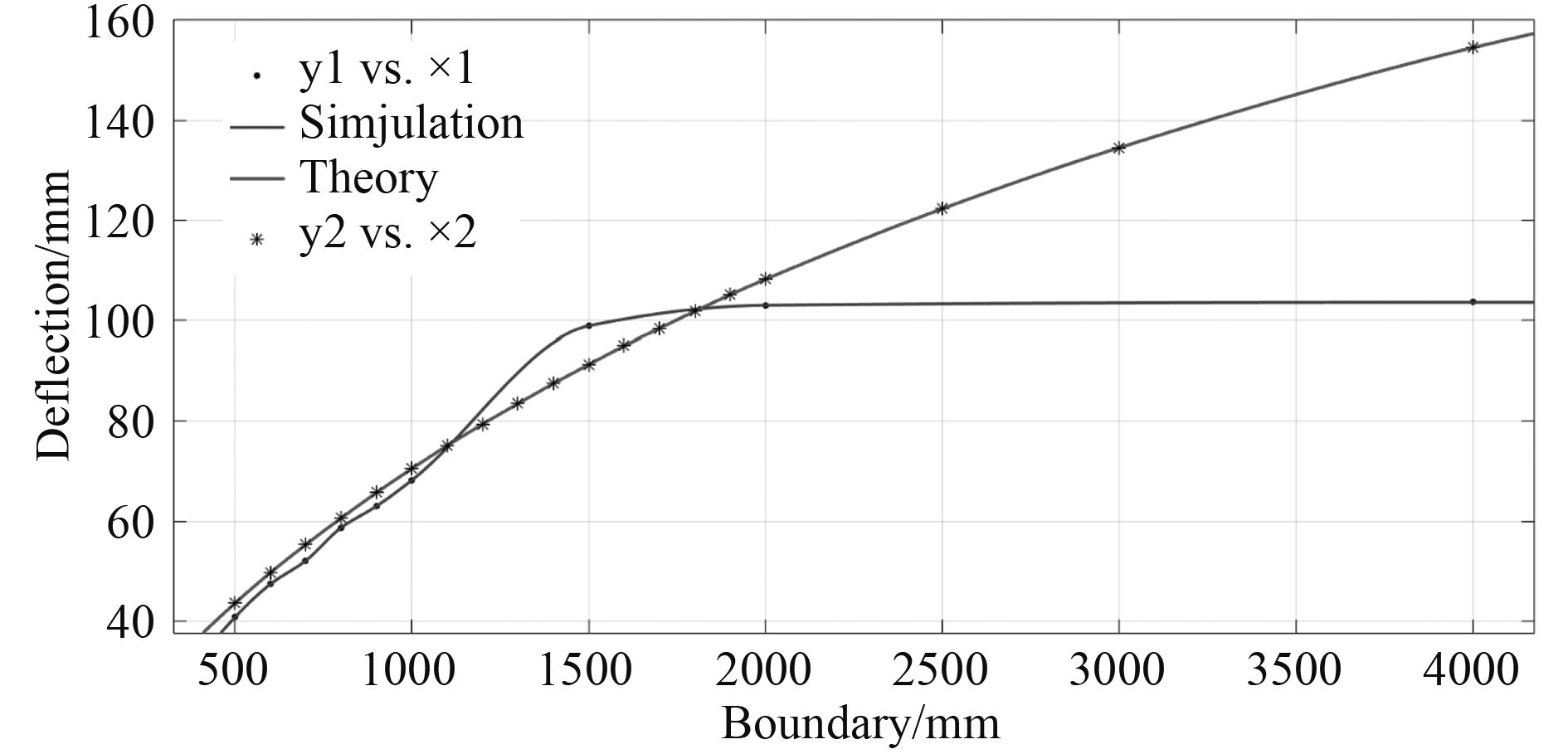
|
图 3 数值模拟与理论计算值对比 Fig. 3 Comparison of simulation values and theoretical values |
对图2两组计算结果定性分析可知,当边界较小时,数值模拟值与理论计算值相近,两者相对偏差在3%~6%之间。随着边界增大,数值模拟计算值趋向于一个恒定值,而理论计算的挠度变形值依旧随边界增大而明显增大。
上述现象表明,当薄板受爆炸冲击载荷作用下,挠度的响应受边界效应影响明显,但随着边界增大,边界效应产生的影响逐渐减小。因此数值模拟结果能可靠且准确的描述挠度随边界增大的变化趋势。与此相反,理论计算在边界增大到一定情况下依旧考虑四边固定边界处塑性绞线的弯曲变形能,显然与实际相悖,故其计算得出的挠度值与实际不符。当薄板边界增大到一定值后,该弹塑性应变能量计算方法已不能准确描述薄板挠度的响应过程。
4 结 语根据以上数值模拟计算结果与文献中实验结果对比,验证了该仿真计算方法有良好的精确度及可靠性。通过对不同边界尺寸下薄板在爆炸冲击载荷作用下挠度的响应情况进行了数值模拟分析,得到以下结论:
薄板四周的约束产生的边界效应会对薄板受冲击载荷后的挠度变化产生影响,但改变不同边界尺寸时挠度对其响应不同。边界尺寸越大,薄板最终挠度变形受边界效应影响越小。当边界尺寸增大到一定数量级后,用弹塑性方法分析薄板挠度变形情况的局限性凸显,由于薄板实际受冲击波作用区域远小于薄板几何尺寸,因此需要对薄板边线处的塑性铰线弯曲变形能进行修正。
| [1] | 袁华, 严必虎. 外军反舰导弹装备使用现状及发展趋势研究[J]. 国防科技, 2014 (6): 46–50. |
| [2] | WIERZBICKI T, FLORENCE A L. A theoretical and experimental investigation of impulsively loading clamped circular viscoplastic plates[J]. Solid and Structures, 1970, 6: 553–568. |
| [3] | RAJENDRAN R, LEE J M. Blast loaded plates[J]. Marine Structures, 2009, 22(2): 99–127. |
| [4] | GANGYI H, FEI X, JUN L. The transient responses of two-layered cylindrical shells attacked by underwater explosive shock waves[J]. Composite Structures, 2010, 92(7): 1551–1560. |
| [5] | 孔祥韶, 吴卫国, 李晓彬, 等. 舰船舱室内部爆炸的数值模拟研究[J]. 中国舰船研究, 2009, (04): 7–11. |
| [6] | 郑成, 孔祥韶, 吴卫国. 爆炸载荷下矩形板弹塑性动态响应研究[J]. 中国造船, 2015, (03): 19–30. |
| [7] | 王芳, 冯顺山, 俞为民. 爆炸冲击波作用下靶板的塑性大变形响应研究[J]. 中国安全科学学报, 2003, (03): 61–64+84. http://d.wanfangdata.com.cn/Periodical_zgaqkxxb200303016.aspx |
| [8] | VILLAVICENCIO R, LIU B, SOARES C G. Response of stiffeners with attached plate subjected to lateral impact[J]. Electrical Measuring Instruments and Measurements, 2012: 393. https://www.researchgate.net/profile/Carlos_Guedes_Soares/publication/259177314_Response_of_stiffeners_with_attached_plate_subjected_to_lateral_impact/links/0deec52c18508ddf49000000.pdf |
| [9] | VILLAVICENCIO R, SOARES C G. Impact response of rectangular and square stiffened plates supported on two opposite edges[J]. Thin-Walled Structures, 2013, 68: 164–182. |
| [10] | 张颖军, 朱锡, 梅志远. 冲击波载荷作用下固支正交各向异性薄板挠度特性分析[J]. 海军工程大学学报, 2010, (03): 102–106. |
| [11] | 谢岩梦, 蔺晓红. 爆炸载荷下复合材料层合板的抗冲击性能[J]. 舰船科学技术, 2014 (8): 11–18. http://d.wanfangdata.com.cn/Periodical_jckxjs201408004.aspx |
 2018, Vol. 40
2018, Vol. 40
