近些年来,船舶动力平台在各个方面得到了很大的发展,向着自动化、智能化的方向发展。其包含了越来越多的子系统及装置,也就使得它在结构、感知和控制方面更加复杂。另外,现代船舶任务趋于多样化,海洋环境相对恶劣,也就造成了动力平台在使用过程中会经常发生损坏和任务变换等情况。目前,船舶动力平台的运行主要依靠工作人员进行管理和控制,他们面对这类不确定信息时会遇到很多的困难;另一方面,据统计工作人员的费用占船舶运行费用的很大比重,所以对动力平台系统进行自我感知和自动控制的研究无论是在实际工程领域还是经济领域都有重要的现实意义。
船舶冷却水系统作为船舶管路系统的重要组成部分,对保障船舶动力平台正常运行起着关键作用[2]。船舶中央冷却水系统担负着对全船设备的冷却任务,对全船的冷却水资源进行统一管理和分配,对其实施有效的检测控制对船舶的正常运行具有重要的意义[1]。
实际的船舶设计和使用中,考虑到空间狭小、各元件在使用的过程中有可能损坏而不能正常工作。这就使得在检测控制时信息存在很大的不确定性和不完备性加大了对系统的控制难度。传统的控制方法已难以满足现代船舶的控制需要,因此需要建立一个更加有效的模型来解决上述存在的问题从而改善对系统的感知能力,对系统实现更加全面有效的控制[2]。
贝叶斯网络是一种进行不确定性推理和数据分析的有效工具,很多领域已经开始了不同程度的研究,但是其在船舶管路系统检测控制中的研究很少并且主要集中在静态网络[2,4]。静态贝叶斯网络只是简单的分析各元器件之间的相互影响关系,对前面时刻系统的状态不加考虑,这就使得在系统监测控制时确实很多实时的数据信息造成错误的判断[6]。
动态贝叶斯网络(Dynamic Bayesian Network,DBN)将时间因素添加到了贝叶斯网络中,能使系统根据前面时刻的运行状态推理和诊断未来运行状况。本文对 DBN 在船舶中央冷却水检测控制系统中的应用进行了研究,通过构建动态网络模型并进行网络推理仿真实验,以证明此方法的有效性。
1 贝叶斯网络 1.1 贝叶斯网络定义贝叶斯网络是根据变量之间的相互独立关系建立起来的一种概率图模型。它包含 2 个部分,一个是代表变量之间关系的贝叶斯网络结构图,即向无环图(Directed Acyclic Graph,DAG),实际中存在的各个变量用相应的节点来表示,而变量之间的继承关系和独立关系则用节点之间的连线来表示。另一部分就是表示节点之间关系强弱的条件概率表(Conditional Probability Tables,CPT)。一个贝叶斯网络必须满足以上的条件,才能进行计算和推理[5,7]。
贝叶斯网络中的节点Vi 和其非直接父节点Vj 条件独立与该父节点Pa(Vi ),即:
| $ Pa({V_i}/{V_j},Pa({V_i})) = P({V_i}/Pa({V_i})) \text{,}$ | (1) |
利用条件独立性,可将贝叶斯网络中的n 个变量的联合概率分解为:
| $ P({V_1},{V_2},...,{V_n}) = \prod\limits_{i = 1}^n {P({V_i}/Pa({V_i}))} \text{。}$ | (2) |
因此,贝叶斯网络中的弧表示变量间的直接影响关系,而没有直接影响关系的变量则为相互独立。然而,贝叶斯网络不能表示前后时刻的关系,只能对某一时刻进行推理。动态贝叶斯网络在贝叶斯网络的基础上做了延伸,具备了一定的时序能力。
1.2 动态贝叶斯网络DBN 模型是把时间的因素加入到了静态贝叶斯网络模型里,将静态网络扩展到时态领域充分考虑了时间对系统运行的影响。在建立模型前先进行以下假设:
1)假设在一有限时间内条件概率变化过程对所有t 一致平稳。
2)假设动态概率过程是马氏的(Markovian),即满足:
| $ \begin{array}{l} P(X[t]|X[1],X[2],...,X[t]) = P(X[t + 1]|X[t]) \end{array} \text{。}$ | (3) |
也就是说未来时刻的概率只与当前时刻有关而与过去时刻无关。
3)假设相邻时间的条件概率平稳,即P(X[t + 1]|X[t])与时间t 无关,可容易得到不同时间片之间的转移概率为P(X[t + 1]|X[t])。
基于以上假设,建立在随机过程时间轨迹上的联合概率分布的 DBN 可由 2 部分组成:
1)先验网B0,定义在初始状态X[1] 上的联合概率分布;
2)转移网B→,定义在变量X[1] 与X[2] 上的转移概率P(X[t + 1]|X[t])。
因此,若给定一个 DBN 模型,则在X[0],X[1],…,X[t] 上的联合概率分布为:
| $ \begin{array}{l} P(X[1],X[2],...,X[t]) = \\ \quad \quad \quad {P_{{B_0}}}(X[1])\prod\limits_{t = 1}^T {{P_{{B_ \to }}}(X[t + 1]|X[t])} \end{array} \text{。}$ | (4) |
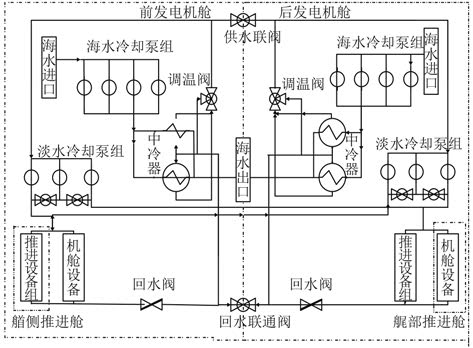
冷却水系统的作用就是冷却动力装置中的发电机组、推进设备、各个辅助设备以及需要冷却的其他装置,使得各个设备得到良好的冷却维持稳定的工作。目前,在新型的电力推进装置中,其需要冷却的设备更多,系统更加复杂这也就对冷却系统提出了更高的标准。当前世界上很多船舶的动力装置冷却方式采用的是半封闭式冷却水系统,其冷却方式是由淡水冷却船舶主机,用海水冷却淡水和其他散热介质,淡水冷却的部分是闭式循环,海水冷却的部分是开式循环[8,9]。图 1 为一典型的中央冷却水系统原型结构图,系统由海水冷却回路和淡水冷却回路。海水冷却在前后机舱各设一个中冷分站,主要部件有机舱海底门、海水过滤器、通海阀、板式冷却器、海水冷却泵、管路及其附件等。淡水冷却系统在前后机舱各设 1 个淡水冷却泵单元,每个单元包括 1 台首部设备兼停泊冷却泵、1 台尾部设备冷却和 1 台备用泵,首部设备有前机舱内各冷却设备和首部推进设备,尾部设备有后机舱内各冷却设备和尾部推进设备。淡水冷却系统还包括中冷器、电子除垢设备、中压发电机组自带水泵、中压发电机组自带淡水冷却器、温控阀、低温淡水膨胀水箱及附件等。该系统的工作原理为:先由海水冷却泵将舷外海水输送到中冷器,在中冷器内完成海水与高温热水的热量交换,使淡水温度维持在一定的范围内。经过热交换的海水会被排除舷外,经过冷却的淡水被输送到所需的设备,对设备冷却之后重新到海水冷却系统进行再循环。
|
图 1 中央冷却水系统原型图 Fig. 1 Prototype of the central cooling water system |
在船舶中央冷却水系统中前后舱的冷却水舱和循环水泵负责整个装置的有效运转,经过简化的管路系统仍涉及 21 个用户和 48 个阀及相关的传感器,在实际中冷却水系统的设备和管路更为复杂并且设有很多的安全保护装置及系统,因此针对这类复杂的系统建立动态贝叶斯网络模型就变得极为复杂。为了降低对船舶中央冷却水系统建立动态贝叶斯网络的复杂性以及提高实验验证的准确性,本文只考虑对资源子系统和 2 个负载子系统建立贝叶斯网络模型。图 2 即为简化的中央冷却水系统,包括有前后舱泵组及中冷器组成的资源子系统和 2 个机舱设备组成的 2 个负载子系统。系统在运行时,中低温的淡水冷却水经过负载子系统的推进装置和机舱设备后进行热量交换形成高温淡水;高温淡水流经资源子系统的中冷器后把热量传递出去形成中低温淡水,进而重新供给负载子系统形成循环。

|
图 2 简化的中央冷却水系统 Fig. 2 Simplified central cooling water system |
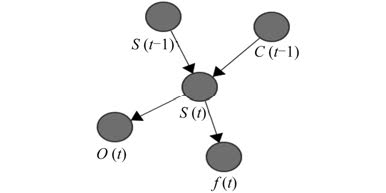
在对 3 个子系统建立动态网络模型前,先对阀或者泵采用的最小组件模型进行介绍。如图 3 所示,该组件状态模型反应了中央冷却水系统中泵、阀、流量在t 时刻和t-1 时刻的状态及相应的变化过程,s(t-1)是组件t-1 时刻的状态,表示为 4 种状态 {开,关,开死,关死},f(t)是组件t 时刻上的流量信息,表示为 3 种状态 {正流,逆流,无流量},c(t-1)是t-1 时刻组件得到的执行命令,表示为 2 种状态 {开,关},o(t)是组件的开关状态,表示为 2 种 {开,关}。
|
图 3 单个组件的 DBN 模型 Fig. 3 DBN model of a single component |
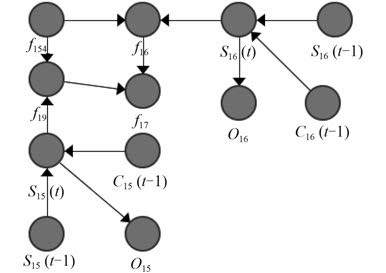
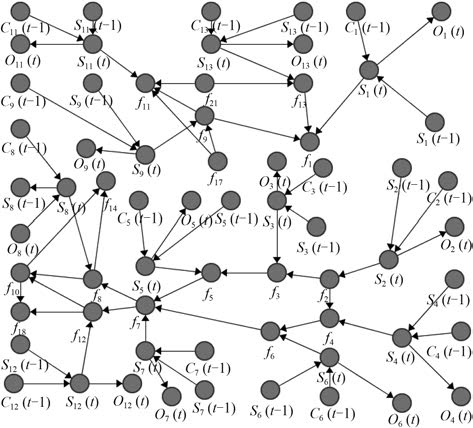
综合上述介绍,所有的有向无环图都是在满足马尔科夫特性的前提下,在 2 个时间片t-1 和t 上建立起来的。它由部分在t-1 时间片的节点和所有在时间片t 的节点组成,在时间片t-1 的节点只包含那些与时间片t 有动态边的节点。在初始时刻,t0 时间片内并且跟t1 时间片的节点有动态边的节点有着统一的分布。在t 时间片内,每个t-1 的节点是通过 DBNs 的信度更新算法P(vi (t-1)|y(t-1))加入软证据进行更新的。本文中,控制系统只需要当前的状态计算并不用进行复杂的耗费时间的平滑和预测。根据 DBN 的原理,对中央冷却水系统进行建模,同时对阀和泵采用最小组件级建模,它们对应的结构如图 4~图 6 所示。图中负载子系统 1 和资源子系统有共同的网络节点f14 和f17,负载子系统 2 跟资源子系统有着共同节点f18 和f21。3 个子系统通过一条链连接组成一个简单的树形结构,其满足贝叶斯网络内部的运行特性,D-分离。在 3 个子系统形成的贝叶斯网络中,节点f14 的父节点f8 和f10 都是在资源子系统的贝叶斯网络中;节点f17 的父节点f15 和f16 都是在负载子系统 1 的贝叶斯网络中。同样,在负载子系统 2 的叶斯网络和资源子系统贝叶斯网络中也存在相似的节点关系,节点f18 的父节点f10 和f12 都是资源子系统贝叶斯网络的节点;节点f21 的父节点f19 和f20 都是负载子系统 2 贝叶斯网络的节点。像 {f14,f17} 和 {f18,f21} 这 2 组节点所满足的条件,即为 D-分离的定义。
|
图 4 负载子系统 1 的 DBN 模型 Fig. 4 DBN model of load subsystem 1 |
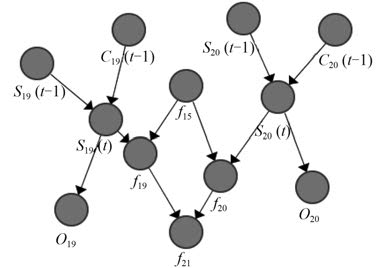
|
图 5 负载子系统 2 的 DBN 模型 Fig. 5 Model of load subsystem 2 |
|
图 6 资源子系统 DBN 模型 Fig. 6 DBN model of resource subsystem |
本文采用的 BK 算法是一种有参的近似推理算法,它是利用参数的方法对系统信度状态进行近似。它是基于变量之间的弱相关性来生成相对独立的团,不需要执行传统联合树构建中的正规化和三角化的操作,这就使得计算的效率得到了显著提高。在 1.5 联合树推理算法中,将接口中的所有节点当成一个团,如果接口规模太大,推理在计算机上将变得难以处理。BK 算法是将接口分解为若干子团,并通过边际化操作获得每个子团的概率分布,然后将这些子团的概率分布乘积作为联合概率分布的近似,即有
| $ P({I_t}|{Y_{1:t}}) \approx \prod\nolimits_{c = 1}^C {P(I_t^c|{Y_{1:t}})} \text{,}$ | (5) |
式中右侧是团C 中节点的概率分布。BK 算法是利用参数的方法对系统状态变量的概率进行近似,利用系统不同部分之间的弱交互性,人工的在弱交互的子系统之间加入独立性。BK 算法人工的将系统W 划分成了相对独立的子系统W = {W1,W2,…,Wk },其中Wk 是其子系统。整个系统状态变量的概率分布表示成因式的形式,每个因式是关于每个子系统局部化的概率分布。DBNs 的联合概率分布可表示为:
| $ P(X) \approx \prod\nolimits_{i = 1}^k {P({X^{{W_i}}})} \text{。}$ | (6) |
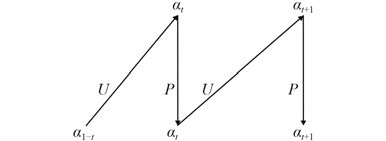
下面介绍 BK 算法的推理过程,由于接口的节点可分为几个子团,这些团在作为下一时间片的先验信息之前先经过证据采集和分发来实现更新;在加入新的证据后,需要对这些团的概率分布进行更新,并作为下一时间片的先验信息,来实现传播。图 7 所示为信息的前向传播过程。
|
图 7 BK 算法更新投影过程 Fig. 7 Updated projection process of BK algorithm |
由图 7 可看出,信息的传播是先从 DBNs 因式形式的先验联合概率分布αt-1 开始,加入新的证据对概率分布进行更新,得到 DBNs 耦合形式的联合概率分布αt ,即图中的U 步操作;然后通过执行概率函数和效用函数的边际化操作,将耦合形式的后验概率分布αt 投影到因式形式的联合概率分布αt ,投影是对概率分布的一种近似操作,即为图中P 步操作。
5 仿真实验为了验证动态贝叶斯网络在船舶中央冷却水系统中应用的正确性和有效性,本文采用了 BayesianLab 软件进行了仿真实验。该软件采用图形化建模界面,具有良好的交互性。并且,该软件具有精确推理算法和近似推理算法,能够进行动态贝叶斯网络推理,操作方便,应用广泛。使用时首先在 BayesianLab 内构建前面所讲述的船舶中央冷却水的模型,然后再根据专家经验和实际船舶上的数据得到动态贝叶斯网络的先验概率表并将其输入到软件里面。在对中央冷却水系统建模完成之后,设定冷却水系统的运行工况为:开始时刻,所有元器件状态为完好并正常工作的、所有流量节点为可观察的、各阀门开度也可观察、资源利用率为 0.8、仿真实验数据采集的间隔为 4 s,总的仿真时间为 120 s、负载 1 的温度高于额定值而负载 2 的温度低于额定值。仿真的结果如图 8~图10 所示。

|
图 8 负载的温度变化情况 Fig. 8 The temperature change of the load |
|
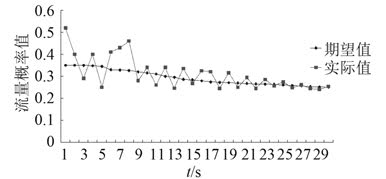
图 9 负载 1 的流量概率值变化趋势 Fig. 9 Change trend of flow probability of load 1 |
|
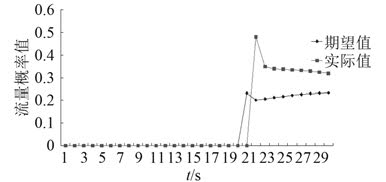
图 10 负载 2 的流量概率值变化趋势 Fig. 10 Change trend of flow probability of load 2 |
在初始时刻,负载 1 的温度高于额定温度,而负载 2 的温度低于额定温度。因此,开始时刻只有负载 1 需要更多的冷却水来降低自己的温度,在图 9 冷却水的流量概率值期望值和实际值都大于 0。负载 2 开始时刻的温度低于额定的值,所以其流量概率值为 0,但是随着功率的不断输入并且功率利用率只有 0.8,则有 20% 的功转变为热量造成图中所示的负载 2 温度升高。大约在t = 96 s 时,负载 2 的温度超过了额定值,所以在图 10 中可以看到负载 2 的流量期望值增大不再为 0。
在仿真的结果中可以看出,实际值一直跟随期望值的趋势变化,表明了动态贝叶斯网络会根据前面时刻的状态给出合理的控制命令来控制冷却水系统。综上所述,根据这个算例可以得到动态贝叶斯网络会随时间的变化经过状态推理给出合理的控制命令。
6 结 语本文针对复杂的船舶中央冷却水系统自动感知的问题,建立了其动态贝叶斯网络模型,采用动态贝叶斯网络的 BK 算法进行感知和状态推理。推理的结果证明了在加入时间的因素之后,动态贝叶斯网络在船舶复杂管路系统应用的可行性和合理性。研究动态贝叶斯网络在船舶中央冷却水系统中的应用具有重要的实际意义和理论价值。
| [1] |
刘富斌, 田志定, 向征涛. 混流式中央冷却系统设计探讨[J]. 船海工程 , 2002 (2) :49–52.
LIU Fu-bin, TIAN Zhi-ding, XIANG Zheng-tao. Design study of mixed flow central cooling system[J]. Ship&Boat , 2002 (2) :49–52. |
| [2] |
付尧, 曾凡明, 陈于涛, 等. 舰用柴油机冷却水系统贝叶斯状态推理方法[J]. 舰船科学技术 , 2014, 36 (8) :42–45.
FU Yao, ZENG Fan-ming, CHEN Yu-tao, et al. Research on the Bayesian state reasoning methods for marine diesel cooling water system[J]. Ship Science and Technology , 2014, 36 (8) :42–45. |
| [3] | XIANG Yang, POOLE D, BEDDOES M P. Multiply sectioned Bayesian networks and junction forests for large knowledge-based systems[J]. Computational Intelligence , 1993, 9 (2) :171–220. DOI:10.1111/coin.1993.9.issue-2 |
| [4] |
王三民, 王宝树. 贝叶斯网络在战术态势评估中的应用[J]. 系统工程与电子技术 , 2004, 26 (11) :1620–1623.
WANG San-min, WANG Bao-shu. Application of Bayesian networks in tactical situation assessment[J]. Systems Engineering and Electronics , 2004, 26 (11) :1620–1623. |
| [5] |
奚海荣, 马文丽, 梁斌. 基于贝叶斯网络SP算法的改进研究[J]. 计算机技术与发展 , 2009, 19 (3) :155–157.
XI Hai-rong, MA Wen-li, LIANG Bin. Improvement of SP algorithm based on Bayesian networks[J]. Computer Technology and Development , 2009, 19 (3) :155–157. |
| [6] |
赵晓辉, 姚佩阳, 张鹏. 动态贝叶斯网络在战场态势估计中的应用[J]. 光电与控制 , 2010, 17 (1) :44–47.
ZHAO Xiao-hui, YAO Pei-yang, ZHANG Peng. Application of dynamic Bayesian network in battlefield situation assessment[J]. Electronics Optics&Control , 2010, 17 (1) :44–47. |
| [7] |
宫义山, 高媛媛. 基于信息融合的诊断贝叶斯网络研究[J]. 计算机技术与发展 , 2009, 19 (6) :106–108.
GONG Yi-shan, GAO Yuan-yuan. Diagnostic Bayesian networks research based on information fusion[J]. Computer Technology and Development , 2009, 19 (6) :106–108. |
| [8] | MIHAJLOVIC V, PETKOVIC M. Dynamic Bayesian networks:a state of the art[R]. CTIT technical reports series, TR-CTIT-34, University of Twente Document Repository, 2001. |
| [9] | COOPER G F. The Computational complexity of probabilitic inference using Bayesian belief networks[J]. Artificial Intelligence , 1990, 42 (2/3) :393–405. |
| [10] | MURPHY K P. Dynamic Bayesian networks:representation, inference and learning[D]. Berkeley, Fall:University of California, 2002. |
| [11] |
胡大伟. 动态贝叶斯网络的近似推理算法研究[D]. 合肥:合肥工业大学, 2009.
HU Da-wei. The research on approximate reasoning algorithm for dynamic Bayesian networks[D]. Hefei:Hefei Polytechnic University, 2009. |
| [12] |
俞奎. 贝叶斯网络建模及推理算法研究[D]. 合肥:合肥工业大学, 2007.
YU Kui. The research of learning and inference algorithm for bayesian networks[D]. Hefei:Hefei Polytechnic University, 2007. |
| [13] |
刘俊娜. 贝叶斯网络推理算法研究[D]. 合肥:合肥工业大学, 2007.
LIU Jun-na. Research on the Bayesian networks inference[D]. Hefei:Hefei Polytechnic University, 2007. |
| [14] |
董晨. 贝叶斯网络在电力系统故障中的应用研究[D]. 沈阳:沈阳工业大学, 2010.
DONG Chen. Applications and research of the Bayesian network in power system fault diagnosis[D]. Shenyang:Shenyang University of Technology, 2010. |
 2016, Vol. 38
2016, Vol. 38
