2. 船舶振动噪声重点实验室, 湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
空气弹簧作为机械系统减振降噪的关键部件,其机械阻抗特性与隔振效果有着紧密的联系。机械阻抗是描述弹性元件动态特性的重要参数,它反映了弹性元件激励与响应之间的关系,是弹性元件隔振设计和性能优化的主要指标。机械阻抗参数的获取主要有实验测试和解析计算2种方法[1],对于一般的空气弹簧模型来说,由于材料的非线性、几何结构的复杂性使得机械阻抗很难通过解析计算的方法来精确地获得,更多的是依赖于实验测试[2-3]。此外,在研究空气弹簧时一般都是基于气体状态方程,近似地认为内部各部位的气压均匀变化甚至是相同的[4-6],忽略由于空气体积元的扰动所产生的声压对机械阻抗特性的影响。
基于以上问题,本文通过建立一个理想化的筒式空气弹簧模型,用近似解析算法基于线性空气波动理论求解出空气弹簧内部声压场的分布规律,分析内部声压在机械阻抗中所起的作用;讨论了相关参数对机械阻抗特性的影响规律。这对于空气弹簧以及空气管路系统减振元件的传递特性研究具有一定的借鉴意义。
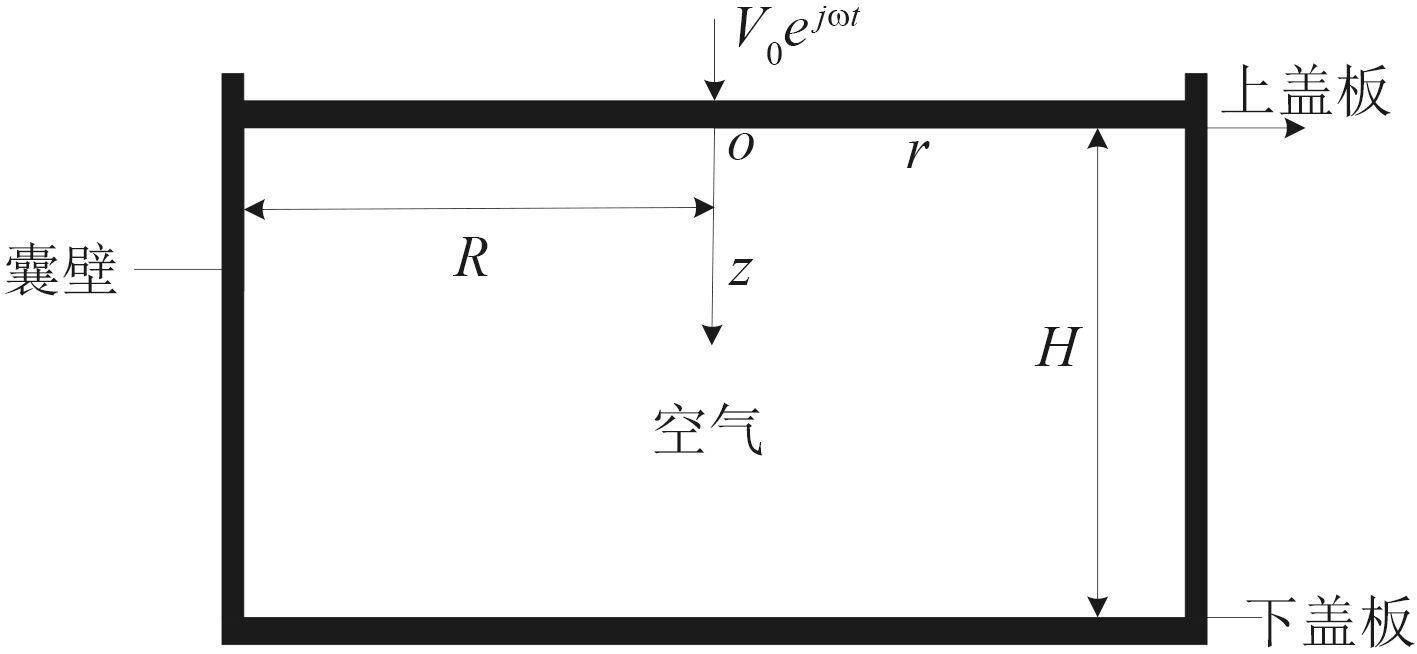
1 数学模型本文所建立的理想化筒式空气弹簧模型如图 1 所示。它由上下盖板、囊壁以及内部空气组成。在所建模型中,为了便于计算有很多理想化的假设:上盖板在小振幅谐波激励下近似当作线性来处理;盖板在振动过程中不考虑其形状的变化以及与其他部件可能会发生的共振;忽略盖板振动过程中与内壁的摩擦;将空气弹簧的囊壁看成是刚性体。
|
图 1 理想化的筒式空气弹簧模型 Fig. 1 Idealized cylinder type air-spring mode |
当上盖板受到谐波激励时,会对与上盖板毗邻的空气体积元产生一个扰动,对于空气振动声场,其声压分布用下述声波方程来描述[7]:
| $\frac{1}{\rho {{c}^{2}}}\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}+\nabla (-\frac{1}{\rho }(\nabla p-q))=Q。$ | (1) |
当不存在声源时偶极子辐射源 q 与单极子辐射源 Q 均为 0,为便于计算,引入势函数Φ,它与声压之间的关系为:
| $\phi =\int{\frac{p}{{{\rho }_{0}}}}\text{d}t。$ | (2) |
令$ \varPhi {\rm{ = }}\Theta {e^{jwt}}$,函数转化到频域即为亥姆霍兹方程${\nabla ^2}\Theta + {k^2}\Theta= 0 \; (k = \omega /c)$。下盖板固定,以上盖板圆面中心为原点,建立柱坐标系 ORZ。当模型内壁是刚体时,内部声压是由气体的垂向运动产生。采用分离变量法可得势函数在柱坐标中的表达式为:
| $\begin{align} & \phi ={{e}^{j\omega t}}\sum\limits_{n=0}^{\infty }{\left[ {{A}_{n}}{{J}_{n}}\left( {{k}_{r}}r \right)+{{B}_{n}}{{N}_{n}}\left( {{k}_{r}}r \right) \right]}\times \\ & ({{A}_{1}}\cos h{{k}_{z}}z+{{B}_{1}}\sin h{{k}_{z}}z)\cos \left( n\varphi -{{\varphi }_{n}} \right)。 \\ \end{align}$ | (3) |
由柱诺依曼函数在零点发散的性质可知式中 Bn = 0 [8]。当上盖板做等幅同相振动,即在 z = 0 处$\dot V{(z,t)_{z = 0}} = {\dot V_0}{e^{j\omega t}}$时,势函数是一个与φ、r 无关的表达式。由式(3)可知,要使势函数表达式与φ无关,则需 n = 0,可得:
| $\phi ={{e}^{jwt}}{{J}_{0}}\left( {{k}_{r}}r \right)(A\cos h{{k}_{z}}z+B\sin h{{k}_{z}}z)\text{。}$ | (4) |
空气弹簧内壁为刚体时,内部气体单元在壁面处的边界条件是径向速度为 0,即
| ${{\dot{V}}_{r}}{{\left( r,z,t \right)}_{r=R}}=-{{\frac{\partial \text{ }\phi }{\partial r}}_{r=R}}=0\text{,}$ | (5) |
由式(5)得 Jl(krR) = 0,用${\tau _{0m}}$表示此表达式的根,对应于不同的 m 值,可得到不同的轴向与径向波数表达式,式(5)可变为:
| $\begin{align} & \Phi ={{e}^{jwt}}\sum\limits_{m=0}^{\infty }{{{J}_{0}}\left( \frac{{{\tau }_{0m}}}{R}r \right)({{A}_{m}}\cos h\sqrt{{{k}^{2}}-{{(\frac{{{\tau }_{0m}}}{R})}^{2}}}z}+ \\ & {{B}_{m}}\sin h\sqrt{{{k}^{2}}-{{(\frac{{{\tau }_{0m}}}{R})}^{2}}}z)。 \\ \end{align}$ | (6) |
由式(6)可知,要使势函数表达式与轴向 r 无关,则需 m = 0,可得:
| $\phi =(A\cos hkz+B\sin hkz){{e}^{jwt}}。$ | (7) |
此时在空气弹簧内部只有沿管轴方向传播的均匀平面波,即只有(0,0)次简正波。由上下盖板处边界条件$\dot V{(z,t)_{z = 0}} = {\dot V_0}{e^{jwt}}$、$\dot V{(z,t)_{z = 0}} = 0$可得式(7)中系数 A和B 的值。综上可得空气弹簧内部声压表达式为:
| $P(z,t)=j{{\rho }_{0}}c\frac{{{{\dot{V}}}_{0}}}{\sin hkH}\cos h\left[ k(H-z) \right]{{e}^{jwt}}。$ | (8) |
空气弹簧模型可以看成是由惯性和弹性元件并联而成的无阻尼约束的单自由度系统,惯性元件由盖板质量组成,弹性元件由内部空气组成。由机械阻抗的定义可知当上盖板受到谐波激励时输入阻抗和传递阻抗表达式为[9]:
| $\left\{ \begin{matrix} {{Z}_{11}}=j\omega M+{{k}_{1}}/j\omega , \\ {{Z}_{12}}={{k}_{2}}/j\omega , \\ \end{matrix} \right.$ | (9) |
式中: M 为上盖板质量;k1和k2 分别为在上下盖板处的动刚度。由声压表达式(8)可知,在上盖板 z = 0 和下盖板 z = H 处由声压所产生的动态力分别为:
| $\left\{ \begin{matrix} {{F}_{p}}=j{{e}^{jwt}}{{\rho }_{0}}c{{{\dot{V}}}_{0}}\pi {{R}^{2}}\cos h(kH)/\sin h(kH), \\ F{{'}_{p}}=j{{e}^{jwt}}{{\rho }_{0}}c{{{\dot{V}}}_{0}}\pi {{R}^{2}}/\sin h(kH), \\ \end{matrix} \right.$ | (10) |
由式(10)可得此时动刚度 k1和k2 表达式为:
| $\left\{ {\matrix{ {{k_1} = {\rho _0}c\omega \cos h(kH)/\sin h(kH)\pi {R^2},} \cr {{k_2} = {\rho _0}c\omega \pi {R^2}/\sin h(kH).} \cr } } \right.$ | (11) |
由式(9)和式(11)可得此时输入阻抗与传递阻抗的表达式为:
| $\left\{ {\matrix{ {{Z_{11}} = j\omega m - j{\rho _0}c\pi {R^2}\cos h(kH)/\sin h(kH),} \cr {{Z_{12}} = - j{\rho _0}c\pi {R^2}/\sin h(kH).} \cr } } \right.$ | (12) |
在评估隔振器隔振效果时力传递率是一个常用的指标,它定义为传递至基础的动态力与激励力的比值[9]。当基础是刚性体时,力传递率可以近似地认为是传递阻抗与输入阻抗的比值。可得力传递率的表达式为:
| $\lambda \text{=}\frac{-j{{\rho }_{0}}c\pi {{R}^{2}}/\sin kH}{j\omega m-j{{\rho }_{0}}c\cot (kH)\pi {{R}^{2}}}\text{。}$ | (13) |
由于模型中上下盖板以及囊壁均考虑成刚体,上盖板在振动过程中不会存在内部声压场与边界的耦合问题。采用 ComsolMultiphysics 软件中的声学模块,对体积为 Ω,在边界$\partial \Omega $处流速为 f 的空气其声压场 p 的计算可归结为求解如下标准的边值问题[10]:
| $\left\{ {\matrix{ { - \nabla (a\nabla P) + bP = 0,} \cr {{{\partial P} \over {\partial \vec n}}\left| {\partial \Omega } \right. = f.} \cr } } \right.$ | (14) |
式中:f 为与边界处流速相关的函数,a和b 为在体积上与频率相关的函数;$\partial \vec n$为在边界外法线上的单位向量。
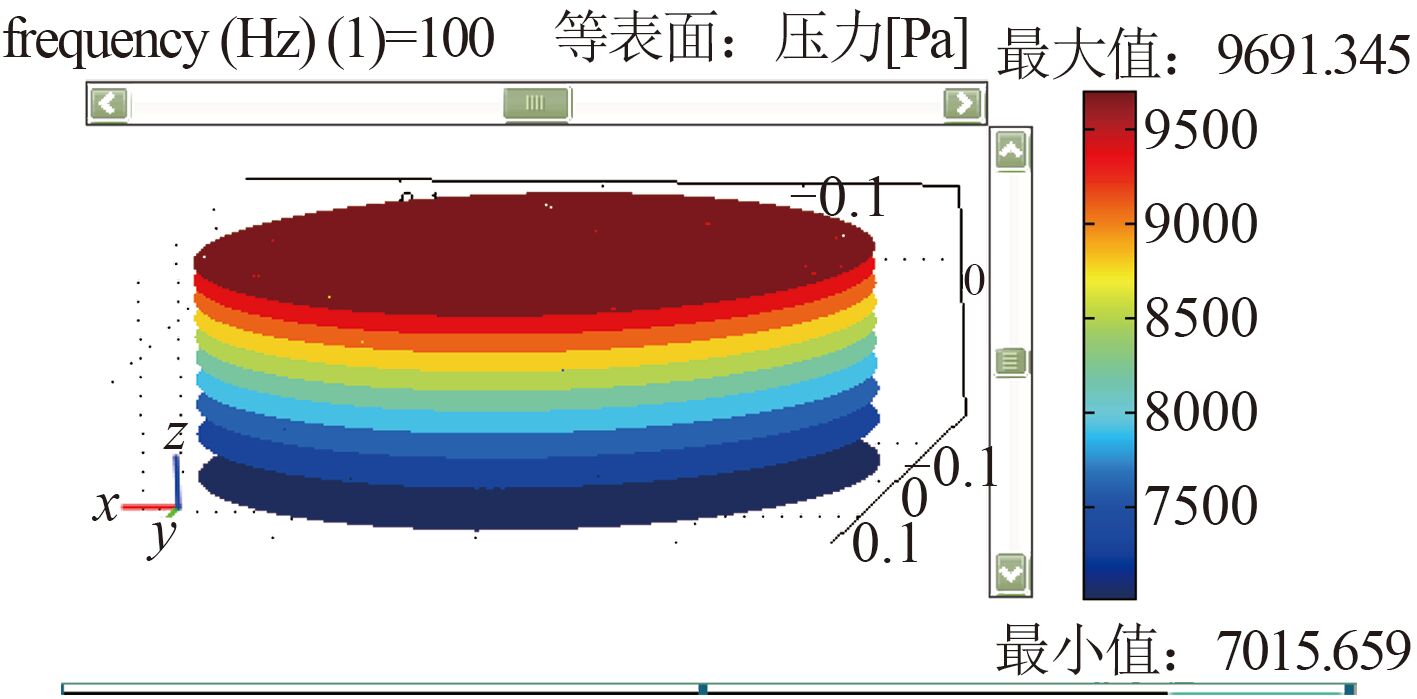
空气弹簧模型相关参数见表 1,对于垂向的振动,求出声压场分布后对上下盖板边界进行积分即可求得内部声压对上下盖板处的动态力。垂向振动计算结束后,选取振动频率为 100 Hz 时空气弹簧声压场切片,如图 2 所示。由图可知,沿轴向同一高度其声压值大小相等,与表达式(8)所得到的结论相吻合,即此时空气弹簧内部的声压表达式是一个关于高度 z 的函数。
|
|
表 1 空气弹簧模型参数 Tab.1 The parameters of air-spring mode |
|
图 2 100 Hz 时空气弹簧声压场 Fig. 2 The pressure field of air-spring at 100 Hz |
机械阻抗近似解析计算与仿真计算得到的结果对比如图 3 所示。由图可知,近似解析计算与仿真计算的结果吻合良好,验证该近似计算方法的正确性。

|
图 3 机械阻抗计算与仿真对比 Fig. 3 The contrast of mechanical impedance between FEM and analytic algorithm |
由阻抗曲线可看出,输入阻抗表现出了标准的刚度区、共振区和质量区,区域的划分主要由盖板质量、空气弹簧刚度这2个因素相互制约共同作用。此时空气弹簧的刚度特性完全由内部空气来体现,刚度值比较小,固有频率值比较低,使得刚度区的频段范围比较窄。在低频段空气弹簧的刚度起主要作用,在共振区两者平分秋色,随着频率的增加,盖板质量的作用越来越显著,在高频段系统的动态特性主要取决于盖板的质量,系统的振动主要受惯性力的支配,此时会产生明显的波动现象。在影响空气弹簧机械阻抗特性的诸多因素中盖板质量、初始压力是2个重要的因素,下面分别分析这2个参数对空气弹簧机械阻抗特性的影响规律。
3.1 上盖板质量的影响不同盖板质量的空气弹簧输入阻抗如图 4 所示,力传递率曲线如图 5 所示。由阻抗表达式可知上盖板质量对传递阻抗没有影响,影响的是输入阻抗。影响的区域主要是共振区与质量区。在低频段(固有频率值左侧)空气弹簧的输入阻抗随着盖板质量的增加而降低;随着频率的升高(固有频率值右侧),空气弹簧的输入阻抗随着盖板质量的增加而提高,盖板质量的作用越来越显著表现为质量区。固有频率随着盖板质量的增加而降低,而在固有频率点的阻抗值随着盖板质量的增加而提高。力传递率的值在共振峰处最大,随着频率的升高在高频段会出现共振峰。

|
图 4 不同盖板质量时的输入阻抗 Fig. 4 The mechanical impedance at different cover plate mass |

|
图 5 不同盖板质量时的力传递率 Fig. 5 The force transmissibility at different cover plate mass |
初始压力是分析空气弹簧机械阻抗特性的一个很重要的参数。一方面它起到承载的作用,另一方面,对于密闭空间中不同压力的气体介质其密度、声速不同,使得波数不同,进而影响空气弹簧内部的声压分布。对理想气体有绝热物态方程:
| $P={{\rho }^{n}}\cdot const,$ | (15) |
式中:P 为空气内部压力;n 为传热指数;const 为常数。将声波过程近似认为是绝热的,则此时的 n = 1.4,依据波速 c 的定义可线性近似得出下列方程:
| $P={{c}^{2}}\cdot \rho $ | (16) |
由式(15)和(16)可得空气弹簧不同初始压力状态下的声速比和波数比分别为:
| $\left\{ \begin{array}{*{35}{l}} {{c}_{1}}/{{c}_{0}}={{\left( {{p}_{1}}/{{p}_{0}} \right)}^{\frac{n-1}{2n}}} \\ {{k}_{1}}/{{k}_{0}}={{\left( {{p}_{1}}/{{p}_{0}} \right)}^{-\frac{n-1}{2n}}} \\ \end{array} \right.$ | (17) |
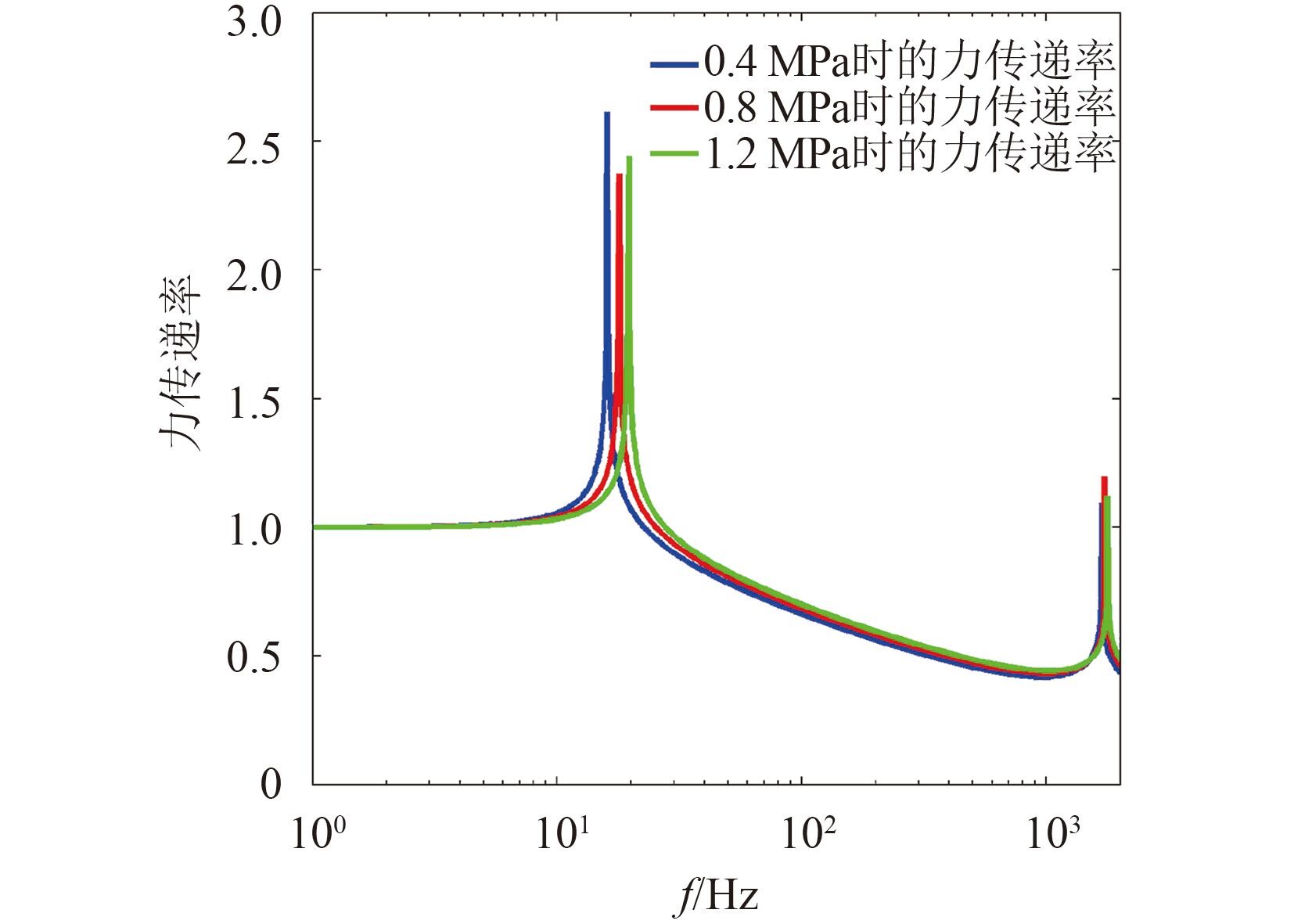
不同初始压力下的阻抗曲线图与力传递率曲线如图 6~图 7 所示。
由图可知,初始压力对输入阻抗和传递阻抗均有影响,它实质上是影响空气弹簧的刚度特性。空气弹簧的固有频率随着压力的增加而变大。对传递阻抗,随着初始压力的增加阻抗值提高,对输入阻抗初始压力影响的主要是刚度区和共振区。在刚度区随着初始压力的增加输入阻抗值提高,在固有频率点右侧附近随着初始压力的增加输入阻抗值降低,随着频率的进一步增加初始压力的影响逐渐减弱,此时的阻抗特性主要由质量特性来体现。

|
图 6 不同初始压力时的机械阻抗 Fig. 6 The mechanical impedance at different initial pressure |
|
图 7 不同初始压力时的阻抗曲线 Fig. 7 The force transmissibility at different initial pressure |
本文提出一种基于空气波动理论的理想化筒式空气弹簧的近似解析解算法,通过有限元仿真表明该方法合理可行。通过该方法可以定性定量的分析参数的变化对空气弹性机械阻抗特性的影响规律。依据该方法通过调整相应的参数就可得到相应的阻抗曲线,为分析结构更复杂的空气弹簧提供理论依据。对所建模型,文中有很多理想化的假设,而在实际情况中盖板和囊壁不是绝对的刚性体,这样会影响空气弹簧模型内部声压的分布,并且还会存在着声压场与内壁结构的耦合问题,对这些问题还有待于进一步的深入研究。
| [1] |
王锁泉, 周庆云, 席亦农, 等. 隔振元件机械阻抗测量与数据处理方法研究[J]. 舰船科学与技术 , 2006, 28 (S2) :107–111.
WANG Suo-quan, ZHOU Qing-yun, XI Yi-nong, et al. Study on the measurement technique and data processing on mechanical impedance of vibration isolator elements[J]. Ship Science and Technology , 2006, 28 (S2) :107–111. |
| [2] |
孙健, 朱石坚, 吕志强. 隔振器机械阻抗特性研究[J]. 船海工程 , 2003 (4) :25–29.
SUN Jian, ZHU Shi-jian, LV Zhi-qiang. A study on the mech-anical impedance characteristics of vibration isolator[J]. Ship and Ocean Engineering , 2003 (4) :25–29. |
| [3] |
王汉刚, 帅长庚, 郭伟, 等. 气囊隔振器垂向阻抗及其传递特性研究[J]. 噪声与振动控制 , 2010, 30 (6) :192–194.
WANG Han-gang, SHUAI Chang-geng, GUO Wei, et al. Study on impedance and transfer characteristics of air-spring with rubber bellow[J]. Noise and Vibration Control , 2010, 30 (6) :192–194. |
| [4] |
楼京俊, 朱石坚. 单囊式空气弹簧参数计算[J]. 海军工程大学学报 , 2001, 13 (2) :64–66.
LOU Jing-jun, ZHU Shi-jian. Single-bagged air spring's parameter calculation[J]. Journal of Naval University of Engineering , 2001, 13 (2) :64–66. |
| [5] |
莫荣利, 谢建藩, 杨军. 空气弹簧隔振性能及试验研究[J]. 噪声与振动控制 , 2005, 12 (6) :41–43.
MO Rong-li, XIE Jian-fan, YANG Jun. Study of the characteristics and testing research of air springs for isolating vibration[J]. Noise and Vibration Control , 2005, 12 (6) :41–43. |
| [6] |
黄映云, 吴善越, 朱石坚. 囊式空气弹簧隔振器的特性计算研究[J]. 振动工程学报 , 2004, 17 (2) :249–252.
HUANG Ying-yun, WU Shan-yue, ZHU Shi-jian. The characteristics calculation of pneumatic vibration isolator[J]. Journal of Vibration Engineering , 2004, 17 (2) :249–252. |
| [7] | 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2001 . |
| [8] | 何祚镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1981 . |
| [9] | 左鹤声. 机械阻抗方法与应用[M]. 机械工业出版社, 1987 . |
| [10] | ZIMMERMAN W B J. Comsol Multiphysics有限元法多物理场建模与分析[M].中仿科技公司,译.北京:人民交通出版社, 2007. |
| [11] | 朱石坚, 何琳. 船舶机械振动控制[M]. 北京: 国防工业出版社, 2006 . |
 2016, Vol. 38
2016, Vol. 38
