| 支撑剂指数设计方法在压裂充填施工中的应用研究 |
2. 中海石油(中国)有限公司天津分公司, 天津 300459
2. CNOOC China Limited, Tianjin Branch, Tianjin 300459, China
压裂裂缝参数优化是压裂充填设计的难点与重点。目前国内外压裂充填参数优化设计方法主要有两种:数值模拟方法和支撑剂指数设计方法。数值模拟方法是通过构建储层与压裂裂缝间的渗流数学模型,获得不同施工参数下压裂井的生产动态数据,进而进行方案优选[1]。此种方法考虑全面,优化过程复杂,结果相对准确,但是需要参数较多,在现场应用过程中受到一定的限制。支撑剂指数设计方法,以获得最优增产效果为核心,建立油藏与压裂裂缝匹配关系,从而获得最优的压裂充填裂缝参数。目前已在国内外压裂充填方案设计中得到了广泛的应用[2-7]。
支撑剂指数设计方法以获得最优裂缝无因次导流能力为目标,即无因次裂缝导流能力达到1.6,来进行裂缝缝长与缝宽的优化[8]。因此低渗储层需要形成长而窄的裂缝,而中高渗储层需要形成短而宽的裂缝。压裂充填工艺可借助端部脱砂技术来提高裂缝内净压力,从而实现增加裂缝宽度的目的,以达到增产要求。而在现场应用中发现,受施工设备能力、储层参数以及施工安全等因素影响,压裂充填施工中净压力值不足以获得优化所需的裂缝宽度,导致支撑剂指数设计方法与现场施工实际情况脱节,达不到最优的参数优化设计目的。因此支撑剂指数设计方法在高渗疏松砂岩储层压裂充填施工应用中还需结合现场施工能力,来获得最终的优化方案。
1 压裂充填井基础信息以南海东部某油田为例,利用支撑剂指数设计方法进行压裂充填参数优化设计。该油田属于典型的中高渗疏松砂岩稠油油藏,主力油层厚度15 m,岩性以细砂岩、粉砂岩泥岩为主,泥质胶结,胶结强度低,泊松比为0.28,杨氏模量为6000 MPa,生产中极易出砂。储层物性较好,平均地层渗透率为400×10-3 μm2,泥质含量20%,地层原油黏度为111.18~277.77 mPa·s。油田采用300 m×300 m的正方形井网生产。本井裂缝渗透率为70 000×10-3 μm2。
区块内A3井采取简易防砂完井方式投产,初期产量为65 m3/d。生产一年后,产量降低至停产,酸化后无效果。随后进行关井测试,试井解释表皮系数为2,污染半径为15 m。对本井进行大修作业,发现油层段筛管滤砂网表面均已被原油及泥砂堵塞,严重影响本井产能。故决定对本井进行压裂充填改造解除近井伤害,同时借助高导流压裂裂缝减缓地层微粒运移以达到增产稳产的目的。为达到最优的增产目的,采用支撑剂指数方法对本井进行压裂充填裂缝参数优化。
2 支撑剂指数设计方法及问题支撑剂指数设计方法是Valko与Economides在1998年首次提出,考虑了压裂裂缝与地层的匹配关系,以获得最优无因次裂缝导流能力为目标对裂缝参数进行优化。2002年Valko与Economides等给出了矩形泄油面积内不同形状因子下支撑剂指数裂缝参数设计方法[2-4],详细如下[6]。
根据达西公式,采液指数计算如下:
| $ J = \frac{q}{{\bar P - {P_{{\rm{wf}}}}}} = \frac{{2\pi Kh}}{{\alpha B\mu }}{J_{\rm{D}}} $ | (1) |
无因次采液指数计算为:
| $ {J_{\rm{D}}} = \frac{1}{{\ln \frac{{{r_{\rm{e}}}}}{{{r_{\rm{w}}}}} - 0.75 + {S_{\rm{f}}}}} $ | (2) |
式中:J为采液系数,m3/(MPa·d);q为油井产量,m3/d;P为地层压力,MPa;Pwf为地层流压,MPa;K为储层渗透率,10-3 μm;h为油层厚度,m;B为体积系数,无因次;μ为原油黏度,MPa·s;re为泄油半径,m;rw为井筒半径,m;Sf为表皮系数,无因次。
支撑剂指数定义为裂缝支撑体积与单井控制油藏体积的比值,物理意义为裂缝渗流能力的改善及其影响范围在整个油藏中所占的比例,在边长为Xe的正方形井网中,公式如下:
| $ {N_{{\rm{prop}}}} = \frac{{4X_{\rm{f}}^2}}{{r_{\rm{e}}^2}}{C_{{\rm{fd}}}} = \frac{{2{K_{\rm{f}}}{V_{\rm{p}}}}}{{K{V_{\rm{r}}}}} $ | (3) |
其中:
| $ \begin{array}{l} {V_{\rm{p}}} = 2{X_{\rm{f}}}wh\\ {V_{\rm{r}}} = X_{\rm{e}}^2h \end{array} $ |
式中:Nprop为支撑剂指数,无因次;Xf为裂缝半长,m;re为泄油半径,m;Cfd为无因次裂缝导流能力,无因次;Kf为裂缝渗透率,10-3 μm2;VP为支撑剂体积,m3;Vr为本井泄油体积,m3。
压裂后无因次采液指数计算如下:
| $ \begin{array}{l} {J_{{\rm{DF}}}} = \frac{1}{{ - 0.629 + 0.5\ln \frac{{{C_{{\rm{fd}}}}}}{{{N_{{\rm{prop}}}}}} + f\left( {{C_{{\rm{fd}}}}} \right)}}\\ f\left( {{C_{{\rm{fd}}}}} \right) = \frac{{1.65 - 0.328u + 0.116{u^2}}}{{1 + 0.18u + 0.064{u^2} + 0.005{u^3}}}\\ u = \ln {C_{{\rm{fd}}}} \end{array} $ | (4) |
根据无因次裂缝导流能力以及支撑剂体积获得裂缝参数计算如下:
| $ {X_{\rm{f}}} = {\left( {\frac{{{V_{\rm{f}}}{K_{\rm{f}}}}}{{{C_{{\rm{fd}}}}hK}}} \right)^{1/2}} $ | (5) |
| $ W = {\left( {\frac{{{C_{{\rm{fd}}}}{V_{\rm{f}}}K}}{{h{K_{\rm{f}}}}}} \right)^{1/2}} $ | (6) |
式中:Vf为裂缝体积,m3;W为裂缝宽度,m。
采用支撑剂指数设计方法对本井进行方案优化。当支撑剂量在5~25 m3时,优化裂缝缝宽范围为0.04~0.09 m,裂缝长度为4.2~9.5 m,压裂后获得无因次采液指数范围为0.2~0.26,而本井投产无因次采液指数为0.11,由此确定可实现增产倍比为1.8~2.36(图 1)。
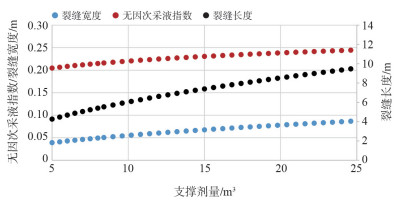 |
| 图 1 支撑剂指数设计方法结果图 |
根据帕金斯模型[9]计算,缝宽为0.04~0.09 m时,施工所需净压力为8.5~19 MPa。压裂充填施工中净压力受储层物性、施工能力等因素制约,需要在一个合理数值范围内,才能保证压裂充填施工顺利完成。如渤海与西非等地区疏松砂岩储层压裂现场数据表明施工中净压力一般为3 MPa,最高不超过6 MPa[10-11]。由此可知,现场施工条件难以满足支撑剂指数优化设计结果,需要对优化设计方法进行调整。
3 方法改进及现场应用效果根据油田周边井压裂施工经验,考虑储层力学参数以及施工排量、压裂液流变性能等参数影响,利用压裂软件进行模拟确定压裂施工净压力低于3 MPa时,本井可实现顺利加砂。根据帕金斯模型计算,净压力为3 MPa时,本井压裂裂缝宽度为0.013 m。以此为基础采用支撑剂指数设计方法进行参数优化计算,结果见图 2。
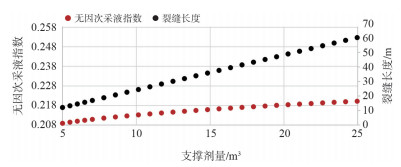 |
| 图 2 综合各因素后支撑剂指数优化设计方法结果图 |
支撑剂量在5~25 m3时,优化裂缝长度为12~60 m,压裂施工后无因次采液指数为0.2~0.22,优化的增产效果低于图 1。原因为:相同加砂规模条件下,方法改进后优化所用的裂缝宽度降低,导致无法实现最优的无因次裂缝导流能力,即无因次导流能力未达到1.6。
考虑到压裂裂缝需穿过近井污染带,故压裂裂缝缝长优化为18 m,对应的优化加砂规模为7.8 m3,压裂后无因次采液指数可达到0.21,可实现增产倍比1.9(图 2)。
该井于2017年年底施工,施工用压裂液112 m3,实际加砂8.3 m3,施工过程中压力平稳,净压力为1.1~2.9 MPa(图 3)。施工一个月后本井产能稳定在日产油135 m3/d,实现增产倍比2.0,与优化结果基本相近,起到了良好的增产目的。
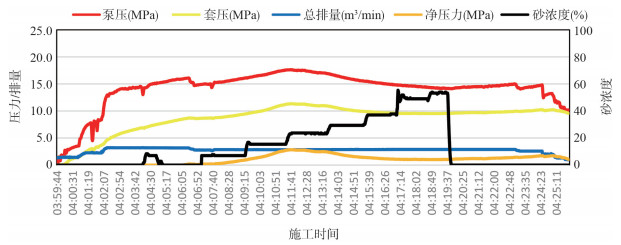 |
| 图 3 A3井压裂施工曲线图 |
4 结论
(1)相比于数值模拟优化设计方法,支撑剂指数优化设计方法具有操作简单、方便快捷的优点,方便现场优化设计应用。
(2)支撑剂指数优化设计方法是以获得最优裂缝无因次导流能力为目标进行裂缝参数优化,在中高渗疏松砂岩储层中应用需结合储层物性、工艺需求等多因素进行综合考虑。
(3)压裂施工中净压力是影响压裂裂缝缝宽的关键因素,需结合区块以往施工经验以及作业设备等情况,确定合理的施工净压力数值。
| [1] |
卞晓冰, 张士诚, 王雷. 海上疏松砂岩稠油油藏压裂充填优化设计[J]. 油气井测试, 2012, 21(1): 39-41. |
| [2] |
蒋廷学, 胥云. 低渗透油藏基于支撑剂指数的压裂优化设计方法研究[J]. 石油钻采工艺, 2008, 30(3): 87-89. |
| [3] |
郭建春, 梁豪, 赵志红. 基于最优支撑剂指数法优化低渗气藏裂缝参数[J]. 西南石油大学学报(自然科学版), 2013, 35(1): 93-98. |
| [4] |
赵春艳, 赵廷峰. 低渗透油藏整体压裂井裂缝参数优化研究[J]. 油气藏评价与开发, 2017, 7(5): 50-53. |
| [5] |
黄杰, 巩永刚, 徐延涛, 等. G函数分析在压裂充填施工中的应用研究[J]. 海洋石油, 2019, 39(2): 57-61. |
| [6] |
卢宗平. 压裂防砂在埕岛油田的应用[J]. 海洋石油, 2006, 26(4): 47-51. |
| [7] |
Demarchos A S, Chomatas A S, Economides M J, et al. Pushing the Limits in Hydraulic Fracture Design//SPE International Symposium and Exhibition on Formation Damage Control[C]. Lafayette, Louisiana: Society of Petroleum Engineers, 2004.
|
| [8] |
Cinco-Ley, H., Samaniego, F. Critical Data Needs of Design of Frac-pack Completions in Today's Oilfield Environment. SPE 10179, 1981.
|
| [9] |
王鸿勋. 水力压裂原理[M]. 北京: 石油工业出版社, 1987: 94-101.
|
| [10] |
Liu L Y, Deng J M, Ma Y W, et al. Single-trip, Multiple-Zone Frac Packing Offshore sand Control: Overview of 58 Case Histories//International Oil & Gas Conference and Exhibition in China[C]. Beijing, China: Society of Petroleum Engineers, 2006.
|
| [11] |
Cipolla C L, Shucart J K, Lafitte J R. Evolution of Frac-Pack Design, Modeling, and Execution in the Ceiba Field, Equatorial Guinea//SPE Annual Technical Conference and Exhibition[C]. Dallas, Texas: Society of Petroleum Engineers, 2005.
|
 2020, Vol. 40
2020, Vol. 40

