| 渤海普Ⅱ类稠油过渡带弱凝胶驱增油预测模型 |
渤海普Ⅱ类稠油(地下原油黏度大于350 mPa·s)资源丰富[1],近年来,渤海油田一直在探索此类稠油的高效开发技术。开发实践表明,距内含油边界大于200 m的纯油区储量通过多元热流体吞吐的方式进行有效的动用并取得了较好的开发效果[2-3]。渤海油田目前已探明的普Ⅱ类稠油距内含油边界小于200 m的过渡带储量比例占到50%。此类储量由于油稠、距内含油边界近,常规的边水驱开发和热采开发均难以有效动用[4-7]。BN油田地下原油黏度为413~741 mPa·s,是渤海投入开发最早的普Ⅱ类稠油油藏,过渡带储量比例占45%。2013年弱凝胶调驱动用过渡带储量以来,相比于常规边水驱,已经实现累增油15×104 m3,增油井区的地下原油黏度为413~741 mPa·s,矿场注入井建立的视阻力系数在1.1~2.9[8-11]。为了更好地推广应用,需要对增油潜力进行全面的评价。然而,由于油稠,国内外此类稠油弱凝胶调驱应用实例少,难以提供全面的借鉴和参考,其增油潜力预测方面的文献尚未见到。为此,以BN油田应用效果为基础,借助油藏数值模拟技术,基于拉丁超立方实验建立均匀设计样本集,并采用多元回归方法建立过渡带调驱增油潜力预测模型[12-15]。与常规的数模预测相比,建立的预测模型保证精度的同时能够方便快捷地实现过渡带弱凝胶驱增油潜力预测。
1 典型油藏数值模拟模型BN油田位于渤海西部海域,油藏埋深-900~-1 100 m,具有高孔高渗的储层物性。油藏沉积时属高弯度曲流河沉积环境,泥包砂沉积特征明显,单层厚度大都介于5~8 m。地下原油黏度介于413~741 mPa·s,属于海上典型的普Ⅱ类稠油油藏。BN油田共有3口井实施弱凝胶调驱先导试验,3个注入井组共有9口井取得了明显的降水增油效果,区块含水由65%下降到59%,日产油提高29.7%(图 1)。矿场试验结果表明,弱凝胶驱对改善高黏的普Ⅱ类稠油开发效果是行之有效的。
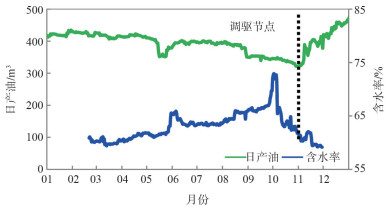 |
| 图 1 2017年BN油田日产油和含水率变化曲线 |
以BN油田应用效果为基础,利用加拿大CMG数值模拟软件的STARS模块,建立能够准确描述弱凝胶动用过渡带储量的数值模型(图 2)。模型网格划分为40×46×21,平面网格尺寸为15 m,纵向网格尺寸为0.4 m。模型地质储量为60×104 m3。基于实际的注采关系,建立1注1采井网,注采井距为300 m。注入井为定向井,位于过渡带,油层厚度全射开;生产井为水平井,水平段长度为300 m,位于纯油区,中上部布井。生产控制条件为含水98%和日产油5 m3/d。模型数值参数如表 1所示。
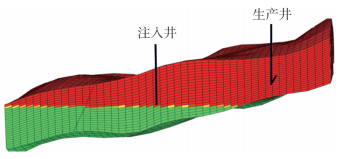 |
| 图 2 油藏数值模型井间剖面 |
| 表 1 模型数值参数 |
模拟中弱凝胶是通过具有吸附性能的聚合物与交联剂(Cr3+)发生交联反应生成得到,凝胶动力学模型见式(1)。
凝胶动力学模型:
| $ \mathit{a}\;{\rm{ }}\mathit{Polymer}{\rm{ + }}\mathit{b\;Xlinker}{\rm{ = }}\mathit{c\;Gel} $ | (1) |
式(1)中:a为参与反应的聚合物质量浓度,mg/L;b为参与反应的交联剂(Cr3+)质量浓度,mg/L;c为反应生成的凝胶质量浓度,mg/L。
交联反应参数通过拟合室内物理模拟实验得到,文中使用的交联反应参数a、b、c分别取值1000、20、1 020。模型中弱凝胶机理主要考虑增加注入流体黏度、凝胶吸附、降低渗透率以及不可及孔隙体积,参数取值通过拟合实验数据和矿场动态确定,弱凝胶驱数值表征参数如表 2所示,其中非线性黏浓和吸附表征参数如表 3所示。
| 表 2 弱凝胶驱数值表征参数 |
| 表 3 非线性黏浓和吸附表征参数 |
2 增油预测模型 2.1 单因素影响函数关系
基于建立的典型数值模型,通过分析油藏数值模拟结果回归确定弱凝胶调驱增油量单因素影响函数关系。通过统计渤海相似普Ⅱ类稠油的地质油藏特征参数,共确定了8个单因素,其取值范围为:平均渗透率(1 000~9 000)×10-3 μm2、变异系数0.1~0.9、边水倍数1~20、井距100~500 m、净毛比0.2~1.0、地层原油黏度为200~1 000 mPa·s、油层厚度4~20 m、生产井距内含油边界距离0~200 m。弱凝胶调驱增油量是指弱凝胶调驱产油量与采用常规边水驱产油量的差值[16]。通过分析增油量能够为后续的经济评价和决策提供直接依据[17]。8个单因素分别开展不同水平下弱凝胶调驱产油、边水驱产油以及增油关系研究。以平均渗透率为例进行说明(图 3)。
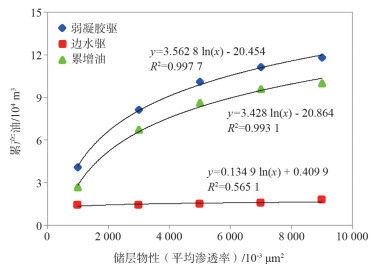 |
| 图 3 不同储层物性条件弱凝胶调驱产油、边水驱产油以及增油关系 |
可以看出,随着平均渗透率逐渐增加,储层物性逐渐变好,地下原油的流度增加,弱凝胶调驱和边水驱产油量均逐渐增加,与平均渗透率均呈现较好的对数关系。将两者产油的差值作为弱凝胶调驱的增油量,在物性变化范围内,弱凝胶调驱增油量在(2.66~9.99)×104 m3之间,与储层物性也呈现对数关系,建立的弱凝胶调驱增油与平均渗透率的影响函数模型见式(2)。
| $ Q = 3.56\ln (k - 20.45) $ | (2) |
式(2)中:Q为弱凝胶调驱增油量,104 m3;k为储层平均渗透率,10-3 μm2。
相同的方法,得到变异系数、边水倍数、注采井距、净毛比、地层原油黏度、油层厚度、生产井距内含油边界距离等7个单因素在不同水平下弱凝胶调驱相比于边水驱开发的增油关系(图 4),并分别得到各单因素对弱凝胶调驱增油的影响函数模型,见式(3)~式(9)。
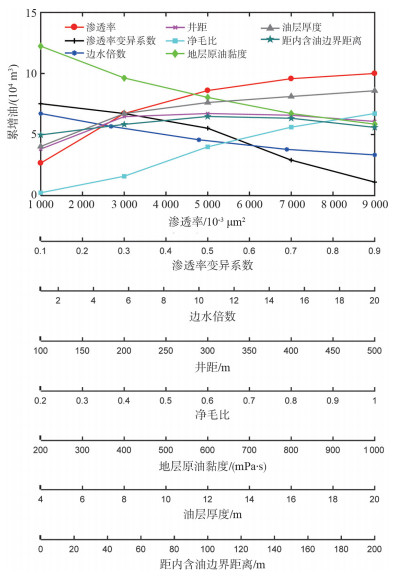 |
| 图 4 各单因素在不同水平下弱凝胶调驱相比于边水驱开发增油变化 |
变异系数:
| $ Q = - 6.07V_{\rm{k}}^2 - 2.26{V_{\rm{k}}} + 7.89 $ | (3) |
边水倍数:
| $ Q = 0.006W_{\rm{b}}^2 - 0.31{W_{\rm{b}}} + 7.03 $ | (4) |
井距:
| $ Q = (2E - 07)D_{\rm{w}}^2 - 0.0002D_{\rm{w}}^2 + 0.07{D_{\rm{w}}} - 0.27 $ | (5) |
净毛比:
| $ Q = - 2.27\mathit{NT}{\mathit{G}^2} + 11.22\mathit{NTG} - 2.11 $ | (6) |
地下原油黏度:
| $ Q = - 140.86\mu _{\rm{o}}^{ - 0.454} $ | (7) |
油层厚度:
| $ Q = 280\ln (h) + 0.45 $ | (8) |
距内含油边界距离:
| $ Q = - 0.0001D_{\rm{n}}^2 + 0.026{D_{\rm{n}}} + 4.92 $ | (9) |
式中:Q为弱凝胶调驱增油量,104 m3;Vk为渗透率变异系数,小数;Wb为边水倍数,无量纲;Dw为注采井距,m;NTG为净毛比,小数;μo为地下原油黏度,mPa·s;h为油层厚度,m;Dn为距内含油边界距离,m。
可以看出,随着变异系数增加,储层非均质性增强,弱凝胶调驱在过渡带增油逐渐降低,两者呈现较好的二次多项式关系;随着边水倍数增加,边水驱产油量增加,弱凝胶调驱增油量逐渐减小,两者呈现较好的二次多项式关系;随着注采井距增加,弱凝胶调驱增油先快速增加后缓慢减小,两者呈现较好的三次多项式关系;随着净毛比增加,地质储量增加,弱凝胶调驱增油量逐渐增加,两者呈现较好的二次多项式关系;随着地层原油黏度增加,地下原油流动性减弱,弱凝胶调驱增油逐渐减小,两者呈现较好的幂函数关系;随着地层厚度增加,动用地质储量增加,调驱增油逐渐增加,两者呈现较好的对数关系;生产井距内含油边界距离增加,表明生产井距边水越远,调驱增油先快速增加后缓慢减小,两者呈现较好的二次多项式关系。
以弱凝胶调驱增油5×104 m3作为界限临界值,确定8个单因素的筛选界限(表 4)。可以看出,平均渗透率大于1 500×10-3 μm2、变异系数小于0.6、水体倍数小于10倍、注采井距大于150 m、净毛比大于0.7、地下原油黏度小于1 000 mPa·s、油层厚度大于5 m、生产井距内含油边界距离大于50 m的油藏条件下,在过渡带采用弱凝胶调驱能够增油5×104 m3以上。单因素界限的确定能够为相似油田采用弱凝胶调驱增油提供了初步的筛选标准。
| 表 4 单因素界限 |
2.2 预测样本集产生
在单因素分析的基础上,通过多因素影响实验方案设计,建立弱凝胶调驱增油预测样本集。多因素分析共考虑8个因素,每个因素5个水平,全方案需完成390 625个方案。为了能够使得实验设计既可以代表所有因素的变化范围,又能够使得实验数目控制在可操作范围内,为此使用拉丁超立方设计方法进行实验方案设计[18]。这是一种分层抽样方法,它既能保证采样点对变量组合空间的充分覆盖,同时能够确保独立变量采样值间的相关趋势达到最小。利用该方法对8因素5水平的问题进行了实验设计,共产生了128套样本方案。
2.3 预测回归模型基于弱凝胶调驱增油与单因素函数关系,开展多元回归模型研究。随机抽取8个样本作为检验样本,其余120个样本作为拟合样本。在此基础上,采用Levenberg-Marquard算法对120个拟合样本进行多元线性回归,得到的多元回归模型见式(10),式中各符号的物理意义同上。
| $ \begin{array}{l} \;\;\;\;\;\;Q = 3.42\ln (k) - 5.76V_{\rm{k}}^2 - 2.49{V_{\rm{k}}} + 0.0051W_{\rm{b}}^2 - \\ 0.28{W_{\rm{b}}} + (1.70E - 07)D_{\rm{w}}^3 - 0.00019D_{\rm{w}}^2 + 0.068{D_{\rm{w}}} - \\ 3.26NT{G^2} + 12.14NTG - 17.40\mu _{\rm{o}}^{0.117} + 2.58\ln (h) - \\ 0.00014D_{\rm{n}}^2 + 0.031{D_{\rm{n}}} - 5.05 \end{array} $ | (10) |
回归得到的预测模型的拟合相关系数为0.990 6,统计参数F=3 995,设定显著水平α=0.005,查F(8,111)表的临界值λ=2.01。由于F>λ,所以认为8个单因素对弱凝胶调驱增油量的影响非常显著。利用随机抽取的8个检验样本对模型精度进行检验,检验样本的平均误差在1.3%~3.6%之间,平均误差为2.1%。
3 应用实例利用此预测模型,对BN油田过渡带弱凝胶调驱的典型井N16井进行增油量预测以进一步检验模型精度。该井基础参数及预测结果如表 5所示。
| 表 5 N16井模型预测增油量与数模预测增油量对比 |
目前N16井累产5.45×104 m3,含水77%,到含水98%时,数模预测采用弱凝胶调驱能够增油8.91×104 m3,本文建立的增油模型预测能够增油9.13×104 m3,两者误差仅为2.5%,预测模型精度满足工程应用的要求。相比数值模拟,预测模型保证预测精度的同时具有方便快捷的特点。
借助增油潜力预测模型,结合过渡带高含水长停井治理,对BN油田的过渡带弱凝胶调驱潜力进行评价,共筛选出4口潜力井位,通过低部位高含水井转注弱凝胶增加动用储量140×104 m3,预计增加油田可采储量12×104 m3。下一步将建立的预测模型用于渤海普Ⅱ类稠油过渡带储量动用潜力筛查,以进一步增加此类边际储量的动用程度。
4 主要结论(1)以弱凝胶调驱增油5×104 m3作为界限临界值,确定8个单因素的筛选界限:平均渗透率大于1 500×10-3 μm2、变异系数小于0.6、水体倍数小于10倍、注采井距大于150 m、净毛比大于0.7、地下原油黏度小于1 000 mPa·s、油层厚度大于5m、生产井距内含油边界距离大于50 m。单因素界限的确定能够为相似油田采用弱凝胶调驱增油提供初步筛选标准。
(2)模型适用范围:平均渗透率(1 000~9 000)×10-3 μm2、变异系0.1~0.9、边水倍数1~20、井距100~500 m、净毛比0.2~1.0、地层原油黏度为200~1 000 mPa·s、油层厚度4~20 m、生产井距内含油边界距离0~200 m。模型预测增油量与实际产量相对平均误差为2.5%,满足工程应用精度要求。
(3)利用该模型对油田过渡带调驱潜力进行筛选,动用储量增加140×104 m3,预计增加油田可采储量12×104 m3。预测模型对渤海普Ⅱ类稠油过渡带储量动用具有重要意义。
| [1] |
薛艳霞, 廖新武, 霍春亮, 等. 海上河流相储层应用地质模型计算储量的不确定性分析[J]. 油气藏评价与开发, 2018, 8(4): 1-5. |
| [2] |
李萍, 刘志龙, 邹剑, 等. 渤海旅大27-2油田蒸汽吞吐先导试验注采工程[J]. 石油学报, 2016, 37(2): 242-247. |
| [3] |
王磊, 郑伟, 余华杰, 等. 渤海稠油多元热流体多轮次吞吐开发效果评价[J]. 重庆科技学院学报(自然科学版), 2016, 18(4): 29-32. |
| [4] |
李彪. 海上S油田优化注水的研究及实践[J]. 海洋石油, 2018, 38(2): 54-57. |
| [5] |
Pan G, Chen J, et al. Combined Technology of Weak Gel Flooding assisting Thermal Huff and Puff Enhances Oil Recovery for Offshore Heavy Oil Field//Proceedings of SPE Annual Technical Conference and Exhibition[C]. Dubai, UAE: SPE, 2016.
|
| [6] |
潘广明, 张彩旗, 刘东, 等. 海上稠油油藏弱凝胶调驱提高采收率技术[J]. 特种油气藏, 2018, 25(3): 140-143. |
| [7] |
唐孝芬, 吴奇, 刘戈辉, 等. 区块整体弱凝胶调驱矿场试验及效果[J]. 石油学报, 2003, 24(4): 58-61. |
| [8] |
赵军, 郑继龙, 陈平, 等. 弱凝胶调驱技术在旅大5-2油田的应用[J]. 石油与天然气化工, 2013, 42(4): 401-403. |
| [9] |
黄波, 熊开昱, 陈平, 等. 绥中36-1油田弱凝胶调驱实验研究[J]. 中国海上油气, 2008, 20(4): 239-242, 249. |
| [10] |
潘广明, 吴金涛, 张彩旗, 等. 海上稠油油藏弱凝胶驱辅助吞吐增油效果研究[J]. 特种油气藏, 2017, 24(6): 134-138. |
| [11] |
王旭东, 杨俊茹, 康晓东, 等. 海上油田早期弱凝胶驱矿场见效规律及效果评价[J]. 重庆科技学院学报(自然科学版), 2017, 19(2): 64-68. |
| [12] |
李相远, 侯健, 杜庆军. 基于潜力预测模型的聚合物驱参数敏感性分析[J]. 油田化学, 2005, 22(2): 163-167. |
| [13] |
施雷庭, 朱诗杰, 邹剑, 等. 聚合物驱有效流度控制时间范围及其影响因素研究[J]. 油气藏评价与开发, 2019, 9(4): 31-35. |
| [14] |
江厚顺. 边水油藏调剖调驱潜力评价与效果分析[J]. 石油天然气学报, 2009, 31(2): 107-110. |
| [15] |
侯健, 王树涛, 杜庆军, 等. 海上稠油油藏蒸汽吞吐效果预测模型[J]. 石油天然气学报, 2013, 35(7): 118-122. |
| [16] |
Sun C, Hou J, Pan G M, et al. Optimized Polymer Enhanced Foam Flooding for Ordinary Heavy Oil Reservoir After Crosslinked Polymer Flooding[J]. Journal of Petroleum Exploration and Production Technology, 2016, 6(4): 777-785. |
| [17] |
Hou J, Pan G M, Lu X J, et al. The Distribution Characteristics of Additional Extracted Oil Displaced by Surfactant-polymer Flooding and Its Genetic Mechanisms[J]. Journal of Petroleum Science and Engineering, 2013, 112: 322-334. |
| [18] |
宫汝祥, 杜庆军, 吴海君, 等. 海上稠油多元热流体吞吐周期产能预测模型[J]. 特种油气藏, 2015, 22(5): 117-120. |
 2020, Vol. 40
2020, Vol. 40

