| 页岩Ⅰ区块体积压裂缝网模拟研究 |
随着陆上常规油气资源开发逐渐进入开发中后期,储量动用难度越来越大,产量越来越低。为满足国家战略资源储备要求,非常规能源——页岩气以其储量丰富且清洁无污染的优点,越来越受到世界各国的重视。在北美地区,页岩气的商业化开发在很大程度上改变了其能源结构,对社会经济产生了深远的影响。北美页岩气开发经验表明[1],页岩储层存在低孔隙度、低渗透率等特征,依靠其自身能量难以实现经济有效开采,必须采用压裂技术对储层进行改造,实现天然裂缝和人工裂缝交错的缝网结构,增大裂缝壁面与页岩基质的接触面积,进而提高储层整体渗透率,达到体积压裂的效果。因此,实现页岩气的有效开发,必须验证页岩气储层能否实现体积压裂改造,形成有效缝网。
1 地质特征页岩Ⅰ区块总体为我国南方丘陵山地,在这一区域地层受到来自北西方向挤压应力作用,主要形成正向构造,背斜带之间的分界主要是宽缓向斜带。本区块的主要开发目的层段位于下志留统龙马溪组下部-上奥陶统五峰组,目的层厚度约为80 m,层段内主要为含气泥页岩。相关岩心资料显示,储层有机碳含量为0.55% ~5.89%,平均值为2.55%,有机碳含量随着储层深度的增加逐渐增加。
储层脆性矿物含量高,平均脆性矿物含量约为56.5%,最小脆性矿物含量约为33.9%,最高脆性矿物含量达80.3%。储集空间主要为纳米级有机质孔隙和黏土矿物间微孔隙,同时发育晶间孔隙、次生溶蚀孔隙,孔径总体尺寸为中孔隙,含气层平均孔隙度约为4.87%,最小孔隙度为1.17%,最大孔隙度达到8.61%。页岩气层水平渗透率在(0.001~355)×10-3 μm2范围内,其中基质渗透率普遍低于1×10-3 μm2,最小值为0.001 5×10-3 μm2,最大值为5.71×10-3 μm2,平均值为0.25×10-3 μm2,而层间缝渗透率普遍高于1×10-3 μm2,最高可达355.2×10-3 μm2。该区块目的层岩石力学参数如下:杨氏模量23~37 GPa,泊松比为0.2,体积模量为14 ~18 GPa,剪切模量10~ 14 GPa,最大主应力为60.50 MPa,最小主应力为52.25 MPa,应力差为8.25 MPa。该区块流速不敏感,中偏强~强水敏,临界盐度2%,酸敏指数0.67~0.75,中~强酸敏,中等偏强应力敏。
2 缝网形成可行性验证 2.1 地质条件页岩储层压裂缝网形成的可行性是页岩地质、储层特征的综合反映,影响因素主要包括泊松比、杨氏模量、石英含量、脆性系数、地应力差异系数、天然裂缝发育程度等。北美页岩气可压性评价指标与页岩Ⅰ区块相关参数对比见表 1。
| 表 1 可压性综合评价 |
页岩Ⅰ区块各项地质参数均符合评价指标,在地质条件上具有体积压裂缝网形成的可行性。
2.2 力学条件体积压裂的力学关键是在地层形成主裂缝后提升缝内净压力,从而进一步促进天然裂缝以及储层弱面张开,形成缝网,达到体积压裂的效果。压裂形成体积缝网的力学条件基础是天然裂缝性储层裂缝扩展规则[2]。目前,Warpinski和Teufel提出的线性扩展准则是国内外应用最为广泛的裂缝扩展准则。
根据Warpinski和Teufel的裂缝扩展准则,当天然裂缝发生张性断裂时,有:
| $ p > {\sigma _{\rm{n}}} $ | (1) |
式中:p为地层流体压力,MPa;σn为法向正应力,MPa。
当作用于天然裂缝的剪应力较大时,天然裂缝在剪应力的作用下十分容易发生剪切滑移,此时:
| $ \left| \tau \right| > {\tau _0} + {K_{\rm{f}}}\left( {{\sigma _{\rm{n}}} - p} \right) $ | (2) |
式中:τ为剪切应力,MPa;τ0为天然裂缝面的黏聚力,MPa;Kf天然裂缝面的摩擦系数,无量纲;p为地层流体压力,MPa;σn为法向正应力,MPa。
根据二维线弹性理论推演,地层的剪应力和正应力分别为:
| $ \tau = \frac{{{\sigma _{\rm{H}}} + {\sigma _{\rm{h}}}}}{2}\sin 2\theta $ | (3) |
| $ {\sigma _{\rm{n}}} = \frac{{{\sigma _{\rm{H}}} + {\sigma _{\rm{h}}}}}{2} - \frac{{{\sigma _{\rm{H}}} + {\sigma _{\rm{h}}}}}{2}\cos 2\theta $ | (4) |
式中:τ为剪切应力,MPa;σH为最大水平主应力,MPa;σh为最小水平主应力,MPa;θ为裂缝与水平最大主力夹角,°;σn为法向正应力,MPa。
当水力压裂裂缝和天然裂缝相交后,由于两条裂缝已经相互连通,注入地层的大量压裂液将会沿着水力压裂裂缝进入天然裂缝,此时,天然裂缝近壁面的孔隙压力为:
| $ p\left( {x, t} \right) = {\sigma _{\rm{h}}} + {p_{{\rm{net}}}}\left( {x, t} \right) $ | (5) |
式中:p(x,t)为天然裂缝近壁面的孔隙压力,MPa;σh为最小水平主应力,MPa;pnet(x,t)为净压力,MPa。
整理式(1)~式(5)得,地层产生张性断裂裂缝所需要的裂缝净压力范围为:
| $ {p_{{\rm{net}}}}\left( {x, t} \right) > \frac{{{\sigma _{\rm{H}}} - {\sigma _{\rm{h}}}}}{2}\left( {1 - \cos 2\theta } \right) $ | (6) |
式中:pnet(x,t)为净压力,MPa;σH为最大水平主应力,MPa;σh为最小水平主应力,MPa;θ为裂缝与水平最大主力夹角,°。
地层发生剪切断裂时所需要的裂缝净压力范围为:
| $ {p_{{\rm{net}}}}\left( {x, t} \right) > \frac{1}{{{K_{\rm{f}}}}}\left[ {{\tau _0} + \frac{{{\sigma _{\rm{H}}} - {\sigma _{\rm{h}}}}}{2}\left( {{K_{\rm{f}}} - \sin 2\theta - {K_{\rm{f}}}\cos 2\theta } \right)} \right] $ | (7) |
式中:pnet(x,t)为净压力,MPa;τ0为天然裂缝面的黏聚力,MPa;Kf天然裂缝面的摩擦系数,无量纲;σH为最大水平主应力,MPa;σh为最小水平主应力,MPa;θ为裂缝与水平最大主力夹角,°。
当
| $ {p_{{\rm{Zmax}}}} = {\sigma _{\rm{H}}} - {\sigma _{\rm{h}}} $ | (8) |
式中:pZmax为张性断裂时最大净压力,MPa;σH为最大水平主应力,MPa;σh为最小水平主应力,MPa。
当
| $ {p_{{\rm{max}}}} = \frac{{{\tau _0}}}{{{K_{\rm{f}}}}} + \left( {{\sigma _{\rm{H}}} - {\sigma _{\rm{h}}}} \right) $ | (9) |
式中:pmax为最大裂缝净压力,MPa;τ0为天然裂缝面的黏聚力,MPa;Kf天然裂缝面的摩擦系数,无量纲;σH为最大水平主应力,MPa;σh为最小水平主应力,MPa。
一般认为,天然裂缝的黏聚力τ0=0,因此,根据式(9)可得:天然裂缝或地层弱面发生剪切断裂时裂缝净压力的最大值同样为地层水平主应力的差值pZmax。综上所述,页岩I区块天然裂缝扩展的力学基础条件为施工形成的裂缝内净压力值大于地层水平主应力的差值。
2.3 工程条件影响页岩地层体积压裂所形成缝网有效性的工程因素包括施工净压力、施工流体黏度及施工液量。为保证满足施工净压力,必须使用可靠的压裂设备;施工流体黏度尽可能小,以满足形成复杂缝网的需要,目前常用滑溜水(或混合压裂液)作为压裂液进行施工;页岩储层压裂不同于常规储层的压裂,压裂过程中需要大量的压裂液量,因此,需要着重考虑压裂供水问题。页岩I区块位于长江江畔,水资源充足,取水方便,压裂液用水能够得到有效保证。
3 裂缝参数优化 3.1 地质模型建立根据页岩I区块的单井数据、层面数据和微地震数据等相关地质参数,利用Petrel软件建立地质模型。对模型进行网格化,设定网格大小为20 m×20 m,生成平面网格。运用序贯高斯模拟的方法建立砂岩层的孔隙度分布模型。在得到孔隙度模型的基础上,运用协克里金方法,在序贯高斯模拟中对渗透率进行控制,建立渗透率分布模型。利用已给出的页岩气丰度数据建立页岩气丰度分布模型。利用已给出的页岩气含水饱和度数据进行含气饱和度建模(图 1)。
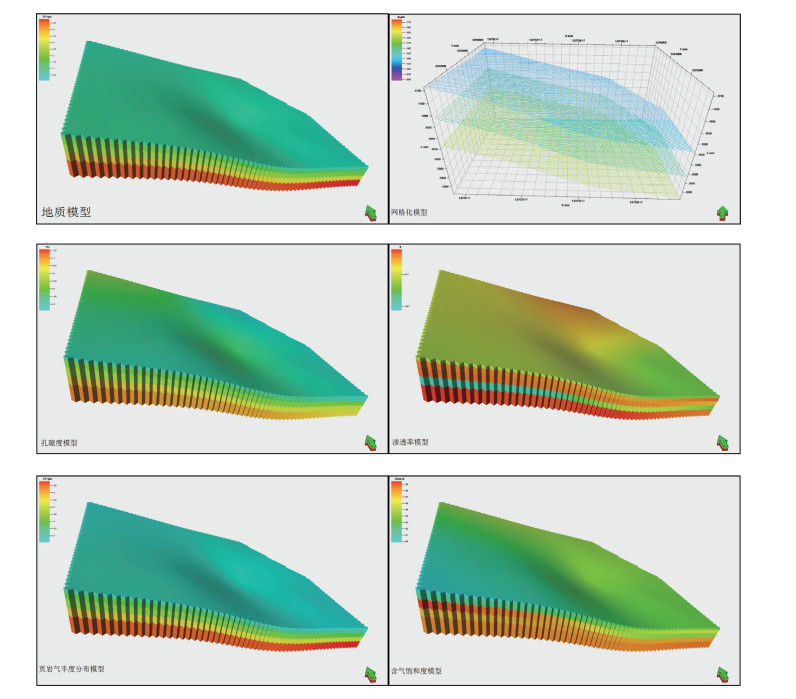 |
| 图 1 页岩I区块相关地质模型 |
将建立的页岩Ⅰ地质模型导入数值模拟软件,利用数值模拟软件对裂缝半长、裂缝段数、导流能力等参数进行优化[3-5]。
3.2 裂缝半长优化分别取140、160、180、200、220、240 m的裂缝半长进行模拟,以20年的采出程度作为评价指标。
模拟结果显示,随着裂缝半长增加,气体的采出程度逐渐增加,但是当裂缝半长大于200 m时,采出程度的增幅减小,因此,优化所得压裂最佳裂缝半长为200 m(图 2)。
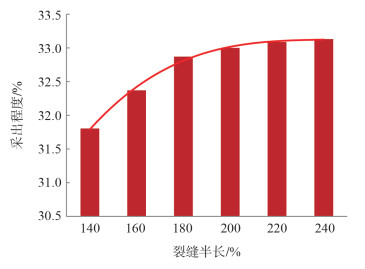 |
| 图 2 不同裂缝半长20年采出程度 |
3.3 裂缝段数优化
以1 000 m的水平井为例,分别布置4、6、8、10、12、14段裂缝进行模拟,模拟时间为20年。
1 000 m的水平井随着压裂分段段数的增加,20年的采出程度逐渐增加,当段数多于10段后采出程度增加幅度很小,因此,最优的裂缝段数为10段(图 3)。
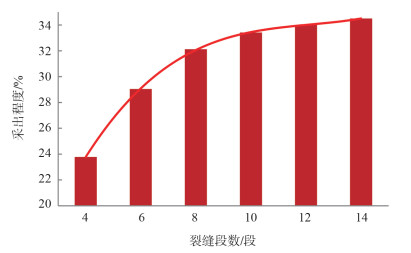 |
| 图 3 不同裂缝段数20年采出程度 |
3.4 裂缝导流能力优化
对比5、7、10、13、15 μm2 · cm五种不同导流能力的裂缝模拟对采出程度的影响,结果如下:
分析得裂缝导流能力小于10 μm2·cm时,采出程度随导流能力的增加变化幅度较大,导流能力大于10 μm2·cm时,采出程度几乎没变化,因此,确定最优的导流能力为10 μm2·cm(图 4)。
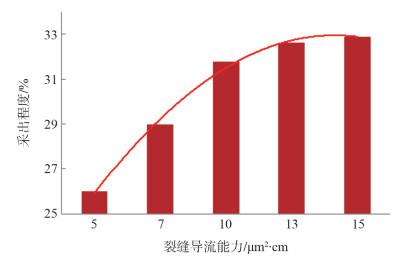 |
| 图 4 不同裂缝导流能力20年采出程度 |
4 裂缝模拟 4.1 裂缝数值模拟方程
根据优化的裂缝参数对体积压裂缝网进行模拟。裂缝模型采用拟三维裂缝扩展模型,数学模型如下:
(1)连续性方程
压裂过程就是压裂液压开地层并充填地层的过程,有质量守恒定律可知,形成裂缝的体积与注入的压裂液的体积相等,即:
| $ \int_0^t {{q_{\rm{D}}}} dt = {V_{\rm{D}}} $ | (10) |
式中:qD为充填裂缝的压裂液流量,m3/min;t为施工时间,min;VD为裂缝体积,m3。
(2)压降方程
压裂裂缝的压降方程如下:
| $ \frac{{\partial p}}{{\partial x}} = {2^{n' + 1}}{\left[ {\frac{{\left( {{2^{n' + 1}}} \right){q_{\rm{D}}}}}{{n'\phi \left( {n'} \right){h_{\rm{D}}}}}} \right]^{n'}}\frac{{K'}}{{W_{\rm{D}}^{2n' + 1}}} $ | (11) |
式中:n'为幂律流体的流态指数,无因次;ϕ(n')为性质因子,在本模型中近似取3π/16;hD为裂缝缝高,m;K'为幂律流体的稠度系数,Pa· sn';WD为裂缝缝宽,cm。
(3)缝宽方程
压裂裂缝缝宽方程如下:
| $ {W_{\rm{D}}} = \frac{{2\left( {1 - {v^2}} \right)}}{E}\left( {{P_{\rm{f}}} - {\sigma _{\min }}} \right){h_{\rm{D}}} $ | (12) |
式中:v为储层泊松比,无因次;E为储层弹性模量,MPa;Pf为裂缝流体压力,MPa;σmin为储层最小水平主应力,MPa。
(4)缝高方程
压裂裂缝缝高控制方程为:
| $ {h_{\rm{D}}} = \frac{{2K_{{\rm{IC1}}}^2}}{{{{\left( {{P_{\rm{f}}} - {\sigma _{\min }}} \right)}^2}{\pi }}} $ | (13) |
式中:KIC1为裂缝断裂韧性,MPa·m1/2;Pf为裂缝流体压力,MPa;σmin为储层最小水平主应力,MPa。
4.2 压裂裂缝模拟结果采用混合压裂液体系,利用滑溜水进行造缝,最后利用线性胶携砂支撑主裂缝,形成较高的导流能力[6-8]。加砂方式采用脉冲加砂,有利于形成复杂缝网。
模拟结果显示,主裂缝铺砂浓度约为4 kg/m3,铺砂均匀效果良好(图 5)。
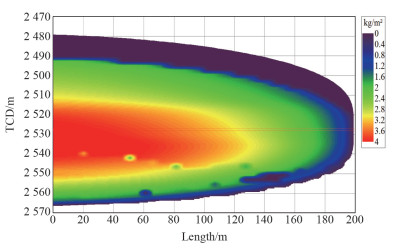 |
| 图 5 裂缝铺砂浓度 |
主裂缝导流能力约为10 μm2·cm,满足优化结果(图 6)。
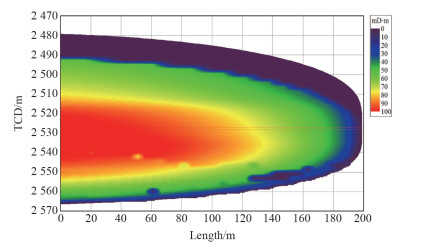 |
| 图 6 裂缝导流能力 |
裂缝三维缝网图显示,区块能够形成有效缝网,对该区块进行体积压裂具有实践性(图 7)。
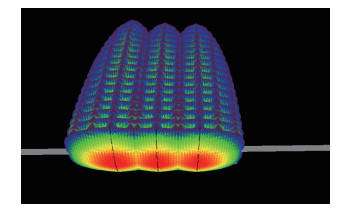 |
| 图 7 三维缝网 |
5 结论
(1)国内外实践经验表明,页岩气开发只有进行体积压裂,形成有效的缝网才具有工业价值。
(2)从地质因素、力学因素以及工程因素三个方面分析了页岩Ⅰ区块具有进行体积压裂的条件。
(3)对页岩Ⅰ区块压裂裂缝参数进行了优化,优化结果为:裂缝半长200 m、裂缝段数为10段、裂缝导流能力为10 μm2·cm。
(4)三维裂缝模拟结果证实页岩Ⅰ区块能够形成有效缝网,并且满足优化的裂缝参数,能够进行体积压裂。
| [1] |
吴奇, 胥云, 刘玉章, 等. 美国页岩气体积改造技术现状及对我国的启示[J]. 石油钻采工艺, 2011, 33(2): 1-7. DOI:10.3969/j.issn.1000-7393.2011.02.001 |
| [2] |
程远方, 李友志, 时贤, 等. 页岩气体积压裂缝网模型分析及应用[J]. 天然气工业, 2013, 33(9): 53-59. |
| [3] |
张士诚, 牟松茹, 崔勇. 页岩气压裂数值模型分析[J]. 天然气工业, 2011, 31(12): 81-84. DOI:10.3787/j.issn.1000-0976.2011.12.014 |
| [4] |
雷群, 胥云, 蒋廷学, 等. 用于提高低-特低渗透油气藏改造效果的缝网压裂技术[J]. 石油学报, 2009, 30(2): 237-241. DOI:10.3321/j.issn:0253-2697.2009.02.013 |
| [5] |
任俊杰, 郭平, 王德龙, 等. 页岩气藏压裂水平井产能模型及影响因素[J]. 东北石油大学学报, 2012, 36(6): 76-81. |
| [6] |
Fathi E, Akkutlu I Y. Matrix Heterogeneity Effects on Gas Transport and Adsorption in Coalbed and Shale Gas Reservoirs[J]. Transport in Porous Media, 2009, 80(2): 281-304. DOI:10.1007/s11242-009-9359-4 |
| [7] |
闪从新, 李晓平, 秦海菲, 等. 多裂缝水平井非稳态产能模型及计算方法研究[J]. 油气井测试, 2008, 17(6): 5-7. DOI:10.3969/j.issn.1004-4388.2008.06.002 |
| [8] |
杨树坤, 张博, 常振, 等. 基于流线方法的压裂水平井注水开发渗流机理研究[J]. 海洋石油, 2016(4): 40-44. DOI:10.3969/j.issn.1008-2336.2016.04.040 |
 2019, Vol. 39
2019, Vol. 39

