| 水下井口波致疲劳力学分析 |
2. 上海霞为石油设备技术服务有限公司, 上海 201414
2. Shanghai SUPWEE Co., Ltd., Shanghai 201414, China
水下钻井井口疲劳寿命是井口研发公司必须满足的基本要求之一。井口疲劳载荷来自于下部挠性接头的张力、剪力和弯矩的不断变化。波浪和洋流作用于平台和隔水管系统而引起的周期载荷被传递到底部挠性接头,载荷传递经过挠性接头后,载荷幅值大大减少。被传递下去的载荷继续通过下隔水管组[LMRP(Lower Marine Riser Package)]、防喷器[BOP(Blowout Preventer)]和井口系统。井口系统载荷一部分从高压井口连接的表层套管传递,另一部分从高压井口和低压井口座挂台阶传递到外层导管,并最终传递到海底土壤中去;从表层套管传递的载荷一部分通过水泥传递到导管并最终传递到土壤中;另一部分则传递到套管深处直至平衡[1]。由此可见,由波浪等引起的周期载荷的传递路径都会从最薄弱的井口焊接剖口传递;低压井口焊接剖口由于在防喷器(BOP)和下隔水管组(LMRP)重力以及套管重力的作用下一直处于压缩状态,对疲劳裂纹的产生有抑制作用;但是,高压井口焊接剖口处没有压缩载荷的作用,在变化载荷作用下会产生较明显的疲劳损伤。因此,在设计时,应重点优化高、低压井口与表层套管连接处的焊接剖口。
由此,通过ABAQUS量化井口设备热点处的疲劳寿命成为优化设计井口疲劳寿命的选择之一,本文将着重阐述基于谱分析方法的井口疲劳计算的力学过程,并通过算例验证计算的合理性[2]。
1 水下井口及隔水管力学性能分析模型基于波致疲劳载荷的传递路径,井口疲劳力学模型应当包含平台系统、隔水管系统和井口悬挂系统。波浪作用于钻井平台的响应RAO分析可通过专业的软件进行计算,不同的平台、波浪和洋流对应不同的RAO,详细的计算流程不再赘述,主要讨论隔水管及井口力学问题。
1.1 隔水管受力分析隔水管系统力学模型包括从上部挠性接头到下部挠性接头之间的管柱、接头和附件(浮块、辅助液压管汇等),主要受到波浪和洋流作用于钻井船的船体运动(3个平动自由度和3个转动自由度),船体运动再作用于隔水管顶部并传导到隔水管系统、隔水管自重、隔水管浮力、由波浪和洋流产生的隔水管惯性力(加速度产生)和拖拽力(速度产生)。底部挠性接头载荷大小受波浪力载荷影响较小,受隔水管顶部张力(T0)和平台偏移距离(S0)的影响较大。由此,隔水管疲劳载荷应在顶部张力和偏移距离的预载下施加波浪的变化载荷。为了获取隔水管系统的传递函数,需建立隔水管系统的预载微分平衡方程(式(1)),并通过有限元方法求解微分方程组,在波浪和洋流作用下隔水管及井口系统力学分析模型如图 1所示。
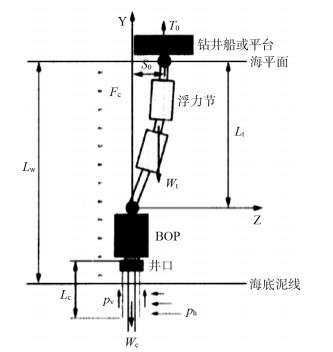 |
| 图 1 隔水管及井口系统力学分析模型[3] |
| $ \frac{{{d^2}}}{{d{z^2}}}[EI(z)\frac{{{d^2}y}}{{d{z^2}}}] + T(z)\frac{{{d^2}y}}{{d{z^2}}} + w(z)\frac{{dy}}{{dz}} - f(z) $ | (1) |
式中:EI为隔水管的抗弯刚度,N · m2;T为有效轴向力(顶部张力与隔水管浮重之和),N;W为隔水管单位长度的重量(包括内部钻井液和浮力节的总重量),N/m;f为沿水平方向作用于隔水管单位长度上的波流联合作用力[4],N。隔水管的波流联合作用力是基于Morison方程的线性假定,即波浪水质点加速度和速度与洋流水质点加速度和速度的叠加产生的作用力。
洋流在水平向对单位隔水管长度上产生的拖拽力见式(2)。
| $ {F_{\text{c}}}=0.5{C_{\text{D}}}{\rho _{\text{w}}}D{u_{\text{c}}}\left| {{u_{\text{c}}}} \right| $ | (2) |
式中:Fc为隔水管柱单位长度上的海流载荷,N/m;CD为拖拽力系数;ρw为海水密度,kg/m3;D为隔水管外径,m;uc为海流流速,m/s。
波浪在水平向对单位隔水管长度上产生的拖拽力和惯性力见式3。
| $ F - {F_{\text{D}}}={F_{\text{I}}}=0.5{C_{\text{D}}}{\rho _{\text{w}}}D{u}\left| u \right| + \frac{{\pi {D^2}}}{4}{C_{\text{M}}}{\rho _{\text{w}}}\frac{{du}}{{dt}} $ | (3) |
式中:F为隔水管柱单位长度上的波浪载荷,N,包括拖拽力FD和惯性力FI两部分,前者是由于水质点的水平速度引起,后者是由于水质点的水平加速度引起;CM为惯性力系数;ρw为海水密度,kg/m3;D为隔水管外径,m;u为波浪引起的水质点速度,m/s。
洋流和波浪联合作用下采用Morison方程得到的隔水管柱单位长度上的水平向载荷,见式(4)。
| $ f\left( z \right)={F_{\text{c}}} + F=0.5{C_{\text{D}}}{\rho _{\text{w}}}D\left( {u + {u_{\text{c}}}} \right)\left| {u + {u_{\text{c}}}} \right| + \frac{{\pi {D^2}}}{4}{C_{\text{M}}}{\rho _{\text{w}}}\frac{{du}}{{dt}} $ | (4) |
式中:uc为海流引起的水质点速度,m/s;u为波浪引起的水质点速度,m/s;du/dt为波浪引起的水质点加速度m/s2。
洋流由于在z向(水平向)速度恒定,则洋流在水平向上的加速度为0。其余方向的受力平衡微分方程可以类似获取[5]。
1.2 井口受力分析通过隔水管力学分析,获取波浪谱不同Bins在底部挠性接头处的弯矩、剪力和张力的RMS(Root Mean Square)。接下来需要建立从底部挠性接头到泥线以下100 m左右的井口系统模型,其中包括LMRP、井口防喷器、井口设备、导管、套管、水泥环以及泥土等。井口疲劳损伤多发生在高低井口与其焊接管柱区域,该区域一方面由于几何不连续导致的应力集中使其疲劳损伤增加;另一方面由于焊接材料及焊接初始微裂纹导致的疲劳强度降低,并在海水腐蚀作用下进一步降低疲劳强度。因此,井口设备的疲劳问题主要是焊接区域的疲劳问题。其力学模型见图 2。
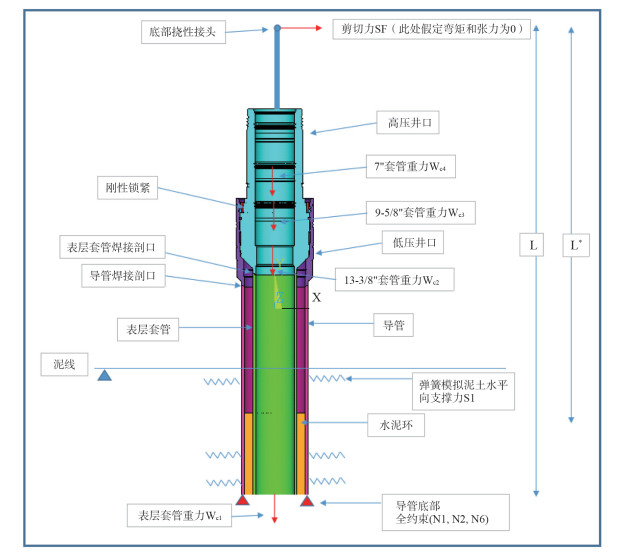 |
| 图 2 井口系统力学分析模型 |
由图 2可见,井口受到的载荷包括底部挠性接头传递的剪力,各层套管的悬挂重力,海底泥土壤的径向支撑力,导管底部的刚性支撑力。系统稳定情况下应满足水平向平衡,轴向平衡和力矩平衡,其方程表达如下:
| $ SF={N_1} + {S_1} $ | (5) |
| $ {W_{{\text{c1}}}} + {W_{{\text{c2}}}} + {W_{{\text{c3}}}} + {W_{{\text{c4}}}}={N_2} $ | (6) |
| $ SF \times={S_1} \times {L^*} + {N_6} $ | (7) |
式中:SF表示挠性接头处的剪切力,N;N1表示导管底部的水平向反力,N;N2表示导管底部轴向反力,N;N6表示导管底部垂直于剖面的弯矩力,N;S1表示泥土水平向当量支撑力,N;Wc1表示表层套管的重力,N;Wc2表示13-3/8″套管的重力,N;Wc3表示9-5/8"套管的重力,N;Wc4表示7"套管的重力,N;L表示从底部挠性接头到导管底部的距离,m;L*表示从底部挠性接头到海土壤水平当量支撑力作用点的距离,m,可以认为海底土壤弹簧支撑力最大点为当量支撑力作用点。其中弯矩计算方程未考虑井口偏斜下重力产生的弯矩[6]。
井口焊接区域产生疲劳的外载基于三种载荷:张力、剪力以及弯矩力。焊接区域响应的应力通常为第一主应力和第三主应力,焊接区域的应力变化如下:
| $ \Delta f\left( {S,M,T} \right)=\frac{{\partial f\left( {S,\bar M,\bar T} \right)}}{{\partial S}}\Delta S + \frac{{\partial f\left( {M,\bar S,\bar T} \right)}}{{\partial M}}\Delta M + \frac{{\partial f\left( {T,\bar M,\bar S} \right)}}{{\partial T}}T $ | (8) |
式中:S表示挠性接头处的剪切力,N;M表示挠性接头处的弯矩力,N;T表示挠性接头处的张力,N;T表示挠性接头处的张力为恒定值,N;S表示挠性接头处的剪力为恒定值,N;M表示挠性接头处的弯矩力为恒定值,N;f(S, M, T)表示焊接区域处于底部挠性接头之间的应力传递函数;Δ表示变化值,N;
2 井口疲劳计算工况本文的井口疲劳以钻井工况为准,实际工况中还应包含完井、修井和生产导致的疲劳损伤,完井、修井和生产导致的疲劳损伤计算方法和钻井一样。由此,总的疲劳损伤应为:
| $ {D_{{\text{total}}}}={D_{{\text{rilling}}}} + {D_{{\text{completion}}}} + {D_{{\text{workover}}}} + {D_{{\text{production}}}} $ | (9) |
式中:Dtotal为总的疲劳损伤;Ddrilling为钻井产生的疲劳损伤;Dcompletion为完井产生的疲劳损伤;Dworkover为修井产生的疲劳损伤;Dproduction为生产导致的疲劳损伤。
在实际工况中,钻井和完井仅仅发生在起初阶段,修井根据实际情况可能会发生,只有生产是经历大部分时间段的工况。因此,井口疲劳损伤计算应以生产工况作为主要计算部分,钻井、完井和修井工况作为预损伤部分:
| $ {D_{{\text{predamage}}}}={D_{{\text{drilling}}}} + {D_{{\text{completion}}}} + {D_{{\text{workover}}}} $ | (10) |
| $ {D_{{\text{total}}}}={D_{{\text{predamage}}}} + {D_{{\text{production}}}} $ | (11) |
式中:Dpredamage为钻井、完井和修井工况产生的初始疲劳损伤,它是某一时期产生的疲劳损伤,不具备周期性。
相反,生产工况产生的疲劳损伤具有周期性,该部分可根据短期(如,1年期)波浪散步数据推出长期疲劳损伤,若井口总损伤为1时,认为井口疲劳失效。例如,假如Dpredamage总计损伤为0.2,Dproduction of 1 year在1年中损伤为0.05,则实际疲劳寿命Nf为16年,计算如下:
| $ {D_{{\text{total}}}}={D_{{\text{predamage}}}} + {D_{{\text{production}}}}={\text{ }}0.2{\text{ }} + {N_{\text{f}}}{D_{{\text{production of 1 year}}}}={\text{ }}1 $ | (12) |
| $ {N_{\text{f}}}=0.8/{D_{{\text{production of 1 year}}}}=0.8/{\text{ }}0.05=16 $ | (13) |
井口疲劳计算从上而下通过传递函数获取在环境载荷作用下井口热点区域的应力响应幅值,结合材料S-N曲线,依据Miner准则计算疲劳寿命,详细流程见图 3。
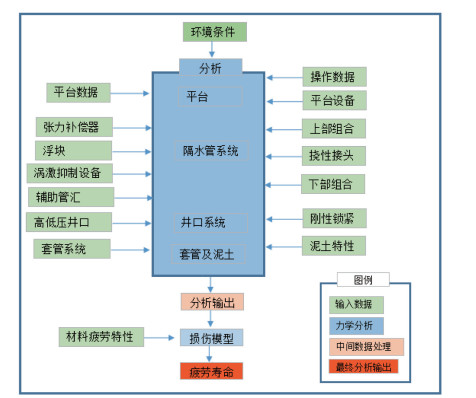 |
| 图 3 井口系统疲劳分析计算流程[7] |
4 算例
中国南海某井所处海水深度600 m,半潜式平台,假设海底浅部地层0~100 m为黏土层,其水下平均容重为7 kN/m3,不排水平均抗剪强度为75 kPa,S-N曲线采用DNV-E。其他主要参数见表 1。
| 表 1 计算参数 |
(1)计算平台RAO(图 4)
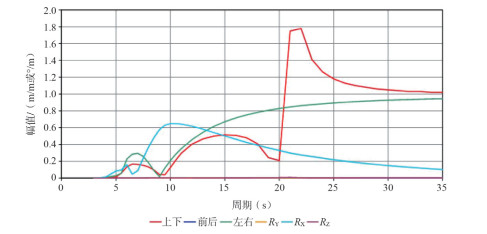 |
| 图 4 平台RAO |
(2)计算隔水管底部挠性接头的RMS(统计均方根)值(表 2)
| 表 2 波浪散布图作用下挠性接头的部分载荷 |
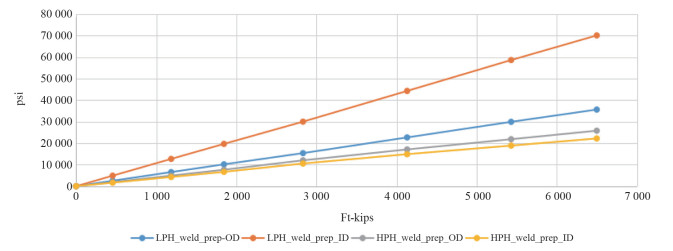 |
| 图 5 拉伸边疲劳热点传递函数 |
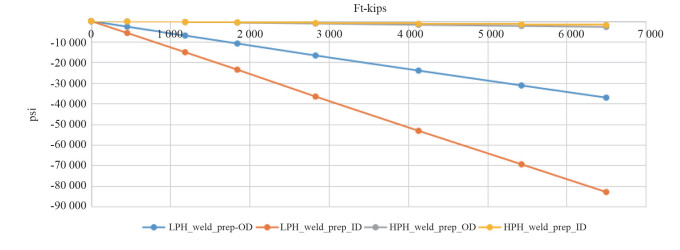 |
| 图 6 压缩边疲劳热点传递函数 |
(4)井口系统热点疲劳(表 3)
| 表 3 井口系统热点疲劳寿命(单位:a) |
5 结论
从上述研究分析中,我们得出结论如下:
(1)对深海井口疲劳力学问题进行系统全面阐述,提供一种行之有效的海洋井口设备疲劳计算方法。
(2)实际算例表明,压缩边的传递函数斜率比拉伸边的传递函数斜率大,导致压缩边的疲劳寿命比拉伸边的疲劳寿命小。如果井口完全对称,则压缩边和伸张边的应力变化幅值应该一样,但是在实际受载中,刚性锁紧环为C型环,导致受压边的载荷变化大于拉伸边的载荷变化;另一方面,DNV方法中不考虑压缩状态下对疲劳裂纹的抑制作用,所以最终结果压缩边的疲劳寿命反而低于拉伸边。
(3)低压井口承受来自BOP以及悬挂的轴向载荷,低压井口一直处于压缩状态,波浪载荷的周期作用幅值作用下,低压井口也处于压缩状态中,但是基于疲劳损伤原理,只要有应力幅值就会产生疲劳损伤。如果受压状态下计算出的疲劳寿命低于DNV要求,可以考虑适当修正压缩状态下裂纹闭合不增长而延长疲劳寿命的因子。
(4)实际算例中,低压井口头内侧表面比外侧表面的寿命低,高压井口头外侧表面比内侧表面的寿命低,这是因为高低压井口焊接剖口局部载荷变化幅值与局部承载截面受到的轴向重力和弯矩载荷综合作用有关。
(5)计算结果表明,该井口满足DNV的疲劳寿命要求。
| [1] |
方华灿. 海洋石油钻采装备与结构[M]. 北京: 石油工业出版社, 1990: 129-146.
|
| [2] |
杨进, 曹式敬. 深水石油钻井技术现状及发展趋势[J]. 石油钻采工艺, 2008, 30(2): 10-13. DOI:10.3969/j.issn.1000-7393.2008.02.002 |
| [3] |
管志川, 苏堪华, 苏义脑. 深水钻井导管和表层套管横向承载能力分析[J]. 石油学报, 2009, 30(2): 285-290. DOI:10.3321/j.issn:0253-2697.2009.02.023 |
| [4] |
刘彩虹, 杨进, 曹式敬, 等. 海洋深水钻井隔水管力学特性分析[J]. 石油钻采工艺, 2008, 30(2): 28-31. DOI:10.3969/j.issn.1000-7393.2008.02.005 |
| [5] |
贾星兰, 方华灿. 海洋钻井隔水管的动力响应[J]. 石油机械, 1995, 23(8): 18-23. |
| [6] |
魏路.西非JDZ-2-1井深水钻井井口稳定性分析研究[D].青岛: 中国石油大学(华东), 2009. http://d.wanfangdata.com.cn/Thesis/Y1542882
|
| [7] |
刘续, 吴永良, 张文学, 等. 水下井口头疲劳寿命分析[J]. 海洋石油, 2016, 36(4): 104-107. |
| [8] |
DNVGL-RP-E104 Wellhead fatigue analysis[R]. 2018: 33-157.
|
 2019, Vol. 39
2019, Vol. 39

