| 基于交叉偶极子阵列声波资料精细评价地应力方法 |
地应力一直以来是油气藏研究中的基础且重要的参数之一,不仅在分析地质构造发展与演化、断层形成与展布、油气运移方向等工作中应用广泛,而且在后期储层裂缝预测、油气压裂设计、开发井网设计、水平井身轨迹设计等同样起到重要作用[1-2]。因此,地应力分析广受重视,目前针对地应力分析,常用方法可分为3种:有限元数值模拟、室内岩心实验分析和利用测井资料计算。其中利用测井资料计算地应力因其方便、快速、实惠而应用广泛[3-4],而且计算方法也日趋成熟。如利用测井资料提供的井径数据、电成像数据及阵列声波数据计算地应力大小与方向[5-8],其中前两者利用的是直观的地层数据进行的应力分析,而后者是通过声波传播原理与地层压实效应进行的理论计算。在此过程中,有人认为最大主应力方向对应的就是快横波传播方向[9],而有人认为在主应力最大方向有大量裂缝存在时,最大主应力方向对应慢横波传播方向[10]。在此,通过研究发现,声波测井往往受井眼与地层的影响,计算出的地应力方向与其他方法略有不同。因此,探究影响声波在分析地应力精度的因素,提高利用声波数据进行地应力分析的精度是一项重要的工作。
1 成像与声波地应力分析模型地应力分析包括地应力大小计算与方向判断,前者主要依靠电成像地层倾角测井资料提供井径数据与阵列声波提供的岩石物理参数结合的方式,利用三维弹性模型为基础,求取地层最大与最小水平主应力大小[11]。公式如下:
| $ {\sigma _{\text{h}}}=\frac{\mu }{{1 - \mu }}{\sigma _{\text{v}}} - \frac{\mu }{{1 - \mu }}{\alpha _{{\text{ven}}}}{p_{\text{p}}} + {\alpha _{{\text{hor}}}}{p_{\text{p}}} + \frac{E}{{1 - {\mu ^2}}}{\varepsilon _{\text{h}}} + \frac{{\mu E}}{{1 - {\mu ^2}}}{\varepsilon _{\text{H}}} $ | (1) |
| $ {\sigma _{\text{H}}}=\frac{\mu }{{1 - \mu }}{\sigma _{\text{v}}} - \frac{\mu }{{1 - \mu }}{\alpha _{{\text{ven}}}}{p_{\text{p}}} + {\alpha _{{\text{hor}}}}{p_{\text{p}}} + \frac{E}{{1 - {\mu ^2}}}{\varepsilon _{\text{H}}} + \frac{{\mu E}}{{1 - {\mu ^2}}}{\varepsilon _{\text{h}}} $ | (2) |
式中:σh为最小水平主应力,MPa;σH为最大水平主应力,MPa;σv为总垂直压力,MPa;αvert为垂直方向的有效压力系数,无量纲;αhor为水平方向的有效压力系数,无量纲;μ为静泊松比,无量纲;pp为孔隙压力,MPa;E为静态杨氏模量,MPa;εh为最小水平主应力的应变,无量纲;εH为最大水平主应力方向的应变,无量纲。
地应力方向的判断,最直接的方法是根据电成像提供的井眼崩落与诱导裂缝进行最大、最小主应力分析。其理论分析基础为:钻井引起地层应力释放,造成了椭圆井眼,并且造成井壁特定方向上产生井壁垮塌或者诱导裂缝,而此时切向正应力最大值出现于最小水平主应力方位[12]。因此,可以通过分析井眼形状与裂缝产状来分析地应力方向。
地应力方向分析的另一种方法是利用阵列声波各向异性提供的快慢横波方位分析地应力方向。此方法理论依据为:原始地层在未受应力释放的影响下,在最大水平主应力方向,地层压实最强烈,地层较为致密,因此,是快横波的传播方位。但是,在钻井过程中,最大主应力方向应力释放强烈,造成了该方向上形成了大量诱导裂缝和微裂隙,造成了该方向上的高声阻抗。因此,此时最大主应力方向成为了慢横波传播方向。而大量作业实践发现,钻井引起地应力释放形成的诱导裂缝往往并非垂直于最大主应力方向,而是多以燕列式排列的高角度裂缝,即诱导缝的走向与最大水平主应力存在一定夹角(图 1)。其中σ1最大水平主应力;σ3最小水平主应力;α为诱导裂缝与最大主应力σ1的夹角;F1、F2为地层诱导裂缝。模型分析认为,地层应力释放后,在最大主应力方向上产生大量高角度诱导裂缝,裂缝面并非完全垂直于最大水平主应力,且往往并非平直,而是呈一定的弧度,因此必然导致快横波的传播方位发生变化,此时的快横波传播方位往往与最大主应力方向呈小角度相交。
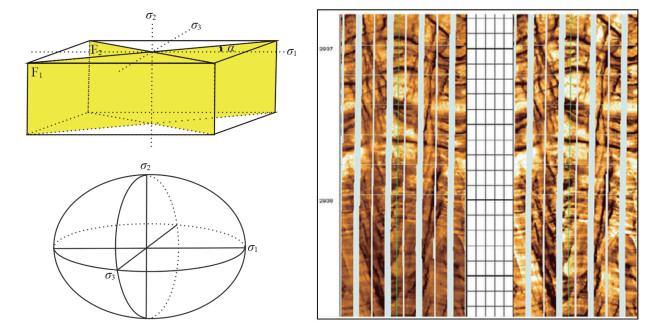 |
| 图 1 地层诱导缝产状及地应力特征图 |
2 诱导裂缝对声波判断地应力方向的影响
以上分析了实际地层中由于应力释放造成的诱导裂缝对快横波传播方位的影响。在以往研究中通常以理想地层模型为指导,简单地把快横波传播方位作为最大水平主应力方向(地层裂缝不发育)或最小主应力方向(地层裂缝发育),而在实际生产中往往遇到的与理想理论模型不一致的现象。此时,需要充分分析地层中裂缝的发育状况,结合其他测井资料,对影响声波判断地层水平最大主应力方向的各因素进行详细研究,最终提高声波判断应力方向的准确性与科学性。以东海某井为例,结合该井电成像研究成果,重点分析诱导裂缝对声波快横波传播方位的影响。
2.1 诱导裂缝发育层段该段上部为频繁交互的砂泥岩,下部为一套稳定的厚层中细砂岩。电成像资料显示,这两套地层中明显发育了延伸长、产状稳定的诱导裂缝,放大比例尺后,丰富、稳定的诱导裂缝清晰可见(图 2);声波各向异性图像显示,这两段地层快、慢横波的波列与时差分离明显,各向异性系数大,声波各向异性方向图中显示为两道近北北东-南西西向的棕红色宽条带,反映了强烈的声波各向异性、快横波方向稳定。通过与该井其他层段对比发现,正是丰富的诱导裂缝导致了上述两个层段的强声波各向异性,分别统计两段地层的快横波传播方位,统计结果显示为NNE向。
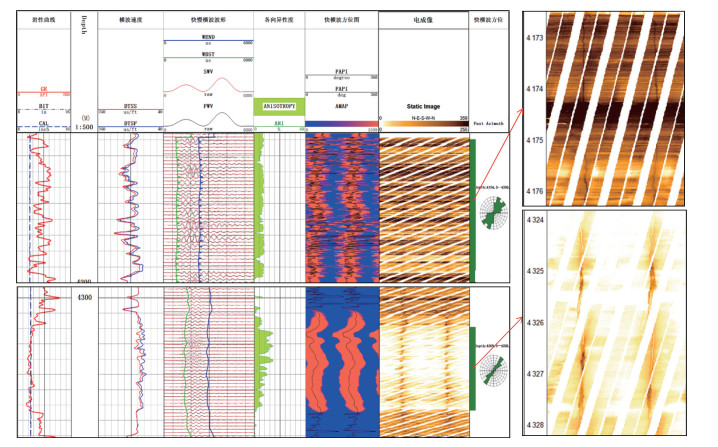 |
| 图 2 成像及声波各向异性层段诱导裂缝特征图 |
2.2 诱导裂缝较发育层段
该段为两套稳定的厚层中细砂岩。电成像资料显示,这两套砂岩中发育了延伸较短、产状不稳定的诱导裂缝,放大比例尺后,发现诱导裂缝缝面较窄、断续不稳定(图 3);声波各向异性图像显示,这两套砂体中快、慢横波的波列与时差分离较明显,各向异性系数较大,声波各向异性方向图中显示为两道近北东-南西向的棕红色不连续窄条带,反映了较强的声波各向异性、快横波方向较稳定。对比该井其他层段,并结合成像与声波资料发现,上述两套砂体内较强的声波各向异性正是由于地层中断续不稳定的诱导裂缝引起的,分别统计两段砂体中快横波传播方位,统计结果显示为NE向。
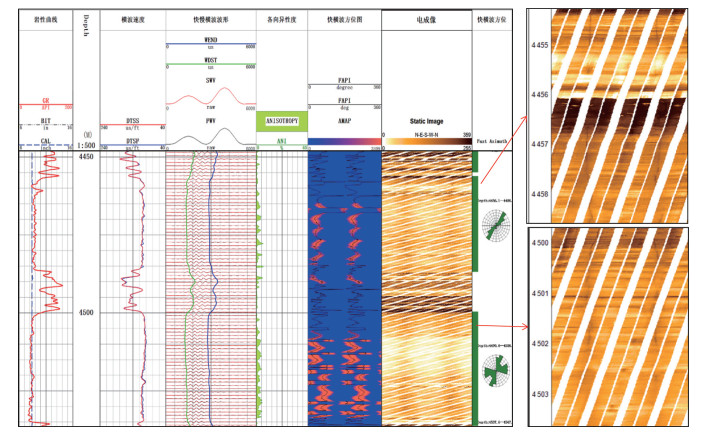 |
| 图 3 成像及声波各向异性层段较少诱导裂缝特征图 |
2.3 诱导裂缝不发育层段
该段上部为中层细砂岩,下部为一套厚层泥岩。电成像资料显示,这两套砂岩中不发育诱导裂缝(图 4);声波各向异性图像显示,这两段地层中快慢、横波的波列与时差分离不明显,声波各向异性方向图中显示为较弱的声波各向异性(未见棕红色条带)。分别统计两段地层中快横波传播方位,统计结果显示为快横波传播方位为近WE向。
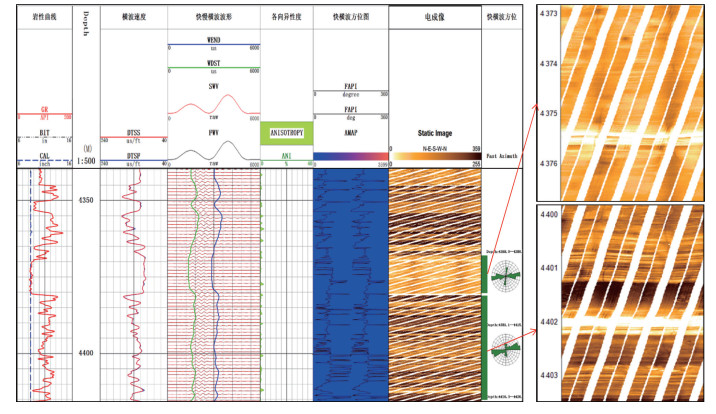 |
| 图 4 成像及声波各向异性层段不发育诱导裂缝特征图 |
电成像资料显示,该井发育丰富的井眼崩落及应力释放造成的诱导裂缝,通过统计该井段井眼崩落及诱导裂缝的产状,得出该区最大水平主应力方向为近WE向,该方向与诱导裂缝不发育层段中声波快横波传播方位相近,与裂缝发育层段中快横波方位有小角度差(45°左右),这与上述中的诱导裂缝应力模型相符。因此,以电成像资料为准,利用声波进行地应力方向判断的时候,应选择地应力释放弱的层段为研究对象,排除因应力释放而产生的诱导裂缝对快横波传播方位的影响。
3 结论通过建立诱导裂缝形成的地应力模型,分析诱导裂缝的产生对声波传播的影响,选取典型层段为研究实例,以电成像资料为标准,评价诱导裂缝对利用声波判断地应力的影响。
(1)地层诱导裂缝应力模型显示,裂缝倾向与最大水平主应力方向相同,但裂缝面并不总是垂直于最大主应力方向,而是与其呈小角度夹角,并且裂缝面也并非平直,这就影响了快横波传播路径,从而对利用声波判断主应力方向产生了影响。
(2)分析诱导裂缝发育程度对快横波传播路径影响,以电成像为标准,发现诱导裂缝发育层段中快横波传播方位与地应力方向呈小角度相交,而诱导裂缝不发育层段快横波方位能够代表最大水平主应力方向。
(3)通过理论与实践结合,提出在利用声波进行地应力判断时,应注意地应力释放形成的诱导裂缝的影响,最好选择弱声波各向异性段,即地应力释放较弱层段,此时的快横波方位才能代表真实的最大水平主应力方位。
| [1] |
周文. 油气藏现今地应力场评价方法及其应用[M]. 北京: 地质出版社, 2007: 12-17.
|
| [2] |
赵良孝. 用测井资料分析压裂漏失及井壁应力崩落的机理和特征[J]. 钻井液与完井液, 1995, 12(1): 14-21. |
| [3] |
葛洪魁, 王顺昌. 地应力测试及其在勘探开发中的应用[J]. 石油大学学报(自然科学版), 1998, 22(1): 94-99. |
| [4] |
欧阳健. 测井地应力分析——以库车坳陷克拉2井气藏解释为例[J]. 新疆石油地质, 1999, 20(3): 213-217. DOI:10.3969/j.issn.1001-3873.1999.03.009 |
| [5] |
王晓杰, 彭仕宓, 吕本勋, 等. 用正交偶极阵列声波测井研究地层地应力场[J]. 中国石油大学学报(自然科学版), 2008, 32(4): 42-46. DOI:10.3321/j.issn:1673-5005.2008.04.009 |
| [6] |
袁仕俊, 刘国良, 周阳, 等. 大北地区高陡构造异常高压地层地应力测井计算方法[J]. 测井技术, 2014, 38(4): 469-473. DOI:10.3969/j.issn.1004-1338.2014.04.018 |
| [7] |
黄继新, 彭仕宓, 王小军, 等. 成像测井资料在裂缝和地应力研究中的应用[J]. 石油学报, 2006, 27(6): 65-69. DOI:10.3321/j.issn:0253-2697.2006.06.014 |
| [8] |
程道解, 孙宝佃, 成志刚, 等. 基于测井资料的地应力评价现状及前景展望[J]. 测井技术, 2014, 38(4): 379-383. DOI:10.3969/j.issn.1004-1338.2014.04.001 |
| [9] |
Esmersoy C, Koster K, Williams M, et al. Dipole shear Anisotropy Logging//Proceedings of 1994 SEG Annual Meeting[C]. Los Angeles: SEG, 1994: 1139-1142.
|
| [10] |
范宜仁, 魏周拓, 陈雪莲. 基于测井资料的地层应力计算及其影响因素研究[J]. 测井技术, 2009, 33(5): 415-420. DOI:10.3969/j.issn.1004-1338.2009.05.003 |
| [11] |
马建海, 孙建孟. 用测井资料计算地层应力[J]. 测井技术, 2002, 26(4): 347-351. DOI:10.3969/j.issn.1004-1338.2002.04.022 |
| [12] |
杜启振, 杨慧珠. 方位各向异性介质的裂缝预测方法研究[J]. 石油大学学报(自然科学版), 2003, 27(4): 32-36. DOI:10.3321/j.issn:1000-5870.2003.04.009 |
 2019, Vol. 39
2019, Vol. 39

