| TTI各向异性速度建模在涠西探区的应用研究 |
宏观速度模型反演方法主要从数据的理解、模型表达、正演这三个方面展开。目前在反演框架下的宏观速度模型估计方法主要有层析成像与基于偏移的速度反演这两类,统称为速度反演。文章讨论的速度建模属于层析范围[1]。
各向同性介质时,地震波沿各个方向的传播速度为常数,波前面为正圆形;各向异性介质时,地震波沿不同方向的传播速度不同,波前面不再呈圆形。当地下介质为各向异性时,采用各向同性的速度进行偏移[2],虽然能够在近偏移距处较好成像,但远偏移距往往存在校不平的现象,而且成像的深度普遍比钻井测量深度更深,存在明显的井震误差。此时需要引入各向异性的偏移成像,引入DELTA校平近中偏移距,再加入EPSILON来校平远偏移距,经过各向异性模型迭代,最终得到较好的成像结果。地震波速度[3]和时距关系复杂,需要进行各向异性处理[4]。
涠西地区断层发育、构造复杂、地层横向变化大、小断层刻画不清楚,导致储层精细刻画难度大,砂体预测、流体预测的准确度不够高。在涠西探区应用各向异性速度建模与成像技术,可以较好解决复杂断块构造成像,落实多级断层和构造;提高资料信噪比和横纵向分辨率;同时满足目的层储层预测和精细油藏研究认识需要。
1 各向异性PSDM速度建模 1.1 层析成像理论与实现在各向同性速度建模中,最常用的是旅行时层析方法[5]。层析根据数据拟合残差求取模型更新量,拟合的数据构成数据空间,求取的数据构成模型空间。
将S(炮点)→ X(反射点)→ R(检波点)这一反射过程(图 1)拆分为X → S和X → R这两个透射过程(图 2)。
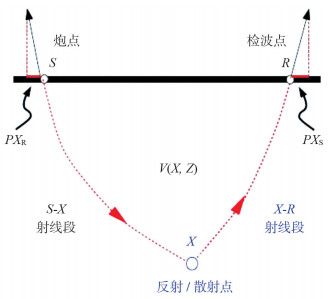 |
| 图 1 一个完整的反射 |
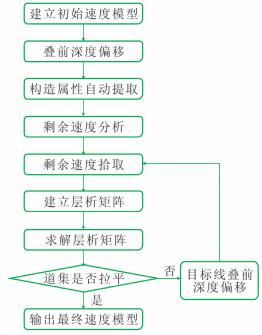 |
| 图 2 网格层析流程 |
层析需要提供一个初始的深度域速度模型,如果是时间域的模型需要转换到深度域。在速度模型和地震数据基础上按照设定的网格进行叠前深度偏移得到网格道集。接着拾取RMO(道集剩余曲率,可以反映道集拉平程度)和道集叠加体的构造属性。根据RMO更新原始速度,然后迭代以上过程,直到得到拉平的道集。
下式完整描述了在广义正交曲线坐标系下,模型空间与立体层析数据空间的线性化关系,即层析矩阵[7]:
| $ \begin{array}{l} \eta \left( {\begin{array}{*{20}{c}} {\Delta {q_1}}\\ {\Delta {p_1}} \end{array}} \right) = \Pi \left( {\sigma , {\sigma _0}} \right)\eta \left( {\begin{array}{*{20}{c}} {\Delta {q_0}}\\ {\Delta {p_0}} \end{array}} \right) + \int\limits_{{\sigma _0}}^\sigma \Pi \left( {\sigma , {\sigma _0}} \right){\Pi ^{ - 1}}\left( {{\sigma _r}, {\sigma _0}} \right)w\left( {{\sigma _{\rm{r}}}} \right)d{\sigma _{\rm{r}}}\\ \Delta w = {\left( {\frac{{\partial \Delta H}}{{\partial p}}, \frac{{\partial \Delta H}}{{\partial q}}} \right)^{\rm{T}}} = {\left( {0, \; - \frac{1}{{{v^2}}}\frac{{\partial \Delta v}}{{\partial q}} + \frac{1}{{{v^3}}}\frac{{\partial v}}{{\partial q}}\Delta v} \right)^{\rm{T}}}\\ \Delta {t_{\rm{s}}} = \frac{{\sin \theta }}{{c\left( {{s_0}} \right)}}\Delta x - \frac{{\cos \theta }}{{v\left( {{s_0}} \right)}}\Delta z - \int\limits_{{s_0}}^{{s_1}} {\frac{{\Delta v}}{{{v^2}}}} ds \end{array} $ | (1) |
式中:
在式(1)的基础上,可以根据数据残差计算模型更新量,通过偏移检查道集是否拉平。
1.2 各向异性建模TTI各向异性模型包括DELTA、EPSILON、PHI、THETA、V0五个参数场。DELTA表示垂向深度差,EPSILON表示横向误差,PHI和THETA是两个正交方位角,在计算过程中起约束作用,V0是应用层析成像已经更新好的各向同性速度场。引入DELTA校平近中偏移距,再加入EPSILON来校平远偏移距,经过各向异性模型迭代,最终得到较好的成像结果。
初始各向异性模型是用各向同性速度与测井误差求取的。对于初始EPSILON因为满足椭圆各向异性假设,设其与DELTA相等,之后再进行EPSILON的更新。通过建立走时场进行克希霍夫叠前深度偏移,根据道集拉平情况进行两轮EPSILON更新,DELTA、THETA和PHI不更新(图 3)。参数更新过程与各向同性速度模型更新过程相同,只是更新量是各向异性参数,而各向同性更新的是速度V0。
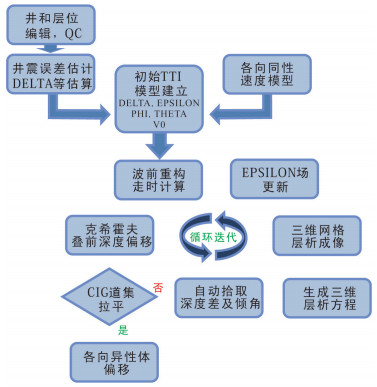 |
| 图 3 TTI各向异性速度模型更新流程 |
2 涠西探区应用
在涠西探区中使用的各向异性速度建模流程如下(图 4):
 |
| 图 4 各向异性速度建模流程 |
V0的求取:输入初始深度域层速度,在旅行时计算之后,进行克希霍夫叠前深度偏移产生网格道集,在道集上进行RMO和倾角拾取,接着进行层析更新速度模型。
其它各向异性参数:结合井[8]、层位信息获得各向异性参数DELTA、EPSILON、PHI、HETA初值,同样在旅行时计算之后,进行克希霍夫叠前深度偏移产生网格道集,在道集上进行RMO和倾角拾取,进行层析成像模型更新,但是仅更新各向异性参数。获得最终TTI各向异性速度模型后进行最终体偏移。与各向同性不同的是旅行时计算的时候需要额外输入四个DELTA、EPSILON、PHI、THETA。
各向异性参数更新的详细过程如下:在更新后的各向同性速度模型基础上,先进行井和层位编辑(详见2.1),然后计算获得各向异性参数(详见2.2);接着进行各向异性模型更新:(1)将速度和各向异性参数作为输入进行走时计算;(2)对经过预处理后的地震数据进行叠前深度偏移生成网格道集;(3)在偏移道集上拾取RMO和倾角;(4)更新EPSILON参数场;(5)重复以上过程。
2.1 井和层编辑经过综合评价,选择使用五套层位(图 5),三口井信息(表 1)进行处理。
 |
| 图 5 深度域解释层位 |
| 表 1 井震误差统计表 |
2.2 各向异性参数获得
通过井标定与解释层位的闭合差,计算出各向同性校正速度,进而通过估算公式计算DELTA(图 6)。
 |
| 图 6 初始DELTA |
Vold是各向同性初始速度,Vnew是各向同性校正速度,通过闭合差计算获得。DELTA是影响垂直介质对称轴方向附近的P波速度大小的参数,DELTA越大也说明P波[9]各向异性程度越强。
对于初始EPSILON因为满足椭圆各向异性假设,设其与DELTA相等,之后再进行更新(图 7)。EPSILON越大表示介质的P波各向异性程度越强,当EPSILON=0时,表示介质中的纵波无各向异性。
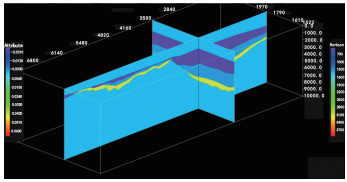 |
| 图 7 初始EPSILON |
THETA和PHI是两个方位角,根据解释层位计算获得(图 8、图 9)。这两个参数作为正确的约束信息,不进行更新。
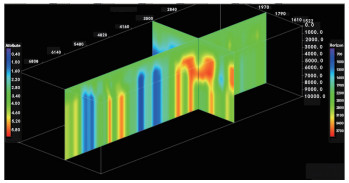 |
| 图 8 初始PHI |
 |
| 图 9 初始THETA |
2.3 EPSILON更新
对初始各向异性速度模型采用波前重构法恢复地下波场,并选择最大能量射线旅行时,进行KirchhoffPSDM处理,对生成的CIG道集进行剩余时差[10]拾取,通过网格层析迭代技术,对初始EPSILON进行更新。
进行网格层析成像之前,需要对道集进行剩余时差分析,自动分析的剩余时差(RMO)曲线是各向异性参数更新的保障(图 10)。
 |
| 图 10 最终EPSILON |
2.4 处理成果分析
试验处理过程中,密切结合层位和测井分层数据,使得求取的各向异性参数与地质吻合程度较高,速度模型更加精细、分辨率更高,成像效果明显更好。且引入各向异性速度建模后,进一步提高了构造成像的可信度。
图 11、图 12展示了研究中TTI-PSDM成像效果与各向同性处理成像效果对比。从成果对比中又明显看到,边界断层成像更加清晰,断层与周围地层的接触关系也更加清楚,波组特征更活跃,小断裂更加干脆,内幕细节也更丰富,基底刻画更合理。断裂和基底部分各向异性处理效果十分明显,充分说明处理成果较好。
 |
| 图 11 各向异性叠前深度偏移剖面 |
 |
| 图 12 各向同性处理剖面 |
3 结论
(1)各向异性叠前深度偏移建模成像较各向同性可以使得边界断层、小断层更加清晰,断层与周围地层接触关系更加清楚,内幕细节更丰富,基底刻画更合理。
(2)各向异性建模技术提高了资料信噪比和横纵向分辨率,满足目的层储层预测和精细油藏研究认识需要。为精细地质解释和反演提供了更好的地震资料。
| [1] |
杨文采, 李幼铭. 应用地震层析成像[M]. 北京: 地质出版社, 1993: 1-230.
|
| [2] |
赵秀莲, 徐翠娥, 陈茂根, 等. 叠前深度偏移技术在东海地区的应用[J]. 海洋石油, 2005, 25(4): 1-5. DOI:10.3969/j.issn.1008-2336.2005.04.001 |
| [3] |
Alkhalifah T, Tsvankin I. Velocity Analysis for Transversely Isotropic Media[J]. Geophysics, 1995, 60(5): 1283-1597. 1550-1566. DOI:10.1190/1.1443865 |
| [4] |
Thomsen L. Weaek Elastic Anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [5] |
马德堂, 朱光明. 横向各向同性介质中的初至波旅行时计算[J]. 石油地球物理勘探, 2006, 41(1): 26-31. DOI:10.3321/j.issn:1000-7210.2006.01.006 |
| [6] |
白海军, 孙赞东, 王学军. 基于波前构建法的TTI介质射线追踪[J]. 石油地球物理勘探, 2011, 46(S1): 1-6. |
| [7] |
Duveneck E. Tomographic Determination of Seismic Velocity Models with Kinematic WavefieldAttributes[MD]. Berlin: Logos Verlag, 2004.
|
| [8] |
李源, 刘伟, 刘微, 等. 各向异性全速度建模技术在山地地震成像中的应用[J]. 石油物探, 2015, 54(2): 157-164. DOI:10.3969/j.issn.1000-1441.2015.02.006 |
| [9] |
韩令贺, 何兵寿, 张会星. VTI介质中准P波方程叠前逆时深度偏移[J]. 地震学报, 2011, 33(2): 209-218. DOI:10.3969/j.issn.0253-3782.2011.02.008 |
| [10] |
杨宽, 曹俊兴, 范欣然. P波资料HTI介质剩余时差校正方法研究[J]. 物探化探计算技术, 2017, 39(3): 367-371. DOI:10.3969/j.issn.1001-1749.2017.03.11 |
 2019, Vol. 39
2019, Vol. 39

