| 斜缆宽频滤波特性研究 |
海上常规地震采集作业是将电缆沉放到同一深度,各检波点鬼波造成的陷波效应集中体现在同一频段。陷波频段与沉放深度有关。沉放越深,陷波频段越靠近低频端,第一通频带越窄,不利于接收高频地震信号,但更有利于接收低频信号。常规地震采集作业时电缆沉放深度一般不会太深(<9 m)。为了兼顾浅深沉放深度鬼波响应各自优势,提高资料频带宽度,Soubaras(2010)提出了“ BraoadSeis(宽频地震)”的概念,从最近的接收道开始,检波器的深度随偏移距的增加而加深,产生不同的鬼波效应,陷波效应分散在多个频段,叠加后拓宽了地震信号的频带宽度,这就是斜缆采集技术[1-2]。
斜缆采集技术在中国海域应用案例不少,取得了较好效果[3-5]。
唐进等提出了基于斜缆采集的鬼波滤波算子的平均叠加脉冲响应谱方法分析了斜缆的宽频采集特点。该方法先计算每个检波器的频谱,再计算所有检波器的算术平均振幅谱[6]。该方法计算简单,但比较粗略。
与上述算术平均谱计算方法不同,本文提出了一种叠加归一化谱的方法,通过将不同检波器的上行波校正到同一时间,下行波相应调整,然后叠加得到一个时间信号,进而计算该叠加信号的振幅谱。基于本方法得到的一维滤波特性,对影响直斜缆滤波特性的关键参数进行了分析。同样利用本方法求取了针对任意斜缆的二维滤波特性,并对5种不同缆型滤波特性进行了对比。
1 直斜缆一维滤波特性 1.1 直斜缆模型直斜缆检波器具有相同的深度间隔,上行波和下行波(即鬼波)到达时(不考虑偏移距)都为等差数列,处理过程中会将上行波校正到同一时间,这样下行波的到达时仍为等差数列,公差是原来的两倍。经过叠加,上行波同时叠加,下行波错时叠加,达到压制下行波的目的。
1.2 一维滤波特性公式推导在一维情况下,也即上行波垂直入射海水面再反射到接收点处,则上行波和下行波到达的时间间隔∆t(单位:s)为:
| $ \Delta t = \frac{{2\Delta h}}{v} $ | (1) |
式中:∆h为直斜缆检波器深度间隔,m;v为地震波传播速度,m/s。
每一道的信号为fn(t)(无量纲),道数为n(无量纲),信号的形态相同,为信号函数f(无量纲),两道之间时延为∆t,所有道叠加的时间信号为x(t)(无量纲)。
| $ \begin{array}{l} x\left( t \right) = {f_1}\left( t \right) + {f_2}\left( t \right) + \ldots + {f_{\rm{n}}}\left( t \right)\\ \;\;\;\;\;\;\; = f\left( t \right) - f\left( {t + \Delta t} \right) + f\left( t \right) - f\left( {t + 2\Delta t} \right) + \cdots + f\left( t \right) - f\left( {t + n\Delta t} \right)\\ \;\;\;\;\;\;\; = nf\left( t \right) - f\left( {t + \Delta t} \right) - f\left( {t + 2\Delta t} \right) - \cdots - f\left( {t + n\Delta t} \right)\\ \;\;\;\;\;\;\; = nf(t) - \sum\limits_{i = 1}^n f \left( {t + k\Delta t} \right) \end{array} $ | (2) |
对(2)式子波做傅里叶变换,根据傅里叶变换的时移性,
| $ \begin{array}{l} F[x(t)] = F\left[ {nf(t) - \sum\limits_{k = 1}^n f (t + k\Delta t)} \right]\\ \;\;\;\;\;\;\;\;\;\;\; = nF(f) - \sum\limits_{k = 1}^n F (f){e^{ - 2{\rm{ \mathsf{ π} }}ifk\Delta t}}\\ \;\;\;\;\;\;\;\;\;\;\; = F(f)\left[ {n - \sum\limits_{k = 1}^n F (f){e^{ - 2{\rm{ \mathsf{ π} }}ifk\Delta t}}} \right]\\ \;\;\;\;\;\;\;\;\;\;\; = F(f)\left\{ {n - \sum\limits_{k - 1}^n {\left[ {\cos \left( {2{\rm{ \mathsf{ π} }}fk\Delta t} \right) - i\sin \left( {2{\rm{ \mathsf{ π} }}fk\Delta t} \right)} \right]} } \right\} \end{array} $ | (3) |
令θ=2πf∆t,(θ无量纲),则
| $ \begin{array}{*{20}{l}} { = F(f)\left[ {n - \sum\limits_{k = 1}^n {(\cos k\theta + i\sin k\theta )} } \right]}\\ { = F(f)\left( {n - \sum\limits_{k = 1}^n {\cos } k\theta + i\sum\limits_{k = 1}^n {\sin } k\theta } \right)} \end{array} $ | (4) |
令
| $ H(f) = n - \sum\limits_{k = 1}^n {\cos } k\theta + i\sum\limits_{k = 1}^n {\sin } k\theta $ | (5) |
计算振幅谱|H(f)|并做归一化,(H(f)无量纲),得叠加归一化振幅谱
| $ \frac{{|H(f)|}}{{2n}} = \frac{{\sqrt {{{\left( {n - \sum\nolimits_{k = 1}^n {\cos k\theta } } \right)}^2} + {{\left( {\sum\nolimits_{k = 1}^n {\sin k\theta } } \right)}^2}} }}{{2n}} $ | (6) |
对叠加归一化振幅谱取极限,计算检波器数量无限多时的频谱
| $ \begin{array}{l} \mathop {\lim }\limits_{n \to \infty } \frac{{|H(f)|}}{{2n}} = \mathop {\lim }\limits_{n \to \infty } \frac{{\sqrt {{{\left( {n - \sum\nolimits_{k = 1}^n {\cos k\theta } } \right)}^2} + {{\left( {\sum\nolimits_{k = 1}^n {\sin k\theta } } \right)}^2}} }}{{2n}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathop {\lim \frac{1}{2}}\limits_{n \to \infty } \sqrt {{{\left( {1 - \frac{{\sum\nolimits_{k = 1}^n {\cos k\theta } }}{n}} \right)}^2} + {{\left( {\frac{{\sum\nolimits_{k = 1}^n {\sin k\theta } }}{n}} \right)}^2}} \end{array} $ | (7) |
(7)式中
| $ \sum\limits_{k = 1}^n {\cos k\theta } \approx \int_0^n {\cos } x\theta dx = \frac{1}{\theta }\sin (n\theta ) \in \left[ { - \frac{1}{\theta },\frac{1}{\theta }} \right] $ | (8) |
| $ \sum\limits_{k = 1}^n {\sin } k\theta \approx \int_0^n {\sin } x\theta dx = \frac{1}{\theta } - \frac{1}{\theta }\cos (n\theta ) \in \left[ {0,\frac{2}{\theta }} \right] $ | (9) |
θ为频率的函数,且不为零,所以当给定频率值,
| $ \mathop {\lim }\limits_{n \to \infty } \frac{{\sum\nolimits_{k = 1}^n {\cos k\theta } }}{n} = 0 $ | (10) |
| $ \mathop {\lim }\limits_{n \to \infty } \frac{{\sum\nolimits_{k = 1}^n {\sin k\theta } }}{n} = 0 $ | (11) |
将(10)(11)式代入(7)式
| $ \mathop {\lim }\limits_{n \to \infty } \frac{{|H(f)|}}{{2n}} = \frac{1}{2} $ | (12) |
由于常用振幅值用分贝表示(单位:dB)为
| $ A = 20 \cdot \log \frac{{|H(f)|}}{{2n}} $ | (13) |
特别的当
| $ \frac{{|H(f)|}}{{2n}} = \frac{1}{2} $ | (14) |
时,对应的分贝值为
| $ A = 20 \cdot \log \frac{1}{2} = - 6 $ | (15) |
通过式(15)可以看出,当检波点个数无限多时,叠加得到的频谱特性曲线为一条沿着-6 dB的直线,对应的子波为脉冲波,电缆端鬼波相对于有效信号的比值为零,无需对电缆端去鬼波处理。
实际斜缆的滤波特性越接近于该极限条件的滤波特性,滤波效果越好。这是分析斜缆滤波特性优劣的依据。
1.3 与平均谱的区别平均谱[6]是一种常用研究斜缆频谱的方法,其优点是计算简单,能粗略地反应斜缆的滤波效应,不过它与叠加归一化谱有一定的偏差(图 1)。
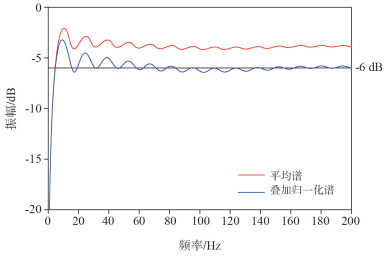 |
| 图 1 平均谱与叠加归一化谱的区别 |
图中红线为平均谱的计算结果,蓝线为本次计算的叠加归一化谱的计算结果,模型参数为最浅沉放深度5 m,最深沉放深度53 m,缆长6000 m。从图中可见,平均谱振幅大于叠加归一化谱,叠加归一化谱极限收敛到-6 dB,平均谱并不收敛到-6 dB。
1.4 直斜缆滤波特性关键影响因素影响直斜缆的滤波特性因素主要包括4方面:①最浅沉放深度;②最深沉放深度;③缆长;④检波器道间距。其中道间距一般固定为12.5 m,所以滤波特性主要对前三个影响因素进行分析。
通过给定直斜缆最浅最深沉放深度、缆长及道间距计算垂向深度间隔,用式(6)进行叠加归一化的频谱数值模拟,分析这几个因素对滤波特性影响。
1.4.1 最深沉放深度最浅沉放深度和缆长不变,分析最深沉放深度对滤波特性的影响。计算滤波特性使用表 1中的参数,最浅沉放深度为5 m,缆长6 000 m,最深沉放深度从53 m变化到29 m。
| 表 1 最深沉放深度变化参数 |
图 2计算的频谱曲线中,红线更接近-6 dB的理想情况,效果较好,蓝色次之,绿色最差。所以,最浅沉放深度和缆长不变的情况下,最深沉放深度越大,频谱特性越好。
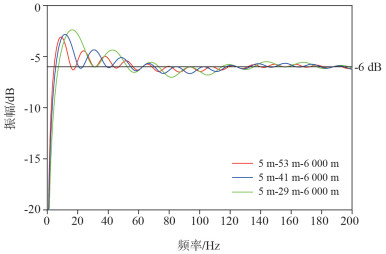 |
| 图 2 最深沉放深度对滤波特性的影响 |
1.4.2 最浅沉放深度
保持最浅沉放深度与最深沉放深度的深度差不变以及缆长不变,分析不同最浅沉放深度组合对滤波特性的影响。计算滤波特性使用表 2中的参数,深度差为24 m,最浅沉放深度从5 m变化到15 m,缆长6 000 m。
| 表 2 深度上下平移变化参数 |
图 3计算的频谱曲线中,红线更接近-6 dB的理想情况,效果较好,蓝色次之,绿色最差。所以,深度差不变,缆长不变的情况下,沉放深度越小,频谱特性越好。
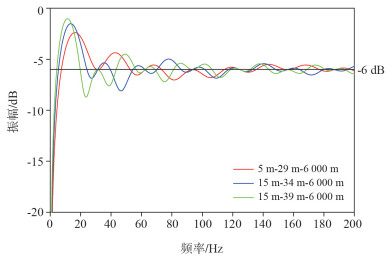 |
| 图 3 等深度差不同最浅沉放深度对频谱的影响 |
1.4.3 电缆长度
控制最浅和最深沉放深度不变,分析直斜缆缆长对滤波特性的影响。计算滤波特性使用表 3中的参数,最浅沉放深度为5 m,最深沉放深度为53 m,缆长从6 000 m变化到200 m。
| 表 3 缆长变化(深度范围不变)参数 |
图 4计算的频谱曲线中,三条曲线与-6 dB接近程度相近。所以,最浅沉放深度和最深沉放深度不变的情况下,不同缆长的频谱特性变化不大。
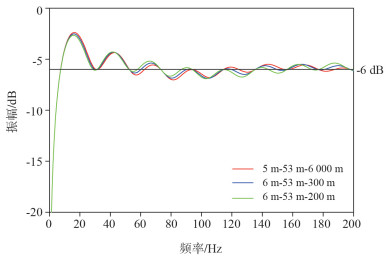 |
| 图 4 缆长变化(深度范围不变)对频谱的影响 |
综上所述,斜缆滤波特性关键的影响因素是近远道的深度变化范围。当深度变化范围较合适(如5~53 m)时,增加缆长对滤波特性影响不大。在实际生产中,应尽量加大近远道的深度变化范围,近偏移距道沉放尽量浅。
2 任意斜缆二维滤波特性及斜缆缆型选择 2.1 任意斜缆二维滤波特性计算方法在二维情况下,地震波不再是理想状态下的垂直传播。任意斜缆的二维滤波特性求取过程如下:
① 计算旅行时
二维的旅行时[3]为
| $ {t_1} = \frac{{\sqrt {{{\left( {2H - {Z_{\rm{s}}} - {Z_{\rm{r}}}} \right)}^2} + {x^2}} }}{v} $ | (16) |
| $ {t_2} = \frac{{\sqrt {{{\left( {2H - {Z_{\rm{s}}} - {Z_{\rm{r}}}} \right)}^2} + {x^2}} }}{v} $ | (17) |
式中:t1为上行波的旅行时,s;t2为下行波的旅行时,s;x为偏移距,m;H为地层深度,m;Zs为震源深度,m;Zr为电缆深度,m;v为地震波传播速度,m/s。
式(16)、式(17)中,v、Zs和H为定值,Zr为x的函数,所以只有一个自变量x,计算出t1和t2与偏移距x的关系。
② 上行波校平
计算时差t=t2-t1,当上行波旅行时校正到0时刻时,下行波旅行时为t。于是得到上行波和下行波校正后与偏移距的关系。
③ 叠加信号
然后将不同偏移距的上行波和下行波信号在时间轴上叠加,生成一个一维信号。其中上行波为正相位,下行波为负相位。
④ 计算叠加信号频谱
通过傅里叶变换计算叠加信号的振幅谱。
2.2 5种缆型滤波特性对比选取5种常见缆型:5 m深平缆、50 m深平缆、犁式缆、抛物线型缆和直线型缆。缆型参数见表 4,形态图见图 5(a),其中犁式缆、抛物线型缆和直斜缆的深度变化范围均为5~50 m。
| 表 4 5种缆型参数表 |
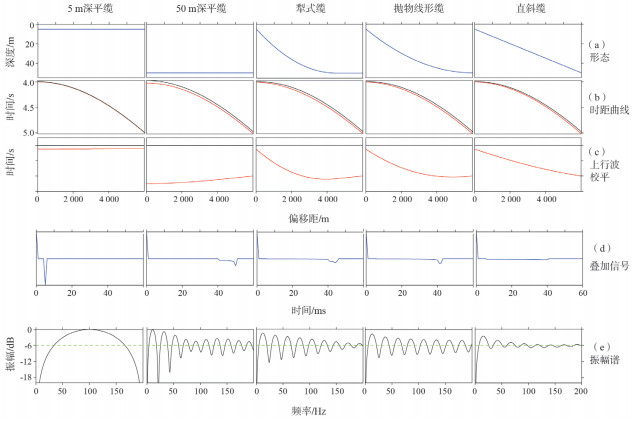 |
| 图 5 5种缆型滤波特性对比图 |
震源沉放深度为5 m,不考虑震源端鬼波效应。模型为单一水平层,深度4 000 m,速度2 000 m/s。
利用式(16)、式(17)计算不同缆型上行波和下行波的旅行时,绘制时距曲线见图 5(b),黑色为上行波,红色为下行波(下同)。
对时距曲线,拉平上行波,下行波随之做相应校正,得到上行波与下行波信号随偏移距的变化,见图 5(c)。
对动校正的信号做水平叠加,得到一维信号(图 5(d))。上行波为正相位,下行波为负相位。
对一维叠加信号做振幅谱分析,得到信号的频谱图(图 5(e))。
从振幅谱可以看出犁式缆、抛物线型缆和直线型缆均优于平缆,其中直斜缆又优于犁式和抛物线型,频谱最为平滑,趋近于-6 dB线。虽然三种缆型检波器分布均为5~50 m,但是犁式和抛物线型缆检波器在深度范围分布不均匀,导致某一深度下行波叠加信号增强,在频谱上出现陷波效果。
从直斜缆的叠加信号和频谱特征可以看出,通过叠加就能很好地压制电缆端鬼波。
3 结论(1)斜缆滤波特性关键影响因素是近远道深度变化范围。变化范围越大,滤波特性越好。在实际生产中,应尽量加大深度变化范围,近偏移距道沉放深度尽量浅一些。
(2)当近远道深度变化范围一定时,增加缆长对滤波特性影响不大。简而言之,检波器在深度方向上的密度对滤波特性影响不大。
(3)通过5种缆型的滤波特性对比,直斜缆压制鬼波的效果最好。实际施工中,应将检波器尽量均匀分布在不同深度,以达到鬼波错时叠加的目的。
| [1] |
Lin D C, RussierD, Gao Y, et al. Challenges in processing variable-depth streamer data//2011 SEG Annual Meeting[C]. San Antonio, Texas: Society of Exploration Geophysicists, 2011.
|
| [2] |
Lin D C, Sablon R, Gao Y, et al. Optimizing the processing flow for variable-depth streamer data[J]. First Break, 2011, 29(9): 89-95. |
| [3] |
钟明睿.倾斜电缆地震处理技术在南海某工区的应用[D].长春: 吉林大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016091730.htm
|
| [4] |
张振波, 李东方. 斜缆宽频地震勘探技术在珠江口盆地的应用[J]. 石油地球物理勘探, 2014, 49(3): 451-456. |
| [5] |
许自强, 方中于, 顾汉明, 等. 海上变深度缆数据最优化压制鬼波方法及其应用[J]. 石油物探, 2015, 54(4): 404-413. DOI:10.3969/j.issn.1000-1441.2015.04.006 |
| [6] |
唐进, 杨凯, 顾汉明, 等. 海上变深度缆地震采集宽频机理分析[J]. 地球物理学进展, 2015, 30(5): 2386-2392. |
 2019, Vol. 39
2019, Vol. 39

