| 南海西部岩石力学分析系统研发 |
南海西部特别是北部湾盆地断块发育,地层的非均质性强,不同构造的岩石力学特征差距很大,地层为易垮塌地层,不利于维护井壁稳定,增加了作业风险。在钻井作业过程中,钻遇易坍塌地层导致事故频发,造成井下钻井事故率高,钻井费用大幅上升,增加了石油勘探开发成本[1-3]。
南海西部存在大量胶结致密、软硬夹层交错、可钻性差的地层,导致部分钻头磨损严重、频繁起下钻更换钻头,钻进效率较低,特别是自流沙港组下部及长流组、前第三系地层可钻性变差,机械钻速明显偏低[4-6]。
国内较少有商用岩石力学分析软件,鉴于南海西部地层的复杂性与特殊性,现有国外商用岩石力学分析软件存在的主要问题有:
(1)适用性较差。岩石力学软件计算需要用到大量的参数,且参数的设置因区块而异。另外计算方法有限,如对于坍塌压力计算,基本全井段采用线性库仑-摩尔准则,结果过于保守。而实验与应用结果表明,对于泥岩采用抛物型、砂岩采用双曲型库仑-摩尔准则计算更为合适[7-8]。
(2)数据处理效率低。岩石力学计算需要处理数万行的测井数据,如筛选有效数据用于分析,剔除干扰数据的影响,而现有岩石力学软件基本不具备数据可视化筛选、智能化剔除功能。由于偏离趋势点常为离散分布,人工在表格中进行数据的筛选,工作量巨大,且容易出错。
(3)软件功能单一。钻进参数与岩石力学参数密切相关,而现有岩石力学软件主要基于测井资料进行分析,软件计算中基本没有考虑钻进参数的影响。
(4)软件界面复杂,且价格昂贵。现有软件几乎都为英文界面,界面复杂,操作习惯与中国研究人员差异较大,不利于效率的提高。
针对北部湾盆地特点,自主研发了中海油第一个岩石力学分析软件,软件实用性强、操作简单,为钻完井设计及施工提供可靠的参考依据,并取得了良好的应用效果。
1 岩石力学分析方法 1.1 地层压力计算模型Eaton法是国内外油田公司普遍采用的地层孔隙压力计算方法,它具有计算精度高,使用范围广等特点。Eaton法计算地层孔隙压力梯度的模式如下[7-9]:
| ${G_{\rm{p}}} = {G_{{\rm{op}}}} - \left( {{G_{{\rm{op}}}} - {\rho _{\rm{w}}}} \right){\left( {\frac{{\Delta t}}{{\Delta {t_{\rm{n}}}}}} \right)^{\rm{n}}} $ | (1) |
式中:Gp为井深处的地层孔隙压力梯度当量密度,g/cm3;Gop为井深H处的上覆岩层压力梯度当量密度,g/cm3;ρw为井深H处的地层水密度,g/cm3;Δt为井深H处的实测声波时差值,μs/ft;Δtn井深H处的正常趋势值,μs/ft;n为Eaton指数。
1.2 岩石参数岩石抗压强度是进行钻头选型及使用情况分析的关键参数,主要依据测井资料预测岩石力抗压强度。一般抗压强度高的岩石其波速也大,沉积岩单轴抗压强度与其动态杨氏模量间的经验关系式有[8-11]:
| ${\sigma _{\rm{c}}} = 0.004\;5 \cdot {E_{\rm{d}}}\left( {1 - {V_{{\rm{cl}}}}} \right) + 0.008{E_{\rm{d}}} \cdot {V_{{\rm{cl}}}} $ | (2) |
式中:Vcl为砂岩的泥质含量,小数;Ed为砂岩的动态杨氏模量,MPa。
| ${\sigma _{\rm{c}}} = \alpha \cdot E_{\rm{s}}^\beta $ | (3) |
式中:α、β为与区域有关的系数。
然而传统模型没有考虑围压的影响,而在实际钻进过程中,一般泥浆密度大于地层压力梯度,地层承受一定的压差作用。在围压作用下,岩石的抗压强度会显著增大,这在高压地层中更为明显。因此仅根据单轴抗压强度评价地层可钻性,特别是泥浆比重与地层压力梯度差值较大时,存在不合理性。
针对常规模型在计算时没有考虑泥浆比重对抗压强度的影响,提出了围压作用下的三轴强度计算方法
| ${\sigma _3} = A \cdot P_{\rm{c}}^2 + B \cdot {P_{\rm{c}}} + C + {\sigma _{\rm{c}}} $ | (4) |
式中:σc为地层单轴抗压强度,MPa;A、B、C为计算系数,根据岩石力学三轴实验结果拟合得到;Pc为压差,MPa,计算式为:
| ${P_{\rm{c}}} = \left( {{\rho _{{\rm{泥浆}}}} - \alpha \cdot {\rho _{{\rm{地层}}}}} \right) \cdot H \cdot 0.009\;8 $ | (5) |
式中:ρ泥浆为泥浆密度,g/cm3;ρ地层为地层压力系数,g/cm3;H为地层垂深,m,α为地层压力传递系数,对于纯泥岩取值为0,对于纯砂岩取值为1。
1.3 井壁稳定性分析(1)井周应力分析
令σv为上覆地应力, σH和σh为水平向的两个主地应力, 为方便描述斜井围岩应力状态及其井眼稳定性, 须引主地应力坐标系(1, 2, 3), 与井筒坐标系(x, y, z)。主地应力坐标系(1, 2, 3)分别与主地应力σH, σh, σz方向一致。井筒坐标系(x, y, z), 其中Oz轴对应于井轴, Ox和Oy位于与井轴垂直的平面之中(图 1)[10]。
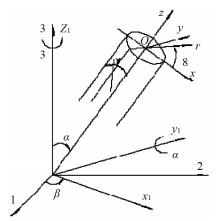 |
| 图 1 定向井井轴坐标变换 |
主地应力坐标系(1,2,3)旋转到坐标系(x,y,z)并得到如下应力转换关系:
| $\left[ {\begin{array}{*{20}{l}} {{\sigma _{{\rm{xx}}}}}&{{\sigma _{{\rm{xy}}}}}&{{\sigma _{{\rm{xz}}}}}\\ {{\sigma _{{\rm{yx}}}}}&{{\sigma _{{\rm{yy}}}}}&{{\sigma _{{\rm{yz}}}}}\\ {{\sigma _{{\rm{zx}}}}}&{{\sigma _{{\rm{zy}}}}}&{{\sigma _{{\rm{zz}}}}} \end{array}} \right] = [L]\left[ {\begin{array}{*{20}{c}} {{\sigma _{\rm{H}}}}&{}&{}\\ {}&{{\sigma _{\rm{h}}}}&{}\\ {}&{}&{{\sigma _{\rm{z}}}} \end{array}} \right]{[L]^{\rm{T}}} $ | (6) |
其中:
| $L = \left[ {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta }&{\cos \alpha \sin \beta }&{ - \sin \beta }\\ { - \sin \beta }&{\cos \beta }&0\\ {\sin \alpha \cos \beta }&{\sin \alpha \cos \beta }&{\cos \beta } \end{array}} \right] $ | (7) |
上面六个地应力分量分别对井周所引起的应力分布线性叠加后,可得到井周应力分布为:
| ${\sigma _{\rm{r}}}{\rm{ }} = \frac{{{R^2}}}{{{r^2}}}P + \frac{{\left( {{\sigma _{{\rm{xx}}}} + {\sigma _{{\rm{yy}}}}} \right)}}{2}\left( {1 - \frac{{{R^2}}}{{{r^2}}}} \right) + \frac{{\left( {{\sigma _{{\rm{xx}}}} - {\sigma _{\rm{yy}}}} \right)}}{2}\left( {1 + \frac{{3{R^4}}}{{{r^4}}} - \frac{{4{R^2}}}{{{r^2}}}} \right)\cos 2\theta \\ + {\sigma _{{\rm{xy}}}}\left( {1 + \frac{{3{R^4}}}{{{r^4}}} - \frac{{4{R^2}}}{{{r^2}}}} \right)\sin 2\theta + \delta \left[ {\frac{{\alpha (1 - 2v)}}{{2(1 - v)}}\left( {1 - \frac{{{R^2}}}{{{r^2}}}} \right) - \phi } \right]\left( {P - {P_{\rm{p}}}} \right){\rm{ }} $ | (8) |
| ${\sigma _\theta } = - \frac{{{R^2}}}{{{r^2}}}P + \frac{{\left( {{\sigma _{{\rm{xx}}}} + {\sigma _{{\rm{yy}}}}} \right)}}{2}\left( {1 + \frac{{{R^2}}}{{{r^2}}}} \right) - \frac{{\left( {{\sigma _{{\rm{xx}}}} - {\sigma _{{\rm{yy}}}}} \right)}}{2}\left( {1 + \frac{{3{R^4}}}{{{r^4}}}} \right)\cos \theta \\ - {\sigma _{{\rm{xy}}}}\left( {1 + \frac{{3{R^4}}}{{{r^4}}} - \frac{{4{R^2}}}{{{r^2}}}} \right)\sin 2\theta + \delta \left[ {\frac{{\alpha (1 - 2v)}}{{2(1 - v)}}\left( {1 - \frac{{{R^2}}}{{{r^2}}}} \right) - \phi } \right]\left( {P - {P_{\rm{p}}}} \right) $ | (9) |
| ${\sigma _{\rm{z}}} = {\sigma _{\rm{zz}}} - v\left[ {2\left( {{\sigma _{{\rm{xx}}}} - {\sigma _{{\rm{yy}}}}} \right){{\left( {\frac{R}{r}} \right)}^2}\cos 2\theta + 4{\sigma _{{\rm{xy}}}}{{\left( {\frac{R}{r}} \right)}^2}\sin 2\theta } \right]\\ \;\;\;\;\;\;\;\;+ \delta \left[ {\frac{{\alpha (1 - 2v)}}{{1 - v}} - \phi } \right]\left( {P - {P_{\rm{p}}}} \right) $ | (10) |
| $\begin{array}{l} {\sigma _{{\rm{r \mathsf{ θ} }}}} = {\sigma _{{\rm{xy}}}}\left( {1 - \frac{{3{R^4}}}{{{r^4}}} + \frac{{2{R^2}}}{{{r^2}}}} \right)\cos 2\theta \\ {\sigma _{{\rm{r}}\mathit{z}}} = {\sigma _{{\rm{y}}\mathit{z}}}\left( {1 + \frac{{{R^2}}}{{{r^2}}}} \right)\cos \theta - {\sigma _{{\rm{xz}}}}\left( {1 + \frac{{{R^2}}}{{{r^2}}}} \right)\sin \theta \\ {\sigma _{{\rm{zr}}}} = {\sigma _{{\rm{x}}\mathit{z}}}\left( {1 - \frac{{{R^2}}}{{{r^2}}}} \right)\cos \theta + {\sigma _{{\rm{yz}}}}\left( {1 - \frac{{{R^2}}}{{{r^2}}}} \right)\sin \theta \end{array} $ | (11) |
通过六个地应力分量,进而可以计算出井壁处任意剪切面处法向应力σn和剪切应力τ。
(2)坍塌压力
从力学的角度来说,造成井壁坍塌的原因主要是由于井内液柱压力较低,使得井壁周围岩石所受应力超过岩石本身的强度而产生剪切破坏所造成的。当井内液柱压力较低时,井壁周围岩石所受应力超过岩石本身的强度而产生剪切破坏。如根据线性库仑-摩尔的研究,岩石破坏时剪切面上的剪应力必须克服岩石的固有剪切强度加上作用于剪切面上的摩擦阻力,即:
| $\tau = {\sigma _{\rm{n}}}{\mathop{tg}\nolimits} \phi + C $ | (12) |
式中:C为岩石剪切强度,MPa,σn为某剪切面处法向应力,MPa,ϕ为岩石内摩擦角,τ为某剪切面处切应力,MPa。
而实验与应用结果表明,强度较低的泥岩采用抛物型库仑-摩尔准则:
| ${\tau ^2} \ge {\sigma _{\rm{t}}}\left( {{\sigma _{\rm{t}}} + {\sigma _{\rm{n}}}} \right) $ | (13) |
式中:σt为岩石抗拉强度,MPa。
对于砂岩或者灰岩,可以考虑采用双曲型库仑-摩尔准则:
| ${\tau ^2} \ge {\left( {{\sigma _{\rm{t}}} + {\sigma _{\rm{n}}}} \right)^2}\tan \eta + \left( {{\sigma _{\rm{t}}} + {\sigma _{\rm{n}}}} \right){\sigma _{\rm{t}}} $ | (14) |
式中:η为岩石强度相关参数。
(3)破裂压力
从力学上说,地层破裂是由于井内泥浆密度过大使岩石所受的周向应力超过岩石的拉伸强度而造成的,即:
| ${\sigma _3} - \zeta {P_{\rm{p}}} = - \left| {{S_{\rm{t}}}} \right| $ | (15) |
式中:St为岩石抗拉强度,MPa;σ3为岩石周向应力,MPa;Pp为地层孔隙压力,MPa;ζ为有效应力系数。
2 岩石力学分析系统研发针对南海西部的需要,同时结合国内外岩石力学软件存在的一些问题,自主研发了中海油岩石力学分析系统,主要模块有数据前处理、泥含量计算、孔隙度分析、上覆压力分析、孔隙压力分析、水平地应力分析、岩石强度计算、钻进参数分析、井壁稳定分析、防砂分析等模块(图 2)。
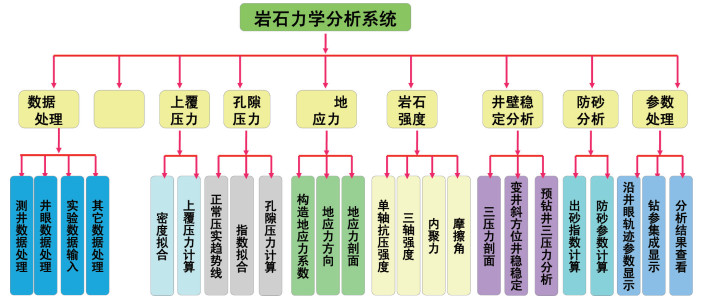 |
| 图 2 岩石力学分析软件模块 |
根据钻井现场的应用特点,要求软件系统安装方便、操作简单、易于维护、功能易于扩展,选择VB语言开发软件,选择EXCEL作为数据库,可以在Win2000以后的Windows操作系统上运行。在实际开发过程中为了提高软件的实用性,软件特色功能如下:
(1)智能化数据筛选功能:可用鼠标在图上直接筛选与剔除异常数据,避免了在表整格中对海量的数据进行筛选,数据处理效率大幅度提升。
(2)数据可视化程度高,信息量大,并将钻进参数、地层特征、钻头使用、岩石强度、将各种信息综合显示与处理,便于岩石力学分析与钻进参数评估,并可为邻井钻头优选提供依据(图 3)。
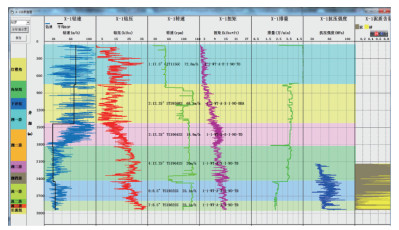 |
| 图 3 岩石力学参数、钻参、钻头、地层信息集成显示 |
(3)实现了多井参数对比功能,可从钻进参数、岩石强度、地层信息进行全方位对比,分析地层特征的差异,进而指导岩石力学分析参数的设置以及钻进参数的控制等。
(4)实现地层参数沿井眼轨迹一体化集成显示功能,数据显示更加直观(图 4),从图上可以直观看出井眼轨迹、地层参数、钻进参数、钻头使用情况等。
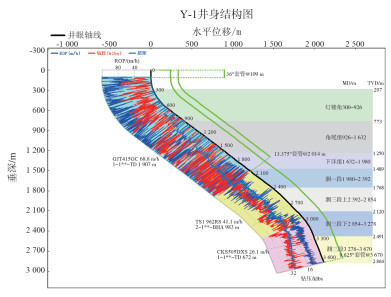 |
| 图 4 地层、钻参沿井眼显示图 |
(5)数据修改方便,采用EXCEL作为数据库输入输出保存数据,可以在EXCEL中直接处理数据,并可以快速批量建模。
3 岩石力学分析系功能分析目前研发的岩石力学分析系统已在南海西部使用,应用证明,该系统可以较为准确的计算岩石力学参数,分析井壁稳定,分析钻参与地层的关系,得到了用户的肯定。模块功能介绍与简要分析如下:
3.1 数据处理模块数据前处理模块中,可以输入计算所需要的测井数据、井斜数据、井身结构数据、钻头使用数据、钻进参数、地质分层数据,并将输入数据转换为软件计算所需要的标准格式。软件对原始输入数据格式具有较好的兼容性,可以自动识别输入的数据。
为提高软件的实用性,软件计算所需要的数据及计算结果数据均存在一个EXCEL文件里面,可以随时打开查看,并直接在EXCEL文件里面修改数据。
3.2 泥质含量计算泥质含量与地层GR关系密切,在计算过程中要用到地层GR的最大最小值。然而计算结果表明,采用地层GR的最大最小值进行计算的结果并不好,采用GR的两个峰值来代替最大最小值效果更好。
在本模块中,自动绘制出了GR频率分布图,可以方便的找出GR的两个峰值用于泥质含量计算;可以选择地层属性为新地层或老地层,计算模型可以采用密度修正或不采用密度修正。计算完成后可以将计算结果以图形的方式显示出来,并且将泥质含量与实测井径、声波、密度数据进行对比(图 5)。
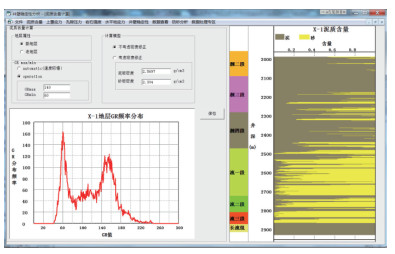 |
| 图 5 泥质含量计算模块 |
3.3 压实趋势线建立
正常压实趋势线是计算孔隙压力的基础,而压实趋势线的建立,需要用较纯泥岩段的声波数据,且与趋势线偏差较远的点不能参与拟合,否则会导致较大的误差,使压实趋势线失真。本系统可以通过泥质含量限定与井径限定对声波数据进行筛选。对偏离趋势的数据点,而在数据表中对偏离趋势的点进行数据剔除工作量巨大,且容易出错。可以在图上将这些点剔除,即可以用鼠标直接将偏离趋势数据点剔除(图 6),操作简单。图中数据点变红说明数据已被剔除,将不用于压实趋势线的拟合,蓝色的点为有效数据,将用于压实趋势线拟合。
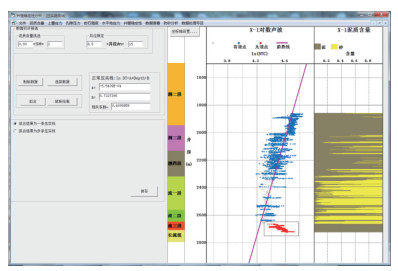 |
| 图 6 正常压实趋势线拟合 |
另外还可以在图上根据声波时差趋势的分布趋势,直接用鼠标手工绘制压实趋势线,系统将自动生成压实趋势线方程。
3.4 上覆压力计算由于一般只在下部井段或储层段才开始测井,上部井段缺少密度数据,因此首先需要拟合上部井段密度数据。拟合密度数据时,应尽量采用泥质含量较高的数据,另外由于在井径较大或较小处,测井数据会失真,不用于计算。
本模块可以通过泥质含量与井径对测井数据进行筛选。偏离趋势异常数据点若参与计算,会严重影响计算精度,本系统可以在图上用鼠标直接将偏离趋势数据点剔除,剔除后数据点显示为红色,将不参与计算(图 7)。
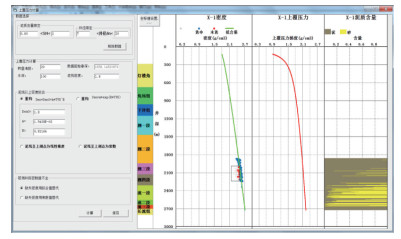 |
| 图 7 上覆压力计算 |
3.5 三轴抗压强度计算
用测井数据即可计算地层单轴抗压强度相关参数的纵向剖面。然而传统模型没有考虑围压的影响,而在实际钻进过程中,一般泥浆密度大于地层压力梯度,地层承受一定的压差作用,在围压作用下,岩石的抗压强度会显著增大,这在高压地层中更为明显。因此仅根据单轴抗压强度评价地层可钻性,特别是泥浆比重与地层压力梯度差值较大时,存在不合理性。
针对常规模型在计算时没有考虑泥浆比重对抗压强度的影响,开发了高压地层岩石抗压强度计算系统,本软件不仅能够计算单轴岩石强度,而且能够计算在围压作用下的三轴强度(图 8)。
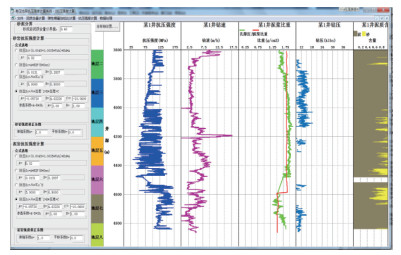 |
| 图 8 三轴抗压强度计算界面 |
3.6 井壁稳定分析
本模块可以计算直井、定向井、水平井等各种井型的三压力剖面,程序内部设有DP、MohrCoulomb线性、Mohr-Coulomb抛物线、MohrCoulomb双曲线模型等可供选择。本系统摒弃了传统模型中全井段使用单一线性库仑-摩尔破坏准则,改进为在泥岩优先采用抛物型、砂岩采用双曲型库仑-摩尔准则。分析时将井壁泥饼渗透等情况考虑在内,并可以考虑井眼适度扩径时的坍塌压力(图 9)。
 |
| 图 9 三压力计算界面 |
另外本模块可以计算全井段的三压力剖面进行计算,还可以计算某段井眼处不同井斜方位坍塌压力及破裂压力。对于易坍塌或漏失地层,可推荐最佳钻井井斜方位,确保安全钻进。
3.7 数据后处理模块数据处理模块中,可以对结果数据进行处理。如在数据统计选项中,可以对岩石抗压强度、机械钻速、钻压等数据进行统计,统计选项中可以选择按地质分层统计、按地层强度范围统计。当选择按地层强度范围统计时,需要输入区间范围(最大值、最小值)、区间数量(图 10)。
 |
| 图 10 结果数据统计界面 |
4 软件应用
南海西部某A油田开发项目共计11口井,其中ϕ311 mm井段钻段钻遇涠二段易坍塌地层,井斜角在17°~85°之间,方位角72°~92°。图 11为A油田坍塌、破裂压力计算结果,可以看出地层破裂压力较高,非断层位置地层破裂漏失风险较小,预测坍塌压力1.34~1.44 g/cm3,而实钻泥浆密度1.37 ~ 1.53 g/cm3,钻井作业过程较为顺利,拟钻井坍塌压力预测值与实钻泥浆比重基本吻合(图 12)。
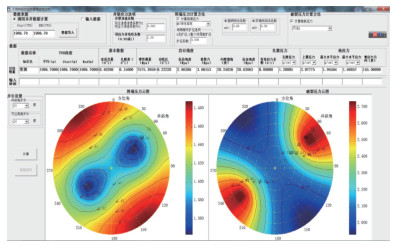 |
| 图 11 某井段坍塌破裂压力分析 |
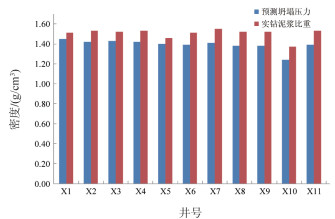 |
| 图 12 南海西部某A油田坍塌压力预测与实钻泥浆密度 |
5 结论
由于南海西部的需要,同时结合国内岩石力学分析软件存在的一些问题,研发了南海西部石力学分析系统,计算精度较高,实用性强,操作简单,为钻完井设计及施工提供可靠的参考依据,取得了良好的效果。该系统有以下特点:
(1)系统化,功能全面,可用于地应力计算、地层压力计算、井壁稳定分等,并首次将钻进参数应用到岩石力学计算中,综合测井数据与钻参进行三轴抗压强度计算。
(2)智能化数据筛选功能:可用鼠标在图上直接筛选与剔除数据,避免了在表整格中对海量的数据进行筛选,数据处理效率大幅度提升。
(3)数据可视化程度高,信息量大,并将钻进参数、地层特征、钻头使用、岩石强度、将各种信息综合显示与处理,实现地层参数沿井眼轨迹显示功能,便于岩石力学分析。
| [1] |
赵宝祥, 陈江华, 徐一龙, 等. 北部湾盆地开发井表层钻井模式[J]. 石油钻采工艺, 2015, 37(6): 23-26. |
| [2] |
北部湾盆地海洋易坍塌地层钻井技术. 石油工业出版社[M]. 北京: 石油工业出社, 2002: 105-120.
|
| [3] |
朱宽亮, 陈金霞, 卢淑芹. 南堡3号构造深层脆性泥页岩井壁稳定机理分析与实践[J]. 钻采工艺, 2016, 39(5): 1-4. DOI:10.3969/J.ISSN.1006-768X.2016.05.01 |
| [4] |
邓金根, 朱海燕, 谢玉洪, 等. 南海西部海域难钻地层特征及破碎机制研究[J]. 岩土力学, 2012, 33(7): 2097-2109. DOI:10.3969/j.issn.1000-7598.2012.07.027 |
| [5] |
黄凯文, 徐一龙, 李磊, 等. 南海西部油田北部湾难钻地层钻井提速技术[J]. 石油钻采工艺, 2013, 35(5): 0020-0028. |
| [6] |
庄林林, 方华良, 雷新超, 等. 北部湾PDC钻头高效钻进及配套技术浅析[J]. 海洋石油, 2015, 35(2): 91-97. DOI:10.3969/j.issn.1008-2336.2015.02.091 |
| [7] |
楼一珊, 金业权. 岩石力学与石油工程[M]. 北京: 石油工业出版社, 2011.
|
| [8] |
陈勉, 金衍, 张广清. 石油工程与岩石力学[M]. 北京: 科学出版社, 2008.
|
| [9] |
蒋涔, 刘苗. 精细压力预测技术研究[J]. 海洋石油, 2016, 36(3): 26-29. DOI:10.3969/j.issn.1008-2336.2016.03.026 |
| [10] |
丁立钦, 王志乔, 吕建国, 等. 基于围岩本体Mogi-Coulomb强度准则的层理性岩层斜井井壁稳定模型[J]. 岩石力学与工程学报, 2017, 36(3): 624-632. |
| [11] |
孟召兰, 邓晗, 韦龙贵, 等. 提高储层出砂预测数值计算精度的方法[J]. 海洋石油, 2017, 37(1): 38-42. |
 2019, Vol. 39
2019, Vol. 39

