| 时深转换技术在巴西某海域3D层速度建模中的应用 |
地震资料解释的最终目标是建立地下介质的三维地质模型,包括由断层和层位组合而成的框架模型以及岩性、物性等属性模型。地下介质是用深度来度量的,因此时间域的地震资料需要通过平均速度模型转换为深度域,即使是深度域地震资料,也必须经过井数据的深度标定而转换为真深度域地震资料。海上井数据稀少,分布不均。地震数据,特别是三维地震数据,密度高,分布较均匀;井点处的VSP(垂直地震剖面)得到的时深数据是目前最准确的时深关系,经过井震标定得到的时深关系则是井上深度与地震时间之间最为合理的时深关系;由地震数据处理得来的水平叠加速度、偏移速度具有纵向精度低的缺点,但在横向上地震速度变化更具合理性;特别是叠前深度偏移处理需要精度较高的层速度模型,其层析反演及迭代偏移技术提供了较合理的三维层速度模型。这些方法各有优缺点,适用于不同的数据条件和要求,需要因地制宜,选择合适的方法和参数进行时深转换。
1 时深转换理论和方法时深转换方法繁多,有井拟合法、井建速度场法、地质构造约束层速度模型法、地震速度场法等。时深转换可分为两种:直接求取平均速度和先建立层速度模型再计算平均速度,分别称为平均速度法和层速度模型法。
1.1 平均速度法平均速度法的目标是直接求取平均速度。平均速度的准确来源是井上VSP(Vertical Seismic Profile)技术得到的时深关系,但此关系不能直接用来对地震数据进行时深转换,其原因是3D或2D地震数据的“时间”与VSP数据的“时间”并不总是一致的,因此对不同的地震数据必须利用合成地震记录完成井震标定,得到最终的平均速度用于时深转换。研究区的条件多样,因此要根据研究区已钻井的情况(无井、单井、多井)以及已钻井的分布情况采用不同的方法进行时深转换。
无井通常代表本区勘探程度低,因此对时深转换精度要求不高,通常采用拟合公式进行时深转换,拟合公式的来源一般为邻区时深关系。此方法的优点是快速、简洁,而缺点则是不适用地下介质情况复杂的地区。另外,没有已钻井,则无法进行井深度校正,转换后的深度不是真深度(真深度即为井深度)。
单井表明该区勘探程度较低,对时深转换的精度要求也较低。平均速度的求取主要有三个关键问题。第一,井震标定得到已钻井点处的时深关系,即利用井震标定建立已钻井点处钻井深度与地震时间之间的对应关系,此项工作越精细得到的时深关系越准确。第二,对已钻井点处的时深关系进行拟合,得到拟合的平均速度用于时深转换,关键是所选择拟合公式和参数;周蒂等研究了珠江口盆地白云凹陷多口探井的时深关系数据,认为乘幂在1和2之间的幂函数拟合式D=atb+c是对深部数据进行时深转换的最优选择[1],常用的多项式时深关系则在中浅部比较适用,因此分段拟合是比较合理的选择。第三,利用井点处的分层进行深度校正,因为只有一口井,选择将井点处的深度校正量在整个工区进行平移。
多井地区一般勘探程度较高,井数据较多,但通常分布不均。首先要对多井的时深关系进行交汇分析,研究利用平均速度进行时深转换的可行性:如果研究区的时深关系一致性较好,则可通过拟合公式或者平均速度插值法实现本区的时深转换工作;相反如果本区的时深关系一致性较差或者很差,那么直接通过平均速度完成时深转换的方法就不适用了。其次,通过分析认为可以利用平均速度进行时深转换,则关键步骤与单井情况类似,其难点在于依靠已知的多个不规则分布的数据来估算相邻位置的数据值,即如何从井点处内插外推到整个研究区,这是一个已经被许多研究者讨论过的经典问题,可借鉴已有的各种方法选择使用,例如传统估值方法、克里金估值、随机模拟等。
必须指出,时深关系中的时间指的是地震波在地下介质中传播的时间,而实际时深关系的时间是地震数据处理后得到的时间。这两个时间并不是一致的,通过井震标定,钻井深度和地震时间相互匹配,同一地区不同的地震数据体可能有不同的时深转换关系。因此,井震标定工作是时深转换过程中至关重要一环。井震标定的时深关系与VSP得到的时深关系相比,其差别表现在两个方面:一是给定初始速度,测井曲线整体漂移,二是通过声波时差曲线些微的拉伸和压缩调整层速度,使井旁道与地震道匹配。
1.2 层速度模型法在构造比较复杂或者时深转换精度要求较高的情况下,直接利用平均速度进行时深转换的方法不再适用,通常会先建立层速度模型,然后再计算出平均速度模型。有两个关键问题:一是在时间域建立层速度模型是否可行有效,二是如何建立合理的层速度模型。
张华军等用一个正演模型说明层速度概念在时深转换中的应用[2]。模型为一“冲断”地质结构,其下盘为一牵引作用形成的向斜构造(图 1a)。正演地震数据经过时间偏移后,其剖面出现正向构造假象(图 1b)。根据时间域的层位和断层解释成果构建时间域地质框架模型,并根据设计的地质模型填上层速度数值,建立时间域层速度模型(图 1c)。利用层速度模型及其转换后的平均速度模型,完成时深转换工作,得到的深度域剖面(图 1d)与设计的深度域地质模型(图 1a)非常接近。这说明只要建立合理的时间域层速度模型,就可以得到较准确的深度域数据体,较好地完成时深转换工作。
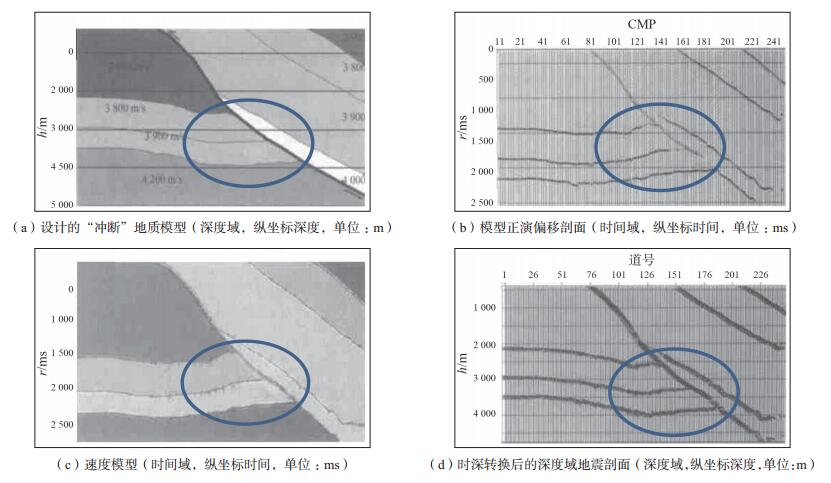 |
| 图 1 层速度概念在时深转换中的应用示意图(引自文献2) |
层速度模型的建立始终离不开井资料,脱离不了内插外推的方式。在构造地形剧烈变化的情况下,引入地质模型约束层速度的内插外推是合理的选择。
地质框架模型的数据基础是层位和断层,关键在于断层之间关系的判断以及断层和层位之间关系的选择。地质模型越合理越精细,则层速度模型的基础就越好。运用地质框架模型进行约束,内部的层速度通常有两种方法进行估算:根据井上速度或者地震速度。有井的地方或者井可以控制的范围优先利用井数据,没有井数据的时候可采用地震数据,两者都有的时候采用井数据[3-7]。
2 研究区时深转换应用分析研究区位于巴西某海域,水深变化大,为被动大陆边缘,构造运动比较简单,但存在大套盐岩沉积,且盐岩流动引发各种盐底辟现象。目前探井及开发井共有109口。为了分析构造特征、计算地质储量、制定及优化开发方案,提出加密井、提高采收率,必须进行储层建模研究工作。
本区速度建模的难点主要有:海水深度变化大、无地震速度体以及时深转换精度要求高。利用Petrel软件,通过追踪海底反射层界面、井震标定、主要构造层位解释,重建地下3D层速度模型,工作流程如图 2所示。
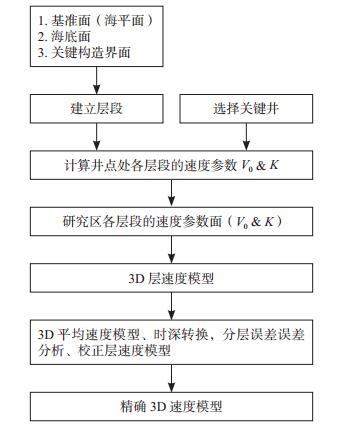 |
| 图 2 速度建模流程图 |
考虑到复杂的地质条件及实际数据,利用井数据及地震数据体进行三维地震资料解释,建立三维层速度模型。框架模型采用标准层、先大后小、先粗后细的原则逐步推进。由于海水深度起伏大,海水变化范围在400 ~ 2 600 m之间,海水与地层速度差异大,反射界面明显,可清晰地追踪出海底反射层,把海底反射层、构造解释层位选为标准层是研究区三维层速度建模的基础(图 3)。
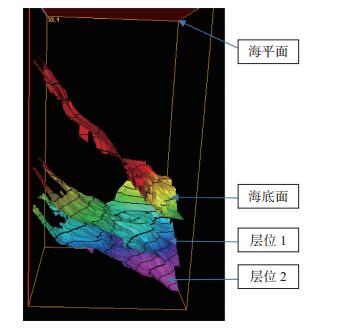 |
| 图 3 速度模型建立所需的层位框架 |
利用研究区内的井数据确立层速度参数V0(某层段顶层速度,m/s)和K(某层段内层速度梯度,1/s),并计算层速度Vz=V0+K(Z - Z0),其中Z为深度,m。选择研究区井震标定相关系数高的探井作为关键井,参与初始速度模型的建立。在海水的影响下时深关系有较大的差异(图 4a),把海水的影响去掉后时深关系比较一致(图 4b),因此建立构造框架时加入了海底。因根据时深关系计算得到的层速度不具有规律性,考虑利用拟合时深关系计算层速度。选用幂指数公式对层速度分段进行拟合得到井点处的参数V0和K(图 5),采用解释的地层时间图作为约束,利用插值外推的方式得到整个研究区的V0和K平面分布图,经过运算,建立了工区三维初始速度模型(图 6)。
 |
| 图 4 部分井时深关系交会图 |
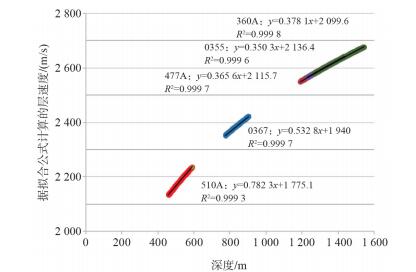 |
| 图 5 据拟合公式计算的层速度随深度变化图(基准面:海底) |
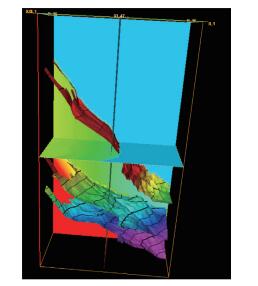 |
| 图 6 构造框架约束下的三维层速度模型 |
考虑到高精度地质建模的需要,框架模型的建立过程中又增加了多个储层解释的层面。当层面之间的厚度变薄,估算速度参数的难度就增大,因此在速度趋势不变的情况下,速度参数就不再重新计算,只需在井分层校正时把所需要的分层选中并对速度模型加以校正即可;如果速度趋势确实有变化,则对层速度进行精细分析处理,然后再估算速度参数V0和K。
利用速度模型进行时深转换,与钻井分层比较,可得到标准层的时深转换误差分布图(图 7)。标准层a与b误差主要分布范围分别在±40 m和±30 m之间。利用关键井的分层数据进行校正,得到校正后的速度模型。利用校正后的速度模型进行时深转换,与钻井分层相比,其误差大幅度降低,标准层a与b误差分别在±2 m和-1 ~ 1.5 m之间(图 8),三维速度模型的精度得到大幅提高。利用建立的三维速度模型,可将时间域的各类数据转换到深度域,为勘探开发提供精确的深度域数据资料。
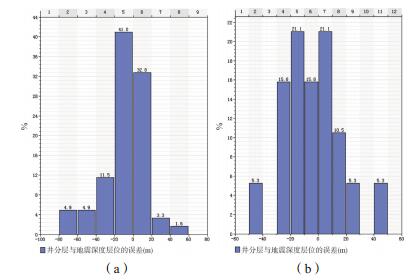 |
| (速度模型校正前) 图 7 研究区标准层a和标准层b时深转换后的深度误差分布图 |
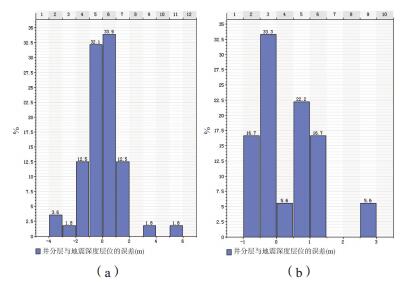 |
| (速度模型校正后) 图 8 研究区标准层a和标准层b时深转换后的深度误差分布图 |
图 9为巴西某海域某标准层位经时深转换后时间域与深度域构造对比图。从时间构造图上可见,东北红色区域为构造高点,西北、东南紫色区域为构造低点,西部为西高东低的斜坡;从深度图上可见,东北红色区域为构造高点,西北紫色区域为构造低点,但西部、东南部变成平缓地带。因此,高精度的层速度模型是本区时深转换的关键,高精度的构造图为本区的构造分析提供了坚实的基础。
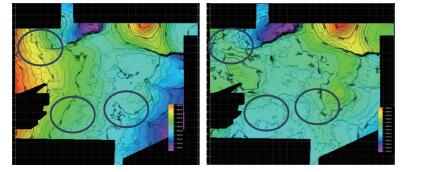 |
| 图 9 研究区某标准层时间构造图(左)和深度构造图(右) |
3 结论
(1)研究区内海底变化大,并存在盐体,导致速度横向变化大,因此采用层速度模型法进行时深转换。由于研究区内存在探井、开发井等多种井别,总数量大,但分布不均,因此本文首先选择部分关键井进行初始层速度模型的建立,最后再利用所有的井进行层速度模型的校正,实践证明这种方法是合理有效的。
(2)层速度模型的建立关键之一是建立层段模型。根据研究区的地质条件和目的层段,海底、目的层顶、目的层底是必须选择的三个层面;其它关键层位可以酌情加入到层段模型的建立当中。
(3)层速度模型的建立关键之二是参数V0和K的建立。本文选用幂函数拟合时深关系,并据此计算层速度,再根据对层速度的拟合得到关键井点处的参数V0和K,并在地震层面的约束下进行外推内插,得到研究区内的参数V0和K。
(4)根据储层建模的需要,添加各个储层的顶底面建立更精细的层段模型,并尽量保持原来的层速度参数面(V0和K)不变,再利用研究区内所有的井进行深度校正,得到高精度的层速度模型,其误差小,满足精细储层建模的要求。
| [1] |
周蒂, 胡登科, 何敏, 等. 深部地层时深转换中的拟合式选择问题[J]. 地球科学——中国地质大学学报, 2008, 33(4): 531-537. |
| [2] |
张华军, 肖富森, 刘定锦, 等. 地质构造约束层速度模型在时深转换中的应用[J]. 石油物探, 2003, 42(4): 521-525. DOI:10.3969/j.issn.1000-1441.2003.04.020 |
| [3] |
李培培, 刘志国, 杨松岭, 等. 虚拟井技术在无井或少井条件下时深转换中的应用[J]. 物探与化探, 2015, 39(5): 994-1000. |
| [4] |
陈林, 邓勇, 盖永浩, 等. 复杂断块构造时深转换方法探讨——以涠西南凹陷为例[J]. 地球物理学进展, 2014, 29(3): 1121-1127. |
| [5] |
凌云, 郭建明, 郭向宇, 等. 油藏描述中的井震时深转换技术研究[J]. 石油物探, 2011, 50(1): 1-13. |
| [6] |
张英德, 彭佳勇, 郝立业, 等. 海外深水复杂地质条件下时深转换难点及技术对策[J]. 地球物理学进展, 2012, 27(4): 1484-1492. |
| [7] |
汪俊, 高红芳, 陈泓君, 等. 基于速度-深度线性模型的时深转换方法及其在南海海盆深水区的应用[J]. 热带海洋学报, 2013, 32(2): 112-117. |
 2019, Vol. 39
2019, Vol. 39

