| 海洋内波能量耗散的数值研究 |
2. 中国科学院南海海洋研究所热带海洋环境国家重点实验室, 广东广州 510301
2. State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, China
海洋内波是海洋中普遍存在的一种动力学过程,当其携带巨大能量时会导致较高的流速,会对海洋石油钻井平台和海底石油管道造成威胁。内波传播过程中,在即将破碎或刚破碎时其水质点速度非常大[1],这会对海上工程设施的安全构成潜在的威胁。Banner等[2]指出,在海岸和海上工程载荷和安全设计时,要考虑由于大尺度波破碎事件引起的作用力和海面下的湍流混合。杜涛等[3]认为内孤立波的波致流以及流的强切变对海上固定设施有很强的破坏力。突然而至的海洋内波会对海洋石油工程作业(如钻井、浮托、吊装等)造成巨大的影响[4-5],引发的事故屡见不鲜。海洋内波形成、传播和耗散的研究,对于海上油气田开发具有重大的意义。因此针对海洋内波的研究是十分必要的。
海洋内波通过浅滩效应、静力不稳定、剪切不稳定、对流不稳定等机制[6-10]实现势能与动能的交换,并通过非线性的波-波相互作用与其它波交换能量,将能量从大的垂直尺度向小的垂直尺度转换,最终以湍流混合的形式耗散掉[11-14]。
Nash等[15]利用海洋观测数据估计内波的能量通量,并分析内波生成、传播和耗散过程。Li等[16]利用非线性浅水方程研究内孤立波的传播,在不考虑底部摩擦的情况下,计算了内孤立波破碎引起的能量耗散。Zheng等[17]利用缓坡方程与波能量平衡方程推导出波破碎和底部摩擦引起的能量耗散因子表达式。李娟等[18]利用Korteweg-de Vries方程的解析解对东海海域内波的传播特性进行了研究。
在许多海洋内波数值研究中,利用线性化了的Boussinesq方程来研究内波的破碎及能量问题,研究中忽略了黏性项和非线性项的影响,而且垂直速度模态数的选取也受到限制。
文中针对内波能量耗散问题,考虑流体黏性和非线性项影响,利用高精度谱方法研究海洋内波传播过程中能量耗散及其机理问题,为海洋石油工程建设提供内波方面的理论指导。
1 内波运动控制方程假设海水不可压缩,其流动由内波引起。压力场可表示为扰动前静力平衡时的压力与扰动压力之和,即
| $ \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial z}=-\frac{1}{{{\rho }_{0}}}\frac{\partial {p}'}{\partial x}+v\left( \frac{{{\partial }^{2}}u}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}u}{\partial {{z}^{2}}} \right) $ | (1) |
| $\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+w\frac{\partial w}{\partial z}=-\frac{1}{{{\rho }_{0}}}\frac{\partial {p}'}{\partial z}+v\left( \frac{{{\partial }^{2}}w}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}w}{\partial {{z}^{2}}} \right)-\frac{{{\rho }''}}{{{\rho }_{0}}}g $ | (2) |
| $ \frac{\partial {\rho }'}{\partial t}+u\frac{\partial {\rho }'}{\partial x}+w\frac{\partial {\rho }'}{\partial z}+w\frac{\partial \bar{\rho }\left( z \right)}{\partial z}=k\left( \frac{{{\partial }^{2}}{\rho }'}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}{\rho }'}{\partial {{z}^{2}}} \right) $ | (3) |
| $ \frac{\partial u}{\partial t}+\frac{\partial w}{\partial z}=0 $ | (4) |
式中:x轴指向东,z轴指向重力的反方向,u为x方向上的速度,m/s;w为z方向上的速度,m/s;v为流体的运动粘度,m2/s;k为热扩散系数,m2/s;g为重力加速度,m/s2;。
为了减少耦合的方程个数,加快计算速度,采用二维的流函数-涡量形式:
| $ \frac{\partial w}{\partial t}=\frac{\partial \left( u\omega \right)}{\partial x}-\frac{\partial \left( u\omega \right)}{\partial z}=v{{\nabla }^{2}}\omega +\frac{\partial {{\rho }^{*}}}{\partial x} $ | (5) |
| $ \omega =\frac{{{\partial }^{2}}\varphi }{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}\varphi }{\partial {{z}^{2}}} $ | (6) |
| $ \frac{\partial {{\rho }^{*}}}{\partial t}=-\frac{\partial \left( {{\rho }^{*}}u \right)}{\partial x}-\frac{\partial \left( {{\rho }^{*}}w \right)}{\partial z}+k{{\nabla }^{2}}{{\rho }^{*}}+w{{N}^{2}} $ | (7) |
其中:
流函数和涡量由下面的式子定义:
| $ u=\frac{\partial \varphi }{\partial z}, w=-\frac{\partial \varphi }{\partial x}, \omega =\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x} $ | (8) |
所有变量均采用周期性边界条件。
2 数值方案采用高精度的谱方法进行空间离散,时间积分采用AB3(Adams-Bashforth 3)方案。物理空间的计算区域
| $ \omega \left( {{x}_{\text{i}}}, {{z}_{\text{j}}}, t \right)=\sum\limits_{k=-{{M}_{\text{x}}}/2}^{{{M}_{\text{x}}}/2-1}{{}}\sum\limits_{l=-{{N}_{\text{z}}}/2}^{{{M}_{\text{z}}}/2-1}{{}}{{{\tilde{\omega }}}_{\text{k, l}}}\left( t \right)\exp \left[ \bar{i}\left( k{{x}_{\text{i}}}, l{{z}_{\text{j}}} \right) \right] $ | (9) |
其中:
| $ \frac{\partial {{{\tilde{\omega }}}_{\text{k, l}}}}{\partial t}=-{{\left[ \frac{\partial \left( \tilde{u}\tilde{\omega } \right)}{\partial x} \right]}_{\text{k, l}}}-{{\left[ \frac{\partial \left( \tilde{w}\tilde{\omega } \right)}{\partial z} \right]}_{\text{k, l}}}-v\left( {{k}^{2}}+{{l}^{2}} \right){{{\tilde{\omega }}}_{\text{k, l}}}+\bar{i}k{{{\tilde{\rho }}}_{k, l}} $ | (10) |
| $ \frac{\partial {{{\tilde{\rho }}}^{*}}_{\text{k, l}}}{\partial t}=-{{\left[ \frac{\partial \left( \tilde{u}{{{\tilde{\rho }}}^{*}} \right)}{\partial x} \right]}_{\text{k, l}}}-{{\left[ \frac{\partial \left( \tilde{w}{{{\tilde{\rho }}}^{*}} \right)}{\partial z} \right]}_{\text{k, l}}}-\frac{v}{\Pr }\left( {{k}^{2}}+{{l}^{2}} \right){{{\tilde{\rho }}}^{*}}_{\text{k, l}}+\tilde{w}{{N}^{2}} $ | (11) |
| $ {{{\tilde{\omega }}}_{\text{k, l}}}=-\left( {{k}^{2}}+{{l}^{2}} \right){{{\tilde{\varphi }}}_{\text{k, l}}} $ | (12) |
| $ {{{\tilde{u}}}_{\text{k,l}}}=\tilde{i}l{{{\tilde{\varphi }}}_{\text{k,l}}},{{{\tilde{w}}}_{\text{k,l}}}=\tilde{i}l{{{\tilde{\varphi }}}_{\text{k,l}}} $ | (13) |
式中:Pr = v/k,上标“ ~”为谱空间中与时间相关的傅立叶系数。谱空间非线性项和时间项的计算过程参见参考文献4。
3 数值计算研究区域设为(0,2π)×(0,2π),网格数为1 024×1 024,周期性边界条件以2π为周期,初始条件为
| 表 1 内波振幅和 Pr 数的取值 |
利用下面的表达式来计算平均的总能量密度及能量耗散率:
| $ \bar{E}=\frac{1}{2S}\int{\left( {{u}^{2}}+{{w}^{2}} \right)}dS+\frac{1}{2S}\int{{{N}^{2}}{{\xi }^{2}}}dS $ | (14) |
| $ \varepsilon =-\frac{d\bar{E}}{dt} $ | (15) |
式中:ξ 为内波波面变化,
为了便于研究内波振幅和Pr数与内波破碎能量耗散率的关系,把内波传播过程划分为三个时期,即破碎前期(before breaking)、破碎期(breaking)、破碎后期(after breaking)。根据平均的总能量密度随时间的变化为一直线关系来识别破碎前期与破碎后期,然后剩下的那部分为破碎期(图 1)。
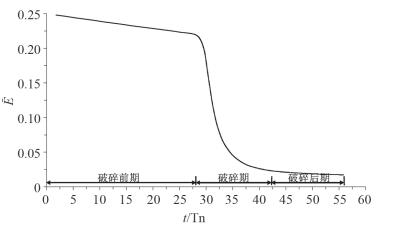 |
| 图 1 内波传播三个时期的划分 |
图 2与图 3分别显示了内波振幅对能量耗散率和平均总能量密度的影响。内波传播过程中,最初能量耗散率基本恒定,随后经过快速上升和下降,再次保持恒定;内波破碎期,振幅越大,能量耗散率的峰值越大,振幅为0.75的最大能量耗散率是振幅为0.256的五十多倍。平均总能量密度总体呈下降趋势,破碎前期缓慢下降,破碎期急剧下降,破碎后期下降变缓。
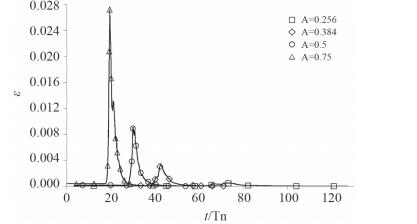 |
| 图 2 内波振幅对能量耗散率的影响 |
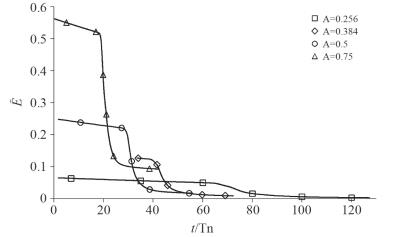 |
| 图 3 内波振幅对平均总能量密度的影响 |
内波传播过程中的平均能量耗散率与初始能量密度的关系见图 4~图 6。内波破碎前期,振幅越大,平均能量耗散率越大,且与初始能量密度(即时刻内波所具有的平均总能量密度)呈线性关系(图 4);破碎期(图 5)和破碎后期(图 6)也有类似的线性关系,破碎期的平均能量耗散率比其它两个阶段的平均耗散率大。这三个时期平均能量耗散率与初始能量密度的拟合关系分别为
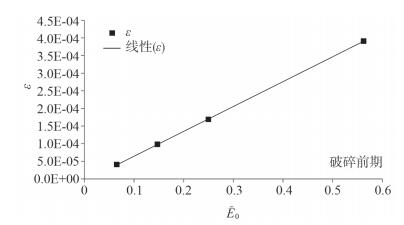 |
| 图 4 内波破碎前期的平均能量耗散率与初始能量密度的关系曲线 |
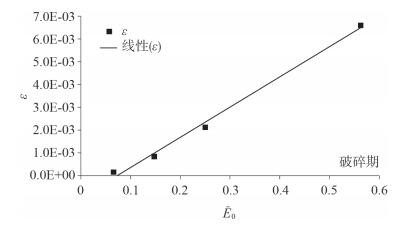 |
| 图 5 内波破碎过程中平均能量耗散率与初始能量密度的关系曲线 |
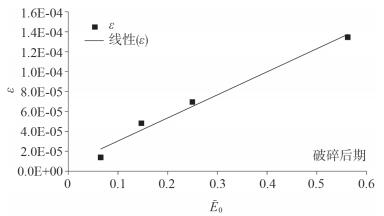 |
| 图 6 内波破碎后期平均能量耗散率与初始能量的关系曲线 |
对同一内波,破碎前期能量耗散比破碎后期的大三倍左右。这是因为内波破碎前所携带的能量较大,流体分子间的无规则运动较强,破碎之后内波所携带的能量减少,流体分子间的无规则运动减弱,相应的能量耗散也减小了。Case1~Case4方案研究结果显示,内波传播过程中能量会被耗散,内波破碎耗散掉初始能量的百分之七十左右,破碎前期和后期耗散掉近百分之二十的能量;振幅越大,能量耗散越大。
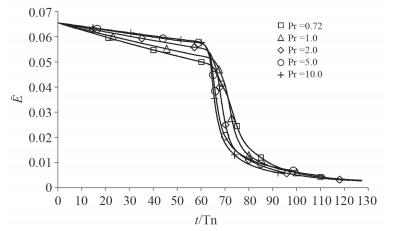
图 7和图 8显示了海水Pr数对能量耗散率ε和平均总能量密度
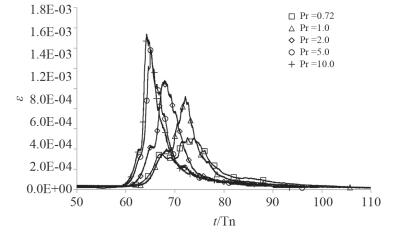 |
| 图 7 Pr数对能量耗散率的影响 |
 |
|
图 8
Pr数对平均的总能量密度 |
内波破碎前期Pr越大,平均能量耗散率越小(图 9),拟合关系式为
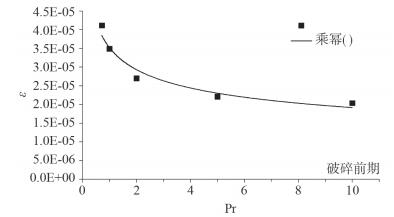 |
| 图 9 内波破碎前期平均能量耗散率与Pr数的关系 |
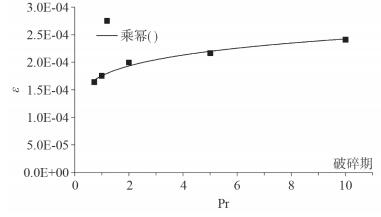 |
| 图 10 内波破碎期平均能量耗散率与Pr数的关系 |
内波失稳破碎,耗散掉大量能量的时间长短与内波振幅有关。图 11给出了Pr数为0.72时内波破碎持续时间T/Tn与内波振幅A的变化曲线。内波振幅越大,内波破碎所经历的时间就越短,即内波携带的能量会在更短时间内耗散掉,两者之间的关系为T/Tn=6.22A-1.36。这是因为振幅越大内波携带的能量越大,内波就越易失稳,而且在内波破碎期振幅越大平均能量耗散率也越大,内波能量耗散就越快,所以振幅越大内波破碎经历的时间T/Tn就越短。
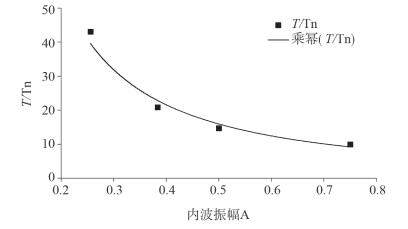 |
| 图 11 内波破碎持续时间与内波振幅的变化曲线(Pr=0.72) |
内波失稳破碎,耗散掉大量能量的时间长短还与海水的Pr数有关。图 12给出了内波振幅为0.256时内波破碎持续时间T/Tn与Pr数的变化关系。Pr数越大,内波破碎经历的时间越短,拟合关系为T/Tn=42.31 Pr-0.08。
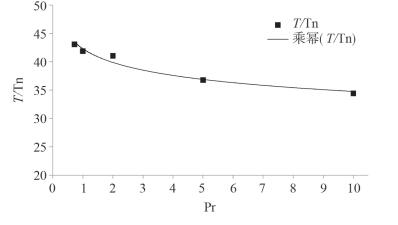 |
| 图 12 内波破碎持续的时间与Pr数的变化曲线(A=0.256) |
5 结论
基于海洋内波对海洋石油工程建设的重大影响,文中采用了高精度的谱方法对内波传播过程中的能量耗散问题进行了数值研究,得到了能量耗散率及内波破碎持续时间分别与内波振幅和Pr之间的关系表达式,为内波能量耗散率和破碎时间的量化提供理论指导。
内波能量耗散与其自身的特性(振幅)有关。研究结果显示,振幅越大,内波携带的能量越大,破碎前期分子之间的无规则运动越剧烈,能量耗散越多;携带的能量越多,内波越易失稳,内波越早破碎,在更短的时间内耗散掉大约百分之七十的能量;破碎后期由于流体分子间的无规则运动比前期的弱,所以破碎后期的平均能量耗散率比前期的要小。内波破碎期大量的能量耗散是由于内波破碎引起的。
内波能量耗散还与传播的物质性质(海水的Pr)有关。研究结果显示,对同一内波,Pr越大,破碎时能量耗散率越大,能量释放也越快,内波破碎时间稍有提前。这是因为当海水运动黏度一定时,Pr越大,分子热扩散系数就越小,破碎前期由分子运动引起的平均能量耗散率越小,内波携带能量较多,内波越易失稳,由内波破碎引起的能量耗散率就越大。
分析可知,内波破碎前期和后期的能量耗散由分子运动主导,破碎期的大量能量耗散由内波破碎引起。研究海洋内波演化过程中引起能量耗散的机制,是认识海洋内波不可缺少的一环,深入的认识能更好地将海洋内波理论应用到海洋石油工程建设中去。
| [1] |
Leichter J J, Deane GB, Stokesm D. Spatial and Temporal Variability of Internal Wave Forcing on A Coral Reef[J]. Journal of Physical Oceanography, 2005, 35(11): 1945-1959. DOI:10.1175/JPO2808.1 |
| [2] |
BannerM L, Babanin A V, Young I R. Breaking Probability for Dominant Waves on the Sea Surface[J]. Journal of Physical Oceanography, 2000, 30(12): 3145-3160. DOI:10.1175/1520-0485(2000)030<3145:BPFDWO>2.0.CO;2 |
| [3] |
杜涛, 方欣华. 潮成内波在物理海洋和相关学科中的影响[J]. 海洋预报, 2003, 20(4): 50-55. DOI:10.3969/j.issn.1003-0239.2003.04.008 |
| [4] |
杨文达, 张异彪, 李斌. 南海琼东南深水海区地质灾害类型与特征[J]. 海洋石油, 2011, 31(1): 1-7. DOI:10.3969/j.issn.1008-2336.2011.01.001 |
| [5] |
周峰. 深水钻井工程风险综述[J]. 海洋石油, 2013, 33(2): 113-118. DOI:10.3969/j.issn.1008-2336.2013.02.113 |
| [6] |
刘国涛, 尚晓东, 陈桂英, 等. 连续层化流体中内波破碎的动力学机制的数值研究[J]. 热带海洋学报, 2009, 28(1): 1-8. DOI:10.3969/j.issn.1009-5470.2009.01.001 |
| [7] |
邓冰, 张宇飞, 朱娟, 等. 海洋剪切流下失稳内波流场及传播的理论分析[J]. 海洋预报, 2016, 33(3): 1-8. |
| [8] |
Koudella C R, Staquet C. Instability Mechanisms of A Two-Dimensional Progressive Internal Gravity Wave[J]. Journal of Fluid Mechanics, 2006, 548: 165-196. DOI:10.1017/S0022112005007524 |
| [9] |
Thorpe S A. The Excitation, Dissipation, and Interaction of Internal Waves in the Deep Ocean[J]. Journal of Geophysical Research, 1975, 80(3): 328-338. DOI:10.1029/JC080i003p00328 |
| [10] |
Teoh SG, Ivey GN, ImbergerJ. Laboratory study ofthe interaction between two internal wave rays[J]. Journal of Fluid Mechanics, 1997, 336: 91-122. DOI:10.1017/S0022112096004508 |
| [11] |
刘国涛, 尚晓东, 陈桂英, 等. 海洋内波破碎及其能量耗散的研究进展[J]. 中山大学学报(自然科学版), 2007, 46(S2): 167-172. |
| [12] |
Xie X H, Liu Q, Shang X D, et al. Poleward Propagation of Parametric Subharmonic Instability-Induced Inertial Waves[J]. Journal of Geophysical Research:Oceans, 2016, 121(3): 1881-1895. DOI:10.1002/2015JC011194 |
| [13] |
Orr M H, Mignerey P C. Nonlinear Internal Waves in the South China Sea:Observation of the Conversion of Depression Internal Waves to Elevation Internal Waves[J]. Journal of Geophysical research:Oceans, 2003, 108(C3): 3064. DOI:10.1029/2001JC001163 |
| [14] |
Wu C H, Nepf H M. Breaking Criteria and Energy Losses for Three-Dimensional Wave Breaking[J]. Journal of Geophysical Research:Oceans, 2002, 107(C10): 3177. DOI:10.1029/2001JC001077 |
| [15] |
Nash J D, Alford M H, Kunze E. Estimating Internal Wave Energy Fluxes in the Ocean[J]. Journal of Atmospheric and Oceanic Technology, 2005, 22(10): 1551-1570. DOI:10.1175/JTECH1784.1 |
| [16] |
Li Y, RaichlenF. Non-Breaking and Breaking Solitary Wave Run-Up[J]. Journal of Fluid Mechanics, 2002, 456(1): 295-318. |
| [17] |
Zheng Y H, Shen Y M, Wu X G, et al. Determination of Wave Energy Dissipation Factor and Numerical Simulation of Wave Height in the Surf Zone[J]. Ocean Engineering, 2004, 31(8-9): 1083-1092. DOI:10.1016/j.oceaneng.2003.10.013 |
| [18] |
李娟, 顾行发, 余涛, 等. 基于Korteweg-de Vries方程解析解的海洋内波模拟研究[J]. 海洋通报, 2011, 30(1): 23-28. DOI:10.3969/j.issn.1001-6392.2011.01.005 |
 2019, Vol. 39
2019, Vol. 39

