| 高温超压地层随钻声波速度预测方法研究 |
莺歌海盆地近期的勘探目标集中于深层高温超压地层[1-2],高温超压地层压力系数达到2.25,温度最高达到190 ℃,受高温超高压温压条件的影响,该区探井稀少,目的层及之上一段地层钻探过程中往往只进行伽马曲线、密度曲线、电阻率曲线测量,缺乏声波测井、VSP资料以及邻井速度资料可借鉴,利用速度体资料进行深度预测及压力预测往往存在较大误差。在高温超压探井钻探过程中需要随时更新深度预测结果,实时监测压力,以确保安全钻探,此外,准确的深度预测能确保目的层之上套管的准确下深位置,因此,在探井随钻过程中对缺失声波的地层进行精确的声波速度预测十分关键。由于常温常压下声波测井一般都具有实测数据,因此前人研究的随钻声波测井曲线预测技术也相对缺乏,声波测井曲线预测的研究工作主要集中于利用伽马曲线进行声波曲线重构[3],利用电阻率曲线应用Faust公式计算[4],利用Gardner公式通过密度测井曲线拟合[5],以及一些其他的声波测井曲线重构方法[6-13],以上声波曲线预测技术解决了不少地区声波速度预测的问题。但在高温超压地层中,砂泥岩速度变化趋势复杂,泥岩存在多条欠压实趋势线[2],单纯利用Gardner公式、Faust公式等经验公式进行声波速度曲线预测精度低,无法满足探井随钻中精细深度预测以及压力预测的要求。因此,针对上述方法存在的问题,研发了一套适用于莺歌海盆地高温超压地层的随钻声波速度预测方法。首先分析了高温超压区岩石物理特征,其次对高温超压带声波速度预测方法展开了研究,将预测的声波速度应用于实际随钻深度预测中。结果显示,预测的声波速度精度高,能够准确预测钻头位置及后续储层深度,为高温超压井套管下深提供准确位置;此外,该方法预测的声波速度能够用于随钻过程中压力分析,保障高温超压井的顺利钻探。
1 高温超压带声波速度预测方法研究为了准确进行莺歌海盆地中深层高温超压地层深度预测,首先分析了莺歌海盆地中深层高温超压地层已钻井X1井岩石物理特征,分析表明(图 1),该区砂岩相对泥岩呈低伽马、低泥质含量、高声波速度、低密度、高纵波阻抗、低纵横波速度比特征,砂泥岩纵波速度差异大,砂岩速度相对稳定,泥岩的速度变化范围大。
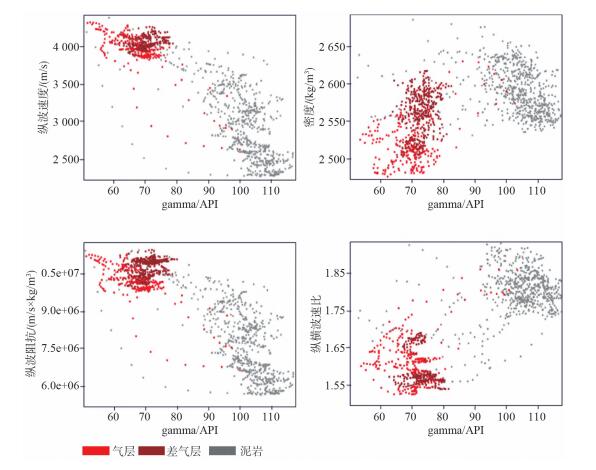 |
| 图 1 X1井岩石物理交会分析图 |
岩石物理分析结果显示,砂泥岩速度差异大,因此,在随钻过程中需要首先判断岩性,本文利用伽马测井曲线采用相对值法计算泥质含量,根据泥质含量的大小判断岩性。
泥质含量计算公式如下[14]:
| $ {V_{{\rm{sh}}}} = \frac{{{2^{{\rm{GCUR}} \cdot {\rm{SH}}}}{\rm{ - }}1}}{{{2^{{\rm{GCUR}}}}{\rm{ - }}1}} $ | (1) |
其中,
| $ SH = \frac{{GR - G{R_{\min }}}}{{G{R_{\max }} - G{R_{\min }}}} $ | (2) |
式中:Vsh为泥质含量,小数;SH为自然伽马相对值,小数;GR为目的层自然伽马测井值,API;GRmin为纯岩性地层的自然伽马测井值,API;GRmax为纯泥岩地层的自然伽马测井值,API;GCUR为与地层年代有关的经验系数,一般新地层取3.7,老地层取2。
其次,通过密度曲线计算地层孔隙度,再利用骨架组分的已知时差,利用体积加权模型计算地层声波时差。
孔隙度计算公式如下[15]:
| $ {\phi _{{\rm{tDEN}}}} = \frac{{{\rho _{{\rm{ma}}}} - \rho }}{{{\rho _{{\rm{ma}}}} - {\rho _{\rm{f}}}}} - {V_{{\rm{sh}}}}\frac{{{\rho _{{\rm{ma}}}} - {\rho _{{\rm{sh}}}}}}{{{\rho _{{\rm{ma}}}} - {\rho _{\rm{f}}}}} $ | (3) |
式中:
体积加权模型计算地层声波时差公式如下:
| $ \mathit{\Delta} t = {t_{{\rm{ma}}}} + CP{\phi _{{\rm{tDEN}}}}\left( {\mathit{\Delta} {t_{\rm{f}}} - \mathit{\Delta} {t_{{\rm{ma}}}}} \right) + CP{V_{{\rm{sh}}}}\left( {\mathit{\Delta} {t_{{\rm{sh}}}} - \mathit{\Delta} {t_{{\rm{ma}}}}} \right) $ | (4) |
式中:Δt为地层声波时差,μs/ft;CP为地层声波压实校正系数,Δtma、Δtf、Δtsh代表骨架、流体、泥质的声波时差,μs/ft。
另外,通过X1井声波速度敏感参数岩石物理分析表明(图 2),若不区分岩性,密度曲线与声波速度之间无良好拟合关系,泥岩段和砂岩段速度趋势差异明显,无法利用统一的方程进行拟合;若区分砂泥岩后,砂岩和泥岩声波速度与密度间都具有良好的拟合关系。统计得到声波速度与密度的拟合关系。
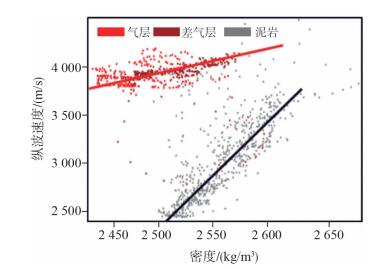 |
| 图 2 X1井声波速度敏感参数分析图 |
其中,泥岩的声波速度与密度的拟合关系为:
| $ {P_{{\rm{vel}}}} = - 28{\rm{ }}989.2 + 12.415{\rm{ }}2 \times {\rm{ }}Density $ | (5) |
砂岩的声波速度与密度的拟合关系为:
| $ {P_{{\rm{vel}}}} = - 1517.{\rm{ }}78 + 2.215{\rm{ }}43 \times {\rm{ }}Density $ | (6) |
式中:Pvel为声波速度,m/s;Density为密度测井值,kg/m3。在具有可靠的密度测井曲线条件下,也可以利用上述声波速度-密度的拟合关系预测随钻过程中的声波速度。
2 实例应用莺歌海盆地中深层LDX区高温超压地层是当前南海西部勘探的重点区域。目前该区探井少,受高温超压条件影响,LDX-3井在目的层及之上一部分地层钻探过程中仅测量了伽马、电阻率和密度曲线,钻探过程中缺少声波测井曲线,而在高温超压层段准确的深度预测不仅关系到目的层深度预测,更关系到目的层之上套管在泥岩中的下深位置以及探井的顺利完钻。因此,为了保证精确的深度预测,首先在LDX-3井钻前利用叠前反演得到的纵波阻抗、纵横波速度比进行岩性预测。通过叠前反演可知(图 3),主要目的层以高纵波阻抗、低纵横波速度比特征为主,根据该区砂泥岩岩石物理特征预测目的层表现为砂岩;在目的层之前,以中等~低阻抗特征、中等~高纵横波速度比特征为主,局部表现出高纵波阻抗、低纵横波速度比的特征,预测目的层之前地层基本为泥岩,局部发育砂岩;并将此岩性预测结果用于LDX-3井钻前套管下深位置设计中。
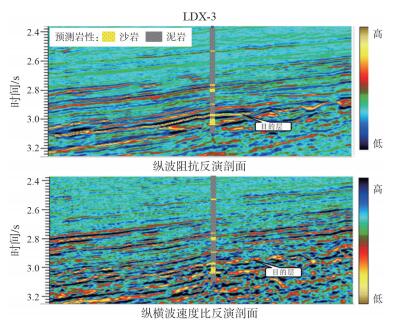 |
| 图 3 LDX-3井钻前叠前反演及岩性预测图 |
在随钻过程中,利用本文研究的两种声波速度预测方法对LDX-3井进行随钻声波速度预测。首先,利用伽马曲线计算泥质含量曲线区分岩性,并通过密度测井曲线计算孔隙度,利用体积加权模型公式计算声波速度。除此之外,分不同岩性采用声波速度-密度的拟合关系进行声波速度预测。利用这两种预测方法得到的曲线进行合成地震记录标定,预测当前钻头所在地震的位置以及主要目的层深度。后续电缆测井补测了该段地层的声波测井曲线,利用电缆补测声波测井曲线与预测声波速度合成地震记录对比(图 4)可以看到,电缆测井声波标定结果与本文提出的两种声波预测曲线标定的结果一致。通过声波速度预测曲线与实际电缆测井声波曲线对比表明(图 5),利用体积加权模型计算的声波速度以及利用声波速度-密度的拟合关系都能很好的预测出声波速度,与实际电缆测井声波速度曲线吻合良好。后续实钻结果表明,预测主要目的层深度与实际钻遇深度误差仅为2 m,说明本文提出的声波速度预测方法精度高,预测的声波速度曲线弥补了高温超压带随钻过程中声波缺失的难题,完全满足该区随钻过程中深度预测的要求。
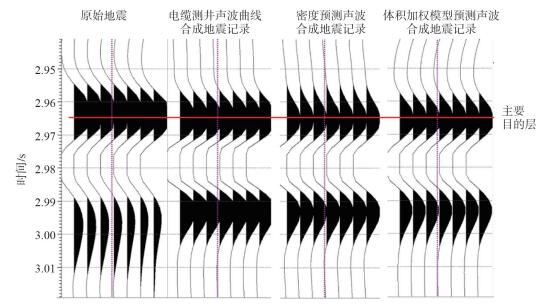 |
| 图 4 不同声波速度曲线制作的合成地震记录对比图 |
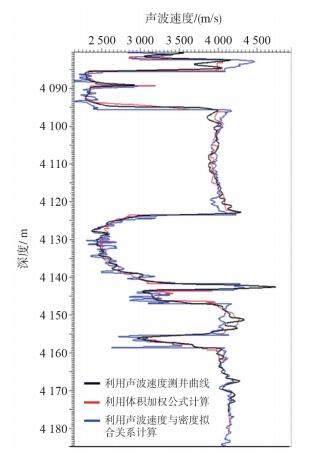 |
| 图 5 不同方法预测的声波速度与电缆声波测井曲线对比图 |
3 结论
受高温超压条件的限制,莺歌海盆地深层探井钻探过程中往往缺少声波测井曲线,随钻过程中高精度的声波速度预测结果不仅能用于深度预测,也能用于随钻过程中的压力预测,因此,高精度的声波速度预测非常关键。岩石物理分析表明,莺歌海盆地高温超压岩石物理特征复杂,砂泥岩声波速度差异大,砂岩速度较稳定,泥岩速度变化范围大,常规声波速度预测方法应用效果不佳。随钻过程中,在具备可靠的伽马测井曲线以及密度测井曲线的条件下,利用体积加权方法可以预测得到准确的声波速度。另外,在区分岩性后,利用不同岩性的声波速度-密度拟合关系同样可以预测得到准确的声波速度。此研究弥补了莺歌海盆地高温超压带随钻过程中声波缺失的难题,高精度的声波速度预测结果能提供准确钻头位置及后续储层深度预测结果,实际应用效果良好,保障了高温超压井的安全钻探及顺利完钻。
| [1] |
裴健翔, 于俊峰, 王立峰, 等. 莺歌海盆地中深层天然气勘探的关键问题及对策[J]. 石油学报, 2011, 32(4): 573-579. |
| [2] |
李芳, 邓勇, 刘仕友, 等. 欠压实低速泥岩对地震反射及AVO的影响[J]. 地质科技情报, 2017, 36(5): 244-248. |
| [3] |
袁全社, 周家雄, 李勇, 等. 声波测井曲线重构技术在储层预测中的应用[J]. 中国海上油气, 2009, 21(1): 23-26. DOI:10.3969/j.issn.1673-1506.2009.01.005 |
| [4] |
陈钢花, 王永刚. Faust公式在声波曲线重构中的应用[J]. 勘探地球物理进展, 2005, 28(2): 125-128. |
| [5] |
Gardner G H F, Gardner L W, Gregory A R. Formation Velocity and Density at the Diagnostic Basics for Stratigraphic Traps[J]. Geophysics, 1974, 39(6): 770-780. DOI:10.1190/1.1440465 |
| [6] |
郭永恒. 随钻测井曲线预测及更新方法研究[J]. 石油钻探技术, 2010, 38(6): 25-28. DOI:10.3969/j.issn.1001-0890.2010.06.006 |
| [7] |
贺懿, 刘怀山, 毛传龙, 等. 多曲线声波重构技术在储层预测中的应用研究[J]. 石油地球物理勘探, 2008, 43(5): 549-556. DOI:10.3321/j.issn:1000-7210.2008.05.011 |
| [8] |
龙国清, 邓宏文, 李玉君, 等. 基于模型正演的测井曲线重构技术在储层表征中的应用[J]. 油气地质与采收率, 2008, 15(1): 66-68, 76. DOI:10.3969/j.issn.1009-9603.2008.01.020 |
| [9] |
熊冉, 高亮, 杨姣, 等. 曲线重构反演在储层横向预测中的应用[J]. 西南石油大学学报(自然科学版), 2012, 34(1): 83-89. DOI:10.3863/j.issn.1674-5086.2012.01.013 |
| [10] |
杨少虎, 黄玉生, 彭文绪, 等. 声波重构技术在储层反演中的应用[J]. 石油地球物理勘探, 2006, 41(2): 171-176. DOI:10.3321/j.issn:1000-7210.2006.02.011 |
| [11] |
姜传金, 马学辉, 周恩红. 拟声波曲线构建的意义及应用[J]. 大庆石油地质与开发, 2004, 23(1): 12-14. DOI:10.3969/j.issn.1000-3754.2004.01.005 |
| [12] |
于文芹, 邓葆玲, 周小鹰. 岩性指示曲线重构及其在储层预测中的应用[J]. 石油物探, 2006, 45(5): 482-486. DOI:10.3969/j.issn.1000-1441.2006.05.009 |
| [13] |
林东成, 张宏, 贾建亮, 等. 声波曲线分层重构反演在岩性预测中的应用[J]. 大庆石油地质与开发, 2010, 29(4): 167-170. DOI:10.3969/J.ISSN.1000-3754.2010.04.038 |
| [14] |
刘卫国, 宋宪生, 郭长林, 等. 利用自然伽马测井数据计算地层泥质含量[J]. 铀矿地质, 2017, 33(1): 45-48, 54. DOI:10.3969/j.issn.1000-0658.2017.01.007 |
| [15] |
毛志强, 谭廷栋. 密度测井和中子测井的相关性及其在识别天然气层中的应用[J]. 地球物理学报, 1996, 39(1): 125-133. DOI:10.3321/j.issn:0001-5733.1996.01.014 |
 2019, Vol. 39
2019, Vol. 39

